Research on the Stability of Open Financial System
Abstract
:1. Introduction
2. New Herd Mechanism
3. Open System in Financial Market
4. Micro Analysis
4.1. Analysis Methods
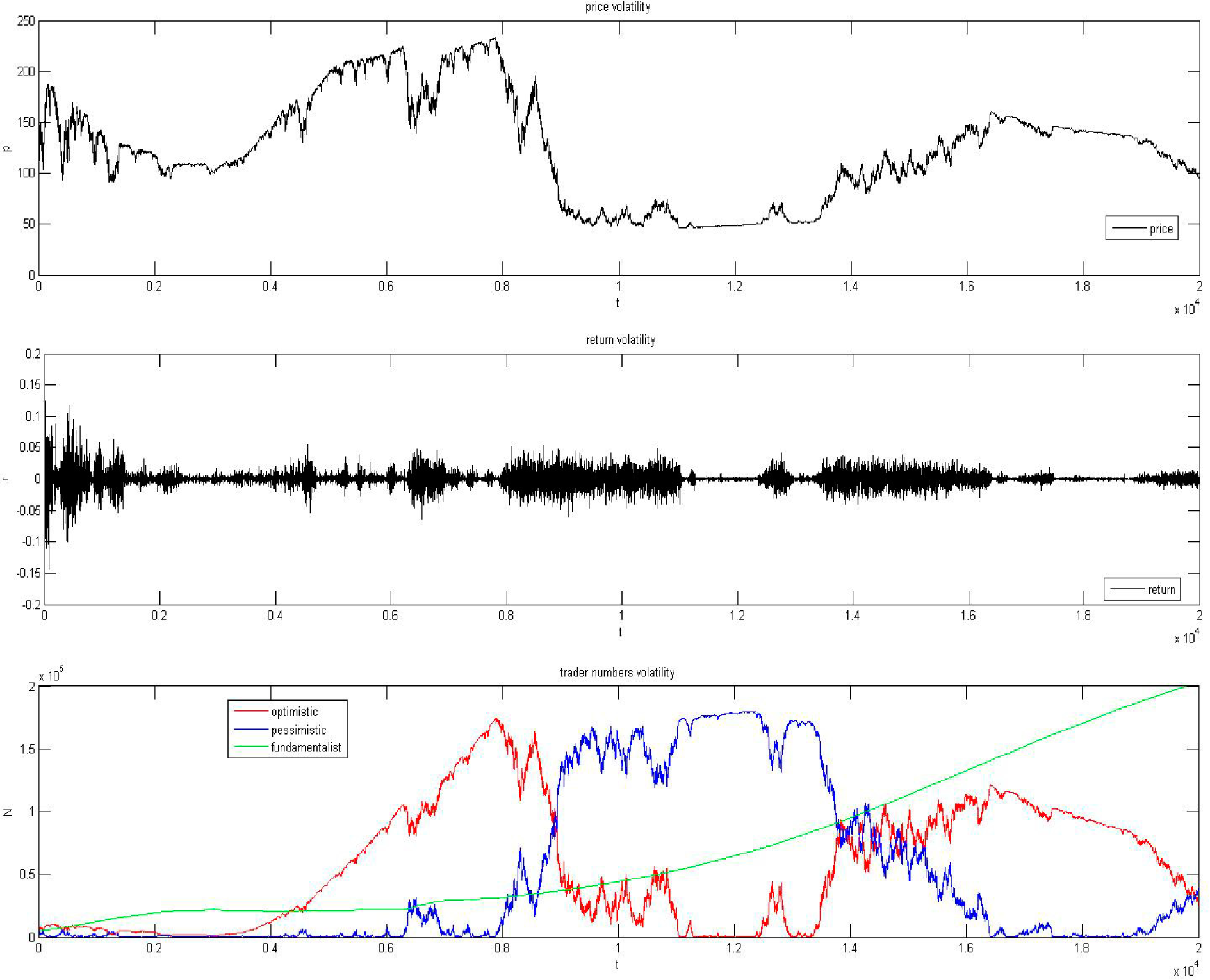
4.2. Simulation
5. Macro Analysis
5.1. Analysis Methods
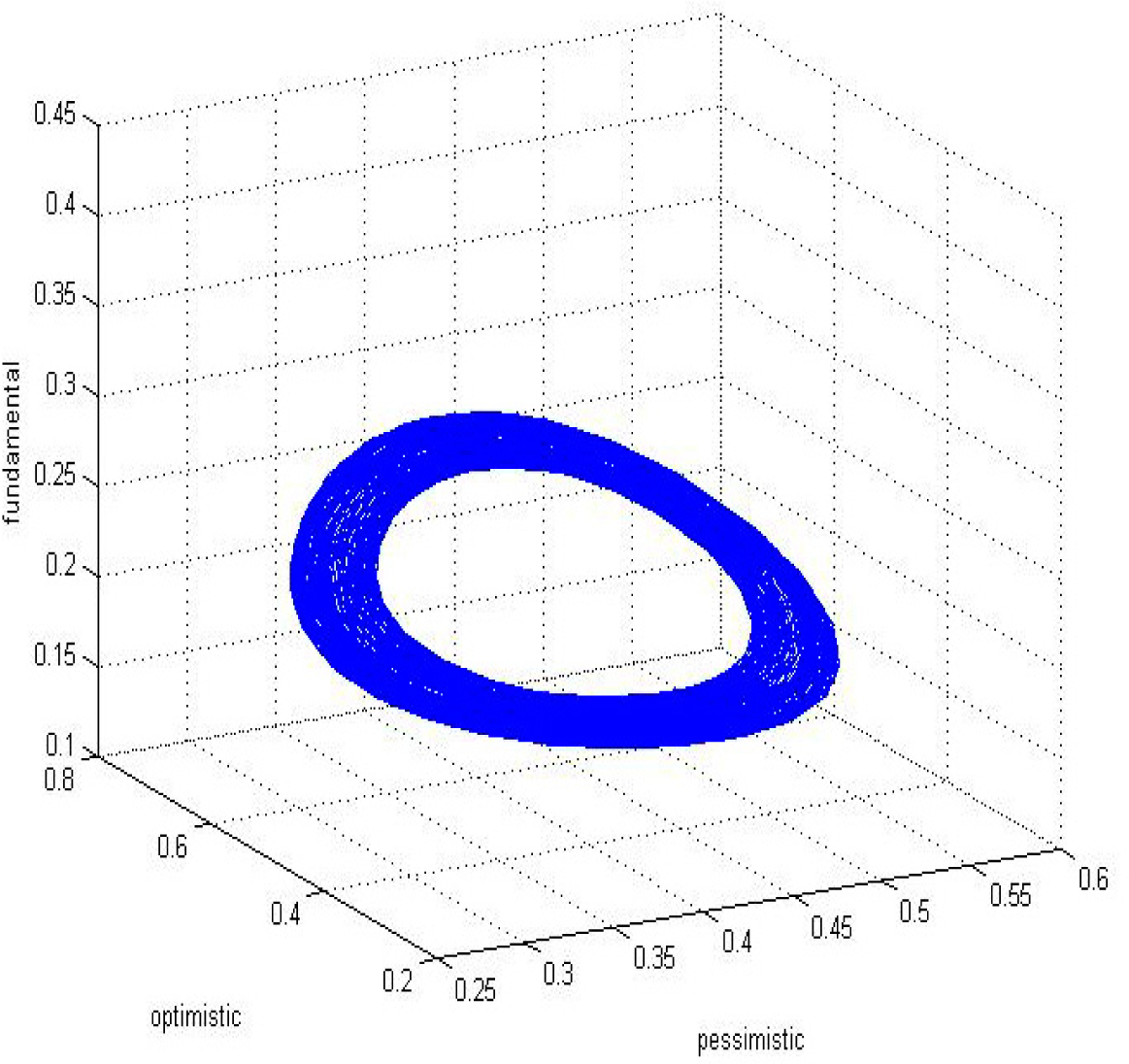
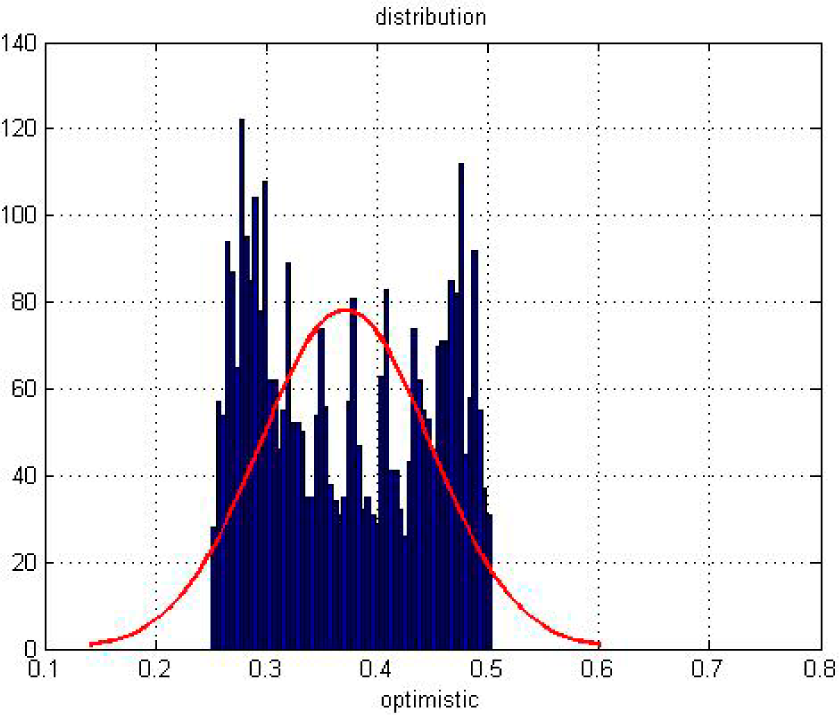
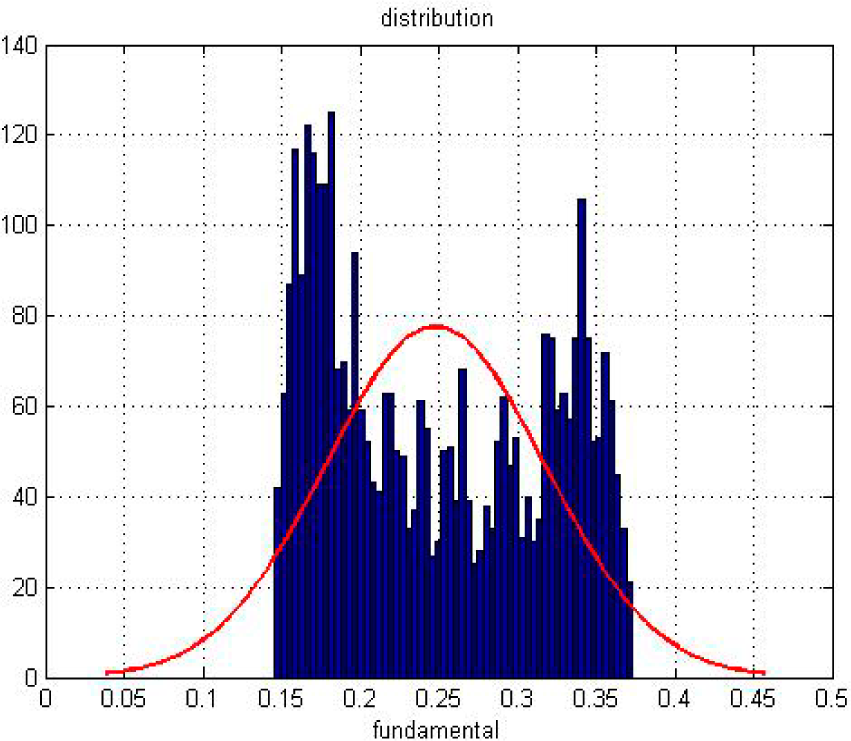
5.2. Result Analysis
6. Conclusions
- We successfully explained the relation between system size and fluctuation of financial market. Especially, through three improvements, we solved the puzzle that the loss of volatility depends on growing system size. The real market’s volatility never vanishes no matter how the market size is changing, because (1) the market is always an open system; (2) the herd behavior is effective among all traders. Besides, we redefined the herd mechanism from the behavior perspective which made the model more practical.
- We have also pointed out the reasons why these financial anomalies, such as bubbles, collapses, and volatility clusters, happened. We derived the price process and return process by using some methods—multivariate Langevin equation and multivariate Fokker–Planck equation. Combining the analysis of these price and return processes which were derived based on our new herd mechanism we can clearly find out that which variables control the market volatility and the relationship between different variables, and all these variables have their actual meaning.
- For the macro level, we employed a non-linear chemistry method to analyze our model and aim at the distribution of different agents with the changing time. The partial differential equations can perfectly describe the stability of the whole system and some statistical variables, such as mean and variance. These findings give us another way to explain the market volatility.
Appendix A
A.1. The multivariate Langevin equation
A.2. Cumulant Generating Function Expansion of the Master Equation
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Figlewski, S. Market “efficiency” in a market with heterogeneous information. J Polit. Econ. 1978, 86, 581–597. [Google Scholar]
- Shiller, R.J.; Fischer, S.; Friedman, B.M. Stock prices and social dynamics. Brook. Pap. Econ. Act. Rev. 1984, 2, 457–498. [Google Scholar]
- Lux, T.; Marchesi, M. Scaling and criticality in a stochastic multi-agent model of a financial market. Nature 1999, 397, 498–500. [Google Scholar]
- Kirman, A. Epidemics of opinion and speculative bubbles in financial markets. Money Financ. Mark. 1991, 354–368. [Google Scholar]
- Kirman, A. Ants, rationality, and recruitment. Q. J. Econ. 1993, 108, 137–156. [Google Scholar]
- De Grauwe, P.; Dewachter, H.; Embrechts, M.J. Exchange Rate Theory: Chaotic Models of Foreign Exchange Markets; Blackwell: Oxford, UK, 1993. [Google Scholar]
- Chen, S.H. Varieties of agents in agent-based computational economics: A historical and an interdisciplinary perspective. J. Econ. Dyn. Control 2012, 36, 1–25. [Google Scholar]
- Levy, M.; Levy, H.; Solomon, S. A microscopic model of the stock market: Cycles, booms, and crashes. Econ. Lett. 1994, 45, 103–111. [Google Scholar]
- Arifovic, J. The behaviour of the exchange rate in the genetic algorithm and experimental economies. J. Polit. Econ. 1996, 104, 510–541. [Google Scholar]
- Arthur, W.B.; Holland, J.H.; LeBaron, B.; Palmer, R.; Tayler, P. Asset pricing under endogenous expectations in an artificial stock market. Econ. Notes 1997, 26, 297–330. [Google Scholar]
- Lux, T.; Marchesi, M. Volatility clustering in financial markets: A microsimulation of interacting agents. Int. J. Theor. Appl. Financ 2000, 3, 675–702. [Google Scholar]
- Yang, H.J.; Gui, P.S. Study on the stability of an artificial stock option market based on bidirectional conduction. Entropy 2013, 15, 700–720. [Google Scholar]
- Giardina, I.; Bouchaud, J.-P. Bubbles, crashes and intermittency in agent based market models. Eur. Phys. J. B 2003, 31, 421–437. [Google Scholar]
- Lux, T.; Schornstein, S. Genetic learning as an explanation of stylized facts of foreign exchange markets. J. Math. Econ. 2005, 41, 169–196. [Google Scholar]
- Cont, R.; Bouchaud, J.P. Herd behaviour and aggregate fluctuations in financial markets. Macroecon. Dyn. 2000, 4, 170–196. [Google Scholar]
- Cont, R.; Wagalath, L. Running for the exit: distressed selling and endogenous correlation in financial markets. Math. Financ 2013, 23, 718–741. [Google Scholar]
- Egenter, E.; Lux, T.; Stauffer, D. Finite-size effects in Monte Carlo simulations of two stock market models. Physica A 1999, 268, 250–256. [Google Scholar]
- Challet, D.; Marsili, M. From minority game to the real markets. Phys. Rev. E 2004, 68, 168–176. [Google Scholar]
- Alfarano, S.; Lux, T.; Wagner, F. Time variation of higher moments in a financial market with heterogeneous agents: An analytical approach. J. Econ. Dyn. Control 2008, 32, 101–136. [Google Scholar]
- Kirman, A.; Teyssiere, G. Microeconomic models for long memory in the volatility of financial time series. Stud. Nonlinear Dyn. Econ. 2002, 5, 281–302. [Google Scholar]
- Horst, U. Financial price fluctuations in a stock market model with many interacting agents. Econ. Theory 2004, 25, 917–932. [Google Scholar]
- Sugiman, T.; Misumi, J. Development of a new evacuation method for emergencies: Control of collective behavior by emergent small group. J. Appl. Psychol 1998, 73, 3–10. [Google Scholar]
- De Grauwe, P.; Kaltwasser, P.R. Animal spirits in the foreign exchange market. J. Econ. Dyn. Control 2012, 36, 1176–1192. [Google Scholar]
- Gillespie, D.T. The chemical Langevin equation. J. Chem. Phys 2000, 113, 297–306. [Google Scholar]



© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Li, L.; Wang, D. Research on the Stability of Open Financial System. Entropy 2015, 17, 1734-1754. https://doi.org/10.3390/e17041734
Yang H, Li L, Wang D. Research on the Stability of Open Financial System. Entropy. 2015; 17(4):1734-1754. https://doi.org/10.3390/e17041734
Chicago/Turabian StyleYang, Haijun, Lin Li, and Deshen Wang. 2015. "Research on the Stability of Open Financial System" Entropy 17, no. 4: 1734-1754. https://doi.org/10.3390/e17041734
APA StyleYang, H., Li, L., & Wang, D. (2015). Research on the Stability of Open Financial System. Entropy, 17(4), 1734-1754. https://doi.org/10.3390/e17041734




