Abstract
The synchronization of loosely-coupled chaotic oscillators, a phenomenon investigated intensively for the last two decades, may realize the philosophical concept of “synchronicity”—the commonplace notion that related events mysteriously occur at the same time. When extended to continuous media and/or large discrete arrays, and when general (non-identical) correspondences are considered between states, intermittent synchronous relationships indeed become ubiquitous. Meaningful synchronicity follows naturally if meaningful events are identified with coherent structures, defined by internal synchronization between remote degrees of freedom; a condition that has been posited as necessary for synchronizability with an external system. The important case of synchronization between mind and matter is realized if mind is analogized to a computer model, synchronizing with a sporadically observed system, as in meteorological data assimilation. Evidence for the ubiquity of synchronization is reviewed along with recent proposals that: (1) synchronization of different models of the same objective process may be an expeditious route to improved computational modeling and may also describe the functioning of conscious brains; and (2) the nonlocality in quantum phenomena implied by Bell’s theorem may be explained in a variety of deterministic (hidden variable) interpretations if the quantum world resides on a generalized synchronization “manifold”.
1. Introduction
Synchronization within networks of oscillators is widespread in nature, even where the mechanisms connecting the oscillators are not immediately apparent. One recalls the example of the synchronization of clocks suspended on a common rigid wall, a paradigm commonly attributed to Huygens [1]. As with similar phenomena of fireflies blinking in unison or female roommates synchronizing hormonal cycles, the pattern suggests a universally valid organizational principle that transcends any detailed causal explanation. Further, from everyday experience, but perhaps related, are the quantum mechanical harmonies between distant parts of a system that are not causally connected. As reviewed in the penultimate section of the paper, quantum mechanics is fundamentally nonlocal in the sense that no interpretation that retains objective reality, in which an observer is assumed to have the free will to alter his choice of what variables to observe while leaving everything else unchanged, is consistent with locality in the observed system. There must either be a grand synchrony between the observer’s choices and the observed system or a synchrony between distant parts of the observed system, maintained by a subtle nonlocal coupling between them.
The study of coupled networks of oscillators in classical physics has focused on regular oscillators with periodic limit-cycle attractors. Such models afford explanations for such surprising relationships as the one observed by Huygens, but other synchronous relationships that are sometimes said to exist in nature are less easily explained. While the synchronization of chaotic oscillators with strange attractors has become familiar in the last two decades, most work on such systems has examined engineered systems, primarily for application to secure communications, using the low-dimensional signal connecting the oscillators as a carrier that is difficult to distinguish from noise. However, examples of synchronized chaos in pairs of systems of partial differential equations that describe physical systems, coupled loosely, have also been given [2–6].
In the philosophical realm, synchronous relationships that are difficult to explain causally have figured prominently in primitive cultures and in traditions commonly associated with Jung [7]. (No reference is made in this paper to the use of archetypes in physical theory or other aspects of Jung’s philosophy.) The notion of “synchronicity” commonly associated with Jung has two essential characteristics beyond the simple simultaneous occurrence of corresponding events: First, the simultaneous occurrences or “synchronicities” must be isolated occurrences. Second, the synchronicities must be “meaningful”. The idea of synchronicity thus goes beyond the synchronization of oscillators in positing a new kind of order in the natural world, schematized by Jung and Pauli (Figure 1) in their book The Interpretation of Nature and of the Psyche [8]. Regular oscillator models fall far short of explaining synchronicities of this type, as Strogatz observed in his popular exposition [9]. A particularly important instance is the synchronization of matter and mind. In this view, mind is not slaved to the objective world, but tends to synchronize with it, based on limited exchange of information. Jung’s examples of synchronicity, and subjective perceptions of synchronicity generally, are often dismissed as the result of chance, but a minority opinion follows Pauli in asserting that a synchronistic order exists in the world alongside the causal one.
Figure 1.
Diagram constructed by Carl Jung, later modified by Wolfgang Pauli, to suggest relationships based on synchronicity as an “acausal connecting principle”, existing alongside causal relationships [8].
While Pauli kept such speculations largely separate from his scientific work, the point of this paper, reached through a review of the author’s and others’ more recent work, is to show that the nonlinear dynamics paradigm of synchronization in networks of loosely-coupled chaotic systems can realize the philosophical notion of synchronicity, or at least approach it much more closely than is possible with regular oscillators. The proposed realization is concrete in nature, without any need for dualism between the mental and material worlds. It is also different from the “dual-aspect monism” ascribed to Jung and Pauli themselves [10], in that material synchronization is put forward as an explanation of synchronous relationships in the mental realm and between mind and matter.
We begin by reviewing work, in the next section, showing that the simple introduction of a time delay in the coupling between the systems can transform a situation of complete synchronization to one of isolated “synchronicities”. In Section 3, we review previous work on an application of synchronized chaos to “data assimilation” of observations of a “real” system into a computational model that is intended to synchronize with truth, analogously to the synchronization of matter and mind. Traditional data assimilation methods, which have been investigated extensively for meteorological modeling [11], can be clarified and augmented within the synchronization framework. “Meaningfulness” is naturally interpreted as internal coherence. A three-way relationship between two parts of a real system and a third system conceived of as an observer is shown to satisfy the requirement for meaningfulness in synchronicities in Section 4.
The objective rational basis for synchronicity that is put forward in this paper suggests applications of the new organizational principle to processes in the brain and in the physical world. In Section 5, we discuss implications of synchronized chaos for neural systems, in view of contemporary ideas about synchronization as a binding mechanism in perception and consciousness and in view of recent work on the synchronization of different computational models of the same objective process with each other. In Section 6, we highlight the role of synchronized chaos in realist interpretations of quantum theory, where determinism is retained, while quantum nonlocality and the Bell correlations are explained. The concluding section speculates on remaining gaps between our objective realization of the synchronicity principle and its original philosophical motivation.
2. Highly Intermittent Synchronization in Loosely-Coupled Chaotic Systems
Extensive interest in synchronized chaotic systems was spurred by the work of Pecora and Carroll [12] (cf. [13,14]), who initially studied the phenomenon in three-variable Lorenz systems [15], a prototypical example of chaos. Slaving the X variable of one Lorenz system to the corresponding variable of a second system, one has:
The systems defined by (X, Y, Z) and (X1 = X, Y1, Z1), respectively, synchronize rapidly: as t → ∞, Y1(t) − Y (t) → 0, Z1(t) − Z(t) → 0, as shown in Figure 2 (synchronization also occurs if the slave system is driven by the master Y variable instead of the X variable, but not if driven by the Z variable). Various schemes to use chaos synchronization for cryptography were motivated by the thought that variables analogous to X in (1) could be used as carrier signals that would be difficult to distinguish from noise [16]: the signal between the two systems defined by X is broadband and has no characteristic frequency. The Takens–Mañé Theorem [17,18] can still be used to infer information about the encoding from a segment of a signal that is sufficiently long, but as one considers higher-dimensional analogues of (1), it becomes increasingly difficult to do so.
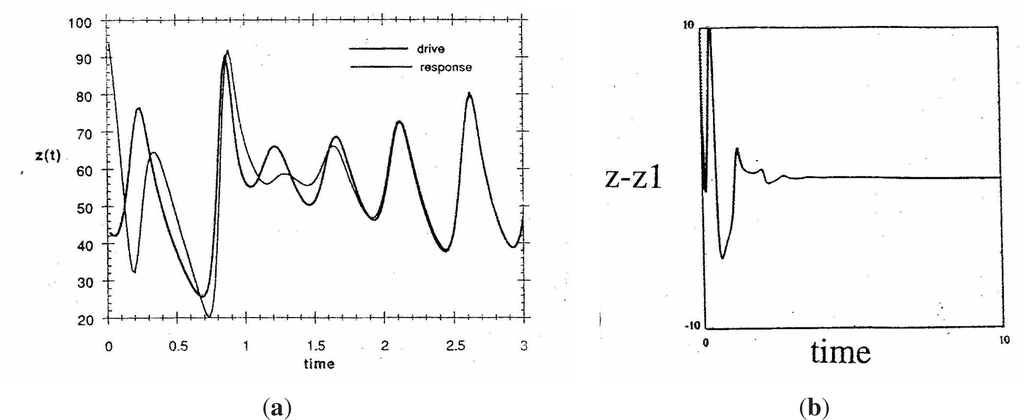
Figure 2.
The trajectories of the synchronously-coupled Lorenz systems in the Pecora–Carroll complete replacement scheme (1) rapidly converge (a). Differences between corresponding variables approach zero (b).
The two connected chaotic systems are conceived to be effectively unpredictable, but exhibit significant correlations if connected by a signal that is conceived to be effectively inscrutable. Taking these views of the systems and their connection as valid, we have an instance of an acausal synchronous relationship. To the extent that relationships between physical systems analogous to (1) occur in nature, synchronism becomes a valid physical principle.
It is important that the “acausal” correlations arise in the context of a perfectly causal, deterministic system. However, the same could be said of the examples of synchronicity given by Jung. Those surprising coincidences occurred in systems that one would imagine to be governed by ordinary deterministic physics, with a history of connection between the two systems, but that connection would not have been readily interpreted as causal. The synchronistic behavior emerges as a higher-order relationship, i.e., an epiphenomenon, in causal systems that could not have been predicted from existing causal theory. Synchronicity thus does not logically contradict causality, but transcends it. In nonlinear computational models governed by causal relationships, synchronicities not predicted from theory are detected in numerical experiments. If physical systems manifest such relationships as in the pair of coupled Lorenz systems, as will be illustrated below, then synchronicity might be accounted for rationally.
Synchronization can indeed occur with weaker forms of coupling than the complete replacement of one variable by its corresponding variable as in (1), but degrades below a threshold coupling strength. Typically, synchronization degrades via on-off intermittency [19], where bursts of desynchronization occur at irregular intervals or as “generalized” synchronization [20], where a strict correspondence remains between the two systems, but that correspondence is given by a less tractable function than the identity. As shown schematically in Figure 3, as differences between the two systems increase, the correspondence changes from the identity to a smooth function that approximates the identity, to one given by a function that is nowhere differentiable. The last case is in fact common [21].
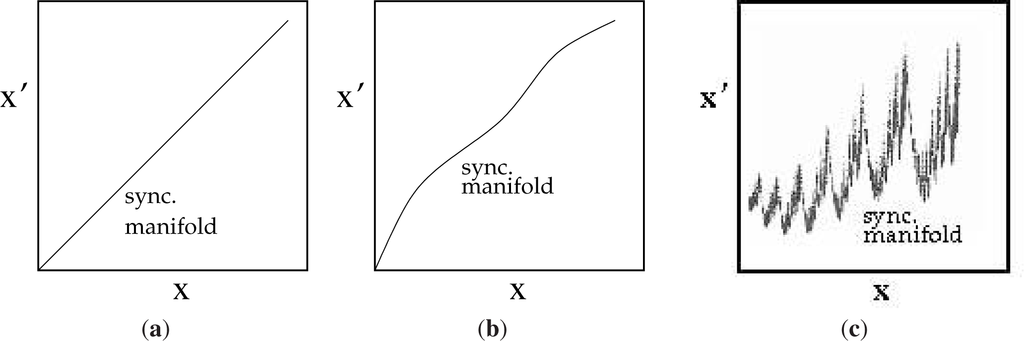
Figure 3.
Transition from identical to generalized synchronization, illustrated by the relationship between a pair of corresponding variables x and x′: projections of the synchronization manifold onto the (x, x′) plane are shown for (a) identical synchronization, (b) generalized synchronization with near-identical correspondence and (c) generalized synchronization with a correspondence function that is nowhere smooth.
While initial research on synchronized chaos was motivated by potential applications to secure communication schemes using electronic circuits, the phenomenon has also been demonstrated in lasers [22] and ferromagnetic materials [23], as well as in the fluid dynamical systems discussed below. In applications to physical systems, it is natural to consider forms of coupling that embody a time delay. If one extends chaos synchronization to the realm of naturally-occurring systems, the delay in transmission ought to be described in terms of the same physics that governs the evolution of the systems separately. To a first approximation, let us assume that the time scale of the delay is the same as some intrinsic dynamical time scale of each system. Consider the following configuration of two Lorenz systems, coupled through an auxiliary variable S that introduces a delay:
System (2) is a generalization of the Pecora–Carroll coupling scheme (1) to a case with bidirectional coupling and where each subsystem is partially driven and partially autonomous.
As Γ → ∞ in (2), with Ṡ finite, S → X − X1. In this limit, the system reduces to a bidirectionally coupled version of (1), which indeed synchronizes. In the general case of the coupled System (2) with finite Γ, the subsystems exchange information more slowly: if X and X1 are slowly varying, then S asymptotes to X − X1 over a time scale 1/Γ. Thus, Γ is an inverse time lag in the coupling dynamics.
Synchronization along trajectories of System (2) is represented in Figure 4 as the difference Z − Z1 vs. time, for decreasing values of Γ. For large Γ, the case represented in Figure 4a, the subsystems synchronize. As Γ is decreased in Figure 4b–d, corresponding to increased time lag, increasingly frequent bursts of desynchronization are observed, until in Figure 4d (uncoupled systems), no portion of the trajectory is synchronized. The bursting behavior can be understood as an instance of on-off intermittency [19,24], the phenomenon that can occur when an invariant manifold containing an attractor loses stability, so that the attractor is no longer an attractor for the entire phase space, but is still effective in portions of the phase space. Trajectories then spend finite periods very close to the invariant manifold, interspersed with bursts away from it.
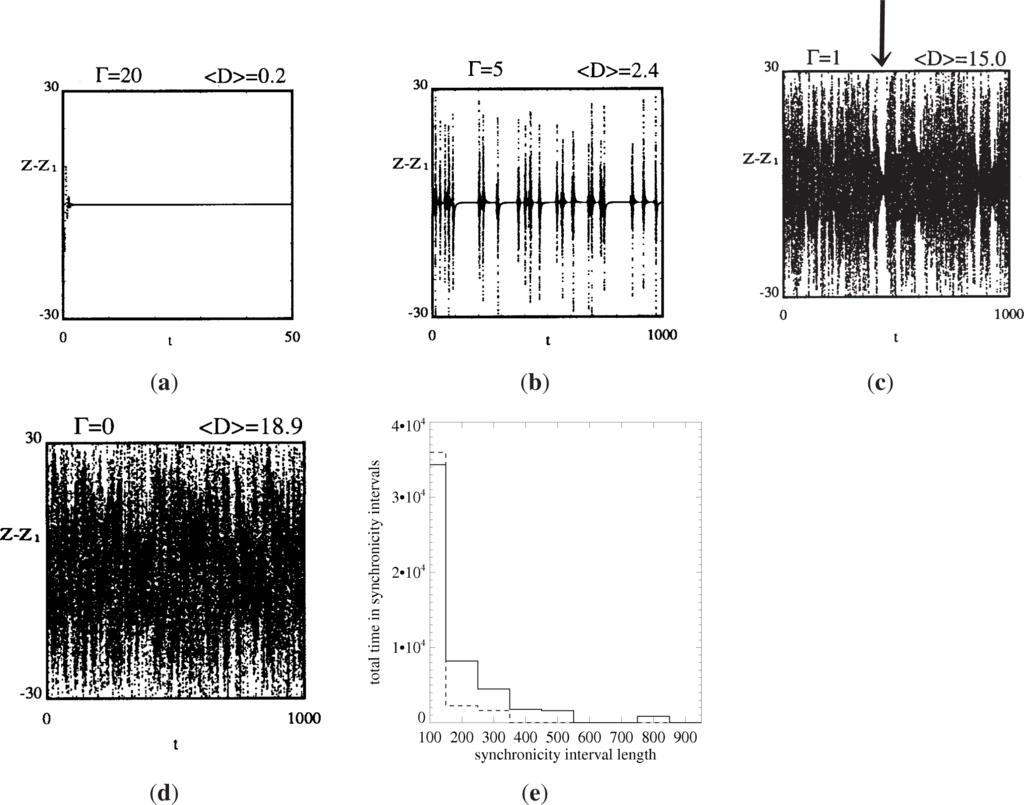
Figure 4.
The difference between the simultaneous states of two Lorenz systems with time-lagged coupling (2), with σ = 10., ρ = 28., and β = 8/3, represented by Z(t) − Z1(t) vs. t for various values of the inverse time lag Γ illustrating complete synchronization (a), intermittent or “on-off” synchronization (b), partial synchronization (c) and de-coupled systems (d). The average Euclidean distance ⟨D⟩ between the states of the two systems in X, Y, Z-space is also shown. A histogram of the lengths of periods of “synchronicity”, such as the one indicated by the arrow in (c), is shown in (e) for the time-delayed coupling case (solid line) and a case of two unrelated Lorenz trajectories (dashed line), where synchronicity intervals are periods during which |Z(t) − Z1(t)| < 5.
The case of a coupling time lag that is of the same order as the prescribed physical time scale in the simple Lorenz system corresponds to Γ = 1, with behavior as in Figure 4c. Although there is little trace of synchronization, the average instantaneous distance between the subsystems is less than it is in the uncoupled case. More interestingly, there is a very short period of nearly complete synchronization. In a very long integration, such “synchronicities”, of moderately short duration, occur more commonly than they would by chance in unrelated systems, as seen in the histograms in Figure 4e, showing the total time in synchronicities of the given duration for the two cases.
System (2) is indeed analogous to the one derived from a pair of geophysical fluid models coupled by standing waves in narrow ducts [2]. Auxiliary variables analogous to S in (2) arise by first decomposing the field into a piece that satisfies the full nonlinear equations with homogeneous boundary conditions and a second piece that satisfies a linear system with matching boundary conditions in the region of the narrow ducts. The linear equations are solved using boundary Green’s functions that effect a time delay. The auxiliary variables are integrals of products of the boundary Green’s functions and differences of corresponding field variables from the two sides of the ducts. Intermittent synchronization of the two ODE systems implies correlations between large-scale weather patterns in the mid-latitude regions of the Northern and Southern Hemispheres, since they are connected by “duct” regions in the tropics, where prevailing winds are westerly and Rossby waves can thus propagate [2].
The relevance of low-order chaos to very high-dimensional geophysical systems may seem questionable, but both chaos and synchronization/control have already been applied to simple models of the the El Niño-Southern Oscillation (ENSO) cycle [25]. ENSO is known to correlate with a large number of global weather phenomena. The intermittency in the synchronization in the two-hemisphere model is a result of the time delay in the coupling between the hemispheres, but such delays play an important role in other geophysical models [26], accounting for the irregularity of the ENSO cycle [27]. If one were to couple a delayed oscillator model of ENSO, such as [27], to models of other climate subsystems that are physically connected, then notwithstanding that the delay here is within a subsystem rather than between subsystems, new geophysical “synchronicities” might emerge, perhaps stronger than the weakly correlated blocking effect, but similarly unexpected.
The co-occurrence of the weather patterns in the two hemispheres could not have been predicted from the mere existence of the narrow connecting ducts. One needs to study the real system, or a sufficiently complex numerical model thereof, to observe the synchronous behavior. The small statistical correlations induced by wave transmission through the ducts were indeed surprising (but not particularly useful), although the “blocking” behavior, to be described in Section 4, had been familiar for several decades. The tendency of blocks to co-occur, which is reminiscent of Huygens’ clocks or synchronized hormonal cycles in female roommates, but constructed from systems that are individually unpredictable, supports the existence of synchronicity as an organizational principle that transcends causality.
Thus, the term “acausal” is interpreted here phenomenologically. One can always find causal mechanisms, as with the wall connection between Huygens’ clocks or the weak molecular signal (a relatively recent discovery) linking female roommates. Subtle causal chains can always be found between any two events that can be linked by a light signal or which have a common history. If one insists, one can regard synchronicity as an epiphenomenon, secondary to the underlying causal relationships. However, it is often more convenient and useful to describe complex systems directly in terms of synchronous patterns without attention to causal mechanisms. It is the assertion of this paper that such an approach potentially applies to all phenomena that philosophers and laypersons have historically categorized as synchronistic.
The impact of chaos synchronization is enhanced greatly by the phenomenon of small-world networks. One can consider a large array of chaotic oscillators with local and/or long-range connections among them. In a small-world network, a few long-range connections are sufficient to sharply decrease the average degree of separation between any two oscillators, as occurs more generally in a scale-free network in which the number of highly connected nodes decreases with the number of their connections according to a power law [9]. Randomly connected networks of this type can be expected to synchronize more readily than regular networks that are connected only in local neighborhoods: the introduction of a few long-range connections can lead to a phase transition to long-range synchronization [28–31].
3. Machine/Human Perception as a Synchronization of Reality and Model
The connection between synchronized chaos and mind-matter synchronicity is best illustrated by another application to meteorology, a field that inspired the modern notion of chaos [15]. Computational models that predict weather include a feature not found in numerical solutions of simpler initial-value problems: as new data are provided by observational instruments, the models are continually re-initialized. This data assimilation procedure combines observations with the model’s prior prediction of the current state, since neither observations nor model forecasts are completely reliable, so as to form an optimal estimate of reality at each instant in time. While similar problems exist in other fields, ranging from financial modeling, to factory automation, to the real-time modeling of biological or ecological systems, data assimilation methods have been researched more extensively and are more developed in meteorology [11,32–34] than in other fields.
Since the problem of data assimilation arises in any situation requiring a computational model of a parallel physical process to track that process as accurately as possible based on limited input, it has been asserted that the broadest view of data assimilation is that of machine perception by an artificially intelligent system [35]. Like a data assimilation system, the human mind forms a model of reality that functions well, despite limited sensory input, and one would like to impart such an ability to the computational model.
The usual approach to data assimilation is to regard it as a tracking problem that can be solved using Kalman filtering or generalizations thereof [11]. However, clearly, the goal of any data assimilation is to synchronize the model with reality, i.e., to arrange for the former to converge to the latter over time. Thus, the synchronously-coupled systems of the previous section are re-interpreted as a “real” system and its model. In System (1), for instance, we imagine that the world is a Lorenz system, that only the variable X is observed and that the observed values are passed to a perfect model.
The above philosophical considerations have motivated efforts to recast data assimilation as a synchronization problem and attempts to thus improve assimilation algorithms [35–37]. It may seem a large stretch from three-variable systems to the human mind, but the use of low-order systems to study problems that arise in numerical weather models is common practice in meteorology, popularized especially by E.N. Lorenz. These numerical models, intended to represent turbulent fluid behavior over a vast range of scales, are among the most complex computational models known. It is remarkable that such models are capable of tracking reality using only a sparse, temporally intermittent set of noisy observations.
To demonstrate the relevance of synchronization in low-order systems, it is first necessary to show that the phenomenon persists as the dynamical dimension of the model is increased to realistic values. Chaos synchronization in the sort of models given by systems of partial differential equations that are of interest in meteorology and other complex modeling situations has indeed been established. Pairs of 1D PDE systems of various types, coupled diffusively at discrete points in space and time, were shown to synchronize by Kocarev et al. [6].
Synchronization in geofluid models that are relevant to weather prediction was demonstrated by Duane and Tribbia [4,5]. The models [38] are given in terms of the stream function ψ(x, y, i, t) in a two-layer (i = 1, 2) channel, contours of which are streamlines of atmospheric flow, as shown in Figure 5, and a derived field variable, the potential vorticity
, with constants as defined in the reference. The dynamical equation for each model is:
where the Jacobian
gives the advective contribution to the Lagrangian derivative D/Dt. Equation (3) states that potential vorticity is conserved on a moving parcel, except for forcing
and dissipation Di, as defined in [5]. The forcing induces a relaxation to a jet-like background flow ψ∗ (Figure 5a,b) with q* ≡ q(ψ*), injecting energy into the system.
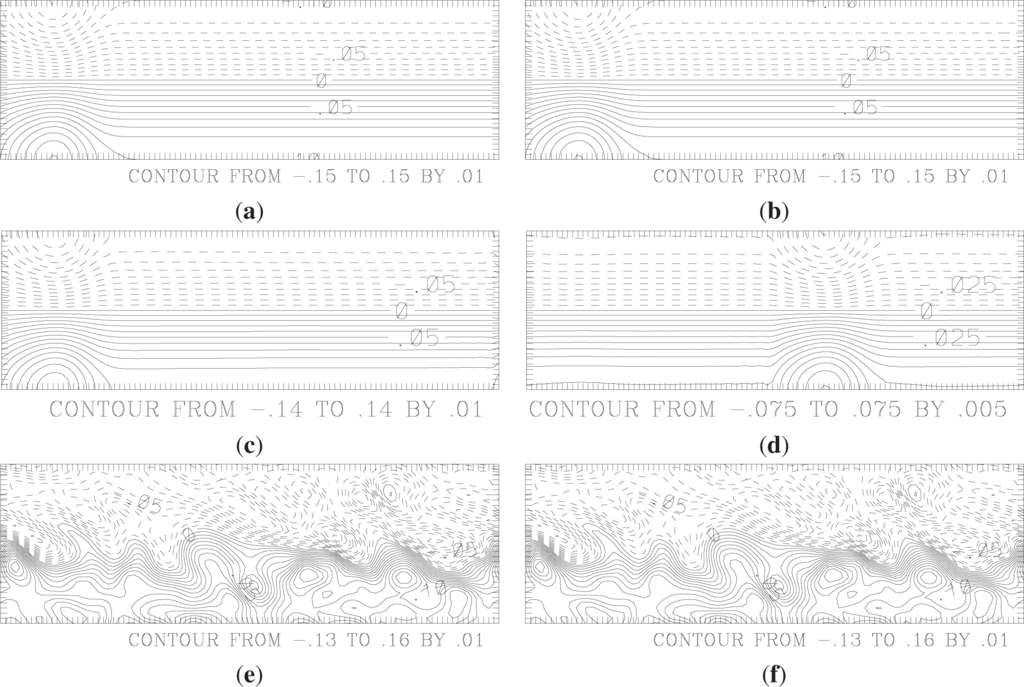
Figure 5.
Stream function (in units of 1.48 × 109 m2s−1) describing the forcing ψ* (a,b), and the evolving flow ψ (c–f), in a parallel channel model with coupling of medium-scale modes for which |kx| > kx0 = 3 or |ky| > ky0 = 2, and |k| ≤ 15, for the indicated numbers n of time steps in a numerical integration (generalizing to bidirectional coupling, for convenience). Parameters are as described previously [5]. An average stream function for the two vertical layers i = 1, 2 is shown. Synchronization occurs by the last time shown (e,f), despite differing initial conditions (c,d).
Two models of the form (3), DqA/Dt = FA+DA and DqB/Dt = FB+DB, were coupled diffusively through a modified forcing term
, where the flow has been decomposed spectrally and the subscript k on each quantity indicates the wave number k spectral component. The two sets of coefficients
and
were chosen to couple the two channels only in some medium range of wavenumbers.
It was found that the two channels rapidly synchronize if only the medium-scale modes are coupled (Figure 5), starting from different initial flow patterns. For unidirectional coupling, the synchronization would effect assimilation of Fourier-space data from the A channel into the B channel. The restriction to coupling of medium-scale modes is a Fourier-space counterpart to assimilating data from discrete, well-separated observation points. It has been shown analytically that optimal synchronization is equivalent to Kalman filtering when the dynamics change slowly in phase space, so that the same linear approximation is valid at each point in time for the real dynamical system and its model. When the dynamics change rapidly, as in the vicinity of a regime transition, one must consider the full nonlinear equations, and there are better synchronization strategies than Kalman filtering or the popular method of ensemble Kalman filtering [39]. The deficiencies of the standard methods, which are well known in such situations, are usually remedied by ad hoc corrections, such as “covariance inflation” [40]. In the synchronization view, such corrections can be derived from first principles [35,41]. In other work by Abarbanel [36], the synchronization view has led to new assimilation algorithms in which nudging coefficients can be made to decrease over time. While neither scheme has been developed for application to practical weather forecasting, these preliminary theoretical results demonstrate the analytical power of viewing perception as synchronization of truth and model.
It is suggested here that biological perception can also be described as synchronization of brains with sensory input. A view of the brain-world relationship in the context of the brain as an open, dissipative system has been put forward by Vitiello [42]. However, as yet, there has been little work on synchronization of neural models with input time series, although synchronization within such models plays a large role in generating realistic EEG patterns (e.g., [43,44]) and in internal organization of information [45]. Some recent work on auditory perception indicates that brain rhythms synchronize with the syllabic rate in speech input, so as to parse syllables [46].
4. Internal Sync vs. Mind-Matter Sync and the Role of Meaning
In the context of data-assimilation/machine-perception, the role of synchronism is indeed reminiscent of Jung’s notion of synchronicity in the relationship between mind and the material world. However, in the latter view, and in the popular culture surrounding the notion, the alleged relationships between events, mental or physical, are detected without close inspection and are “meaningful”. In this section, it is argued that meaningfulness is realized naturally in terms of the internal coherence that is typically present in any system that synchronizes with an external system and, thus, that the scientific view of synchronization should satisfy philosophers in this regard, as well.
Prior use of the idealized geophysical model considered above illustrates how “meaning” would enter. The quasi-geostrophic channel model was originally developed to represent the geophysical “index cycle”, in which the large-scale mid-latitude atmospheric circulation vacillates, at apparently random intervals, between two types of flow [38]. In the “blocked flow” regime, e.g., Figure 6a, a large high-pressure center, typically over the Pacific or Atlantic, interrupts the normal flow of weather from west to east and causes a build-up of extreme conditions (droughts, floods, extreme temperatures) downstream. In the “zonal flow” regime, e.g., Figure 6b, weather patterns progress normally. Synchronization of flow states, complete or partial, implies correlations between the regimes occupied by two coupled channel models at any given time. Such correlations, in the context of synchronization between reality and model, are indeed meaningful to meteorologists and to the residents of the regions downstream of any blocks. Synchronization of two highly simplified versions of the channel model has been used to predict correlations between blocking events in the Northern and Southern Hemispheres [2,3], and synchronization of two channel models has been used to infer conditions under which Atlantic and Pacific blocking events can be expected to anticorrelate [4,5].
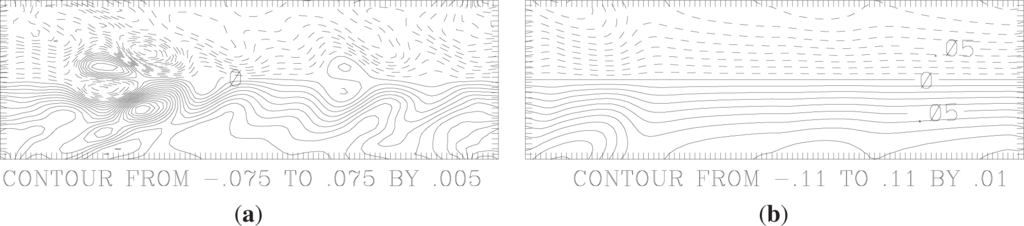
Figure 6.
Stream function (in units of 1.48 × 109 m2s−1) describing a typical blocked flow state (a) and a typical zonal flow state (b) in the two-layer quasi-geostrophic channel model. An average stream function for the two vertical layers i = 1, 2 is shown.
To generalize from the geophysical models, we note that blocks are “coherent structures”, as commonly arise in a variety of nonlinear field theories. Such structures, of which solitons are perhaps the best known example, persist over a period of time because of a balance between nonlinear and dispersive effects. While no generally accepted definition of “coherent structure” has been articulated, one view of their fundamental nature can support the proposed general connection with meaningfulness. For a structure to persist, the different degrees of freedom of the underlying field theory must continue to satisfy a fixed relationship as they evolve separately. That behavior defines generalized synchronization, the phenomenon in which two dynamical systems synchronize, but with a correspondence between states given by a relationship other than the identity [20]. Coherent structures are then characterized by internal generalized synchronization within a system. As state variables that are generally synchronized with other state variables reveal additional information, it is proposed that such relationships capture “meaningfulness” in the usual sense of that term.
Meaningfulness is even more naturally defined as internal synchronization within mind. A response to a given external stimulus by any “element” of mind is likely to be deemed meaningful if there are synchronized, parallel responses of other mental elements.
No reference has been made to the semantic meaning of the meaningful structures. Rather, the function of internal synchronization is that of parsing, or perceptual grouping, which must precede interpretation. Synchronization is indeed known to play a role in perceptual grouping in real neural systems, as discussed below in Section 5. An example is the “cocktail party problem” of how a listener groups sounds in a crowded room into individual voices, to each of which meaning can be assigned. von der Malsburg hypothesized that the grouping occurs when neurons responding to the different frequency components of a given voice, at any given time, momentarily synchronize their spike trains [47]. In the visual domain, the corresponding process is the synchronization of neurons that respond to features in the visual field that belong to the same object, so that meaning can subsequently be assigned to that object at higher levels of processing. In digital image processing, the task of automatic image segmentation into meaningful components is often harder than the task of interpreting those components; cellular neural network architectures have been proposed in which segmentation is manifest as synchronization of units corresponding to each meaningful component within the 2D field and de-synchronization between different meaningful components [48,49] (The synchronization must be delicately controlled to be useful. An excess of synchronization can lead to such pathological conditions as epileptic seizures).
If coherent structures defined by synchronization within a system are meaningful, the question remains of whether the correspondence between two co-occurring structures in two different systems, which might define a synchronicity, is itself meaningful, i.e., whether the structures are properly paired. In the typical case (especially in the case of a real system and its model), there is enough similarity between the synchronizing systems that a meaningful pairing is likely.
It remains to show that internal synchronization is likely in each of a pair of dynamical systems that exhibit synchronized chaos. It has indeed been hypothesized that internal synchronization is required for synchronizability with an external system [50]. The essential role of coherence in synchronizing systems was examined by considering a pair of Hamiltonian systems, for which complete synchronization is precluded, because phase-space volumes of ensembles of trajectories are preserved, by Liouville’s theorem. It turns out that the form of the resulting incomplete, residual synchronization highlights the role of coherent structures.
We consider a nonlinear scalar field theory, in an expanding universe, that gives rise to “oscillons”—coherent structures in the field that oscillate in fixed, randomly-placed locations—as do similar structures that were first noted in vibrating piles of sand [51]. The expansion of the Universe plays a role in the cosmological case that is analogous to the role of frictional dissipation in the sand piles—entropy is cast off to smaller scales in the expanding coordinate system, corresponding to newly created space in a fixed coordinate system. However, unlike the sand piles, the cosmological system is governed by a time-dependent Hamiltonian, and Liouville’s theorem still applies. The one-dimensional model is given by the relativistic scalar field equation, with a nonlinear potential term, in an expanding background geometry described by a Robertson–Walker metric with Hubble constant H. Using covariant derivatives for that metric in place of ordinary derivatives, one obtains the field equation:
The scalar field exhibits oscillon behavior for some forms of the nonlinear potential V (Figure 7a), but not for others (Figure 7b).
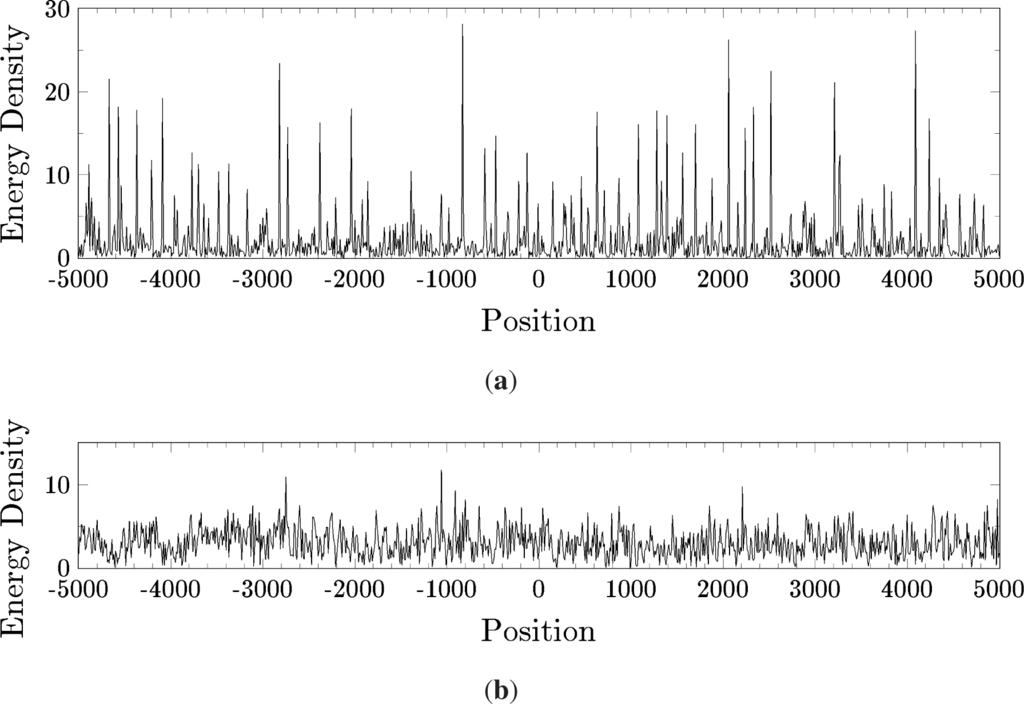
Figure 7.
Energy density ρ = (1/2)e−Ht(ϕx)2 + (1/2)eHt(ϕt)2 + eHtV (ϕ) vs. position x for a numerical simulation of the Scalar Field Equation (4) with the potential V(ϕ) = (1/2)ϕ 2 − (1/4)ϕ4 + (1/6)ϕ 6, exhibiting localized oscillons (a), and a simulation of the same equation, but with a different potential V(ϕ) = (1/2)ϕ2 + (1/4)ϕ4 + (1/6)ϕ6, for which oscillons do not occur (b).
Where oscillons exist, a crude form of synchronized chaos is observed for a pair of loosely-coupled scalar field systems (a configuration that is introduced to study the synchronization patterns, without physical motivation), as seen in Figure 8. The fields do not synchronize, but the oscillons in the two systems tend to form in the same locations. The phases of the oscillons do not necessarily agree, so neither do we have an example of phase synchronization—the celebrated phenomenon [52,53] in which a system that is chaotic can nevertheless be assigned a phase that matches that of a second system. Oscillon frequencies depend on their amplitudes, which are generally different for a pair of oscillons whose positions correspond, and so the phases cannot agree (additionally, it is not clear how one would define a phase for a multi-oscillon system that would capture information about their positions). For a potential that does not support oscillons, the positional coincidence is trivially absent, and there is no correlation between corresponding components of the underlying field. Synchronization in this case can only be interpreted in terms of coherent structures in the separate systems.
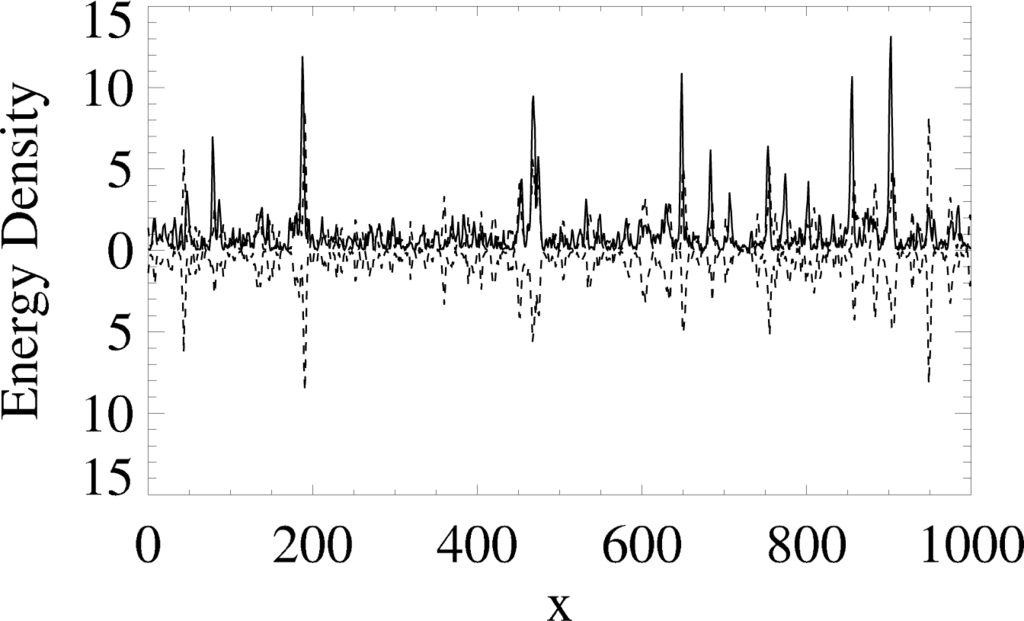
Figure 8.
The local energy density ρ vs. x for two simulations (solid and dashed lines) of the Scalar Field Equation (4), coupled to one another only through modes of wavenumber k ≤ 64, where modes up to kmax = 214 are realized numerically (ρ for the second system (dashed line) is also shown reflected across the x-axis for the ease of comparison). The coincidence of oscillon positions is apparent.
In a system as simple as the three-variable Lorenz model, the hypothesis about the relationship between internal and external synchronization is also validated. In this case, the relationship gives insight about which variables can be coupled to give synchronized chaos. Along the Lorenz attractor, the variables X and Y partially synchronize, resulting in the near-planar shape, while Z is independent. Consistently with the internal-external synchronization hypothesis, either X or Y, but not Z, can be coupled to the corresponding variable in an external system to cause the two systems to synchronize, as is well known.
To summarize, the meaningfulness of a synchronization pattern, as philosophically required, is naturally defined in terms of internal synchronization, or coherent structures, involving some of the variables that synchronize externally. However, external synchronization usually (or, by hypothesis, always) implies the existence of internal synchronization and, hence, meaning.
5. Sync as an Organizational Principle in Mind and in Computational Modeling
If chaos synchronization provides a rational foundation for philosophical synchronicity, it should give deeper insight regarding apparent synchronicity in physical and psychological phenomena and underlying mechanisms. In the psychological realm, it has already begun to appear that synchronized oscillations play a key role. Synchronized firing of neurons has been introduced as a mechanism for grouping of different features belonging to the same physical object [47,54,55]. If a moving bar is presented to a cat, then neurons responding to opposite ends of the bar, which may be widely separated within the visual cortex, synchronize their spike trains, even if the middle of the bar is missing [54]. Analogous neural synchronization phenomena describe the coordination of different muscles involved in motor control for a complex activity. Debates over the physiological basis of consciousness have centered on the question of what groups or categories of neurons must fire in synchrony in a mental process for that process to be a “conscious” one [56]. It was argued previously that patterns of synchronized firing of neurons provide a particularly natural and useful representation of objective grouping relationships, with chaotic intermittency allowing the system to escape locally optimal patterns in favor of global ones [57], following an early suggestion of Freeman’s [58]. Ambiguous figures, of the sort depicted by Escher, for instance, typically arise when more than one grouping of different features is possible. Intermittent synchronization patterns in the fields of neurons that respond to the features would give alternating interpretations of the same figure. The observed, highly intermittent synchronization of 40-Hz neural spike trains could play just such a role, an idea that has been supported in more specific studies of brain function [45].
Since in the experiment with the cat, for instance, the cat’s consciousness is focused on the bar, the role of spike train synchronization in perceptual grouping has led to speculations about the role of synchronization in consciousness [9,47,56,59]. However, here, we suggest a relationship between neural synchronization and consciousness on a more naive basis: the hallmark of conscious thought, defined subjectively, is the ability to focus on one’s own thoughts and to influence them as one would interact with external events. Thus, consciousness can be framed as self-perception and then placed on a similar footing as perception of the objective world. In this view, there must be semi-autonomous parts of a “conscious” mind that perceive one another. In the interpretation of Section 3, these components of the mind synchronize with one another, or in alternative language, they perform “data assimilation” from one another, with a limited exchange of information.
Such a scheme has actually been proposed, and is currently being investigated, for the fusion of alternative computational models of the same objective process in a practical context [60,61]: different numerical models used to predict climate change in the 21st century differ by as much as a factor of two in the amount of globally-averaged warming and differ completely in their projections for specific regions of the globe. Current practice is just to average the results of the different models. By synchronizing a small set of alternative models with each other, a more reliable and detailed consensus could be obtained.
Taking the interpretation of consciousness that motivates such computational schemes seriously, imagine again that the world is a three-variable Lorenz system, perceived by three different components of mind, also represented by Lorenz systems, but with different parameters. The three Lorenz systems also “self-perceive” each other. Three imperfect “model” Lorenz systems were generated by perturbing parameters in the differential equations for a given “real” Lorenz system and adding extra terms. The resulting suite is:
,
,
, and
where (x, y, z) is the real Lorenz system and (xi, yi, zi) i = 1, 2, 3 are the three models. An extra term μ is present in the models, but not in the real system. Because of the relatively small number of variables available in this toy system, all possible directional couplings among corresponding variables in the three Lorenz systems were considered, giving 18 connection coefficients
A = x, y, z i, j = 1, 2, 3 i ≠ j. The constants KA A = x, y, z are chosen arbitrarily so as to effect “data assimilation” from the “real” Lorenz system into the three coupled “model” systems. The configuration is schematized in Figure 9.
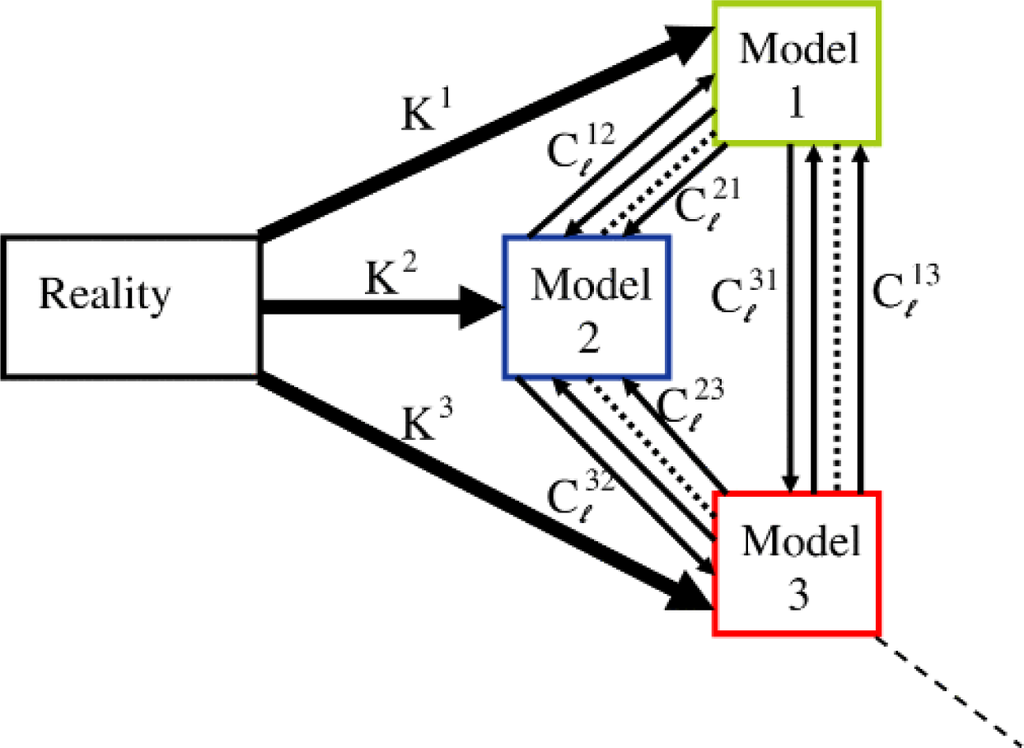
Figure 9.
“Model” Lorenz systems are linked to each other, generally in both directions and to “reality” in one direction. Separate links between models, with distinct values of the connection coefficients
, are introduced for different variables and for each direction of possible influence.
The connections Cij linking the three model systems can be chosen using yet a further extension of the synchronization paradigm: if two systems synchronize when their parameters match, then under some weak assumptions, as was proven in [62], it is possible to prescribe a dynamical evolution law for general parameters in one of the systems, so that the parameters of the two systems, as well as the states will converge. In the present case, the tunable parameters are taken to be the connection coefficients (not the parameters of the separate Lorenz systems), and they are tuned under the peculiar assumption that reality itself is a similar suite of connected Lorenz systems. The general result [62] gives the following adaptation rule for the couplings:
with analogous equations for
and
, where the adaptation rate a is an arbitrary constant and the extra terms with coefficient ∊ dynamically constrain all couplings
to remain in the range (−δ, Cmax) for some small number δ. Without recourse to the formal result on parameter adaptation, the rule (6) has a simple interpretation: time integrals of the first terms on the right-hand side of each equation give correlations between truth-model synchronization error,
, and inter-model “nudging”, xj−xi. We indeed want to increase or decrease the inter-model nudging, for a given pair of corresponding variables, depending on the sign and magnitude of this correlation (The learning algorithm we have described resembles a supervised version of Hebbian learning. In that scheme, “cells that fire together wire together.” Here, corresponding model components “wire together” in a preferred direction, until they “fire” in concert with reality.). The procedure will produce a set of values for the connection coefficients that is at least locally optimal in the multidimensional space of connection values.
A simple case is one in which each of the three model systems contains the “correct” equation for only one of the three variables and “incorrect” equations for the other two. The “real” system could then be formed approximately using large connections for the three correct equations, with other connections vanishing, and the peculiar assumption is strictly true if the large connections become infinite. Other combinations of model equations will also approximate reality.
Several things have been learned from “supermodels”, such as the one defined by (5) and (6). First, it is not difficult to define adequate inter-model connections. In a numerical experiment (Figure 10a), the couplings did not converge, but the coupled suite of “models” did indeed synchronize with the “real” system, even with the adaptation process turned off half-way through the simulation, so that the coupling coefficients
subsequently held fixed values. (The three models also synchronized among themselves nearly identically.) Second, the inter-model connections are needed, despite efforts, common in the modeling community [63], to combine only the outputs of independently run models using Bayesian reasoning. The difference between corresponding variables in the “real” and coupled “model” systems was significantly less than the difference using the average outputs of the same suite of models, not coupled among themselves (Figure 10b). Further, without the model-model coupling, the output of the single model with the best equation for the given variable (in this case, z, modeled best by z1 in Model 1) differed even more from “reality” than the average output of the three models (Figure 10c). Therefore, it is unlikely that any ex post facto weighting scheme applied to the three outputs would give results equaling those of the synchronized suite. Internal synchronization within the multi-model “mind” is essential. Third, the choice of semi-autonomous models to be combined is not essential, as long as the “gene pool” of models is diverse. In a case where no model had the “correct” equation for any variable, results deteriorated only slightly (Figure 10d).
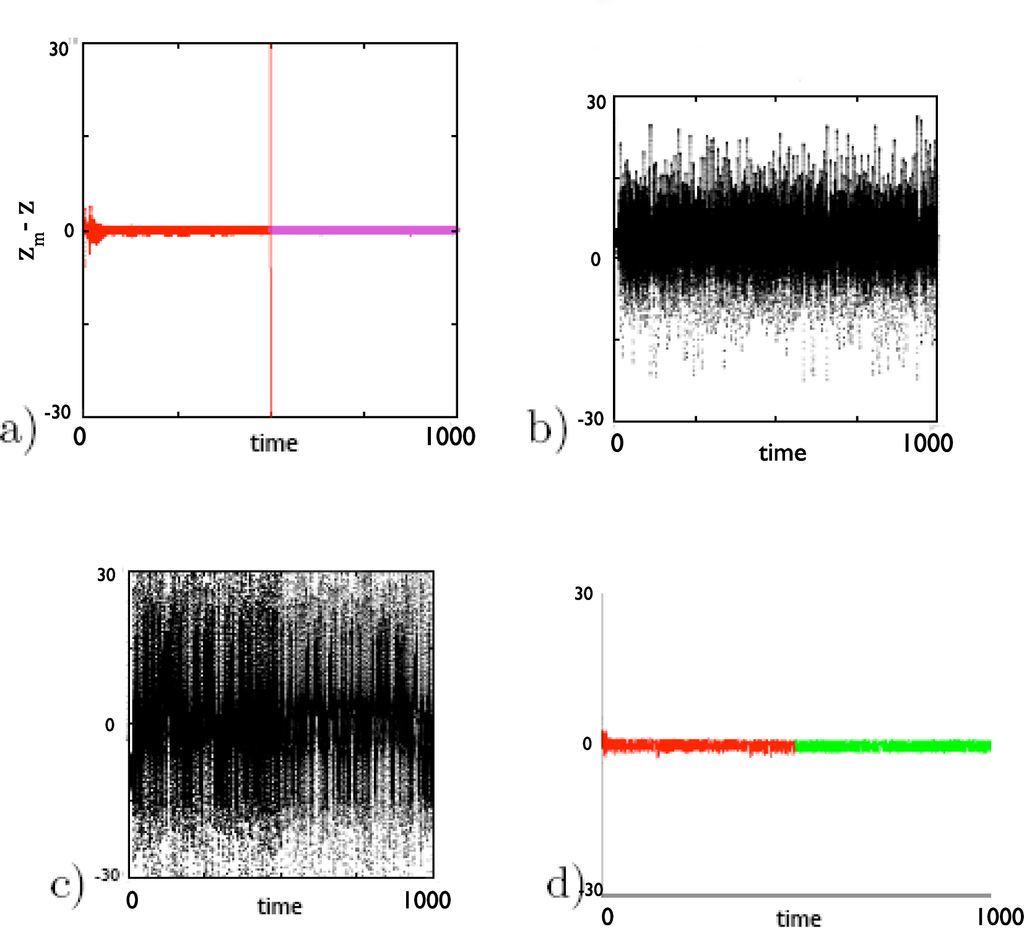
Figure 10.
Difference zm−z between “model” and “real” z vs. time for a Lorenz system with ρ = 28, β = 8/3, σ = 10.0 and an interconnected suite of models with ρ1,2,3 = ρ, β1 = β, σ1 = 15.0, μ1 = 30.0, β2 = 1.0, σ2 = σ, μ2 = −30.0, β3 = 4.0,σ3 = 5.0, μ3 = 0. The synchronization error is shown for (a) the average of the coupled suite zm = (z1 +z2 +z3)/3 with couplings
adapted according to (6) for 0 < t < 500 and held constant for 500 < t < 1,000; (b) the same average zm, but with all
; (c) zm = z1, the output of the model with the best z equation, with
; (d) as in (a), but with β1 = 7/3, σ2 = 13.0, and μ3 = 8.0, so that no equation in any model is “correct” (analogous comparisons for x and y give similar conclusions).
The above scheme for the fusion of imperfect computational/mental models only requires that the models come equipped with a procedure to assimilate new measurements from an objective process in real time and, hence, from one another. Such procedures are indeed available for the long-range climate projection models, which differ significantly among themselves in regard to the magnitude and regional characteristics of expected global warming [64] (to project 21st century climate, the models are disconnected from reality after training, parameters are altered slightly to represent increased greenhouse gas levels, and one assesses changes in the overall shape of the attractor). Toward the intended application, results with Lorenz systems were thoroughly confirmed and extended using a learning method that minimizes synchronization error over finite-length trajectories, instead of the instantaneous error as above, to determine inter-model connections [60,61]. The scheme could also be applied to financial, physiological or ecological models. It could conceivably also describe the combination of individuals to form a society (cf. [65]), in models and in reality.
In the realm of mind, the sharpening of the transition to synchronization as the suite of interconnected systems increases in size (e.g., as in the Kuramoto model [66]) is taken here to bolster the previous suggestions that synchronization plays a fundamental role in conscious mental processing (we have focused on assimilation/perception, but analogous constructions could be applied to the opposite problem of control—the interaction between mind and matter is two-way). For application to mind, we imagine that the systems are neurons or collections of neurons (for a large number of simple systems, a mean field theory could represent the interaction of each system with the collective effect of the others). Note that the proposed role of synchronization is markedly different from Pauli’s view of mental phenomena as “something objectively psychical which cannot and should not be explained by material causes” [10,67]. Here, mental phenomena are grounded in the material reality of neuronal systems, even if their dynamical properties are qualitatively different from those of the much higher dimensional physical world that they represent.
To describe ordinary mental phenomena, one needs a notion of synchronization at slower time scales and higher levels of organization, so that alternative representations of the same objective reality within the brain can fuse to form a conscious percept. Thus, the synchronization view suggests a new direction of research, since it remains to integrate a theory of higher-level synchronization with the known synchronization of 40-Hz spike trains. There is indeed evidence that internal synchronization within the brain is greater during successful encoding of new information and during recognition [68], supporting a connection between higher level brain-reality synchronization and short time scale internal synchronization. It is certainly plausible that synchronization at higher levels could rest on synchronization at shorter time scales. Inter-scale interactions played a similar role in the synchronization of a range of Fourier components of the same field in the synchronously coupled systems of partial differential equations considered in Section 3. Conversely, feedback from the interpretive stages might trigger or reinforce the low-level synchronization. This indeed must occur to explain the known neural phenomena in visual grouping [54], but realistic models remain to be constructed. In such models, with a steady stream of new input data, natural noise or chaos would cause the periods of high-quality synchronization across the system to be brief (as in Figure 4c) (cf. [69]). Analogous neural synchronicities at multiple levels of a processing hierarchy in a real organism would appear subjectively as consciousness.
6. Sync in Quantum Theory
It has been asserted that an “acausal connecting principle” applies not only to the relationship between mind and matter, or to relationships within mind, but also applies to matter itself. Turning to the realm of basic physics, the fundamental role of synchronism is most evident in the surprising long-distance correlations that characterize quantum phenomena. The Einstein–Podolsky–Rosen (EPR) phenomenon, viewed in light of Bell’s theorem, implies that spatially separated physical systems with a common history continue to evolve as though connected with each other and with observers. Bell’s theorem definitively asserts that observed correlations between two spatially separated spin-1/2 particles arising from the decay of a common spin-0 ancestor cannot be explained in terms of a causal relationship to the initial decay conditions alone. Such a relationship would imply that the binary-valued spins A and B are only functions of the orientations a and b of the respective measuring devices and of some hidden variables represented collectively by λ, i.e., A = A(a, λ), B = B(b, λ). In general, λ designates the state of the joint system at some initial time. One then defines the correlation P between the two measured spins as a function of the two orientations a and b, P (a, b) ≡ ∫ ρ(λ)A(a, λ)B(b, λ)dλ, where ρ(λ) is any function specifying a probability distribution of the hidden variables, i.e., ∫ ρ(λ)dλ = 1. One introduces a third orientation b′, and considers the difference P(a, b) − P(a, b′) = −∫ dλρ(λ)[A(a, λ)A(b, λ) − A(a, λ)A(b′, λ)] = ∫ dλρ(λ)A(a, λ)A(b, λ)[A(b, λ)A(b′, λ) − 1] having used the convention A = ±1, B = ±1 and having substituted B(b, λ) = −A(b, λ). It follows that |P (a, b) − P (a, b′)| ≤ ∫ dλρ(λ)[1 − A(b, λ)A(b′, λ)], which is Bell’s inequality [70]:
The standard quantum theoretic result P(a, b) = − cos(a−b) violates (7) (as does any smooth function), so the general hidden-variable form A = A(a, λ), B = B(b, λ), based on spin systems that evolve independently after the initial decay, is ruled out.
A key assumption is that the observer is free to alter his choice of measurement orientation, from b to b′, without changing the initial state parameters λ. If one takes the “superdeterminist” view that negates this sense of free will, so that the observers’ choices are also determined by the initial state, then one can avoid the Bell paradox. That is the route taken by ’t Hooft [71] and by Palmer [72].
However, if one leaves the usual notion of free will intact, the picture of the quantum world that emerges from Bell’s theorem is one in which entanglement and nonlocal connections are pervasive, even among virtual particles in the vacuum, defining a web of relationships similar to the one implied by the ubiquity of chaos synchronization. As with synchronized chaos, quantum entanglement can be used for cryptography, an analogy that was developed in prior work [73].
All of the above considerations are avoided in the standard (Copenhagen) interpretation of quantum mechanics in which the hidden variables λ do not exist, and measured quantities are a result of the act of measurement, with no correspondence to prior properties of the measured system. But there is nonlocality even in the standard interpretation, since a spin-measurement of a particle must also affect the spin of its distant EPR partner. Could the relationship between the two particles resemble that between Huygens’ clocks? If one assumes hidden variables, one may naturally seek an interpretation of EPR correlations in terms of synchronized chaotic oscillators, putting quantum theory on a non-local deterministic footing. Bell’s theorem denies the possibility of either a quantum theory or an underlying hidden-variable theory that is local, so some form of non-locality is required, but that non-locality should still not allow faster-than-light signals, which would violate relativity. Bohm [74,75], rediscovering de Broglie’s suggestion, introduced an explicitly non-local potential to construct a theory that was entirely equivalent in its predictions to standard non-relativistic quantum theory. In a two-slit experiment, for example, a particle can follow one of two paths defined by potential valleys, with the choice of path sensitively dependent on initial conditions, as in a chaotic system. However, the many-body form of the potential is typically unanalyzable, an issue that arises especially in extension to relativistic field theory. The view taken here is that Bohm’s interpretation is an “existence proof” of the possibility of a hidden variable theory, countering von Neumann’s earlier alleged proof that such theories are impossible [76]; and not a satisfactory theory as it stands.
In ’t Hooft’s more recent interpretation [71,77,78], which might ultimately generate testable predictions at the microscale, there is a weaker form of non-locality due to the presence of Planck-scale black holes and an essential entanglement between the choices made by an observer (a and b above) and the observed state, as must arise, since “free will” in making such choices is incompatible with determinism. New conservation principles, not articulated as of yet, are posited to constrain both physical states and observer choices [78]. In this section, in accordance with Bohm’s coordinated “ballet dances” of particles [79] and with ’t Hooft’s new conservation principles, we review and update a previous suggestion [73,80] that chaos synchronization can contribute to a realist interpretation of quantum theory.
In an interpretation based on a granular state-space as with ’t Hooft’s, Palmer [72] has hypothesized that the quantum world lives on a dynamically invariant fractal point set within the higher-dimensional phase space associated with the degrees of freedom that are naively thought to be independent. Membership in the invariant set is an uncomputable property, so theories can only be formulated in terms of the variables of the full phase space, and the emergent “conservation laws” that restrict motion to the invariant set remain implicit. Palmer’s invariant set is in fact a generalized synchronization “manifold” (the common, but improper term, since the “manifold” is nowhere smooth), of the sort suggested by Figure 3c. As discussed in the prior work [80], generalized rather than identical synchronization is the fundamental relationship, because EPR spins anti-correlate.
To bar supraluminal transmission of information, the proposal in [73,80] relies on the mechanism used in synchronization-based cryptography: a signal provided by one variable of a chaotic system is difficult to distinguish from noise and is meaningful only when received by an identical copy of the system. However, it follows from the Takens–Mañé Theorem [17,18] that information can be extracted from such a signal if one considers a long enough time series. Longer time series are required to decode signals produced by more complex systems. For perfect security, one would need a chaotic system with an infinite-dimensional attractor.
Such a situation would arise most naturally in a multi-scale system (e.g., as proposed by Palmer [81]), requiring at least a system of partial differential equations, but something can be learned by considering a family of simpler systems of variable dimension, given by ordinary differential equations [73,80]. It is known that two N-dimensional generalized Rossler systems (GRS’s) (each equivalent to a Rossler system for N = 3) will synchronize for any N, no matter how large, when coupled via only one of the N variables:
Each system has an attractor of dimension ≈ N − 1, for N greater than about 40, and a large number of positive Lyapunov exponents that increases with N. As N → ∞, while the synchronization persists, the signal linking the two systems becomes impossible to distinguish from noise. It was shown [73] that an inequality analogous to Bell’s could be constructed by arbitrarily bisecting the phase space to define final states analogous to spin-up/spin-down and using a GRS parameter as an analogue of measurement orientation. That inequality is in fact violated because of the connection between the systems, but a naive observer would expect it to hold, because he is unable to distinguish the connecting signal from noise.
In Palmer’s view, there is no connecting signal, because the world never leaves the “invariant set” (although the dissipative character of gravitational interactions is assumed to play a role cosmologically in dynamically constraining the Universe to motion on the invariant set in the first place) [72]. In [73,80], on the other hand, we considered the nature of the required “restoring force” if small perturbations transverse to the synchronization manifold are conceived of as physical.
To construct a realistic model, one must move far beyond the simple System (8). The GRS is a questionable model of reality, because its largest Lyapunov exponent hmax → 0 as N → ∞ (the system’s “metric entropy”, the sum of the positive Lyapunov exponents,
, is constant as N → ∞). In other words, the higher the dimension, the less chaotic the system. Such behavior is suspect in a system intended to represent unpredictable quantum fluctuations. Taking the GRS behavior as N → ∞ to be generic, one must reconcile its increasingly mild character with the requirement that the nonlocal “signal” be perfectly masked through chaos. It was noted [80] that the issue is resolved if the GRS is viewed as a spatially asymptotic description of an intrinsically faster dynamics in a highly curved space-time. For reference, recall that an object falling into a black hole is perceived by an observer at a distance from the hole as approaching the horizon with decreasing velocity, but never reaching it. If the physical system that the GRS describes lives in the vicinity of a micro-black hole or wormhole, the variables in the asymptotic description will be slowed, but the actual physical processes will be realistically violent and can couple to each other through “signals” that are perfectly masked. More generally, the synchronizing subsystems can be expected to behave more wildly than the usual physical systems defined by PDEs on a continuum. Some form of granularity in state-space and/or physical space-time is indicated, in agreement with the models of ’t Hooft [78] and of Palmer [72,81].
6.1. Physical vs. Virtual Non-Locality
A Planck-scale foam-like structure in space-time was posited by Hawking [82] in the context of a procedure to quantize classical general relativity where that structure contributes significantly to a sum over alternative Euclidean space-time geometries. The present question is about the possible role of micro-wormholes in long-range synchronization, without transmission of information, in ordinary Lorentzian space-time. That possibility is consistent with theoretical arguments [83] and experimental evidence [84] for fundamental granularity in space-time structure. In the Appendix, it is explained that micro-wormholes could arise in a variant of general relativity defined by equations that are generally covariant, but scale-dependent, and a weak divergence that arises from the recirculation of virtual quanta through wormholes may be avoided if the wormholes are sufficiently narrow. The wormholes envisioned are reminiscent of those in the original construction of Wheeler [85], who suggested that lines of electric force are always closed if positive and negative charges are thus connected at the micro-level. In the absence of a theory of Planck-scale processes, other forms for the non-local physical connection could be considered, but general-relativistic wormholes are a natural starting point for any such construction. Indeed, Maldacena and Susskind have recently suggested that non-traversable wormholes mediate EPR correlations in standard quantum theory [86]. A modicum of traversability, as described in the Appendix, could then support a non-local deterministic interpretation.
If connections are formed by joining micro-black holes, as might coincide with particles in an EPR pair, the systems that must synchronize are defined on two-dimensional horizons at the mouths of the wormholes. This is consistent with the holographic principle [87,88] that such 2D fields capture the essential information about the full three-dimensional systems.
On the other hand, if we stipulate, with Palmer, that the synchronization manifold is fundamental, because the physical world never leaves it, then no wormholes are needed: we have two dynamical systems defining an anticorrelated EPR pair,
and
, with x ∊ RN and y ∊ RN. The dynamics are modified, so as to couple the systems:
and there is some locally-invertible function Φ: RN → RN, such that ||Φ(x) − y|| → 0 as t → ∞. Then, the coupled dynamics are also defined by the two autonomous systems:
without recourse to wormholes or any nonlocal connections, provided we know the badly behaved function Φ exactly. To avoid the implications of Bell’s theorem in this scenario, the correspondence Φ must also depend on the observer choices of measurement orientation.
If the nonlocal connections are assumed to be physical, we must rely on the narrow width and short life of the wormholes to prevent supraluminal transmission of matter or information. Diffraction effects preclude communication, except in highly symmetrical situations, as in EPR, where constructive interference would account for the needed nonlocal connections. The isolated character of such quantum “synchronicities” follows from the rarity of the required symmetrical context.
The existence of the wormholes could shape the synchronization manifold and the correspondence Φ, whether or not the connections continue to play a role in the dynamics. That sparse connections can be sufficient to synchronize two extended systems has already been demonstrated. Kocarev et al. [6] showed that pairs of PDE systems of various types (Kuramoto–Sivashinsky, complex Ginsburg–Landau, etc.) could be synchronized by pinning corresponding variables to one another at a discrete set of points, at discrete instants of time (the example of synchronizing two quasi-geostrophic channel models (Figure 5) establishes essentially the same phenomenon for coupling formulated in Fourier space). A sparse set of wormholes is expected to give synchronization of subsystems on opposite sides in the same way. Once the subsystems are perfectly synchronized, physical connections are no longer needed, if we can rationalize the continued relevance of Equation (10).
The mediation of quantum interconnectedness by intermittent wormholes is perhaps the ultimate home for the marriage [9] between synchronization dynamics and small-world (or “scale-free”) networks. The proposal would also realize the program, favored by a minority of physicists, of quantizing gravity by rooting quantum behavior in space-time geometry, rather than the reverse. The question is essentially whether the construction can reproduce the nonlocal piece of the “quantum potential” in Bohm’s interpretation [74] (the remaining piece corresponding to motion along the synchronization manifold), accounting for the origin of that piece geometrically.
In the synchronization framework, one could also imagine classical entanglement between observer choices and observed states, again with no explicit description of the relationship, as in ’t Hooft’s interpretation. The degrees of freedom corresponding to observer choice must in fact be part of the definition of the overall synchronization manifold on which the world resides. The synchronized chaos framework thus supports a local contextual resolution of the Bell paradox, as well as a natural description of the weak nonlocality that is required if observer free will is retained (as this author prefers). Within the single framework, non-local connections may or may not be present accordingly, or might be vanishingly small and conceivably rooted in cosmological history.
7. Summary and Concluding Remarks
In the foregoing review, we have attempted to show that the synchronization of loosely-coupled chaotic systems approaches the philosophical notion of highly intermittent, meaningful synchronicity more closely than commonly thought. Synchronized chaos is highly intermittent in a natural setting (Section 2). As with philosophical synchronicity, it describes the relationship between the objective world and a perceiving mind or computational model (Section 3). The phenomenon typically involves the coincidence of coherent structures, to which meaning can be attached (Section 4). Central to our thesis is a relationship between internal synchronization within a system and external synchronizability with another physical system or with a model. That relationship, which was described in Section 4, is in accord with common wisdom: an objective system with a high degree of internal synchronization is more easily perceived/understood; an internally coherent individual can more easily engage the world, etc. Accordingly, that relationship is currently proving to be a useful design principle in computational modeling, as described in Section 5.
What is not clear is that even with the isolated character and meaningfulness of synchronicities in coupled chaotic systems, the phenomenon reaches all the way to that of Jung and others, who discussed detailed coincidences between physical events and previous dreams, for instance. The attempt to put relationships of that kind on a rational footing may appear doomed. The mechanisms of deterministic chaos seem barely sufficient. One may dismiss such examples and consider only more restricted forms of synchronicity, or one may imagine that new physical principles emerge. The difficulty of ascribing the more extended notion of synchronicity to material reality may indeed have led to the dual-aspect monist conjecture [10] in which mind is elevated to the same level as matter, and both are aspects of an underlying domain that is not primarily mental or material. In contrast, although mind is semi-autonomous in the picture presented here, our view is decidedly materialist. Our endeavor might be compared to Marx’s attempt to ground Hegel’s dialectic in material reality, a transformation whose legitimacy has sometimes been questioned, notably by Bohm [89].
Closer to physics is the example of Einstein’s relationship to the ideas of Ernst Mach. Einstein was inspired by Mach’s relativism, but Mach castigated Einstein for the latter’s belief that atoms are real, preferring to view them only as useful conceptual constructs [90]. Mach did not hold the extreme position that “all is mind.” He simply had an exaggerated sense of the dependence of scientific observations on the human observer, preventing his full realization of the consequences of ideas he himself had introduced.
As science progresses, it is to be expected that some ideas previously introduced on a religious basis, or by idealist philosophers, are not wrong, but have indeed a hidden justification in material reality. The logical jump required for an objective understanding of Pauli’s synchronicity is shorter yet. Even if our objective realization of the Jung–Pauli notion is only partial, it is the point of view of this paper that it is appropriate for scientists to seriously consider a concept that has captured the popular imagination as widely as has synchronicity and to afford a rational explanation if possible. Therefore, the question is whether nonlinear dynamics has gone far enough as to put philosophical synchronicity on an objective footing to any significant degree.
The question is perhaps sharpest in regard to consciousness and synchronization-based theories thereof. In Section 5, it was argued that previous suggestions about the role of synchronization in the brain were supported by the possibility of highly intermittent synchronization among chaotic oscillators and by the possibility of synchronizing different complex models of the same objective process, giving rise to “self-perception”. However, Penrose has given a well-known argument that the reasoning abilities of conscious beings cannot arise from classical physics or algorithmic processes that describe such physics: for any algorithmic system of ascertaining truth, one can always articulate a true statement, of the sort constructed by Gôdel, that such a being knows to be true, but whose truth cannot be established within the system [91]. Since synchronized chaos is still deterministic, the abilities of conscious beings must come from fundamentally different processes, which Penrose has concluded are quantum mechanical. (If one considers a chaotic system given by differential equations for which infinite precision in initial conditions is needed to predict the outcome even qualitatively, as in Palmer’s earliest proposal [92], a typical basin of attraction for a given outcome is a “fat fractal”: the more precisely the initial conditions are known, the smaller is the probability of error in “guessing” the outcome. That is very unlike quantum indeterminacy.) Additionally, because the randomness in wave-function collapse in the standard interpretation of quantum theory would be inconsistent with its proposed role in consciousness, Penrose also proposed a new interpretation involving an objective and deterministic account of wave-function collapse [91,93].
The discussion of quantum processes in Section 6 was included because they seem to provide the deepest example of synchronicity: the quantum world appears to live on a generalized synchronization “manifold”. However, if Penrose is correct, the converse statement can also be made: synchronicity as manifest in human consciousness is also fundamentally quantum in origin. Correlations in neuronal firing or between neural subsystems can only give rise to consciousness, in this view, if quantum correlations are involved, such correlations arising either as in standard quantum theory or as in deterministic re-interpretations thereof. Synchronicities between states of the mind and of the objective world must somehow follow. Perhaps such an enlarged notion could reach the popular concept and the one of Jung and Pauli. In Penrose’s view, as here, the question of the proper interpretation of quantum phenomena, on the one hand, and that of the origin of synchronism between mind and matter, on the other, are to be resolved jointly. The proposed view differs in that dynamical synchronization, in a properly structured micro-world, would account for quantum correlations, but would also explain macroscopic phenomena, mental and material, directly.
Appendix
A. On the Possibility of Micro-Wormholes
As discussed in Section 6 of the text, if space-time were permeated with micro-scale Wheelerian wormholes, that would be useless for time travel, a synchronistic order could nonetheless emerge: chaos synchronization could combine with small-world effects in the same manner as has been described for more familiar applications. Consideration of synchronicity as a basic physical principle would not be complete without considering Wheeler’s suggestion. In a deterministic theory underlying quantum mechanics, a wormhole might connect the charges in an EPR pair. The role of wormholes in mediating quantum entanglement posited by Maldacena and Susskind [86] would be enlarged in a non-local deterministic theory. Here, we discuss two historical objections to wormholes as they would impact their possible occurrence at the microscale.
A.1. Implications of the Weak-Energy Condition in Ordinary and Higher-Derivative Gravity
While two Schwarzschild black hole solutions to Einstein’s equations can be joined to form a wormhole, solutions of this type are not traversable [94]. The possibility of traversable wormhole solutions is limited by the weak energy condition. That condition states that for any null geodesic, say one parameterized by ζ, with tangent vectors ka = dxa/dζ, an averaged energy along the geodesic must be positive:
where Tαβ is the stress-energy tensor. Traversable wormholes can exist only if (11) is violated for some null geodesics passing through the wormhole, implying the existence of “exotic matter” with negative energy density in the “rest frame” of a light beam described by the null geodesic. The negative energy density is required, in one sense, to hold the wormhole open.
Quantum fluctuations in the vacuum can violate the weak energy condition [95,96]. However, the problem can be avoided at the classical level, as desired if quantum theory is not to be presumed, if a larger class of generally covariant theories are considered. Terms containing higher derivatives of the metric can indeed be added to Einstein’s equations, with effects that are negligible on
all but the smallest scales [97,98]. The situation is analogous to that of the Navier–Stokes equation in fluid dynamics: while the terms involving the co-moving derivative follow simply from Newton’s first law, the dissipative terms are ad hoc and can take many forms. General relativity can likewise be extended to theories of the form:
where
is a quantity involving a total of n derivatives of the metric, L is a fundamental length scale, the cn are dimensionless constants and we have included a cosmological constant Λ for full generality. If L = LP, the Planck length, then the new terms in the extended Theory (12) are negligible on macroscopic scales. They only need be considered if curvature is significant at the Planck length scale. Any metric that solves the ordinary Einstein equations after the substitution
solves (12) for given Tμν. It is plausible that the modified stress-energy tensor
can be made to violate the weak energy condition if the signs of the constants cn are chosen appropriately and, thus, that a traversable micro-wormhole solution is possible.
In a standard quantum mechanical treatment of the micro-wormhole, traversability would emerge in the same manner as does black hole radiation. A theory of the form (12) could come from a deterministic re-interpretation of the quantum mechanical process.
A.2. Vacuum Recirculation Effects for Narrow Wormholes
The paradoxes that one normally associates with closed time-like curves, as would pass through a wormhole, have a quantum counterpart: repeated passage of a virtual particle through a wormhole may lead to a divergence in the stress-energy tensor Tμν, as the loops of a spiral world line pile up to form a closed timelike curve. The derivation of this controversial result is as follows: for each passage of a virtual particle through the wormhole, the contribution to the two-point function
from a trajectory that contains that passage is attenuated by a factor b/D, where b is the wormhole width and D is the spatial length of a geodesic through the wormhole, as measured in the frame of an “observer” traveling along the geodesic from the vicinity of x and x′ through the wormhole once and back to the same vicinity. Here, x and x′ are nearby points in space-time, |Ψ > is the quantum state and
is the field operator associated with the field ϕ. The contribution to the two-point function is found to behave as (b/D)k × 1/σ, where σ is 1/2 the square of the proper distance between x and x′ along the geodesic connecting them through the wormhole, and the power k depends on the number of times that the trajectory traverses the wormhole (contributions from trajectories with k = 0 or 1, that traverse the wormhole only once, dominate). One finds σ ~ DΔt, where Δt is the proper time between x and the nearest null geodesic that passes through the wormhole. As x′ → x, the contribution diverges if x can be joined to itself by a null geodesic that passes through the wormhole. The stress-energy tensor can be expressed in terms of the two-point function [99] and also diverges as σ → 0 or Δt → 0. Specifically, one finds Tμν ~ (b/D)k × 1/D(Δt)3 in natural units, or in dimensional units,
Kim and Thorne [99] argued that the divergence, which is small because of the “diffraction” factor b/D, probably disappears in the proper quantum theory of gravity, allowing wormholes to remain. Quantization of the gravitational field in that theory would be effective on scales of LP, the Planck length, so we only need consider the magnitude of Tμν for Δt ≥ LP. At these scales, referring to (13), Tμν ≤ LP/D in natural units of
, giving energy densities that are far too weak to destroy the wormhole, or have other noticeable effects, for macroscopic D.
Hawking [100], in support of his “chronology protection conjecture”, provided a counter-argument asserting that quantum gravity effects would only enter on much smaller scales, corresponding to the Planck length in the rest-frame of an “observer” traveling on one of the geodesics through the wormhole. The values attained by Tμν on scales larger than Hawking’s reduced length scale would still cause collapse of the wormhole, the instant that recirculation becomes possible.
Let us assume that the predictions of standard quantum theory in curved spacetime survive in whatever deterministic theory underlies quantum mechanics. Here, we note that there is an additional mechanism that might cut off the recirculation divergence for wormholes of very narrow width. Virtual particles of arbitrarily high energy cannot traverse the wormhole. High-energy virtual particles would reverse the effect of the exotic matter or of the higher-derivative terms, so the existence of the wormhole would again be precluded by the weak energy condition. The contribution to the energy flux from the virtual particles is
, where n(ω) is the number density of quanta at frequency ω (as in the Weizsacker -Williams approximation [101], the quanta are assumed not to elongate in the wormhole). At detailed resolution in frequency-space, n(ω) = ∑i niδ(ω − ωi), where ωi is a discrete set of frequencies and {ni} is a set of positive integers. There is a problem from the weak energy condition if any ωi > ωcutoff (with ni ≥ 1), for ωcutoff sufficiently large as to cancel the negative-energy contributions to T00. In a path integral, taken both over particle trajectories and over geometries, one need only consider histories in which more energetic particles either collapse the wormhole or are reflected and do not traverse it. In contrast, for wormholes of macroscopic width, histories must be included in the path integral for which the energies of recirculating virtual quanta outside the wormhole are anomalously large (treating the geometry itself classically). The cutoff in the former case implies that the term 1/σ in the two-point function is replaced by a term like
, which does not diverge.
Thus, for sufficiently narrow wormholes, the original position of Kim and Thorne that that vacuum recirculation divergence is damped may be correct. The behavior discussed above is on the borderline between the non-traversability of Einstein–Rosen bridges, which mediate entanglement in ordinary quantum theory according to the recent proposal [86], and traversable wormhole behavior that could give rise to full nonlocality. Although finite wormhole lifetime would be required to mediate long-range synchronization, highly intermittent wormhole behavior may be enough, in accordance with previous findings [6] for other types of PDEs. Additionally, the collapse of a wormhole triggered by the entrance of a particle on one side would have measurable effects on the other side; perhaps the only effects of traversability in the underlying classical theory where virtual particles do not appear. In the absence of a detailed Planck-scale theory, the question of traversability remains open.
Acknowledgments
The author is grateful for discussions over the past decade with Joe Tribbia, Jeff Weiss, Alan Guth, Frank Hoppensteadt, Ljupco Kocarev, Tim Palmer, David Peat, and Mickael Chekroun. Michael Ghil and Anastasios Tsonis are thanked for their encouragement. Part of this work was supported under NSF Grants #0327929 and #0838235, DOE Grant #DE-SC0005238, and European Research Council Grant #266722.
Conflicts of Interest
The author declares no conflict of interest.
References
- Huygens, C. Horologium Oscilatorium; F. Muguet: Paris, France, 1673. [Google Scholar]
- Duane, G.S. Synchronized chaos in extended systems and meteorological teleconnections. Phys. Rev. E 1997, 56, 6475–6493. [Google Scholar]
- Duane, G.S.; Webster, P.J.; Weiss, J.B. Co-occurrence of Northern and Southern Hemisphere blocks as partially synchronized chaos. J. Atmos. Sci. 1999, 56, 4183–4205. [Google Scholar]
- Duane, G.S.; Tribbia, J.J. Synchronized chaos in geophysical fluid dynamics. Phys. Rev. Lett. 2001, 86, 4298–4301. [Google Scholar]
- Duane, G.S.; Tribbia, J.J. Weak Atlantic-Pacific teleconnections as synchronized chaos. J. Atmos. Sci. 2004, 61, 2149–2168. [Google Scholar]
- Kocarev, L.; Tasev, Z.; Parlitz, U. Synchronizing spatiotemporal chaos of partial differential equations. Phys. Rev. Lett. 1997, 79, 51–54. [Google Scholar]
- Peat, F.D. Synchronicity: The Bridge Between Matter and Mind; Bantam: New York, NY, USA, 1987. [Google Scholar]
- Jung, C.G.; Pauli, W. The Interpretation of Nature and the Psyche; Pantheon: New York, NY, USA, 1955. [Google Scholar]
- Strogatz, S.H. Sync: The Emerging Science of Spontaneous Order; Theia: New York, NY, USA, 2003. [Google Scholar]
- Atmanspacher, H.A. Dual-aspect monism á la Pauli and Jung. J. Conscious. Stud. 19, 96–120.
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Pecora, L.M.; Carrol, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar]
- Afraimovitch, V.S.; Verichev, N.N.; Rabinovich, M.I. Stochastic synchronization of oscillations in dissipative systems. Inv. VUZ Radiofiz. RPQAEC 1986, 29, 795–803. [Google Scholar]
- Fujisaka, H.; Yamada, T. Stability theory of synchronized motion in coupled-oscillator systems. Prog. Theor. Phys. 1983, 69, 32–47. [Google Scholar]
- Lorenz, E.N. Deterministic non-periodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar]
- Pecora, L.M.; Carroll, T.L.; Johnson, G.A.; Mar, D.J.; Heagy, J.F. Fundamentals of synchronization in chaotic systems, concepts, and applications. Chaos 1997, 7, 520–543. [Google Scholar]
- Mañé, R. On the dimension of the compact invariant sets of certain nonlinear maps. In Dynamical Systems and Turbulence, Warwick 1980; Lecture Notes in Mathematics, Volume 898; Springer: Berlin/Heidelberg, Germany, 1981; pp. 230–242. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Lecture Notes in Mathematics, Volume 898; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Ott, E.; Sommerer, J.C. Blowout bifurcations: The occurrence of riddled basins and on-off intermittency. Phys. Lett. A 1994, 188, 39–47. [Google Scholar]
- Rulkov, N.; Sushchik, M.; Tsimring, L.; Abarbanel, H. Generalized synchronization of chaos in directionally coupled chaotic systems. Phys. Rev. E 1995, 51, 980–994. [Google Scholar]
- So, P.; Barreto, E.; Josic, K.; Sander, E.; Schiff, S. Limits to the experimental detection of nonlinear synchrony. Phys. Rev. E 2002, 65, 046225. [Google Scholar]
- Roy, R.; Thornburg, K.S. Experimental synchronization of chaotic lasers. Phys. Rev. Lett. 1994, 72, 2009–2012. [Google Scholar]
- Peterman, D.W.; Ye, M.; Wigen, P.E. High frequency synchronization of chaos. Phys. Rev. Lett. 1995, 74, 1740–1742. [Google Scholar]
- Platt, N.; Spiegel, E.A.; Tresser, C. On-off intermittency—a mechanism for bursting. Phys. Rev. Lett. 1993, 70, 279–282. [Google Scholar]
- Tziperman, E.; Scher, H.; Zebiak, S.E.; Cane, M.A. Controlling spatiotemporal chaos in a realistic El Niǹo prediction model. Phys. Rev. Lett. 1997, 79, 1034–1037. [Google Scholar]
- Ghil, M.; Childress, S. Topics in Geophysical Fluid Dynamics: Atmospheric Dynamics, Dynamo Theory, and Climate Dynamics; Springer: New York, NY, USA, 1987. [Google Scholar]
- Ghil, M.; Zaliapin, I.; Thompson, S. A delay differential model of ENSO variability: Parametric instability and the distribution of extremes. Nonlinear Process. Geophys. 2008, 15, 417–433. [Google Scholar]
- Barahona, M.; Pecora, L.M. Synchronization in small-world systems. Phys. Rev. Lett. 2002, 89, 054101. [Google Scholar]
- Huang, L.; Park, K.; Lai, Y.-C.; Yang, L.; Yang, K.-Q. Abnormal synchronization in complex clustered networks. Phys. Rev. Lett. 2006, 97, 164101. [Google Scholar]
- Lago-Fernandez, L.F.; Huerta, R.; Corbacho, F.; Siguenza, J.A. Fast response and temporal coherent oscillations in small-world networks. Phys. Rev. Lett. 2000, 84, 2758–2761. [Google Scholar]
- Zhang, Z.; Zhou, S.; Zou, T. Self-similarity, small-world, scale-free scaling, disassortativity, and robustness in hierarchical lattices. Eur. Phys. J. 2007, 56, 259–271. [Google Scholar]
- Bengtsson, L.; Ghil, M.; Källén, E. (Eds.) Dynamic Meteorology: Data Assimilation Methods; Springer: New York, NY, USA and Heidelberg/Berlin, Germany, 1981.
- Ghil, M.; Malanotte-Rizzoli, P. Data assimilation in meteorology and oceanography. Adv. Geophys. 1991, 33, 141–266. [Google Scholar]
- Talagrand, O. Assimilation of observations, an introduction. J. Meteorol. Soc. Jpn. 1997, 75, 191–209. [Google Scholar]
- Duane, G.S.; Tribbia, J.J.; Weiss, J.B. Synchronicity in predictive modeling: A new view of data assimilation. Nonlinear Process. Geophys. 2006, 13, 601–612. [Google Scholar]
- Abarbanel, H.D.I.; Creveling, D.R.; Farsian, R.; Kostuk, M. On dynamical state and parameter estimation. SIAM J. Appl. Dyn. Syst. 2009, 8, 1341–1381. [Google Scholar]
- Yang, S.-C.; Baker, D.; Li, H.; Cordes, K.; Huff, M.; Nagpal, G.; Okereke, E.; Villafañe, J.; Kalnay, E.; Duane, G.S. Data assimilation as synchronization of truth and model: Experiments with the three-variable Lorenz system. J. Atmos. Sci. 2006, 63, 2340–2354. [Google Scholar]
- Vautard, R.; Legras, B.; Déqué, M. On the source of mid-latitude lowfrequency variability. Part I: A statistical approach to persistence. J. Atmos. Sci. 1988, 45, 2811–2843. [Google Scholar]
- Evensen, G. Data Assimilation: The Ensemble Kalman Filter; Springer: Berlin, Germany, 2007. [Google Scholar]
- Anderson, J.L. An ensemble adjustment Kalman filter for data assimilation. Mon. Weather Rev. 2001, 129, 2884–2903. [Google Scholar]
- Duane, G.S. Data assimilation as artificial perception and supermodeling as artificial consciousness. In Concensus and Synchronization in Complex Networks; Kocarev, L., Ed.; Springer: New York, NY, USA and Heidelberg/Berlin, Germany, 2012; pp. 209–226. [Google Scholar]
- Vitiello, G. My Double Unveiled: The Dissipative Quantum Model of Brain (Advances in Consciousness Research); John Benjamins Pub Co: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Gong, P.; Nikolaev, A.R.; Leeuwen, C.V. Intermittent dynamics underlying the intrinsic fluctuations of the collective synchronization patterns in electrocortical activity. Phys. Rev. E 2007, 76, 011904. [Google Scholar]
- Kezys, D.; Plikynas, D. Prognostication of human brain EEG signal dynamics using a refined coupled oscillator energy exchange model. NeuroQuantology 2014, 12, 337–349. [Google Scholar]
- Buzsáki, G. Rhythms of the Brain; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Doelling, K.B.; Arnal, L.H.; Ghitza, O.; Poeppel, D. Acoustic landmarks drive delta-theta oscillations to enable speech comprehension by facilitating perceptual parsing. NeuroImage 2014, 85, 761–768. [Google Scholar]
- Von der Malsburg, C.; Schneider, W. A neural coctail-party processor. Biol. Cybern. 1986, 54, 29–40. [Google Scholar]
- Terman, D.; Wang, D.L. Global competition and local cooperation in a network of neural oscillators. Physica D 1995, 81, 148–176. [Google Scholar]
- Wang, D.L.; Terman, D. Image segmentation based on oscillatory correlation. Neural Comput 1997, 9, 805–836. [Google Scholar]
- Duane, G.S. Synchronization of extended systems from internal coherence. Phys. Rev. E 2009, 80, 015202. [Google Scholar]
- Umbanhower, P.B.; Melo, F.; Swinney, H.L. Localized excitations in a vertically vibrated granular layer. Nature 1996, 382, 793–796. [Google Scholar]
- Pikovsky, A.S.; Rosenblum, M.G.; Osipov, G.V.; Kurths, J. Phase synchronization of choatic oscillators by external driving. Physica D 1997, 104, 219–238. [Google Scholar]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. Phase synchronization of chaotic oscillators. Phys. Rev. Lett. 1996, 76, 1804–1807. [Google Scholar]
- Gray, C.M.; Konig, P.; Engel, A.K.; Singer, W. Oscillatory responses in cat visual-cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature 1989, 338, 334–337. [Google Scholar]
- Schechter, B. How the brain gets rhythm. Science 1996, 274, 339–340. [Google Scholar]
- Koch, C.; Greenfield, S. How does consciousness happen? Sci. Am. 2007, 297, 76–83. [Google Scholar]
- Duane, G.S. A “cellular neuronal” approach to optimization problems. Chaos 2009, 19, 033114. [Google Scholar]
- Freeman, W.J. Chaos in the brain—possible roles in biological intelligence. Int. J. Intell. Syst. 1995, 10, 71–88. [Google Scholar]
- Rodriguez, E.; George, N.; Lachaux, J.P.; Martinerie, J.; Renault, B.; Varela, F.J. Perception’s shadow: Long-distance synchronization of human brain activity. Nature 1999, 397, 430–433. [Google Scholar]
- Mirchev, M.; Duane, G.S.; Tang, W.S.; Kocarev, L. Improved modeling by coupling imperfect models. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2471–2751. [Google Scholar]
- Van den Berge, L.A; Selten, F.M.; Wiegerinck, W.; Duane, G.S. A multi-model ensemble method that combines imperfect models through learning. Earth Syst. Dyn. Discuss. 2010, 1, 247–296. [Google Scholar]
- Duane, G.S.; Yu, D.-C.; Kocarev, L. Identical synchronization, with translation invariance, implies parameter estimation. Phys. Lett. A 2007, 371, 416–420. [Google Scholar]
- Tebaldi, C.; Knutti, R. The use of the multi-model ensemble in probabilistic climate projection. Philos. Trans. R. Soc. A 2007, 365, 2053–2075. [Google Scholar]
- Duane, G.S.; Tribbia, J.; Kirtman, B. Consensus on long-range prediction by adaptive synchronization of models, Presented at EGU General Assembly, Vienna, Austria, 19–24 April 2009; p. 13324.
- Plikynas, D.; Masteika, S.; Basinskas, G.; Kezys, D.; Kumar, P.; Laukaitis, A. Social systems in terms of coherent individual neurodynamics: Conceptual premises and experimental scope. Int. J. General Syst. 2014, 43, 434–469. [Google Scholar]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Springer: New York, NY, USA, 1984. [Google Scholar]
- Von Meyenne, K. (Ed.) Wolfgang Pauli. Wissenschaftlicher Briefwechsel mit Bohr, Einstein, Heisenberg, u.a, Band II: 1930–1939; Springer: Berlin, Germany, 1985; pp. 340–341.
- Kahana, M.J. The cognitive correlates of human brain oscillations. J. Neurosci 2006, 26, 1669–1672. [Google Scholar]
- Ashwin, P.; Buescu, J.; Stewart, I. Bubbling of attractors and synchronization of chaotic oscillators. Phys. Lett. A 1994, 193, 126–139. [Google Scholar]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar]
- ’t Hooft, G. The cellular automaton interpretation of quantum mechanics: A view on the quantum nature of our universe, compulsory or impossible? 2014, arXiv, 1405.1548.
- Palmer, T.N. The Invariant Set Postulate: A new geometric framework for the foundations of quantum theory and the role played by gravity. Proc. R. Soc. Lond. A 2009, 465, 3165–3185. [Google Scholar]
- Duane, G.S. Violation of Bell’s inequality in synchronized hyperchaos. Found. Phys. Lett. 2001, 14, 341–353. [Google Scholar]
- Bohm, D. A suggested interpretation of the quantum theory in terms of “hidden” variables, I and II. Phys. Rev. 1952, 85, 166–193. [Google Scholar]
- Bohm, D.; Hiley, B.J. The Undivided Universe; Routledge: London, UK, 1992. [Google Scholar]
- Von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin, Germany, 1932. [Google Scholar]
- ’t Hooft, G. Quantum gravity as a dissipative deterministic system. Class. Quant. Grav. 1999, 16, 3263–3279. [Google Scholar]
- ’t Hooft, G. Entangled quantum states in a local deterministic theory 2009, arXiv, 0908.3408.
- Bohm, D. A new theory of the relationship of mind and matter. Philos. Psychol. 1990, 3, 271–286. [Google Scholar]
- Duane, G.S. Quantum nonlocality from synchronized chaos. Int. J. Theor. Phys. 2005, 44, 1917–1932. [Google Scholar]
- Palmer, T.N. A granular permutation-based representation of complex numbers and quaternions: Elements of a possible realistic quantum theory. Proc. R. Soc. Lond. A 2004, 460, 1039–1055. [Google Scholar]
- Hawking, S.W. Spacetime foam. Nucl. Phys. B 1978, 144, 349–362. [Google Scholar]
- Bombelli, L.; Lee, J.; Meyer, D.; Sorkin, R.D. Space-time as a causal set. Phys. Rev. Lett. 1987, 59, 521–524. [Google Scholar]
- Amelino-Camelia, G.; Piran, T. Planck-scale deformation of Lorentz symmetry as a solution to the ultrahigh energy cosmic ray and the Tev-photon paradoxes. Phys. Rev. D 2001, 64, 036005. [Google Scholar]
- Wheeler, J.A. Geometrodynamics; Academic Press: New York, NY, USA, 1962. [Google Scholar]
- Maldacena, J.; Susskind, L. Cool horizons for entangled black holes. Fortschr. Phys. 2013, 61, 781–811. [Google Scholar]
- Susskind, L. The world as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar]
- ’t Hooft, G. Dimensional reduction in quantum gravity 1993, arXiv, gr-qc/9310026.
- Peat, F.D. Infinite Potential: The Life and Times of David Bohm; Addison-Wesley: Reading, MA, USA, 1996. [Google Scholar]
- Yourgrau, P. A World Without Time: The Forgotten Legacy of Gödel and Einstein; Allen Lane: London, UK, 2005. [Google Scholar]
- Penrose, R. The Emperor’s New Mind; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Palmer, T.N. A local deterministic model of quantum spin measurement. Proc. R. Soc. Lond. A 1995, 451, 585–608. [Google Scholar]
- Hameroff, S.; Penrose, R. Consciousness in the universe A review of the “Orch OR” theory. Phys. Life Rev. 2014, 11, 39–78. [Google Scholar]
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar]
- Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes, time machines, and the weak energy condition. Phys. Rev. Lett. 1988, 61, 1446–1449. [Google Scholar]
- Candelas, P. Vacuum polarization in Schwarzschild spacetime. Phys. Rev. D 1980, 21, 2185–2202. [Google Scholar]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Stelle, K.S. Renormalization of higher-derivative quantum gravity. Phys. Rev. D 1977, 16, 953–969. [Google Scholar]
- Kim, S.-W.; Thorne, K.S. Do vacuum fluctuations prevent the creation of closed timelike curves? Phys. Rev. D 1991, 43, 3929–3947. [Google Scholar]
- Hawking, S.W. The chronology protection conjecture. Phys. Rev. D 1992, 46, 603–611. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; Wiley: New York, NY, USA, 1962. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).