Weakest-Link Scaling and Extreme Events in Finite-Sized Systems
Abstract
:1. Introduction
1.1. Mathematical Preliminaries
- In the case of fracture strength, Rℓ(x) is the probability that the system has not failed if the external load takes values that do not exceed x.
- In the case of earthquake return times, the survival function is the probability that there are no successive earthquakes separated by a time interval less than or equal to x.
- In the case of annual rainfall maxima, Rℓ(x) gives the probability that the maximum rainfall over the support area for the duration of one year does not exceed the value x.
2. Weakest-Link Scaling Theory
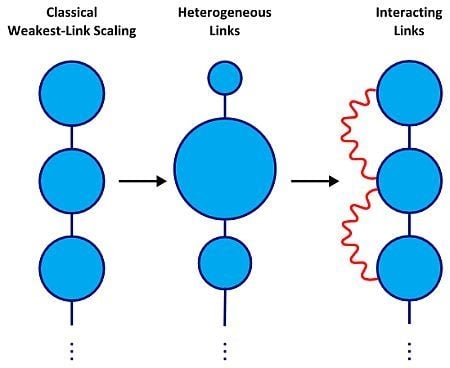
2.1. Systems Composed of Interacting Links
2.2. Hazard Function for Links with Variable Parameters
2.3. Observed Distributions for Non-ergodic Conditions
3. Exponential and Non-Exponential Link Survival Functions
3.1. Weibull Link Ansatz
3.2. Non-Exponential Link Ansatz
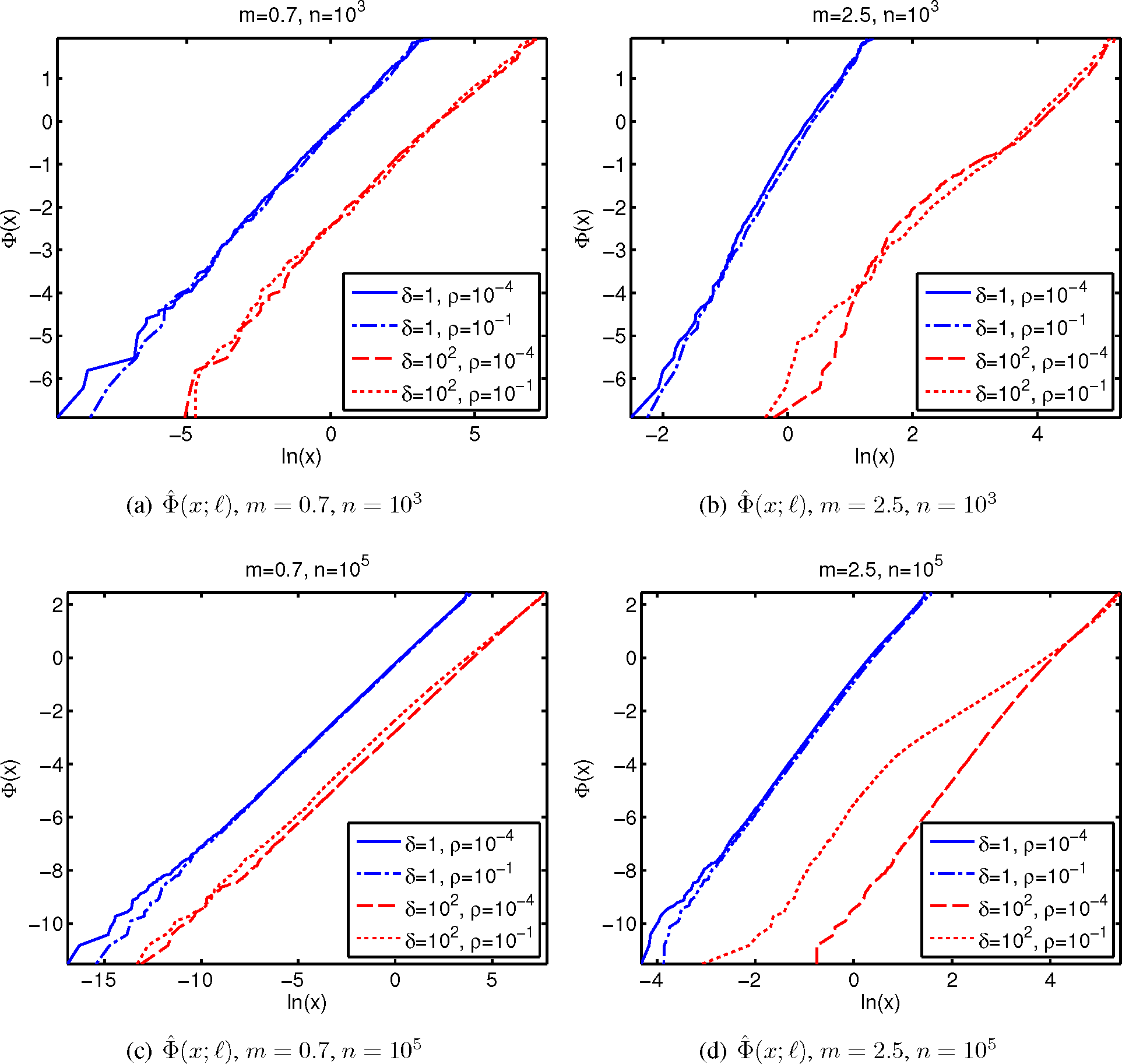
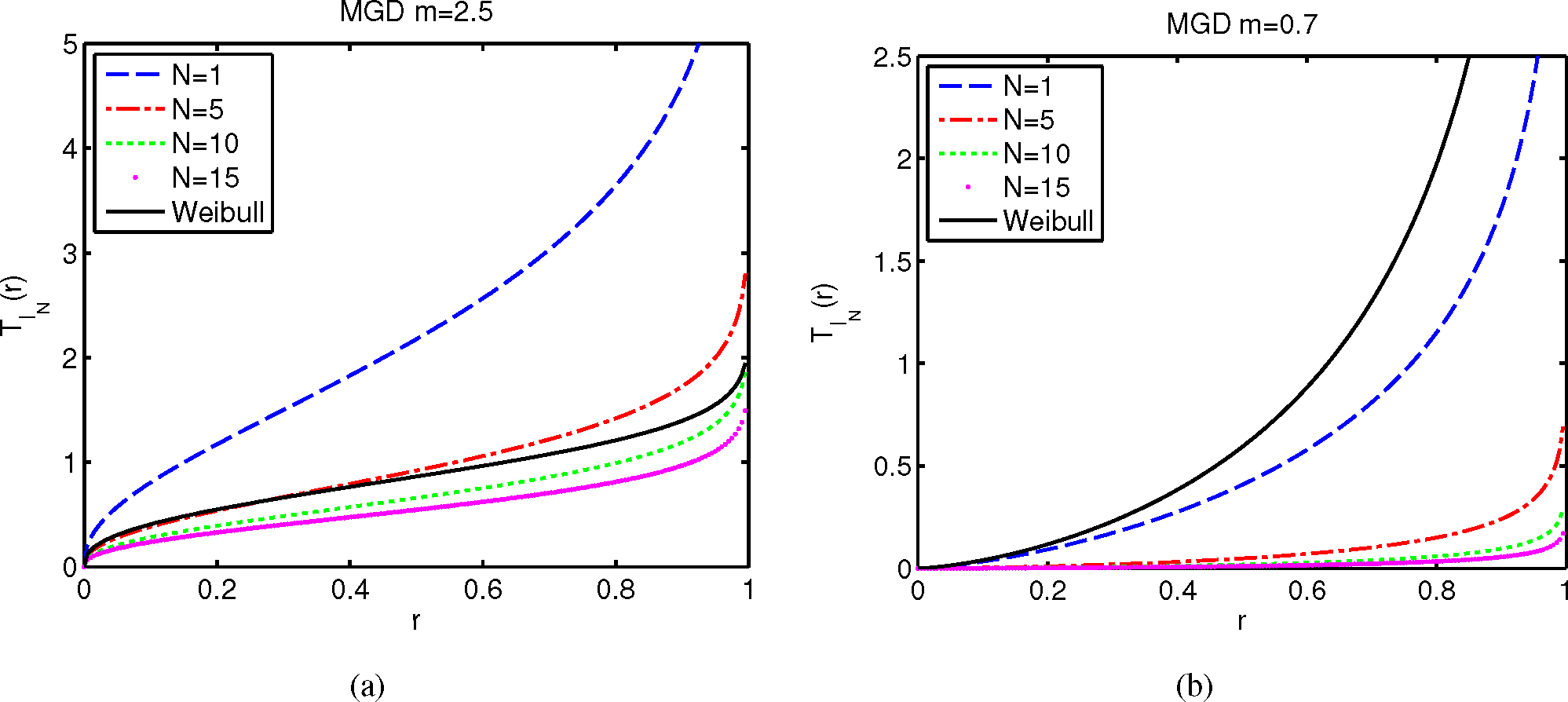
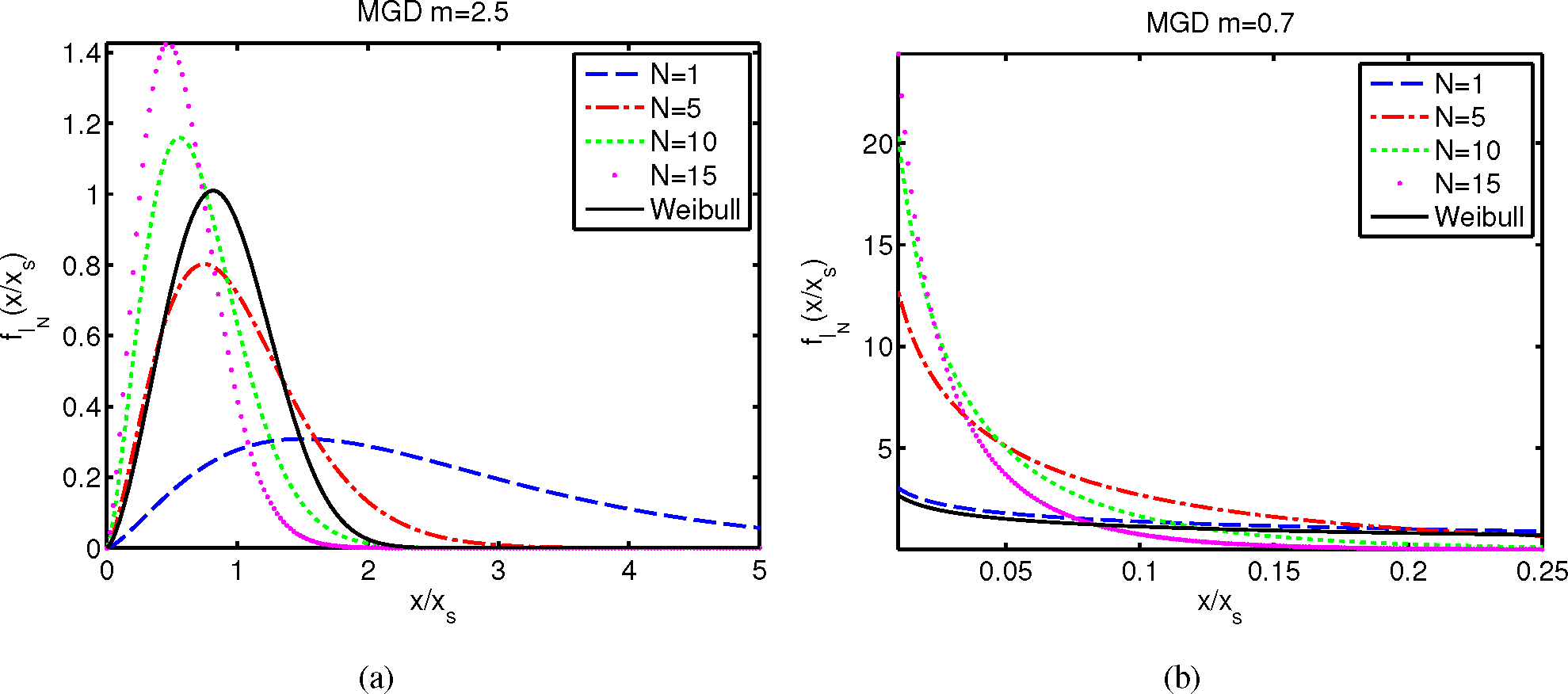
4. Finite-Size System with Gamma Link Distribution
4.1. The Gamma Distribution
4.2. The Modified Gamma Distribution
4.3. Motivation and Properties
5. Finite-Sized System with κ-Weibull Distribution
5.1. The κ-exponential and κ-logarithm Functions
5.2. The κ-Weibull Function
5.3. Motivation and Properties
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Sornette, D. Critical Phenomena in Natural Sciences; Springer: Berlin, Germany, 2004. [Google Scholar]
- Gumbel, E.J. Les valeurs extrêmes des distributions statistiques. Annales de l’Institut Henri Poincaré 1935, 5, 115–158. [Google Scholar]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar]
- Eliazar, I.; Klafter, J. Randomized central limit theorems: A unified theory. Phys. Rev. E 2010, 82, 021122. [Google Scholar]
- Barlow, R.E.; Proschan, F. Mathmatical Theory of Reliability; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Hristopulos, D.T.; Uesaka, T. Structural disorder effects on the tensile strength distribution of heterogeneous brittle materials with emphasis on fiber networks. Phys. Rev. B 2004, 70, 064108. [Google Scholar]
- Pang, S.D.; Bažant, Z.; Le, J.L. Statistics of strength of ceramics: Finite weakest-link model and necessity of zero threshold. Int. J. Fract. 2008, 154, 131–145. [Google Scholar]
- Amaral, P.M.; Fernandes, J.C.; Rosa, L.G. Weibull statistical analysis of granite bending strength. Rock Mech. Rock Eng. 2008, 41, 917–928. [Google Scholar]
- Hagiwara, Y. Probability of earthquake occurrence as obtained from a Weibull distribution analysis of crustal strain. Tectonophysics 1974, 23, 313–318. [Google Scholar]
- Rikitake, T. Recurrence of great earthquakes at subduction zones. Tectonophysics 1976, 35, 335–362. [Google Scholar]
- Rikitake, T. Assessment of earthquake hazard in the Tokyo area, Japan. Tectonophysics 1991, 199, 121–131. [Google Scholar]
- Holliday, J.R.; Rundle, J.B.; Turcotte, D.L.; Klein, W.; Tiampo, K.F.; Donnellan, A. Space-Time Clustering and Correlations of Major Earthquakes. Phys. Rev. Lett. 2006, 97, 238501. [Google Scholar]
- Abaimov, S.G.; Turcotte, D.L.; Rundle, J.B. Recurrence-time and frequency-slip statistics of slip events on the creeping section of the San Andreas fault in central California. Geophys. J. Int. 2007, 170, 1289–1299. [Google Scholar]
- Abaimov, S.G.; Turcotte, D.; Shcherbakov, R.; Rundle, J.B.; Yakovlev, G.; Goltz, C.; Newman, W.I. Earthquakes: Recurrence and Interoccurrence Times. Pure Appl. Geophys. 2008, 165, 777–795. [Google Scholar]
- Hristopulos, D.T.; Mouslopoulou, V. Strength statistics and the distribution of earthquake interevent times. Physica A 2013, 392, 485–496. [Google Scholar]
- Conradsen, K.; Nielsen, L.; Prahm, L. Review of Weibull statistics for estimation of wind speed distributions. J. Clim. Appl. Meteorol. 1984, 23, 1173–1183. [Google Scholar]
- Van den Brink, H.; Können, G. The statistical distribution of meteorological outliers. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E. Superstatistics. Physica A 2003, 322, 267–275. [Google Scholar]
- Sornette, D.; Knopoff, L. The paradox of the expected time until the next earthquake. Bull. Seismol. Soc. Am. 1997, 87, 789–798. [Google Scholar]
- Chakrabarti, B.K.; Benguigui, L.G. Statistical Physics of Fracture and Breakdown in Disordered Systems; Clarendon Press: Oxford, UK, 1997. [Google Scholar]
- Curtin, W.A. Size Scaling of Strength in Heterogeneous Materials. Phys. Rev. Lett. 1998, 80, 1445–1448. [Google Scholar]
- Alava, M.J.; Phani, K.V.V.N.; Zapperi, S. Statistical models of fracture. Adv. Phys. 2006, 55, 349–476. [Google Scholar]
- Alava, M.J.; Phani, K.V.V.N.; Zapperi, S. Size effects in statistical fracture. J. Phys. D 2009, 42, 214012. [Google Scholar]
- Ditlevsen, O.D.; Madsen, H.O. Structural Reliability Methods; Wiley: Chichester, UK and New York, NY, USA, 1996. [Google Scholar]
- Mouslopoulou, V.; Hristopulos, D.T. Patterns of tectonic fault interactions captured through geostatistical analysis of microearthquakes. J. Geophys. Res. Solid Earth. 2011, 116. [Google Scholar] [CrossRef]
- Cohen, E. Superstatistics. Physica D 2004, 193, 35–52. [Google Scholar]
- Hristopulos, D.T.; Petrakis, M.; Kaniadakis, G. Finite-size Effects on Return Interval Distributions for Weakest-link-scaling Systems. Phys. Rev. E 2014, 89, 052142. [Google Scholar]
- Bažant, Z.P.; Le, J.L.; Bažant, M.Z. Scaling of strength and lifetime probability distributions of quasi-brittle structures based on atomistic fracture mechanics. Proc. Natl. Acad. Sci. USA. 2009, 1061, 11484–11489. [Google Scholar]
- Daniels, H.E. The statistical theory of the strength of bundles of threads. Proc. R. Soc. A 1945, 183, 405–435. [Google Scholar]
- Smith, R.L.; Phoenix, S.L. Asymptotic distributions for the failure of fibrous materials under series-parallel structure and equal load sharing. J. Appl. Mech. 1981, 48, 75–82. [Google Scholar]
- Kaniadakis, G. Statistical mechanics in the context of special relativity II. Phys. Rev. E 2005, 72, 036108. [Google Scholar]
- Clementi, F.; Di Matteo, T.; Gallegati, M.; Kaniadakis, G. The κ-generalized distribution: A new descriptive model for the size distribution of incomes. Physica 2008, 387, 3201–3208. [Google Scholar]
- Kaniadakis, G. Maximum Entropy Principle and power-law tailed distributions. Eur. Phys. J. B 2009, 70, 3–13. [Google Scholar]
- Clementi, F.; Gallegati, M.; Kaniadakis, G. A κ-generalized statistical mechanics approach to income analysis, 2009; arXiv:0902.0075.
- Kaniadakis, G. Theoretical Foundations and Mathematical Formalism of the Power-Law Tailed Statistical Distributions. Entropy 2013, 15, 3983–4010. [Google Scholar]
- Bažant, Z.P.; Pang, S.D. Activation energy based extreme value statistics and size effect in brittle and quasi-brittle fracture. J. Mech. Phys. Solids. 2007, 55, 91–131. [Google Scholar]
- Tsubo, Y.; Isomura, Y.; Fukai, T. Power-Law Inter-Spike Interval Distributions Infer a Conditional Maximization of Entropy in Cortical Neurons. PLoS Comput. Biol. 2012, 8, e1002461. [Google Scholar]
- Manzato, C.; Shekhawat, A.; Nukala, P.K.V.V.; Alava, M.J.; Sethna, J.P.; Zapperi, S. Fracture Strength of Disordered Media: Universality, Interactions, and Tail Asymptotics. Phys. Rev. Lett. 2012, 108, 065504. [Google Scholar]

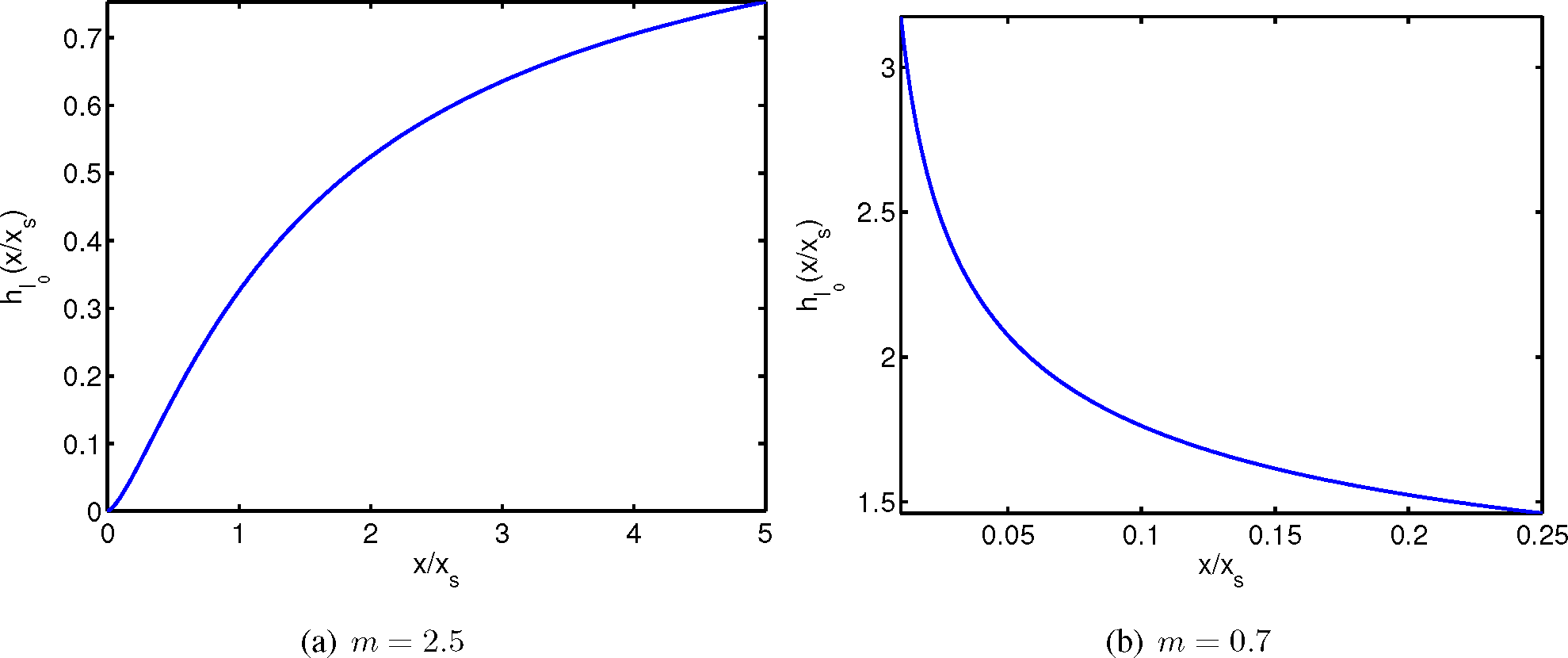
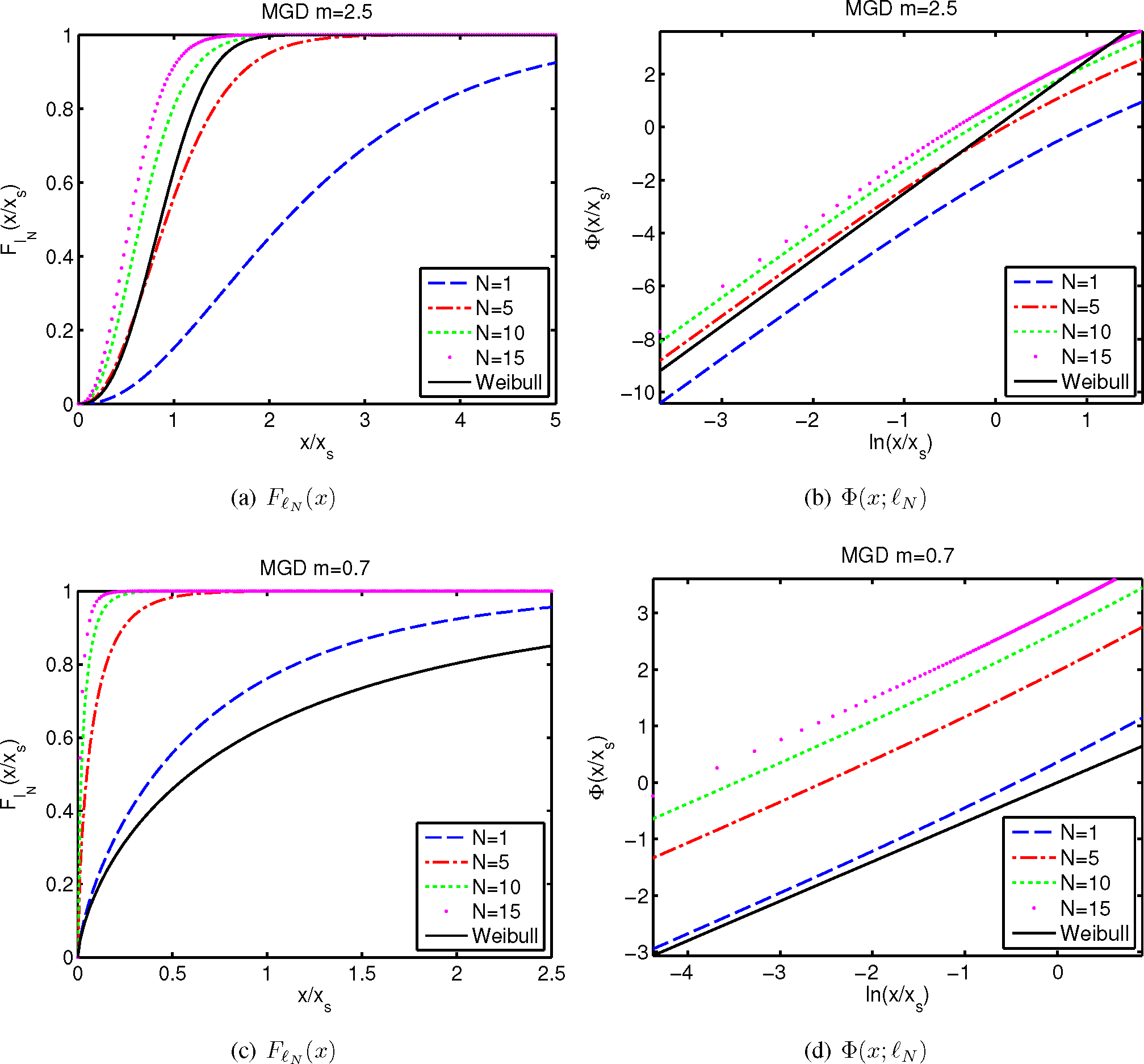

| m = 0.7 | m = 2.5 | |||||
|---|---|---|---|---|---|---|
| N | δ | ρ | ||||
| 103 | 1 | 10−4 | 1.39 | 0.688 | 1.42 | 2.14 |
| 10−1 | 1.55 | 0.694 | 1.54 | 2.25 | ||
| 100 | 10−4 | 45.6 | 0.592 | 51.8 | 1.23 | |
| 10−1 | 43.6 | 0.634 | 49.6 | 1.38 | ||
| 105 | 1 | 10−4 | 1.40 | 0.689 | 1.42 | 2.19 |
| 10−1 | 1.50 | 0.691 | 1.52 | 2.23 | ||
| 100 | 10−4 | 57.0 | 0.679 | 59.3 | 1.94 | |
| 10−1 | 42.9 | 0.611 | 48.4 | 1.30 | ||
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hristopulos, D.T.; Petrakis, M.P.; Kaniadakis, G. Weakest-Link Scaling and Extreme Events in Finite-Sized Systems. Entropy 2015, 17, 1103-1122. https://doi.org/10.3390/e17031103
Hristopulos DT, Petrakis MP, Kaniadakis G. Weakest-Link Scaling and Extreme Events in Finite-Sized Systems. Entropy. 2015; 17(3):1103-1122. https://doi.org/10.3390/e17031103
Chicago/Turabian StyleHristopulos, Dionissios T., Manolis P. Petrakis, and Giorgio Kaniadakis. 2015. "Weakest-Link Scaling and Extreme Events in Finite-Sized Systems" Entropy 17, no. 3: 1103-1122. https://doi.org/10.3390/e17031103
APA StyleHristopulos, D. T., Petrakis, M. P., & Kaniadakis, G. (2015). Weakest-Link Scaling and Extreme Events in Finite-Sized Systems. Entropy, 17(3), 1103-1122. https://doi.org/10.3390/e17031103