Projective Synchronization for a Class of Fractional-Order Chaotic Systems with Fractional-Order in the (1, 2) Interval
Abstract
:1. Introduction
2. Problem Statement and Main Result
- , for any x(t),
- , .
3. Illustrative Example
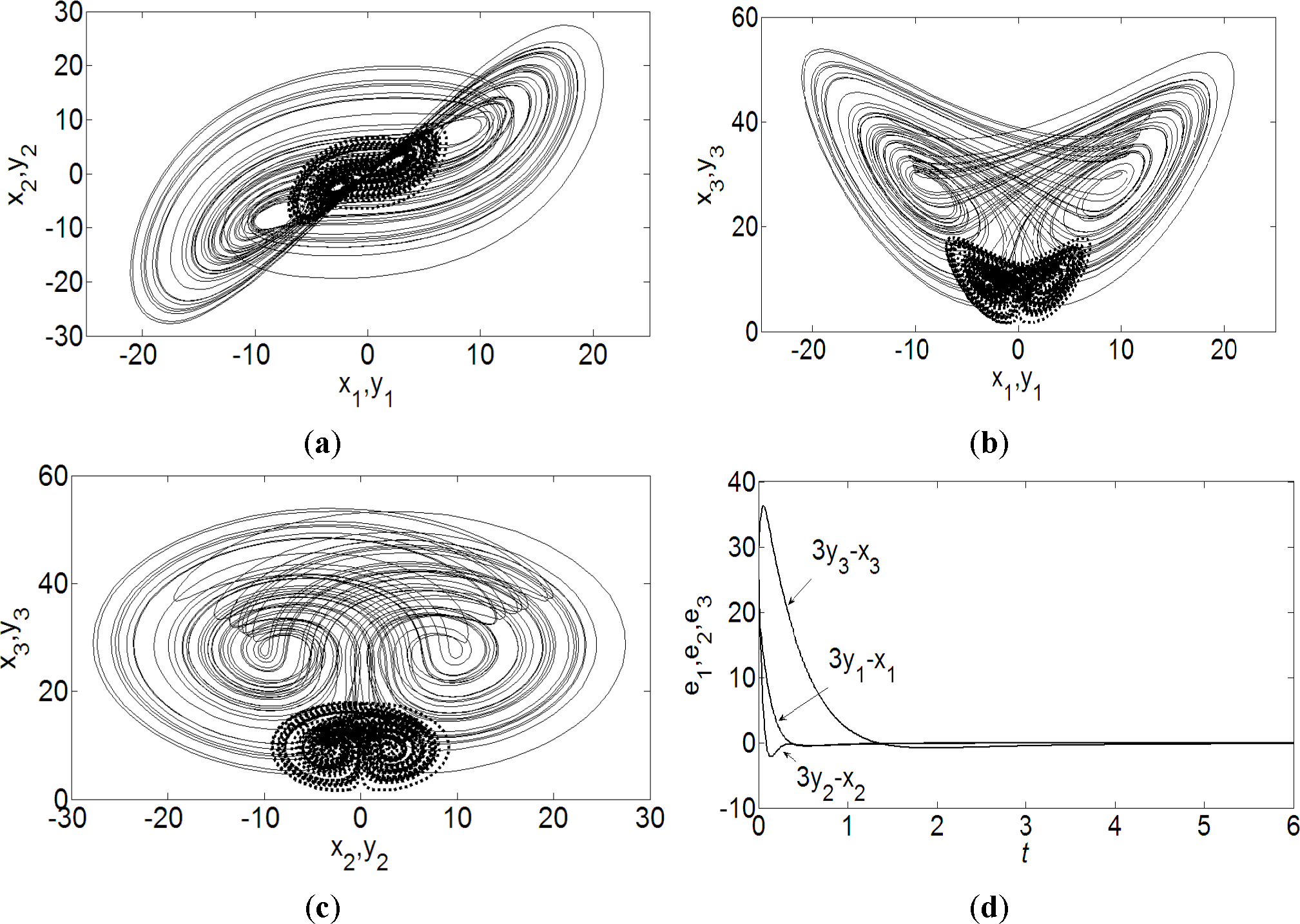
3.1. Projective Synchronization of Fractional-Order Lorenz Chaotic System with 1<q <2
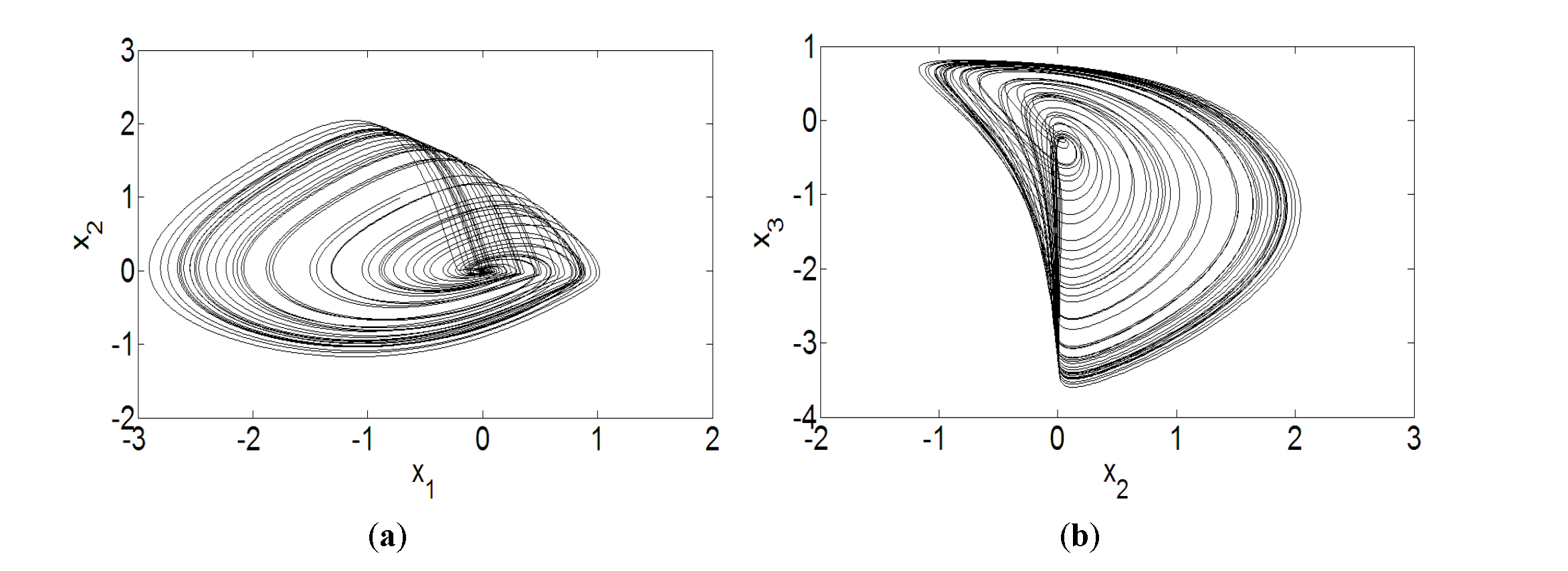
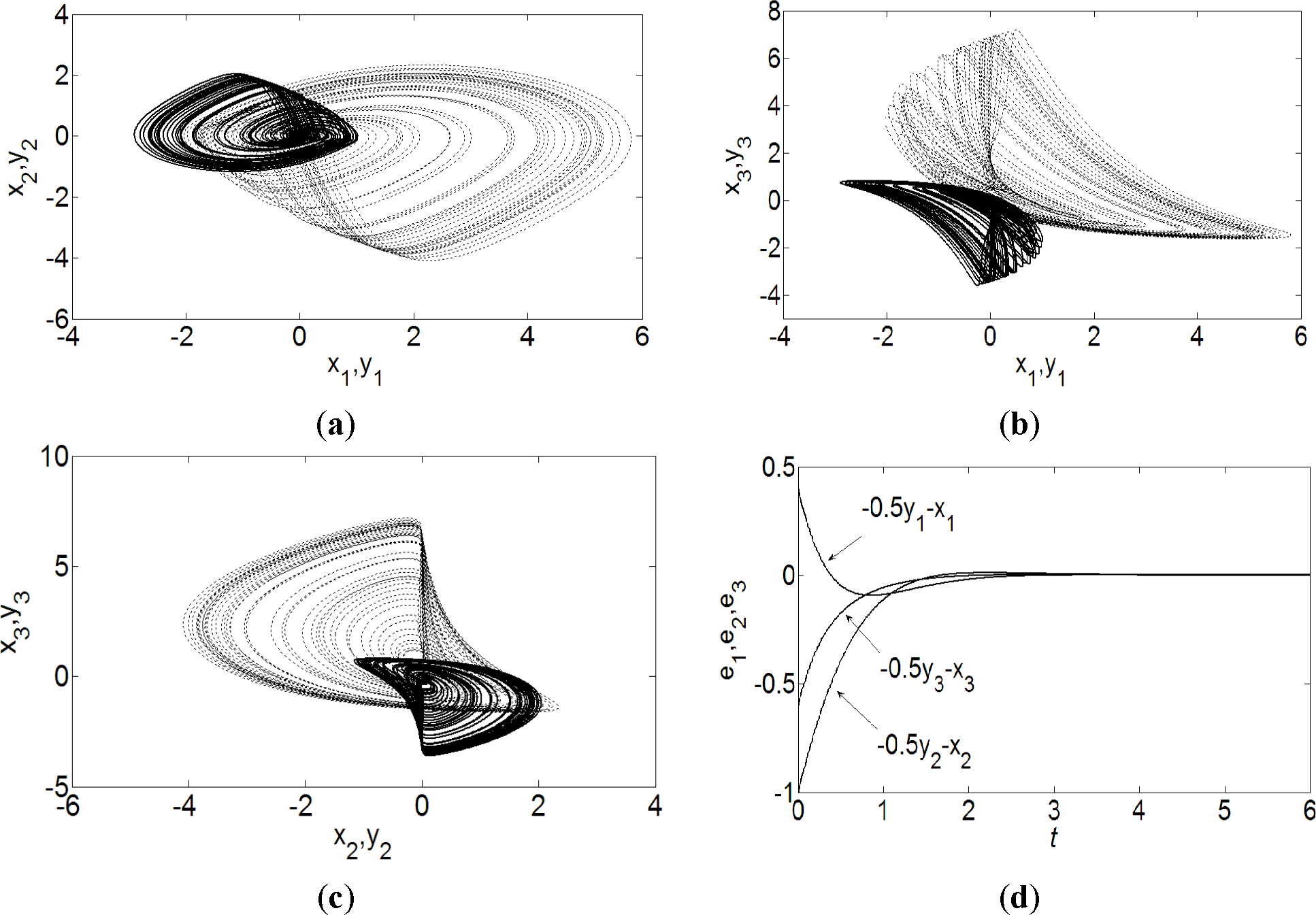
3.2. Projective Synchronization of Fractional-Order Modified Chua’s Chaotic System with 1<q<2
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Chen, L.P.; He, Y.G.; Chai, Y.; Wu, R.C. New results on stability and stabilization of a class of nonlinear fractional-order systems. Nonlinear Dyn. 2014, 75, 633–641. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, Singapore, 2000. [Google Scholar]
- Naber, M. Time fractional Schrodinger equation. J. Math. Phys. 2004, 45, 3339–3352. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, 1999. [Google Scholar]
- Grigorenko, I.; Grigorenko, E. Chaotic dynamics of the fractional Lorenz system. Phys. Rev. Lett. 2003, 91, 034101–034104. [Google Scholar]
- Zhou, P.; Ding, R.; Cao, Y.X. Multi drive-one response synchronization of fractional-order chaotic systems. Nonlinear Dyn. 2012, 67, 1263–1271. [Google Scholar]
- Xiao, M.; Zheng, W.X.; Cao, J.D. Approximate expressions of a fractional order Van der Pol oscillator by the residue harmonic balance method. Math. Comput. Simul. 2013, 89, 1–12. [Google Scholar]
- Zhou, P.; Yang, F.Y. Hyperchaos, chaos, and horseshoe in a 4D nonlinear system with an infinite number of equilibrium points. Nonlinear Dyn. 2014, 76, 473–480. [Google Scholar]
- Liu, J. Complex modified hybrid projective synchronization of different dimensional fractional-order complex chaos and real hyper-chaos. Entropy 2014, 16, 6195–6211. [Google Scholar]
- Xi, H.L.; Li, Y.X.; Huang, X. Generation and nonlinear dynamical analyses of fractional-order memristor-based Lorenz Systems. Entropy 2014, 16, 6240–6253. [Google Scholar]
- Chen, G.R.; Dong, X. From Chaos to Order Perspectives, Methodologies and Applications; World Scientific: Singapore, Singapore, 1998. [Google Scholar]
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Mainieri, R.; Rehacek, J. Projective synchronization in three-dimensional chaotic systems. Phys. Rev. Lett. 1999, 82, 3042–3045. [Google Scholar]
- Zhou, P.; Zhu, W. Function projective synchronization for fractional-order chaotic systems. Nonlinear Anal. RWA. 2011, 12, 811–816. [Google Scholar]
- Wang, X.Y.; Song, J.M. Synchronization of the fractional order hyperchaos Lorenz systems with activation feedback control. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3351–3357. [Google Scholar]
- Zhang, R.X.; Yang, S.P. Adaptive synchronization of fractional-order chaotic systems via a single driving variable. Nonlinear Dyn. 2011, 66, 831–837. [Google Scholar]
- Zhang, W.; Cai, X.; Holm, S. Time-fractional heat equations and negative absolute temperatures. Comput. Math. Appl. 2014, 67, 164–171. [Google Scholar]
- Beghin, L.; Orsingher, E. The telegraph process stopped at stable-distributed times and its connection with the fractional telegraph equation. Fract. Calc. Appl. Anal. 2003, 6, 187–204. [Google Scholar]
- Gafiychuk, V.; Datsko, B. Mathematical modeling of different types of instabilities in time fractional reaction-diffusion systems. Comput. Math. Appl. 2010, 59, 1101–1107. [Google Scholar]
- Mainardi, F. The fundamental solutions for the fractional diffusion-wave equation. Appl. Math. Lett. 1996, 9, 23–28. [Google Scholar]
- Gorenflo, R.; Mainardi, F.; Moretti, D.; Pagnini, G.; Paradisi, P. Fractional diffusion: Probability distributions and random walk models. Physica A 2002, 305, 106–112. [Google Scholar]
- Li, C.P.; Zhao, Z.G.; Chen, Y.Q. Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion. Comput. Math. Appl. 2011, 62, 855–875. [Google Scholar]
- Ge, Z.M.; Jhuang, W.R. Chaos, control and synchronization of fractional order rotational mechanical system with a centrifugal governor. Chaos Solitons Fractals. 2007, 33, 270–289. [Google Scholar]
- Muthuswamy, B.; Chua, L.O. One simplest chaotic circuit. Int. J. Bifurc. Chaos. 2010, 20, 1567–8150. [Google Scholar]
- De la Sen, M. About robust stability of Caputo linear fractional dynamics systems with time delays through fixed theory. Fixed Point Theory A 2011. [Google Scholar] [CrossRef]
- Ye, H.; Gao, J.; Ding, Y. A generalized Gronwall inequality and its application to a fractional equation. J. Math. Anal. Appl. 2007, 328, 1075–1081. [Google Scholar]
- Tang, J.N.; Huang, C.T. Impulsive control and synchronization analysis of complex dynamical networks with non-delayed and delayed coupling. Int. J. Innov. Comput. Inf. Control. 2013, 9, 4555–4564. [Google Scholar]
- Smaoui, N.; Karouma, A.; Zribi, M. Adaptive synchronization of hyperchaotic Chen systems with spplication to secure sommunication. Int. J. Innov. Comput. Inf. Control. 2013, 9, 1127–1144. [Google Scholar]
- Li, F.; Shi, P.; Wu, L.; Zhang, X. Fuzzy-model-based D-stability and non-fragile control for discrete-time descriptor systems with multiple delays. IEEE Trans. Fuzzy Syst. 2014, 22, 1019–1025. [Google Scholar]
- Chua, L.O. Memristor—the missing circuit element. IEEE Trans. Circuit Theory. 1971, 18, 507–519. [Google Scholar]

© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, P.; Bai, R.; Zheng, J. Projective Synchronization for a Class of Fractional-Order Chaotic Systems with Fractional-Order in the (1, 2) Interval. Entropy 2015, 17, 1123-1134. https://doi.org/10.3390/e17031123
Zhou P, Bai R, Zheng J. Projective Synchronization for a Class of Fractional-Order Chaotic Systems with Fractional-Order in the (1, 2) Interval. Entropy. 2015; 17(3):1123-1134. https://doi.org/10.3390/e17031123
Chicago/Turabian StyleZhou, Ping, Rongji Bai, and Jiming Zheng. 2015. "Projective Synchronization for a Class of Fractional-Order Chaotic Systems with Fractional-Order in the (1, 2) Interval" Entropy 17, no. 3: 1123-1134. https://doi.org/10.3390/e17031123
APA StyleZhou, P., Bai, R., & Zheng, J. (2015). Projective Synchronization for a Class of Fractional-Order Chaotic Systems with Fractional-Order in the (1, 2) Interval. Entropy, 17(3), 1123-1134. https://doi.org/10.3390/e17031123




