Analysis of Neural Oscillations on Drosophila’s Subesophageal Ganglion Based on Approximate Entropy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Object
2.2. Data Collection
2.3. Data Processing
2.4. The ApEn Extraction Algorithm
- (1)
- The sequence {u(i)} composes the m-dimensional vector X(i):X(i) = [u(i), u(i + 1) … u(i + m − 1)], i = 1, 2, ..., N − m + 1
- (2)
- For every i value, the distance between vector X(i) and another vector X(j) is calculated:d[X(i),X(j)] = max|u(i + k) − u(j + k)|, k = 0, 1, …, m − 1
- (3)
- Given the threshold value ( > 0), for each i value, statistical number of d [X (i), X (j)] < r is calculated .And the ratio of number to total N − m + 1 is called :
- (4)
- logarithm is obtained and the average i value is calculated, denoted as , namely:
- (5)
- For m + 1, repeat from step 1 to step 4 and get ;
- (6)
- Finally, the results are as follows:
2.5. Evaluation of ApEn
2.6. Clustering Analysis
3. Results
3.1. Statistical Indicators of Oscillation
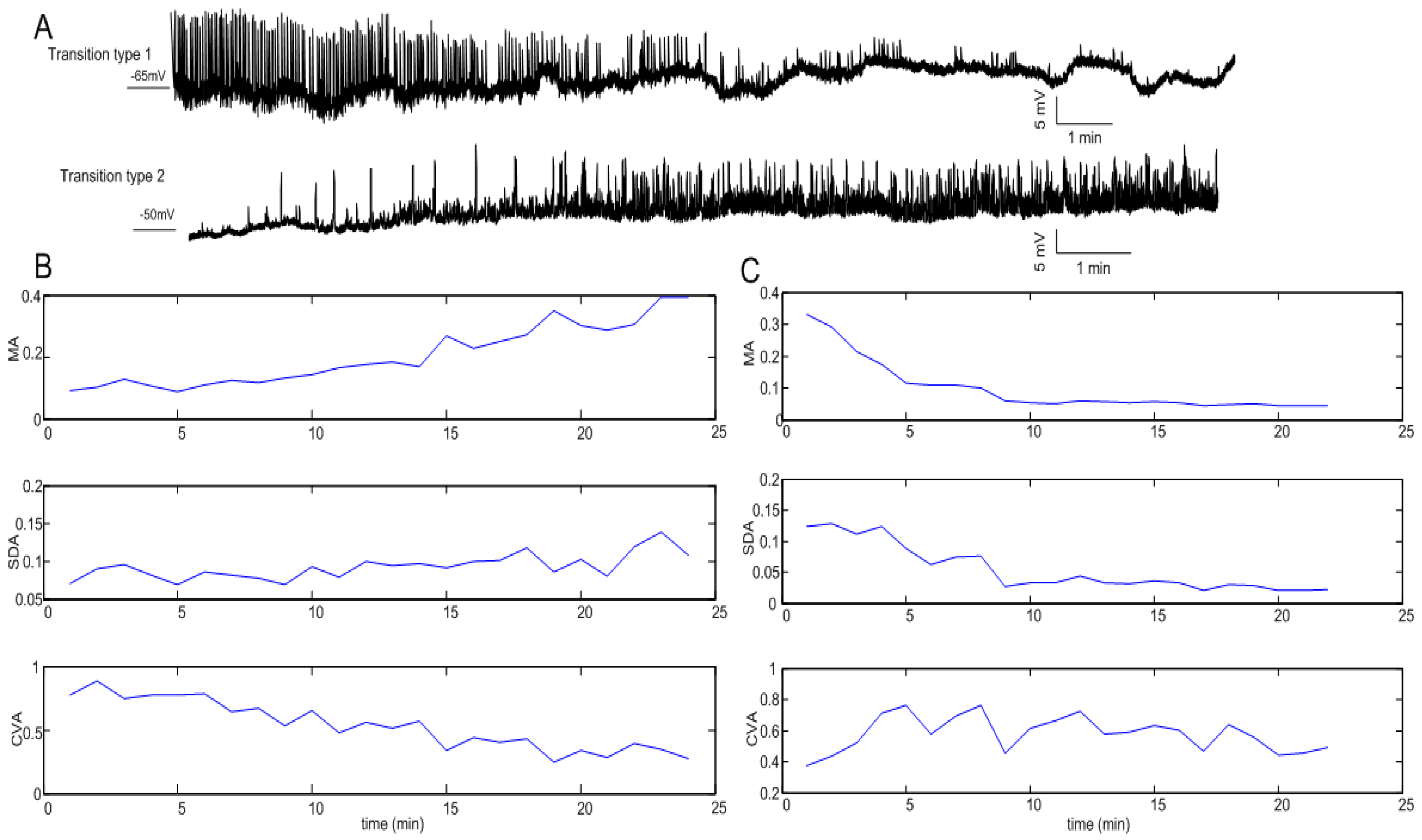
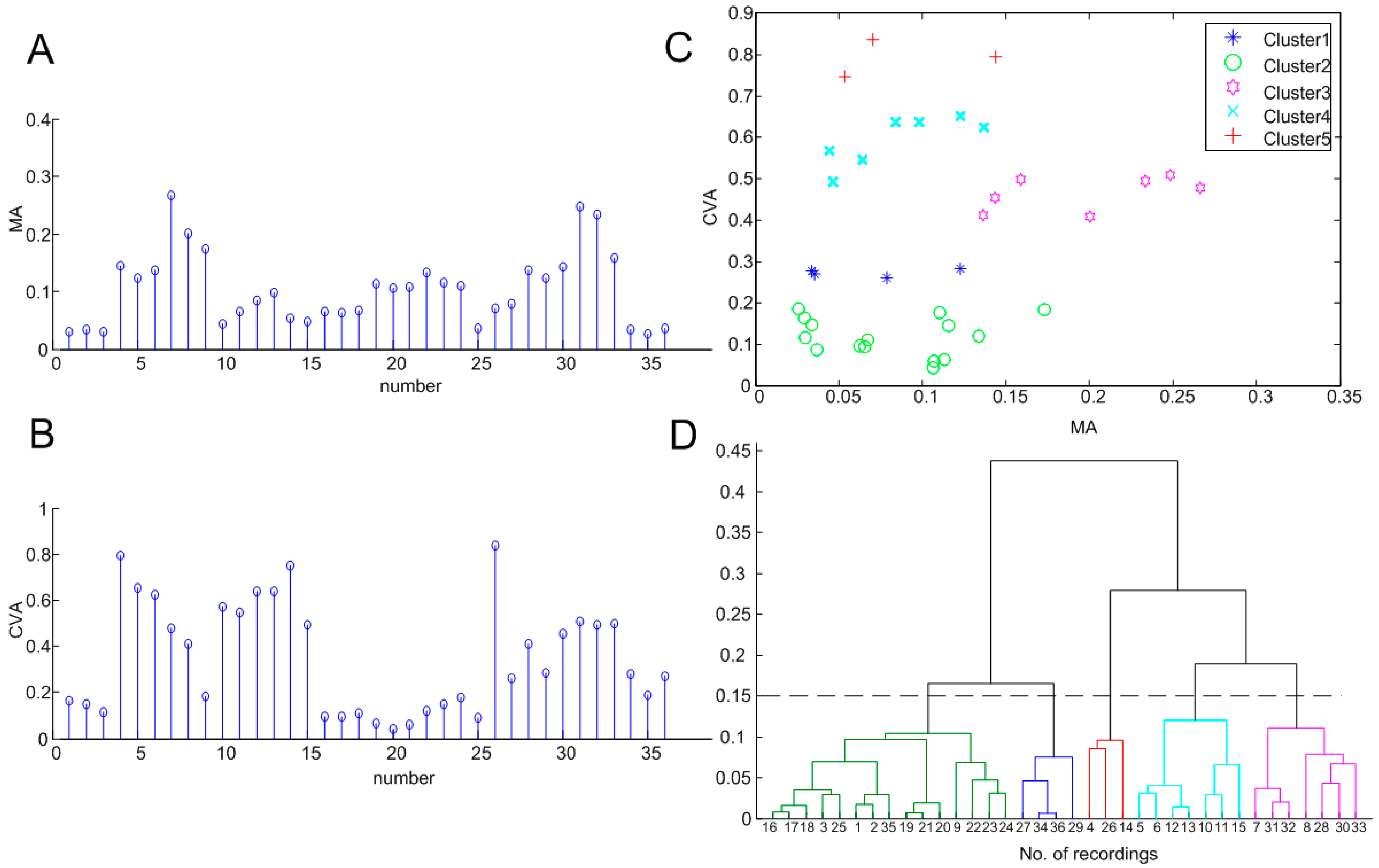
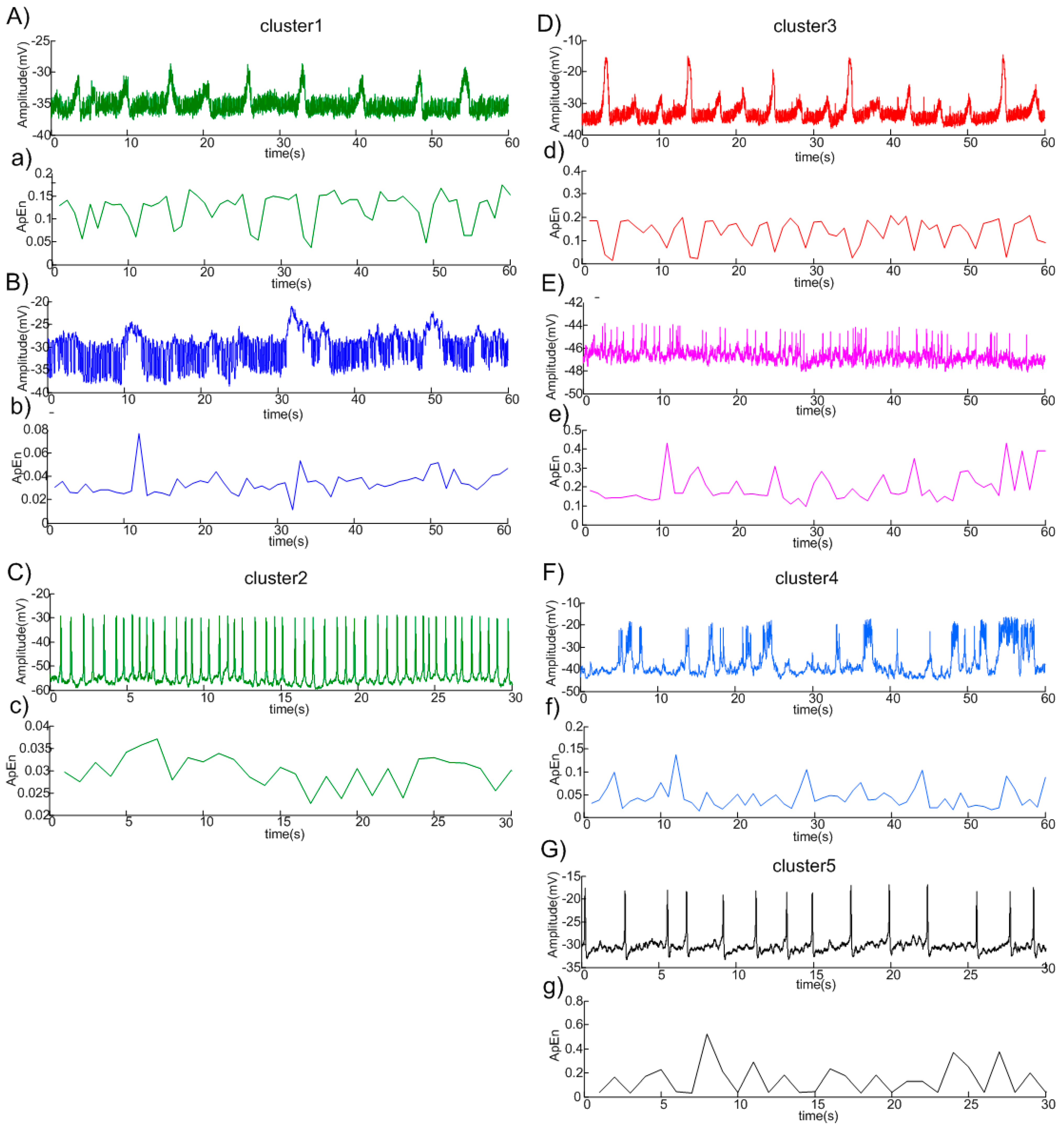
3.2. Clustering Results
| No. of Recordings | No. of Oscillations | No. of ApEn Values for every Oscillation | Kruskal–Wallis Test |
|---|---|---|---|
| 1 | 1/2/3 | 60 | p < 0.01 |
| 2 | 4/5/6 | 60 | p = 0.182 |
| 3 | 7/8/9 | 60 | p < 0.01 |
| 4 | 10/11/12 | 60 | p < 0.01 |
| 5 | 13/14/15 | 60 | p < 0.01 |
| 6 | 16/17/18 | 60 | p < 0.01 |
| 7 | 19/20/21 | 60 | p < 0.01 |
| 8 | 22/23/24 | 60 | p < 0.01 |
| 9 | 25/26/27 | 60 | p < 0.01 |
| 10 | 28/29/30 | 60 | p < 0.01 |
| 11 | 31/32/33 | 60 | p < 0.01 |
| 12 | 34/35/36 | 60 | p < 0.01 |
| Total | 36 | 2160 | p < 0.01 |
3.3. Transformation of Oscillation
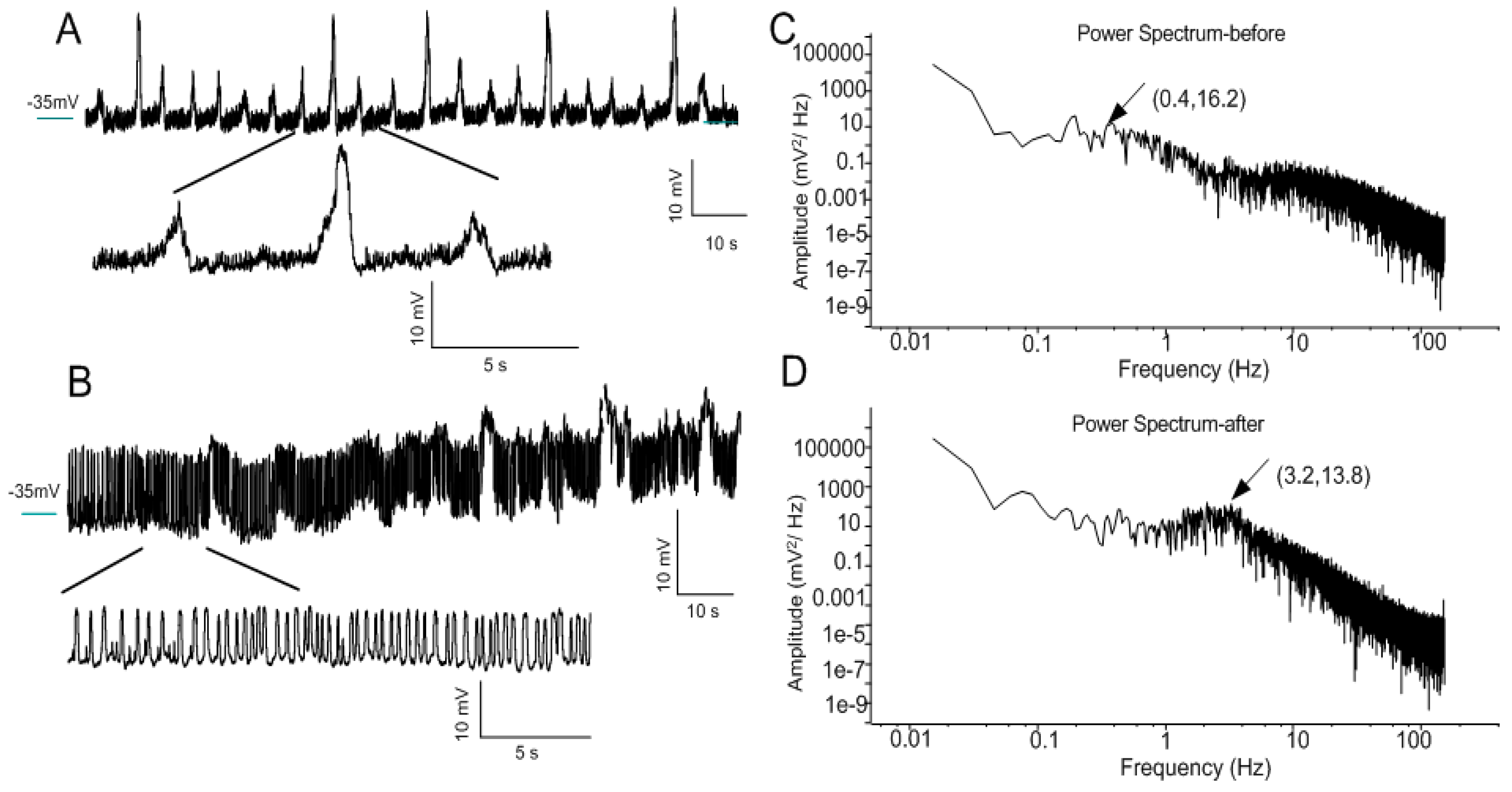
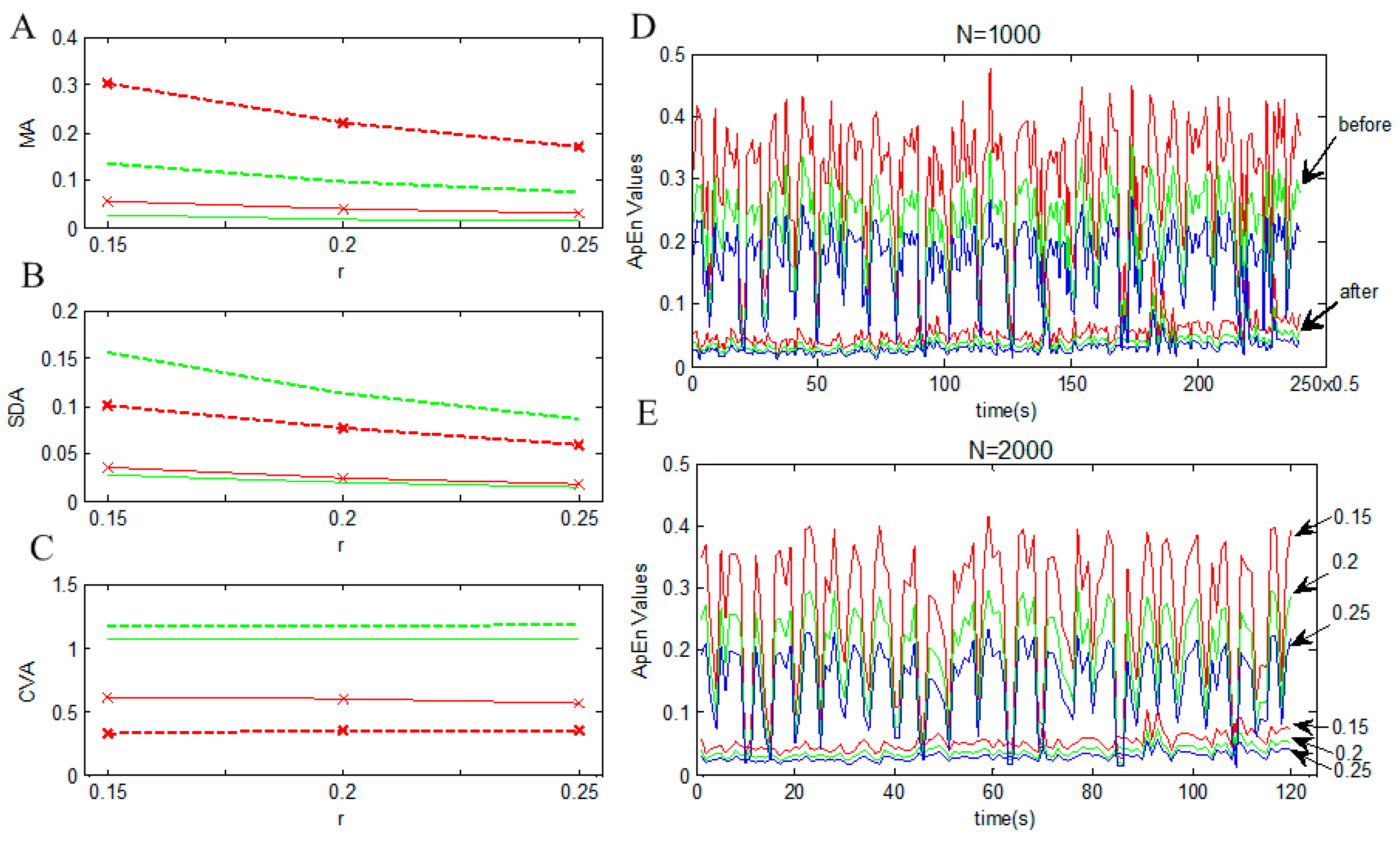
| Sample Points(N) | The Threshold Coefficient(r) | MA-before | MA-after | SDA-before | SDA-after | CVA-before | CVA-after |
|---|---|---|---|---|---|---|---|
| 1000 | 0.15 | 0.302 | 0.057 | 0.100 | 0.035 | 0.332 | 0.616 |
| 1000 | 0.2 | 0.220 | 0.040 | 0.076 | 0.024 | 0.347 | 0.596 |
| 1000 | 0.25 | 0.169 | 0.031 | 0.060 | 0.018 | 0.355 | 0.564 |
| 2000 | 0.15 | 0.134 | 0.026 | 0.157 | 0.028 | 1.168 | 1.067 |
| 2000 | 0.2 | 0.097 | 0.019 | 0.114 | 0.020 | 1.178 | 1.064 |
| 2000 | 0.25 | 0.074 | 0.015 | 0.087 | 0.016 | 1.180 | 1.064 |
3.4. The Location of Neurons with Certain Pattern
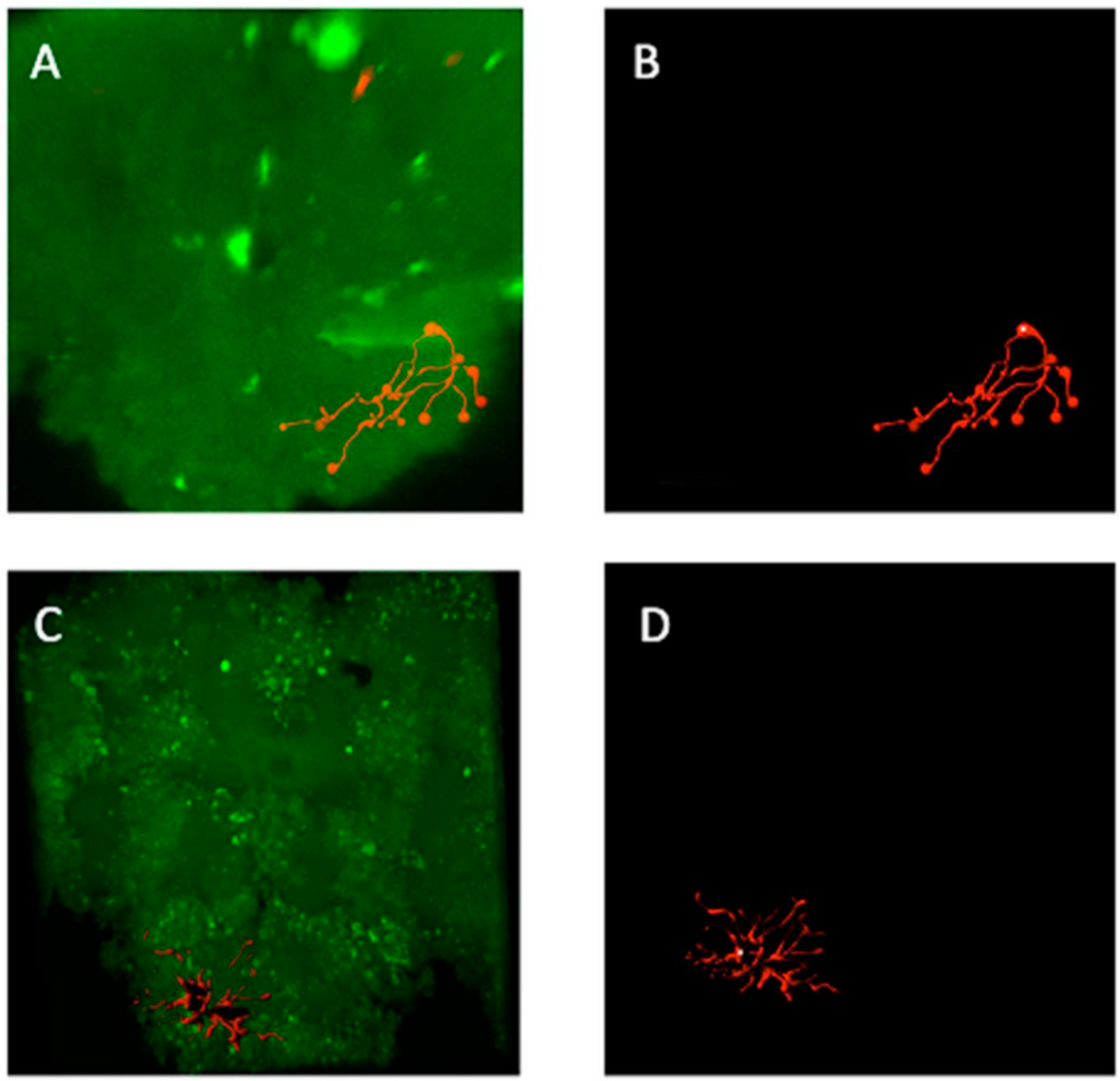
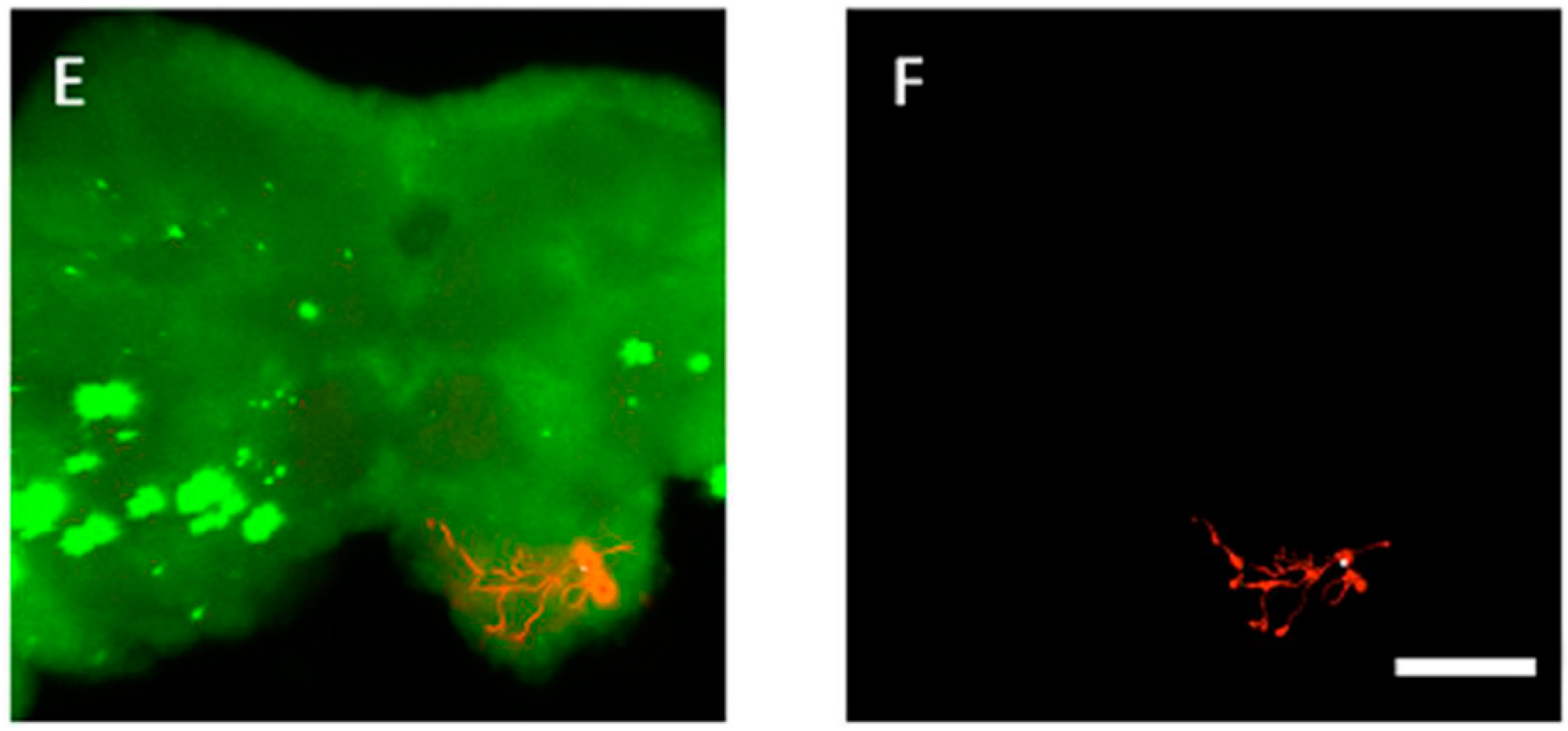
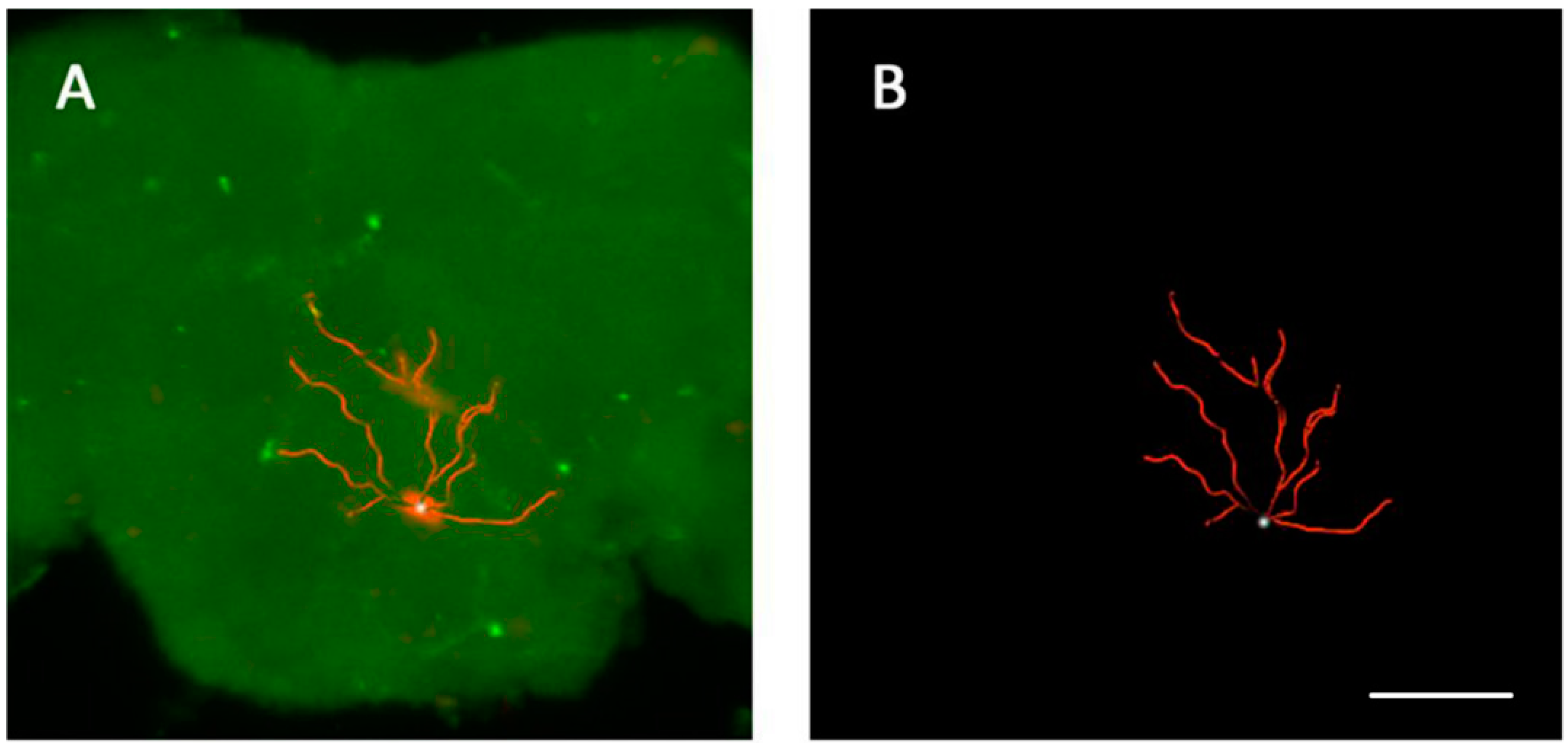
4. Discussion
4.1. ApEn of Neuron Oscillation
4.1.1. Three Indicators
4.1.2. Clustering of Different Patterns
4.2. Oscillations in SOG Region
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Olsen, S.R.; Wilson, R.I. Cracking neural circuits in a tiny brain: New approaches for understanding the neural circuitry of drosophila. Trends Neurosci. 2008, 31, 512–520. [Google Scholar] [CrossRef] [PubMed]
- Muqit, M.M.K.; Feany, M.B. Opinion: Modelling neurodegenerative diseases in drosophila: A fruitful approach? Nat. Rev. Neurosci. 2002, 3, 237–243. [Google Scholar] [CrossRef] [PubMed]
- Feany, M.B.; Bender, W.W. A drosophila model of parkinson’s disease. Nature 2000, 404, 394–398. [Google Scholar] [CrossRef] [PubMed]
- Braun, H.A.; Schwabedal, J.; Dewald, M.; Finke, C.; Postnova, S.; Huber, M.T.; Wollweber, B.; Schneider, H.; Hirsch, M.C.; Voigt, K.; et al. Noise-induced precursors of tonic-to-bursting transitions in hypothalamic neurons and in a conductance-based model. Chaos 2011, 21. [Google Scholar] [CrossRef] [PubMed]
- Scott, K.; Brady, R., Jr.; Axel, R.; Morozov, P.; Rzhetsky, A.; Cravchik, A.; Zuker, C. A chemosensory gene family encoding candidate gustatory and olfactory receptors in drosophila. Cell 2001, 104, 661–673. [Google Scholar] [CrossRef]
- Ito, I.; Bazhenov, M.; Ong, R.C.-Y.; Raman, B.; Stopfer, M. Frequency transitions in odor-evoked neural oscillations. Neuron 2009, 64, 692–706. [Google Scholar] [CrossRef] [PubMed]
- Masse, N.Y.; Turner, G.C.; Jefferis, G.S.X.E. Olfactory information processing in drosophila. Curr. Biol. 2009, 19, R700–R713. [Google Scholar] [CrossRef] [PubMed]
- Martinez, D.; Montejo, N. A model of stimulus-specific neural assemblies in the insect antennal lobe. PLoS Comput. Biol. 2008, 4. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Xu, Y.; Deng, S.; Huang, N.; Yang, Y.; Qiu, J.; Liu, J.; Wang, X.; Yang, G.; Gu, H. A pair of identified giant visual projection neurons demonstrates rhythmic activities before eclosion. Neurosci. Lett. 2013, 550, 156–161. [Google Scholar] [CrossRef] [PubMed]
- Ran, D.; Cai, S.; Gu, H.; Wu, H. Di (2-ethylhexyl) phthalate modulates cholinergic mini-presynaptic transmission of projection neurons in drosophila antennal lobe. Food Chem. Toxicol. 2012, 50, 3291–3297. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Yan, Y.; Zou, X.; Zhang, C.; Zhang, H.; Xu, Y.; Wang, X.; Gu, H.; Yang, Z.; Janos, P. Static magnetic field modulates rhythmic activities of a cluster of large local interneurons in drosophila antennal lobe. J. Neurophysiol. 2011, 106, 2127–2135. [Google Scholar] [CrossRef] [PubMed]
- Tenney, J.R.; Fujiwara, H.; Horn, P.S.; Vannest, J.; Xiang, J.; Glauser, T.A.; Rose, D.F. Low- and high-frequency oscillations reveal distinct absence seizure networks. Ann. Neurol. 2014, 76, 558–567. [Google Scholar] [CrossRef] [PubMed]
- Flint, R.D.; Lindberg, E.W.; Slutzky, M.W.; Jordan, L.R.; Miller, L.E. Accurate decoding of reaching movements from field potentials in the absence of spikes. J. Neural Eng. 2012, 9. [Google Scholar] [CrossRef] [PubMed]
- Kirli, K.K.; Ermentrout, G.B.; Cho, R.Y. Computational study of nmda conductance and cortical oscillations in schizophrenia. Front. Comput. Neurosci. 2014, 8. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Orlandi, J.G.; Soriano, J.; Stetter, O.; Geisel, T.; Battaglia, D. Transfer entropy reconstruction and labeling of neuronal connections from simulated calcium imaging. PLoS ONE 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Wichmann, T.; Soares, J. Neuronal firing before and after burst discharges in the monkey basal ganglia is predictably patterned in the normal state and altered in parkinsonism. J. Neurophysiol. 2006, 95, 2120–2133. [Google Scholar] [CrossRef] [PubMed]
- Rinzel, J.; Huguet, G. Nonlinear dynamics of neuronal excitability, oscillations, and coincidence detection. Commun. Pur. Appl. Math. 2013, 66, 1464–1494. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S. Approximate entropy as an irregularity measure for financial data. Economet. Rev. 2008, 27, 329–362. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Z.; Zhou, Y.; Du, S.; Zhang, Y.; Mei, T.; Tian, X. Construction of rules for seizure prediction based on approximate entropy. Clin. Neurophysiol. 2014, 125, 1959–1966. [Google Scholar] [CrossRef] [PubMed]
- Burioka, N.; Cornelisson, G.; Halberg, F.; Kaplan, D.T.; Suyama, H.; Sako, T.; Shimizu, E.I. Approximate entropy of human respiratory movement during eye-closed waking and different sleep stages. Chest 2003, 123, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Levy, W.J.; Pantin, E.; Mehta, S.; McGarvey, M. Hypothermia and the approximate entropy of the electroencepbalogram. Anesthesiology 2003, 98, 53–57. [Google Scholar] [CrossRef] [PubMed]
- Kalayci, T.; Ozdamar, O. Wavelet preprocessing for automated neural network detection of EEG spikes. IEEE Eng. Med. Biol. 1995, 14, 160–166. [Google Scholar] [CrossRef]
- Sanders, T.H.; Clements, M.A.; Wichmann, T. Parkinsonism-related features of neuronal discharge in primates. J. Neurophysiol. 2013, 110, 720–731. [Google Scholar] [CrossRef] [PubMed]
- Gu, H.; O’Dowd, D.K. Cholinergic synaptic transmission in adult drosophila kenyon cells in situ. J. Neurosci. 2006, 26, 265–272. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Holzinger, A.; Jurisica, I. Knowledge Discovery and Data Mining in Biomedical Informatics: The Future is in Integrative, Interactive Machine Learning Solutions; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–18. [Google Scholar]
- Mayer, C.C.; Bachler, M.; Hoertenhuber, M.; Stocker, C.; Holzinger, A.; Wassertheurer, S. Selection of entropy-measure parameters for knowledge discovery in heart rate variability data. BMC Bioinform. 2014, 15. [Google Scholar] [CrossRef] [PubMed]
- Perkel, D.H.; Gerstein, G.L.; Moore, G.P. Neuronal spike trains and stochastic point processes. I. The single spike train. Biophys. J. 1967, 7, 391–418. [Google Scholar] [CrossRef]
- Markus, B.; Schiemann, J.; Roeper, J.; Schneider, G. Measuring burstiness and regularity in oscillatory spike trains. J. Neurosci. Methods 2011, 201, 426–437. [Google Scholar]
- Witham, C.L.; Baker, S.N. Information theoretic analysis of proprioceptive encoding during finger flexion in the monkey sensorimotor system. J. Neurophysiol. 2015, 113, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Tang, H.; Han, X.; Bi, Q. Bursting mechanism in a time-delayed oscillator with slowly varying external forcing. Commun. Nonlinear Sci. 2014, 19, 1175–1184. [Google Scholar] [CrossRef]
- Manis, G. Fast computation of approximate entropy. Comput. Methods Programs Biomed. 2008, 91, 48–54. [Google Scholar] [CrossRef] [PubMed]
- Davies, R.M.; Gerstein, G.L.; Baker, S.N. Measurement of time-dependent changes in the irregularity of neural spiking. J. Neurophysiol. 2006, 96, 906–918. [Google Scholar] [CrossRef] [PubMed]
- Meyer, A.; Galizia, C.G.; Nawrot, M.P. Local interneurons and projection neurons in the antennal lobe from a spiking point of view. J. Neurophysiol. 2013, 110, 2465–2474. [Google Scholar] [CrossRef] [PubMed]
- Wild, J.; Prekopcsak, Z.; Sieger, T.; Novak, D.; Jech, R. Computational neuroscience: Performance comparison of extracellular spike sorting algorithms for single-channel recordings. J. Neurosci. Methods 2012, 203, 369–376. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.; Yan, Y.; Xu, Y.; Jin, Y.; Lei, J.; Zou, X.; Ran, D.; Zhang, H.; Luan, S.; Gu, H. Alumina nanoparticles alter rhythmic activities of local interneurons in the antennal lobe of drosophila. Nanotoxicology 2013, 7, 212–220. [Google Scholar] [CrossRef] [PubMed]
- Qiao, J.; Zou, X.; Lai, D.; Yan, Y.; Wang, Q.; Li, W.; Deng, S.; Xu, H.; Gu, H. Azadirachtin blocks the calcium channel and modulates the cholinergic miniature synaptic current in the central nervous system of drosophila. Pest Manag. Sci. 2014, 70, 1041–1047. [Google Scholar] [CrossRef] [PubMed]
- Pita-Almenar, J.D.; Yu, D.; Lu, H.-C.; Beierlein, M. Mechanisms underlying desynchronization of cholinergic-evoked thalamic network activity. J. Neurosci. 2014, 34, 14463–14474. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chen, L.; Deng, Y.; Luo, W.; Wang, Z.; Zeng, S. Detection of bursts in neuronal spike trains by the mean inter-spike interval method. Prog. Nat. Sci. 2009, 19, 229–235. [Google Scholar] [CrossRef]
- Holt, G.R.; Softky, W.R.; Koch, C.; Douglas, R.J. Comparison of discharge variability in vitro and in vivo in cat visual cortex neurons. J. Neurophysiol. 1996, 75, 1806–1814. [Google Scholar] [PubMed]
- Shinomoto, S.; Kim, H.; Shimokawa, T.; Matsuno, N.; Funahashi, S.; Shima, K.; Fujita, I.; Tamura, H.; Doi, T.; Kawano, K.; et al. Relating neuronal firing patterns to functional differentiation of cerebral cortex. PLoS Comput. Biol. 2009, 5. [Google Scholar] [CrossRef] [PubMed]
- Christodoulou, C.; Bugmann, G. Coefficient of variation vs. Mean interspike interval curves: What do they tell us about the brain? Neurocomputing 2001, 38, 1141–1149. [Google Scholar] [CrossRef]
- Maimon, G.; Assad, J.A. Beyond poisson: Increased spike-time regularity across primate parietal cortex. Neuron 2009, 62, 426–440. [Google Scholar] [CrossRef] [PubMed]
- Kumbhare, D.; Baron, M.S. A novel tri-component scheme for classifying neuronal discharge patterns. J. Neurosci. Methods 2015, 239, 148–161. [Google Scholar] [CrossRef] [PubMed]
- Taube, J.S. Interspike interval analyses reveal irregular firing patterns at short, but not long, intervals in rat head direction cells. J. Neurophysiol. 2010, 104, 1635–1648. [Google Scholar] [CrossRef] [PubMed]
- Machens, C.K.; Romo, R.; Brody, C.D. Flexible Control of Mutual Inhibition: A Neural Model of Two-Interval Discrimination. Science 2005, 307, 1121–1124. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, N.K.; Stopfer, M.; Ito, K. Odor-evoked neural oscillations in drosophila are mediated by widely branching interneurons. J. Neurosci. 2009, 29, 8595–8603. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, T.; Qiao, J.; Zhou, Y.; Gu, H.; Chen, Z.; Tian, X.; Gu, K. Analysis of Neural Oscillations on Drosophila’s Subesophageal Ganglion Based on Approximate Entropy. Entropy 2015, 17, 6854-6871. https://doi.org/10.3390/e17106854
Mei T, Qiao J, Zhou Y, Gu H, Chen Z, Tian X, Gu K. Analysis of Neural Oscillations on Drosophila’s Subesophageal Ganglion Based on Approximate Entropy. Entropy. 2015; 17(10):6854-6871. https://doi.org/10.3390/e17106854
Chicago/Turabian StyleMei, Tian, Jingda Qiao, Yi Zhou, Huaiyu Gu, Ziyi Chen, Xianghua Tian, and Kuiying Gu. 2015. "Analysis of Neural Oscillations on Drosophila’s Subesophageal Ganglion Based on Approximate Entropy" Entropy 17, no. 10: 6854-6871. https://doi.org/10.3390/e17106854
APA StyleMei, T., Qiao, J., Zhou, Y., Gu, H., Chen, Z., Tian, X., & Gu, K. (2015). Analysis of Neural Oscillations on Drosophila’s Subesophageal Ganglion Based on Approximate Entropy. Entropy, 17(10), 6854-6871. https://doi.org/10.3390/e17106854





