Quantum Secure Direct Communication Based on Dense Coding and Detecting Eavesdropping with Four-Particle Genuine Entangled State
Abstract
:1. Introduction
2. Description of Protocol
- (1)
- Bob prepares N pairs of Bell states in order and inserts M pairs of four-particle genuine entangled states .
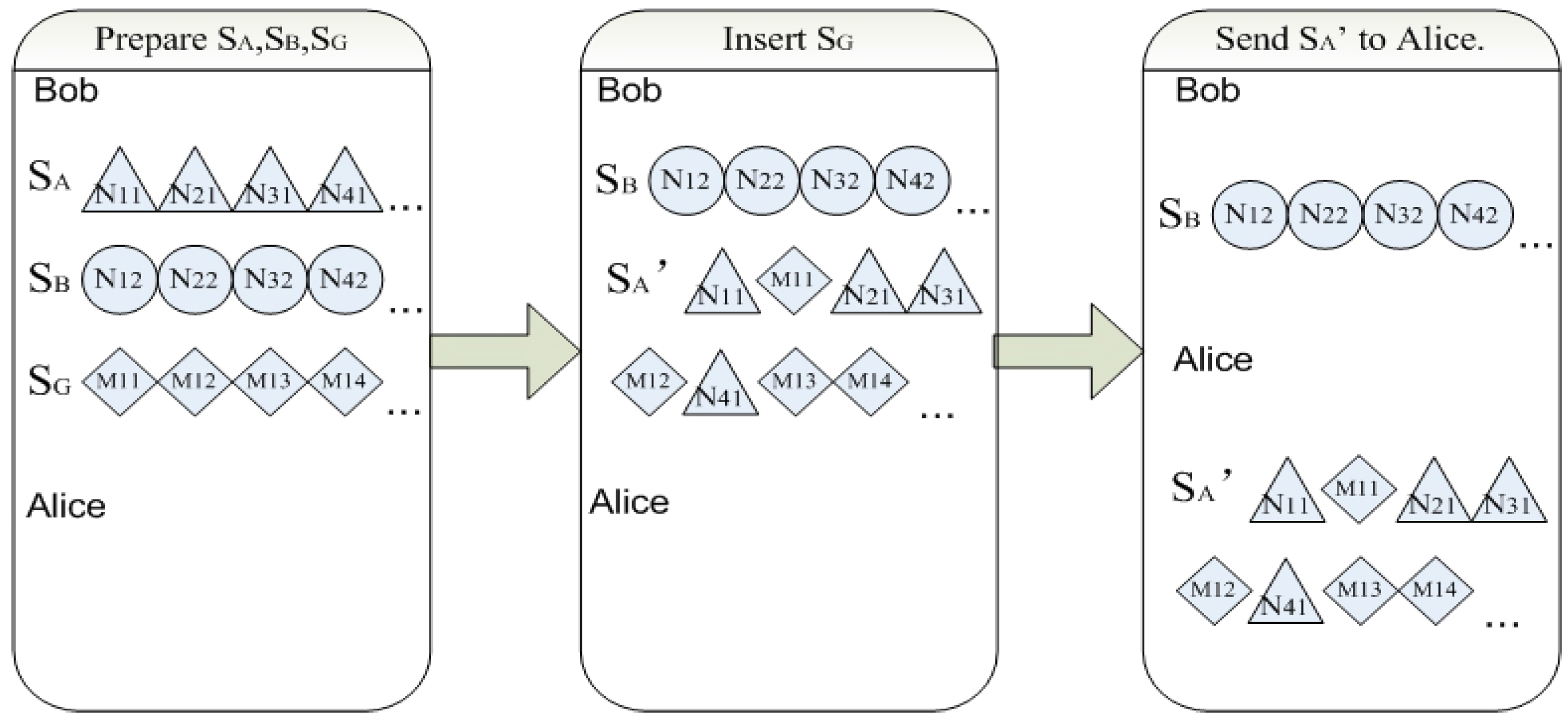
- (2)
- The detection of eavesdropping.
- (3)
- Alice encodes her secure message on remaining photons based on dense coding.
- (4)
- Bob decodes the cipher text with the Bell measurement.
- (5)
- The FGEP protocol ends successfully.
3. The Security Analysis of the Protocol
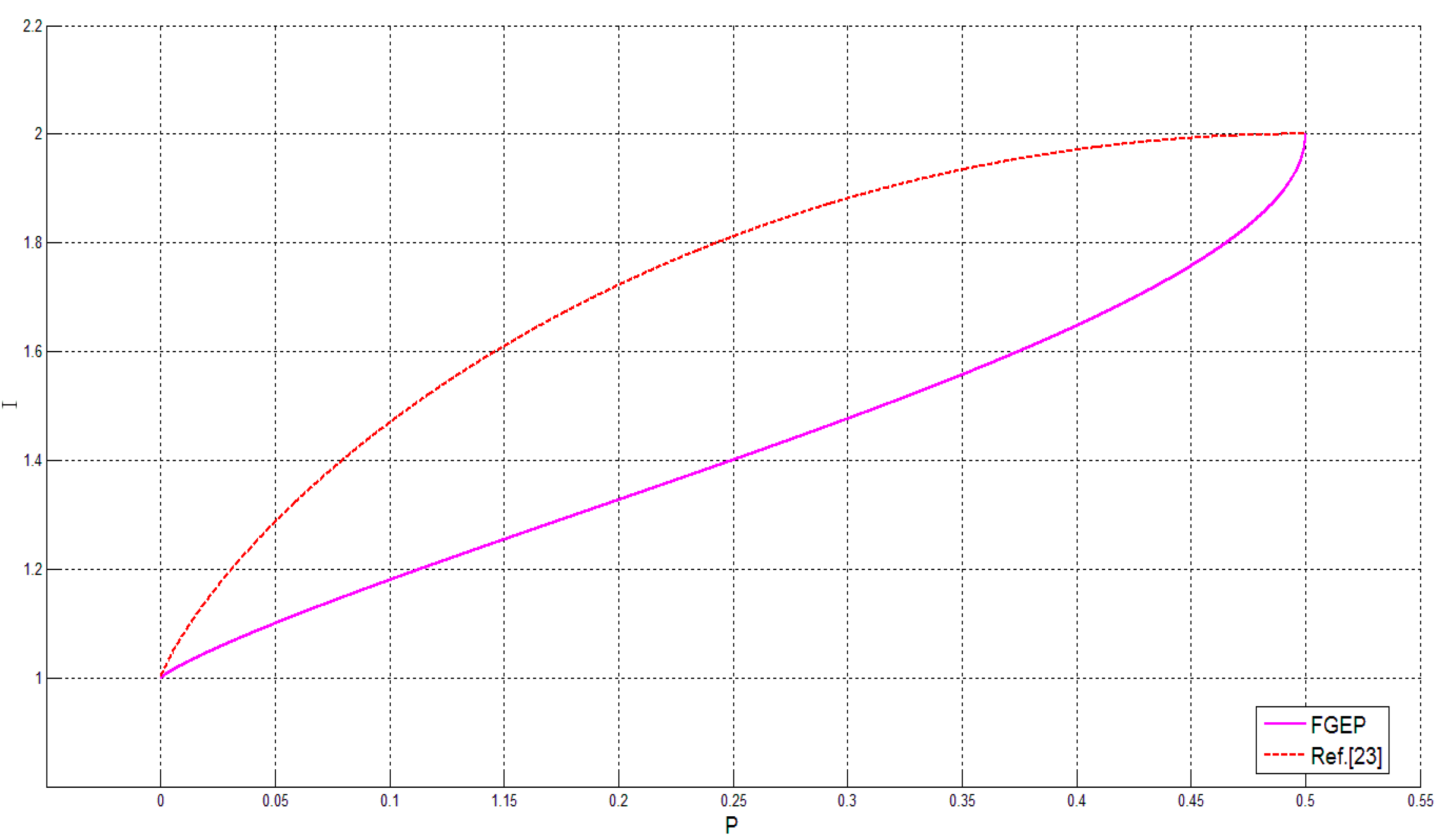
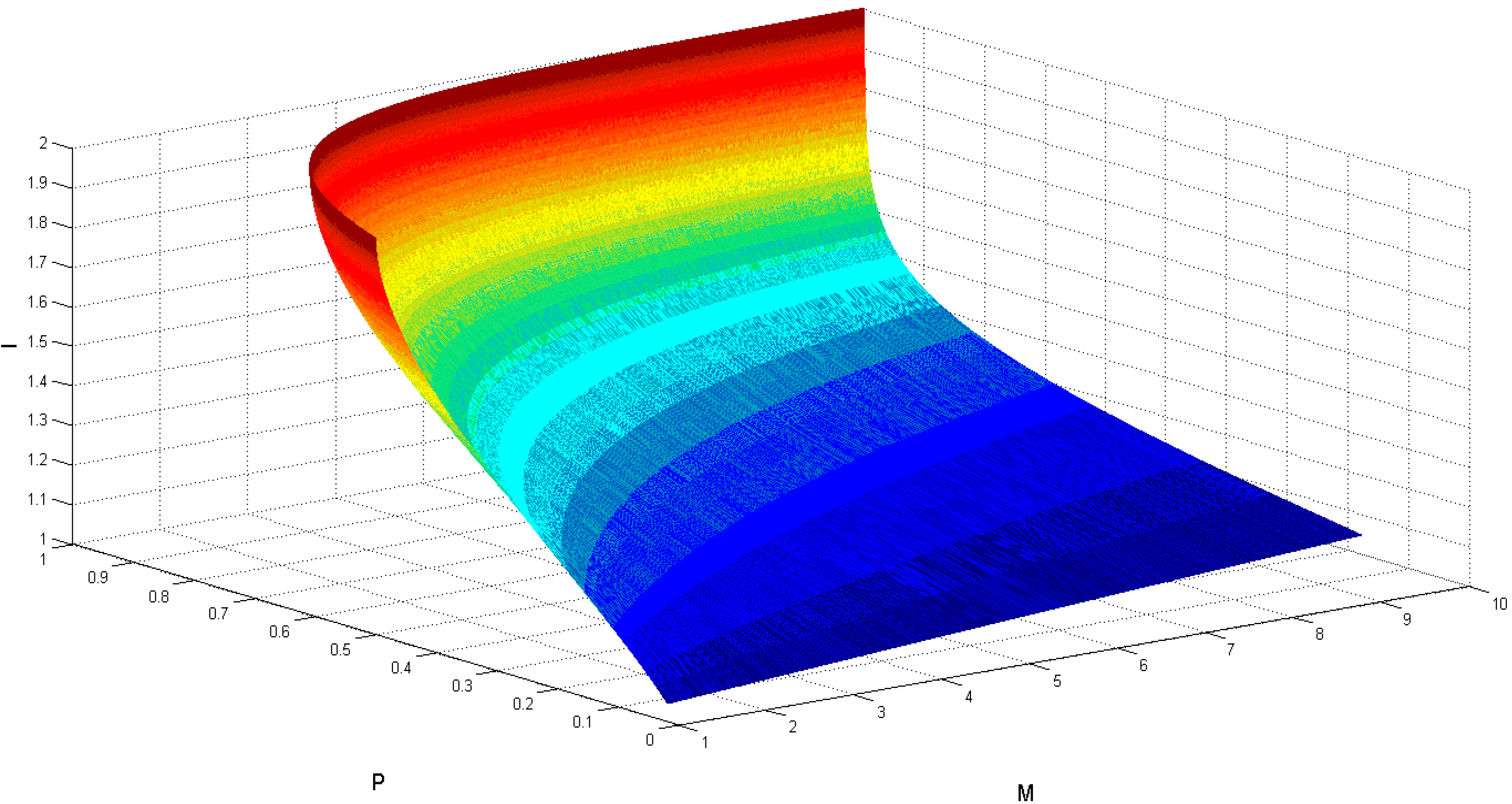
4. Conclusions
- (i)
- The eavesdropping detection method using the four-particle genuine entangled state as decoy photons in the FGEP protocol is similar to the method using the control mode [23].
- (ii)
- In the FGEP protocol, the Bell states are prepared by Bob rather than by Alice. This guarantees that the home qubits could not leak to Eve, and the Bell states that carries the secure message can be reused.
- (iii)
- The FGEP protocol is based on the four-particle genuine entangled state, which can reduce the times of detection.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Computer Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Deng, F.G.; Li, X.H.; Zhou, H.Y.; Zhang, Z.-J. Improving the security of multiparty quantum secret sharing against Trojan horse attack. Phys. Rev. A 2005, 72. [Google Scholar] [CrossRef]
- Song, T.T.; Wen, Q.Y.; Gao, F.; Chen, H. Participant attack and improvement to multiparty quantum secret sharing based on GHZ states. Int. J. Theor. Phys. 2013, 52, 293–301. [Google Scholar] [CrossRef]
- Adhikari, S.; Roy, S.; Chakraborty, S.; Chakraborty, S.; Jagadish, V.; Haris, M.K.; Kumar, A. Controlled secret sharing protocol using a quantum cloning circuit. Quantum Inf. Process. 2014, 13, 2071–2080. [Google Scholar] [CrossRef]
- Liao, C.H.; Yang, C.W.; Hwang, T. Dynamic quantum secret sharing protocol based on GHZ state. Quantum Inf. Process. 2014, 13, 1907–1916. [Google Scholar] [CrossRef]
- Wu, Y.; Cai, R.; He, G.; Zhang, J. Quantum secret sharing with continuous variable graph state. Quantum Inf. Process. 2014, 13, 1085–1102. [Google Scholar] [CrossRef]
- Wang, C.; Liu, J.-W.; Liu, X.; Shang, T. A Novel Deterministic Secure Quantum Communication Scheme with Einstein—Podolsky—Rosen Pairs and Single Photons. Commun. Theor. Phys. 2013, 60. [Google Scholar] [CrossRef]
- Kao, S.H.; Tsai, C.W.; Hwang, T. Comment on: Supervisory Asymmetric Deterministic Secure Quantum Communication. Int. J. Theor. Phys. 2012, 51, 3868–3875. [Google Scholar] [CrossRef]
- Huang, W.; Wen, Q.Y.; Liu, B.; Gao, F.; Chen, H. Deterministic secure quantum communication with collective detection using single photons. Int. J. Theor. Phys. 2012, 51, 2787–2797. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, Q.; Hong, L.; Yin, W.-J.; Xu, D.; Zhou, J. Scheme for Deterministic Secure Quantum Communication with Three-qubit GHZ State. Int. J. Theor. Phys. 2014, 53, 2558–2564. [Google Scholar] [CrossRef]
- Deng, F.G.; Long, G.L.; Liu, X.S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 2003, 68. [Google Scholar] [CrossRef]
- Stefano, L.M.M. Secure Deterministic Communication without Entanglement. Phys. Rev. Lett 2005. [Google Scholar] [CrossRef]
- Lucamarini, M.; Mancini, S. Secure deterministic communication without entanglement. Phys. Rev. Lett. 2005, 94. [Google Scholar] [CrossRef]
- Li, W.; Chen, J.; Wang, X.; Li, C. Quantum Secure Direct Communication Achieved by Using Multi-Entanglement. Int. J. Theor. Phys. 2014, 54, 100–105. [Google Scholar] [CrossRef]
- Yan, C.; Zhang, S.-B.; Yan, L.-L.; Sheng, Z.-W. A multiparty controlled bidirectional quantum secure direct communication and authentication protocol based on EPR pairs. Chin. Phys. Lett. 2013, 30. [Google Scholar] [CrossRef]
- Li, J.; Jin, H.F.; Jing, B. Improved eavesdropping detection strategy based on four-particle cluster state in quantum direct communication protocol. Chin. Sci. Bull. 2012, 57, 4434–4441. [Google Scholar] [CrossRef]
- Deng, F.G.; Li, X.H.; Li, C.Y.; Zhou, P.; Zhou, H.Y. Quantum secure direct communication network with Einstein–Podolsky–Rosen pairs. Phys. Lett. A 2006, 359, 359–365. [Google Scholar] [CrossRef]
- Hwang, T.; Li, C.M; Lee, N.Y. Secure direct communication using deterministic BB84 protocol. Int. J. Mod. Phys. C 2008, 19, 625–635. [Google Scholar] [CrossRef]
- Bin, G.; Yu-Gai, H.; Xia, F.; Yi, Z.C. A two-step quantum secure direct communication protocol with hyperentanglement. Chin. Phys. B 2011, 20. [Google Scholar] [CrossRef]
- Chang, Y.; Xu, C.; Zhang, S.; Yan, L. Controlled quantum secure direct communication and authentication protocol based on five-particle cluster state and quantum one-time pad. Chin. Sci. Bull. 2014, 59, 2541–2546. [Google Scholar] [CrossRef]
- Du, R.; Sun, Z.; Wang, B.; Long, D. Quantum secret sharing of secure direct communication using one-time pad. Int. J. Theor. Phys. 2012, 51, 2727–2736. [Google Scholar] [CrossRef]
- Gu, B.; Zhang, C.Y.; Cheng, G.S.; Huang, Y.G. Robust quantum secure direct communication with a quantum one-time pad over a collective-noise channel. Sci. China Phys. Mech. Astron. 2011, 54, 942–947. [Google Scholar] [CrossRef]
- Boström, K.; Felbinger, T. Deterministic secure direct communication using entanglement. Phys. Rev. Lett. 2002, 89. [Google Scholar] [CrossRef]
- Gu, B.; Xu, F.; Ding, L.; Zhang, Y. High-capacity three-party quantum secret sharing with hyperentanglement. Int. J. Theor. Phys. 2012, 51, 3559–3566. [Google Scholar] [CrossRef]
- Chang, Y.; Zhang, S.B.; Li, J.; Yan, L.L. Robust EPR-pairs-based quantum secure communication with authentication resisting collective noise. Sci. China Phys. Mech. Astron. 2014, 57, 1907–1912. [Google Scholar] [CrossRef]
- Wang, T.Y.; Cai, X.Q. An Efficient Quantum Secret Sharing Scheme with Decoy States. Int. J. Mod. Phys. B 2012, 26. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Pan, Z.; Sun, F.; Chen, Y.; Wang, Z.; Shi, Z. Quantum Secure Direct Communication Based on Dense Coding and Detecting Eavesdropping with Four-Particle Genuine Entangled State. Entropy 2015, 17, 6743-6752. https://doi.org/10.3390/e17106743
Li J, Pan Z, Sun F, Chen Y, Wang Z, Shi Z. Quantum Secure Direct Communication Based on Dense Coding and Detecting Eavesdropping with Four-Particle Genuine Entangled State. Entropy. 2015; 17(10):6743-6752. https://doi.org/10.3390/e17106743
Chicago/Turabian StyleLi, Jian, Zeshi Pan, Fengqi Sun, Yanhua Chen, Zheng Wang, and Zuozhi Shi. 2015. "Quantum Secure Direct Communication Based on Dense Coding and Detecting Eavesdropping with Four-Particle Genuine Entangled State" Entropy 17, no. 10: 6743-6752. https://doi.org/10.3390/e17106743
APA StyleLi, J., Pan, Z., Sun, F., Chen, Y., Wang, Z., & Shi, Z. (2015). Quantum Secure Direct Communication Based on Dense Coding and Detecting Eavesdropping with Four-Particle Genuine Entangled State. Entropy, 17(10), 6743-6752. https://doi.org/10.3390/e17106743




