Two-Dimensional Lattice Boltzmann for Reactive Rayleigh–Bénard and Bénard–Poiseuille Regimes
Abstract
:1. Introduction
2. Thermal Decomposition of Nitrous Oxide
- The continuity equation
- The Navier–Stokes equation with buoyant forces (G).
- The infinitesimal balance of heat transfer, based on the Fourier’s law, including effects of natural convection and viscous dissipation.
- The linear Bousinesq equation of state.
- The gaseous fluid (air and different species involved in the thermal decomposition of the laughing gas) is incompressible and Newtonian.
- The thermal conductivity, viscosity, coefficient of thermal expansion and coefficient of diffusion of chemical species are all constant throughout the studied temperature range.
- The variation of density is only significant in terms of buoyant forces.
- Viscous dissipation is negligible.
- The Reynolds number is small (for Bénard–Poiseuille flow).
- The laughing gas decomposition is the only chemical reaction that takes place in the system.
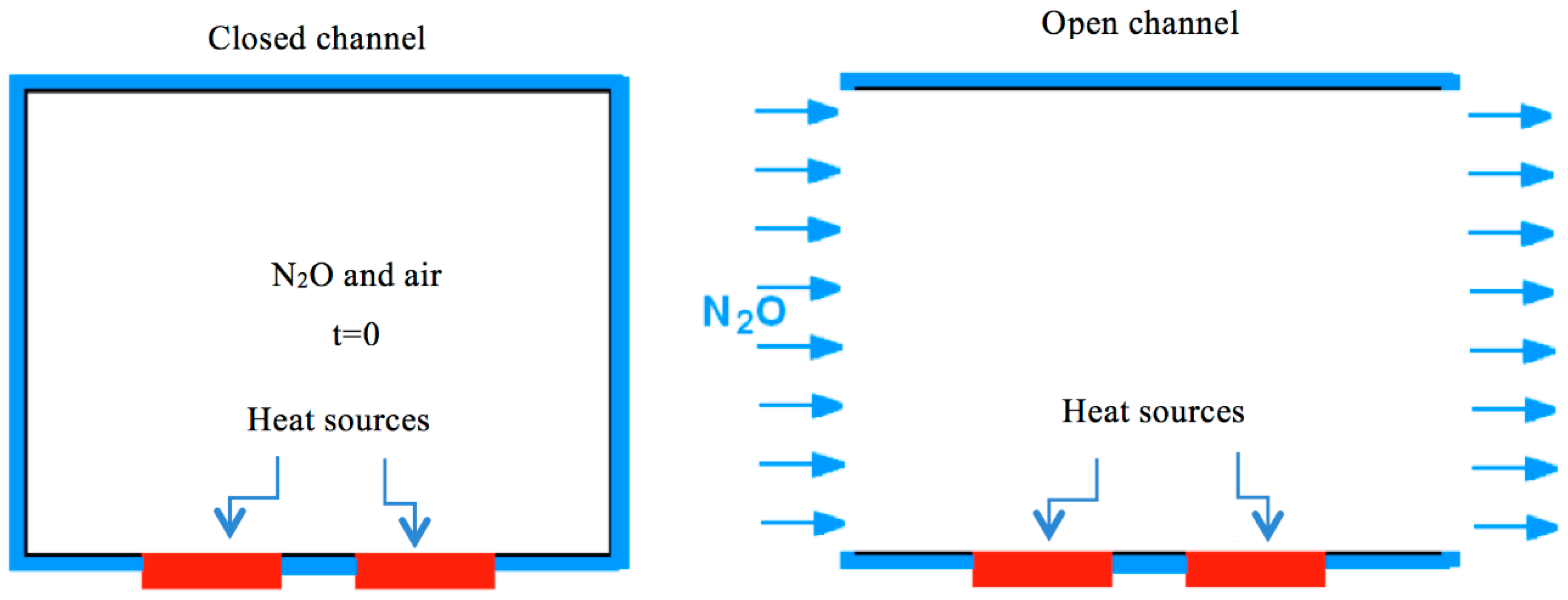
- In the top and bottom plates, temperature is constant. This means that the heat generated by the chemical reaction is assumed to be efficiently removed from the system.
- In the bottom plates, there are two heat sources (or hot spots) for both the opened and closed channels at a higher temperature than the low constant temperature set in 7. These heat sources trigger the (N2O decomposition) reaction.
- The concentrations of chemical species are kept sufficiently small so that they dominate the properties of air during the phenomenon of natural convection.
3. The Lattice Botlzmann Model
3.1. Open Channel
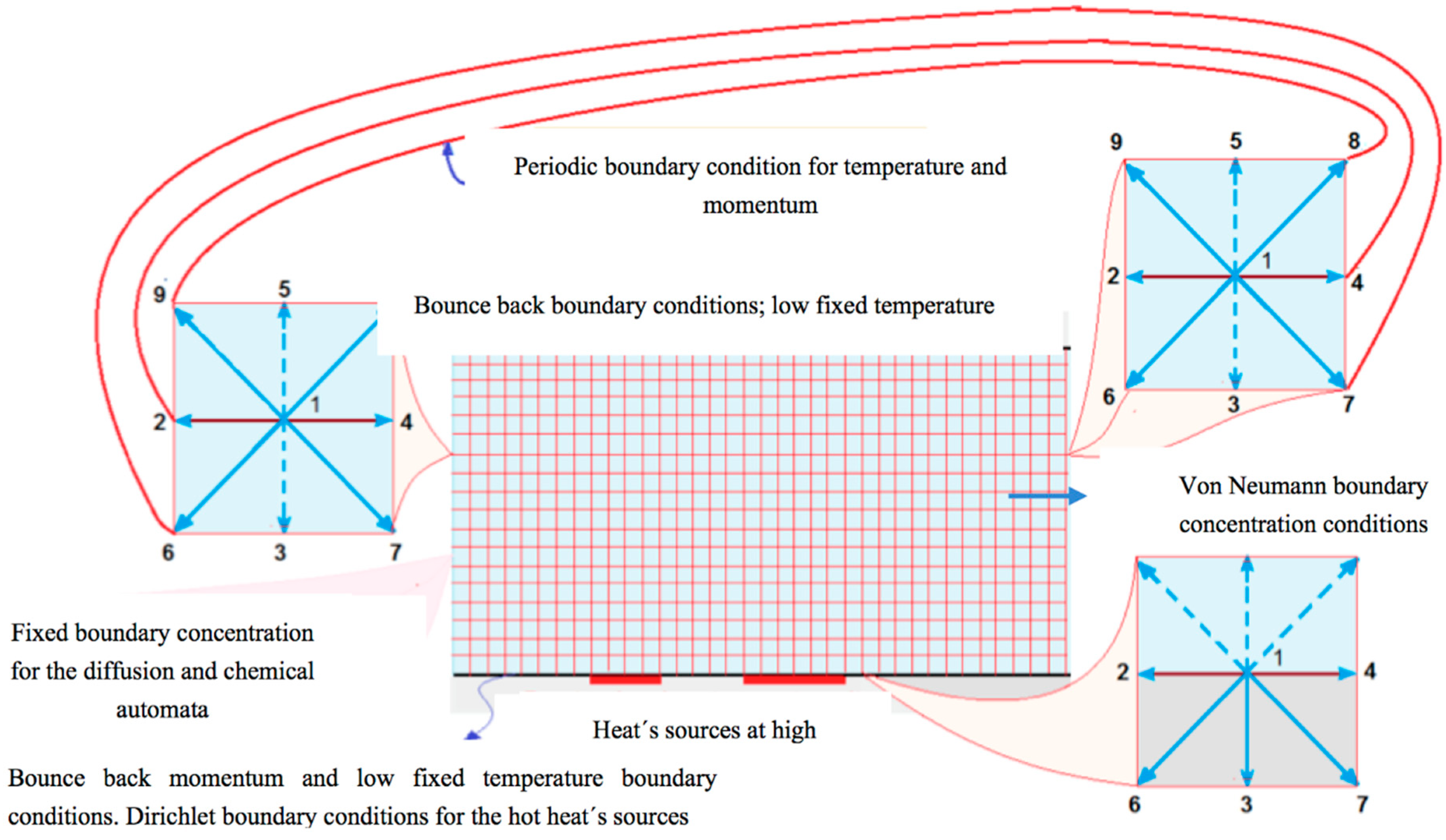
- For the top plate, bounce back boundary conditions for the fluid dynamic LBE and a low constant isothermal boundary conditions for the thermic LBE are used.
- Inlet and outlet periodic boundary conditions, for the moment and thermal LBE, are set.
- For the bottom plate, bounce back boundary conditions are imposed in all the nodes for the hydrodynamic LBE, while for thermal LBE we used bounce back conditions as well, except in the heat sources sites where Dirichlet boundary conditions are set.
- Top and bottom bounce back boundary conditions.
- Invariable concentration in the inlet of the channel.
- Null gradient concentration in the outlet of the channel (von Neumann condition).
3.2. Closed Channel
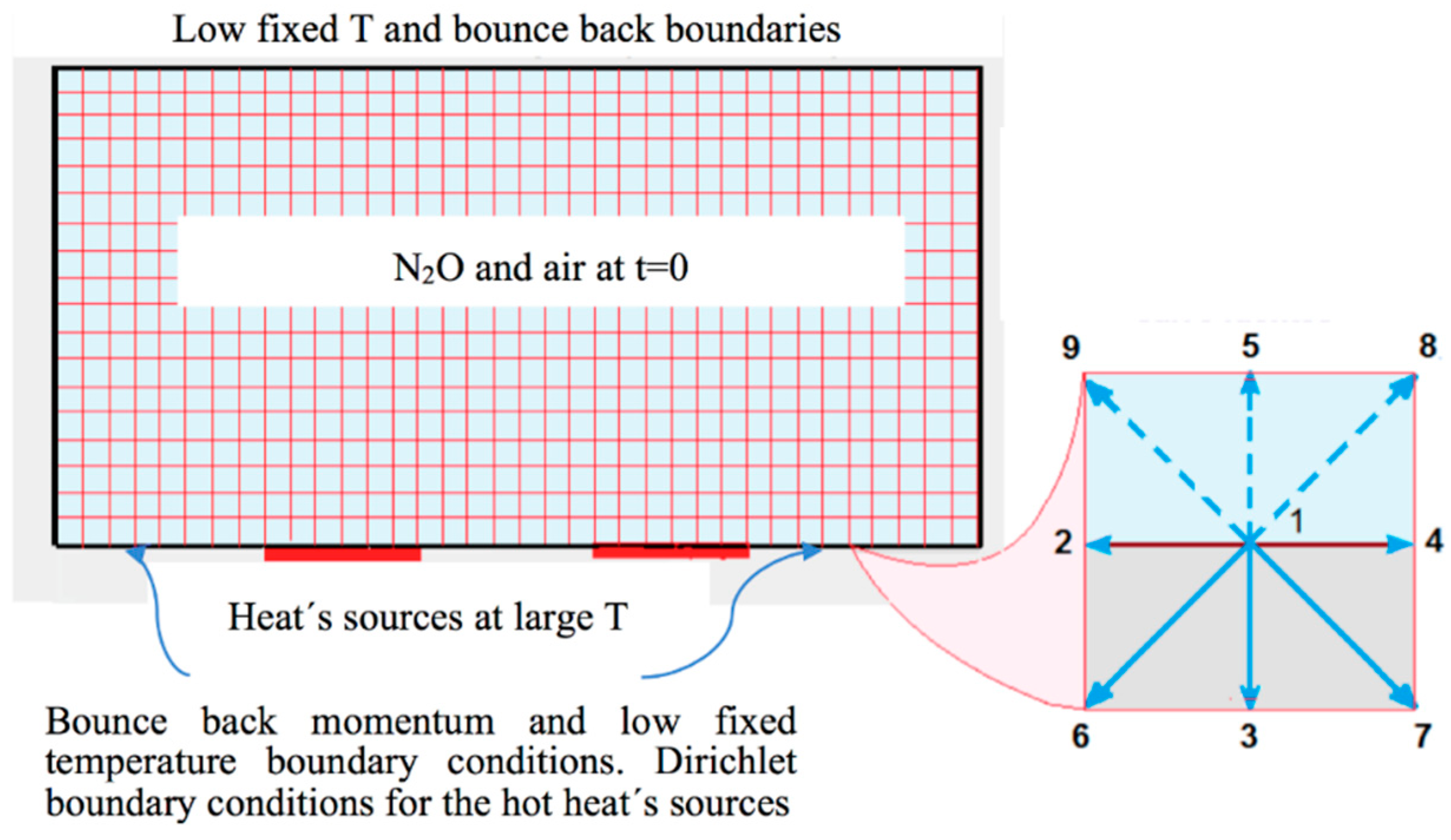
- Bounce back boundary conditions at all the sites for the fluid and thermal LBE on all borders, except at the heat’s sources.
- Diritchlet boundary conditions at all high temperature sites (heat sources).
- Initial state with uniformly distributed nitrous oxide in the closed vessel, with initial concentration C0 and initial temperature T0, smaller than the temperature of the sources.
- Bounce back boundary conditions at all the sites for the reaction-diffusion LBE on all borders.
4. The Lattice Botlzmann Algorithm
4.1. Open Channel
- The distribution functions f and g for the velocity u and temperature T fields, respectively, were evaluated simultaneously in a coupled fashion, taking into account iterative calculations performed by the following steps:
- 1.1
- Propagation (streaming) of the f and g distribution functions.
- 1.2
- Calculation of the distribution functions at equilibrium; feq and geq.
- 1.3
- Actualization of the f and g distribution functions.
- 1.4
- Introduction of thermal and fluid dynamics boundary conditions.
- 1.5
- Calculation of the u and T fields from the new f and g distribution functions.
- 1.6
- Assessment of the new and preceding values of u and T, if they are closed enough, finish the iterations; else, return to step 1.1.
- Once obtaining the steady temperature and velocity profiles, the temporal evolution of the distribution functions hi for each one of the three chemical species is calculated, solving the LBM equations for the reaction-diffusion advection phenomena. This is a non-iterative procedure, structured practically by the same steps as the ones in the thermo-hydrodynamic analysis, except for that in the formulation of the diffusional distribution functions for each chemical species. The chemical kinetics term (Arrhenius law also considered) is introduced, keeping the 1:1:1/2 stoichiometric relationships between reactants and products.
4.2. Closed Channel
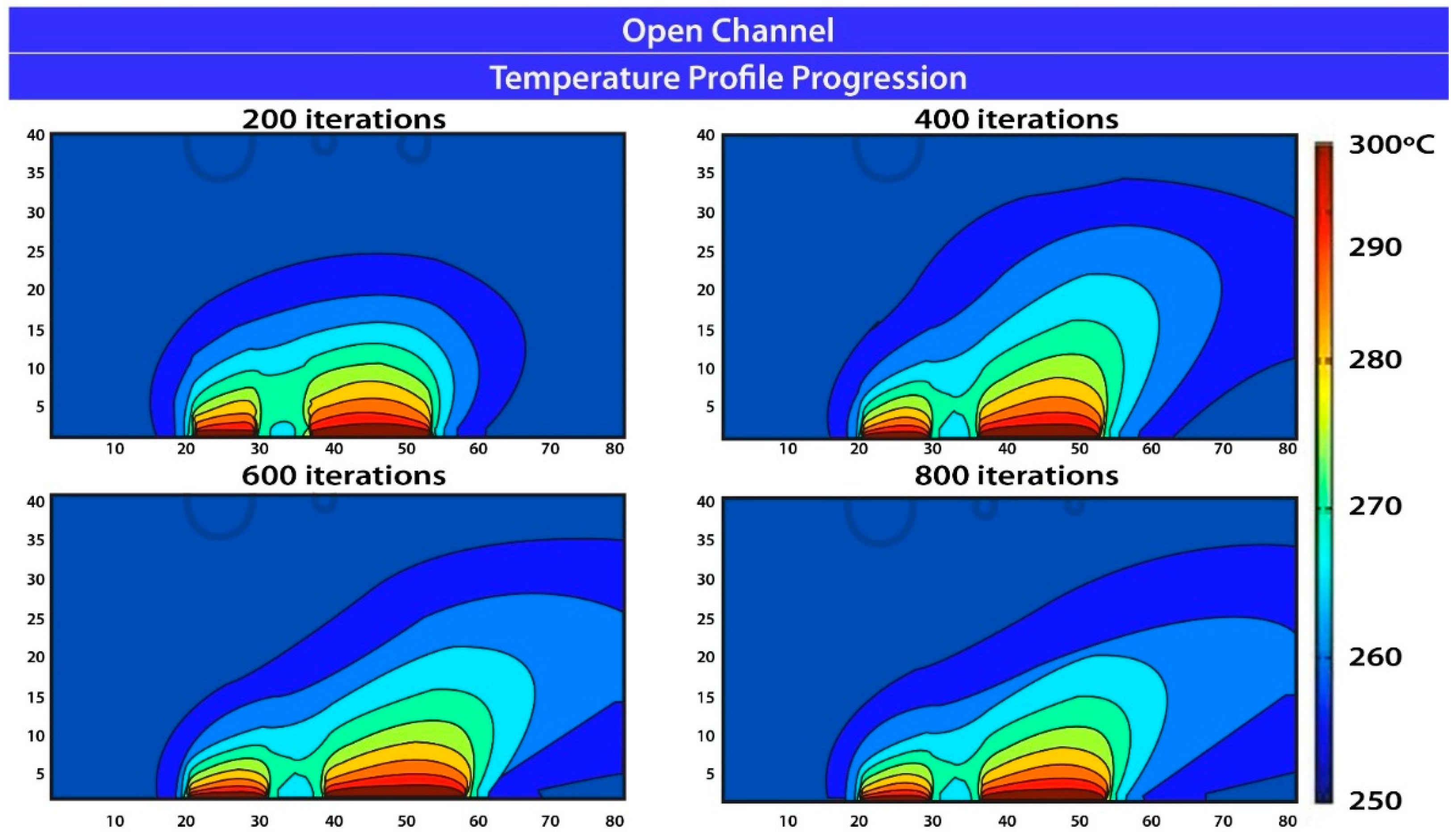
5. Results and Conclusions
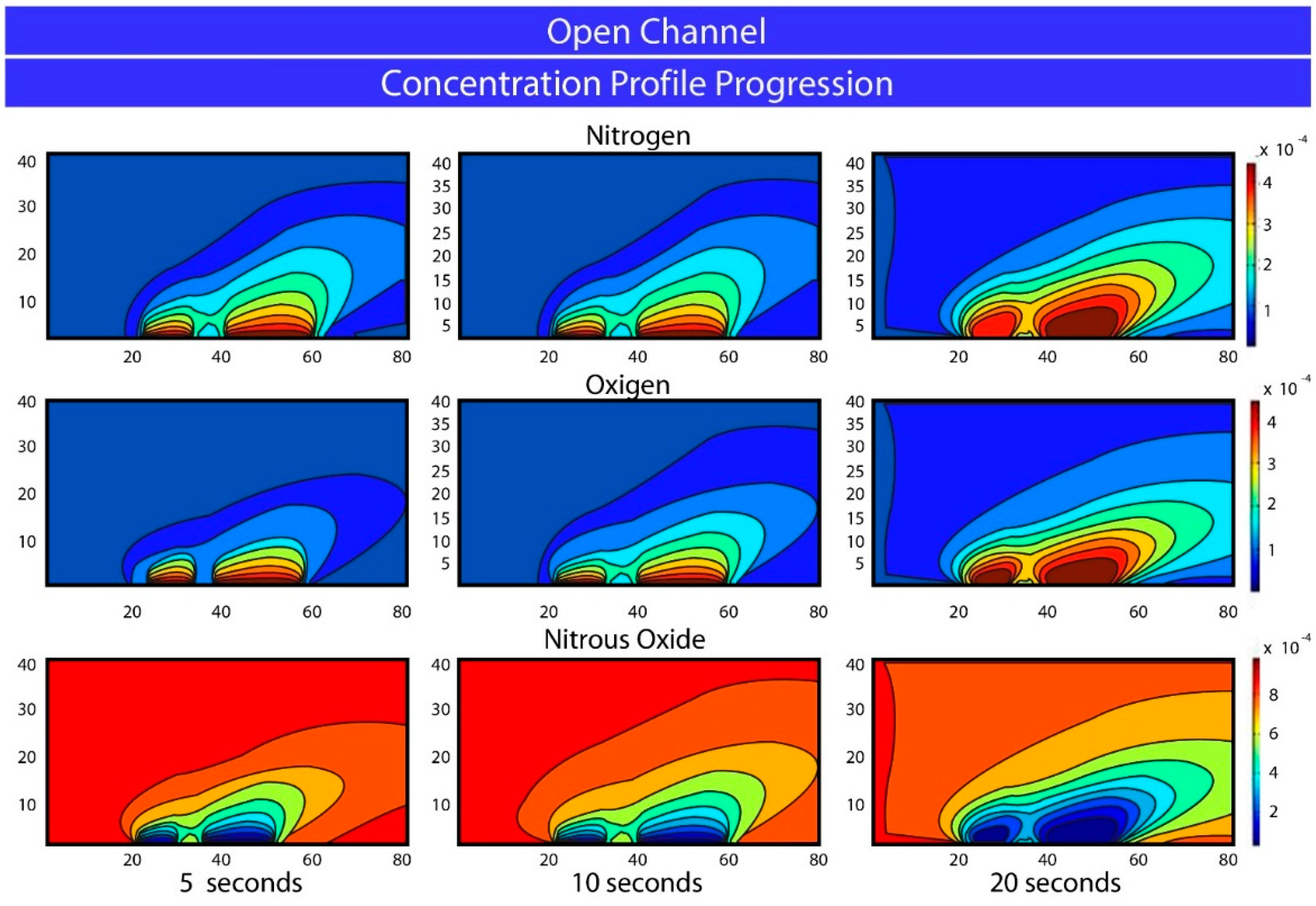
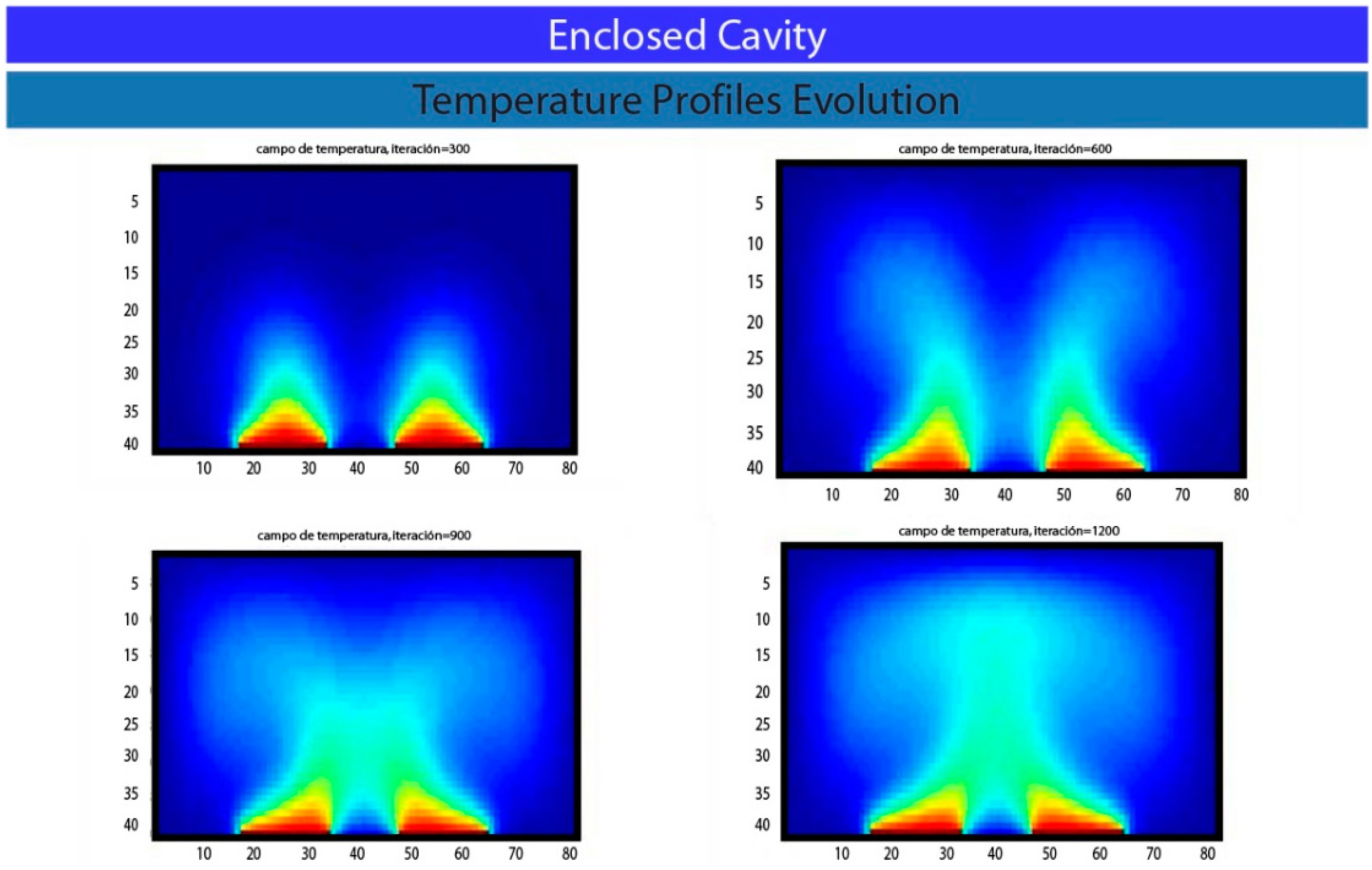
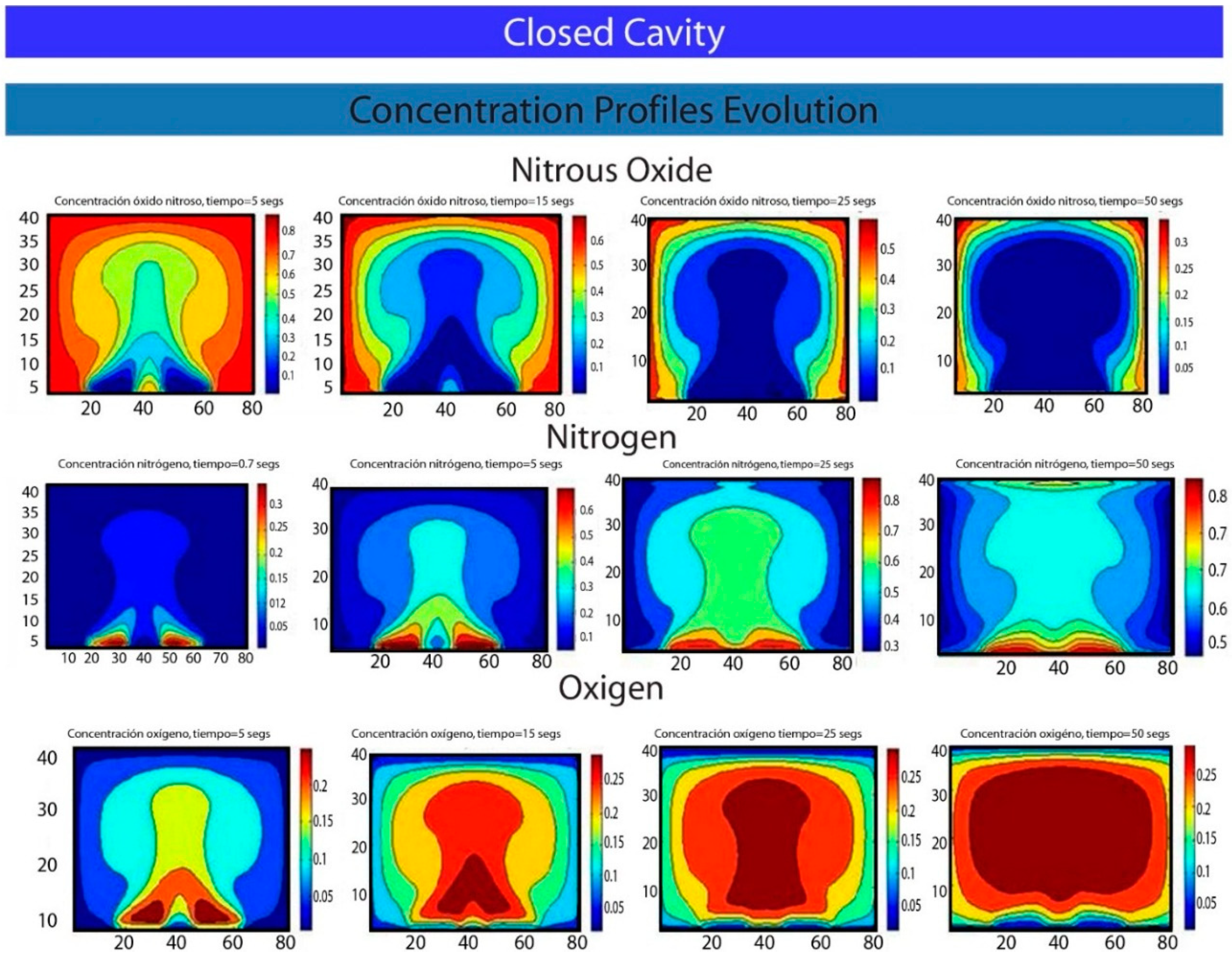
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dragani, W.C. A feature model of surface pressure and wind fields associated with passage of atmospheric cold fronts. Comp. Geosci. 1999, 25, 1149–1157. [Google Scholar] [CrossRef]
- Agee, E.M. Mesoscale cellular convection over the oceans. Dyn. Atmos. Oceans 1987, 10, 317–341. [Google Scholar] [CrossRef]
- Nicolas, X. Revue bibliographique sur les écoulements de Poiseuille–Rayleigh–Bénard: écoulements de convection mixte en conduites rectangulaires horizontales chauffées par le bas. Int. J. Therm. Sci. 2002, 41, 961–1016. [Google Scholar] [CrossRef]
- Bograchev, D.A.; Davidov, A.D.; Volgin, V.M. Linear stability of Rayleigh–Benard–Posieuille convection for electrochemical system. Int. J. Heat Mass Transf. 2008, 51, 4886–4891. [Google Scholar] [CrossRef]
- Kakuda, K.; Miura, S. Finite element simulation of three- dimensional Rayleigh–Bénard convection. Int. J. Comput. Fluid Dyn. 2001, 15. [Google Scholar] [CrossRef]
- Murty, V.D. A numerical investigation of Benard convection using finite elements. Comp. Fluids 1986, 14, 379–391. [Google Scholar] [CrossRef]
- Lan, C.H.; Ezekoye, O.A.; Howell, J.R.; Ball, K.S. Stability analysis for three-dimensional Rayleigh–Bénard convection with radioactively participating medium using spectral methods. Int. J. Heat Mass Transf. 2003, 46, 1371–1383. [Google Scholar] [CrossRef]
- Howle, L.E. A comparison of the reduced galerkin and pseudo-spectral methods for simulation of steady Rayleigh–Bénard convection. Int. J. Heat Mass Transf. 1996, 39, 2401–2407. [Google Scholar] [CrossRef]
- Luo, X.; Chen, W.-K. A discussion on finite-difference schemes for low Prandtl number Rayleigh–Bénard convection. In Advanced Computational Methods in Heat Transfer; Sundén, B., Brebbia, C.A., Eds.; WIT Press: Ashurst, UK, 1994. [Google Scholar]
- Park, H.M.; Ryu, D.H. Rayleigh–Bènard convection of viscoelastic fluids in finite domains. J. Non-Newton. Fluid Mech. 2001, 98, 169–184. [Google Scholar] [CrossRef]
- Tzeng, P.-Y.; Liu, M.-H. Direct-simulation Monte Carlo modeling on two-dimensional Rayleigh–Bénard instabilities of rarefied gas. Numer. Heat Transf. A Appl. 2005, 47, 805–823. [Google Scholar] [CrossRef]
- Zhang, J.; Fan, J. Kinetic study of the Rayleigh–Bénard flows. Chin. Sci. Bull. 2009, 54, 364–368. [Google Scholar] [CrossRef]
- Higuera, F.J.; Succi, S. Simulating the flow around a circular cylinder with a Lattice Boltzmann equation. Europhys. Lett. 1989, 8, 517–521. [Google Scholar] [CrossRef]
- Benzi, R.; Succi, S.; Vergassola, M. The lattice Boltzmann equation: theory and applications. Phys. Rep. 1992, 222, 145–197. [Google Scholar] [CrossRef]
- Shan, X.W. Simulation of Rayleigh–Bénard convection using a lattice Boltzmann method. Phys. Rev. E 1997, 55, 2780–2788. [Google Scholar] [CrossRef]
- Kao, P.-H.; Yang, R.-J. Simulating oscillatory flow in Rayleigh–Bénard convection using the lattice Boltzmann method. Int. J. Heat Mass Trans. 2007, 50, 3315–3328. [Google Scholar] [CrossRef]
- Barrios, G.; Rechtman, R.; Rojas, J.; Tovar, R. The lattice Boltzmann equation for natural convection in a two-dimensional cavity with a partially heated wall. J. Fluid Mech. 2005, 522, 91–100. [Google Scholar] [CrossRef]
- Chandrasekar, S. Hydrodynamic and Hydromagnetic Stabilities; Clarendon Press: Oxford, UK, 1961. [Google Scholar]
- Massaioli, F.; Benzi, R.; Succi, S. Exponential tails in 2-dimensional Rayleight–Bérnard convection. Europhys. Lett. 1993, 21, 305–310. [Google Scholar] [CrossRef]
- Benzi, R.; Tripiccione, R.; Massaioli, F.; Succi, S.; Ciliberto, S. On the scaling of the velocity and temperature structure functions in Rayleigh–Bénard convection. Europhys. Lett. 1994, 25, 341–346. [Google Scholar] [CrossRef]
- Moussaoui, M.A.; Jami, M.; Mezrhab, A.; Naji, H. Lattice Boltzmann simulation of convective heat transfer from heated blocks in a horizontal channel. Numer. Heat Transf. A Appl. 2009, 56, 422–443. [Google Scholar] [CrossRef]
- Amaya-Ventura, G.; Rodríguez-Romo, S. 2D Lattice Boltzmann Simulation of Chemical Reactions within Rayleigh–Bénard and Poiseuille–Bénard Convection Systems. In Proceedings of the International Conference on Numerical Analysis and Applied Mathematics 2011 (ICNAAM 2011), Halkidiki, Greece, 19–25 September 2011; pp. 1798–1801.
- Chen, S.Y.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- He, X.Y.; Chen, S.Y.; Doolen, G.D. A novel thermal model for the lattice Boltzmann method in incompressible limit. J. Comput. Phys. 1998, 146, 282–300. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, M. Modeling of electrokinetic reactive transport in micropore using a coupled lattice Boltzmann method. J. Geophys. Res. Solid Earth 2015, 120, 2877–2890. [Google Scholar] [CrossRef]
- Yamamoto, K.; He, X.Y.; Doolen, G.D. Simulation of combustion field with lattice Boltzmann method. J. Stat. Phys. 2002, 107, 367–383. [Google Scholar] [CrossRef]
- Chiavazzo, E.; Karlin, I.V.; Gorban, A.N.; Boulouchos, K. Coupling of the model reduction technique with the lattice Boltzmann method for combustion simulations. Combust. Flame 2010, 157, 1833–1849. [Google Scholar] [CrossRef]
- Chiavazzo, E.; Karlin, I.V.; Gorban, A.N.; Boulouchos, K. Efficient simulations of detailed combustion fields via the lattice Boltzmann method. Int. J. Numer. Methods Heat Fluid Flow 2011, 21, 494–517. [Google Scholar]
- Charru, F. Hydrodynamic Instabilities, 1st ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Levenspiel, O. Ingeniería de las Reacciones Químicas; Reverté: Barcelona, Spain, 1987. (In Spanish) [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Romo, S.; Ibañez-Orozco, O. Two-Dimensional Lattice Boltzmann for Reactive Rayleigh–Bénard and Bénard–Poiseuille Regimes. Entropy 2015, 17, 6698-6711. https://doi.org/10.3390/e17106698
Rodríguez-Romo S, Ibañez-Orozco O. Two-Dimensional Lattice Boltzmann for Reactive Rayleigh–Bénard and Bénard–Poiseuille Regimes. Entropy. 2015; 17(10):6698-6711. https://doi.org/10.3390/e17106698
Chicago/Turabian StyleRodríguez-Romo, Suemi, and Oscar Ibañez-Orozco. 2015. "Two-Dimensional Lattice Boltzmann for Reactive Rayleigh–Bénard and Bénard–Poiseuille Regimes" Entropy 17, no. 10: 6698-6711. https://doi.org/10.3390/e17106698
APA StyleRodríguez-Romo, S., & Ibañez-Orozco, O. (2015). Two-Dimensional Lattice Boltzmann for Reactive Rayleigh–Bénard and Bénard–Poiseuille Regimes. Entropy, 17(10), 6698-6711. https://doi.org/10.3390/e17106698




