Spatiotemporal Scaling Effect on Rainfall Network Design Using Entropy
Abstract
:1. Introduction
2. Methodology
2.1. Spatiotemporal Scale
2.2. Kriging
2.3. Entropy
2.4. Optimization of Network Design
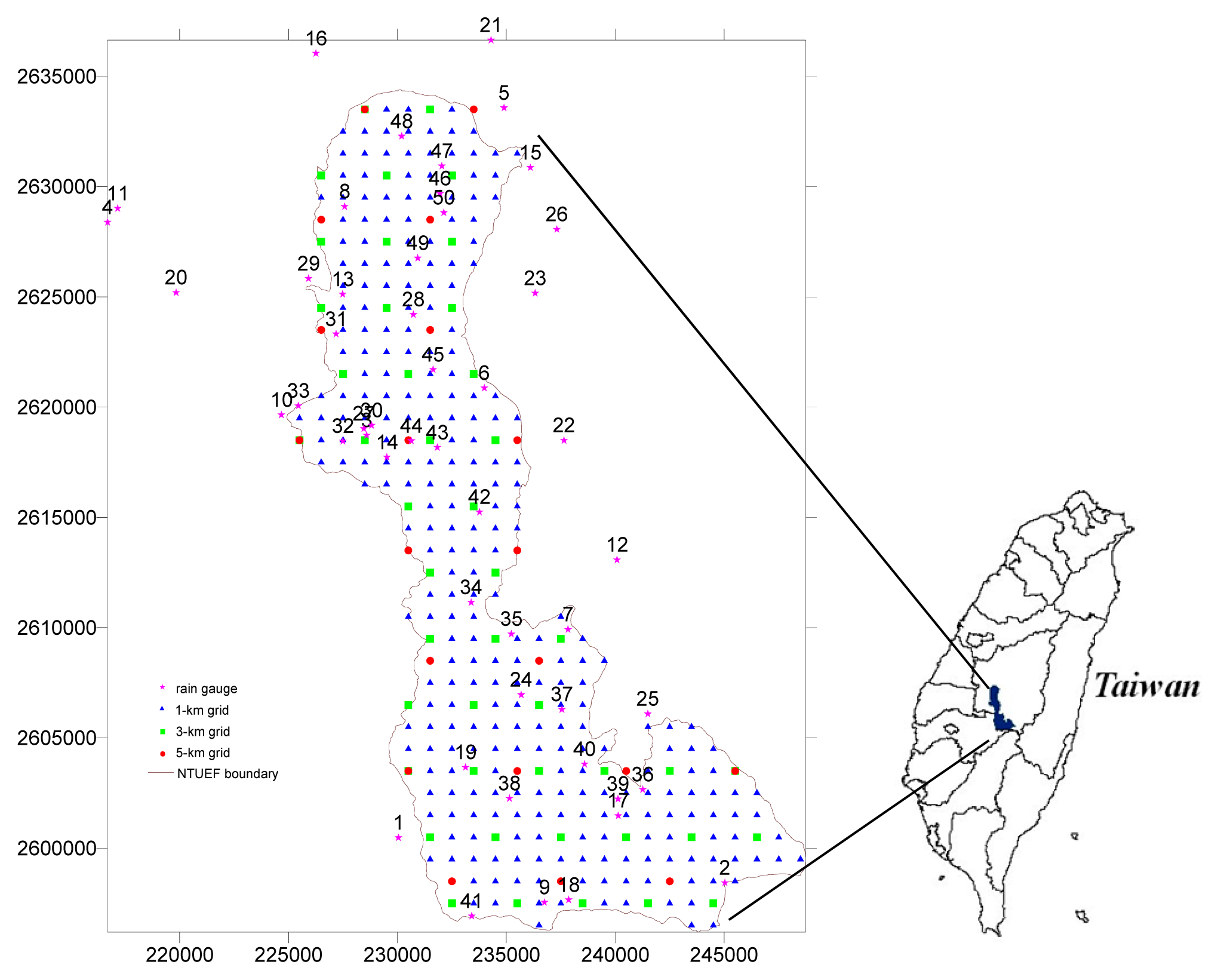
2.5. Study Area and Data
3. Result and Discussion
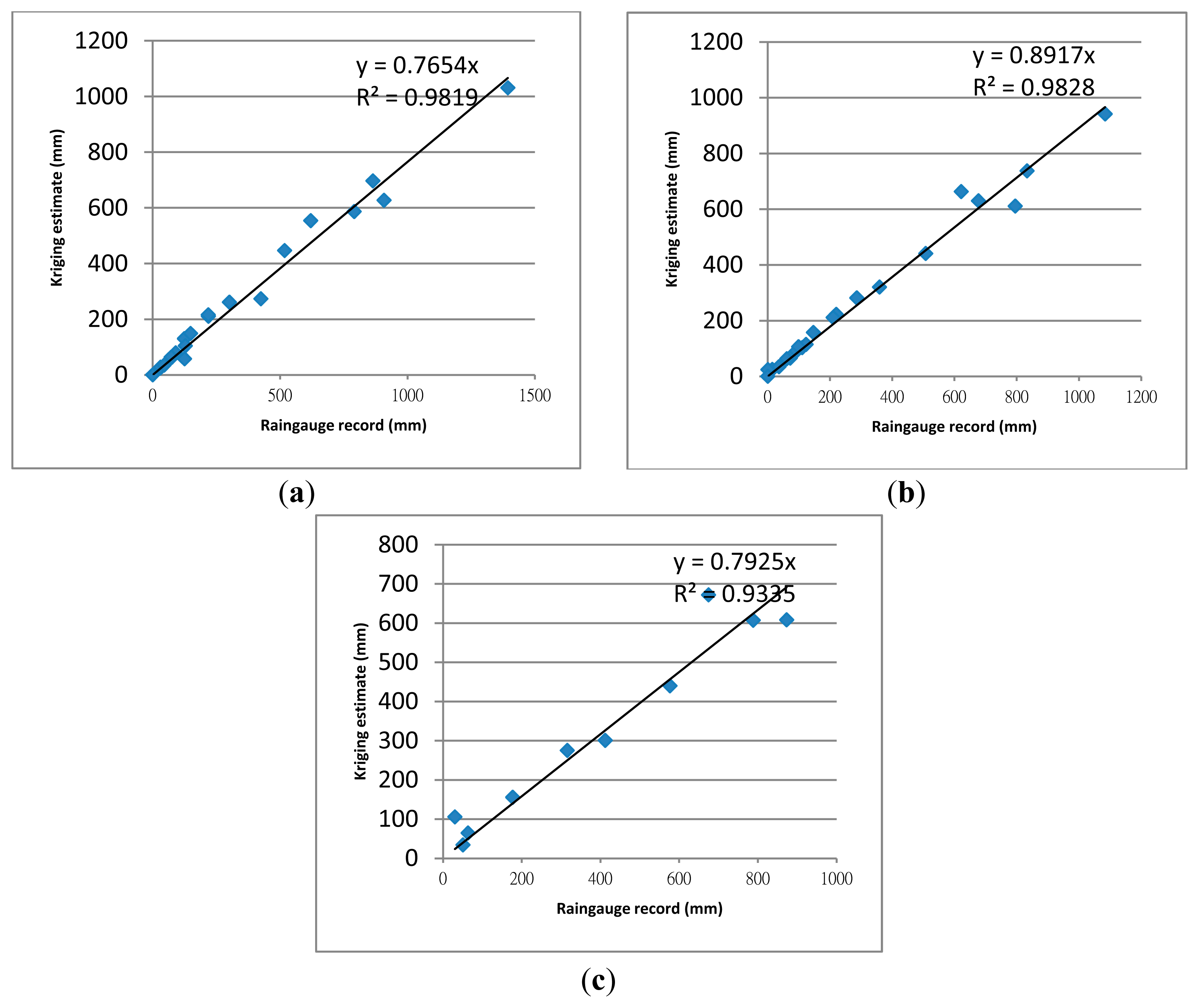
3.1. Validation of Kriging Estimates
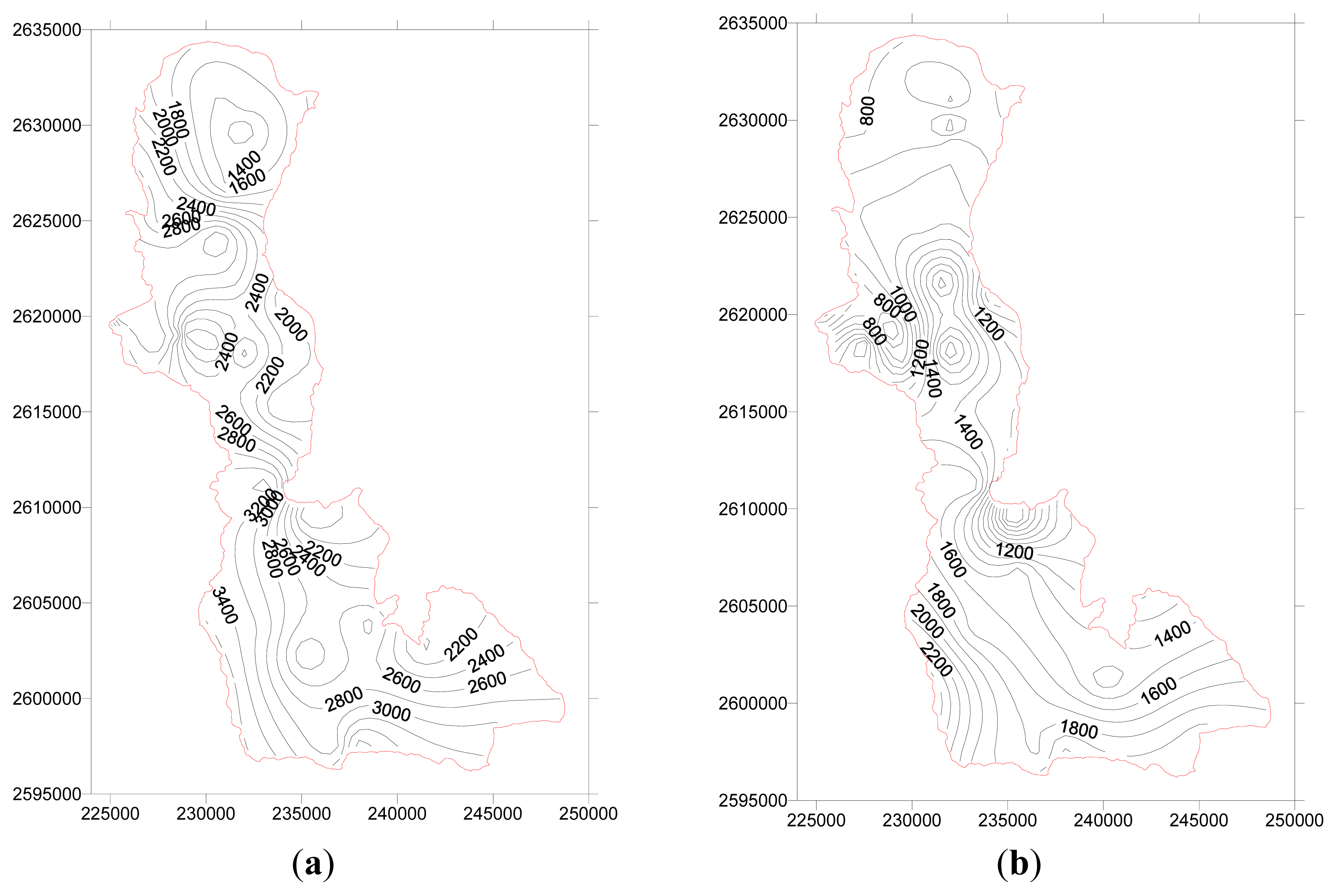
3.2. Uncertainty Distributed in Space
3.3 Spatial Scale Effect
3.4. Temporal Scale Effect
3.5. Optimal Rain Gauge Station Network of the NTUEF Area
4. Conclusions
- (1)
- It exhibits different locations for first prioritized candidate rain gauges between spatiotemporal scales.
- (2)
- The effect of spatial scales is insignificant in comparison to temporal scales for network design. From the joint entropy value, the difference between hourly and monthly scales is more significant than the six dry, wet months and annual rainfall. However, the difference is significant across the spatial scale.
- (3)
- A smaller number and a lower percentage of required stations (PRS) are needed to reach stable joint entropy of long duration (six months or year) at finer spatial scale. Compromising the accuracy and network density, we suggest the optimal network design comprising of 13 candidate stations be suitable across all spatiotemporal scales.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hackett, O.M. National water data program. J. Am. Water Work Assoc 1966, 58, 786–792. [Google Scholar]
- Campbell, S.A. Sampling and Analysis of Rain; American Society of Testing and Materials: West Conshohocken, PA, USA, 1983. [Google Scholar]
- World Meteorological Organisation (WMO), Guide to Hydrometeorological Practices; WMO Technical Paper 82; WMO: Geneva, Switzerland, 1970.
- Markus, M.H.; Knapp, V.; Tasker, G.D. Entropy and generalized least square methods in assessment of the regional value of streamgauges. J. Hydrol 2003, 283, 107–121. [Google Scholar]
- Cheng, K.S.; Lin, Y.C.; Liou, J.J. Rain-gauge network evaluation and augmentation using geostatistics. Hydrol. Process 2008, 22, 2554–2564. [Google Scholar]
- Harmancioglu, N. Measuring the information content of hydrological processes by the entropy concept. J. Civ. Eng. Facul. Ege Univ 1981, 13–40. [Google Scholar]
- Awumah, K.; Goulter, I. Assessment of reliability in water distribution networks using entropy based measures. Stoch. Hydrol. Hydraul 1990, 4, 309–320. [Google Scholar]
- Awumah, K.; Goulter, I.; Bhatt, S.K. Entropy-based redundancy measures in water-distribution networks. J. Hydraul. Eng 1991, 117, 595–614. [Google Scholar]
- Krstanovic, P.F.; Singh, V.P. Evaluation of rainfall network using entropy II: Application. Water Resour. Manag 1992, 6, 295–314. [Google Scholar]
- Al-Zahrani, M.; Husain, T. An algorithm for designing a precipitation network in the southwestern region of Saudi Arabia. J. Hydrol 1998, 205, 205–216. [Google Scholar]
- Ozkul, D.S.; Harmancioglu, N.B.; Singh, V.P. Entropy-based assessment of water quality monitoring networks. J. Hydraul. Eng 2000, 5, 90–100. [Google Scholar]
- Mogheir, Y.; Singh, V.P. Application of information theory to groundwater quality monitoring networks. Water Resour. Manag 2002, 16, 37–49. [Google Scholar]
- Mogheir, Y.; de Lima, J.L.M.P.; Singh, V.P. Characterizing the spatial variability of groundwater quality using the entropy theory: I. Synthetic data. Hydrol. Process 2004, 18, 2165–2179. [Google Scholar]
- Nunes, L.M.; Cunha, M.C.; Ribeiro, L. Groundwater Monitoring Network Optimization with Redundancy Reduction. J. Water Resour. Plann. Manag 2004, 130, 33–43. [Google Scholar]
- Masoumi, F.; Kerachian, R. Assessment of the groundwater salinity monitoring network of the Tehran region: Application of the discrete entropy theory. Water Sci. Technol 2008, 58, 765–771. [Google Scholar]
- Mogheir, Y.; Singh, V.P.; de Lima, J.L.M.P. Spatial assessment and redesign of a groundwater quality monitoring network quality using entropy theory, Gaza Strip, Palestine. Hydrogeol. J 2006, 14, 700–712. [Google Scholar]
- Yoo, C.; Jung, K.; Lee, J. Evaluation of rain gauge network using entropy theory: Comparison of mixed and continuous distribution function applications. J. Hydrol. Eng 2008, 13, 226–235. [Google Scholar]
- Mogheir, Y.; de Lima, J.L.M.P.; Singh, V.P. Entropy and multi-objective based approach for groundwater quality monitoring network assessment and redesign. Water Resour. Manag 2009, 23, 1603–1620. [Google Scholar]
- Alfonso, L.; Lobbreche, A.; Price, R. Information theory-based approach for location of monitoring water level gauges in polder. Water Resour. Res 2010, 46, W03528. [Google Scholar]
- Alfonso, L.; Lobbrecht, A.; Price, R. Optimization of water level monitoring network in polder systems using information theory. Water Resour. Res 2010, 46, W12553. [Google Scholar]
- Li, C.; Singh, V.P.; Mishra, A.K. Entropy theory-based criterion for hydrometric network evaluation and design: Maximum information minimum redundancy. Water Resour. Res 2012, 48, W5521. [Google Scholar]
- Gong, W.; Gupta, H.V.; Yang, D.W.; Sricharan, K.; Hero, A.O. Estimating epistemic and aleatory uncertainty during hydrologic modeling: An information theoretic approach. Water Resour. Res 2013, 49, 2253–2273. [Google Scholar]
- Chen, Y.C.; Wei, C.; Yeh, H.C. Rainfall network design using kriging and entropy. Hydrol. Process 2008, 22, 340–346. [Google Scholar]
- Yeh, H.C.; Chen, Y.C.; Wei, C.; Chen, R.H. Entropy and Kriging Approach to Rainfall Network Design. Paddy Water Environ 2011, 9, 343–355. [Google Scholar]
- Awadallah, A.G. Selecting optimum locations of rainfall stations using kriging and entropy. Int. J. Civil Environ. Eng 2012, 12, 36–41. [Google Scholar]
- Amorocho, J.; Espildora, B. Entropy in the assessment of uncertainty in hydrologic systems and models. Water Resour. Res 1973, 9, 1511–1522. [Google Scholar]
- Chapman, T.G. Entropy as a measure of hydrologic data uncertainty and model performance. J. Hydrol 1986, 85, 111–126. [Google Scholar]
- Harmancioglu, N.; Yevjevich, V. Transfer of hydrologic information among river points. J. Hydrol 1987, 91, 103–118. [Google Scholar]
- Yang, Y.; Burn, D.H. An entropy approach to data collection network design. J. Hydrol 1994, 157, 307–324. [Google Scholar]
- Singh, V.P. The Use of Entropy in Hydrology and Water Resources. Hydrol. Process 1997, 11, 587–626. [Google Scholar]
- Kawachi, T.; Maruyama, T.; Singh, V.P. Rainfall entropy for delineation of water resources zones in Japan. J. Hydrol 2001, 246, 36–44. [Google Scholar]
- Mishra, A.K.; Coulibaly, P. Hydrometric network evaluation for Canadian watersheds. J. Hydrol 2010, 380, 420–437. [Google Scholar]
- Memarzadeh, M.; Mahjouri, N.; Kerachian, R. Evaluating sampling locations in river water quality monitoring networks: Application of dynamic factor analysis and discrete entropy theory. Environ. Earth Sci 2013, 70, 2577–2585. [Google Scholar]
- Sivapalan, M.; Grayson, R.; Woods, R. Preface Scale and scaling in hydrology. Hydrol. Process 2004, 18, 1369–1371. [Google Scholar]
- Viney, N.R.; Sivapala, M. A framework for scaling of hydrologic conceptualizations based on a disaggregation–aggregation approach. Hydrol. Process 2004, 18, 1395–1408. [Google Scholar]
- Serra, Y.L.; Mcphaden, M.J. Multiple Time- and Space-Scale Comparisons of ATLAS Buoy Rain Gauge Measurements with TRMM Satellite Precipitation Measurements. J. Appl. Meteorol 2003, 42, 1045–1059. [Google Scholar]
- Singh, V.P. Entropy Theory and Its Application in Environmental and Water Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Stewart, J.B.; Engman, E.T.; Feddes, R.A.; Kerr, Y. Scaling up in Hydrology Using Remote Sensing; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Matheron, G. Traite De Geostatistique Appliqué, Tome 1; Editions Technip: Paris, France, 1962. (In French) [Google Scholar]
- Rodriguez-Iturbe, I.; Sanabria, M.G.; Bras, R.L. A geomorphoclimatic theory of the instantaneous unit hydrograph. Water Resour. Res 1982, 18, 877–886. [Google Scholar]
- Chiles, J.-P.D.P. Geostatistics-Modeling Spatial Uncertainty; Willey: New York, NY, USA, 1999. [Google Scholar]
- Wackernagel, H. Multivariate Geostatistics; Springer-Verlag: Berlin, Germany, 2003. [Google Scholar]
- Kebaili, B.Z.; Chebbi, A. Comparison of two kriging interpolation methods applied to spatiotemporal rainfall. J. Hydrol 2009, 365, 56–73. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J 1948, 27, 623–656. [Google Scholar]
- Shannon, C.E.; Weaver, W. Mathematical Theory of Communication; University of Illinois Press: Champaign, IL, USA, 1949. [Google Scholar]
- Kay, P.A.; Kutiel, H. Some remarks on climatic maps of precipitation. Clim. Res 1994, 4, 233–241. [Google Scholar]
- Kutiel, H.; Kay, P.A. Effects of network design on climatic maps of precipitation. Clim. Res 1996, 7, 1–10. [Google Scholar]





| No. | Rain Gauge Station | Elevation (m) | TM2 (m) | Hourly Rainfall for Typhoon Events (mm) | Monthly Rainfall (mm) | Annual Rainfall (mm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Easting | Northing | Maximum | Minimum | Mean | Standard Deviation | Maximum | Minimum | Mean | Standard Deviation | Maximum | Minimum | Mean | Standard Deviation | |||
| 1 | AliShan | 2,413 | 230,043 | 2,600,476 | 123.0 | 0.0 | 25.8 | 25.6 | 3,346.0 | 0.0 | 336.6 | 438.1 | 5,886.7 | 2,196.5 | 4,039.2 | 1,140.9 |
| 2 | Mt. Jade | 3,845 | 245,030 | 2,598,435 | 64.0 | 0.0 | 14.7 | 13.4 | 2,189.9 | 0.0 | 254.8 | 299.0 | 4,705.2 | 1,702.7 | 3,058.2 | 830.3 |
| 3 | Xitou Nursery | 1,169 | 228,583 | 2,618,722 | 110.0 | 0.0 | 17.0 | 20.6 | 1,770.0 | 0.0 | 202.3 | 246.1 | 4,053.0 | 1,291.0 | 2,455.3 | 673.5 |
| 4 | Jushan-NTU | 156 | 216,693 | 2,628,383 | 145.0 | 0.0 | 10.2 | 18.1 | 1,173.0 | 0.0 | 181.0 | 214.8 | 2,821.6 | 1,355.1 | 2,221.0 | 449.4 |
| 5 | Shueli-NTU | 295 | 234,893 | 2,633,571 | 123.5 | 0.0 | 10.5 | 17.2 | 1,512.5 | 0.0 | 150.7 | 200.4 | 2,816.0 | 2,12.5 | 1,835.9 | 724.6 |
| 6 | Nemoupu-NTU | 509 | 233,987 | 2,620,868 | 125.5 | 0.0 | 11.2 | 15.8 | 1,008.0 | 0.0 | 153.3 | 175.4 | 2,805.0 | 946.0 | 1,820.9 | 491.0 |
| 7 | Heshe-NTU | 780 | 237,830 | 2,609,920 | 74.0 | 0.0 | 11.2 | 14.3 | 1,258.0 | 0.0 | 154.2 | 185.0 | 2,688.5 | 1,062.0 | 1,855.9 | 498.8 |
| 8 | Chinshueigao-NTU | 520 | 227,576 | 2,629,098 | 100.0 | 0.0 | 9.2 | 14.5 | 1,271.6 | 0.0 | 187.6 | 222.1 | 4,275.0 | 680.5 | 2,234.6 | 852.4 |
| 9 | Hsingouko | 2,540 | 236,749 | 2,597,543 | 112.5 | 0.0 | 16.8 | 15.9 | 2,203.0 | 0.0 | 241.7 | 294.0 | 4,524.5 | 787.0 | 2,828.7 | 1,068.2 |
| 10 | Dann | 1,528 | 224,672 | 2,619,646 | 75.5 | 0.0 | 8.6 | 11.2 | 945.0 | 0.0 | 180.7 | 197.9 | 3,154.0 | 773.0 | 2,088.8 | 627.1 |
| 11 | Jushan | 151 | 217,157 | 2,629,012 | 170.0 | 0.0 | 8.9 | 16.9 | 1,133.5 | 0.0 | 177.6 | 207.3 | 3,205.0 | 613.0 | 2,047.8 | 611.7 |
| 12 | Wanshian | 2,403 | 240,080 | 2,613,075 | 85.0 | 0.0 | 12.8 | 15.0 | 1,633.5 | 0.0 | 208.3 | 247.9 | 3,642.0 | 924.0 | 2,421.6 | 832.5 |
| 13 | Phoenix Garden | 878 | 227,485 | 2,625,117 | 141.0 | 0.0 | 11.9 | 18.4 | 1,292.0 | 0.0 | 218.2 | 235.6 | 3,671.0 | 948.0 | 2,522.5 | 741.5 |
| 14 | Xitou Observation | 1,771 | 229,514 | 2,617,731 | 61.0 | 0.0 | 9.2 | 9.6 | 1,053.5 | 0.0 | 192.8 | 203.2 | 3,139.0 | 909.5 | 2,219.5 | 629.0 |
| 15 | Long-Shen Bridge | 339 | 236,100 | 2,630,858 | 130.5 | 0.0 | 9.0 | 15.0 | 900.0 | 0.0 | 164.5 | 179.4 | 2,812.5 | 1,133.5 | 1,921.2 | 653.3 |
| 16 | Ji-Ji | 235 | 226,257 | 2,636,039 | 103.5 | 0.0 | 8.3 | 13.2 | 975.0 | 0.0 | 188.7 | 210.0 | 3,100.5 | 1,504.5 | 2,256.7 | 923.4 |
| 17 | GuanShan | 1,780 | 240,135 | 2,601,472 | 81.5 | 0.0 | 14.8 | 15.4 | 1,171.5 | 0.0 | 227.7 | 225.2 | 3,695.9 | 1,296.5 | 2,444.9 | 820.9 |
| 18 | Pasture | 2,677 | 237,860 | 2,597,660 | 136.0 | 0.0 | 18.3 | 17.4 | 2,383.5 | 0.0 | 304.1 | 387.7 | 5,218.8 | 1,653.5 | 3,719.5 | 1,025.3 |
| 19 | Shenmu Village | 1,595 | 233,125 | 2,603,668 | 91.5 | 0.0 | 16.4 | 17.0 | 2,141.5 | 0.0 | 260.1 | 330.5 | 4,649.5 | 1,653.5 | 3,114.4 | 1,664.2 |
| 20 | Chungshinlun | 661 | 219,839 | 2,625,192 | 63.5 | 0.0 | 9.4 | 12.6 | 1,075.0 | 0.0 | 231.0 | 264.0 | 3,682.0 | 1,554.5 | 2,731.8 | 1,468.3 |
| 21 | Shueli | 593 | 234,295 | 2,636,644 | 110.0 | 0.0 | 10.2 | 17.5 | 911.0 | 0.0 | 193.9 | 218.3 | 3,094.0 | 1,451.0 | 2,341.8 | 1,276.9 |
| 22 | Fongchiou | 1,151 | 237,647 | 2,618,491 | 84.5 | 0.0 | 11.1 | 14.3 | 1,211.0 | 0.0 | 166.9 | 210.1 | 2,938.0 | 1,088.0 | 2,021.5 | 1,114.5 |
| 23 | ShangAn | 781 | 236,321 | 2,625,167 | 66.0 | 0.0 | 8.6 | 12.2 | 804.5 | 0.0 | 162.0 | 190.1 | 2,914.0 | 1,193.0 | 1,973.3 | 1,074.3 |
| 24 | Hsin-shin Bridge | 897 | 235,680 | 2,606,957 | 96.5 | 0.0 | 14.2 | 17.2 | 1,751.5 | 0.0 | 193.9 | 266.1 | 3,277.5 | 1,291.0 | 2,425.1 | 1,297.9 |
| 25 | Dongpu | 887 | 241,493 | 2,606,091 | 67.0 | 0.0 | 10.2 | 11.8 | 1,307.0 | 0.0 | 169.6 | 219.2 | 2,917.0 | 1,107.0 | 2,092.9 | 1,138.7 |
| 26 | Siluang | 1,001 | 237,315 | 2,628,058 | 78.5 | 0.0 | 10.7 | 15.5 | 963.5 | 0.0 | 186.7 | 217.3 | 3,061.0 | 1,313.5 | 2,193.8 | 1,218.5 |
| 27 | Xitou office | 1,156 | 228,453 | 2,619,028 | 56.0 | 0.0 | 13.5 | 12.9 | 1,218.5 | 0.0 | 223.2 | 277.4 | 4,005.5 | 1,125.5 | 3,053.3 | 1,369.3 |
| 28 | TienDi | 787 | 230,728 | 2,624,199 | 53.5 | 0.0 | 11.3 | 12.6 | 1,360.5 | 0.0 | 140.3 | 266.4 | 3,122.5 | 137.0 | 2,326.5 | 973.3 |
| 29 | GuangHsin | 645 | 225,917 | 2,625,831 | 49.5 | 0.0 | 9.8 | 12.2 | 1,190.5 | 0.0 | 238.9 | 286.9 | 3,628.5 | 329.0 | 3,124.5 | 1,299.3 |
| 30 | No.3 Gully | 1,185 | 228,811 | 2,619,174 | 25.0 | 0.0 | 4.2 | 5.7 | 776.0 | 0.0 | 167.2 | 180.2 | 3,339.5 | 712.5 | 1,937.0 | 907.2 |
| 31 | Neihu elementary school | 772 | 227,181 | 2,623,316 | 52.0 | 0.0 | 9.8 | 11.7 | 1,214.5 | 0.0 | 201.6 | 258.7 | 3,560.5 | 901.0 | 3,090.3 | 1,157.6 |
| 32 | Lower University Gully | 1,197 | 227,492 | 2,618,456 | 106.0 | 0.0 | 15.1 | 16.8 | 1,663.0 | 0.5 | 255.6 | 402.7 | 3,956.0 | 222.5 | 3,334.2 | 1,207.7 |
| 33 | Wushio | 1,495 | 225,450 | 2,620,064 | 32.0 | 0.0 | 7.3 | 7.5 | 2,296.5 | 0.0 | 212.4 | 394.3 | 3,941.0 | 610.0 | 3,400.8 | 1,221.4 |
| 34 | Yashanpin | 1,390 | 233,383 | 2,611,144 | 86.0 | 0.0 | 17.5 | 19.4 | 1,872.5 | 0.0 | 269.3 | 367.1 | 4,221.0 | 2,264.5 | 3,534.0 | 1,478.1 |
| 35 | Alibudon | 1,208 | 235,227 | 2,609,712 | 31.5 | 0.0 | 4.8 | 7.9 | 823.5 | 0.0 | 135.8 | 162.1 | 2,876.0 | 530.5 | 1,549.0 | 780.0 |
| 36 | Salishian | 1,216 | 241,259 | 2,602,664 | 61.5 | 0.0 | 10.3 | 12.3 | 1,211.5 | 0.0 | 208.0 | 274.3 | 3,284.5 | 824.5 | 1,941.2 | 799.8 |
| 37 | Neuchangpin | 1,306 | 237,549 | 2,606,292 | 83.0 | 0.0 | 13.8 | 16.5 | 1,500.0 | 0.0 | 185.3 | 247.9 | 2,672.5 | 1,768.5 | 2,302.8 | 1,008.6 |
| 38 | Shenmu | 1,315 | 235,142 | 2,602,259 | 75.0 | 0.0 | 12.9 | 15.5 | 1,490.5 | 0.5 | 297.5 | 413.5 | 3,885.0 | 425.0 | 2,185.3 | 955.8 |
| 39 | 32-compartment | 1,823 | 240,123 | 2,602,231 | 59.0 | 0.0 | 15.6 | 13.5 | 1,714.5 | 0.0 | 223.5 | 298.9 | 3,073.0 | 2,050.5 | 2,318.0 | 1,157.2 |
| 40 | 30-compartment | 2,097 | 238,588 | 2,603,814 | 66.0 | 0.0 | 14.8 | 14.4 | 1,725.0 | 0.0 | 227.2 | 341.3 | 4,294.0 | 1,134.5 | 2,903.7 | 1,244.7 |
| 41 | 29-compartment | 2,298 | 233,408 | 2,596,924 | 80.5 | 0.0 | 20.2 | 20.7 | 2,307.5 | 0.0 | 347.0 | 466.6 | 5,450.5 | 974.5 | 3,453.3 | 1,774.8 |
| 42 | 20-compartment | 967 | 233,765 | 2,615,241 | 72.0 | 0.0 | 12.8 | 15.1 | 1,372.5 | 15.0 | 174.8 | 282.1 | 2,010.0 | 603.0 | 1,456.5 | 573.6 |
| 43 | 21-compartment | 1,280 | 231,832 | 2,618,174 | 99.5 | 0.0 | 22.3 | 24.4 | 2,243.5 | 7.0 | 296.3 | 433.4 | 2,946.0 | 2,048.5 | 2,518.5 | 1,023.4 |
| 44 | 22-compartment | 892 | 230,636 | 2,618,475 | 79.0 | 0.0 | 13.7 | 17.1 | 1,403.0 | 3.0 | 198.1 | 259.8 | 2,859.5 | 1,859.5 | 2,129.6 | 877.4 |
| 45 | 24-compartment | 1,278 | 231,635 | 2,621,701 | 107.0 | 0.0 | 18.9 | 21.2 | 2,042.0 | 0.0 | 171.1 | 339.8 | 2,820.5 | 442.0 | 1,582.8 | 797.0 |
| 46 | 13-compartment | 454 | 231,953 | 2,629,686 | 51.5 | 0.0 | 7.9 | 11.0 | 708.5 | 8.5 | 178.2 | 193.9 | 2,728.5 | 1,003.5 | 1,870.9 | 804.6 |
| 47 | 16-compartment | 1,002 | 232,038 | 2,630,932 | 71.0 | 0.0 | 10.6 | 14.9 | 303.0 | 2.5 | 114.4 | 203.5 | 1,473.5 | 508.5 | 1,058.4 | 458.3 |
| 48 | 17-compartment | 454 | 230,194 | 2,632,283 | 51.0 | 0.0 | 8.9 | 10.4 | 343.0 | 0.0 | 166.6 | 259.3 | 1,403.0 | 409.5 | 1,110.8 | 300.3 |
| 49 | 11-compartment | 1,228 | 230,931 | 2,626,757 | 60.0 | 0.0 | 12.9 | 14.5 | 915.0 | 21.0 | 216.6 | 207.2 | 2,998.0 | 1,402.0 | 2,219.9 | 929.7 |
| 50 | 9-compartment | 1,213 | 232,127 | 2,628,823 | 57.0 | 0.0 | 10.4 | 12.3 | 755.0 | 21.5 | 216.4 | 189.2 | 2,391.5 | 1,301.5 | 1,839.6 | 762.0 |
| Typhoon | Date | Maximum Wind (m/s) | Rainfall Duration (h) | Damage (Billion, NT) |
|---|---|---|---|---|
| Herb | 29 July–1 August 1996 | 53 | 44 | 39.3 |
| Toraji | 28–31 July 2001 | 38 | 24 | 14.7 |
| Mindulle | 28 June–3 July 2004 | 45 | 72 | 6.5 |
| Kalmeigi | 16–18 July 2008 | 33 | 32 | 3.4 |
| Silaku | 11–16 September 2008 | 51 | 75 | 5.6 |
| Marakot | 5–10 August 2009 | 40 | 96 | 47.7 |
| Saola | 30 July–3 August 2012 | 38 | 42 | 16.2 |
| Temporal Scale | b (Sill, mm2) | a (Range Parameter, m) | Kriging Variance (mm2) |
|---|---|---|---|
| Hour | 165 ± 292 | 40,243 ± 25,538 | 21 ± 62 |
| Month | 23,529 ± 67,316 | 39,481 ± 67,316 | 3,154 ± 7,760 |
| Dry six months | 43,209 ± 52,813 | 50,926 ± 22,708 | 3,198 ± 4,184 |
| Wet six months | 583,324 ± 560,410 | 39,499 ± 27,171 | 64,250 ± 58,808 |
| Annual | 645,623 ± 654,175 | 31,337 ± 29,685 | 104,080 ± 107,613 |
| Scale | Candidate Station Number | Hour | Month | Six Dry Months | Six Wet Months | Year |
|---|---|---|---|---|---|---|
| 1-km | 346 | 126 (36.4%) | 143 (41.3%) | 3(0.9%) | 2(0.6%) | 4 (1.1%) |
| 3-km | 45 | 26 (57.8%) | 28 (62.2%) | 5(11.1%) | 3(6.7%) | 4 (8.9%) |
| 5-km | 20 | 14 (70.0%) | 13 (65.0%) | 6(30%) | 3(15%) | 3 (15.0%) |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wei, C.; Yeh, H.-C.; Chen, Y.-C. Spatiotemporal Scaling Effect on Rainfall Network Design Using Entropy. Entropy 2014, 16, 4626-4647. https://doi.org/10.3390/e16084626
Wei C, Yeh H-C, Chen Y-C. Spatiotemporal Scaling Effect on Rainfall Network Design Using Entropy. Entropy. 2014; 16(8):4626-4647. https://doi.org/10.3390/e16084626
Chicago/Turabian StyleWei, Chiang, Hui-Chung Yeh, and Yen-Chang Chen. 2014. "Spatiotemporal Scaling Effect on Rainfall Network Design Using Entropy" Entropy 16, no. 8: 4626-4647. https://doi.org/10.3390/e16084626
APA StyleWei, C., Yeh, H.-C., & Chen, Y.-C. (2014). Spatiotemporal Scaling Effect on Rainfall Network Design Using Entropy. Entropy, 16(8), 4626-4647. https://doi.org/10.3390/e16084626





