Abstract
The intention of this paper is to evaluate the sensitivity of the Storm Water Management Model (SWMM) output to its input parameters. A global parameter sensitivity analysis is conducted in order to determine which parameters mostly affect the model simulation results. Two different methods of sensitivity analysis are applied in this study. The first one is the partial rank correlation coefficient (PRCC) which measures nonlinear but monotonic relationships between model inputs and outputs. The second one is based on the mutual information which provides a general measure of the strength of the non-monotonic association between two variables. Both methods are based on the Latin Hypercube Sampling (LHS) of the parameter space, and thus the same datasets can be used to obtain both measures of sensitivity. The utility of the PRCC and the mutual information analysis methods are illustrated by analyzing a complex SWMM model. The sensitivity analysis revealed that only a few key input variables are contributing significantly to the model outputs; PRCCs and mutual information are calculated and used to determine and rank the importance of these key parameters. This study shows that the partial rank correlation coefficient and mutual information analysis can be considered effective methods for assessing the sensitivity of the SWMM model to the uncertainty in its input parameters.1. Introduction
Urban drainage models are widely used for planning, design and management of urban drainage systems. These models have become very complex. Sensitivity analysis of models has been identified to be an essential component in building models and evaluating the performance of models [1]. Sensitivity analysis can be applied to identify the relative influence of each model input parameter on the model outputs. Generally speaking, there are two main groups of sensitivity analysis: local and global approaches [2]. Local sensitivity analysis evaluates how the outputs change by varying one input parameter at a time. On the contrary, the global sensitivity analysis (GSA) considers a variation of all parameters simultaneously and evaluates their contribution to the uncertainty. The local approach has apparent limitations in complex hydrological models (e.g., SWMM), which often involve many nonlinear relationships between input and output variables [3,4].
This study is focused primarily on the global sensitivity analysis (GSA) methods. There are numerous methods available for performing sensitivity analyses. Widely used GSA methods include variance-based methods [5], sampling-based methods such as Latin hypercube sampling with partial rank correlation coefficient index (LHS-PRCC) [6], global screening methods [7], regression-based methods and others [8].
Storm Water Management Model (SWMM) [9] by the U.S. Environmental Protection Agency (EPA) is chosen for this study to simulate various hydrologic/hydraulic processes in urban areas. It is designed for single event or long-term (continuous) simulation of rainfall-runoff transformation, hydraulic performance and water quality. SWMM has four principle hydrologic/hydraulic processes: precipitation, rainfall losses, runoff transformation and flow routing. It is necessary to conduct a detailed sensitivity analysis to evaluate the main parameters of the SWMM which are the most sensitive parameters affecting the rainfall-runoff-routing simulation in the model.
Although several global sensitivity analysis (GSA) methods have been proposed in many fields of science and engineering, there are not many reports on global sensitivity analysis in the urban drainage field [10]. The Morris screening and the standardised regression coefficients (SRCs) were applied to a sewer flow and water quality model by Gamerith et al. [11]. Vezzaro and Mikkelsen [12] recently applied a variance decomposition GSA method combined with the General Likelihood Uncertainty Estimation (GLUE) in order to identify the major sources of uncertainty in a storm-water quality model. Freni et al. [13] briefly discussed parameter sensitivity in urban stormwater quality modeling within general likelihood uncertainty estimation (GLUE) approach; Dotto et al. [14] analyzed parameter sensitivities using the formal Bayesian approach. Prat et al. [15] investigated sensitivities in an integrated model study of the sewer system and the waste water treatment plant with Monte Carlo simulations and Partial Correlation Coefficients (PCC).
One of the methods of global analysis is the Partial Rank Correlation Coefficient Analysis, a method that is based on the Pearson correlation coefficient and that assumes a monotonic relationship between the input and the output variables [16]. The partial rank correlation coefficient (PRCC) is widely used for sensitivity analysis [17,18].
While there are several approaches to quantify the magnitude (strength) of relations between variables, the mutual information, derived from information theory, provides a general measure of dependencies between variables. The concept of mutual information proposed by Shannon and Weaver in 1949 [19] was developed to quantify shared information between data sets. Unlike correlation that is only applicable to the linear relationship between two variables, the mutual information is theoretically able to identify various types of relations [20]. Mutual information is well suited for solving the hydrological problems, because there rarely exists the linear relationship between any two hydrological variables [21]. This problem can be avoided by analyzing mutual information which measures the statistical dependence between two hydrological variables. Bonnlander et al. [22] demonstrated the application of mutual information for selecting the key input variables of neural network models. Mishra et al. [23] described three global sensitivity methods, that is, stepwise regression, mutual information analysis and classification tree for determining uncertainty importance, and showed some sample applications for ground water models. Zeng et al. [24] compared stepwise regression analysis and mutual entropy analysis for identifying the key uncertainty variables affecting the parameters of normal groundwater level series.
In this study, two GSA methods—LHS-PRCC and mutual information (entropy) analysis—are applied to a conceptual hydrologic-hydraulics model (SWMM) in order to, (i) provide a compare of both methods concerning the similarity of results and their effectiveness; (ii) identify and rank the important model parameters for selected model output variables. The two methods are selected for comparison because these potentially powerful sensitivity analysis techniques are not well known in the hydrologic modeling literature.
The structure of this paper is as follows. In Section 2, we describe two GSA methods: partial rank correlation coefficient (PRCC) and mutual information analysis. We also introduce our working example. SWMM model is described briefly. In Section 3, the applicability of PRCC and mutual information analysis is demonstrated using results from SWMM model application at the Ya-hua garden district in Changsha city. The Latin Hypercube Sampling (LHS) method is used to generate 1000 sets of parameter samples. Sensitivities are evaluated using different model outputs. Finally, some conclusions of the study are given in Section 4.
2. Materials and Methods
2.1. Study Site
The selected study area was Ya-hua garden district in Changsha city, and the drainage area was approximately 11.7 ha (Figure 1). Mean annual precipitation in the region is between 1200-2000 mm, and the maximum recorded daily precipitation was 338mm in 1996.
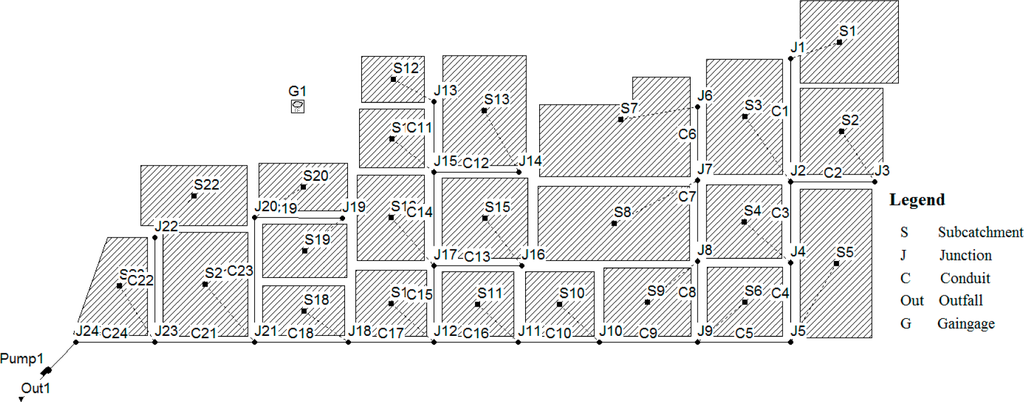
The total impervious area of the study area was 56%, and pervious area was 44%. The overland average slope was 0.3%. The study area was subdivided into 24 sub-catchments with the size of each varying from 0.24–0.96 ha, based on the existing land use, conduit diameter, topography and drainage characteristics, etc. The total number of conduits was 23, and the number of node was 24. The catchment was drained by a separate sewage drainage system, and the storm water runoff flowed past 23 conduits to the catchment outlet labeled OUT1 (Figure 1). Rainfall was measured by rain gauges installed within the catchment. Table 1 presents the total runoff volume and peak discharge of the monitored rainfall events. The parameters of SWMM model are calibrated by three measurement data on 12/08/01, 28/07/02, 25/08/03. A detailed description of the catchment is given in Ren [25].

2.2. Model Description
The Environment Protection Agency (EPA) Storm Water Management Model (SWMM) is chosen for this study. SWMM is a physically-based distributed model, which means that a study area can be subdivided into any number of irregular sub-catchments. The model is capable of simulating all the hydrologic-hydraulic processes that occur in the urban drainage system [26]. SWMM consists of four functional program blocks, plus a coordinating executive block. SWMM has been widely applied to plan and design of the urban drainage system.
In the present study, two primary functional blocks, the Runoff block and the Extran block, are considered to route flows. The Runoff block is designed to simulate continuous runoff hydrographs for each sub-catchment in the drainage basin. Runoff hydrographs from the various sub-catchments are taken as input to the Extran block. The Extran block completes complex hydraulic analysis of the open and closed conduit systems. The Extran block solves the complete Saint-Venant equations accounting for channel storage, backwater effects, surcharged flow and reverse flow.
SWMM generates catchment’s surface runoff from rainfall using a distributed non-linear reservoir model, taking into account depression loss, infiltration and evaporation. Infiltration is rain water that soaks into the ground from precipitation. This water is considered removed from the runoff process. The major loss considered in the rainfall and runoff modeling is infiltration loss. In SWMM, each sub-catchment is further divided into three subareas: an impervious area with depression storage, an impervious area without depression storage and a pervious area with depression storage. The infiltration losses is considered only from the pervious areas. For the pervious areas of a sub-catchment, SWMM has three different methods for computing infiltration loss: the Horton, Green-Ampt and Curve Number models. The Horton model will be used in this study.
2.3. Model Parameters
In general, uncertainty sources in urban drainage modeling include parameter, data and model structure. Only model parameters are used as factors in the sensitivity analysis in this study, neglecting the contribution of model structure. The model hydrology parameters within the SWMM Runoff Block are: sub-catchment slope, sub-catchment width, sub-catchment area, Manning roughness coefficient (n) for pervious and impervious area, minimum and maximum infiltration rates, impervious area with depression storage, and impervious area without depression storage. Whereas in the Extran Block the principal input parameters are: conduit length, Manning’s n for the conduit, cross-sectional geometry.
In this study, three scaling factors (i.e., Pct-Area, K-Width, K-Slope) [27] are introduced to replace sub-catchment area, sub-catchment width and sub-catchment slope. The actual values of the model’s input parameters are equal to the product of the scaling factor and the measured values of parameters. Sub-catchment area is greatly affected by the subjectivity of model generalization, especially in the case of small study area; uncertainty of sub-catchment area is more obvious. The model parameters and their variation ranges are shown in Table 2. Parameter values have been set at reasonable values based on results coming from the literature and from the field measurements of the study site. For assessing the influence of varying inputs on model outputs, all model parameters are assumed to be uniformly distributed, and thus the parameters have the same probability of taking any value within a specified range. The parameter values of SWMM model vary from sub-watershed to sub-watershed depending on soil types, land cover (percent impervious, etc.), topography and/or other characteristics of the sub-watershed.

2.4. Sensitivity Analysis Methods
2.4.1. Latin Hypercube Sampling
In this paper, the Latin Hypercube Sampling method (LHS) is adopted to generate samples of input variables, which can avoid the repeated sampling. The LHS method is one of the stratified sampling methods, and was first introduced by McKay et al. [28]. The LHS can significantly reduce the required number of simulations compared to the conventional Monte Carlo (MC) method [29]. In LHS the range of each of the model inputs is divided into N equivalent intervals, where N is the number of simulations. One representive parameter value from each interval is randomly selected. The representative values for each random variable are then combined so that each representative value is considered only once in the simulation process. The objective of LHS is to ensure the full coverage of the range of the input variables. In this way, all possible values of the random variables are represented in the simulation. As the number of parameters increases, the sample size required generally increases. For uncertainty analysis, the number of simulation samples should be at least k+1, where k is the number of model input parameters, but much larger sample sizes are usually necessary to obtain reasonable results [16].
In this study, we used the LHS method to generate 1000 parameter samples from the range of values for each uncertain parameter in Table 2. Ranges of parameter values were determined based on either literature values or field measurements (Table 2). Correlations between parameters were neglected when performing the sampling and each uncertain parameter was assumed to follow a uniform distribution. This assumption can led to some overestimation of uncertainty and a reduction in confidence in model results [30].
2.4.2. Partial Rank Correlation Coefficient (PRCC)
The choice of the sensitivity analysis method to use significantly depends on the assumed relationship between the input parameters and model output. For nonlinear but monotonic relationship between two variables, PRCC [16,31] appears to be the best choice, because it provides a measure of monotonicity between parameters and model output after removing the linear effects of all parameters except the parameter of interest. We have chosen in the present work to use PRCC as the preferred method for sensitivity analysis, as one of the most efficient and reliable sampling-based techniques. A correlation coefficient (CC) between input xj and output y is calculated as follows:
To measure the potential nonlinear but monotonic relationships between xj and y, we calculated the PRCC, which is a robust sensitivity measure as long as little to no correlation exists between the inputs [16]. It represents a partial correlation on rank-transformed data: xj and y are first rank transformed, then the linear regression models described in Equation (2) are built. A higher positive PRCC indicates that the parameter has a greater positive control on the response variable of interest, while a higher (absolute value) negative PRCC indicates a greater negative control [32]. In contrast, a PRCC value close to 0 indicates a poor effect on the response variable of interest.
PRCC is often combined with LHS for conducting sensitivity analysis. By combining the uncertainty analyses with PRCC, we are able to reasonably assess the sensitivity of our output variable to parameter variation.
2.4.3. Mutual Information (Entropy) Analysis
Entropy is a measure of the uncertainty associated with random variables, or, alternatively, a measure of the amount of information contained in a distribution [33]. It is closely related to sensitivity, since it is expected that a model will be more sensitive to a parameter carrying more information than to another one carrying less. Mutual information, which is based on the concept of entropy, provides a general framework for dealing with possible non-monotonicity in input-output relationships—which cannot be handled by linear correlation and regression based approaches [22,34].
As suggested by Mishra and Knowlton [35], the combination of the mutual information concept and contingency table analysis can be used to perform global sensitivity analysis. Table 3 is an example of n×m contingency table [36]. A contingency table such as Table 3 is used to examine whether or not the two variables are independent.

Table 3 consists of n rows and m columns that correspond to the n categories of the variable x and the m categories of the variable y. We let fij denote the joint frequency for (i, j), where the first subscript refers to the row number and the second is the column number. The marginal frequencies represent the row-wise and column-wise sums of the frequencies in the table, denoted by fi and fj, respectively.
The entropies of input variable x and output variable y can be defined by:
The values of discrete random variable x take xi, i=1,2,…,n; And the values of discrete random variable y take yj, i=1,2,…,m, The conditional entropy H(x|y) is the average additional information provided by observing the variable x when the variable y is already known. The conditional entropy H(x|y) of x given y is defined as:
The joint entropy H(x,y) of x and y denotes the average total information gained by observing both x and y. The joint entropy H(x,y) of x and y is defined as:
The mutual information I(x,y) of x and y is the amount of information shared by x and y. The mutual information I(x,y) is defined in terms of their entropies:
The mutual information is always non-negative: I(x,y) ≥0 for any two random variables x and y. The mutual information is zero if and only if x and y are independent. So, the mutual information between the random variables x and y can be considered a measure of dependence between these variables, or better yet, the statistical correlation of x and y.
In mutual entropy method, the sensitivity of the output to input variables is estimated by the following two indicators [24].
The first indicator is the uncertainty coefficient as a quantitative measure of association, defined by the two limits identified above:
This measure lies between 0 (corresponding to no association between the x and y) and 1 (completely association).
R-statistic is another alternative measure of association defined on the basis of mutual information:
3. Results and Discussion
In the following sections, the results are presented and discussed in detail for the investigated model outputs.
3.1. Statistics Analysis of Model Outputs
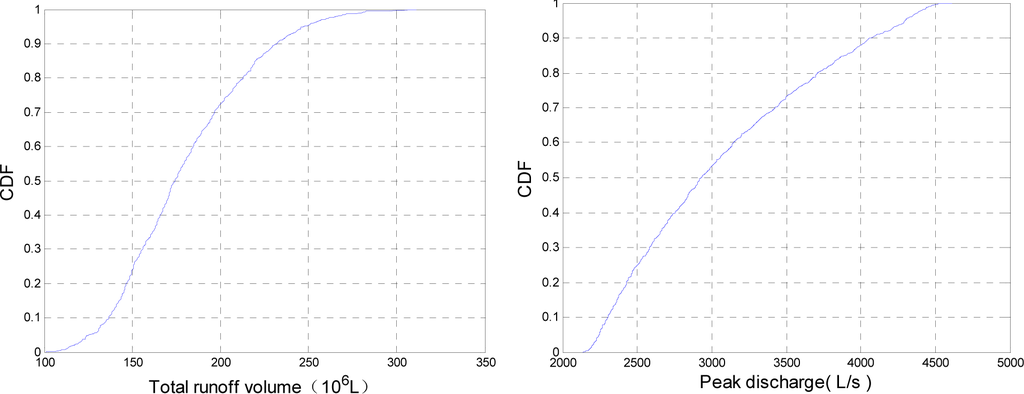
The LHS method was used to explore the effects of the input parameter uncertainty on the three output variables: the peak discharge (Qp), the total runoff volume (V) and the time to peak (Tp). Using Latin hypercube sampling, 1000 samples were generated from a uniform distribution of the parameter ranges. The model parameters had been assigned as uniform distributions and the parameters were changed within the ranges of Table 2.
The results of the simulation runs of the SWMM model consist of N observations of each output variable. Distribution functions for each of the output variables can be directly derived and characterized by simple descriptive statistics. The empirical frequency distribution for three output variables were directly derived from the results of the uncertainty analysis, these distributions are presented in Figure 2. The descriptive statistics for these distributions are given in Table 4. The results show high output variability due to the high degree of estimation uncertainty for the initial value of the input parameters. The sample size N is set to 1000. Figure 2 shows the cumulative distribution functions (CDFs) for the outputs of the SWMM model. These descriptive statistics cannot be used to identify which of the input variables are the most important in contributing to the model output; consequently, partial rank correlation coefficients were calculated in order to identify these key variables.

3.2. PRCC Analysis
The primary model outputs of interest for the sensitivity analyses were the peak discharge (Qp), the total runoff volume (V) and the time to peak (Tp). PRCC were calculated between each of the 12 input parameters and three output variables. Based on the magnitude of the absolute value of the PRCC, we ranked the relative importance of the 12 input parameters. PRCC values of the parameters are presented in Table 5. Figure 3 shows partial rank scatter plots of the ranks for the total runoff volume and each of the 12 input parameters. This visualisation shows how strongly an output variable is influenced by the input parameters. The visual analysis shows a negative impact of Con-Mann and total runoff volume (a high parameter leads to a low total runoff volume value).

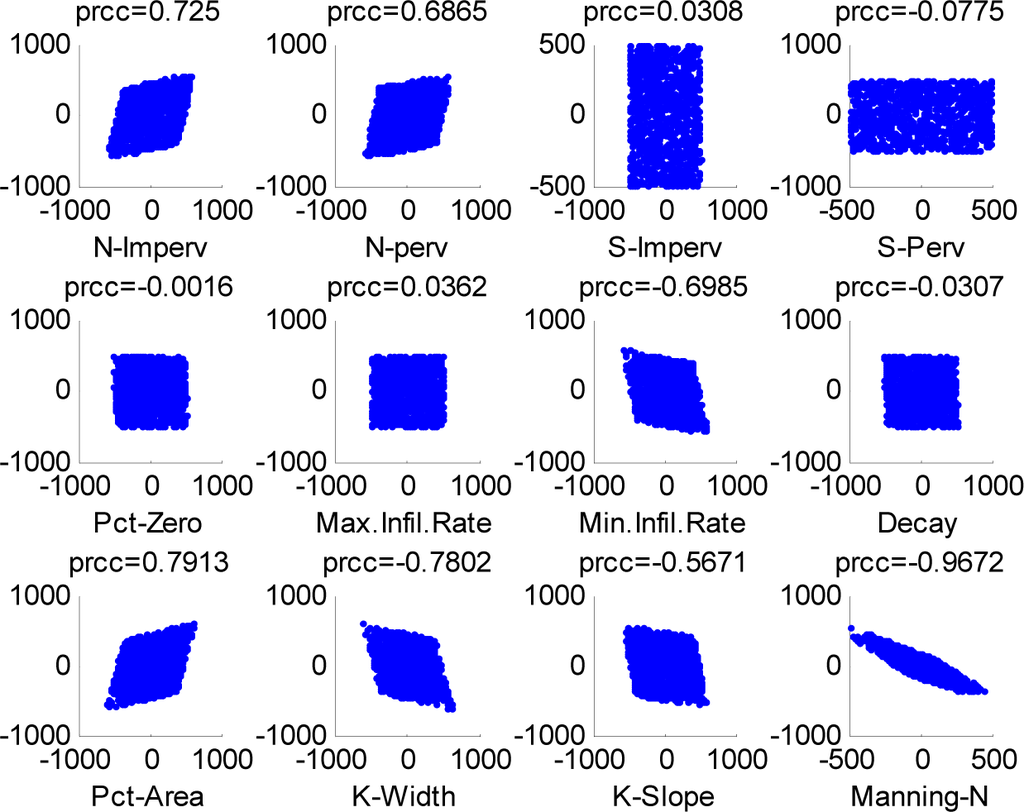
The PRCC results for the total runoff volume show that the Con-Mann has the highest influence on the results, followed by the Pct-Area and K-Width. Pct-Area, N-Imperv and N-Perv are strongly positively correlated with the total runoff volume. On the other hand, Con-Mann, K-Width, Min. Infil. Rate and K-Slope are strongly negatively correlated to the total runoff volume. Table 4 shows that the ranking of relative importance of parameter could vary among different output variables. For example, Con-Mann has a relatively low influence on the time of peak, but a high influence on the peak discharge and total runoff volume.
3.3. Mutual Entropy Analysis
Mutual entropy analysis can be conducted using contingency tables. A contingency table is a statistical table that shows the relationships between two variables. To construct a contingency table, the first step is to bin the range of values, and then count the number of observations in each bin. Since Mishra et al. [23] pointed out that 10–15 classes for each variable give stable results, we used a 10 × 10 table. The 1000 calculated output values and the corresponding sampled values of all input parameters were divided into 10 equiprobable intervals. Mutual information were calculated from the contingency table based on the data. R statistic to determine the importance ranking of input parameters is shown in Table 6–8. In Table 6–8, the first column and the second column show the variables in order of decreasing importance. The third column denotes the values of the joint entropy H(x,y) as given by Equation (4). The mutual entropy I (x,y) (given in the fourth column) and the uncertainty coefficient U(x,y) (given in the fifth column) are calculated from Equations (6) and (7), respectively. The sixth column shows the R statistic value calculated using Equation (8).


The most important parameter for total runoff volume and peak discharge identified via the R statistic is Con-Mann, which clearly dominates the importance ranking. For the time to peak, both methods identify N-Imperv as the most important parameter. For the other parameters, however, ranking from PRCCs and mutual information slightly differs.
The entropy analysis indicates the similar parameter importance ranking as PRCCs analysis, indicating the absence of any important non-monotonic relationships between inputs and outputs.
4. Conclusions
Sensitivity analysis of an urban drainage model with respect to uncertain model-input parameters is presented in this paper. We review and compare two global sensitivity analysis methods that have proven to be among the most reliable and efficient, namely a PRCC and a mutual information method. One example is presented to demonstrate the applicability of the selected global sensitivity analysis methods. Twelve model input parameters and three model outputs are investigated. LHS is used to generate input data from the assigned distributions and ranges in the SWMM model. A sensitivity analysis based on PRCC and mutual information method has been conducted in order to identify the parameter importance of SWMM model.
Statistics analysis of SWMM model outputs reveals high output variability due to uncertain estimates of various model parameter values. However, only a few key input parameters are important in contributing to the model outputs. PRCC and entropy analysis are used to identify and rank the importance of these key input parameters. The example demonstrates how PRCC can be used to identify key input parameters in sample data sets derived from numerical simulations. Scatter plots offer a straightforward way to visualize the relationship between input parameter and output variable. However, the applicability of PRCC is restricted to nonlinear but monotonic relationships between outputs and inputs. The mutual information has the strength of identifying non-monotonic sensitivities. Therefore, using mutual information on stochastic models can complement LHS/PRCC results.
Sensitivity measures of PRCC and entropy-based are found to give similar ranking of the SWMM input parameters. The PRCC and mutual information are found to be sufficient to identify the most important parameters of the SWMM model.
The choice of model output variables significantly influence the importance and ranking of the parameters. It is essential to investigate more than one model output for assessing sensitivities over the range of possible model responses.
Acknowledgements
This research was supported by the Special Fund for Public Welfare Industry (No. 201301057) and Shandong Province Provincial Key Hydraulic Research Projects (No. SDSLKY 201403).
Author Contributions
All authors have contributed substantially to the study. All authors have read and approved the final manuscript.
Conflicts of Interests
The authors declare no conflict of interest.
References
- Jakeman, A.J.; Letcher, R.A.; Norton, J.P. Ten iterative steps in development and evaluation of environmental models. Environ. Model. Softw. 2006, 21, 602–614. [Google Scholar]
- Saltelli, A.; Torantola, S.; Chan, K.P.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics. 1999, 41, 39–56. [Google Scholar]
- Cukier, R.I.; Levine, H.B.; Shuler, K.E. Nonlinear sensitivity analysis of multiparameter model systems. J. Comput. Phys. 1978, 26, 1–42. [Google Scholar]
- Muleta, M.K.; Nicklow, J.W. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar]
- Sobol, I.M. On sensitivity estimates for nonlinear mathematical models. Matematicheskoe Modelirov. 1990, 2, 112–118. [Google Scholar]
- Helton, J.C.; Davis, F.J. Illustration of sampling-based methods for uncertainty and sensitivity analysis. Risk Anal. 2002, 22, 591–622. [Google Scholar]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics. 1991, 33, 161–174. [Google Scholar]
- Freni, G.; Mannina, G. The identifiability analysis for setting up measuring campaigns in integrated water quality modelling. Phys. Chem. Earth 2012, 42, 52–60. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual Version 5.0.EPA/600/R-05/040, National Risk Management Research Laboratory; United States Environmental Protection Agency: Cincinnati, OH, USA, 2009. [Google Scholar]
- Gamerith, V.; Neumann, M.B.; Muschalla, D. Applying global sensitivity analysis to the modelling of flow and water quality in sewers. Water Res. 2013, 47, 4600–4611. [Google Scholar]
- Gamerith, V.; Neumann, M.B.; Muschalla, D. Applied Global Sensitivity Analysis in Sewer Flow and Water Quality Modelling, Proceeding of the 12th International Conference of Urban Drainage, Porto Alegre, Brazil, 10–15 September 2011.
- Vezzaro, L.; Mikkelsen, P.S. Application of global sensitivity analysis and uncertainty quantification in dynamic modeling of micropollutants in stormwater runoff. Environ. Model. Softw. 2012, 27, 40–41. [Google Scholar]
- Freni, G.; Mannina, G.; Viviani, G. Uncertainty in urban stormwater quality modeling: the effect of acceptability threshold in the GLUE methodology. Water Res. 2008, 42, 2061–2072. [Google Scholar]
- Dotto, C.B.S.; Kleidorfer, M.; Deletic, A.; Rauch, W.; McCarthy, D.T. Performance and sensitivity analysis of stormwater models using a Bayesian approach and long-term high resolution data. Environ. Model. Softw. 2011, 26, 1225–1239. [Google Scholar]
- Prat, P.; Benedetti, L.; Corominas, L.; Comas, J.; Poch, M. Model-based knowledge acquisition in environmental decision support system for wastewater integrated management. Water Sci. Technol. 2012, 65, 1123–1129. [Google Scholar]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar]
- Blower, S.M.; Dowlatabadi, H. Sensitivity and uncertainty analysis of complex-models of disease transmission—An HIV model, as an example. Int. Stat. Rev. 1994, 62, 229–243. [Google Scholar]
- Blower, S.M.; Hartel, D.; Dowlatabadi, H.; Anderson, R.M.; May, R.M. Drugs, sex and HIV: a mathematical model for New York City. Phil. Trans. Royal Soc. 1991, 331, 171–187. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Francois, D.; Rossi, F.; Wertz, V.; Verleysen, M. Resampling methods for parameter-free and robust feature selection with mutual information. Neurocomputing 2007, 70, 1276–1288. [Google Scholar]
- Harrold, T.I.; Sharma, A.; Sheather, S. Selection of a kernel bandwidth for measuring dependence in hydrologic time series using the mutual information criterion. Stoch Environ. Res. Risk Assess. 2001, 15, 310–324. [Google Scholar]
- Bonnlander, B.V.; Weigend, A.S. Selecting input variables using mutual information and nonparametric density estimation, Proceedings of the International Symposium on Artificial Neural Networks (ISANN’94), Tainan, Taiwan; 1994; pp. 42–50.
- Mishra, S.; Deeds, N.; Ruskauff, G. Global sensitivity analysis techniques for probabilistic ground water modeling. Ground Water. 2009, 47, 727–744. [Google Scholar]
- Zeng, X.; Wang, D.; Wu, J. Sensitivity analysis of the probability distribution of groundwater level series based on information entropy. Stoch Environ. Res. Risk Assess. 2012, 26, 345–356. [Google Scholar]
- Ren, B. Study on the Urban Design Rainstorm and Rainfall Runoff Calculation Model. Ph.D. Thesis, Chongqing University, Chongqing, China, 2004. [Google Scholar]
- Huber, W.C.; Dickinson, R.E. Storm water management model user’s manual, version 4; US Environmental Protection Agency: Athens, GA, USA, 1992. [Google Scholar]
- Wang, H.; Du, P.; Zhao, D. Global sensitivity analysis for urban rainfall-runoff model. China Environ. Sci. 2008, 28, 725–729. [Google Scholar]
- Mckay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of 3 methods for selecting values of input variables in the analysis of output from a computer code. Technometrics. 1979, 21, 239–245. [Google Scholar]
- Iman, R.; Helton, J.H. An investigation of uncertainty and sensitivity analysis techniques for computer models. Risk Anal. 1988, 8, 71–90. [Google Scholar]
- Zaehle, S.; Sitch, S.; Smith, B.; Hatterman, F. Effects of parameter uncertainties on the modeling of terrestrial biosphere dynamics. Glob. Biogeochem. Cycles. 2005, 19, GB3020. [Google Scholar]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar]
- Jiang, Y.; Zhuang, Q.; Schaphoff, S.; Sitch, S.; Sokolov, A.; Kicklighter, D.; Melillo, J. Uncertainty analysis of vegetation distribution in the northern high latitudes during the 21st century with a dynamic vegetation model. Ecol. Evol. 2012, 2, 593–614. [Google Scholar]
- Ihara Shunsuke, I. Information Theory for Continuous Systems; World Scientific: Singapore, Singapore, 1993. [Google Scholar]
- Helton, J.C. Uncertainty and sensitivity analysis techniques for use in performance assessment for radioactive waste disposal. Reliab. Eng. Syst. Saf. 1993, 42, 327–367. [Google Scholar]
- Mishra, S.; Knowlton, R.G. Testing for input-output dependence in performance assessment models, Proceedings of the 10th International High-Level Radioactive Waste Management Conference, Las Vegas, Nevada, IL: American Nuclear Society, 30 March–2 April 2003; pp. 882–887.
- Mogheir, Y.; de Lima, J.; Singh, V.P. Characterizing the spatialvariability of groundwater quality using the entropy theory: I. Synthetic data. Hydrol. Process. 2004, 18, 2165–2179. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).