A Quantitative Analysis of an EEG Epileptic Record Based on MultiresolutionWavelet Coefficients
Abstract
:1. Introduction
- We develop a novel extension of this methodology, using the wavelet leaders for the corresponding information theory quantifier evaluation.
- We exemplify both treatments with the analysis of a scalp epileptic EEG signal and compare the results of both methodologies for a scalp EEG recorded in the right central location (Channel C4), obtained from one patient.
2. Wavelet Methodology and Information Theory Quantifiers
2.1. Wavelet Transform
2.2. Discrete Wavelet Transform and Quantifiers
2.3. Wavelet Leaders and Quantifiers
- Via the Mallat algorithm [40], compute cj,k for the resolution levels j = 1, ⋯, jmax (see Equation (16)). Considering the data series {f(n) : n = 1, ⋯, N} at the finest level, then jmax ≤ log2(N).
- From the definition given by Equation (19), estimate the wavelet leaders using the following equation:
- Calculate Sf(n) and Cf(n) for the resolution level jmax, using Equations (24)–(26), entering the Jensen-Shannon divergence (Equation (12)) in the Q definition.
3. qEEG Analysis of a Tonic-Clonic Epileptic Signal
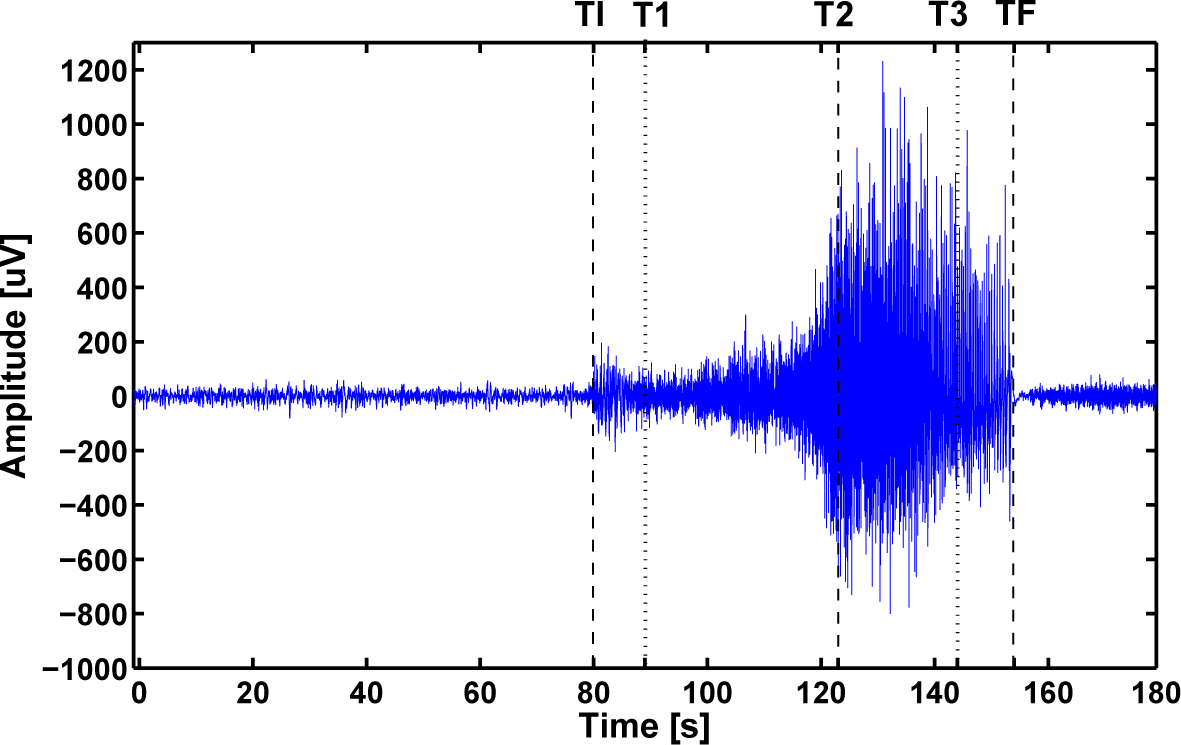
3.1. Clinical Data and the Experimental Setup
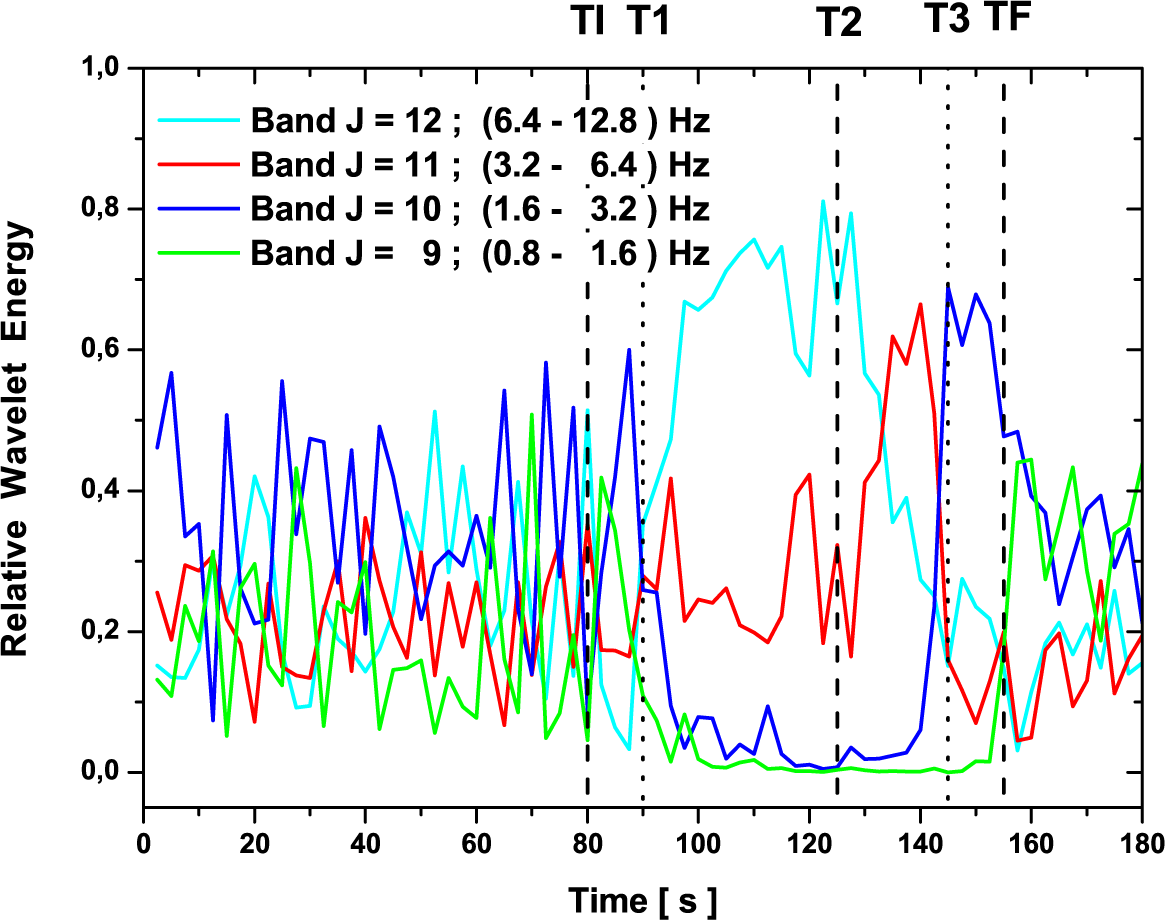
3.2. Analysis Based on a Set of ODWT Coefficients
3.3. Analysis Based on a Set of Wavelet Leader Coefficients
3.4. Discussion
4. Final Remarks
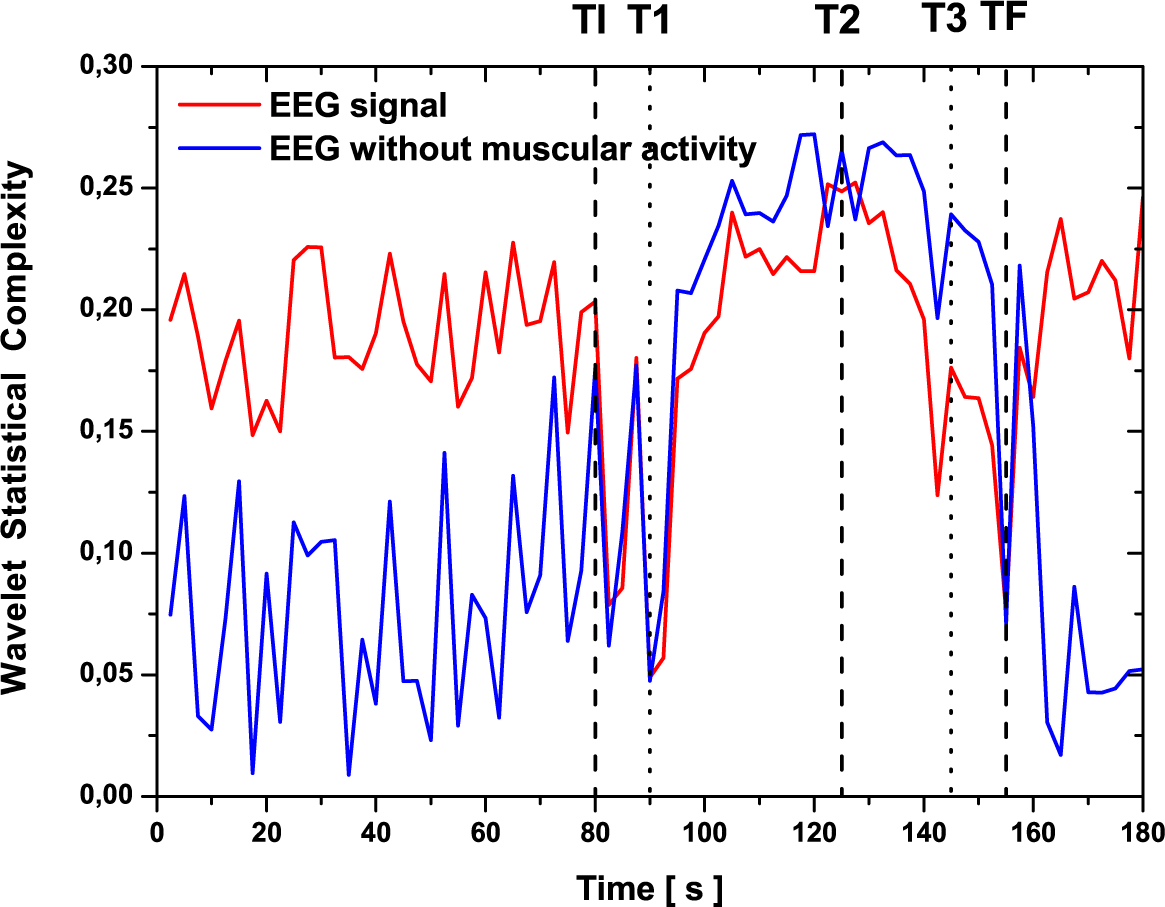
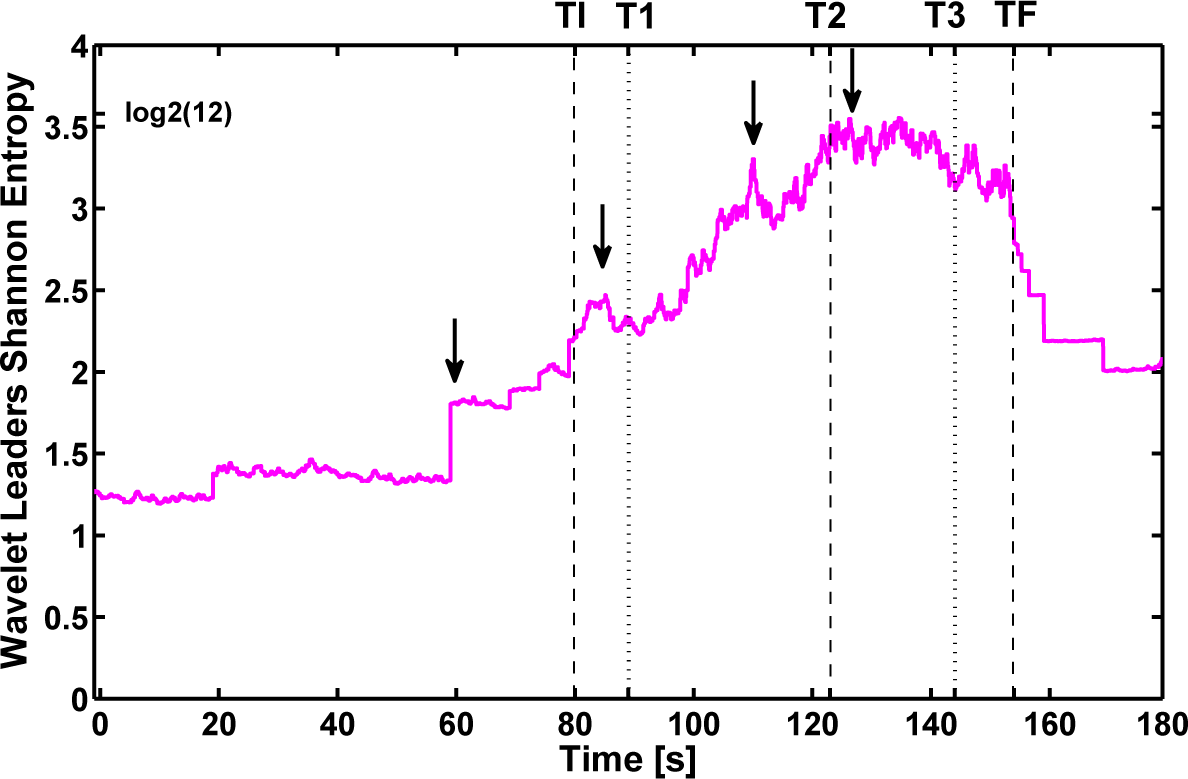
- The analysis is local, and wavelet leader-based quantifiers can detect a higher resolution in the changes of the signals than Shannon wavelet entropy and wavelet statistical complexity. Moreover, the video recordings of the patient present some inaccurate information on these changes.
- As mentioned above, the results obtained for the filtered signal (i.e., without the contribution of muscle-noise contaminated bands) is essentially identical to the original signal. This property has two advantages, it reduces the use of mathematical tools, such as signal pre-processing filters, and second, it simplifies the calculation process.
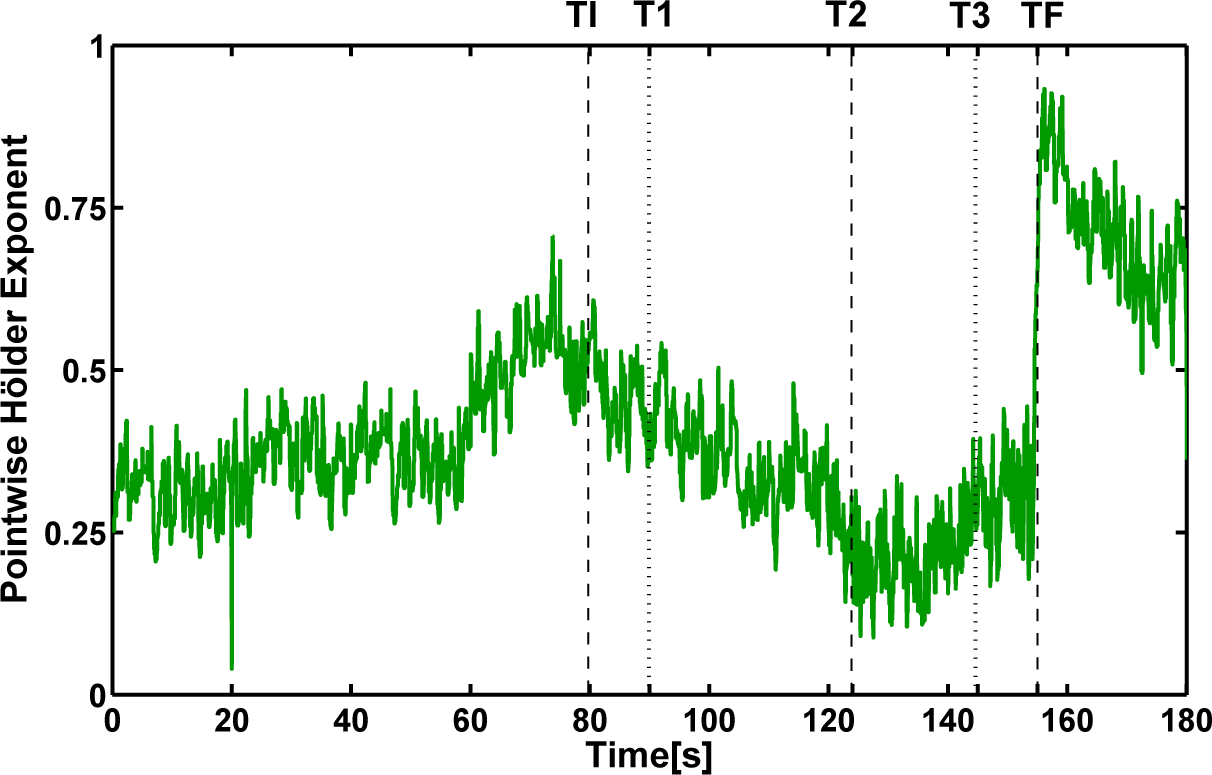
- Pre-seizure and post-seizure fluctuation values in the evaluation of SWS and WSC quantifiers make average evaluation necessary to find the plateau that occurs naturally in wavelet leader-based quantifiers (WLSS and WLSC). Moreover, this fact clearly marks discontinuities in the signal (such as shown at ~60 s).
- The maximum wavelet leader Shannon entropy WLSS occurs slightly after 120 s, marking a transition from the tonic to the clonic phase, in agreement with what was found by computing the SWS and WSC.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Niedermeyer, E.; Lopes da Silva, F.H. Electroencephalography, Basic Principles, Clinical Applications, and Related Field; Urban and Schwarzenberg: Baltimore, MD, USA, 1987. [Google Scholar]
- Casdagli, M.C.; Iasemedis, L.D.; Savit, R.S.; Gilmore, R.L.; Roper, S.N.; Sackellares, J.C. Non-linearity in invasive EEG recordings from patients with temporal lobe epilepsy. Electroencephalogr. Clin. Neurophysiol. 1997, 102, 98–105. [Google Scholar]
- Lehnertz, K.; Elger, C.E. Can epileptic seizures be predicted? Evidence from nonlinear time series analysis of brain electrical activity. Phys. Rev. Lett. 1998. [Google Scholar]
- Kowalik, Z.J.; Elbert, T. Changes of chaoticness in spontaneous EEG/EMG. Integr. Physiol. Behav. Sci. 1994, 29, 270–282. [Google Scholar]
- Iasemedis, L.D.; Sackellares, J.C.; Zaveri, H.P.; Williams, W.J. Phase space topographyand Lyapunov exponent of electrocorticograms in partial seizures. Brain Topogr. 1990, 2, 187–201. [Google Scholar]
- Iasemedis, L.D.; Sackellares, J.C. The evolution with time of spatial distribution of the largest Lyapunov exponent on the human epileptic cortex. In It Measuring Chaos in Human Brain; Duke, D., Pritchards, W., Eds.; World Scientific: Singapore, Singapore, 1991; pp. 49–82. [Google Scholar]
- Rosso, O.A.; Mairal, M.L. Characterization of time dynamical evolution of electroencephalographic epileptic records. Physica A 2002, 312, 469–504. [Google Scholar]
- Pijn, J.P.; van Neerven, J.; Noestt, A.; Lopes da Silva, F.H. Chaos or noise in EEG signals: Dependence on state and brain site. Electroencephalogr. Clin. Neurophysiol. 1991, 79, 371–381. [Google Scholar]
- Powell, G.E.; Percival, I.C. A spectral entropy method for distinguishing regular and irregular motion of Hamiltonian systems. J. Phys. A Math. Gen. 1979, 12, 2053–2071. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing, 3rd ed.; Academic Press: Burlington, MA, USA, 2009. [Google Scholar]
- Samar, V.; Bopardikar, A.; Rao, R.; Swartz, K. Wavelet analysis of neuroelectric waveforms: A conceptual tutorial. Brain Lang. 1999, 66, 7–60. [Google Scholar]
- Blanco, S.; Figliola, A.; Quian Quiroga, R.; Rosso, O.A.; Serrano, E. Time-Frequency analysis of electroencephalogram series (III): Information transfer function and wavelets packets. Phys. Rev. E 1998. [Google Scholar]
- Rosso, O.A.; Martín, M.T.; Figliola, A.; Keller, K.; Plastino, A. EEG analysis using wavelet-based informational tools. J. Neurosci. Methods 2006, 153, 163–182. [Google Scholar]
- Rosso, O.A.; Blanco, S.; Yordanova, J.; Kolev, V.; Figliola, A.; Schürmann, M.; Başar, E. Wavelet entropy: A new tool for the analysis of short duration brain electrical signals. J. Neurosci. Methods 2001, 105, 65–75. [Google Scholar]
- Rosso, O.A.; Martín, M.T.; Plastino, A. Brain electrical activity analysis using wavelet based informational tools. Physica A 2002, 313, 587–608. [Google Scholar]
- Rosso, O.A.; Blanco, S.; Rabinowicz, A. Wavelet analysis of generalized Tonic-Clonic epileptic seizures. Signal Process. 2002, 83, 1275–1289. [Google Scholar]
- Rosso, O.A.; Martín, M.T.; Plastino, A. Brain electrical activity analysis using wavelet based informational tools (II): Tsallis non-extensivity and complexity measurements. Physica A 2003, 320, 497–511. [Google Scholar]
- Rosso, O.A.; Figliola, A. Order/Disorder in brain electrical activity. Rev. Mex. Física 2004, 50, 149–155. [Google Scholar]
- Rosso, O.A.; Martín, M.T.; Plastino, A. Evidence of self-organization in brain electrical activity using wavelet based informational tools. Physica A 2005, 347, 444–464. [Google Scholar]
- Rosso, O.A.; Hyslop, W.; Gerlach, R.; Smith, R.L.L.; Rostas, J.; Hunter, M. Quantitative EEG analysis of the maturational changes associated with childhood absence epilepsy. Physica A 2005, 356, 184–189. [Google Scholar]
- Rosso, O.A. Entropy changes in brain function. Int. J. Psychophysiol. 2007, 64, 75–80. [Google Scholar]
- Pereyra, M.; Lamberti, P.W.; Rosso, O.A. Wavelet Jensen-Shannon divergence as a tool for studying the dynamics of frequency band components in EEG epileptic seizures. Physica A 2007, 379, 122–132. [Google Scholar]
- Rosso, O.A.; Mendes, A.; Rostas, J.A.; Hunter, M.; Moscato, P. Distinguishing childhood absence epilepsy patients from controls by the analysis of their background brain electrical activity. J. Neurosci. Methods 2009, 177, 461–468. [Google Scholar]
- Rosso, O.A.; Mendes, A.; Berreta, R.; Rostas, J.A.; Hunter, M.; Moscato, P. Distinguishing childhood absence epilepsy patients from controls by the analysis of their background brain activity (II): A combinatorial optimization approach for electrode selection. J. Neurosci. Methods 2009, 181, 257–267. [Google Scholar]
- Quian Quiroga, R.; Rosso, O.A.; Başar, E.; Schürmann, M. Wavelet-entropy in event-related potentials: A new method shows ordering of EEG oscillations. Biol. Cybern. 2001, 84, 291–299. [Google Scholar]
- Kolev, V.; Rosso, O.A.; Yordanova, J. A transient dominance of theta ERP component characterizes passive auditory processing: Evidence from developmental study. Neuroreport 2001, 12, 2791–2796. [Google Scholar]
- Yordanova, J.; Kolev, V.; Rosso, O.A.; Schürmann, M.; Sakowitz, O.W.; Özgören, M.; Bas¸ar, E. Wavelet entropy analysis of event-related potentials indicates modality-independent theta dominance. J. Neurosci. Methods 2002, 117, 99–109. [Google Scholar]
- Schüett, A.; Rosso, O.A.; Figliola, A. A discovery of new features of gastropod local field potentials by application of wavelet tools. J. Neurosci. Methods 2002, 119, 89–104. [Google Scholar]
- Yordanova, J.; Rosso, O.A.; Kolev, V. A transient dominance of theta event-related brain potential component characterizes stimulus processing in auditory oddball task. Clin. Neurophysiol. 2003, 114, 529–540. [Google Scholar]
- Schüett, A.; Rosso, O.A.; Figliola, A. Wavelet analysis can sensitively describe dynamics of ethanol evoked spiky local field potential wave of slug (Limax marginatus) brain. Clin. Neurophysiol. 2003, 129, 135–150. [Google Scholar]
- Rosenblatt, M.; Serrano, E.; Figliola, A. An entropy based in wavelet leaders to quantify the local regularity of a signal and its application to analyze the Dow Jones index. Int. J. Wavelets Multiresolution Inf. Process. 2012, 10, 1250048. [Google Scholar]
- Jaffard, S. Oscillation spaces: Properties and applications to fractal and multifractal functions. J. Math. Phys. 1998, 39, 4129–4141. [Google Scholar]
- Jaffard, S. Wavelet techniques in multifractal analysis. Proc. Symp. Pure Math. Am. Math. Soc. 2004, 72, 91–151. [Google Scholar]
- Arneodo, A.; Bacry, E.; Muzy, J.F. The thermodynamics of fractals revisited with wavelets. Physica A 1995, 213, 232–275. [Google Scholar]
- Lashermes, B.; Roux, S.G.; Abry, P.; Jaffard, S. Comprehensive multifractal analysis of turbulent velocity using the wavelet leaders. Eur. Phys. J. B 2008, 61, 201–215. [Google Scholar]
- Wendt, H.; Roux, S.G.; Abry, P.; Jaffard, S. Wavelet leaders and bootstrap for multifractal analysis of images. Signal Process. 2009, 89, 1100–1114. [Google Scholar]
- Leonarduzzi, R.F.; Schlotthauer, G.; Torres, M.E. Wavelet leader based multifractal analysis of heart rate variability during myocardial ischaemia, Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Buenos Aires, Argentina, 31 August–4 Septermber 2010; pp. 110–113.
- Abry, P.; Roux, S.G.; Jaffard, S. Detecting oscillating singularities in multifractal analysis: Application to hydrodynamic turbulence, Proceedings of the IEEE International Conference On Acoustics, Speech, and Signal Processing, Prague, Czech Republic, 22–27 May 2011.
- Mallat, S. Multiresolution approximations and wavelet orthonormal bases of L2. Trans. Am. Math. Soc. 1989, 315, 69–87. [Google Scholar]
- Meyer, Y. Ondelettes et Opérateurs; Hermann: Paris, France, 1990. [Google Scholar]
- Unser, M. Splines a perfect fit for signal and image processing. IEEE Signal Process. Mag. 1999, 16, 22–38. [Google Scholar]
- Thevenaz, P.; Blue, T.; Unser, M. Interpolation revisited. IEEE Trans. Med. Imaging 2000, 19, 739–758. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Technol. J. 1948, 27. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Kolmogorov, A.N. A new metric invariant of transitive dynamic system and automorphysms in Lebesgue spaces. Dokl. Akad. Nauk. SSSR 1958, 119, 861–864. [Google Scholar]
- Sinai, Y.G. On the concept of entropy of dynamical system. Dokl. Akad. Nauk. SSSR 1959, 124, 768–771. [Google Scholar]
- Feldman, D.P.; Crutchfield, J.P. Measures of statistical complexity: Why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar]
- López-Ruiz, R.; Mancini, H.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar]
- Martín, M.T.; Plastino, A.; Rosso, O.A. Statistical complexity and disequilibrium. Phys. Lett. A 2003, 311, 126–132. [Google Scholar]
- Lamberti, P.W.; Martín, M.T.; Plastino, A.; Rosso, O.A. Intensive entropic nontriviality measure. Physica A 2004, 334, 119–131. [Google Scholar]
- Grosse, I.; Bernaola-Galván, P.; Carpena, P.; Román-Roldán, R.; Oliver, J.; Stanley, H.E. Analysis of symbolic sequences using the Jensen-Shannon divergence. Phys. Rev. E 2002, 65, 041905. [Google Scholar]
- Martín, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical complexity measures: Geometrical and analytical properties. Physica A 2006, 369, 439–462. [Google Scholar]
- Lopez-Ruiz, R.; Sañudo, J.; Romera, E.; Calbet, X. Statistical Complexity and Fisher—Shannon Information: Applications; Springer Netherlands: Berlin, Germany, 2012. [Google Scholar]
- Legrand, P. Local regularity and multifractal methods for image and signal analysis. In Scaling, Fractals and Wavelets; Abry, P., Gonçalvès, P., Lévy Vehel, J., Eds.; Iste and Wiley: London, UK, 2009; pp. 367–409. [Google Scholar]
- Lévy Véhel, J.; Seuret, S. Two-microlocal formalism. Fractal Geom. Appl. Jubil. Benoit Mandelbrot Proc. Symp. Pure Math. 2004, 72, 153–215. [Google Scholar]
- Meyer, Y. Wavelets, Vibrations and Scalings; American Mathematical Society - CRM: Providence, RI, USA, 1997. [Google Scholar]
- Jaffard, S. Exposants de Hölder en des points donnés et coefficients d’ondelettes. C R. Acad. Sci. Ser. I Math. 1989, 308, 79–81. [Google Scholar]
- Gevins, A.; Rémond, R. (Eds.) Handbook of Electroencephalography and Clinical Neurophysiology, Vol. I: Methods of Analysis of Brain Electrical and Magnetic Signals; Elsevier: Amsterdam, The Netherlands, 1987.
- Lopes da Silva, F.H.; van Leeuwen, S.; Rémond, A. Handbook of Electroencephalography and Clinical Neurophysiology, Vol. II: Clinical Applications of Computer Analysis of EEG and other Neurophysiological Signals; Elsevier: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Daly, D.D.; Pedley, T.A. (Eds.) Current Practice of Clinical Electroencephalography, 2nd ed.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 1990.
- Gastaut, H.; Fischer-Williams, M. Handbook of Physiology; Field, J., Magoun, H.W., Hall, V.E., Eds.; Williams & Wilkins: Baltimore, MD, USA, 1959; Volume 1. [Google Scholar]
- Gastaut, H.; Broughton, R. Epileptic Seizures; Thomas: Springfield, IL, USA, 1972. [Google Scholar]
- Gotman, J.; Ives, J.R.; Gloor, P. Frequency content of EEG and EMG at seizure onset: Possibility of removal of EMG artifact by digital filtering. Clin. Neurophysiol. 1981, 52, 626–639. [Google Scholar]
- Shang, P.; Lu, Y.; Kama, S. The application of Hölder exponent to traffic congestion warning. Physica A 2006, 370, 769–776. [Google Scholar]
- Quiroga, R.Q. Quantitative Analysis of EEG Signals: Time-Frequency Methods and Chaos Theory. Ph.D. Thesis, Institute of Physiology and Institute of Signal Processing, Medical University of Lübeck, Lübeck, Germany, 1998. [Google Scholar]
- Darcey, T.M.; Willamson, P.D. Spatio-temporal EEG measures and their application to human intracranial recorded epileptic seizures. Electroencephalogr. Clin. Neurophysiol. 1985, 61, 573–587. [Google Scholar]







| Bj | ωmin (Hz) | ωmax (Hz) | j-Level | EEG Band |
|---|---|---|---|---|
| B14 | 25.6 | 51.2 | 14 | β, γ |
| B13 | 12.8 | 25.6 | 13 | β |
| B12 | 6.4 | 12.8 | 12 | θ, α |
| B11 | 3.2 | 6.4 | 11 | θ |
| B10 | 1.6 | 3.2 | 10 | δ |
| B9 | 0.8 | 1.6 | 9 | δ |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosenblatt, M.; Figliola, A.; Paccosi, G.; Serrano, E.; Rosso, O.A. A Quantitative Analysis of an EEG Epileptic Record Based on MultiresolutionWavelet Coefficients. Entropy 2014, 16, 5976-6005. https://doi.org/10.3390/e16115976
Rosenblatt M, Figliola A, Paccosi G, Serrano E, Rosso OA. A Quantitative Analysis of an EEG Epileptic Record Based on MultiresolutionWavelet Coefficients. Entropy. 2014; 16(11):5976-6005. https://doi.org/10.3390/e16115976
Chicago/Turabian StyleRosenblatt, Mariel, Alejandra Figliola, Gustavo Paccosi, Eduardo Serrano, and Osvaldo A. Rosso. 2014. "A Quantitative Analysis of an EEG Epileptic Record Based on MultiresolutionWavelet Coefficients" Entropy 16, no. 11: 5976-6005. https://doi.org/10.3390/e16115976
APA StyleRosenblatt, M., Figliola, A., Paccosi, G., Serrano, E., & Rosso, O. A. (2014). A Quantitative Analysis of an EEG Epileptic Record Based on MultiresolutionWavelet Coefficients. Entropy, 16(11), 5976-6005. https://doi.org/10.3390/e16115976






