The Measurement of Information Transmitted by a Neural Population: Promises and Challenges
Abstract
:1. Introduction
1.1. Methods for Estimating Information Content in Single Spike Trains
1.2. The Fourier Method
1.2.1. Representing Neural Signals in the Frequency Domain
1.2.2. The Fast Fourier Transform
1.2.3. Entropy in the Neural Signal
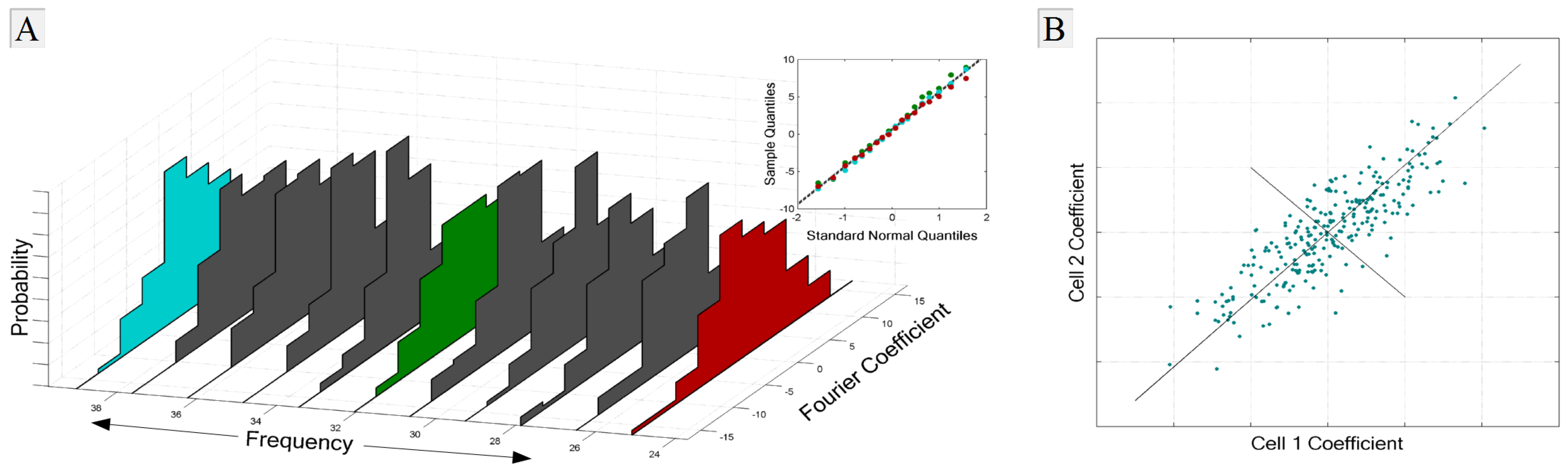
1.2.4. Noise and Signal Entropies
1.3. Overview
2. Methods
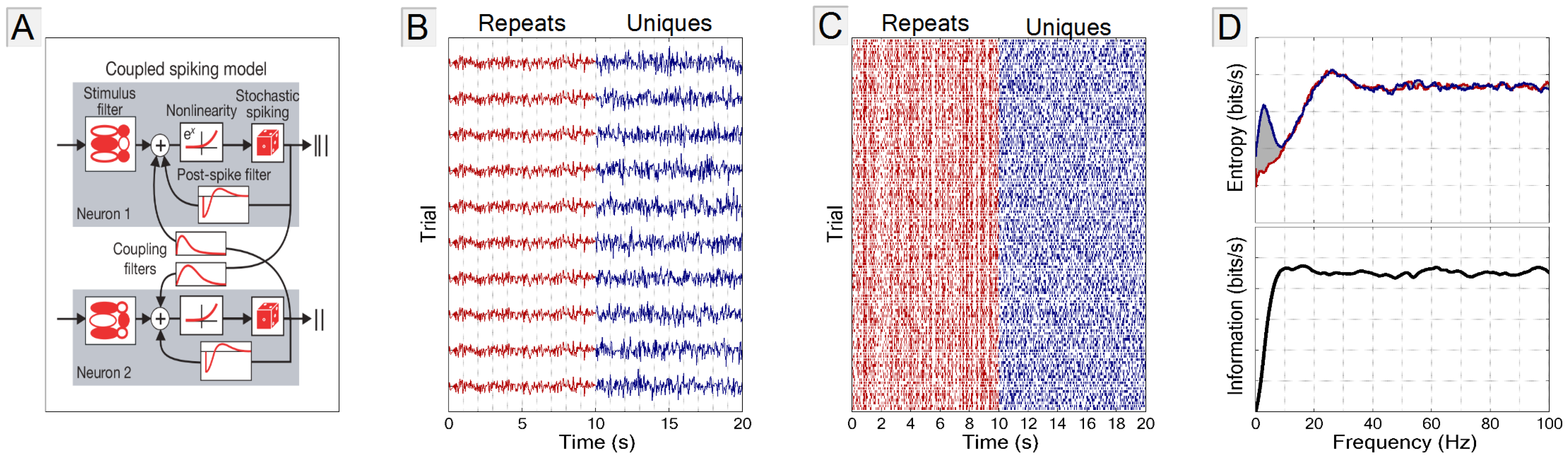
2.1. The GLM Simulation
2.2. Stimulus
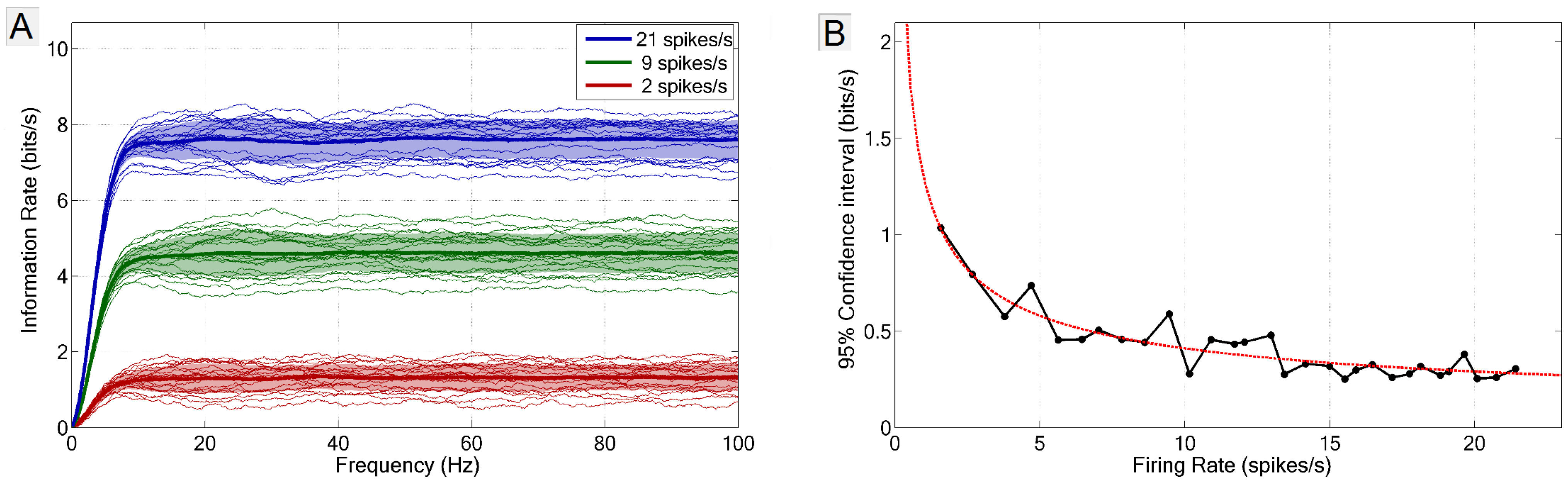
2.3. Frequency vs. Information Plots
2.4. Measurement of Error and Confidence
3. Results
3.1. Comparison with the Direct Method
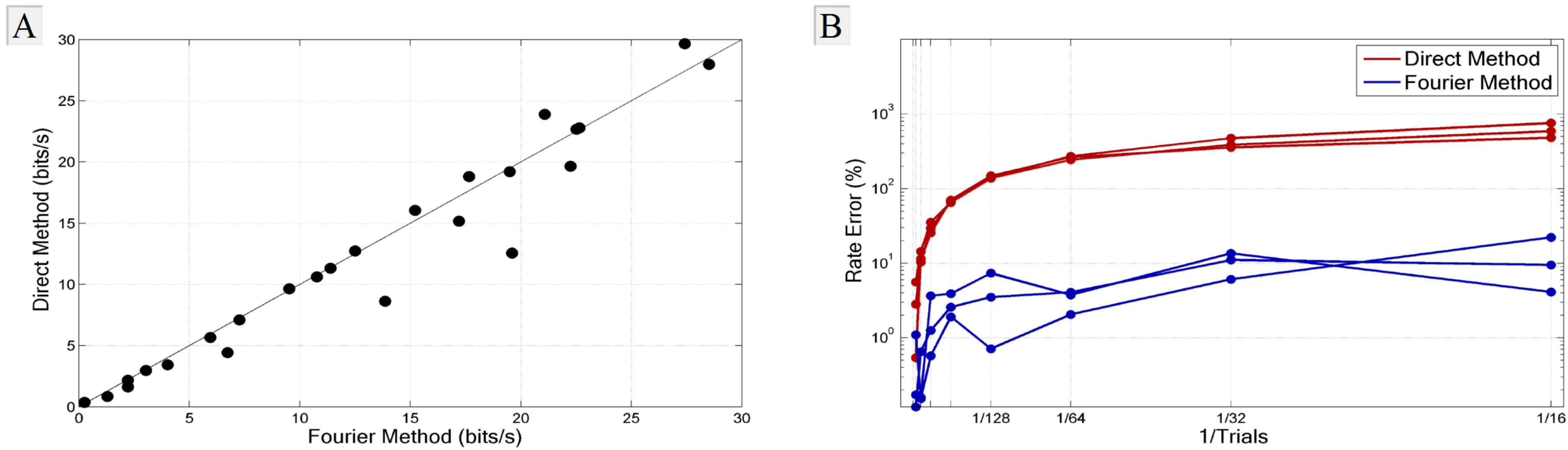
3.2. Experimental Requirements

3.3. Recording Pitfalls
- Firing non-stationarity
- Spike-to-neuron assignment errors during spike sorting
- Biased estimation of noise entropy
3.3.1. Firing Rate Non-Stationarity
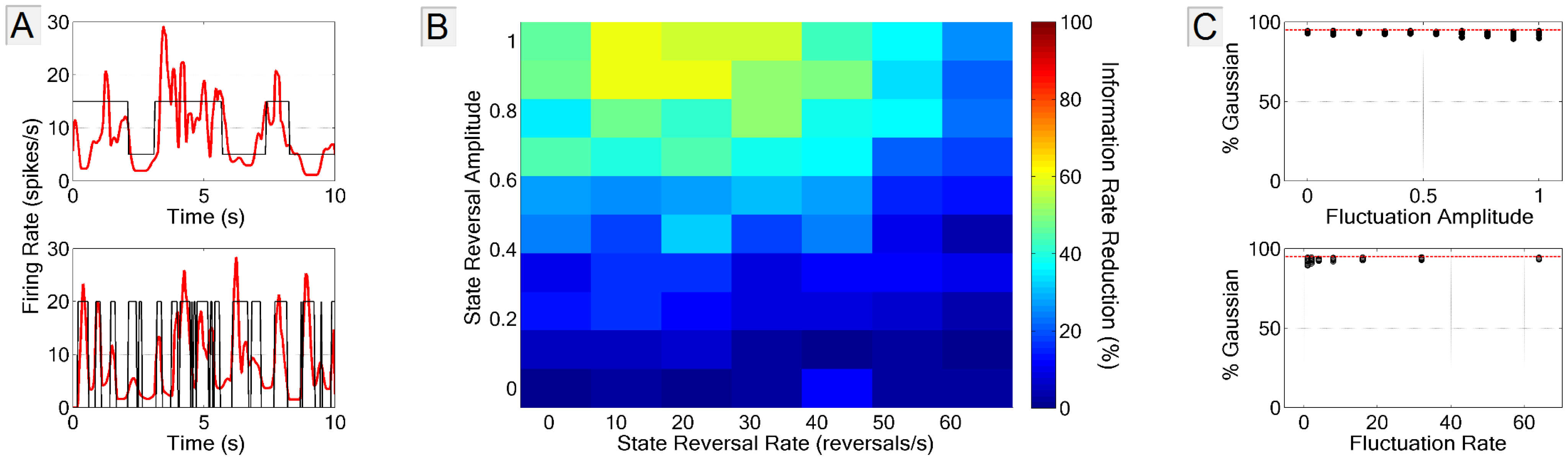
3.3.2. Spike-Neuron Misassignment
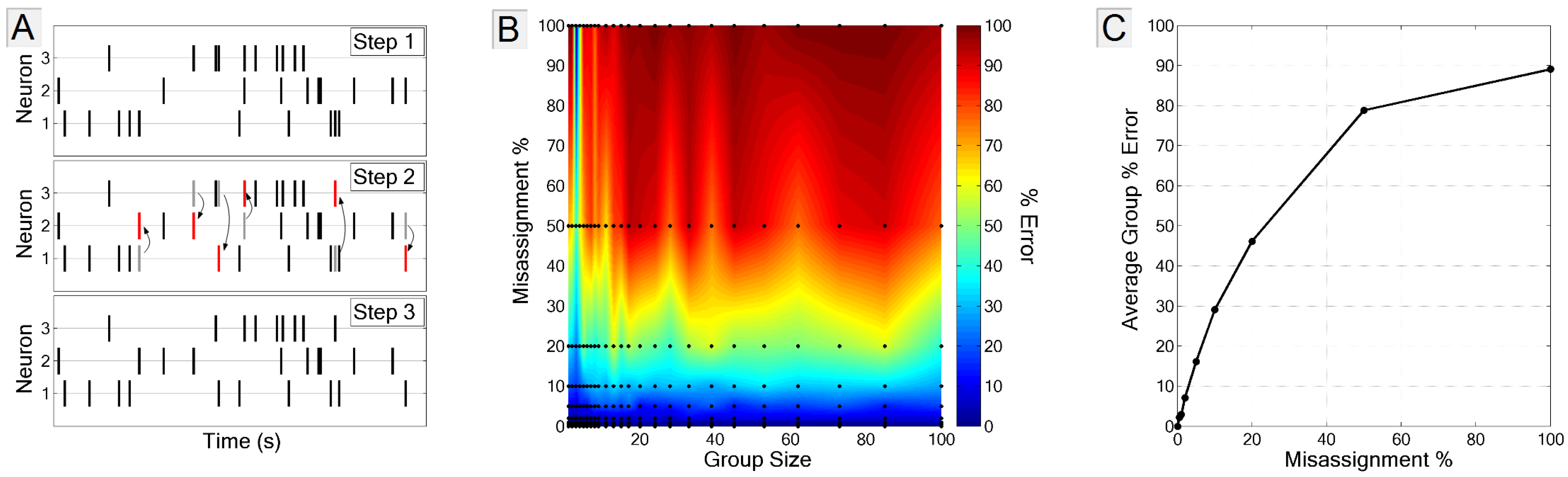
3.3.3. Biased Estimate of Noise Entropy
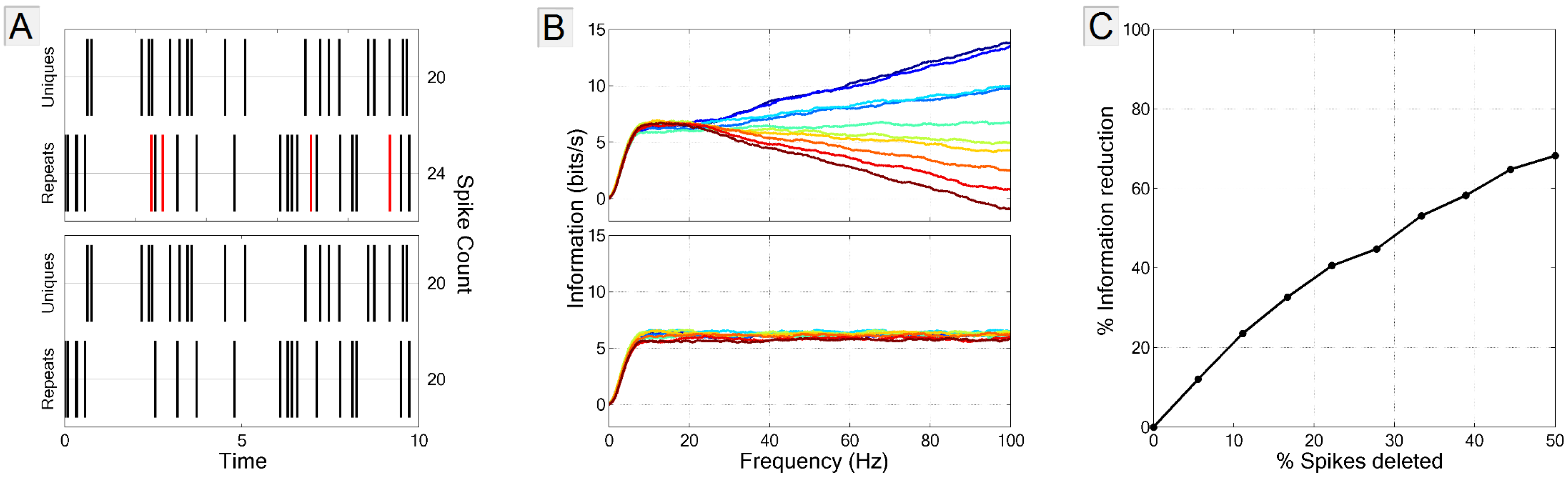
3.4. Multi-Neuron Information and Redundancy
3.4.1. Signal and Intrinsic Correlations

3.4.2. Application to Large Populations
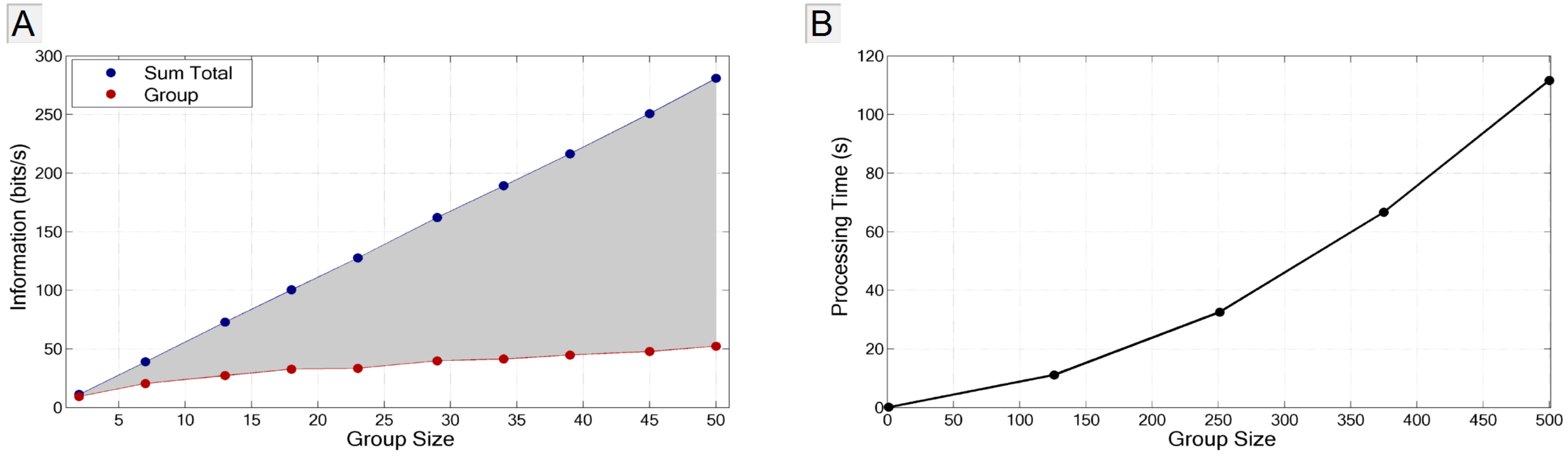
4. Summary and Conclusions
Acknowledgements
Conflicts of Interest
References
- Nicolelis, M.A.L.; Ribeiro, S. Multielectrode recordings: The next steps. Curr. Opin. Neurobiol. 2002, 12, 602–606. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656, Reprinted with corrections. Available online: http://cm.bell-labs.com/cm/ms/what/shannonday/shannon1948.pdf (accessed on 8 May 2013). [Google Scholar]
- Panzeri, S.; Senatore, R.; Montemurro, M.A.; Petersen, R.S. Correcting for the sampling bias problem in spike train information measures. J. Neurophysiol. 2007, 98, 1064–1072. [Google Scholar] [CrossRef]
- Quiroga, R.Q.; Panzeri, S. Extracting information from neuronal populations: Information theory and decoding approaches. Nat. Rev. Neurosci. 2009, 10, 173–185. [Google Scholar] [CrossRef] [PubMed]
- Ince, R.A.A.; Senatore, R.; Arabzadeh, E.; Montani, F.; Diamond, M.E.; Panzeri, S. Information-theoretic methods for studying population codes. Neural Netw. 2010, 23, 713–727. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Crumiller, M.; Knight, B.; Kaplan, E. Estimating the amount of information carried by a neuronal population. Front. Comput. Neurosci. 2010, 4. [Google Scholar] [CrossRef] [PubMed]
- Crumiller, M.; Knight, B.; Yu, Y.; Kaplan, E. Estimating the amount of information conveyed by a population of neurons. Front. Neurosci. 2011, 5. [Google Scholar] [CrossRef] [PubMed]
- Pillow, J.W.; Paninski, L.; Uzzell, V.J.; Simoncelli, E.P.; Chichilnisky, E.J. Prediction and decoding of retinal ganglion cell responses with a probabilistic spiking model. J. Neurosci. 2005, 25, 11003–11013. [Google Scholar] [CrossRef] [PubMed]
- Paninski, L.; Pillow, J.; Lewi, J. Statistical models for neural encoding, decoding, and optimal stimulus design. Prog. Brain Res. 2007, 165, 493–507. [Google Scholar] [PubMed]
- Strong, S.P.; Koberle, R.; de Ruyter van Steveninck, R.R.; Bialek, W. Entropy and information in neural spike trains. Phys. Rev. Lett. 1998, 80, 197–200. [Google Scholar] [CrossRef]
- Linkser, R. Self-organization in a perceptual network. Computer 1988, 21, 105–117. [Google Scholar]
- Pillow, J.W.; Shlens, J.; Paninski, L.; Sher, A.; Litke, A.M.; Chichilnisky, E.J.; Simoncelli, E.P. Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature 2008, 454, 995–999. [Google Scholar] [CrossRef] [PubMed]
- Destexhe, A.; Rudolph, M.; Paré, D. The high-conductance state of neocortical neurons in vivo. Nat. Rev. Neurosci. 2003, 4, 739–751. [Google Scholar] [CrossRef] [PubMed]
- Destexhe, A.; Paré, D. Impact of network activity on the integrative properties of neocortical pyramidal neurons in vivo. J. Neurophysiol. 1999, 81, 1531–1547. [Google Scholar] [PubMed]
- Wilson, C. Up and down states. Scholarpedia J. 2008, 3. [Google Scholar] [CrossRef]
- Sherman, S.M. Tonic and burst firing: Dual modes of thalamocortical relay. Trends Neurosci. 2001, 24, 122–126. [Google Scholar] [CrossRef]
- Reinagel, P.; Godwin, D.; Sherman, S.M.; Koch, C. Encoding of visual information by LGN bursts. J. Neurophysiol. 1999, 81, 2558–2569. [Google Scholar] [PubMed]
- De Charms, R.C.; Merzenich, M.M. Primary cortical representation of sounds by the coordination of action-potential timing. Nature 1996, 381, 610–613. [Google Scholar] [CrossRef] [PubMed]
- Carr, C.E. Processing of temporal information in the brain. Annu. Rev. Neurosci. 1993, 16, 223–243. [Google Scholar] [CrossRef] [PubMed]
- Braitenberg, V. Cell assemblies in the cerebral cortex. Lecture Notes Biomath. 1978, 21, 171–188. [Google Scholar]
- Sakurai, Y. Population coding by cell assemblies–what it really is in the brain. Neurosci. Res. 1996, 26, 1–16. [Google Scholar] [CrossRef]
- Gawne, T.J.; Richmond, B.J. How independent are the messages carried by adjacent inferior temporal cortical neurons? J. Neurosci. 1993, 13, 2758–2771. [Google Scholar] [PubMed]
- Meister, M.; Lagnado, L.; Baylor, D.A. Concerted signaling by retinal ganglion cells. Science 1995, 270, 1207–1210. [Google Scholar] [CrossRef]
- Oram, M.W.; Hatsopoulos, N.G.; Richmond, B.J.; Donoghue, J.P. Excess synchrony in motor cortical neurons provides redundant direction information with that from coarse temporal measures. J. Neurophysiol. 2001, 86, 1700–1716. [Google Scholar] [PubMed]
- Eckhorn, R.; Bauer, R.; Jordan, W.; Brosch, M.; Kruse, W.; Munk, M.; Reitboeck, H.J. Coherent oscillations: A mechanism of feature linking in the visual cortex? Biol. Cybern. 1988, 60, 121–130. [Google Scholar] [CrossRef] [PubMed]
- Gray, C.M.; König, P.; Engel, A.K.; Singer, W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature 1989, 338, 334–337. [Google Scholar] [CrossRef] [PubMed]
- Vaadia, E.; Haalman, I.; Abeles, M.; Bergman, H.; Prut, Y.; Slovin, H.; Aertsen, A. Dynamics of neuronal interactions in monkey cortex in relation to behavioural events. Nature 1995, 373, 515–518. [Google Scholar] [CrossRef] [PubMed]
- Steinmetz, P.N.; Roy, A.; Fitzgerald, P.J.; Hsiao, S.S.; Johnson, K.O.; Niebur, E. Attention modulates synchronized neuronal firing in primate somatosensory cortex. Nature 2000, 404, 187–190. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Iliescu, B.F.; Ma, J.; Josić, K.; Dragoi, V. Adaptive changes in neuronal synchronization in macaque V4. J. Neurosci. 2011, 31, 13204–13213. [Google Scholar] [CrossRef] [PubMed]
- Nirenberg, S.; Carcieri, S.M.; Jacobs, A.L.; Latham, P.E. Retinal ganglion cells act largely as independent encoders. Nature 2001, 411, 698–701. [Google Scholar] [CrossRef] [PubMed]
- Levine, M.W.; Castaldo, K.; Kasapoglu, M.B. Firing coincidences between neighboring retinal ganglion cells: Inside information or epiphenomenon? Biosystems 2002, 67, 139–146. [Google Scholar] [CrossRef]
- Averbeck, B.B.; Lee, D. Neural noise and movement-related codes in the macaque supplementary motor area. J. Neurosci. 2003, 23, 7630–7641. [Google Scholar] [PubMed]
- Golledge, H.D.R.; Panzeri, S.; Zheng, F.; Pola, G.; Scannell, J.W.; Giannikopoulos, D.V.; Mason, R.J.; Tovée, M.J.; Young, M.P. Correlations, feature-binding and population coding in primary visual cortex. Neuroreport 2003, 14, 1045–1050. [Google Scholar] [PubMed]
- Brenner, N.; Strong, S.P.; Koberle, R.; Bialek, W.; de Ruyter van Steveninck, R.R. Synergy in a neural code. Neural Comput. 2000, 12, 1531–1552. [Google Scholar] [CrossRef] [PubMed]
- Abbott, L.F.; Dayan, P. The effect of correlated variability on the accuracy of a population code. Neural Comput. 1999, 11, 91–101. [Google Scholar] [CrossRef] [PubMed]
- Latham, P.E.; Nirenberg, S. Synergy, redundancy, and independence in population codes, revisited. J. Neurosci. 2005, 25, 5195–5206. [Google Scholar] [CrossRef] [PubMed]
- Abeles, M.; Bergman, H.; Margalit, E.; Vaadia, E. Spatiotemporal firing patterns in the frontal cortex of behaving monkeys. J. Neurophysiol. 1993, 70, 1629–1638. [Google Scholar] [PubMed]
- Maldonado, P.E.; Gerstein, G.L. Neuronal assembly dynamics in the rat auditory cortex during reorganization induced by intracortical microstimulation. Exp. Brain Res. 1996, 112, 431–441. [Google Scholar] [CrossRef] [PubMed]
- Nicolelis, M.A.; Lin, R.C.; Chapin, J.K. Neonatal whisker removal reduces the discrimination of tactile stimuli by thalamic ensembles in adult rats. J. Neurophysiol. 1997, 78, 1691–1706. [Google Scholar] [PubMed]
- Ikegaya, Y.; Aaron, A.; Cossart, R.; Aronov, D.; Lampl, I.; Ferster, D.; Yuste, R. Synfire chains and cortical songs: Temporal modules of cortical activity. Science 2004, 304, 559–564. [Google Scholar] [CrossRef] [PubMed]
- Watkins, D.S. Fundamental of Matrix Computations, 1st ed.; Wiley: New York, NY, USA, 1991; p. 84. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Crumiller, M.; Knight, B.; Kaplan, E. The Measurement of Information Transmitted by a Neural Population: Promises and Challenges. Entropy 2013, 15, 3507-3527. https://doi.org/10.3390/e15093507
Crumiller M, Knight B, Kaplan E. The Measurement of Information Transmitted by a Neural Population: Promises and Challenges. Entropy. 2013; 15(9):3507-3527. https://doi.org/10.3390/e15093507
Chicago/Turabian StyleCrumiller, Marshall, Bruce Knight, and Ehud Kaplan. 2013. "The Measurement of Information Transmitted by a Neural Population: Promises and Challenges" Entropy 15, no. 9: 3507-3527. https://doi.org/10.3390/e15093507
APA StyleCrumiller, M., Knight, B., & Kaplan, E. (2013). The Measurement of Information Transmitted by a Neural Population: Promises and Challenges. Entropy, 15(9), 3507-3527. https://doi.org/10.3390/e15093507



