Information Entropy As a Basic Building Block of Complexity Theory
Abstract
:1. Introduction
2. The Origin of Information Entropy
3. Entropy in Classical Thermodynamics
4. Entropy Maximizing Probability Distributions
- (1)
- Exponential distribution, with PDF given by:maximizes entropy under the constraint that the mean of the random variable, X, which is , is fixed.This entropy maximization property is perhaps one of the main reasons why we encounter exponential distributions so frequently in mathematics and physics. For example, a Poisson process is defined through exponential temporal or spatial intervals, while the sojourn times of Markov processes are exponentially distributed [20]. Exponential distribution is also very relevant to ergodic chaotic systems, as recurrence times of chaotic systems follow exponential distributions [22,23]. Exponential laws play an even more fundamental role in physics, since the basic laws in statistical mechanics and quantum mechanics are expressed as exponential distributions, while finite spin glass systems are equivalent to Markov chains.
- (2)
- When mean, μ, and variance, , are given, the distribution that maximizes entropy is the normal distribution with mean, μ, and variance, , .The fundamental reason that normal distributions maximize entropy is the Central Limit theorem—a normal distribution may be considered an attractor, since the sample mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed.
5. Entropy and Complexity
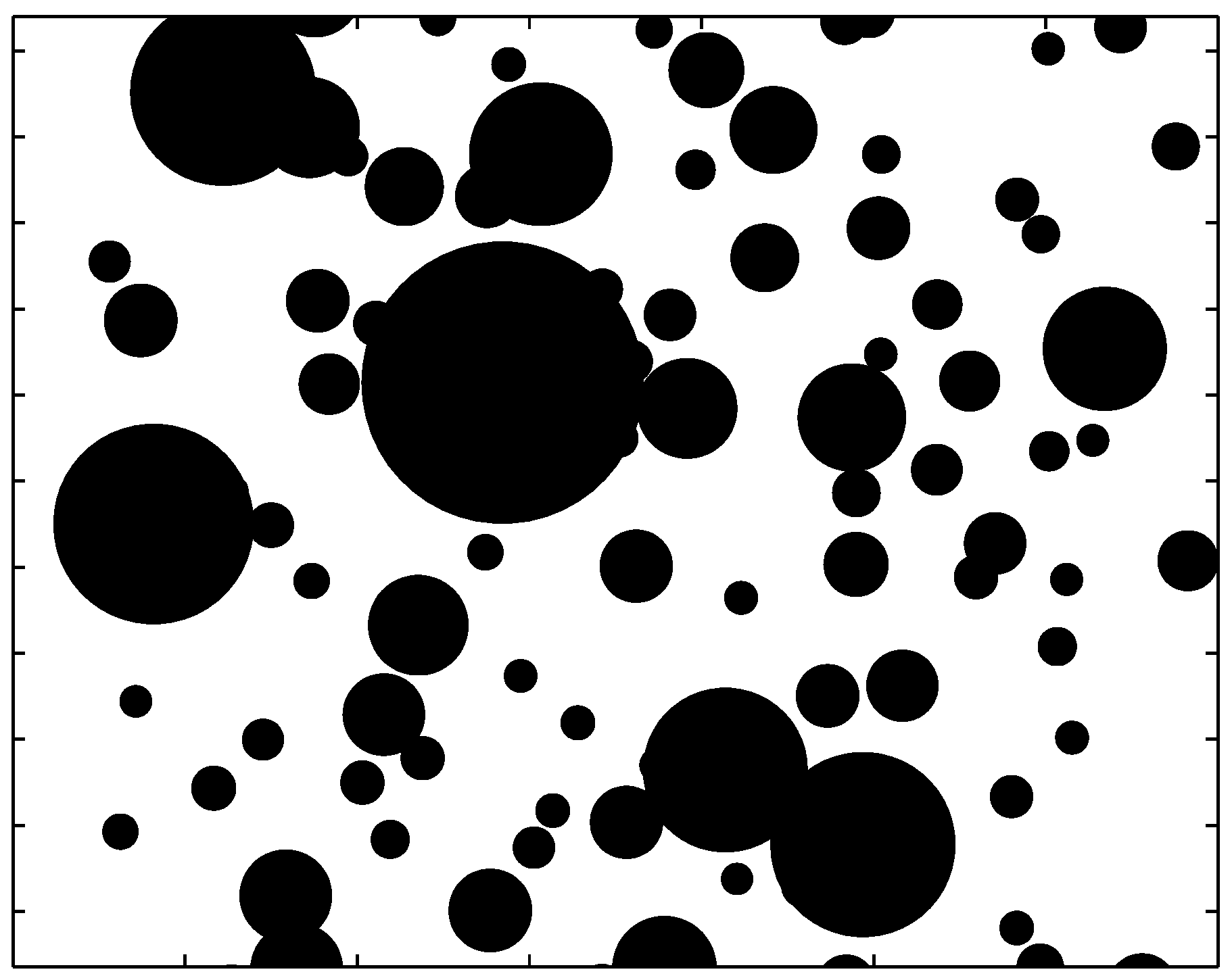
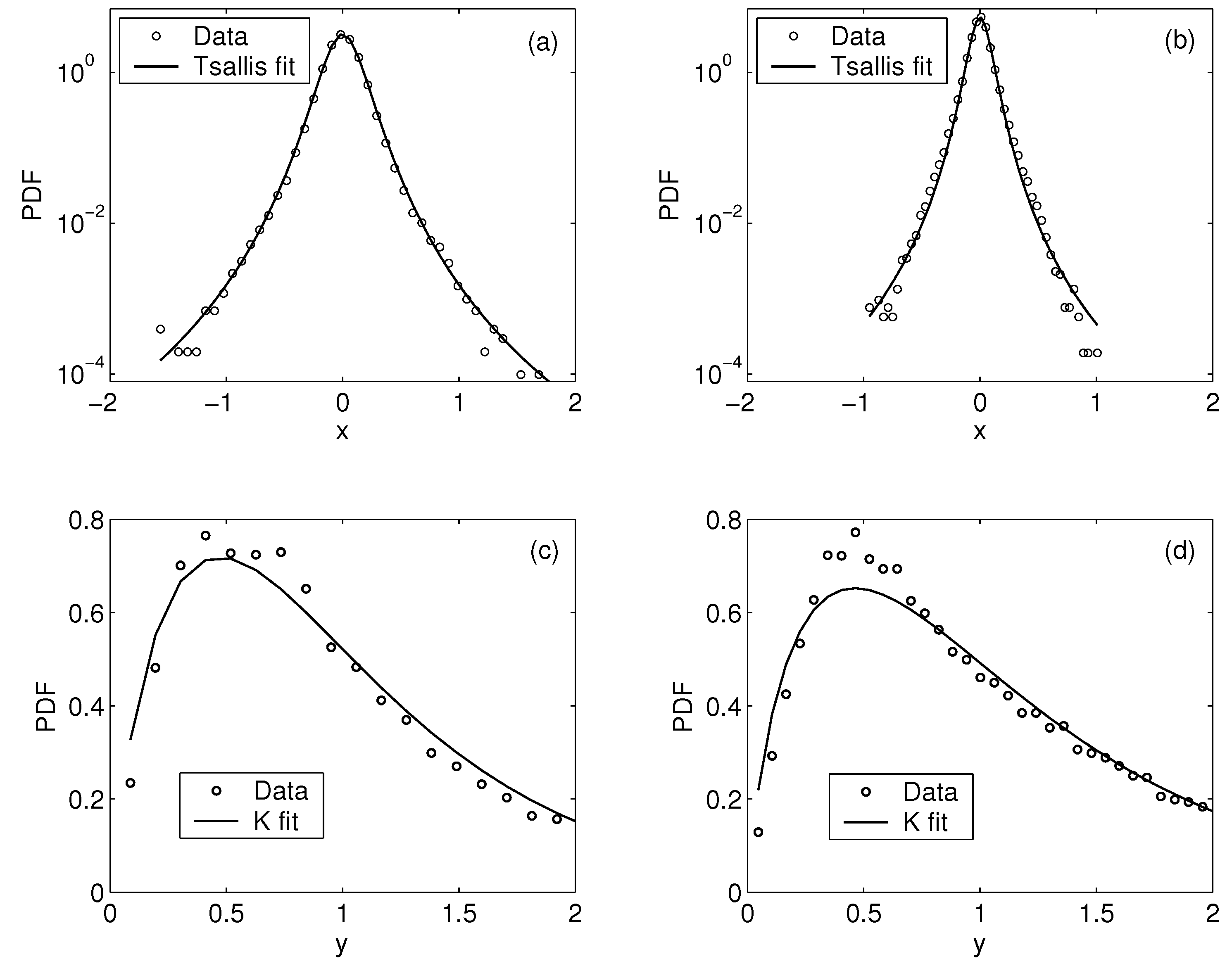
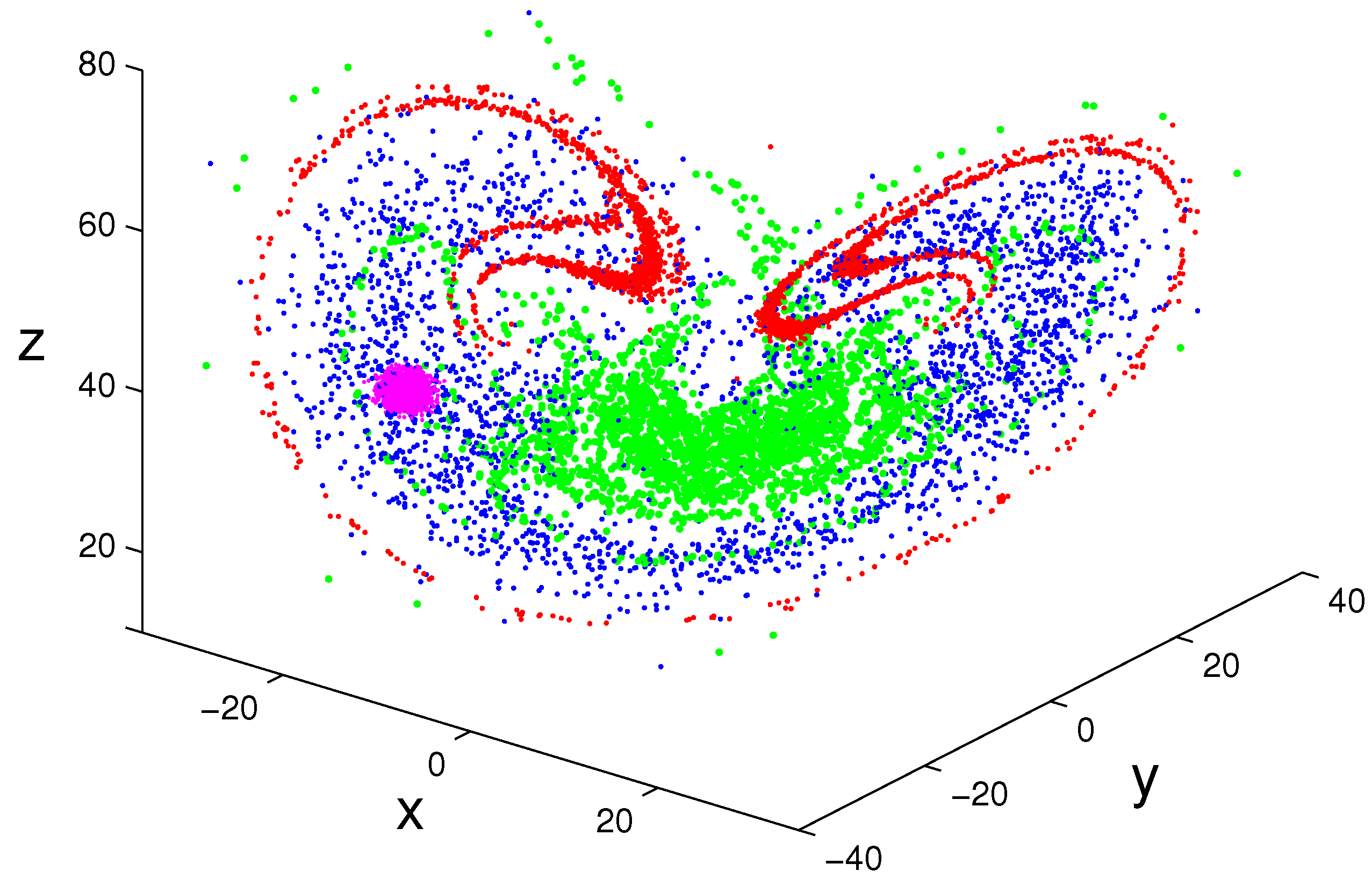
6. Time’s Arrow
7. Entropy in an Inter-Connected World: Examples of Applications and Future Perspectives
7.1. Estimating Entropy from Complex Data: The Use of the Lempel-Ziv Complexity
- Scheme 1: Let denote a finite length, 0–1 symbolic sequence; denote a substring of S that starts at position i and ends at position j, that is, when , and when , , the null set. Let denote the vocabulary of a sequence, S. It is the set of all substrings, or words, of S, (i.e., for ; ). For example, let , we then have . The parsing procedure involves a left-to-right scan of the sequence, S. A substring, , is compared to the vocabulary that is comprised of all substrings of S up to , that is, . If is present in , then update and to and , respectively, and the process repeats. If the substring is not present, then place a dot after to indicate the end of a new component, update and to (the single symbol in the position) and , respectively, and the process continues. This parsing operation begins with and continues until , where n is the length of the symbolic sequence. For example, the sequence, 1011010100010, is parsed as . By convention, a dot is placed after the last element of the symbolic sequence. In this example, the number of distinct words is six.
- Scheme 2: The sequence, , is sequentially scanned and rewritten as a concatenation, , of words, , chosen in such a way that and is the shortest word that has not appeared previously. In other words, is the extension of some word, , in the list, , where and s is either zero or one. The above example sequence, 1011010100010, is parsed as . Therefore, a total of seven distinct words are obtained. This number is larger than the six of Scheme 1 by one.
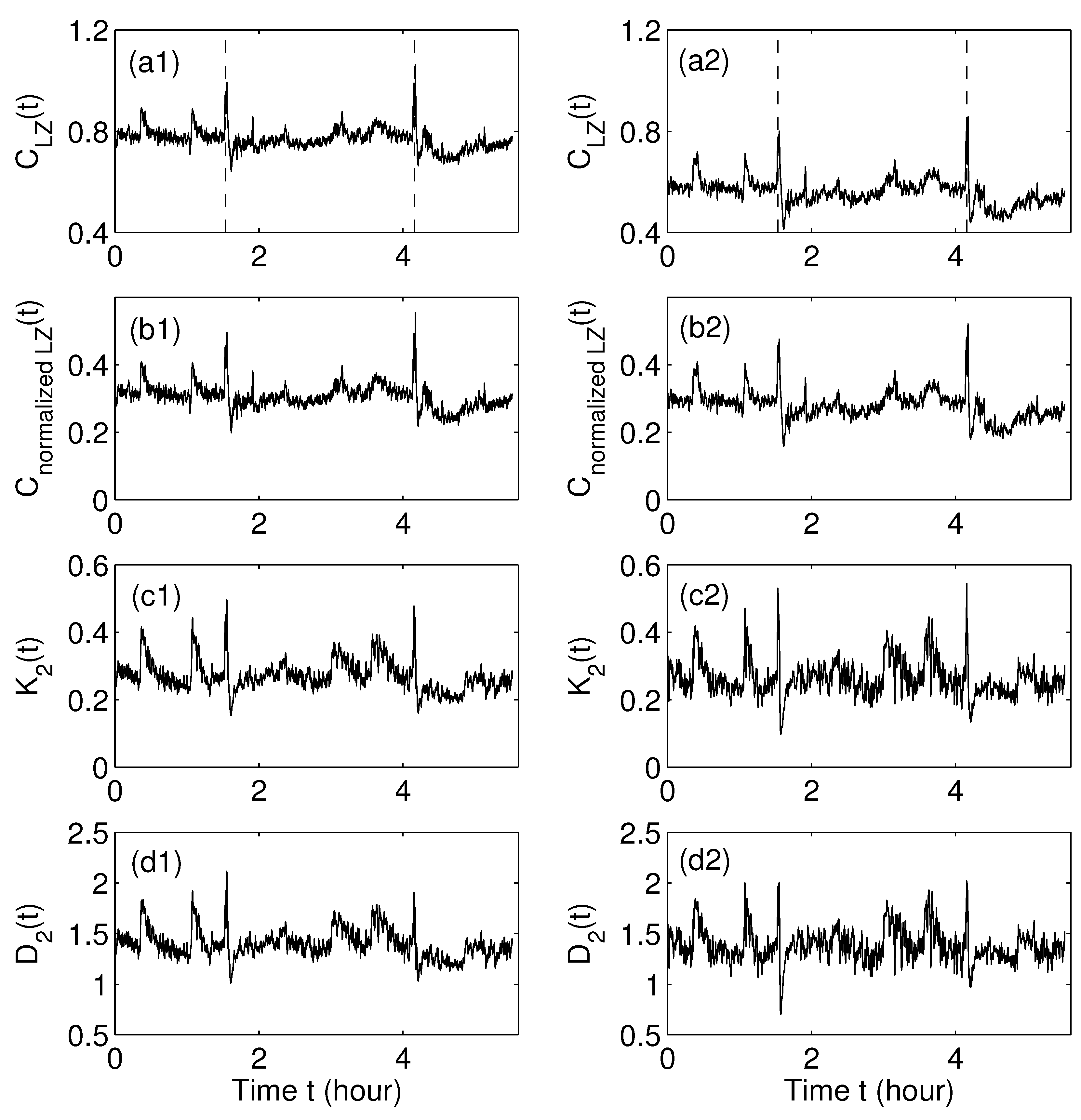
7.2. Future Perspectives
Acknowledgments
Conflicts of Interest
References
- Kastens, K.A.; Manduca, C.A.; Cervato, C.; Frodeman, R.; Goodwin, C.; Liben, L.S.; Mogk, D.W.; Spangler, T.C.; Stillings, N.A.; Titus, S. How geoscientists think and learn. Eos Trans. Am. Geophys. Union 2009, 90, 265–272. [Google Scholar] [CrossRef]
- Lin, C.C.; Shu, F.H. On the spiral structure of disk galaxies. Astrophys. J. 1964, 140, 646–655. [Google Scholar] [CrossRef]
- Vasavada, A.R.; Showman, A. Jovian atmospheric dynamics: An update after Galileo and Cassini. Rep. Progr. Phys. 2005, 68, 1935–1996. [Google Scholar] [CrossRef]
- Zhang, G.M.; Yu, L. Emergent phenomena in physics (in Chinese). Physics 2010, 39, 543–549. [Google Scholar]
- Hemelrijk, C.K.; Hildenbrandt, H. Some causes of the variable shape of flocks of birds. PLoS One 2011, 6, e22479. [Google Scholar] [CrossRef] [PubMed]
- Hildenbrandt, H.; Carere, C.; Hemelrijk, C.K. Self-organized aerial displays of thousands of starlings: A model. Behav. Ecol. 2010, 21, 1349–1359. [Google Scholar] [CrossRef]
- Shaw, E. Schooling fishes. Am. Sci. 1978, 66, 166–175. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- D’Orsogna, M.R.; Chuang, Y.L.; Bertozzi, A.L.; Chayes, L.S. Self-propelled particles with soft-core interactions: Patterns, stability, and collapse. Phys. Rev. Lett. 2006, 96, e104302. [Google Scholar] [CrossRef]
- Hemelrijk, C.K.; Hildenbrandt, H. Self-organized shape and frontal density of fish schools. Ethology 2008, 114, 245–254. [Google Scholar] [CrossRef]
- Kroy, K.; Sauermann, G.; Herrmann, H.J. Minimal model for sand dunes. Phys. Rev. Lett. 2002, 88, e054301. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Champaign, IL, USA, 1949. [Google Scholar]
- Khinchin, A.I. Mathematical Foundations of Information Theory; Courier Dover Publications: Mineola, NY, USA, 1957. [Google Scholar]
- Erill, I. Information theory and biological sequences: Insights from an evolutionary perspective. In Information Theory: New Research; Deloumeayx, P., Gorzalka, J.D., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2012; pp. 1–28. [Google Scholar]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Ziv, J.; Lempel, A. Compression of individual sequences via variable-rate coding. IEEE Trans. Inf. Theory 1978, 24, 530–536. [Google Scholar] [CrossRef]
- Shor, P. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 1995, 52, R2493–R2496. [Google Scholar] [CrossRef] [PubMed]
- Hamming, R. The Art of Probability for Scientists and Engineers; Addison-Wesley: Boston, MA, USA, 1991. [Google Scholar]
- Tribus, M. The Maximum Entropy Formalism; Levine, R.D., Tribus, M., Eds.; MIT Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Gao, J.B.; Cao, Y.H.; Tung, W.W.; H, J. Multiscale Analysis of Complex Time Series—Integration of Chaos and Random Fractal Theory, and Beyond; Wiley Interscience: New York, NY, USA, 2007. [Google Scholar]
- Gatlin, L.L. Information Theory and the Living System; Columbia University Press: New York, NY, USA, 1972. [Google Scholar]
- Gao, J.B. Recurrence time statistics for chaotic systems and their applications. Phys. Rev. Lett. 1999, 83, 3178–3181. [Google Scholar] [CrossRef]
- Gao, J.B.; Cai, H.Q. On the structures and quantification of recurrence plots. Phys. Lett. A 2000, 270, 75–87. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Tung, W.W.; Cao, Y.H.; Sarshar, N.; Roychowdhury, V.P. Assessment of long range correlation in time series: How to avoid pitfalls. Phys. Rev. E 2006, 73, e016117. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Tung, W.W. Facilitating joint chaos and fractal analysis of biosignals through nonlinear i adaptive filtering. PLoS One 2011, 6, e24331. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Gouyet, J.F. Physics and Fractal Structures; Springer: New York, NY, USA, 1995. [Google Scholar]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Falconer, K.J. Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons: Chichester, UK, 1990. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C.; Levy, S.V.F.; Souza, A.M.C.; Maynard, R. Statistical-mechanical foundation of the ubiquity of levy distributions in nature. Phys. Rev. Lett. 1995, 75, 3589–3593. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Tung, W.W.; Gao, J.B. A new way to model non-stationary sea clutter. IEEE Signal Process. Lett. 2009, 16, 129–132. [Google Scholar] [CrossRef]
- Atmanspacher, H.; Scheingraber, H. A fundamental link between system theory and statistical mechanics. Found. Phys. 1987, 17, 939–963. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591–2593. [Google Scholar] [CrossRef]
- Osborne, A.R.; Provenzale, A. Finite correlation dimension for stochastic-systems with power-law spectra. Phys. D Nonlinear Phenom. 1989, 35, 357–381. [Google Scholar] [CrossRef]
- Provenzale, A.; Osborne, A.R.; Soj, R. Convergence of the K2 entropy for random noises with power law spectra. Phys. D Nonlinear Phenom. 1991, 47, 361–372. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Tung, W.W.; Cao, Y.H. Distinguishing chaos from noise by scale-dependent Lyapunov exponent. Phys. Rev. E 2006, 74, e066204. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Mao, X.; Tung, W.W. Detecting low-dimensional chaos by the “noise titration” technique: Possible problems and remedies. Chaos Solitons Fractals 2012, 45, 213–223. [Google Scholar] [CrossRef]
- Gao, J.B.; Hwang, S.K.; Liu, J.M. When can noise induce chaos? Phys. Rev. Lett. 1999, 82, 1132–1135. [Google Scholar] [CrossRef]
- Gao, J.B.; Tung, W.W.; Hu, J. Quantifying dynamical predictability: The pseudo-ensemble approach (in honor of Professor Andrew Majda’s 60th birthday). Chin. Ann. Math. Ser. B 2009, 30, 569–588. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Tung, W.W.; Zheng, Y. Multiscale analysis of economic time series by scale-dependent Lyapunov exponent. Quant. Financ. 2011, 13, 265–274. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Tung, W.W. Entropy measures for biological signal analysis. Nonlinear Dyn. 2012, 68, 431–444. [Google Scholar] [CrossRef]
- Feldman, D.P.; Crutchfield, J.P. Measures of statistical complexity: Why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Feldman, D.P.; Crutchfield, J.P. Structural information in two-dimensional patterns: Entropy convergence and excess entropy. Phys. Rev. E 2003, 67, e051104. [Google Scholar] [CrossRef]
- Emmert-Streib, F. Statistic complexity: Combining Kolmogorov complexity with an ensemble approach. PLoS One 2010, 5, e12256. [Google Scholar] [CrossRef] [PubMed]
- Zunino, L.; Soriano, M.C.; Rosso, O.A. Distinguishing chaotic and stochastic dynamics from time series by using a multiscale symbolic approach. Phys. Rev. E 2012, 86, e046210. [Google Scholar] [CrossRef]
- Torcini, A.; Grassberger, P.; Politi, A. Error propagation in extended chaotic systems. J. Phys. A Math. Gen. 1995. [Google Scholar] [CrossRef]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Growth of non-infinitesimal perturbations in turbulence. Phys. Rev. Lett. 1996. [Google Scholar] [CrossRef]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Predictability in the large: An extension of the concept of Lyapunov exponent. J. Phys. A Math. Gen. 1997, 30, 1–26. [Google Scholar] [CrossRef]
- Gaspard, P.; Wang, X.J. Noise, chaos, and (ϵ, τ)-entropy per unit time. Phys. Rep. 1993, 235, 291–343. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, e021906. [Google Scholar] [CrossRef]
- Prigogine, I. From Being to Becoming; W.H. Freeman and Company: New York, NY, USA, 1980. [Google Scholar]
- Lebowitz, J.L. Microscopic origins of irreversible macroscopic behavior. Phys. A Stat. Mech. Appl. 1999, 263, 516–527. [Google Scholar] [CrossRef]
- Feynman, R. The Character of Physical Law; MIT Press: Cambridge, MA, USA, 1967; p. 112. [Google Scholar]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Springer-Verlag: Berlin, Germany, 1978; p. 71. [Google Scholar]
- Kac, M. Probability and Related Topics in Physical Sciences; Interscience Publishers: Hoboken, NJ, USA, 1959; Lectures in Applied Mathematics, Series; Volume 1A, p. 62. [Google Scholar]
- Villani, C. A review of mathematical topics in collisional kinetic theory. Handb. Math. Fluid Dyn. 2002, 1, 71–74. [Google Scholar]
- Wang, G.M.; Sevick, E.M.; Emil Mittag, Searles, D.J.; Evans, D.J. Experimental demonstration of violations of the second law of thermodynamics for small systems and short time scales. Phys. Rev. Lett. 2002, 89, e050601. [Google Scholar] [CrossRef]
- Schrodinger, E. What is Life? Macmillan Publishers: London, UK, 1946. [Google Scholar]
- Penrose, R. The Emperor’s New Mind: Concerning Computers, Minds, and The Laws of Physics; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Kolmogorov, A.N. Three approaches to the quantitative definition of “information”. Probl. Inf. Transm. 1965, 1, 1–7. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Logical basis for information theory and probability theory. IEEE Trans. Inf. Theory 1968, IT-14, 662–664. [Google Scholar] [CrossRef]
- Zhang, X.S.; Roy, R.J.; Jensen, E.W. EEG complexity as a measure of depth of anesthesia for patients. IEEE Trans. Biomed. Eng. 2001, 48, 1424–1433. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, R. Quantifying physiological data with Lempel-Ziv complexity: Certain issues. IEEE Trans. Biomed. Eng. 2002, 49, 1371–1373. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Rapp, P.E.; Cellucci, C.J.; Korslund, K.E.; Watanabe, T.A.A.; Jiménez-Montaño, M.A. Effective normalization of complexity measurements for epoch length and sampling frequency. Phys. Rev. E 2001, 64, e016209. [Google Scholar] [CrossRef]
- Hu, J.; Gao, J.B.; Principe, J.C. Analysis of biomedical signals by the Lempel-Ziv complexity: The effect of finite data size. IEEE Trans. Biomed. Eng. 2006, 53, 2606–2609. [Google Scholar] [PubMed]
- Gao, J.B.; Hu, J.; Tung, W.W. Complexity measures of brain wave dynamics. Cogn. Neurodyn. 2011, 5, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Loewenstern, D.; Yianilos, P.N. Significantly lower entropy estimates for natural DNA sequences. J. Comput. Biol. 1999, 6, 125–142. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, P.R.; Munteanu, C.R.; Escobar, M.; Prado-Prado, F.; Martn-Romalde, R.; Pereira, D.; Villalba, K.; Duardo-Snchez, A.; Gonzlez-Daz, H. New Markov-Shannon entropy models to assess connectivity quality in complex networks: From molecular to cellular pathway, Parasite-Host, Neural, Industry, and Legal-Social networks. J. Theor. Biol. 2012, 293, 174–188. [Google Scholar] [CrossRef] [PubMed]
- Cattani, C. On the existence of wavelet symmetries in Archaea DNA. Comput. Math. Methods Med. 2012. [Google Scholar] [CrossRef] [PubMed]
- Cattani, C.; Pierro, G. On the fractal geometry of DNA by the binary image analysis. Bull. Math. Biol. 2013, 1, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishnan, N.; Bose, R. Dipole entropy based techniques for segmentation of introns and exons in DNA. Appl. Phys. Lett. 2012. [Google Scholar] [CrossRef]
- Cattani, C. Uncertainty and Symmetries in DNA Sequences. In Proceedings of the 4th International Conference on Biomedical Engineering in Vietnam, Ho Chi Minh, Vietnam, 10–12 January 2012; Springer: Berlin/Heidelberg, Germany, 2013; pp. 359–369. [Google Scholar]
- Jani, M.; Azad, R.K. Information entropy based methods for genome comparison. ACM SIG Bioinform. 2013. [Google Scholar] [CrossRef]
- Luce, R.D. Whatever happened to information theory in psychology? Rev. Gen. Psychol. 2003, 7, 183–188. [Google Scholar] [CrossRef]
- Hirsh, J.B.; Mar, R.A.; Peterson, J.B. Psychological entropy: A framework for understanding uncertainty-related anxiety. Psychol. Rev. 2012, 119, 304–320. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.Z.; Wong, M.S.; Wang, J.Z.; Zhao, Y.L. Analysis of airborne particulate matter (PM2.5) over Hong Kong using remote sensing and GIS. Sensors 2012, 12, 6825–6836. [Google Scholar] [CrossRef] [PubMed]
- Georgescu-Roegen, N. The Entropy Law and Economic Process; Harvard University Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Solow, R. A contribution to the theory of economic growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Swan, T. Economic growth and capital accumulation. Econ. Record 1956, 32, 334–361. [Google Scholar] [CrossRef]
- McCauley, J.L. Thermodynamic analogies in economics and and finance: Instability of markets. Phys. A Stat. Mech. Appl. 2003, 329, 199–212. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Mao, X.; Zhou, M.; Gurbaxani, B.; Lin, J.W.B. Entropies of negative incomes, Pareto-distributed loss, and financial crises. PLoS One 2011, 6, e25053. [Google Scholar] [CrossRef] [PubMed]
- Mimkes, J. Stokes integral of economic growth: Calculus and Solow model. Phys. A Stat. Mech. Appl. 2010, 389, 1665–1676. [Google Scholar] [CrossRef]
- Manyika, J.; Chui, M.; Brown, B.; Bughin, J.; Dobbs, R.; Roxburgh, C.; Byers, A.H. Big data: The next frontier for innovation, competition, and productivity. 2011. Available online: http://www.mckinsey.com/insights/business technology/big data the next frontier for innovation (accessed on 26 March 2013).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gao, J.; Liu, F.; Zhang, J.; Hu, J.; Cao, Y. Information Entropy As a Basic Building Block of Complexity Theory. Entropy 2013, 15, 3396-3418. https://doi.org/10.3390/e15093396
Gao J, Liu F, Zhang J, Hu J, Cao Y. Information Entropy As a Basic Building Block of Complexity Theory. Entropy. 2013; 15(9):3396-3418. https://doi.org/10.3390/e15093396
Chicago/Turabian StyleGao, Jianbo, Feiyan Liu, Jianfang Zhang, Jing Hu, and Yinhe Cao. 2013. "Information Entropy As a Basic Building Block of Complexity Theory" Entropy 15, no. 9: 3396-3418. https://doi.org/10.3390/e15093396
APA StyleGao, J., Liu, F., Zhang, J., Hu, J., & Cao, Y. (2013). Information Entropy As a Basic Building Block of Complexity Theory. Entropy, 15(9), 3396-3418. https://doi.org/10.3390/e15093396




