Outer Synchronization between Fractional-Order Complex Networks: A Non-Fragile Observer-based Control Scheme
Abstract
:1. Introduction
2. Preliminaries and Network Model
2.1. Basic Concepts and Lemmas
- (1)
- ;
- (2)
- ;
- (3)
- .
2.2. Network Model
3. Global Outer Synchronization Analysis
4. Numerical Simulations
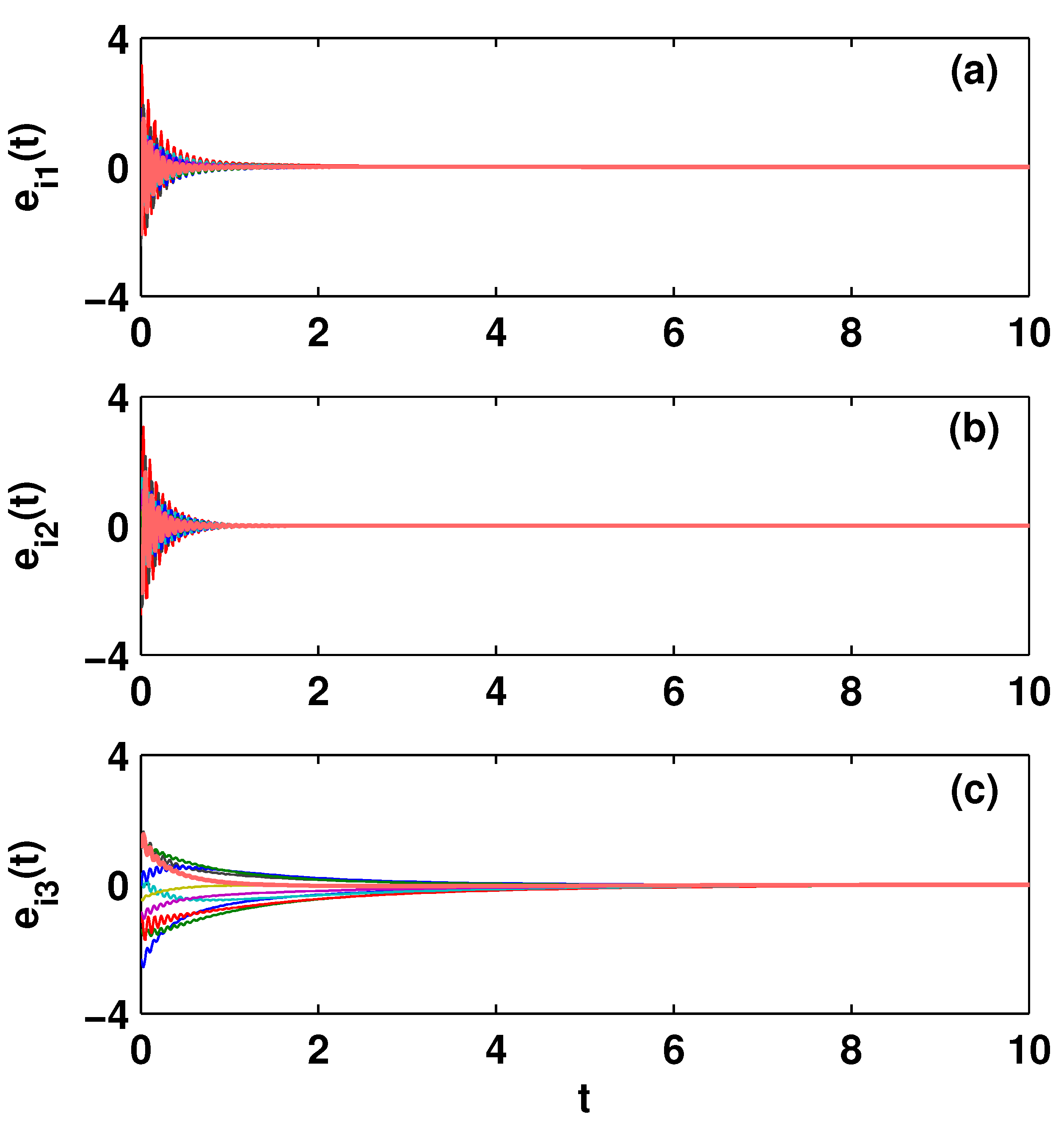
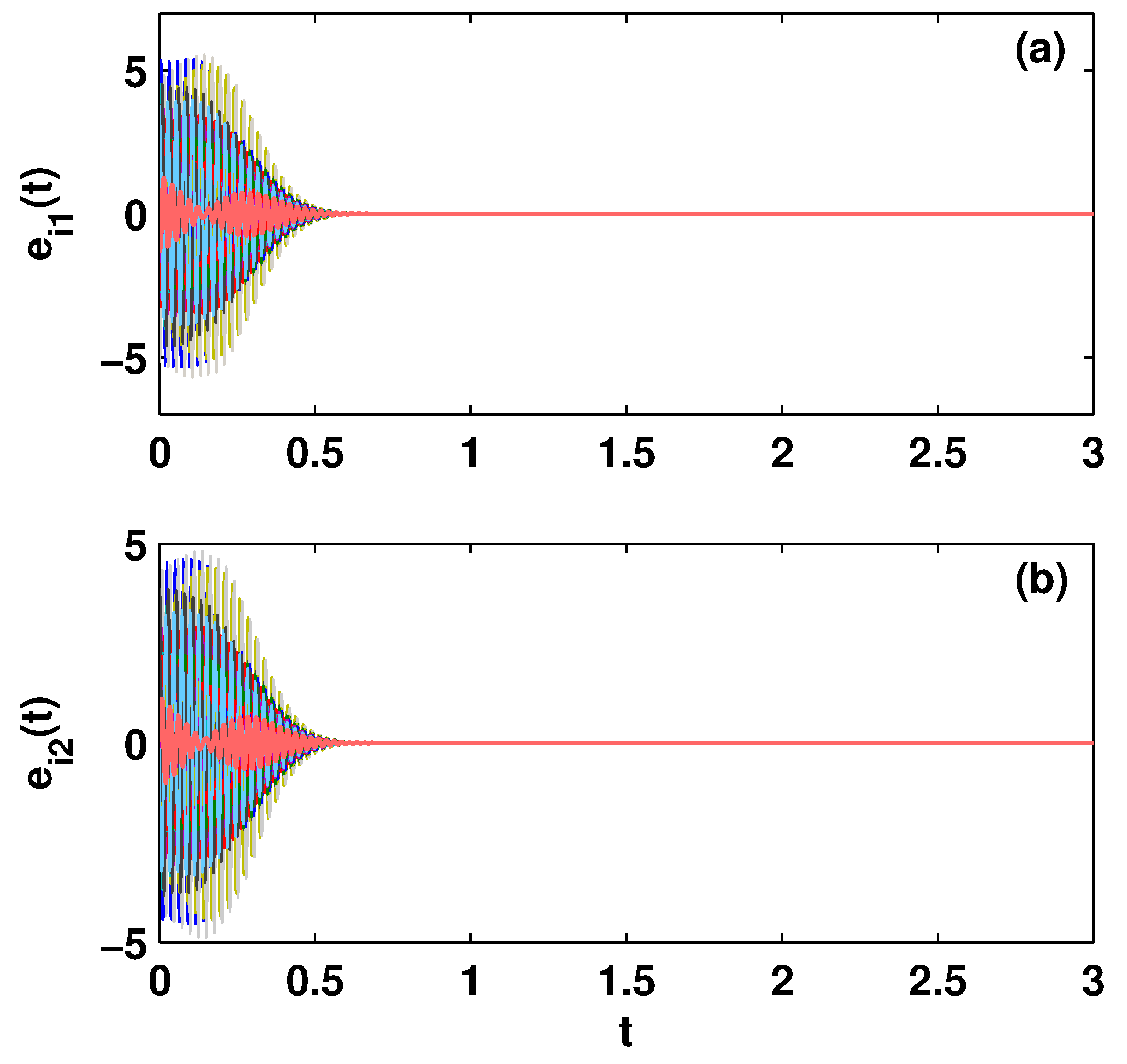
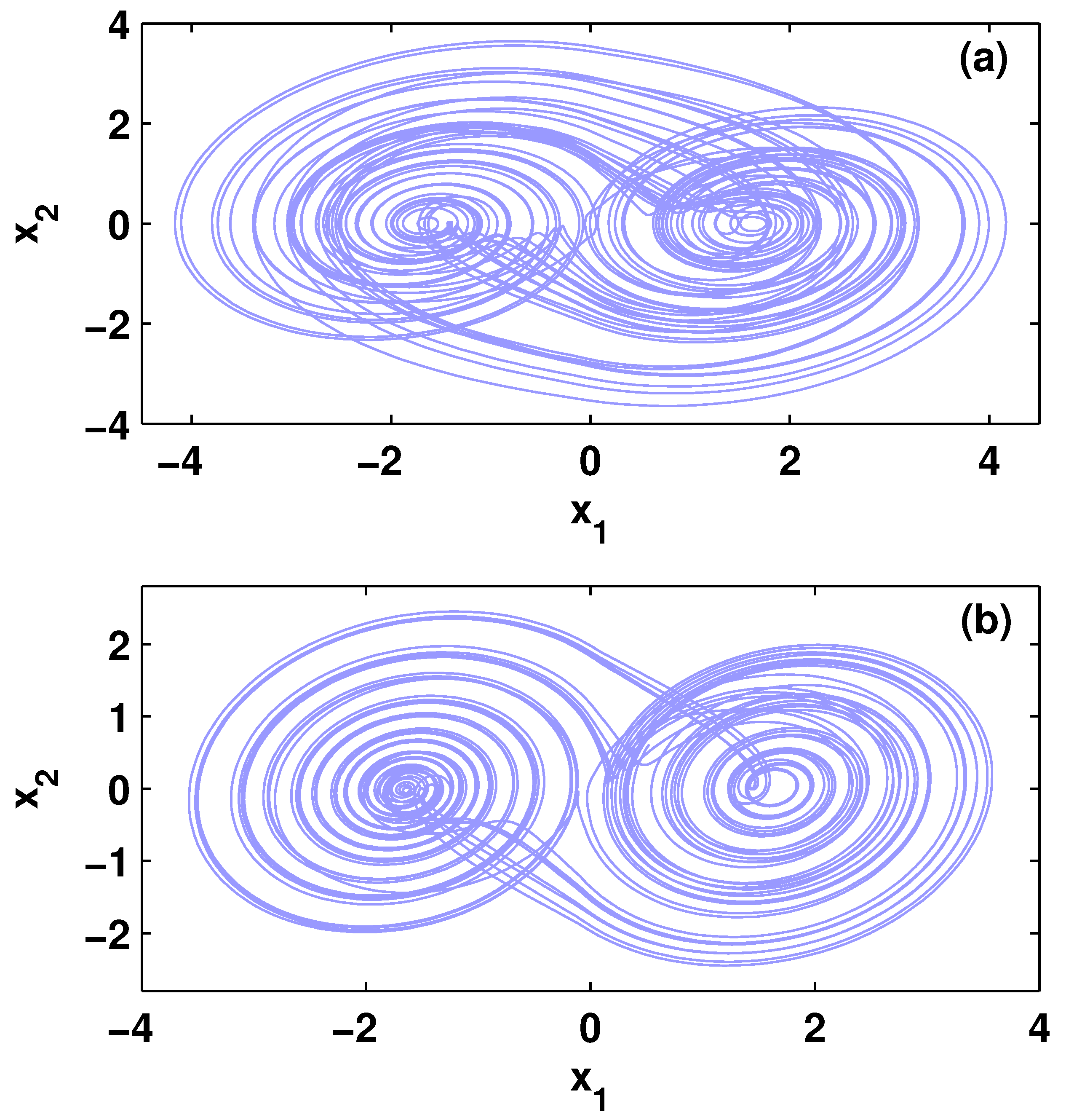
4.1. Outer Synchronization between Two FCNs with Nearest-Neighbor Network Topology
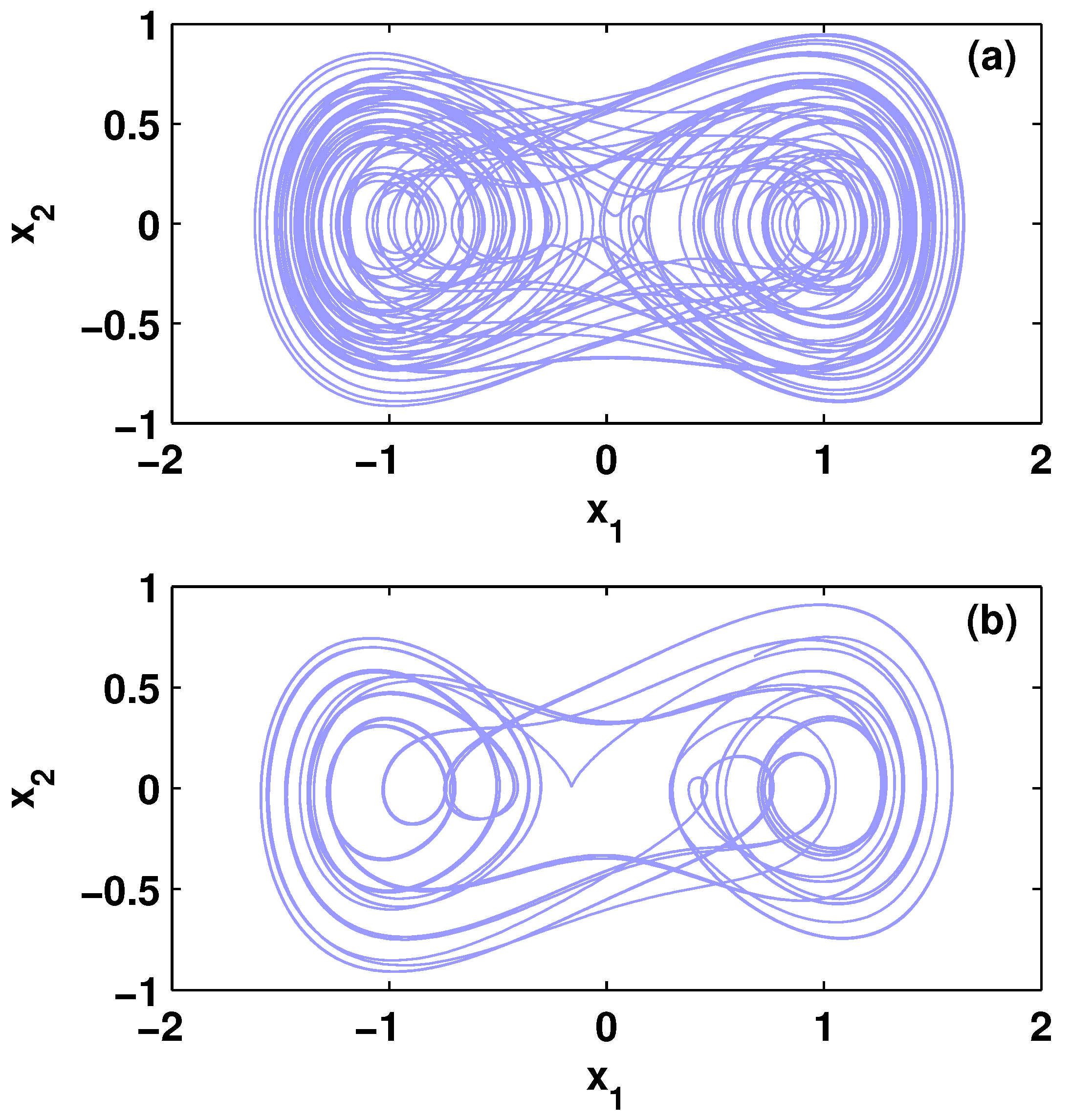
4.2. Outer Synchronization between Two FCNs with Small-World Network Topology
5. Conclusions
Acknowledgements
References
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.-U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Balanov, A.; Janson, N.; Postnov, D.; Sosnovtseva, O. Synchronization: From Simple to Complex; Springer-Verlag: Berlin, Germany, 2010. [Google Scholar]
- Ren, W.; Beard, R.W. Distributed Consensus in Multi-vehicle Cooperative Control; Springer-Verlag: London, UK, 2008. [Google Scholar]
- Li, Z.K.; Duan, Z.S.; Chen, G.R.; Huang, L. Consensus of multiagent systems and synchronization of complex networks: A unified viewpoint. IEEE Trans. Circuits Syst. I 2010, 57, 213–224. [Google Scholar]
- Seo, J.H.; Shim, H.; Back, J. Consensus of high-order linear systems using dynamic output feedback compensator: Low gain approach. Automatica 2009, 45, 2659–2664. [Google Scholar] [CrossRef]
- Lü, J.; Yu, X.; Chen, G.; Cheng, D. Characterizing the synchronizability of small-world dynamical networks. IEEE Trans. Circuits Syst. I 2004, 51, 787–796. [Google Scholar] [CrossRef]
- Lü, J.; Chen, G. A time-varying complex dynamical network model and its controlled synchronization criteria. IEEE Trans. Autom. Control 2005, 50, 841–846. [Google Scholar]
- Zhang, Q.; Lu, J.; Lü, J.; Tse, C.K. Adaptive feedback synchronization of a general complex dynamical network with delayed nodes. IEEE Trans. Circuits Syst. II 2008, 55, 183–187. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Lü, J. On pinning synchronization of complex dynamical networks. Automatica 2009, 45, 429–435. [Google Scholar] [CrossRef]
- Yang, X.; Cao, J.; Lu, J. Stochastic synchronization of complex networks with nonidentical nodes via hybrid adaptive and impulsive control. IEEE Trans. Circuits Syst. I 2012, 59, 371–384. [Google Scholar] [CrossRef]
- Nixon, M.; Fridman, M.; Ronen, E.; Friesem, A.A.; Davidson, N.; Kanter, I. Controlling synchronization in large laser networks. Phys. Rev. Lett. 2012, 108, 214101:1–214101:5. [Google Scholar] [CrossRef] [PubMed]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Lü, J.; Chen, G.; Yu, X. Modelling, Analysis and Control of Multi-Agent Systems: A Brief Overview. In Proceedings of the 2011 IEEE International Symposium on Circuits and Systems, Rio de Janeiro, Brazil, 15–18 May 2011; pp. 2103–2106.
- Chen, Y.; Lü, J.; Han, F.; Yu, X. On the cluster consensus of discrete-time multi-agent systems. Syst. Control Lett. 2011, 60, 517–523. [Google Scholar] [CrossRef]
- Zhu, J.; Lü, J.; Yu, X. Flocking of multi-agent non-holonomic systems with proximity graphs. IEEE Trans. Circuits Syst. I 2013, 60, 199–210. [Google Scholar] [CrossRef]
- Lu, X.; Lu, R.; Chen, S.; Lü, J. Finite-time distributed tracking control for multi-agent systems with a virtual leader. IEEE Trans. Circuits Syst. I 2013, 60, 352–362. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastsava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Miller, K.S.; Ross, B. Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley: New York, NY, USA, 1993. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. On the fractional calculus model of viscoelastic behavior. J. Rheol. 1986, 30, 133–155. [Google Scholar] [CrossRef]
- Cao, Y.; Li, Y.; Ren, W.; Chen, Y.Q. Distributed coordination of networked fractional-order systems. IEEE Trans. Syst. Man Cybernet. B 2010, 40, 362–370. [Google Scholar]
- Shen, J.; Cao, J.; Lu, J. Consenus of fractional-order systems with non-uniform input and communication delays. J. Syst. Control Eng. 2012, 226, 271–283. [Google Scholar]
- Tang, Y.; Wang, Z.; Fang, J.A. Pinning control of fractional-order weighted complex networks. Chaos 2009, 19, 013112. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, Y. Network synchronization in a population of star-coupled fractional nonlinear oscillators. Phys. Lett. A 2010, 374, 1464–1468. [Google Scholar] [CrossRef]
- Delshad, S.S.; Asheghan, M.M.; Beheshti, M.H. Synchronization of N-coupled incommensurate fractional-order chaotic systems with ring connection. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 3815–3824. [Google Scholar] [CrossRef]
- Sun, W.; Li, Y.; Li, C.; Chen, Y.Q. Convergence speed of a fractional order consensus algorithm over undirected scale-free networks. Asian J. Control 2011, 13, 936–946. [Google Scholar] [CrossRef]
- Chen, L.; Chai, Y.; Wu, R.; Sun, J.; Ma, T. Cluster synchronization in fractional-order complex dynamical networks. Phys. Lett. A 2012, 376, 2381–2388. [Google Scholar] [CrossRef]
- Wang, J.; Xiong, X. A general fractional-order dynamical network: Synchronization behavior and state tuning. Chaos 2012, 22, 023102:1–023102:9. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Li, C. Synchronization in fractional-order differential systems. Physica D 2005, 212, 111–125. [Google Scholar] [CrossRef]
- Li, C.P.; Sun, W.G.; Kurths, J. Synchronization between two coupled complex networks. Phys. Rev. E 2007, 76, 046204. [Google Scholar] [CrossRef] [PubMed]
- Li, C.P.; Xu, C.X.; Sun, W.G.; Xu, J.; Kurths, J. Outer synchronization of coupled discrete-time networks. Chaos 2009, 19, 013106:1–013106:7. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.J.; Cao, J.D.; Lu, J.Q. Outer synchronization between two nonidentical networks with circumstance noise. Physica A 2008, 389, 1480–1488. [Google Scholar] [CrossRef]
- Li, Z.C.; Xue, X.P. Outer synchronization of coupled networks using arbitrary coupling strength. Chaos 2010, 20, 023106:1–023106:7. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Lu, J.A.; Lü, J.H.; Hill, D.J. Structure identification of uncertain general complex dynamical networks with time delay. Automatica 2009, 45, 1799–1807. [Google Scholar] [CrossRef]
- Zhao, J.C.; Li, Q.; Lu, J.A.; Jiang, J.P. Topology identification of complex dynamical networks. Chaos 2010, 20, 023119:1–023119:7. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, R.; Grosu, I.; Dana, S.K. Antisynchronization of two complex dynamical networks. LNICST 2009, 4, 1072–1082. [Google Scholar]
- Wu, X.; Zheng, W.X.; Zhou, J. Generalized outer synchronization between complex dynamical networks. Chaos 2009, 19, 013109:1–013109:9. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Zeng, C.Y.; Tian, L.X. Linear generalized synchronization between two complex networks. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2162–2167. [Google Scholar] [CrossRef]
- Wu, X.J.; Lu, H.T. Outer synchronization between two different fractional-order general complex dynamical networks. Chin. Phys. B 2010, 19, 070511:1–070511:12. [Google Scholar]
- Asheghan, M.M.; Míguez, J.; Hamidi-Beheshti, M.T.; Tavazoei, M.S. Robust outer synchronization between two complex networks with fractional order dynamics. Chaos 2011, 21, 033121:1–033121:12. [Google Scholar] [CrossRef] [PubMed]
- Keel, L.H.; Bhattacharyya, S.P. Robust, Fragile, or Optimal? IEEE Trans. Autom. Control 1997, 42, 1098–1105. [Google Scholar] [CrossRef]
- Matignon, D. Stability results of fractional differential equations with applications to control processing. IMACS, IEEE-SMC 1996, 2, 963–968. [Google Scholar]
- Laub, A.J. Matrix Analysis for Scientists and Engineers; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Lu, J.G.; Chen, Y.Q. Robust stability and stabilization of fractional-order interval systems with the fractional order α: the case 0 < α < 1. IEEE Trans. Autom. Control 2010, 55, 152–158. [Google Scholar]
- Khargonekar, P.P.; Petersen, I.R.; Zhou, K. Robust stabilization of uncertain linear systems: quadratic stabilizability and H∞ control theory. IEEE Trans. Autom. Control 1990, 35, 356–361. [Google Scholar] [CrossRef]
- Boyd, S.; Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Glad, T.; Ljung, L. Control Theory (Multivariable and Nonlinear Methods); Taylor and Francis: London, UK, 2000. [Google Scholar]
- Chen, Y.Q.; Ahn, H.S.; Podlubny, I. Robust stability check of fractional order linear time invariant systems with interval uncertainties. Signal Process. 2006, 86, 2611–2618. [Google Scholar] [CrossRef]
- Ahmad, W.M.; Sprott, J.C. Chaos in fractional-order autonomous nonlinear systems. Chaos Solitons Fractals 2003, 16, 339–351. [Google Scholar] [CrossRef]
- Li, C.P.; Deng, W.H. Chaos synchronization of fractional-order differential systems. Int. J. Mod. Phys. B 2006, 20, 791–803. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of "small-world" networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhao, M.; Wang, J. Outer Synchronization between Fractional-Order Complex Networks: A Non-Fragile Observer-based Control Scheme. Entropy 2013, 15, 1357-1374. https://doi.org/10.3390/e15041357
Zhao M, Wang J. Outer Synchronization between Fractional-Order Complex Networks: A Non-Fragile Observer-based Control Scheme. Entropy. 2013; 15(4):1357-1374. https://doi.org/10.3390/e15041357
Chicago/Turabian StyleZhao, Meichun, and Junwei Wang. 2013. "Outer Synchronization between Fractional-Order Complex Networks: A Non-Fragile Observer-based Control Scheme" Entropy 15, no. 4: 1357-1374. https://doi.org/10.3390/e15041357
APA StyleZhao, M., & Wang, J. (2013). Outer Synchronization between Fractional-Order Complex Networks: A Non-Fragile Observer-based Control Scheme. Entropy, 15(4), 1357-1374. https://doi.org/10.3390/e15041357