HydroZIP: How Hydrological Knowledge can Be Used to Improve Compression of Hydrological Data
Abstract
:1. Introduction
1.1. Background
1.2. Research Objective
1.3. Related Work
2. Data and Methods
2.1. The MOPEX Hydrological Data Set and Preprocessing
2.2. Benchmark Test Using General Compressors
3. Development of the Specific Compressor: HydroZIP
3.1. Entropy Coding Methods
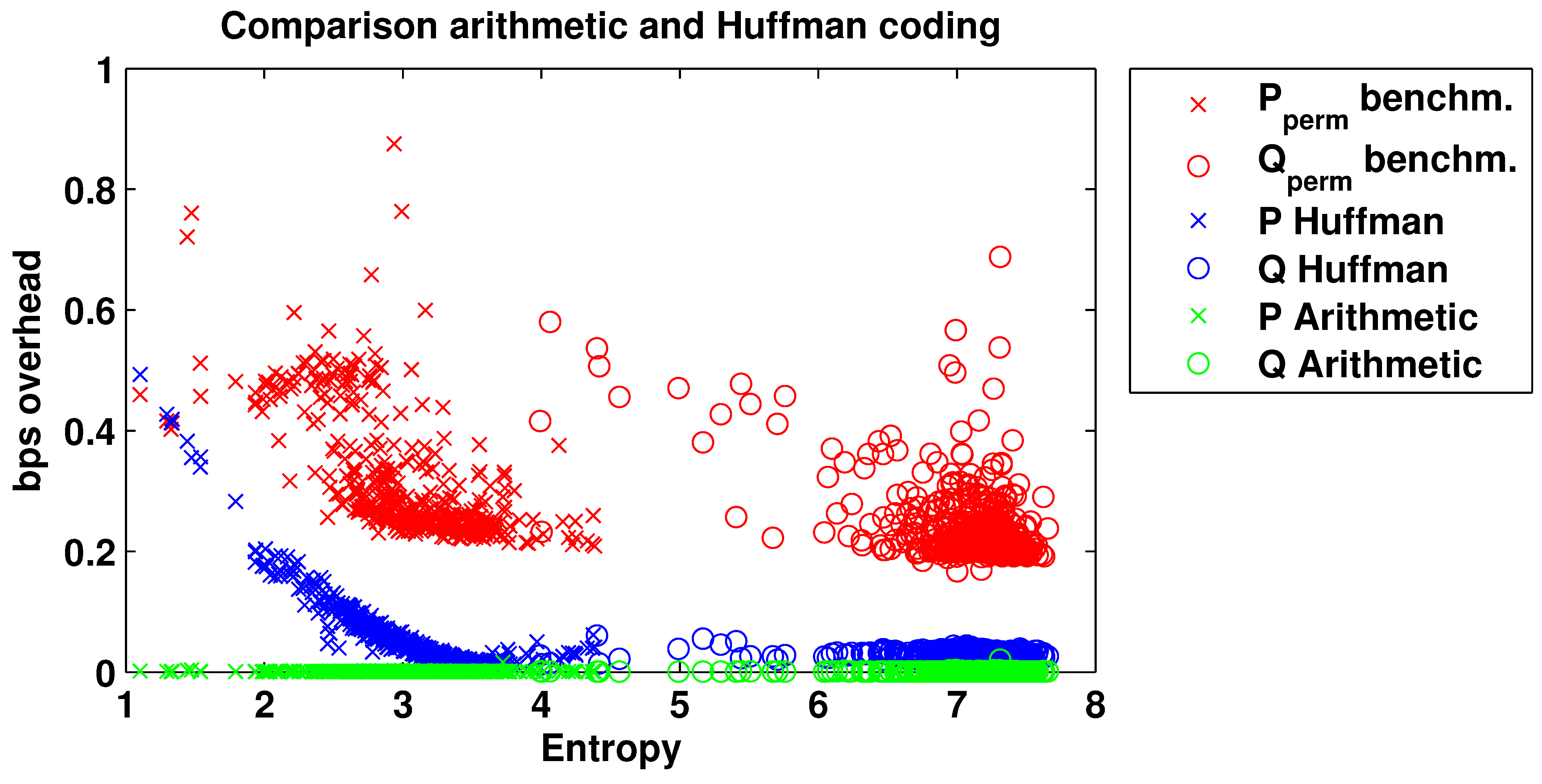
3.2. Reducing the Overhead
3.3. The Structure in Hydrological Data
- Frequency distributions are generally smooth, allowing them to be parametrized instead of stored in a table.
- Often longer dry periods occur, leading to series of zeros in rainfall and smooth recessions in streamflow.
- Autocorrelation is often strong for streamflow, making entropy rate significantly lower than the entropy . Also, distribution of differences from one time step to the next will have a lower entropy: .
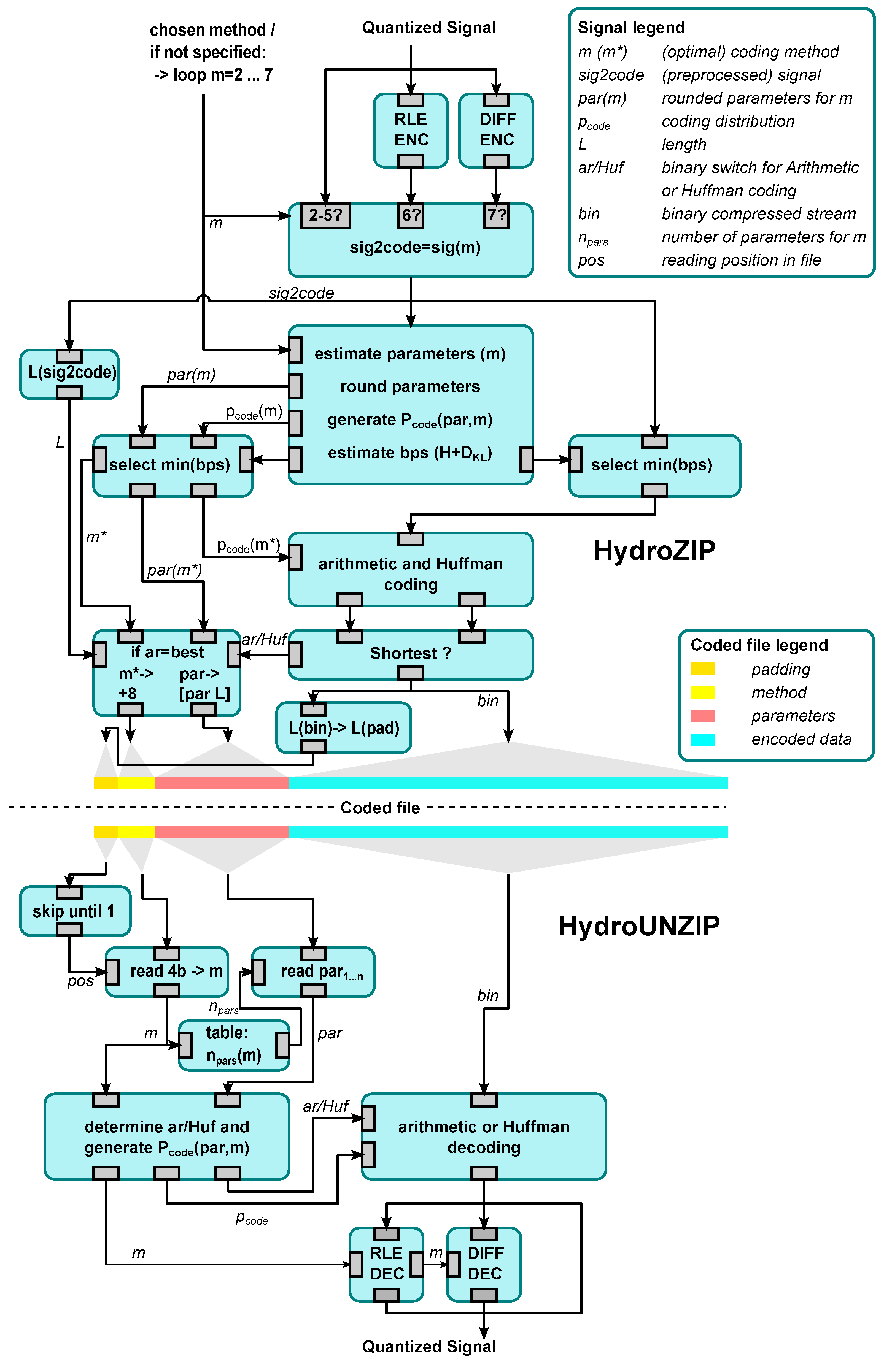
3.4. General Design of the Compressor and Compressed File
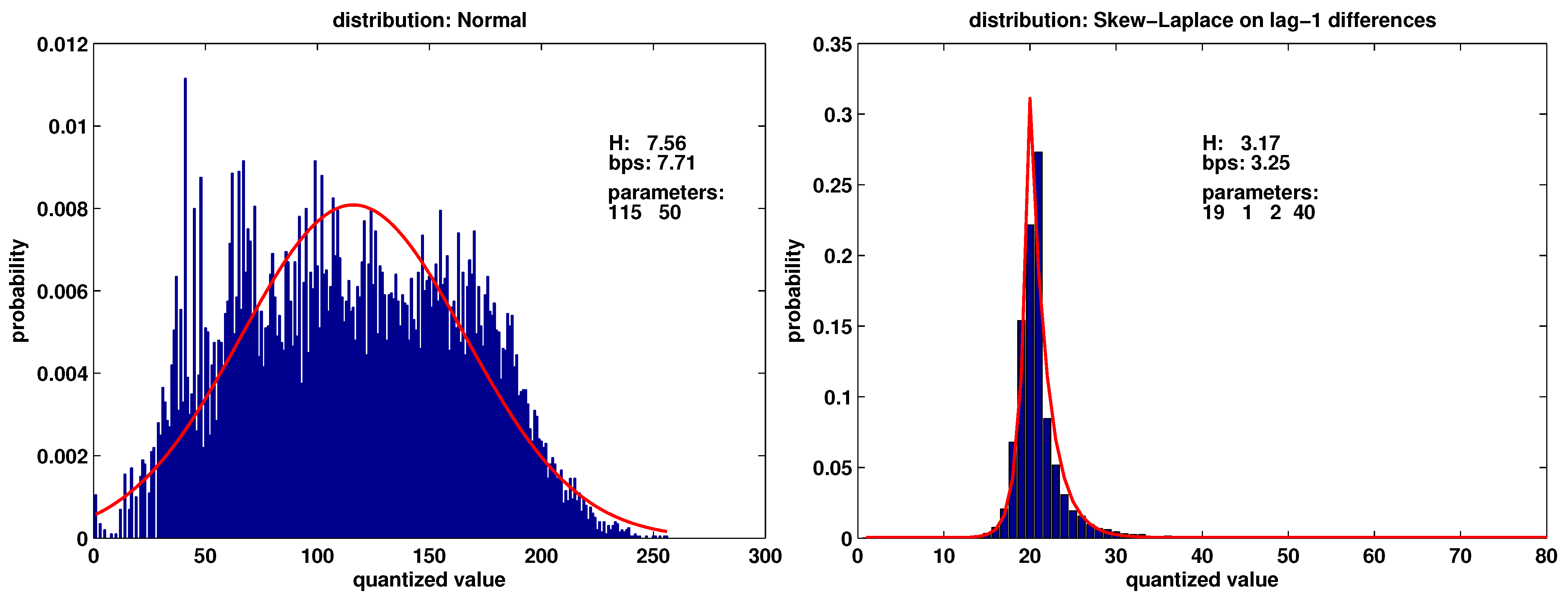
3.5. Encoding the Distribution

3.6. Efficient Description of Temporal Dependencies
3.7. The Coded File
3.8. HydroUNZIP

| Parametric distribution | nr.(Huf) | nr.(ar) | precoding | parameters [range] |
|---|---|---|---|---|
| 2 | 10 | [0-255] | ||
| 3 | 11 | μ[0-255] | ||
| + | 4 | 12 | [0-255]; [0-1] | |
| + | 5 | 13 | [0-5.1]; [0-51]; [0-1] | |
| ++ | 6 | 14 | RLE | [0-5.1]; [0-51]; ,[0-1] |
| skew-Laplace+ K | 7 | 15 | Diff | [0-255], K[0-512] |
4. Results
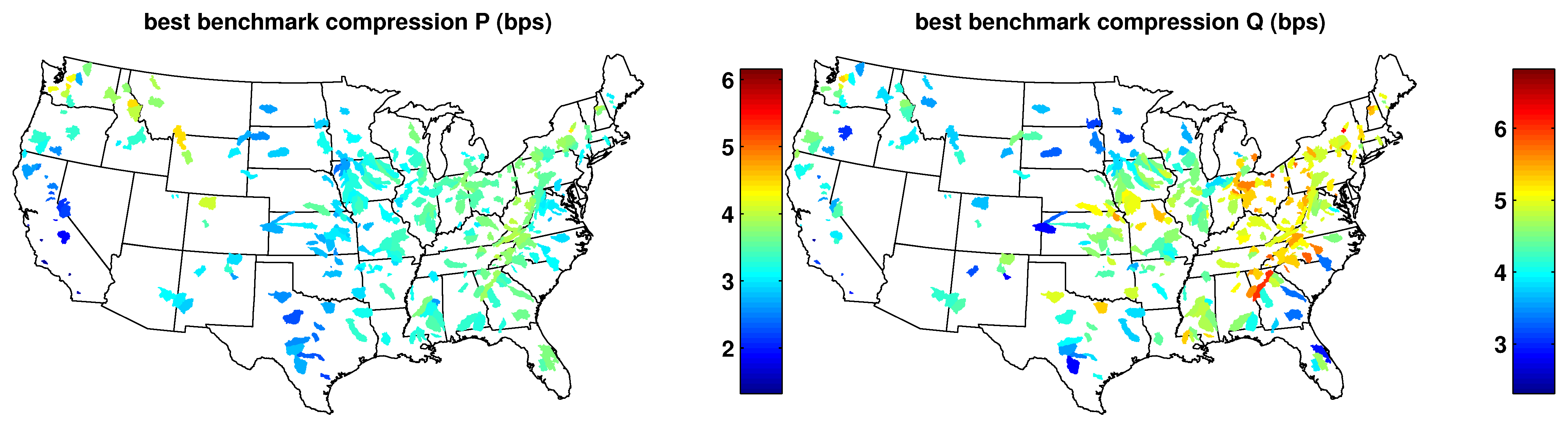
4.1. Results of the Benchmark Algorithms
4.2. Results for Compression with HydroZIP
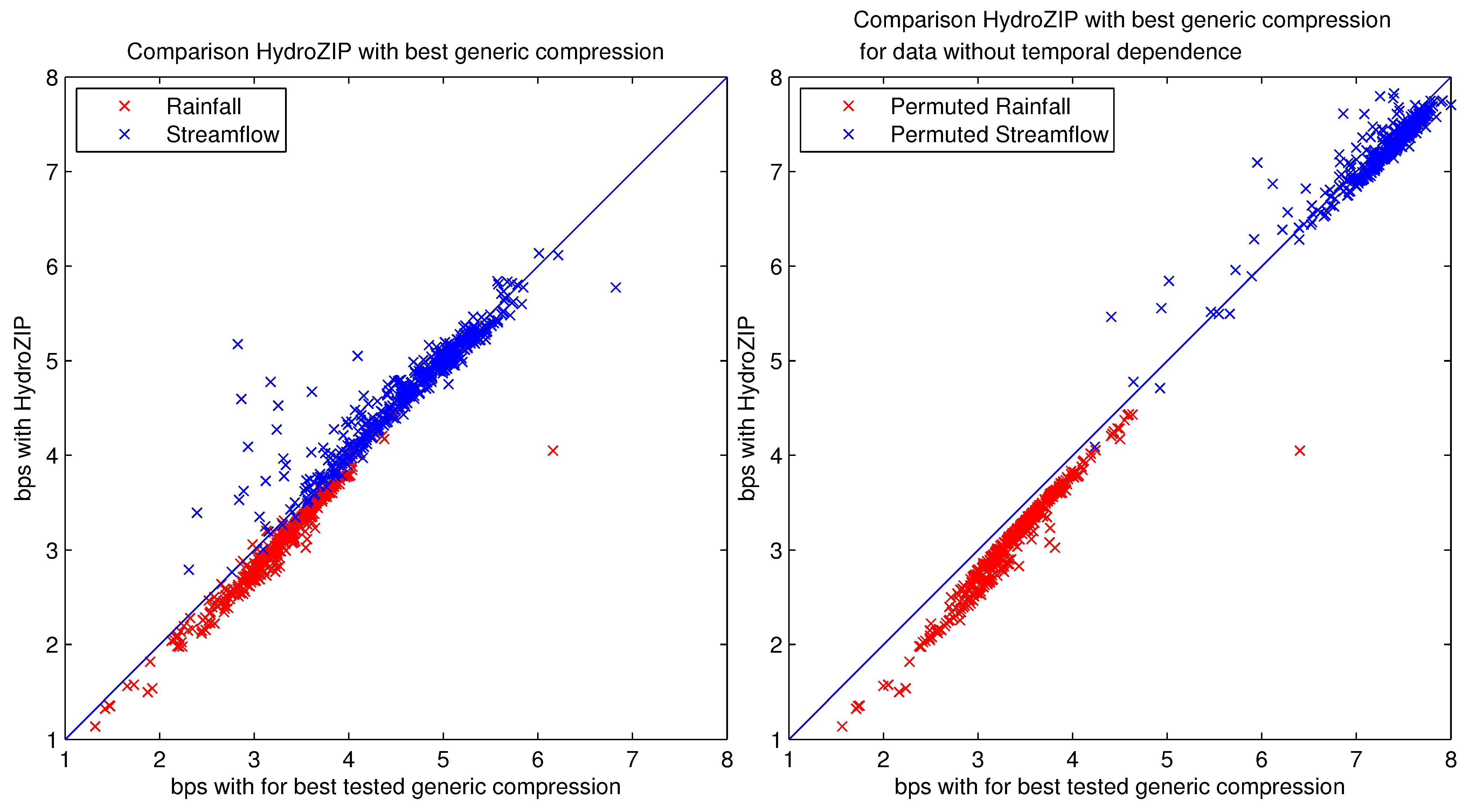
| quantile | file size reduction (%) | |||
|---|---|---|---|---|
| P | Q | Pperm | Qperm | |
| Min | −2.5 | −83.2 | 3.5 | 15.0 |
| 5% | 1.4 | −9.6 | 4.7 | 48.4 |
| 50% | 5.5 | −0.3 | 6.8 | 57.7 |
| 95% | 11.8 | 2.8 | 17.0 | 70.5 |
| Max | 34.2 | 15.4 | 36.7 | 83.5 |
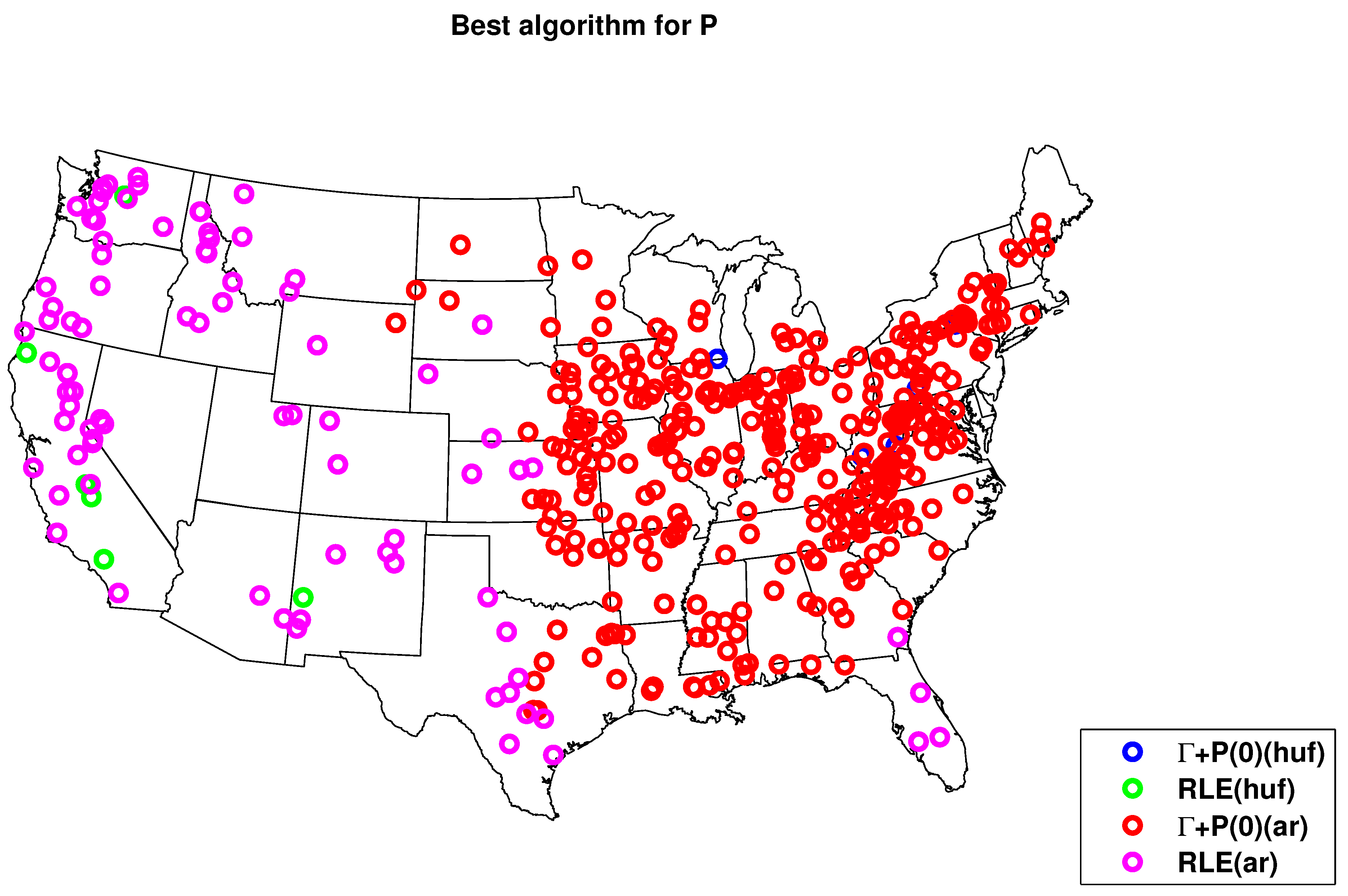
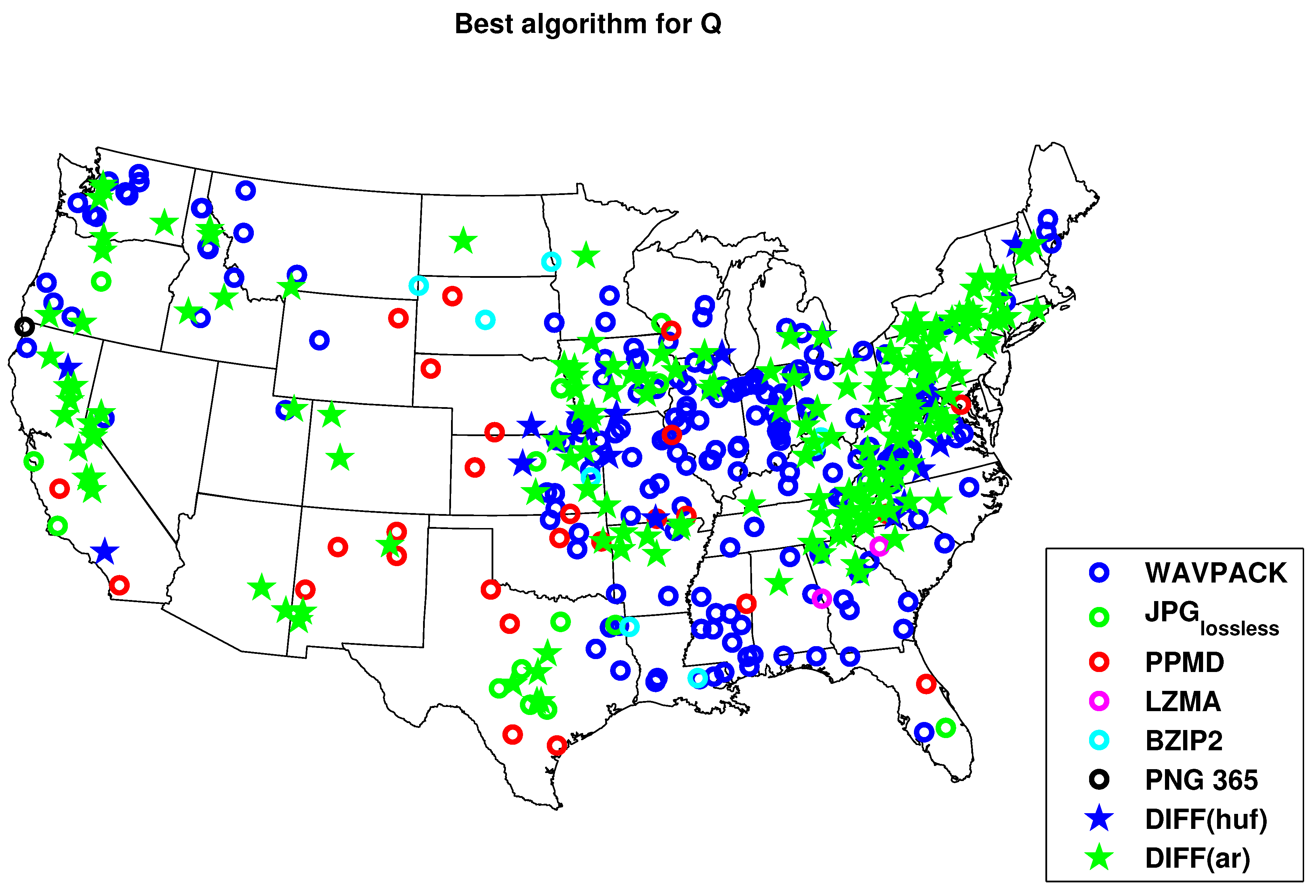
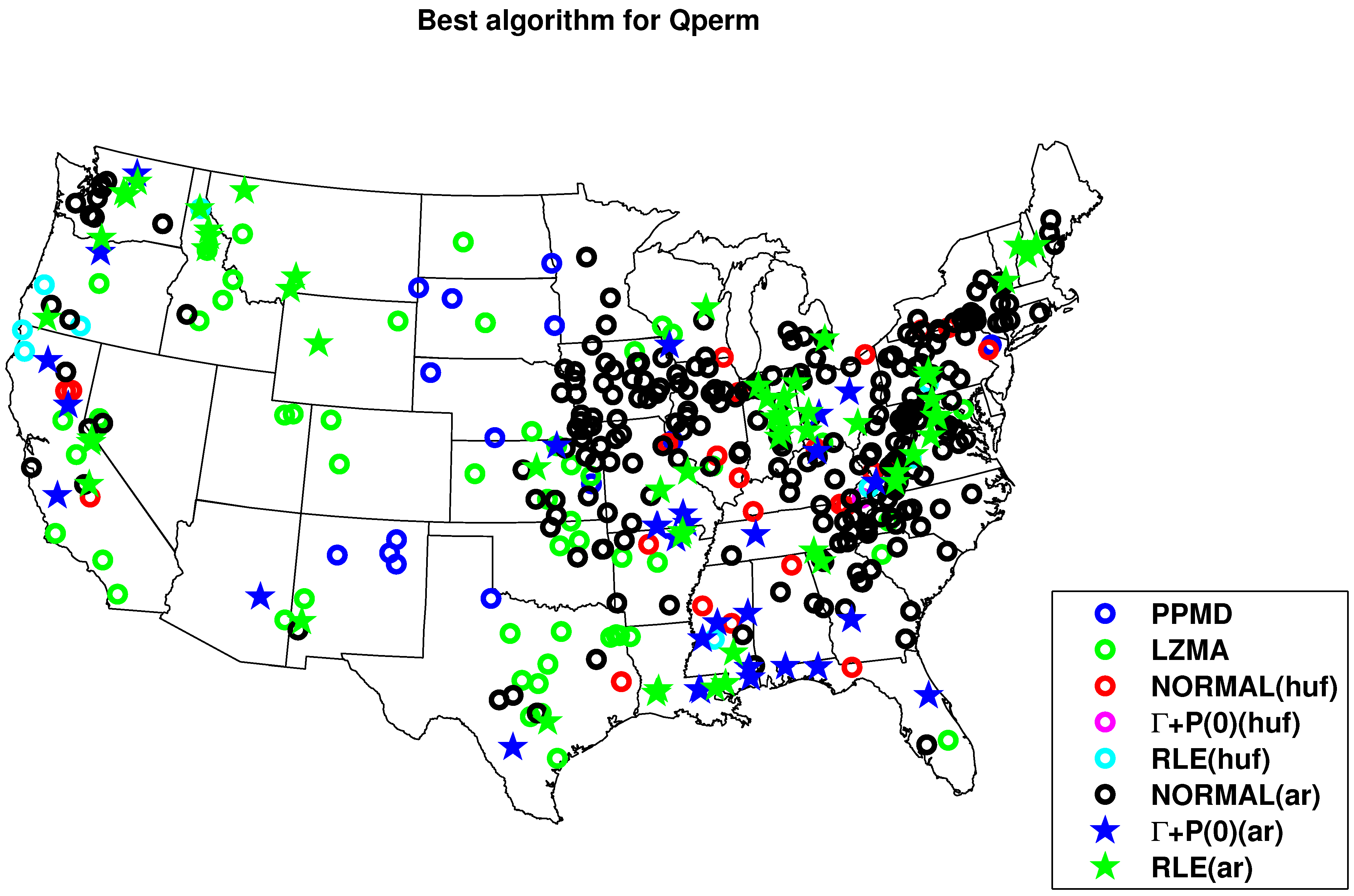
5. Discussion and Conclusion
5.1. Discussion
- rainfall amounts can be described by a smooth, parametric distribution
- dry days may be modeled separately
- dry spells have the tendency to persist for multiple days, or even months
- several candidate distributions from hydrological literature
5.2. Caveats and Future Work
5.3. Conclusion
Acknowledgments
References
- Lehning, M.; Dawes, N.; Bavay, M.; Parlange, M.; Nath, S.; Zhao, F. Instrumenting the Earth: Next-generation Sensor Networks and Environmental Science. In The Fourth Paradigm: Data-Intensive Scientific Discovery; Microsoft Research: Redmond, WA, USA, 2009. [Google Scholar]
- Ryabko, B.; Astola, J. Application of Data Compression Methods to Hypothesis Testing for Ergodic and Stationary Processes. In Proceedings of the International Conference on Analysis of Algorithms DMTCS Proceedings AD, Barcelona, Spain, 6–10 June, 2005; Volume 399, p. 408.
- Ryabko, B.; Astola, J.; Gammerman, A. Application of Kolmogorov complexity and universal codes to identity testing and nonparametric testing of serial independence for time series. Theor. Comput. Sci. 2006, 359, 440–448. [Google Scholar] [CrossRef]
- Cilibrasi, R. Statistical inference through data compression. Ph.D. Thesis, Universiteit van Amsterdam, Amsterdam, The Netherlands, 2007. [Google Scholar]
- Weijs, S.V.; van de Giesen, N.; Parlange, M.B. Data compression to define information content of hydrological time series. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 2029–2065. [Google Scholar] [CrossRef]
- Kavetski, D.; Kuczera, G.; Franks, S.W. Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Beven, K.; Smith, P.; Wood, A. On the colour and spin of epistemic error (and what we might do about it). Hydrol. Earth Syst. Sci. 2011, 15, 3123–3133. [Google Scholar] [CrossRef]
- Singh, S.K.; Bárdossy, A. Calibration of hydrological models on hydrologically unusual events. Adv. Water Resour. 2012, 38, 81–91. [Google Scholar] [CrossRef]
- Gong, W.; Gupta, H.V.; Yang, D.; Sricharan, K.; Hero, A.O. Estimating epistemic & aleatory uncertainties during hydrologic modeling: An information theoretic approach. Water Resour. Res. 2013, in press. [Google Scholar]
- Stedinger, J.R.; Vogel, R.M.; Lee, S.U.; Batchelder, R. Appraisal of the generalized likelihood uncertainty estimation (GLUE) method. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Montanari, A.; Shoemaker, C.A.; van de Giesen, N. Introduction to special section on Uncertainty Assessment in Surface and Subsurface Hydrology: An overview of issues and challenges. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Montanari, A.; Koutsoyiannis, D. A blueprint for process-based modeling of uncertain hydrological systems. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Collins English Dictionary-Complete & Unabridged 10th Edition. Available online: http://www.collinsdictionary.com/dictionary/english/zip (accessed on 14 March 2013).
- Chaitin, G.J. On the length of programs for computing finite binary sequences. J. ACM 1966, 13, 547–569. [Google Scholar] [CrossRef]
- Solomonoff, R.J. A formal theory of inductive inference. Part I. Inform. Control 1964, 7, 1–22. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Int. J. Comput. Math. 1968, 2, 157–168. [Google Scholar] [CrossRef]
- Chaitin, G.J. A theory of program size formally identical to information theory. J. ACM 1975, 22, 329–340. [Google Scholar] [CrossRef]
- Rissanen, J. Information and Complexity in Statistical Modeling; Springer Verlag: New York, NY, USA, 2007. [Google Scholar]
- Schoups, G.; van de Giesen, N.C.; Savenije, H.H.G. Model complexity control for hydrologic prediction. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Hutter, M. On universal prediction and Bayesian confirmation. Theor. Comput. Sci. 2007, 384, 33–48. [Google Scholar] [CrossRef]
- Rathmanner, S.; Hutter, M. A philosophical treatise of universal induction. Entropy 2011, 13, 1076–1136. [Google Scholar] [CrossRef]
- Cilibrasi, R.; Vitányi, P. Clustering by compression. IEEE Trans. Inform. Theory 2005, 51, 1523–1545. [Google Scholar] [CrossRef]
- Vitányi, P.; Balbach, F.; Cilibrasi, R.; Li, M. Normalized Information Distance. In Information Theory and Statistical Learning; Emmert-Streib, F., Dehmer, M., Eds.; Springer: New York, NY, USA, 2009; pp. 45–82. [Google Scholar]
- Cerra, D.; Datcu, M. Expanding the algorithmic information theory frame for applications to earth observation. Entropy 2013, 15, 407–415. [Google Scholar] [CrossRef]
- Szilagyi, J.; Parlange, M. A geomorphology-based semi-distributed watershed model. Adv. Water Resour. 1999, 23, 177–187. [Google Scholar] [CrossRef]
- Beven, K.J. How far can we go in distributed hydrological modelling? Hydrol. Earth Syst. Sci. 2001, 5, 1–12. [Google Scholar] [CrossRef]
- Simoni, S.; Padoan, S.; Nadeau, D.; Diebold, M.; Porporato, A.; Barrenetxea, G.; Ingelrest, F.; Vetterli, M.; Parlange, M. Hydrologic response of an alpine watershed: Application of a meteorological wireless sensor network to understand streamflow generation. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Leung, L.Y.; North, G.R. Information theory and climate prediction. J. Clim. 1990, 3, 5–14. [Google Scholar] [CrossRef]
- Kleeman, R. Measuring dynamical prediction utility using relative entropy. J. Atmos. Sci. 2002, 59, 2057–2072. [Google Scholar] [CrossRef]
- DelSole, T. Predictability and information theory. Part I: Measures of predictability. J. Atmos. Sci. 2004, 61, 2425–2440. [Google Scholar] [CrossRef]
- DelSole, T.; Tippett, M.K. Predictability: Recent insights from information theory. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Roulston, M.S.; Smith, L.A. Evaluating probabilistic forecasts using information theory. Mon. Weather Rev. 2002, 130, 1653–1660. [Google Scholar] [CrossRef]
- Benedetti, R. Scoring rules for forecast verification. Mon. Weather Rev. 2010, 138, 203–211. [Google Scholar]
- Ahrens, B.; Walser, A. Information-based skill scores for probabilistic forecasts. Mon. Weather Rev. 2008, 136, 352–363. [Google Scholar] [CrossRef]
- Tödter, J.; Ahrens, B. Generalization of the ignorance score: Continuous ranked version and its decomposition. Mon. Weather Rev. 2012, 140, 2005–2017. [Google Scholar]
- Weijs, S.V.; van Nooijen, R.; van de Giesen, N. Kullback–Leibler divergence as a forecast skill score with classic reliability–resolution–uncertainty decomposition. Mon. Weather Rev. 2010, 138, 3387–3399. [Google Scholar] [CrossRef]
- Weijs, S.V.; Schoups, G.; van de Giesen, N. Why hydrological predictions should be evaluated using information theory. Hydrol. Earth Syst. Sci. 2010, 14, 2545–2558. [Google Scholar] [CrossRef]
- Harmancioglu, N.B.; Alpaslan, N.; Singh, V.P. Application of the Entropy Concept in Design of Water Quality Monitoring Networks. In Entropy and Energy Dissipation in Water Resources; Singh, V., Fiorentino, M., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992; pp. 283–302. [Google Scholar]
- Alfonso, L.; Lobbrecht, A.; Price, R. Information theory-based approach for location of monitoring water level gauges in polders. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Li, C.; Singh, V.; Mishra, A. Entropy theory-based criterion for hydrometric network evaluation and design: Maximum information minimum redundancy. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Singh, V.P. The use of entropy in hydrology and water resources. Hydrol. Process. 1997, 11, 587–626. [Google Scholar] [CrossRef]
- Lange, H. Are ecosystems dynamical systems. Int. J. Comput. Anticip. Syst. 1998, 3, 169–186. [Google Scholar]
- Lange, H. Time series analysis of ecosystem variables with complexity measures. Int. J. Complex Syst. 1999, 250, 1–9. [Google Scholar]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Toward improved calibration of hydrologic models: Multiple and noncommensurable measures of information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef]
- Vrugt, J.; Bouten, W.; Weerts, A. Information content of data for identifying soil hydraulic parameters from outflow experiments. Soil Sci. Soc. Am. J. 2001, 65, 19–27. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Bouten, W.; Gupta, H.V.; Sorooshian, S. Toward improved identifiability of hydrologic model parameters: The information content of experimental data. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Laio, F.; Allamano, P.; Claps, P. Exploiting the information content of hydrological “outliers” for goodness-of-fit testing. Hydrol. Earth Syst. Sci. 2010, 14, 1909–1917. [Google Scholar] [CrossRef]
- Price, J. Comparison of the information content of data from the Landsat-4 Thematic Mapper and the Multispectral Scanner. Geosci. Remote Sens. IEEE Trans. 1984, 3, 272–281. [Google Scholar] [CrossRef]
- Horvath, K.; Stogner, H.; Weinhandel, G.; Uhl, A. Experimental Study on Lossless Compression of Biometric Iris Data. In Proceedings of the 7th International Symposium on Image and Signal Processing and Analysis (ISPA), Dubrovnik, Croatia, 4–6 September 2011; pp. 379–384.
- Nalbantoglu, O.U.; Russell, D.J.; Sayood, K. Data compression concepts and algorithms and their applications to bioinformatics. Entropy 2009, 12, 34–52. [Google Scholar] [CrossRef] [PubMed]
- Voepel, H.; Ruddell, B.; Schumer, R.; Troch, P.; Brooks, P.; Neal, A.; Durcik, M.; Sivapalan, M. Quantifying the role of climate and landscape characteristics on hydrologic partitioning and vegetation response. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Weijs, S.V.; Mutzner, R.; Parlange, M.B. Could electrical conductivity replace water level in rating curves for alpine streams? Water Resour. Res. 2013, 49, 343–351. [Google Scholar] [CrossRef]
- Huffman, D.A. A method for the construction of minimum-redundancy codes. Proc. IRE 1952, 40, 1098–1101. [Google Scholar] [CrossRef]
- Ziv, J.; Lempel, A. A universal algorithm for sequential data compression. IEEE Trans. Inform. Theory 1977, 23, 337–343. [Google Scholar] [CrossRef]
- Martin, G.N.N. Range Encoding: An Algorithm for Removing Redundancy from a Digitised Message. In Proceedings of the Video & Data Recording Conference, Southampton, UK, 24–27 July 1979.
- Rissanen, J.; Langdon, G.G. Arithmetic coding. IBM J. Res. Dev. 1979, 23, 149–162. [Google Scholar] [CrossRef]
- Burrows, M.; Wheeler, D.J. A Block-sorting Lossless Data Compression Algorithm, Technical report; Systems Research Center: Palo Alto, CA, USA, 1994. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Proceedings of the 2nd International Symposium on Information Theory, Tsahkadsor, Armenia SSR, 2–8 September 1973; pp. 267–281.
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Michel, W.S. Statistical encoding for text and picture communication. Am. Inst. Electr. Eng. Part I Commun. Electron. Trans. 1958, 77, 33–36. [Google Scholar] [CrossRef]
- Katz, R.; Parlange, M. Effects of an index of atmospheric circulation on stochastic properties of precipitation. Water Resour. Res. 1993, 29, 2335–2344. [Google Scholar] [CrossRef]
- Parlange, M.B.; Katz, R.W. An extended version of the Richardson model for simulating daily weather variables. J. Appl. Meteorol. 2000, 39, 610–622. [Google Scholar] [CrossRef]
- Katz, R.W. Extreme value theory for precipitation: Sensitivity analysis for climate change. Adv. Water Resour. 1999, 23, 133–139. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Karl, T.R.; Easterling, D.R.; Knight, R.W.; Jamason, P.F.; Hennessy, K.J.; Suppiah, R.; Page, C.M.; Wibig, J.; Fortuniak, K.; et al. Changes in the probability of heavy precipitation: Important indicators of climatic change. Clim. Chang. 1999, 42, 243–283. [Google Scholar] [CrossRef]
- Semenov, V.; Bengtsson, L. Secular trends in daily precipitation characteristics: Greenhouse gas simulation with a coupled AOGCM. Clim. Dyn. 2002, 19, 123–140. [Google Scholar]
- Papalexiou, S.; Koutsoyiannis, D. Entropy based derivation of probability distributions: A case study to daily rainfall. Adv. Water Resour. 2011, 45, 51–57. [Google Scholar] [CrossRef]
- Szilagyi, J.; Katul, G.G.; Parlange, M.B. Evapotranspiration intensifies over the conterminous United States. J. Water Resour. Plan. Manag. 2001, 127, 354–362. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B.; Tebaldi, C. Stochastic modeling of the effects of large-scale circulation on daily weather in the southeastern US. Clim. Chang. 2003, 60, 189–216. [Google Scholar] [CrossRef]
- Katz, R.W.; Brush, G.S.; Parlange, M.B. Statistics of extremes: Modeling ecological disturbances. Ecology 2005, 86, 1124–1134. [Google Scholar] [CrossRef]
- Beven, K.; Westerberg, I. On red herrings and real herrings: Disinformation and information in hydrological inference. Hydrol. Process. 2011, 25, 1676–1680. [Google Scholar] [CrossRef]
- Weijs, S.V.; van de Giesen, N. Accounting for observational uncertainty in forecast verification: An information–theoretical view on forecasts, observations and truth. Mon. Weather Rev. 2011, 139, 2156–2162. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Weijs, S.V.; Van de Giesen, N.; Parlange, M.B. HydroZIP: How Hydrological Knowledge can Be Used to Improve Compression of Hydrological Data. Entropy 2013, 15, 1289-1310. https://doi.org/10.3390/e15041289
Weijs SV, Van de Giesen N, Parlange MB. HydroZIP: How Hydrological Knowledge can Be Used to Improve Compression of Hydrological Data. Entropy. 2013; 15(4):1289-1310. https://doi.org/10.3390/e15041289
Chicago/Turabian StyleWeijs, Steven V., Nick Van de Giesen, and Marc B. Parlange. 2013. "HydroZIP: How Hydrological Knowledge can Be Used to Improve Compression of Hydrological Data" Entropy 15, no. 4: 1289-1310. https://doi.org/10.3390/e15041289
APA StyleWeijs, S. V., Van de Giesen, N., & Parlange, M. B. (2013). HydroZIP: How Hydrological Knowledge can Be Used to Improve Compression of Hydrological Data. Entropy, 15(4), 1289-1310. https://doi.org/10.3390/e15041289





