Abstract
A method is shown for computing transfer entropy over multiple time lags for coupled autoregressive processes using formulas for the differential entropy of multivariate Gaussian processes. Two examples are provided: (1) a first-order filtered noise process whose state is measured with additive noise, and (2) two first-order coupled processes each of which is driven by white process noise. We found that, for the first example, increasing the first-order AR coefficient while keeping the correlation coefficient between filtered and measured process fixed, transfer entropy increased since the entropy of the measured process was itself increased. For the second example, the minimum correlation coefficient occurs when the process noise variances match. It was seen that matching of these variances results in minimum information flow, expressed as the sum of transfer entropies in both directions. Without a match, the transfer entropy is larger in the direction away from the process having the larger process noise. Fixing the process noise variances, transfer entropies in both directions increase with the coupling strength. Finally, we note that the method can be generally employed to compute other information theoretic quantities as well.
1. Introduction
Transfer entropy [1] quantifies the information flow between two processes. Information is defined to be flowing from system X to system Y whenever knowing the past states of X reduces the uncertainty of one or more of the current states of Y above and beyond what uncertainty reduction is achieved by only knowing the past Y states. Transfer entropy is the mutual information between the current state of system Y and one or more past states of system X, conditioned on one or more past states of system Y. We will employ the following notation. Assume that data from two systems X and Y are simultaneously available at k timestamps: . Then we express transfer entropies as:
Each of the two transfer entropy values TEx→y and TEy→x is nonnegative and both will be positive (and not necessarily equal) when information flow is bi-directional. Because of these properties, transfer entropy is useful for detecting causal relationships between systems generating measurement time series. Indeed, transfer entropy has been shown to be equivalent, for Gaussian variables, to Granger causality [2]. Reasons for caution about making causal inferences in some situations using transfer entropy, however, are discussed in [3,4,5,6]. A formula for normalized transfer entropy is provided in [7].
The contribution of this paper is to explicitly show how to compute transfer entropy over a variable number of time lags for autoregressive (AR) processes driven by Gaussian noise and to gain insight into the meaning of transfer entropy in such processes by way of two example systems: (1) a first-order AR process X = {xn} with its noisy measurement process Y = {yn}, and (2) a set of two mutually-coupled AR processes. Computation of transfer entropies for these systems is a worthwhile demonstration since they are simple models that admit intuitive understanding. In what follows we first show how to compute the covariance matrix for successive iterates of the example AR processes and then use these matrices to compute transfer entropy quantities based on the differential entropy expression for multivariate Gaussian random variables. Plots of transfer entropies versus various system parameters are provided to illustrate various relationships of interest.
Note that Kaiser and Schreiber [8] have previously shown how to compute information transfer metrics for continuous-time processes. In their paper they provide an explicit example, computing transfer entropy for two linear stochastic processes where one of the processes is autonomous and the other is coupled to it. To perform the calculation for the Gaussian processes the authors utilize expressions for the differential entropy of multivariate Gaussian noise. In our work, we add to this understanding by showing how to compute these quantities analytically for higher time lags. We now provide a discussion of differential entropy, the formulation of entropy appropriate to continuous-valued processes as we are considering.
2. Differential Entropy
The entropy of a continuous-valued process is given by its differential entropy. Recall that the entropy of a discrete-valued random variable is given by the Shannon entropy (we shall always choose log base 2 so that entropy will be expressed in units of bits) where pi is the probability of the ith outcome and the sum is over all possible outcomes.
Following [9] we derive the appropriate expression for differential entropies for conditioned and unconditioned continuous-valued random variables. When a process X is continuous-valued we may approximate it as a discrete-value process by identifying pi = fiΔx where fi is the value of the pdf at the ith partition point and Δx is the refinement of the partition. We then obtain:
Note that since the X process is continuous-valued, then, as Δx → 0, we have H(X) → + infinity. Thus, for continuous-valued processes, the quantity h(X), when itself defined and finite, is used to represent the entropy of the process. This quantity is known as the differential entropy of random process X.
Closed-form expressions for the differential entropy of many distributions are known. For our purposes, the key expression is the one for the (unconditional) multivariate normal distribution [10]. Let the probability density function of the n-dimensional random vector x be denoted f(x), then the relevant expressions are:
where detC is the determinant of matrix C, the covariance of x. In what follows, this expression will be used to compute differential entropy of unconditional and conditional normal probability density functions. The case for conditional density functions warrants a little more discussion.
Recall that the relationships between the joint and conditional covariance matrices, CXY and CY|X, respectively, of two random variables X and Y (having dimensions nx and ny, respectively) are given by:
Here blocks Σ11 and Σ22 have dimensions nx by nx and ny by ny, respectively. Now, using Leibniz’s formula, we have that:
Hence the conditional differential entropy of Y, given X, may be conveniently computed using:
This formulation is very handy as it allows us to compute many information-theoretic quantities with ease. The strategy is as follows. We define C(k) to be the covariance of two random processes sampled at k consecutive timestamps {tn−k+2, tn− k+1, …, tn, tn+1}. We then compute transfer entropies for values of k up to k sufficiently large to ensure that their valuations do not change significantly if k is further increased. For our examples, we have found k = 10 to be more than sufficient. A discussion of the importance of considering this sufficiency is provided in [11].
3. Transfer Entropy Computation Using Variable Number of Timestamps
We wish to consider two example processes each of which conforms to one of the two model systems having the general expressions:
and:
Here, vn and wn are zero mean uncorrelated Gaussian noise processes having variances R and Q, respectively. For system stability, we require the model poles to lie within the unit circle.The first model is of a filtered process noise X one-way coupled to an instantaneous, but noisy measurement process Y. The second model is a two-way coupled pair of processes, X and Y.
Transfer entropy (as defined by Schreiber [1]) considers the flow of information from past states (i.e., state values having, timetags ) of one process to the present state of another process. However, note that in the first general model (measurement process) there is an explicit flow of information from the present state of the X process; xn+1 determines the present state of the Y process yn+1 (assuming c− 1 is not zero). To fully capture the information transfer from the X process to the current state of the Y process we must identify the correct causal states [4]. For the measurement system, the causal states include the current (present) state. This state is not included in the definition of transfer entropy, being a mutual information quantity conditioned on only past states. Hence, for the purpose of this paper, we will temporarily define a quantity, “information transfer,” similar to transfer entropy, except that the present of the driving process, xn+1, will be lumped in with the past values of the X process: xn−k+2:xn. For the first general model there is no information transferred from the Y to the X process. We define the (non-zero) information transfer from the X to the Y process (based on data from k timetags) as:
The major contribution of this paper is to show how to analytically compute transfer entropy for AR Gaussian processes using an iterative method for computing the required covariance matrices. Computation of information transfer is additionally presented to elucidate the power of the method when similar information quantities are of interest and to make the measurement example more interesting. We now present a general method for computing the covariance matrices required to compute information-theoretic quantities for the AR models above. Two numerical examples follow.
To compute transfer entropy over a variable number of multiple time lags for AR processes of the general types shown above, we compute its block entropy components over multiple time lags. By virtue of the fact that the processes are Gaussian we can avail ourselves of analytical entropy expressions that depend only on the covariance of the processes. In this section we show how to analytically obtain the required covariance expressions starting with the covariance for a single time instance. Taking expectations, using the AR equations, we obtain the necessary statistics to characterize the process. Representing these expectation results in general, the process covariance matrix C(1)(tn) corresponding to a single timestamp, tn, is:
To obtain an expanded covariance matrix, accounting for two time instances (tn and tn+1), we compute the additional expectations required to fill in the matrix C (2)(tn):
Because the process is stationary, we may write:
where:
Thus we have found the covariance matrix C(2) required to compute block entropies based on two timetags or, equivalently, one time lag. Using this matrix the single-lag transfer entropies may be computed.
We now show how to compute the covariance matrices corresponding to any finite number of time stamps. Define vector . Using the definitions above, write the matrix C(2) as a block matrix and, using standard formulas, compute the conditional mean and covariance Cc of given :
Note that the expected value of the conditional mean is zero since the mean of the process, , is itself zero.
With these expressions in hand, we note that we may view propagation of the state to its value at the next timestamp as accomplished by the recursion:
Here S is the principal square root of the matrix Cc. It is conveniently computed using the inbuilt Matlab function sqrtm. To see analytically that the recursion works, note that using it we recover at each timestamp a process having the correct mean and covariance:
and:
Thus, because the process is Gaussian and fully specified by its mean and covariance, we have verified that the recursive representation yields consistent statistics for the stationary AR system. Using the above insights, we may now recursively compute the covariance matrix C(k) for a variable number (k) of timestamps. Note that C(k) has dimensions of 2k × 2k. We denote 2 × 2 blocks of C(k) as C(k)ij for i, j = 1,2, ..., k , where C(k)ij is the 2-by-2 block of C(k) consisting of the four elements of C(k) that are individually located in row 2i − 1 or 2i and column 2j − 1 or 2j.
The above recursion is now used to compute the block elements of C(3). Then each of these block elements is, in turn, expressed in terms of block elements of C(2). These calculations are shown in detail below where we have also used the fact that the mean of the zn vector is zero:
By continuation of this calculation to larger timestamp blocks (k > 3), we find the following pattern that can be used to extend (augment) C(k−1) to yield C(k). The pattern consists of setting most of the augmented matrix equal to that of the previous one, and then computing two additional rows and columns for C(k), k > 2, to fill out the remaining elements. The general expressions are:
At this point in the development we have shown how to compute the covariance matrix:
Since the system is linear and the process noise wn and measurement noise vn are white zero-mean Gaussian noise processes, we may express the joint probability density function for the 2k variates as:
Note that the mean of all 2k variates is zero.
Finally, to obtain empirical confirmation of the equivalence of the covariance terms obtained using the original AR system and its recursive representation, numerical simulations were conducted. Using the example 1 system (below) 500 sequences were generated each of length one million. For each sequence the C(3) covariance was computed. The error for all C(3) matrices was then averaged, assuming that the C(3) matrix calculated using the method based on the recursive representation was the true value. The result was that for each of the matrix elements, the error was less than 0.0071% of its true value. We are now in position to compute transfer entropies for a couple of illustrative examples.
4. Example 1: A One-Way Coupled System
For this example we consider the following system:
Parameter hc specifies the coupling strength of the Y process to the first-order AR process X, and R and Q are their respective (wn and vn) zero-mean Gaussian process noise variances. For stability, we require |a| <1. Comparing to the first general representation given above, we have m = 0, and . The system models filtered noise xn and a noisy measurement, yn, of xn. Thus the xn sequence represents a hidden process (or model) which is observable by way of another sequence, yn. We wish to examine the behavior of transfer entropy as a function of the correlation ρ between xn and yn. One might expect that the correlation ρ between xn and yn to be proportional of the degree of information flow; however, we will see that the relationship between transfer entropy and correlation is not quite that simple.
Both the X and Y processes have zero mean. Computing the joint covariance matrix C(1) for xn and yn and their correlation we obtain:
Hence the process covariance matrix C(1) corresponding to a single timestamp, tn is:
In order to obtain an expanded covariance matrix, accounting for two time instances (tn and tn+1) we compute the additional expectations required to fill in the matrix C(2):
Thus we have found the covariance matrix C(2) required to compute block entropies based on a single time lag. Using this matrix the single-lag transfer entropies may be computed. Using the recursive process described in the previous section we can compute C(1°). We have found that using higher lags does not change the entropy values significantly.
To aid the reader in understanding the calculations required to compute transfer entropies using higher time lags, it is worthwhile to compute transfer entropy for a single lag. We first define transfer entropy using general notation indicating the partitioning of the X and Y sequences in to past and future and , respectively. We then compute transfer entropy as a sum of block entropies:
Similarly:
The Y states have no influence on the X sequence in this example. Hence TEy→x = 0. Since we are here computing transfer entropy for a single lag (i.e., two time tags tn and tn+1) we have:
By substitution of the expression for the differential entropy of each block we obtain:
For this example, note from the equation for yn+1 that state xn+1 is a causal state of X influencing the value of yn+1. In fact, it is the most important such state. To capture the full information that is transferred from the X process to the Y process over the course of two time tags we need to include state xn+1. Hence we compute the information transfer from x → y as:
Here the notation indicates the determinant of the matrix composed of the rows and columns of C(2) indicated by the list of indices i shown in the subscripted brackets. For example, is the determinant of the matrix formed by extracting columns {1, 2, 3, 4} and rows {1, 2, 3, 4} from matrix C(2). In later calculations we will use slightly more complicated-looking notation. For example, is the determinant of the matrix formed by extracting columns {2, 4 ,…, 18, 20} and the same-numbered rows from matrix C(1°). (Note C(k)[i],[i] is not the same as C(k)ii as used in Section 3).
It is interesting to note that a simplification in the expression for information transfer can be obtained by writing the expression for it in terms of conditional entropies:
From the fact that yn+1 = xn+1 + vn+1 we see immediately that:
Hence we may write:
To compute transfer entropy using nine lags (ten timestamps) assume that we have already computed C(10) as defined above. We partition the sequence into three subsets:
Now, using these definitions, and substituting in expressions for differential block entropies we obtain:
Similarly:
As a numerical example we set hc = 1, Q = 1, and for three different values of a (0.5, 0.7 and 0.9) we vary R so as to scan the correlation ρ between the x and y processes between the values of 0 and 1.
In Figure 1 it is seen that for each value of parameter a there is a peak in the transfer entropy TE(k)x→y. As the correlation ρ between xn and yn increases from a low value the transfer entropy increases since the amount of information shared between yn+1 and xn is increasing. At a critical value of ρ transfer entropy peaks and then starts to decrease. This decrease is due to the fact that at high values of ρ the measurement noise variance R is small. Hence yn becomes very close to equaling xn so that the amount of information gained (about yn+1) by learning xn, given yn, becomes small. Hence h(yn+1 | yn) ‑ h(yn+1 | yn, xn) is small. This difference is TE(2)x→y.
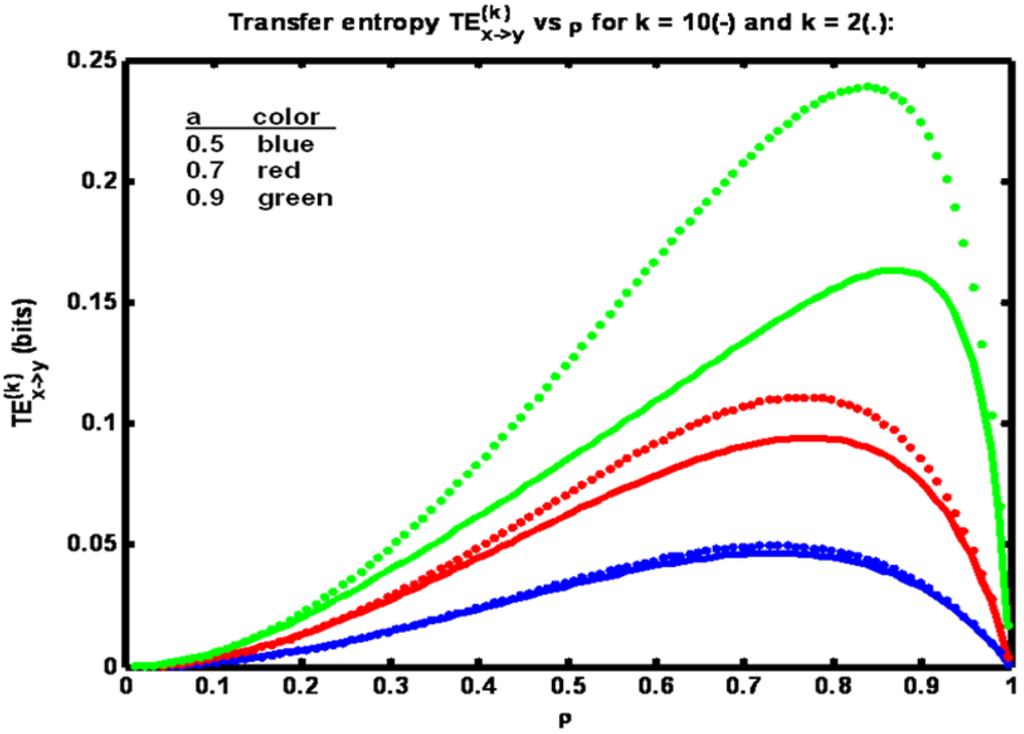
Figure 1.
Example 1: Transfer entropy TE(k)x→y versus correlation coefficient ρ for three values of parameter a (see legend). Solid trace: k = 10, dotted trace: k = 2.
The relationship between ρ and R is shown in Figure 2. Note that when parameter a is increased, a larger value of R is required to maintain ρ at a fixed value. Also, in Figure 1 we see the effect of including more timetags in the analysis. When k is increased from 2 to 10 transfer entropy values fall, particularly for the largest value of parameter a. It is known that entropies decline when conditioned on additional variables. Here, transfer entropy is acting similarly. In general, however, transfer entropy, being a mutual information quantity, has the property that conditioning could make it increase as well [12].
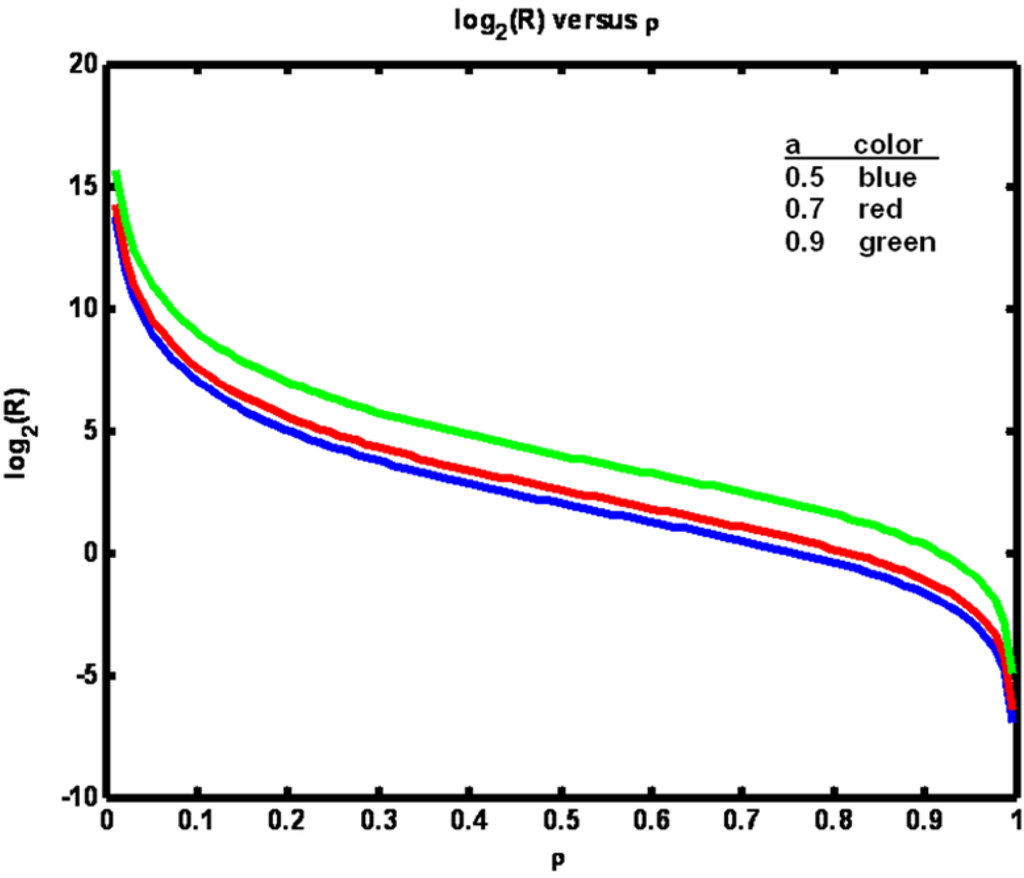
Figure 2.
Example 1: Logarithm of R versus ρ for three values of parameter a (see legend).
The observation that the transfer entropy decrease is greatest for the largest value of parameter a is perhaps due to the fact that the entropy of the X process is itself greatest for the largest a value and therefore has more sensitivity to an increase in X data availability (Figure 3).
From Figure 1 it is seen that as the value of parameter a is increased, transfer entropy is increased for a fixed value of ρ. The reason for this increase may be gleaned from Figure 3 where it is clear that the amount of information contained in the x process, HX, is greater for larger values of a. Hence more information is available to be transferred at the fixed value of ρ when a is larger. In the lower half of Figure 3 we see that as ρ increases the entropy of the Y process, HY, approaches the value of HX. This result is due to the fact that the mechanism being used to increase ρ is to decrease R. Hence as R drops close to zero yn looks increasingly identical to xn (since hc = 1).
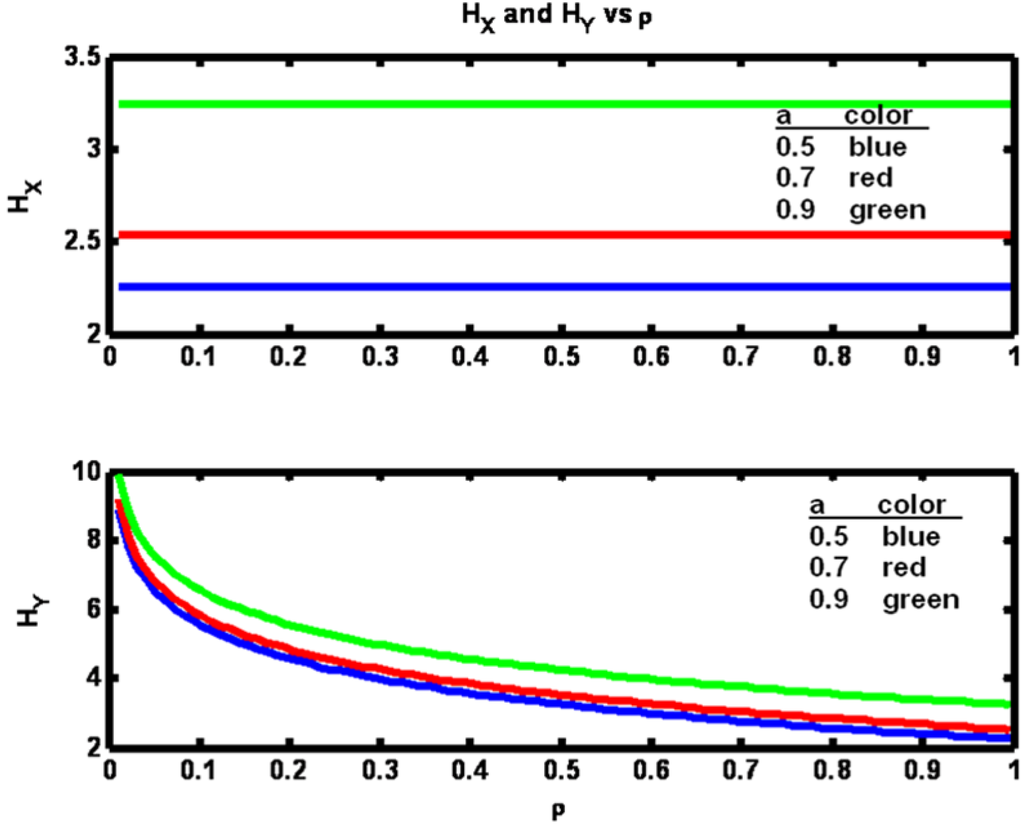
Figure 3.
Example 1: Process entropies HX and HY versus correlation coefficient ρ for three values of parameter a (see legend).
Figure 4 shows information transfer IT(k)x→y plotted versus correlation coefficient ρ. Now note that the trend is for information transfer to increase as ρ is increased over its full range of values. °
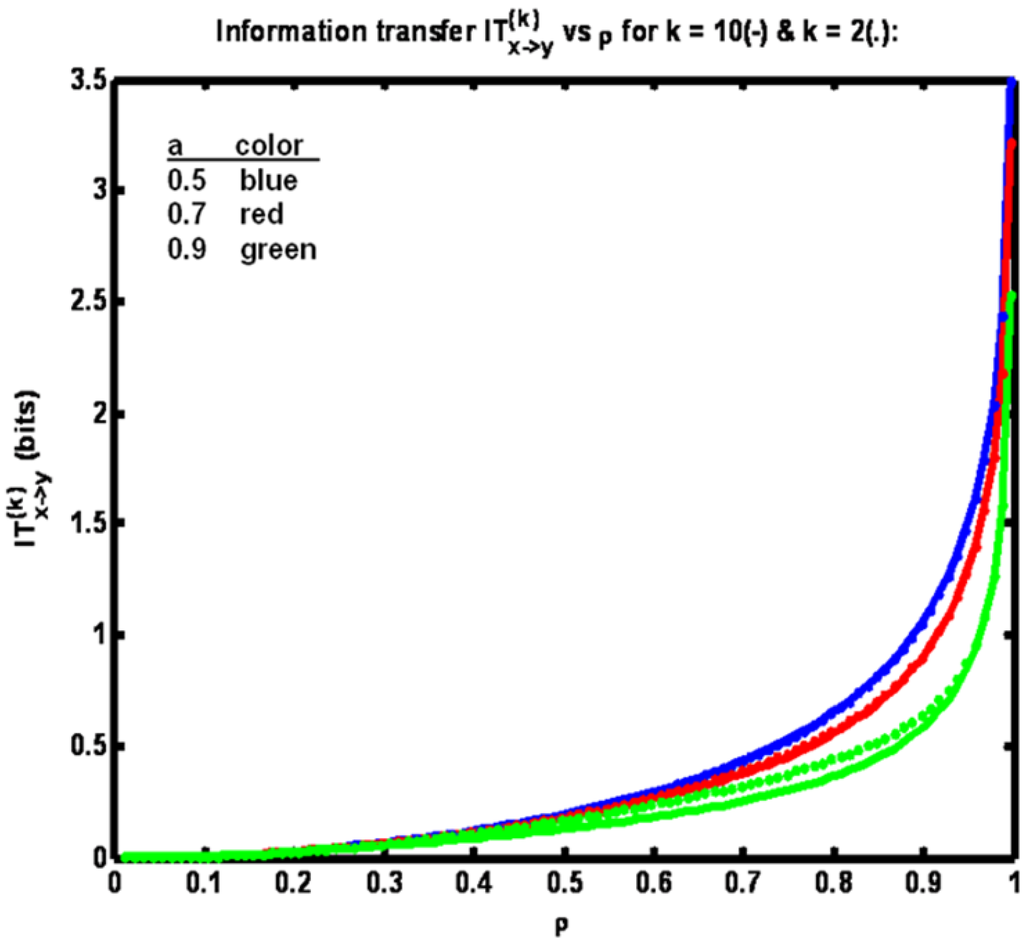
Figure 4.
Example 1: Information transfer IT(k)x→y versus correlation coefficient ρ for three different values of parameter a (see legend) for k = 10 (solid trace) and k = 2 (dotted trace).
This result is obtained since as ρ is increased yn+1 becomes increasingly correlated with xn+1. Also, for a fixed ρ, the lowest information transfer occurs for the largest value of parameter a. We obtain this result since at the higher a values xn and xn+1 are more correlated. Thus the benefit of learning the value of yn+1 through knowledge of xn+1 is relatively reduced, given that yn (itself correlated with xn) is presumed known. Finally, we have IT(10)x→y < IT(2)x→y since conditioning the entropy quantities comprising the expression for information transfer with more state data acts to reduce their difference. Also, by comparison of Figure 2 and Figure 4, it is seen that information transfer is much greater than transfer entropy. This relationship is expected since information transfer as defined herein (for k = 2) is the amount of information that is gained about yn+1 from learning xn+1 and xn, given that yn is already known. Whereas transfer entropy (for k = 2) is the information gained about yn+1 from learning only xn, given that yn is known. Since the state yn+1 in fact equals xn+1, plus noise, learning xn+1 is highly informative, especially when the noise variance is small (corresponding to high values of ρ). The difference between transfer entropy and information transfer therefore quantifies the benefit of learning xn+1, given that xn and yn are known (when the goal is to determine yn+1).
Figure 5 shows how information transfer varies with measurement noise variance R. As R increases the information transfer decreases since measurement noise makes determination of the value of yn+1 from knowledge of xn and xn+1 less accurate. Now, for a fixed R, the greatest value for information transfer occurs for the greatest value of parameter a. This is the opposite of what we obtained for a fixed value of ρ as shown in Figure 4. The way to see the rationale for this is to note that, for a fixed value of information transfer, R is highest for the largest value of parameter a. This result is obtained since larger values of a yield the most correlation between states xn and xn+1. Hence, even though the measurement yn+1 of xn+1 is more corrupted by noise (due to higher R), the same information transfer is achieved nevertheless, because xn provides a good estimate of xn+1 and, thus, of yn+1.
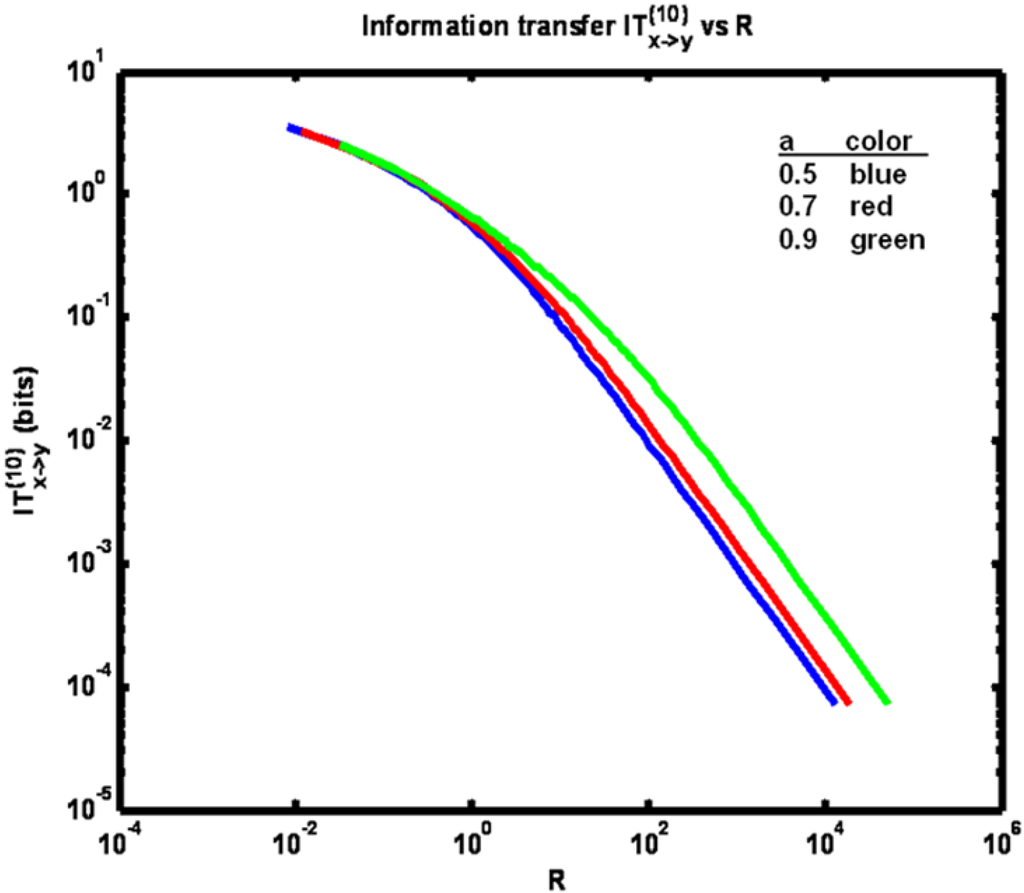
Figure 5.
Example 1: Information transfer IT(10)x→y versus measurement error variance R for three different values of parameter a (see legend).
5. Example 2: Information-theoretic Analysis of Two Coupled AR Processes.
In example 1 the information flow was unidirectional. We now consider a bidirectional example achieved by coupling two AR processes. One question we may ask in such a system is how transfer entropies change with variations in correlation and coupling coefficient parameters. It might be anticipated that increasing either of these quantities will have the effect of increasing information flow and thus transfer entropies will increase.
The system is defined by the equations:
For stability, we require that the eigenvalues of the constant matrix lie in the unit circle. The means of processes X and Y are zero. The terms wn and vn are the X and Y processes noise terms respectively. Using the following definitions:
we may solve for the correlation coefficient ρ between xn and yn to obtain:
Now, as we did previously in example 1 above, compute the covariance C(2) of the variates obtained at two consecutive timestamps to yield:
At this point the difficult part is done and the same calculations can be made as in example 1 to obtain C(k); k = 3,4, …, 10 and transfer entropies. For illustration purposes, we define the parameters of the system as shown below, yielding a symmetrically coupled pair of processes. To generate a family of curves for each transfer entropy we choose a fixed coupling term ε from a set of four values. We set Q = 1000 and vary R so that ρ varies from about 0 to 1. For each ρ value we compute the transfer entropies. The relevant system equations and parameters are:
Hence, we make the following substitutions to compute C(2):
For each parameter set {ε, Q, R} there is a maximum possible ρ, obtained by taking the limit as R→ ∞ of the expression for ρ given above. Doing so, we obtain:
where:
There is a minimum value of ρ also. The corresponding value for R, Rmin, was found by means of the inbuilt Matlab program fminbnd. This program is designed to find the minimum of a function in this case ρ(a, b, c, d, R, Q)) with respect to one parameter (in this case R) starting from an initial guess (here, R = 500). The program returns the minimum functional value (ρmin) and the value of the parameter at which the minimum is achieved (Rmin). After identifying Rmin a set of R values were computed so that the corresponding set of ρ values spanned from ρmin to the maximum in fixed increments of Δρ (here equal to 0.002). This set of R values was generated using the iteration:
For the four selections of parameter ε we obtain the functional relationships shown in Figure 6.
From Figure 6 we see that for a fixed ε, increasing R increases (or decreases) ρ depending on whether R is less than (or greater than) Q (Q = 1000). Note that large increases in R > Q are required to marginally increase ρ when ρ nears its maximum value. The reason that the minimum ρ value occurs when Q equals R is because whenever they are unequal one of the processes dominates the other, leading to increased correlation. Also, note that if R << Q, then increasing ε will cause ρ to decrease since increasing the coupling will cause the variance of the y process Var(yn), a term appearing in the denominator of the expression for ρ, to increase. If Q << R, a similar result is obtained when ε is increased.
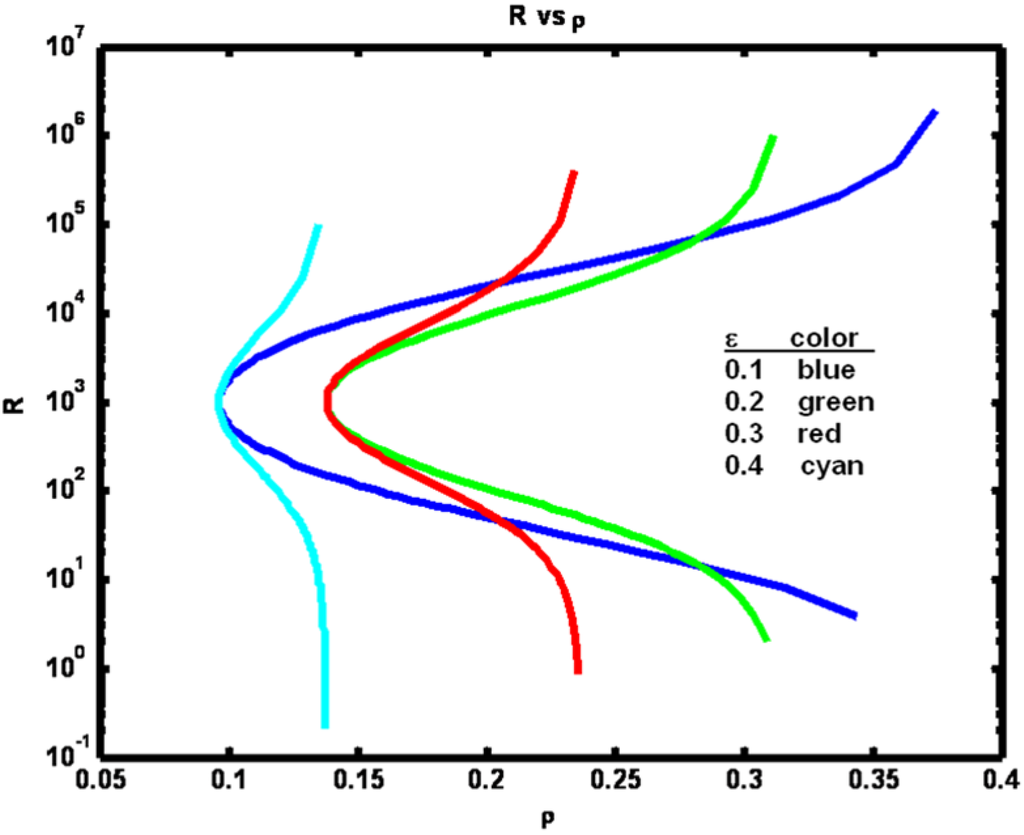
Figure 6.
Example 2: Process noise variance R versus correlation coefficient ρ for a set of ε parameter values (see figure legend).
Transfer entropies in both directions are shown in Figure 7. Fixing ε, we note that as R is increased from a low value both ρ and TEx− >y initially decrease while TEy− >x increases. Then for further increases of R, ρ reaches a minimum value then begins to increase, while TEx→y continues to decrease and TEy→x continues to increase.
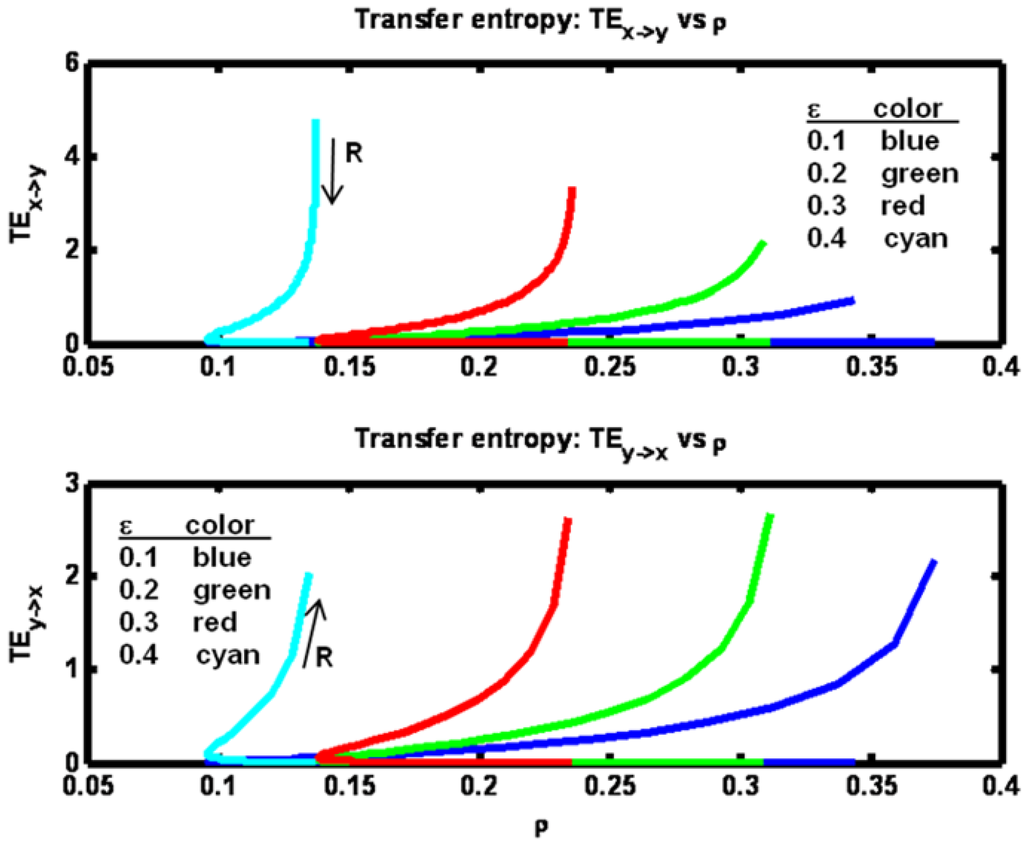
Figure 7.
Example 2: Transfer entropy values versus correlation ρ for a set of ε parameter values (see figure legend). Arrows indicate direction of increasing R values.
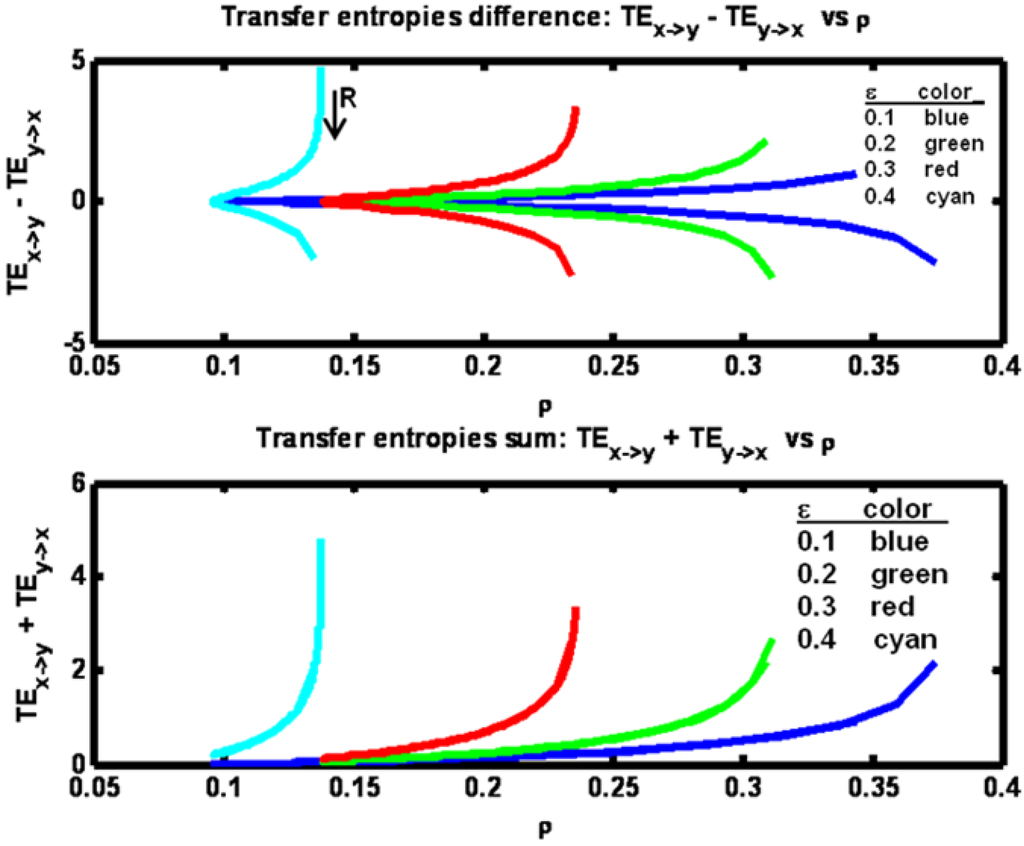
Figure 8.
Example 2: Transfer entropies difference (TEx− >y – TEy − > x) and sum (TEx− > y + TEy− > x) versus correlation ρ for a set of ε parameter values (see figure legend). Arrow indicates direction of increasing R values.
By plotting the difference TEx→y – TEy→x in Figure 8 we see the symmetry that arises as R increases from a low value to a high value. What is happening is that when R is low, the X process dominates the Y process so that TEx→y > TEy→x. As R increases, the two entropies equilibrate. Then, as R rises above Q, the Y process dominates giving TEx→y < TEy→x. The sum of the transfer entropies shown in Figure 8 reveal that the total information transfer is minimal at the minimum value of ρ and increases monotonically with ρ. The minimum value for ρ in this example occurs when the process noise variances Q and R are equal (matched). Figure 9 shows the changes in the transfer entropy values explicitly as a function of R. Clearly, when R is small (as compared to Q = 1000), TEx→y > TEy→x. Also it is clear that at every fixed value of R, both transfer entropies are higher at the larger values for the coupling term ε.
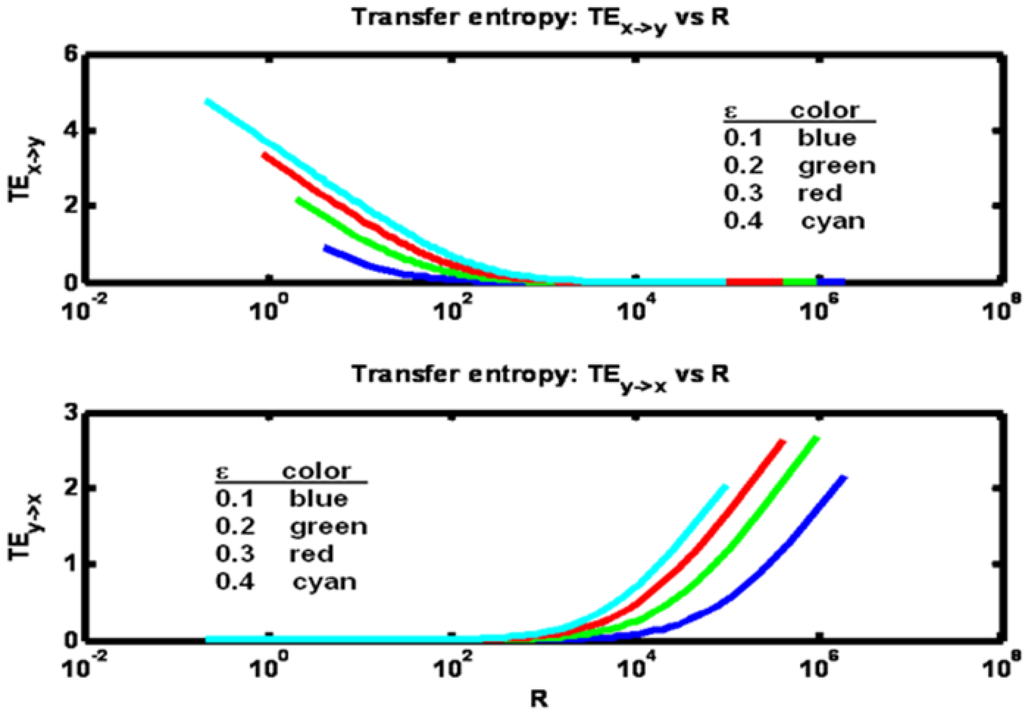
Figure 9.
Example 2: Transfer entropies TEx→y and TEy→x versus process noise variance R for a set of ε parameter values (see figure legend).
Another informative view is obtained by plotting one transfer entropy value versus the other as shown in Figure 10.
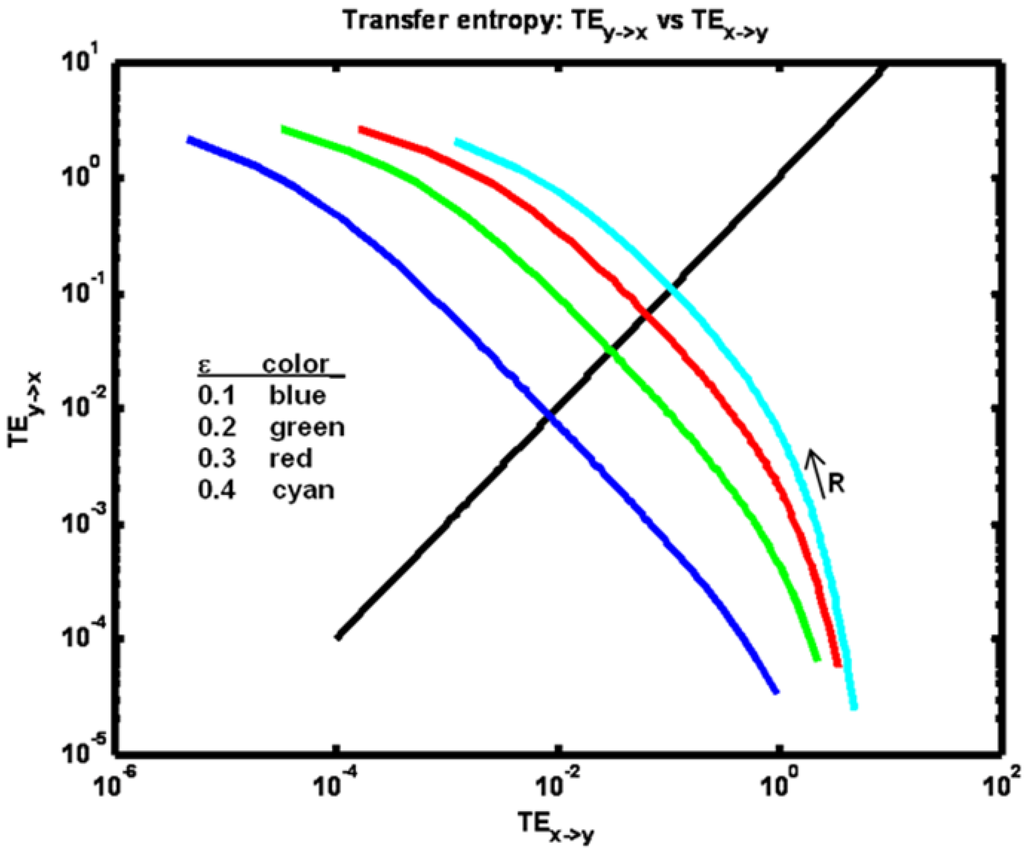
Figure 10.
Example 2: Transfer entropy TEx− > y plotted versus TEy− > x for a set of ε parameter values (see figure legend). The black diagonal line indicates locations where equality obtains. Arrow indicates direction of increasing R values.
Here it is evident how TEy→x increases from a value less than TEx→y to a value greater than TEx→y as R increases. Note that for higher coupling values ε this relative increase is more abrupt.
Finally, we consider the sensitivity of the transfer entropies to the coupling term ε. We reprise example system 2 where now ε is varied in the interval (0, ½) and three values of R (somewhat arbitrarily selected to provide visually appealing figures to follow) are considered:
Figure 11 shows the relationship between ρ and ε, where εx = εy = ε for the three R values. Note that for the case R = Q the relationship is symmetric around ε = ¼. As R departs from equality more correlation between xn and yn is obtained.
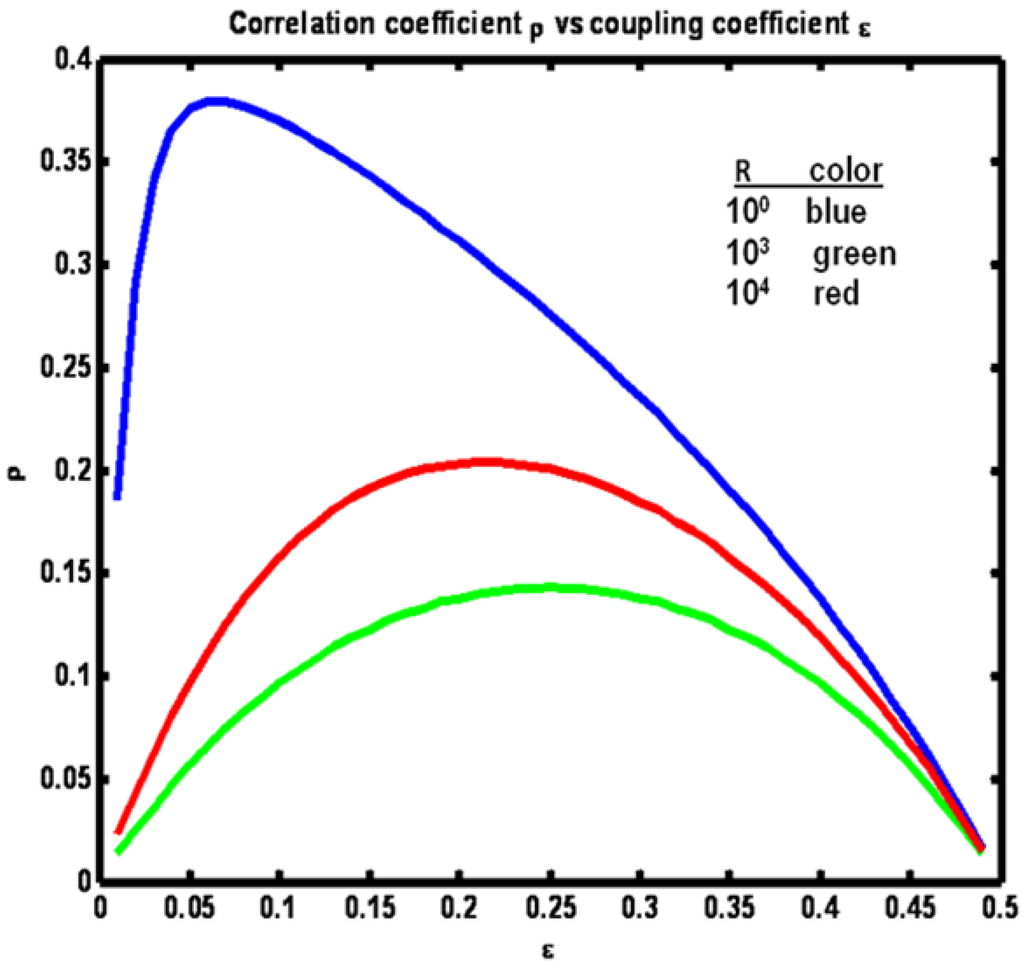
Figure 11.
Example 2: Correlation coefficient ρ vs coupling coefficient ε for a set of R values (see figure legend).
The reason for this increase is that when the noise driving one process is greater in amplitude than the amplitude of the noise driving the other process, the first process becomes dominant over the other. This domination increases as the disparity between the process noise variances increases (R versus Q). Note also that as the disparity increases, the maximum correlation occurs at increasingly lower values of the coupling term ε. As the disparity increases at fixed ε = ¼ the correlation coefficient ρ increases. However, the variance in the denominator of ρ can be made smaller and thus ρ larger, if the variance of either of the two processes can be reduced. This can be accomplished by reducing ε.
The sensitivities of the transfer entropies to changes in coupling term ε are shown in Figure 12. Consistent with intuition, all entropies increase with increasing ε. Also, when R < Q (blue trace) we have TEx‑>y > TEy‑>x and the reverse for R > Q. (red). For R = Q, TEx‑>y = TEy‑>x (green).
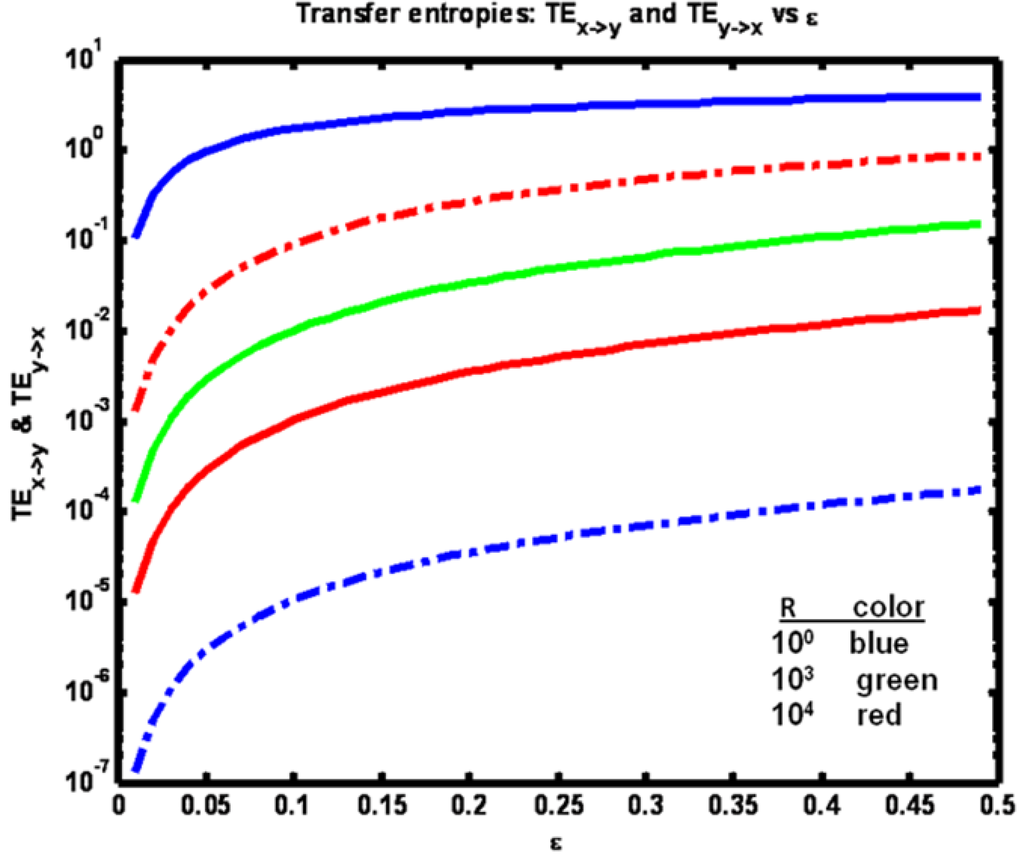
Figure 12.
Example 2: Transfer entropies TEx→y (solid lines) vs TEy→x (dashed lines) vs coupling coefficient ε for a set of R values (see figure legend).
Finally, it is interesting to note that whenever we define three cases by fixing Q and varying the setting for R ( one of R1, R2 and R3 for each case) such that R1 < Q, R2 = Q and R3 = Q2/R1 (so that Ri+1 = QRi/R1 for i = 1 and i = 2) we then obtain the symmetric relationships TEx ‑ >y(R1) = TEy ‑ >x(R3) and TEx ‑ >y(R3) = TEy ‑ >x(R1) for all ε in the interval (1, ½). For these cases we also obtain ρ(R1) = ρ(R3) on the same ε interval.
6. Conclusions
It has been shown how to compute transfer entropy values for Gaussian autoregressive processes for multiple timetags. The approach is based on the iterative computation of covariance matrices. Two examples were investigated: (1) a first-order filtered noise process whose state is measured with additive noise, and (2) two first-order symmetrically coupled processes each of which is driven by independent process noise. We found that, for the first example, increasing the first-order AR coefficient at a fixed correlation coefficient, transfer entropy increased since the entropy of the measured process was itself increased.
For the second example, it was discovered that the relationships between the coupling and correlation coefficients and the transfer entropies is more complicated. The minimum correlation coefficient occurs when the process noise variances match. It was seen that matching of these variances results in minimum information flow, expressed as the sum of both transfer entropies. Without a match, the transfer entropy is larger in the direction away from the process having the larger process noise. Fixing the process noise variances, transfer entropies in both directions increase with coupling strength ε.
Finally, it is worth noting that the method for computing covariance matrices for a variable number of timetags as presented here facilitates the calculation of many other information-theoretic quantities of interest. To this purpose, the authors have computed such quantities as crypticity [13] and normalized transfer entropy using the reported approach.
References
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef] [PubMed]
- Ay, N.; Polani, D. Information Flows in Causal Networks. Adv. Complex Syst. 2008, 11, 17–41. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M. Differentiating information transfer and causal effect. Eur. Phys. J. B 2010, 73, 605‑615. [Google Scholar] [CrossRef]
- Chicharro, D.; Ledberg, A. When two become one: the limits of causality analysis of brain dynamics. PLoS One 2012, 7, e32466. [Google Scholar] [CrossRef] [PubMed]
- Hahs, D.W.; Pethel, S.D. Distinguishing anticipation from causality: anticipatory bias in the estimation of information flow. Phys. Rev. Lett. 2011, 107, 128701. [Google Scholar] [CrossRef] [PubMed]
- Gourevitch, B.; Eggermont, J.J. Evaluating information transfer between auditory cortical neurons. J. Neurophysiol. 2007, 97, 2533–2543. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, A.; Schreiber, T. Information transfer in continuous processes. Physica D 2002, 166, 43–62. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley Series in Telecommunications, Wiley: New York, NY, USA, 1991. [Google Scholar]
- Kotz, S.; Balakrishnan, N.; Johnson, N.L. Continuous Multivariate Distributions, Models and Applications, 2nd ed.; John Wiley and Sons, Inc.: New York, NY, USA, 2000; Volume 1. [Google Scholar]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local information transfer as a spatiotemporal filter for complex systems. Phys. Rev. E 2008, 77, 026110. [Google Scholar] [CrossRef]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. 2010; arXiv:1004:2515. [Google Scholar]
- Crutchfield, J.P; Ellison, C.J.; Mahoney, J.R. Time’s barbed arrow: irreversibility, crypticity, and stored information. Phys. Rev. Lett. 2009, 103, 094101. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).