Entropy in Urban Systems
Abstract
:1. Introduction
2. Entropy Concepts
| Author | Scientific domain | Definition | Interpretation |
|---|---|---|---|
| R. Clausius, 1867 [12] | Physics- thermodynamics | Energy in the system not available to produce work | Unavailable energy tends to increase |
| Boltzmann-Planck, 1900 [13] | Statistical mechanics | Possibilities of arrangement of molecules | Disorder |
| C. Shannon, 1948 [14] | Information theory | Average number of bits necessary to communicate a symbol | Uncertainty |
| E. Jaynes, 1957 [13] | Statistical mechanics | Principle of maximum entropy, where everything goes everywhere unless constraints are imposed | Statistic inference |
| Leopold and Langbein, 1962 [15] | Hydrologic and geomorphic sciences | Entropy in landscape evolution—energy distribution probabilities are as uniform as may be permitted by physical constrains | Maximum entropy |
| A. Wilson, 1970 [3] | Geography | Spatial location and interaction models | People and things tend to be/go everywhere unless constrained to do otherwise |
| H. Thail,1972 [16] | Economy | Relative entropy | Proportion of the maximum uncertainty, spread, dividedness. |
| M. Batty, 1974 [18] | Geography | Spatial entropy—incorporates interval size to weight on the probabilities | Optimization of data categories, or zones for visualization an analysis. Trends in the spread of probabilities across the spatial system. |
| K. Bailey, 1990 [19] | Sociology | Social entropy measures diversity among social parameters, opposes social structure | Low social entropy necessary to maintain good standard of living |
| J. Stepanić et al., 2000 [20] | Sociology | Entropy of a social system | Number of possible social structures the system can adopt |
| F. Parisi, 2002 [21] | Economy | Entropy in property | Property is subject to the fundamental law of entropy |
3. Urban Systems and Urban Sprawl
3.1. Urban Systems
3.2. Urban Sprawl
3.3. Methods Used in Urban Sprawl Studies
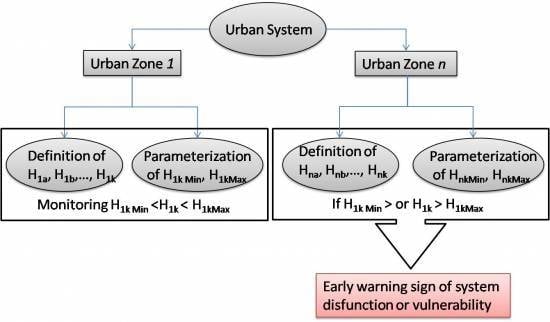
4. Entropy in Urban Systems: A Framework for Monitoring Entropy in Urban Sprawl
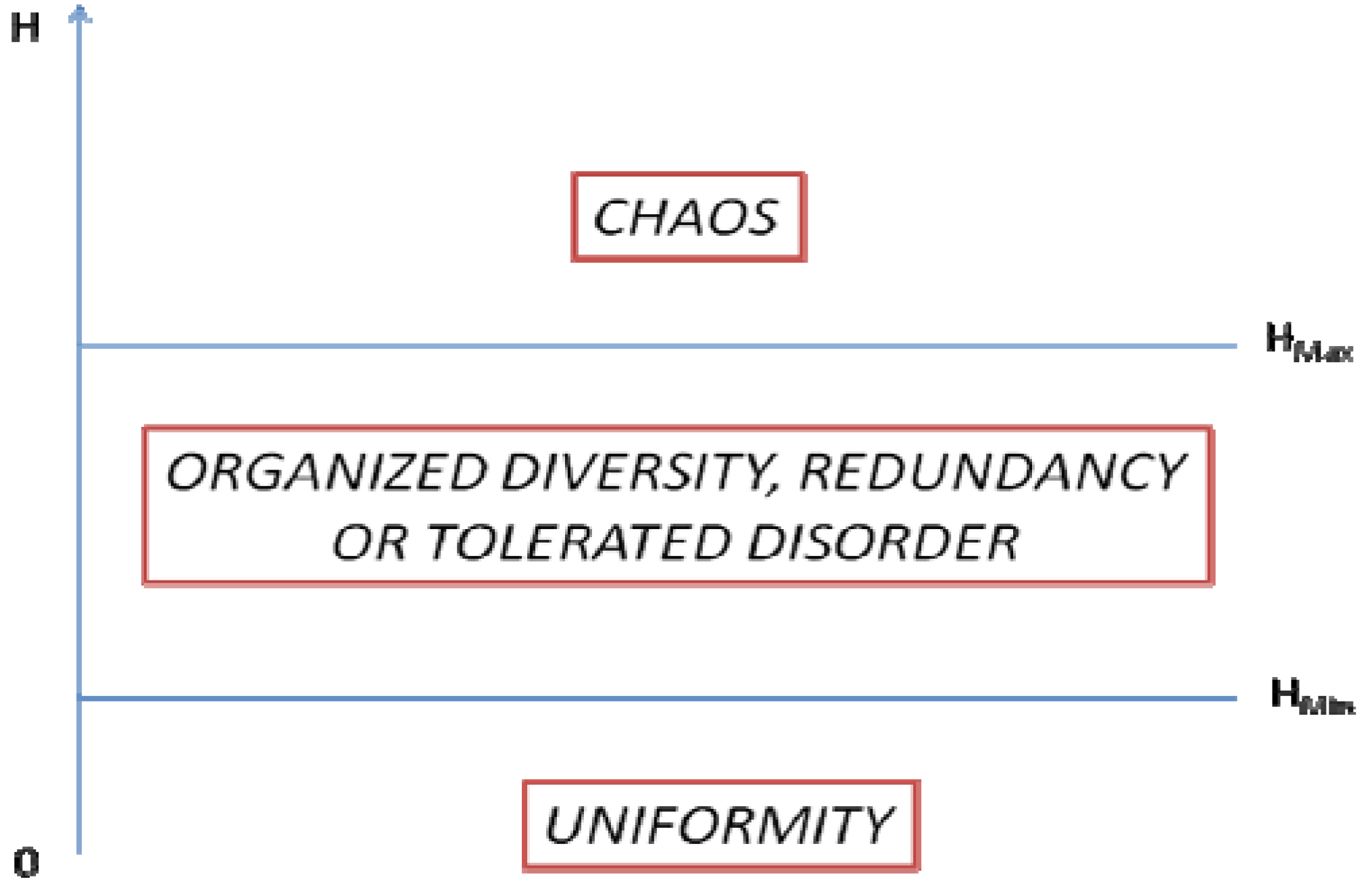
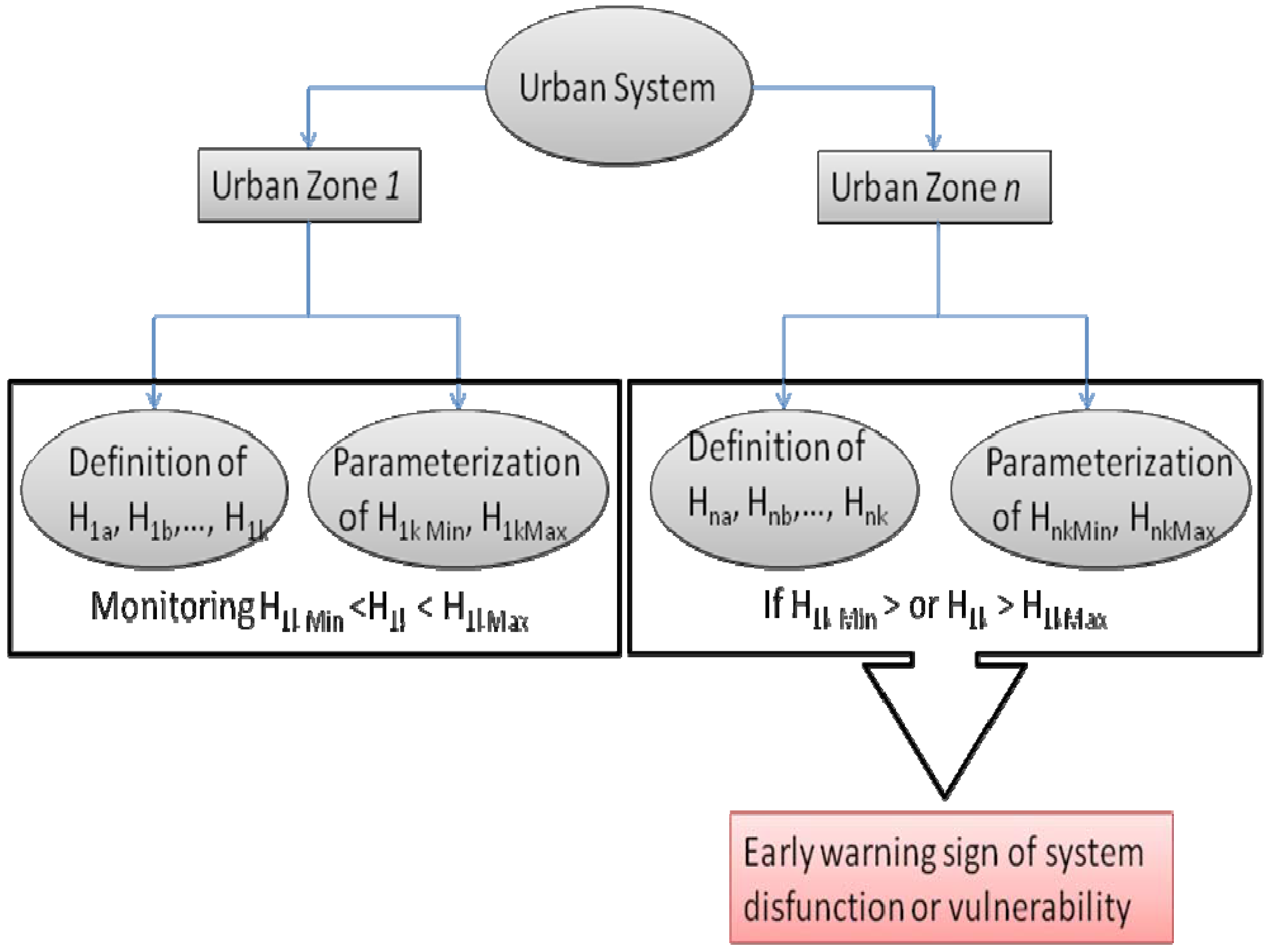
5. Conclusions
Acknowledgment
Conflicts of Interest
References
- Uffink, J. Bluff your way in the second law of thermodynamics. Stud. Hist. Philos. Sci. Part B: Stud. Hist. Philos. Mod. Phys. 2001, 32, 305–394. [Google Scholar] [CrossRef]
- Millennium Ecosystem Assessment. Ecosystems and Human Well-Being: Synthesis; Island Press: Washington, DC, USA, 2005. [Google Scholar]
- Wilson, A. Entropy in urban and regional modelling: Retrospect and prospect. Geogr. Anal. 2010, 42, 364–394. [Google Scholar] [CrossRef]
- Batty, M. Building a science of cities. Cities 2012, 29, S9–S16. [Google Scholar] [CrossRef]
- Niemelä, J.; Saarela, S.-R.; Söderman, T.; Kopperoinen, L.; Yli-Pelkonen, V.; Väre, S.; Kotze, D.J. Using the ecosystem services approach for better planning and conservation of urban green spaces: A Finland case study. Biodivers. Conserv. 2010, 19, 3225–3243. [Google Scholar] [CrossRef]
- Hoffhine Wilson, E.; Hurd, J.D.; Civco, D.L.; Prisloe, M.P.; Arnold, C. Development of a geospatial model to quantify, describe and map urban growth. Remote Sens. Environ. 2003, 86, 275–285. [Google Scholar] [CrossRef]
- Herold, M.; Couclelis, H.; Clarke, K.C. The role of spatial metrics in the analysis and modeling of urban land use change. Comput. Environ. Urban Syst. 2005, 29, 369–399. [Google Scholar] [CrossRef]
- Christiansen, P.; Loftsgarden, T. Drivers behind Urban Sprawl in Europe; Institute of Transport Economics, Norwegian Centre of Transport Research: Oslo, Norway, 2011; p. 29. [Google Scholar]
- Sun, H.; Forsythe, W.; Waters, N. Modeling urban land use change and urban sprawl: Calgary, Alberta, Canada. Networks Spat. Econ. 2007, 7, 353–376. [Google Scholar] [CrossRef]
- Martins, V.N.; Pires, R.; Cabral, P. Modelling of coastal vulnerability in the stretch between the beaches of Porto de Mós and Falésia, Algarve (Portugal). J. Coast. Conserv. 2012, 16, 503–510. [Google Scholar] [CrossRef]
- Cabral, P.; Santos, J.A.; Augusto, G. Monitoring urban sprawl and the national ecological reserve in Sintra-Cascais, Portugal: Multiple OLS linear regression model evaluation. J. Urban Plan. Dev. 2011, 137, 346–353. [Google Scholar] [CrossRef]
- Clausius, R. The Mechanical Theory of Heat: With its Applications to the Steam-Engine and to the Physical Properties of Bodies; J. Van Voorst: London, UK, 1867; p. 376. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Leopold, L.B.; Langbein, W.B. The Concept of Entropy in Landscape Evolution; United States Geological Survey: Washington, DC, USA, 1962. [Google Scholar]
- Thomas, R.W. Information Statistics in Geography; Headey Brothers Ltd, The Invicta Press: Ashford, Kent, UK, 1981. [Google Scholar]
- Yeh, A.G.O.; Li, X. Measurement and monitoring of urban sprawl in a rapidly growing region using entropy. Photogramm. Eng. Remote Sens. 2001, 67, 83–90. [Google Scholar]
- Batty, M. Spatial entropy. Geogr. Anal. 1974, 6, 1–31. [Google Scholar] [CrossRef]
- Bailey, K.D. Social entropy theory: An overview. Syst. Pract. 1990, 3, 365–382. [Google Scholar] [CrossRef]
- Stepanic, J.; Stefancic, H.; Zebec, M.S.; Perackovic, K. Approach to a quantitative description of social systems based on thermodynamic formalism. Entropy 2000, 2, 98–105. [Google Scholar] [CrossRef]
- Parisi, F. Entropy in property. Am. J. Comp. L. 2002, 50, 595–632. [Google Scholar] [CrossRef]
- Miceli, T.J.; Sirmans, C.F. The holdout problem, urban sprawl, and eminent domain. J. Housing Econ. 2007, 16, 309–319. [Google Scholar] [CrossRef]
- The 1755 Lisbon Earthquake: Revisited. In Geotechnical, Geological, and Earthquake Engineering; Springer: Dordrecht, The Netherlands, 2009.
- Wagenaar, M. Townscapes of power. GeoJournal 2000, 51, 3–13. [Google Scholar] [CrossRef]
- Cerdà, I. Teoría General de la Urbanización, 1: y Aplicación de sus Principios y Doctrinas a la Reforma y Ensanche de Barcelona (in Spanish); Imprenta Española: Madrid, Spain, 1867. [Google Scholar]
- Berry, B.J.L. Cities as systems within systems of cities. Pap. Reg. Sci. 2005, 13, 147–163. [Google Scholar] [CrossRef]
- Forrester, J. Systems analysis as a tool for urban planning. IEEE Trans. Syst. Sci. Cybern. 1970, 6, 258–265. [Google Scholar] [CrossRef]
- Sterman, J. Business Dynamics: Systems Thinking and Modeling for a Complex World; Irwin/McGraw Hill Higher Education: Columbus, OH, USA, 2000. [Google Scholar]
- Knaap, G.; Talen, E.; Olshansky, R.; Forrest, C. Government Policy and Urban Sprawl; Illinois Department of Natural Resources, Office of Realty and Environmental Planning: Chicago, IL, USA, 2013. [Google Scholar]
- Frenkel, A.; Ashkenazi, M. The integrated sprawl index: Measuring the urban landscape in Israel. Ann. Reg. Sci. 2007, 42, 99–121. [Google Scholar] [CrossRef]
- Brueckner, J.K. Urban sprawl: Diagnosis and remedies. Int. Reg. Sci. Rev. 2000, 23, 160–171. [Google Scholar] [CrossRef]
- Yeh, A.; Xia, L. Integration of neural networks and cellular automata for urban planning. Geo-Spat. Inf. Sci. 2004, 7, 6–13. [Google Scholar] [CrossRef]
- Johnson, M.P. Environmental impacts of urban sprawl: A survey of the literature and proposed research agenda. Environ. Plan. 2001, 33, 717–735. [Google Scholar] [CrossRef]
- Ewing, R.H. Characteristics, Causes, and Effects of Sprawl: A Literature Review. In Urban Ecology; Marzluff, J.M., Shulenberger, E., Endlicher, W., Alberti, M., Bradley, G., Ryan, C., Simon, U., ZumBrunnen, C., Eds.; Springer US: Boston, MA, USA, 2008; pp. 519–535. [Google Scholar]
- Nechyba, T.J.; Walsh, R.P. Urban sprawl. J. Econ. Perspect. 2004, 18, 177–200. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Z.; Li, W. Analyses of urban ecosystem based on information entropy. Ecol. Model. 2006, 197, 1–12. [Google Scholar] [CrossRef]
- Bhatta, B.; Saraswati, S.; Bandyopadhyay, D. Quantifying the degree-of-freedom, degree-of-sprawl, and degree-of-goodness of urban growth from remote sensing data. Appl. Geogr. 2010, 30, 96–111. [Google Scholar] [CrossRef]
- Sullivan, W.C.; Lovell, S.T. Improving the visual quality of commercial development at the rural–urban fringe. Landsc. Urban Plan. 2006, 77, 152–166. [Google Scholar] [CrossRef]
- Alberti, M. The effects of urban patterns on ecosystem function. Int. Reg. Sci. Rev. 2005, 28, 168–192. [Google Scholar] [CrossRef]
- Burchell, R.W.; Mukherji, S. Conventional development versus managed growth: The costs of sprawl. Am. J. Public Health 2003, 93, 1534–1540. [Google Scholar] [CrossRef] [PubMed]
- Sturm, R.; Cohen, D.A. Suburban sprawl and physical and mental health. Public Health 2004, 118, 488–496. [Google Scholar] [CrossRef] [PubMed]
- Kelly-Schwartz, A.C. Is sprawl unhealthy? A multilevel analysis of the relationship of metropolitan sprawl to the health of individuals. J. Plan. Educ. Res. 2004, 24, 184–196. [Google Scholar] [CrossRef]
- Burchell, R.; Shad, N.; Listokin, D.; Phillips, H.; Downs, A.; Seskin, S.; Davis, J.; Moore, T.; Helton, D.; Gall, M. The costs of sprawl–revisited; Transit Cooperative Research Program: Washington, DC, USA, 1998; p. 40. [Google Scholar]
- Bhatta, B. Analysis of Urban Growth and Sprawl from Remote Sensing Data; Advances in Geographic Information Science; Springer: Heidelberg, Germany and New York, NY, USA, 2010. [Google Scholar]
- Yang, X.; Lo, C.P. Modelling urban growth and landscape changes in the Atlanta metropolitan area. Int. J. Geogr. Inf. Sci. 2003, 17, 463–488. [Google Scholar] [CrossRef]
- Cheng, J.; Masser, I. Urban growth pattern modeling: A case study of Wuhan city, PR China. Landsc. Urban Plan. 2003, 62, 199–217. [Google Scholar] [CrossRef]
- Burchfield, M.; Overman, H.G.; Puga, D.; Turner, M.A. Causes of sprawl: A portrait from space. Q. J. Econ. 2006, 121, 587–633. [Google Scholar] [CrossRef]
- Squires, G. Urban Sprawl: Causes, Consequences, & Policy Responses; Urban Institute Press: Washington, DC, USA, 2002. [Google Scholar]
- Martins, V.N.; Silva, D.S.E.; Cabral, P. Social vulnerability assessment to seismic risk using multicriteria analysis: The case study of Vila Franca do Campo (São Miguel Island, Azores, Portugal). Nat. Hazards 2012, 62, 385–404. [Google Scholar] [CrossRef]
- Wu, F. Urban Development in Post-Reform China: State, Market, and Space; Routledge: Abingdon, Oxon, UK and New York, NY, USA, 2007. [Google Scholar]
- Frederic Deng, F.; Huang, Y. Uneven land reform and urban sprawl in China: The case of Beijing. Prog. Plan. 2004, 61, 211–236. [Google Scholar] [CrossRef]
- Tewolde, M.G.; Cabral, P. Urban sprawl analysis and modeling in Asmara, Eritrea. Remote Sens. 2011, 3, 2148–2165. [Google Scholar] [CrossRef]
- Robert, W. Wassmer causes of urban sprawl in the United States: Auto reliance as compared to natural evolution, flight from blight, and local revenue reliance. J. Policy Anal. Manage. 2008, 27, 536–555. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, United States, 1996. [Google Scholar]
- Angel, S.; Sheppard, S.; Civco, D. The Dynamics of Global Urban Expansion; Transport and Urban Development Department, The World Bank: Washington, DC, USA, 2005. [Google Scholar]
- Almeida, C.M.D.; Monteiro, A.M.V.; Câmara, G.; Soares-Filho, B.S.; Cerqueira, G.C.; Pennachin, C.L.; Batty, M. GIS and remote sensing as tools for the simulation of urban land-use change. Int. J. Remote Sens. 2005, 26, 759–774. [Google Scholar] [CrossRef]
- Hardin, P.J.; Jackson, M.W.; Otterstrom, S.M. Mapping, Measuring, and Modeling Urban Growth. In Geo-Spatial Technologies in Urban Environments; Jensen, D.R.R., Gatrell, D.J.D., McLean, D.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 141–176. [Google Scholar]
- Torrens, P.; Alberti, M. Measuring Urban Sprawl; Working Paper Series; Centre for Advances Spatial Analysis, University College London: London, UK, 2000. [Google Scholar]
- Tsai, Y.-H. Quantifying urban form: Compactness versus “sprawl”. Urban Stud. 2005, 42, 141–161. [Google Scholar] [CrossRef]
- Araya, Y.H.; Cabral, P. Analysis and modeling of urban land cover change in Setúbal and Sesimbra, Portugal. Remote Sens. 2010, 2, 1549–1563. [Google Scholar] [CrossRef]
- Herold, M.; Scepan, J.; Clarke, K.C. The use of remote sensing and landscape metrics to describe structures and changes in urban land uses. Environ. Plan. 2002, 34, 1443–1458. [Google Scholar] [CrossRef]
- Cabral, P. Délimitation d‘aires urbaines à partir d‘une image Landsat ETM+ : Comparaison de méthodes de classification. Can. J. Remote Sens. 2007, 33, 422–430. (in French). [Google Scholar] [CrossRef]
- Portugali, J. Self-Organization and the City; Springer Series in Synergetics; Springer: New York, NY, USA, 1999. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cabral, P.; Augusto, G.; Tewolde, M.; Araya, Y. Entropy in Urban Systems. Entropy 2013, 15, 5223-5236. https://doi.org/10.3390/e15125223
Cabral P, Augusto G, Tewolde M, Araya Y. Entropy in Urban Systems. Entropy. 2013; 15(12):5223-5236. https://doi.org/10.3390/e15125223
Chicago/Turabian StyleCabral, Pedro, Gabriela Augusto, Mussie Tewolde, and Yikalo Araya. 2013. "Entropy in Urban Systems" Entropy 15, no. 12: 5223-5236. https://doi.org/10.3390/e15125223
APA StyleCabral, P., Augusto, G., Tewolde, M., & Araya, Y. (2013). Entropy in Urban Systems. Entropy, 15(12), 5223-5236. https://doi.org/10.3390/e15125223