The general model behavior in uniform-compression simulations is described in [
21]. The jamming phase transition in the analyzed case occurs at
. It is accompanied by a rapid increase of the internal pressure,
p, the fraction of non-rattler grains (defined here as grains with at least two contacts) and the mean contact number,
,
i.e., changes indicative of the percolation of the contact and force network. Additional simulations performed with different values of the GSD exponent,
α, showed that, not surprisingly, the jamming packing fraction,
, increases with decreasing
α (the wider the GSD, the denser the packing fraction attainable), but the course of the jamming transition (for example, the shape of the
curve) remains almost unaffected. This suggests that the results presented here are relevant for a wider range of model parameters than those actually used in the simulations.
3.1. Shear Jamming: General Characteristics
The general behavior of the modeled system under pure shear deformation depends on the packing fraction,
A, and the strain rate,
ϵ [
8]. At low
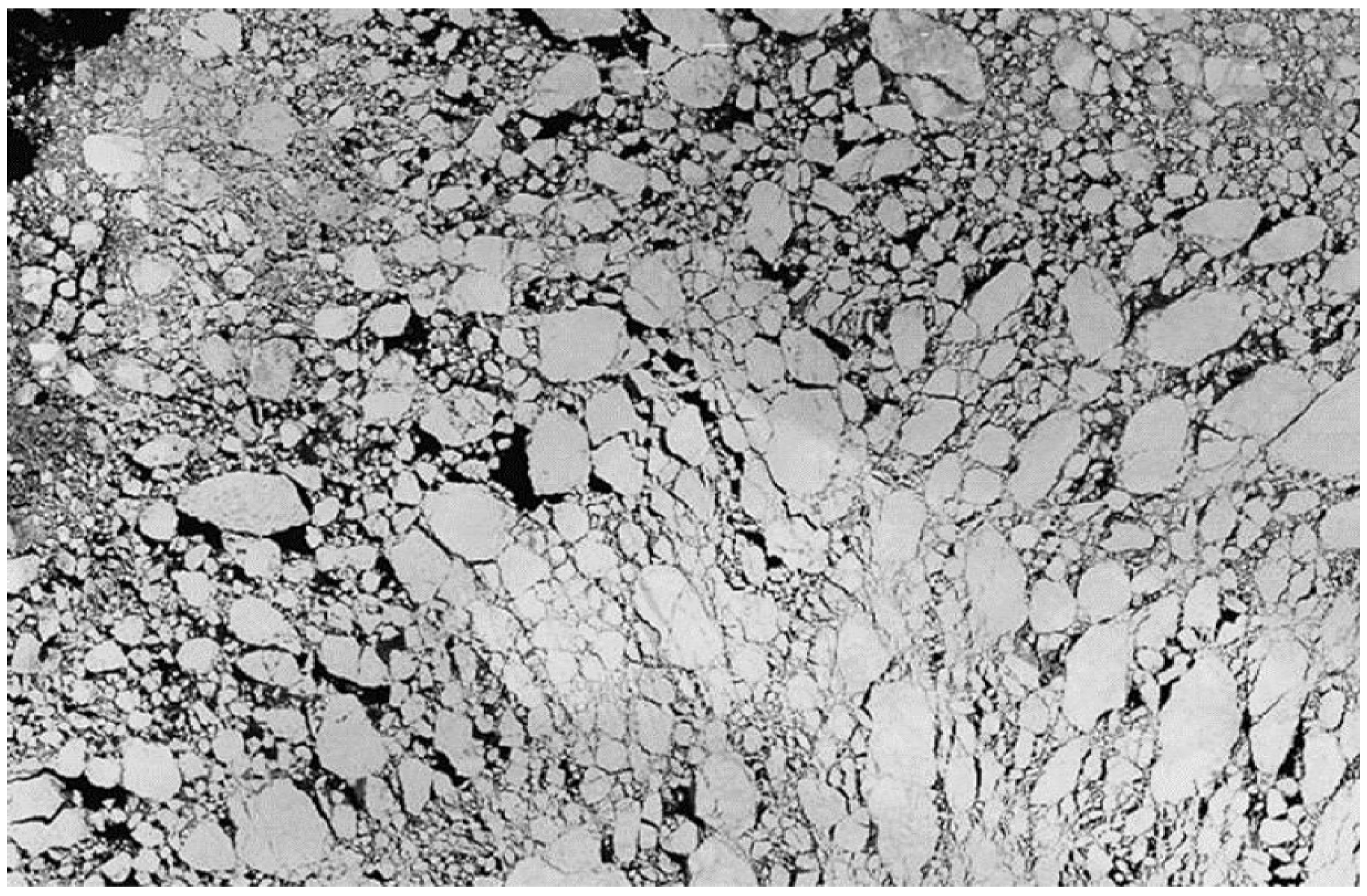
A, the system remains in an unjammed state, in which the internal stress is generated via short, binary collisions between neighboring grains. Regions of jammed, more densely packed grains develop only locally (
Figure 2); they are short-lived and disperse, due to interactions with the surrounding, more loosely packed regions. Hence, the internal stress level at the system scale remains very low, a few orders of magnitude lower than in the jammed states (
Figure 3), when the force network between grains percolates the whole system (
Figure 2) and the neighboring grains remain in contact for many seconds or even minutes (see further
Section 3.2),
i.e., periods of time up to a few orders of magnitude longer than the duration of a typical binary collision.
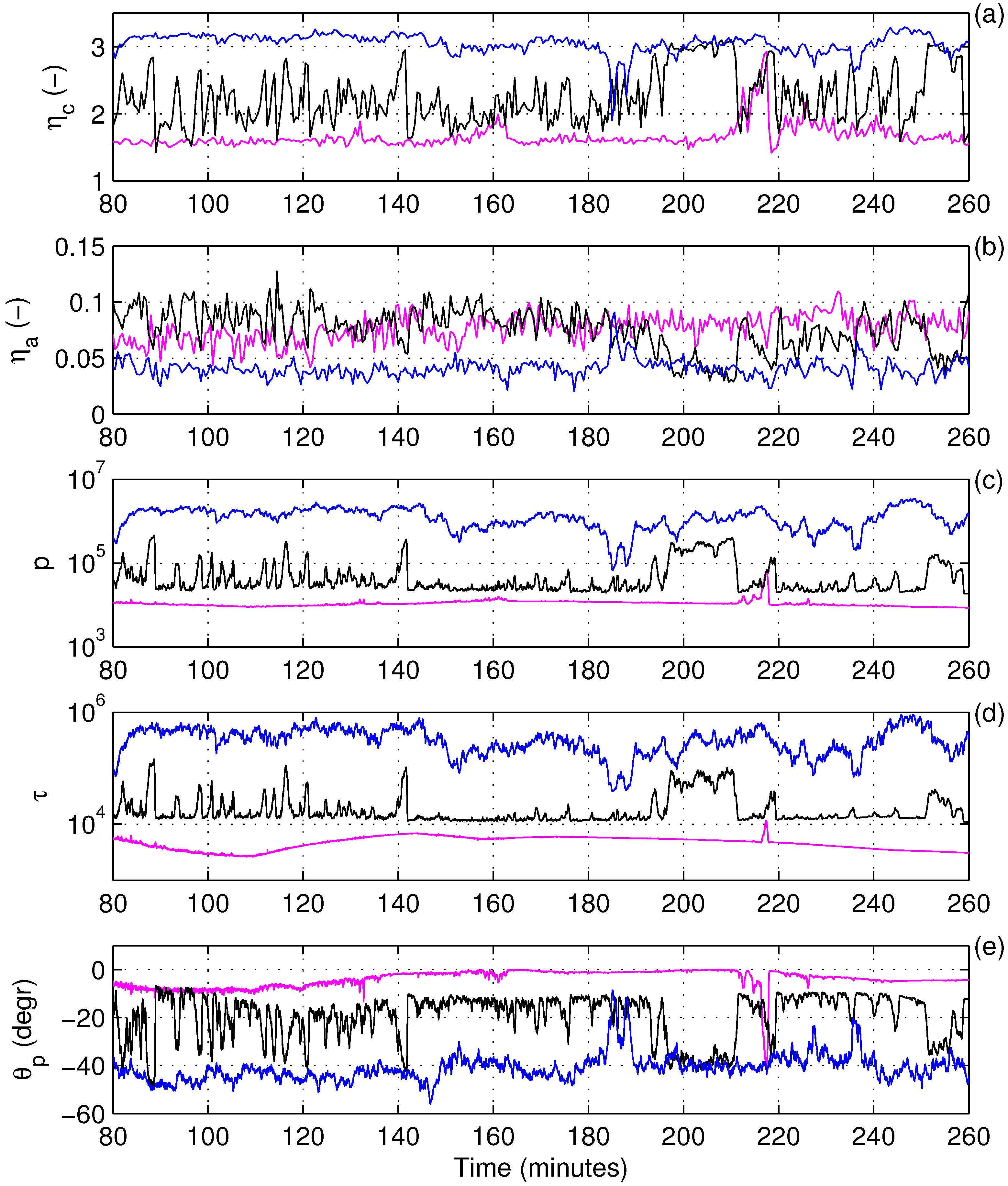
Figure 3.
Time series of the average contact number, (a), force-network anisotropy (b), pressure p (c), shear stress τ (d) and the principal angle, (e), during simulations with: and m/s (blue); and m/s (black); and m/s (magenta).
Figure 3.
Time series of the average contact number, (a), force-network anisotropy (b), pressure p (c), shear stress τ (d) and the principal angle, (e), during simulations with: and m/s (blue); and m/s (black); and m/s (magenta).
The large-scale system behavior can be described by means of the properties of the stress and fabric tensors: the pressure
and the shear stress
are calculated from the principal stresses,
and
; the mean contact number
and the contact-network anisotropy
are calculated from the eigenvalues of the fabric tensor,
and
(see [
8,
21] for details). Both in the jammed and unjammed states, far from the jamming-transition point, those four large-scale system characteristics—
p,
τ,
and
—remain relatively stable in time, and the system recovers fast from short rearrangement events that sporadically take place (
Figure 3). In between those two extremes, the system undergoes rapid changes and shifts from unjammed to jammed states and
vice versa (black lines in
Figure 3). Between those two extremes, the force networks often have a fragile, “openwork” structure, with relatively large unjammed areas where the stress remains very low and with forces transmitted via long “strands” of approximately linearly aligned grains. As in the case of fragile states observed recently [
8], those force networks may span the whole model domain in only one (compressive) direction, giving the material anisotropic strength in response to deformation, which manifests itself in high values of
(see, also,
Section 3.2). The present results suggest that, even in constant strain conditions, the fragile states are short-lived, at least in the range of
A and
ϵ combinations analyzed here.
Apart from the properties of the stress and contact-fabric tensors, a signature of jamming is also present in the grains’ velocity, both means and their anomalies. Let us define and , as the mean and standard deviation, respectively, of the velocity of all grains that at time t have their y-coordinate within a certain small distance, δ, from y (i.e., that lie inside a stripe of length and width ). Further, let and denote the time mean of and over the whole simulation time and —the velocity anomaly of grain i, i.e., .
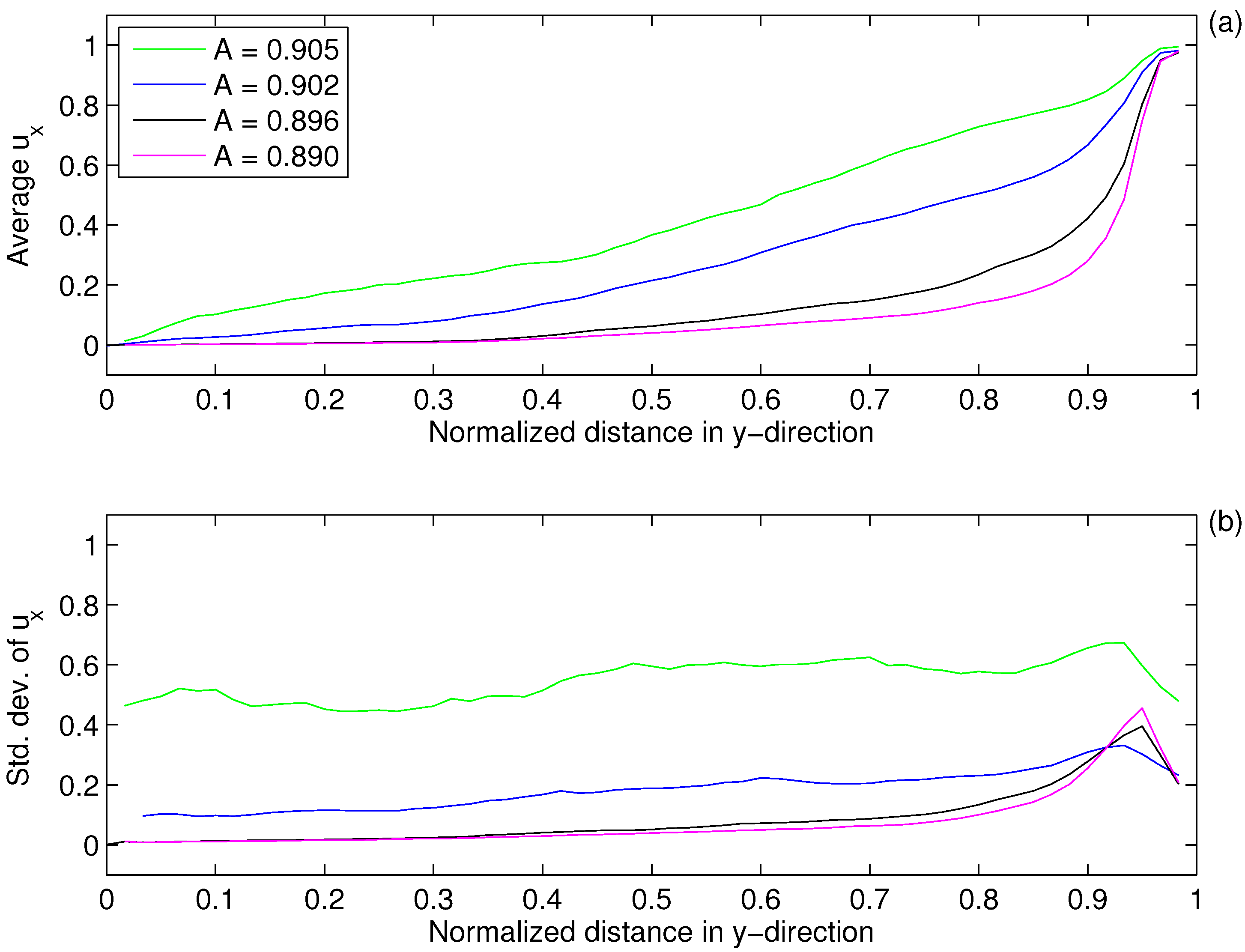
Figure 4.
Profiles of the average (a) and standard deviation (b) of the x-component of grain velocity in the function of the normalized y-distance ( at the “frozen” boundary and at the moving boundary). Results obtained with m/s.
Figure 4.
Profiles of the average (a) and standard deviation (b) of the x-component of grain velocity in the function of the normalized y-distance ( at the “frozen” boundary and at the moving boundary). Results obtained with m/s.
The profiles of
and
are shown in
Figure 4 for a range of
A values corresponding to unjammed and jammed states. At low packing fractions, the motion of the grains is confined to the region close to the moving boundary, and a narrow zone of strong shear separates this region from the rest of the model domain, remaining almost at rest. To the contrary, jammed states are characterized by an almost constant velocity gradient
and constant standard deviation of velocity
, independently on the distance from the moving boundary,
i.e., the strain is distributed over the whole system.
In order to characterize the variability of velocity anomalies, it is convenient to define a measure analogous to entropy (as used in statistical mechanics), characterizing the spread of velocity anomalies of individual grains at a given time,
t:
where
n denotes the number of bins of the discrete pdfof
,
is the probability density of the
i-th bin and
—a normalization constant, introduced so that the maximum value of
. In order to account for different ranges of
in different model runs, the pdfs were estimated by dividing the range,
, into
bins of equal width, where
,
denote the 1% and 99% quantiles of the data, respectively. Thus,
E analyzed here reflects the shape of the pdfs within the respective inter-quantile range, and not their widths, which, as shown in
Figure 4b, is much larger in the jammed than in the unjammed states.
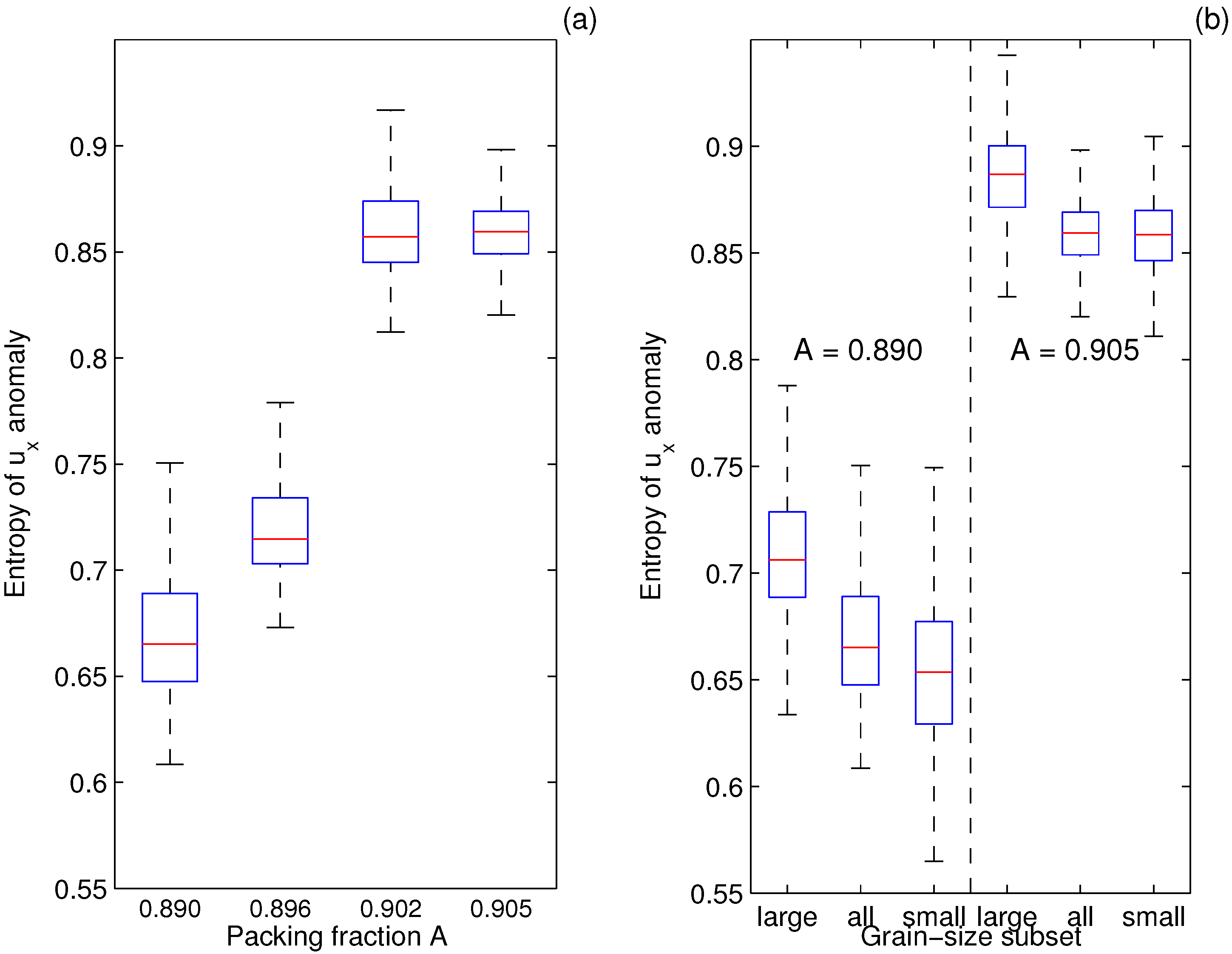
Figure 5.
Normalized entropy E of the anomalies, , in the function of the grain packing fraction, A (a), and grain size (b). On each box, the central mark is the median, the edges of the box are the 25th and 75th percentiles and the whiskers extend to the most extreme data points not considered outliers. In (b), for the two selected values of A (0.890 and 0.905), the statistics are calculated three times: for all N grains and for the subsets of the 10% largest and 10% smallest grains, respectively. Results obtained with m/s.
Figure 5.
Normalized entropy E of the anomalies, , in the function of the grain packing fraction, A (a), and grain size (b). On each box, the central mark is the median, the edges of the box are the 25th and 75th percentiles and the whiskers extend to the most extreme data points not considered outliers. In (b), for the two selected values of A (0.890 and 0.905), the statistics are calculated three times: for all N grains and for the subsets of the 10% largest and 10% smallest grains, respectively. Results obtained with m/s.
As can be seen in
Figure 5a,
E increases with increasing packing fraction
A. It has highest values, exceeding 0.85, and lowest time variability (see the boxes and whiskers in
Figure 5) in shear-jammed states. In unjammed states,
E, most of the time remains within the 0.65–0.7 range. Thus, the range of instantaneous velocity anomalies in jammed systems is significantly larger, even corrected for the width of the respective pdfs. On the other hand, jamming is associated with a transition from local to global correlations of
, as illustrated in
Figure 6 and
Figure 7, showing the linear correlation coefficient,
C, between pairs of grains in two selected model runs (for two grains,
i and
j,
C is a Pearson correlation coefficient between the
x-components of
and
over time
min). At low
A, statistically significant correlation of velocity anomalies is observed only between grains within a small spatial distance from each other. At high
A, the correlation remains high within the whole model domain. Those two facts—velocity anomalies correlated on the system-scale and high values of
E—indicate that in a jammed state, the grains tend to have large velocity anomalies that are of the same sign.
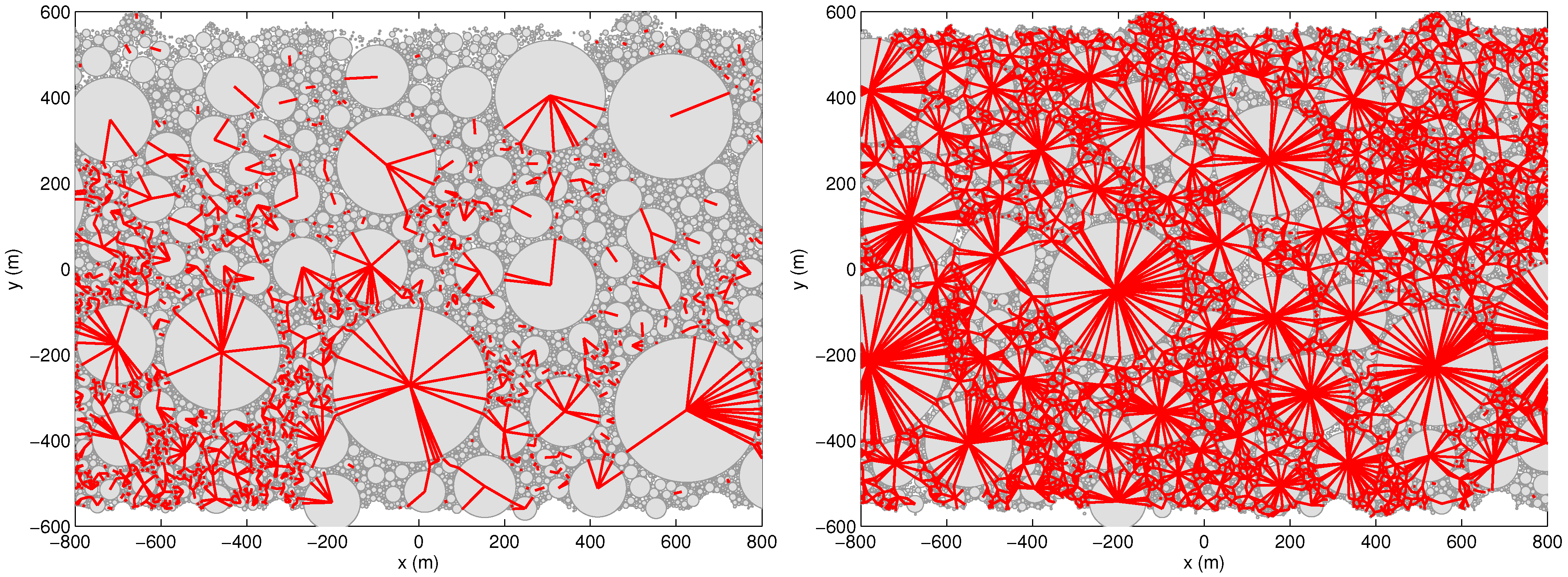
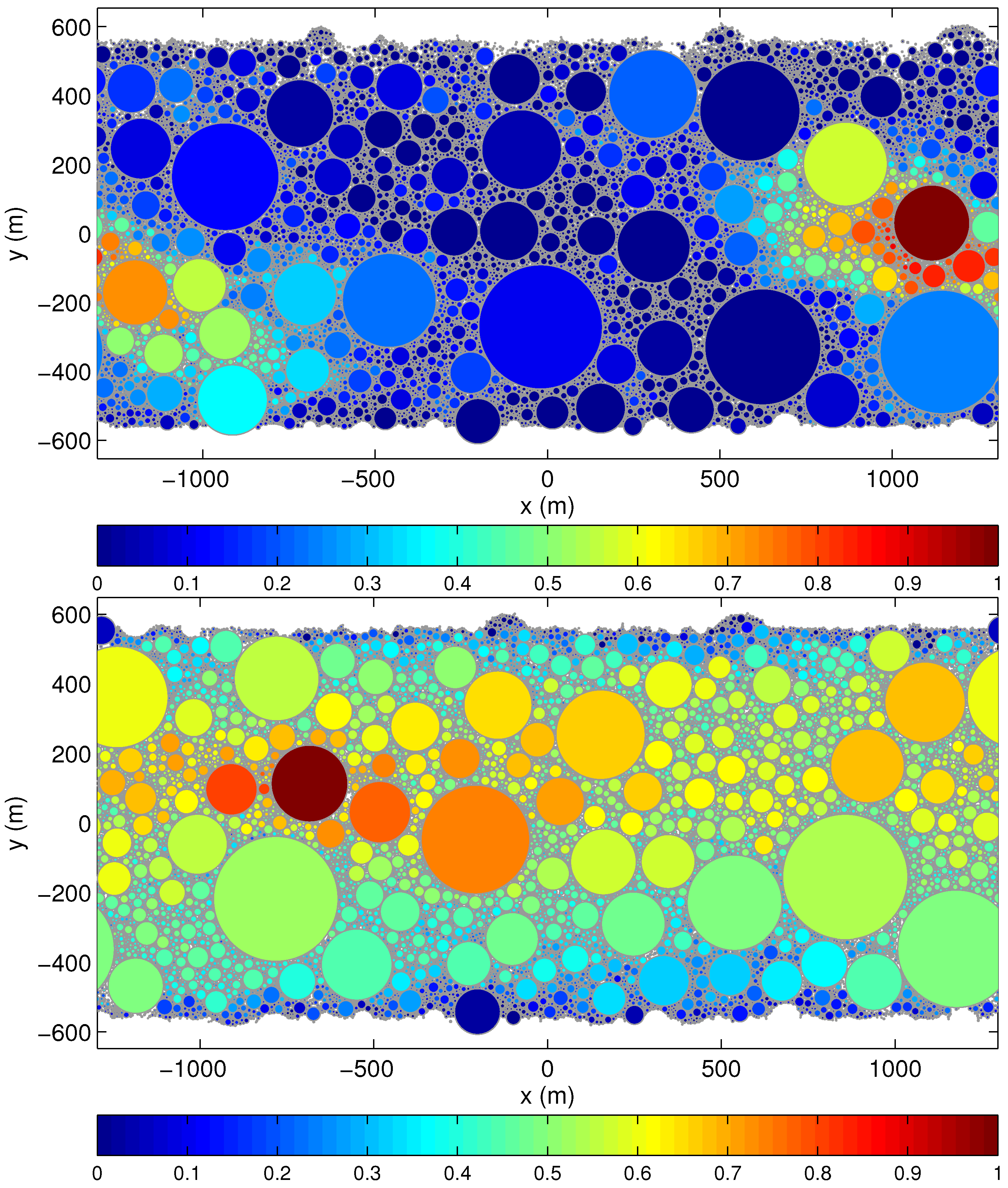
Figure 6.
Snapshots of the modeled system for m/s and the packing fraction (a) and (b), showing the linear correlation coefficient, C, between the velocity anomalies, , of a selected grain (dark brown, ) and all other grains in the system. C was calculated for a period of time equal to 100 minutes. Grains belonging to the “frozen” and moving boundaries are not shown.
Figure 6.
Snapshots of the modeled system for m/s and the packing fraction (a) and (b), showing the linear correlation coefficient, C, between the velocity anomalies, , of a selected grain (dark brown, ) and all other grains in the system. C was calculated for a period of time equal to 100 minutes. Grains belonging to the “frozen” and moving boundaries are not shown.
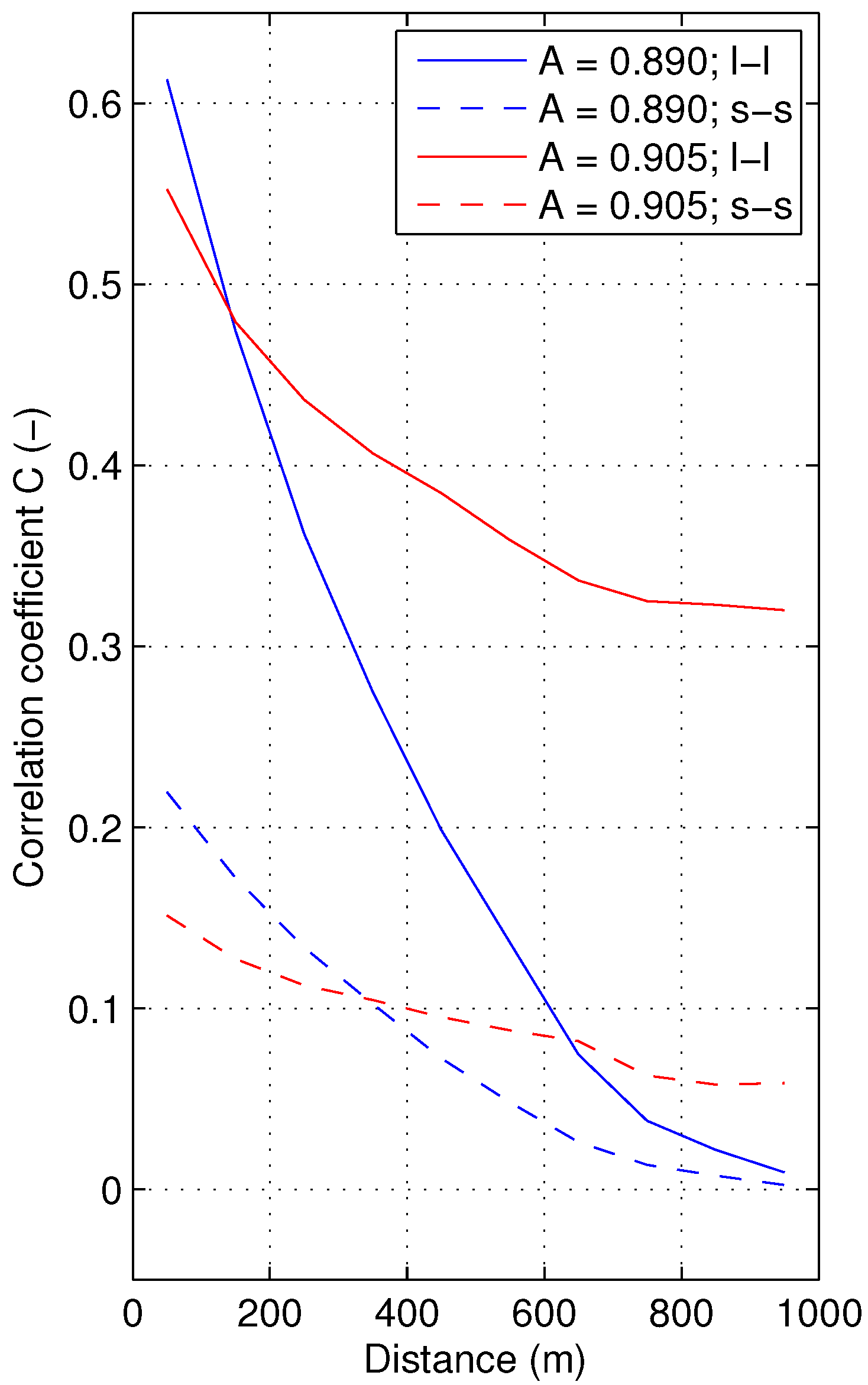
Figure 7.
The correlation coefficient, C, between the velocity anomalies, , calculated for pairs of grains from a subset of the 10% largest (continuous lines) and 10% smallest (dashed lines) grains in the whole ensemble, in the function of the grain-grain distance. Results of simulations with m/s and (blue), (red).
Figure 7.
The correlation coefficient, C, between the velocity anomalies, , calculated for pairs of grains from a subset of the 10% largest (continuous lines) and 10% smallest (dashed lines) grains in the whole ensemble, in the function of the grain-grain distance. Results of simulations with m/s and (blue), (red).
3.2. The Role of Polydispersity
In systems with power-law GSD, the largest grains occupy a substantial part of the model domain (even with increasing system size
N), and it is their locations and relative movement that have a deciding influence on the system as a whole. Sub-regions of the model domain that at a given time instance are filled with small grains can change their shape (and thus react to strain deformation) more easily than assemblies of large grains. In many respects, assemblies of very small grains act as a plastic, easily deformable ‘filler’ occupying empty spaces between very large grains. An analysis of animations illustrating the time evolution of the modeled system reveal that the rapid jamming and un-jamming events mentioned earlier (black curves in
Figure 3) tend to be associated with reorganization of the positions of the largest grains. This observation seems confirmed by the fact that, at high packing fractions, the analyzed measures of the grains’ velocity anomalies, like the entropy,
E, are strongly correlated to the global instantaneous pressure,
p, and shear stress
τ and that this correlation is higher for a subset of the largest grains than for the whole system. For example, in the model run with
and
m/s, the correlation of
E with
equals 0.83 and 0.95 for, respectively, all and the subset of 10% of the largest grains.
Previous experiments with an earlier version of the model demonstrated that polydispersity plays an important role in many aspects of the dynamics of sea ice composed of floes with power-law size distribution, including the formation of clusters in response to wind [
19,
20]. Not surprisingly, polydispersity also influences the behavior of the sheared systems studied here. Many global characteristics of the system, including those analyzed above, have different values when they are calculated for a subset of the largest or smallest grains, revealing their different response to the forcing and interactions with neighboring grains. In particular, the entropy,
E, of velocity anomalies of the largest grains in an ensemble is higher than the system average at all packing fractions analyzed,
i.e., both in jammed and unjammed states (
Figure 5b). The emergence of long-range correlations between velocity anomalies at the jamming transition, described in the previous section, takes place almost exclusively due to correlations between the largest grains in the system (
Figure 7 and
Figure 8). Similarly, at low
A, the high values of
C within clusters (0.5–0.6 on average) are observed only for pairs of the largest grains. Furthermore, whereas at low
A, those values drop rapidly with increasing grain-grain distance, the rate of that decrease is much slower in jammed states (compare the continuous curves in
Figure 7), resulting in a shift of the pdf of
C towards larger values, representing statistically significant correlation (
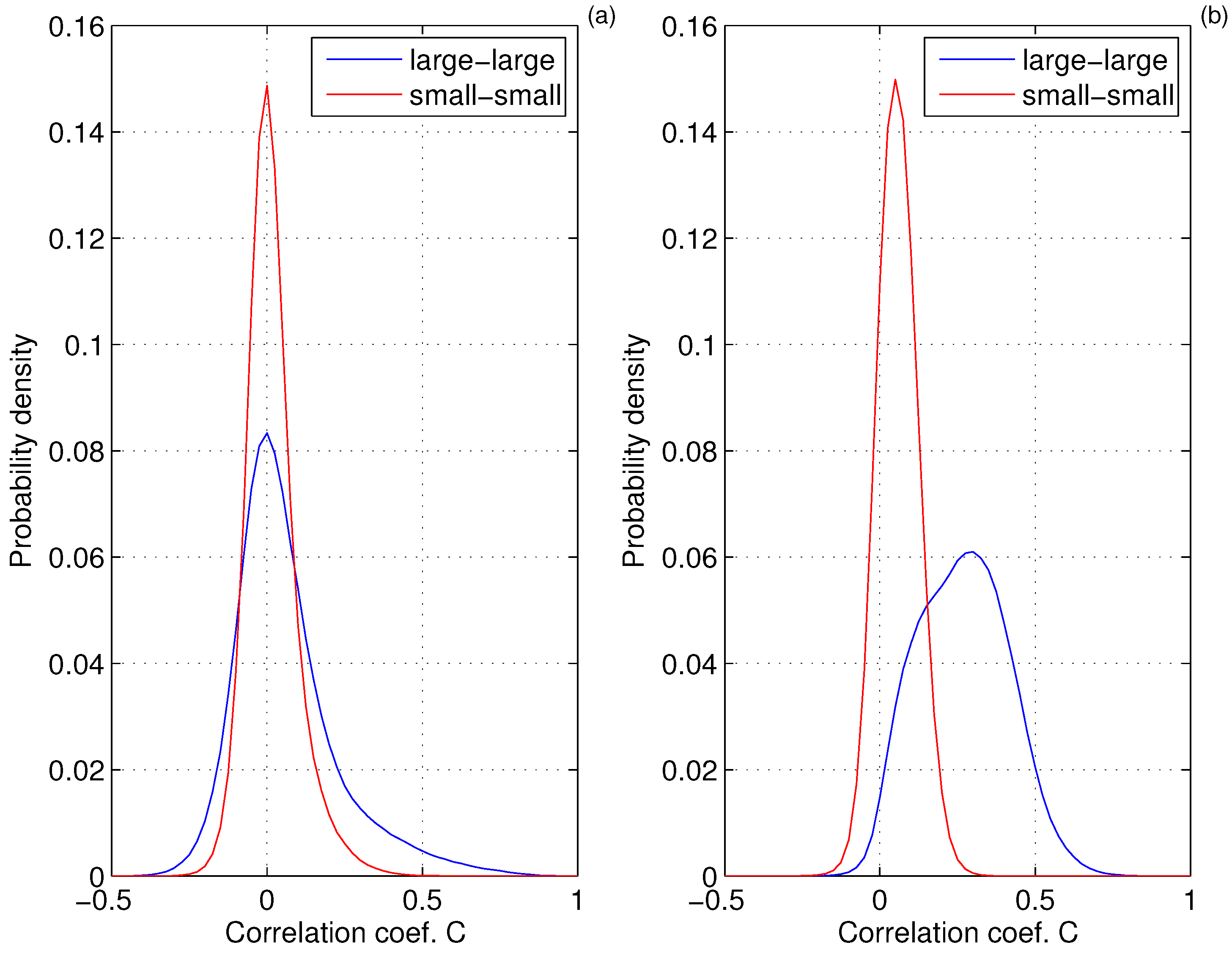
Figure 8b). To the contrary, the pdfs of
C of the smallest grains (in this case,
m) hardly change at the jamming transition, with most values of
C remaining at a very low, statistically insignificant level.
Figure 8.
pdfsof the correlation coefficient, C, between the velocity anomalies, , calculated for pairs of grains from a subset of the 10% largest (blue) and 10% smallest (red) grains in the whole ensemble. Results of simulations with m/s and (a), (b).
Figure 8.
pdfsof the correlation coefficient, C, between the velocity anomalies, , calculated for pairs of grains from a subset of the 10% largest (blue) and 10% smallest (red) grains in the whole ensemble. Results of simulations with m/s and (a), (b).
Thus, the increase of the packing fraction,
A, towards jamming is accompanied by the growth of clusters of coordinated motion of the relatively small subset of the largest grains (notably, the range of sizes of those grains is still very wide, between 6.5 and 180 m). It is worth noting that similar behavior has been described recently for sheared bidisperse granular systems, in which the dominant dynamical modes were associated with reorganization of grains within localized clusters [
10]. Similarly, Weeks and colleagues [
27] observed cooperative motion of particles within clusters in colloidal supercooled fluids, with the size of clusters rapidly increasing when the system approached the glass transition.
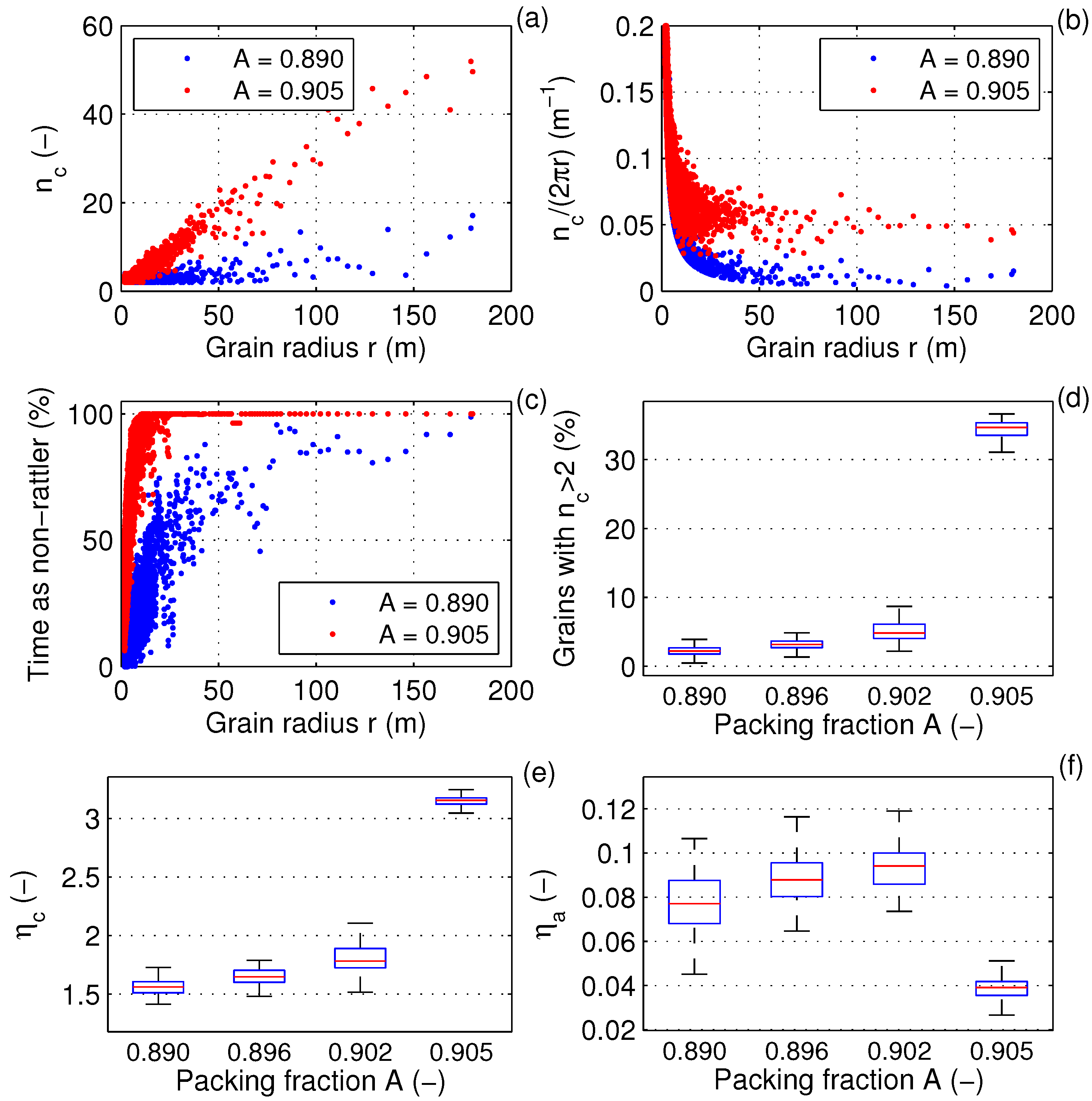
Figure 9.
Selected properties of the contact networks in the modeled system for a number of packing fractions,
A: number of contacts of individual non-rattler grains,
(
a);
scaled with grain perimeter
(
b); percentage of the simulation time when individual grains were non-rattler grains (
c); percentage of grains with at least three contacts (
d); average contact number
(
e); and contact-network anisotropy
(
f). In (
d–
f), the elements of the box symbols are the same as in
Figure 5; they reflect the time variability of the analyzed variables during the simulation.
Figure 9.
Selected properties of the contact networks in the modeled system for a number of packing fractions,
A: number of contacts of individual non-rattler grains,
(
a);
scaled with grain perimeter
(
b); percentage of the simulation time when individual grains were non-rattler grains (
c); percentage of grains with at least three contacts (
d); average contact number
(
e); and contact-network anisotropy
(
f). In (
d–
f), the elements of the box symbols are the same as in
Figure 5; they reflect the time variability of the analyzed variables during the simulation.
Due to obvious geometrical reasons, in strongly polydisperse materials, the number of contacts of individual grains strongly varies. Interestingly, the jamming transition (inferred from the size of the largest connected cluster) in the analyzed cases still takes place when the average contact number,
, exceeds the value of three (packing fraction
in
Figure 9e), similarly as in monodisperse and weakly polydisperse systems ([
8] and
Figure 10). For the large grains from the tail of the GSD, the contact number of individual grains,
, is an approximately linear function of their radius (and perimeter), with
in the jammed state (
Figure 9a,b), e.g.,
for
m. A linear relationship for
has been obtained recently by Shaebani and colleagues [
28] in simulations of 2D uniformly compressed, weakly polydisperse systems, in agreement with their mean-field solution. In our simulations, smaller grains often have just one or two neighbors (hence the points on the left side of
Figure 9b tend to lie on the
curve), and importantly, it is their incorporation into the system-wide contact network that leads to its consolidation at the jamming transition: whereas the largest grains are non-rattler grains most of the time, even in unjammed states, the smallest grains switch at jamming from predominantly freely moving to predominantly non-rattler (
Figure 9c; see also
Figure 2). Consequently, jamming is associated with a decrease of the mean radius of grains forming the main contact network (not shown). On the other hand, it is the largest grains that build the stable skeleton of the global contact and force network, in the sense that the great majority of grains, predominantly from the left part of the GSD, does not participate in its formation. Even in a jammed state, only
% of grains have three or more contacts (
Figure 9d), and even though
, the mean contact number for the 90% smaller grains (
i.e., excluding the 10% largest) is smaller than three. The “sparse” character of the grain-grain contacts is clearly seen in
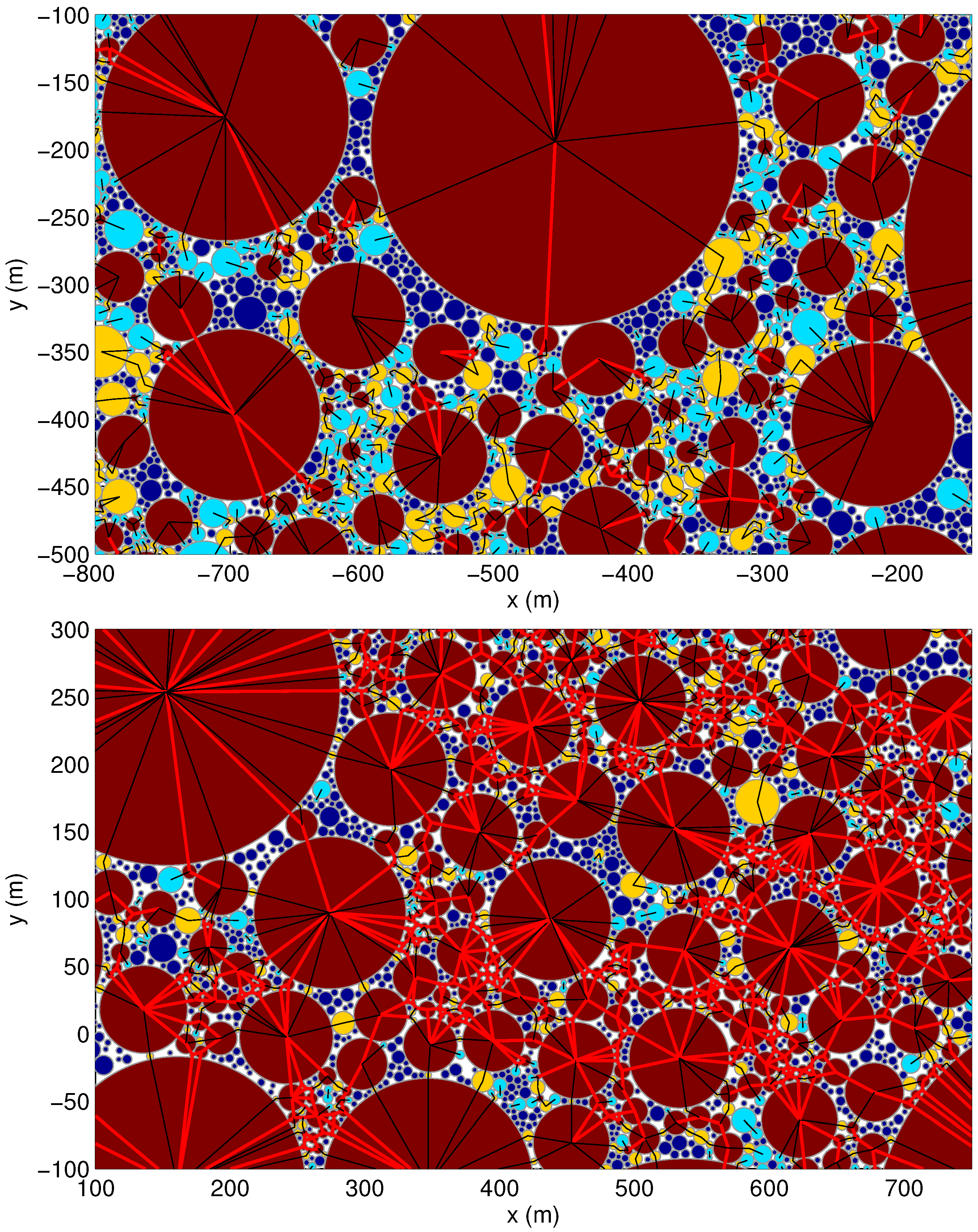
Figure 11. In the jammed state at
, the force network percolates the whole model domain (see also
Figure 2), but it has an “openwork” structure, with the largest grains incorporated into long force chains and irregular “cells”, surrounding unjammed regions, usually filled with very small grains. As already mentioned, the assemblies of the smallest grains act as a semi-plastic “filler”, adjusting its shape to the deforming cells of the main force network.
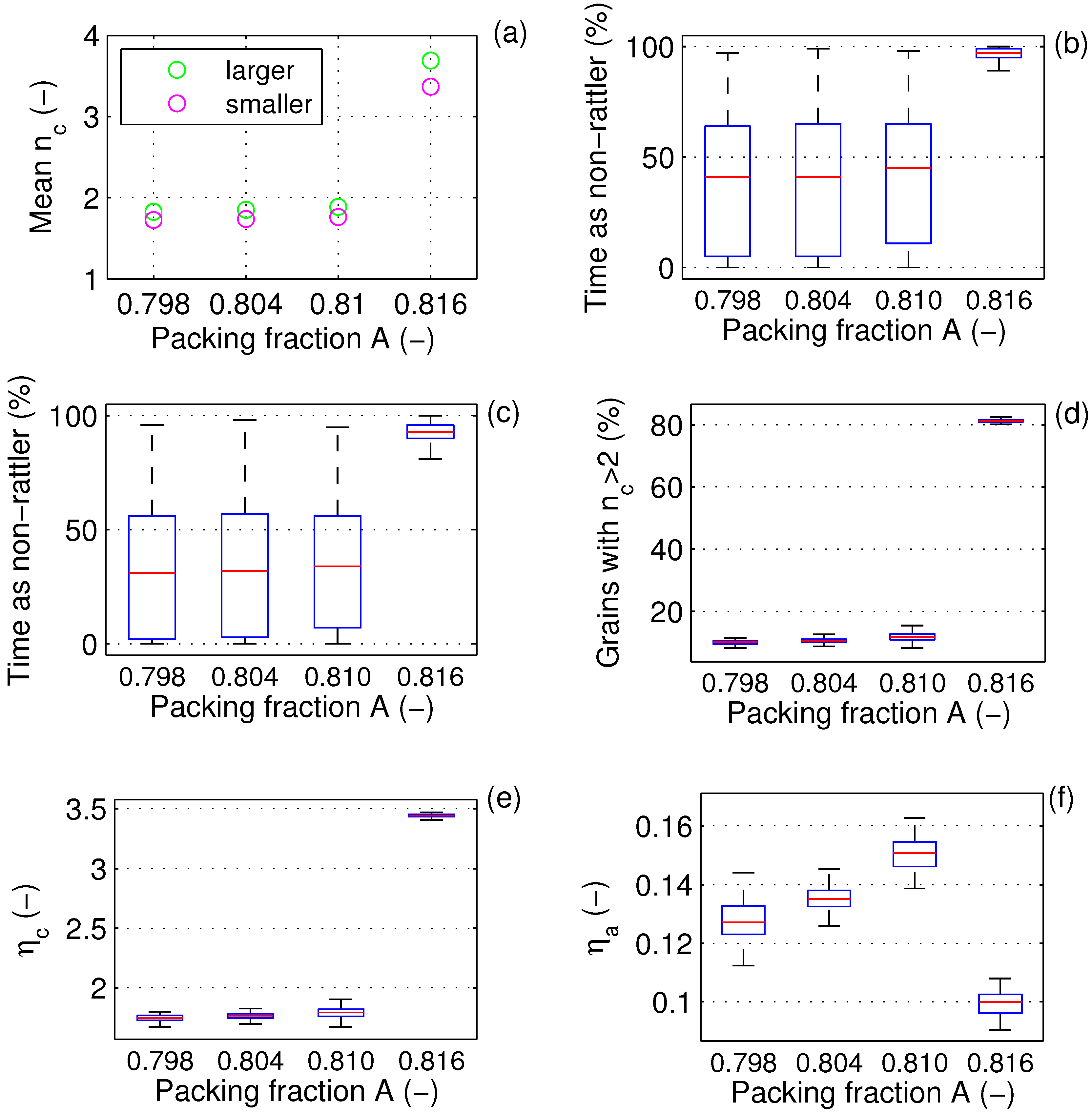
All those properties of the analyzed system are directly related to its extreme polydispersity. In the bidisperse reference case (
Figure 10), the jamming transition is much more rapid in terms of the amount of grains that are incorporated into the global contact network: as soon as
exceeds the value of three, roughly 80% of grains become non-rattler grains (
Figure 10d,e). Moreover, the coarser and finer fractions contribute similarly to the contact network (compare
Figure 10b,c), and the (very small) difference between the average number of neighbors of individual grains from the two fractions (
Figure 10a) results simply from the difference between their perimeters.
Back to the PL-GSD simulation, it is also worth noticing that although the contact numbers of the largest grains are high independent of the packing fraction (
Figure 9c and
Figure 11), in unjammed states, most of those contacts do not form part of stable force strains, but reflect individual collisions as they ‘fight their way’ among smaller neighbors (in
Figure 11 at
, most of the lines outgoing from the centers of the largest grains are black,
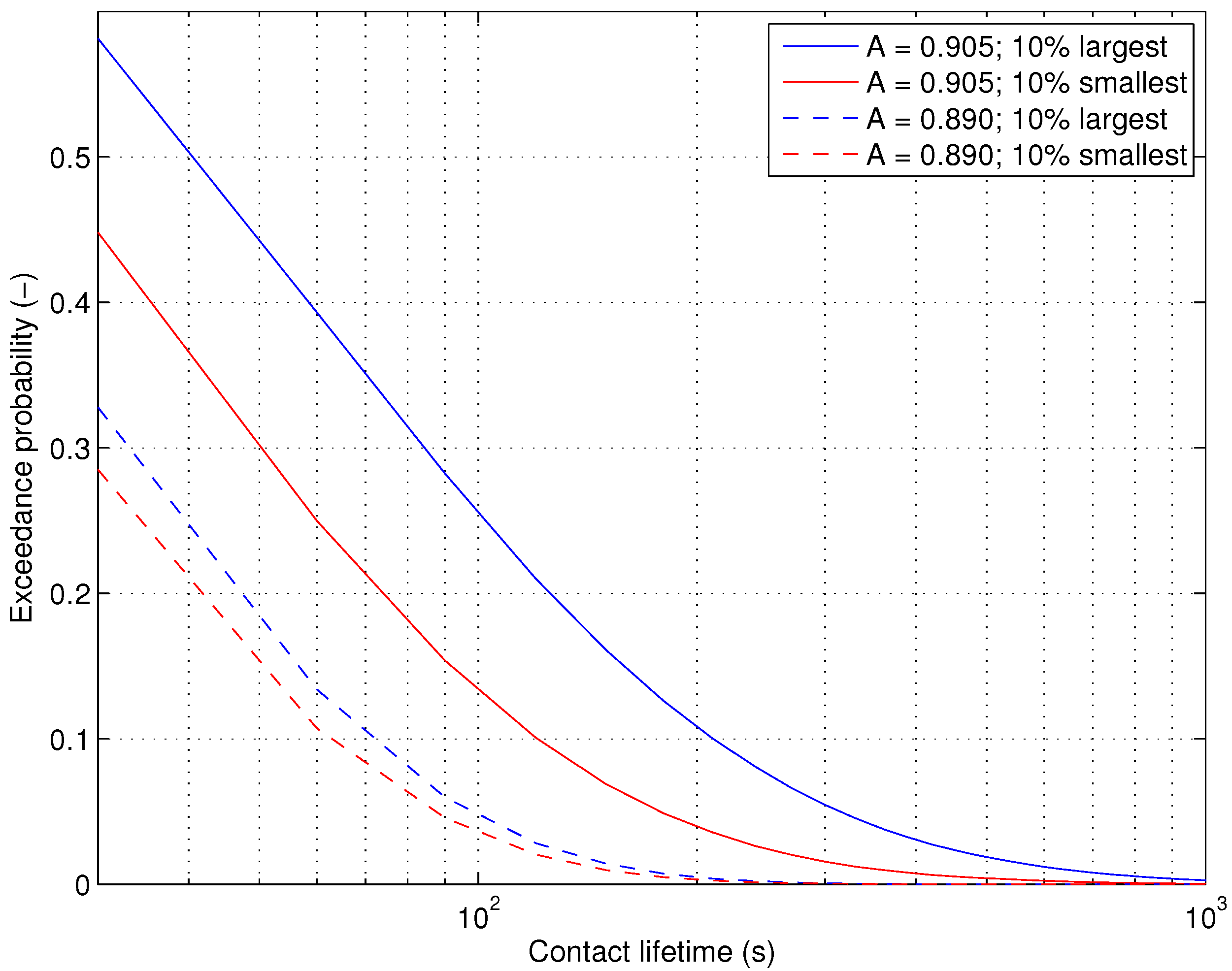
i.e., they lead to grains with a number of contacts lower than three). Such contacts rarely survive more than a few seconds. Indeed, the exceedance probability of contact lifetime is at low
A similar for all grain sizes (
Figure 12) and only ∼10% of contacts survive for longer than one minute, as compared to ∼25% and 40% of contacts between the smallest and largest grains, respectively, observed in the jammed state.
Moreover, it must be remembered that the condition,
, alone is not sufficient to stabilize the position of individual grains within the contact network. The arrangement of the contacts around the grain’s perimeter is important, as well. For a given grain,
i, this arrangement is determined by a set of vectors,
, for all
(see
Section 2.1), which divide the grain into
sectors. The central angle of the widest of those sectors (for brevity, we will call it the maximum contact angle,
) provides a useful measure of the above-mentioned stability of the
i-th grain within the force network. Obviously,
, possible only if
, is necessary for stability;
is possible only if
.
Figure 10.
Selected properties of the contact networks in the bidisperse (BD) model case for a number of packing fractions,
A: mean number of contacts of individual non-rattler grains,
, from the finer and coarser fractions (
a); percentage of the simulation time when individual grains from the finer (
b) and coarser (
c) fraction were non-rattler grains; percentage of grains with at least three contacts (
d); average contact number
(
e); and contact-network anisotropy
(
f). In (
b–
f), the elements of the box symbols are the same as in
Figure 5; they reflect the time variability of the analyzed variables during the simulation.
Figure 10.
Selected properties of the contact networks in the bidisperse (BD) model case for a number of packing fractions,
A: mean number of contacts of individual non-rattler grains,
, from the finer and coarser fractions (
a); percentage of the simulation time when individual grains from the finer (
b) and coarser (
c) fraction were non-rattler grains; percentage of grains with at least three contacts (
d); average contact number
(
e); and contact-network anisotropy
(
f). In (
b–
f), the elements of the box symbols are the same as in
Figure 5; they reflect the time variability of the analyzed variables during the simulation.
As can be seen in
Figure 11b, many non-rattler grains,
i.e., those with
, have
. In fact, ∼14% out of the ∼35% of grains building the percolated contact network (
i.e., ∼5% of the total) have
. For comparison, out of 82–83% of grains building the global network in the BD case, only ∼1% are unstable.
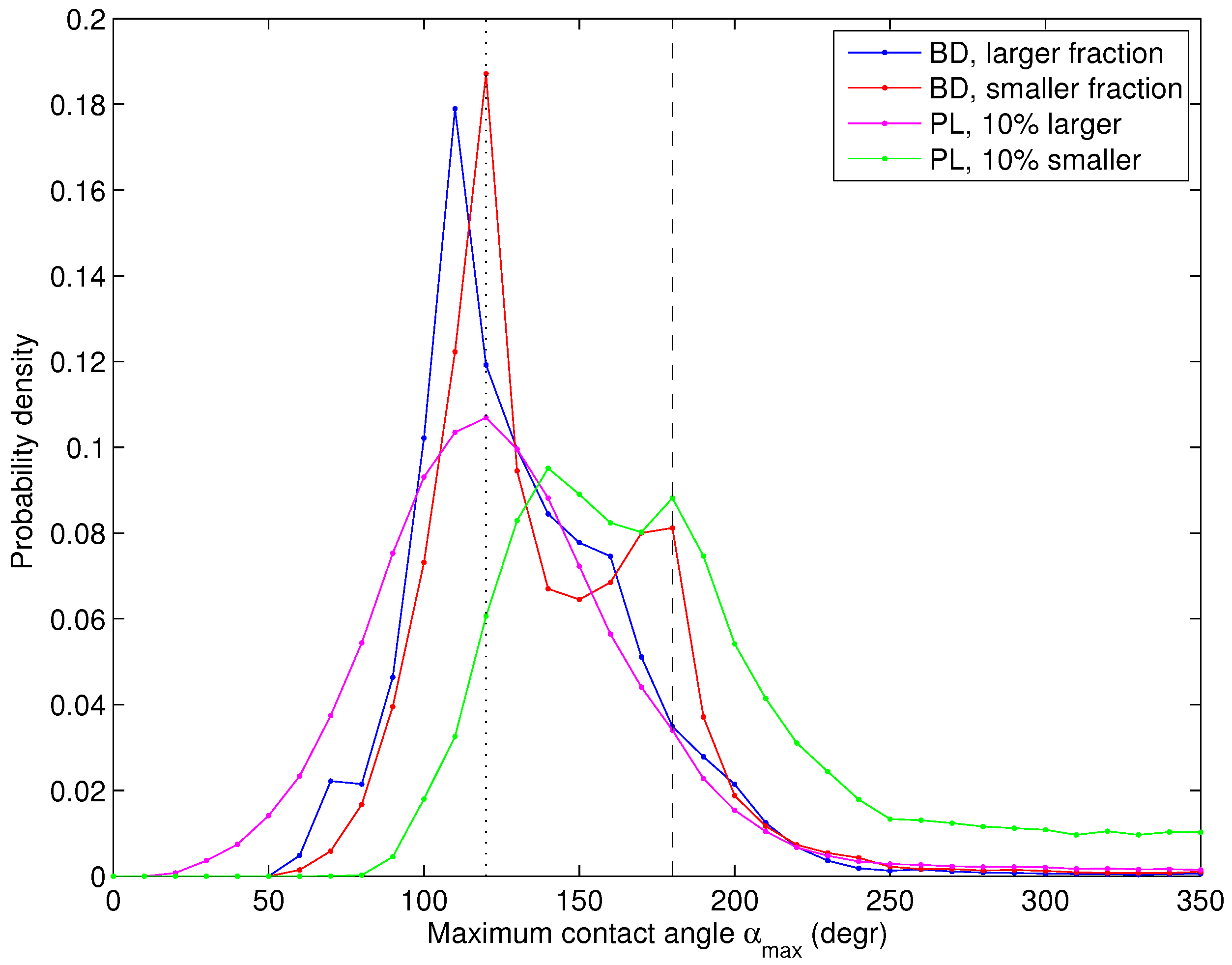
Figure 13 shows the pdfs of
for the PL and BD cases in shear-jammed states. In the BD simulations, the pdfs have high peaks close to the 120
value, indicating the prevailing—very stable—contact arrangement with
and roughly uniform distribution of neighbors around the grain’s perimeter. Notably, the pdfs for the coarser and finer fractions have very similar shapes, with an exception of a small second peak close to 180
for the finer fraction. To the contrary, in the PL simulations, the pdf of
of the smallest grains has a wide maximum shifted towards the unstable region and a long tail corresponding to individual, instantaneous collisions.
Figure 11.
Zoomed fragments of the modeled system (top:
; bottom:
) corresponding to the situations shown in
Figure 2. Color scale: number of contacts,
, of individual grains (dark blue: zero; light blue: one; yellow: two; brown: three or more). Red lines: forces between grains with
; black lines: the remaining forces.
Figure 11.
Zoomed fragments of the modeled system (top:
; bottom:
) corresponding to the situations shown in
Figure 2. Color scale: number of contacts,
, of individual grains (dark blue: zero; light blue: one; yellow: two; brown: three or more). Red lines: forces between grains with
; black lines: the remaining forces.
Finally, another very important property of force networks in sheared systems is their anisotropy,
. It has been identified as an order parameter for shear-jammed states, in that it is non-zero in such states and zero in isotropically jammed systems [
8]. The values of
obtained in this work, in the BD and, especially, PL simulations, are lower than those reported in [
8], which may be related to the details of the contact-model formulation. Characteristically, for the PL case, the
values are roughly 50% higher for the 10% largest grains than the ensemble mean (not shown), again underlying the special role of those grains in shaping the force network structure. The overall variability of
is, however, similar in both PL and BD simulations,
i.e., a rapid drop of
is observed at jamming, preceded by a slight increase when the jamming is approached from below (
Figure 9f and
Figure 10f). The strongest anisotropy was obtained in those model runs, in which the system underwent strong shifts between unjammed and jammed states (black curves in
Figure 3).
Figure 12.
Exceedance probability of the contact lifetime (in seconds) for two values of the packing fraction (, dashed lines; , continuous lines), calculated for contacts between the 10% largest (blue) and 10% smallest (red) grains.
Figure 12.
Exceedance probability of the contact lifetime (in seconds) for two values of the packing fraction (, dashed lines; , continuous lines), calculated for contacts between the 10% largest (blue) and 10% smallest (red) grains.
Figure 13.
pdfs of the maximum contact angle, , for two model runs: with bidisperse (BD; ) and power-law (PL; ) grain-size distribution. For the BD case, the pdfs are calculated separately for the coarser and finer grain fraction; for the PL case—for the subsets of 10% largest and 10% smallest grains. The vertical dotted and dashed lines mark the values and , respectively (see the text for a description).
Figure 13.
pdfs of the maximum contact angle, , for two model runs: with bidisperse (BD; ) and power-law (PL; ) grain-size distribution. For the BD case, the pdfs are calculated separately for the coarser and finer grain fraction; for the PL case—for the subsets of 10% largest and 10% smallest grains. The vertical dotted and dashed lines mark the values and , respectively (see the text for a description).