Elastic Properties of CaSiO3 Perovskite from ab initio Molecular Dynamics
Abstract
:1. Introduction
2. Method
3. Results
| Parameter | Value |
|---|---|
| V0 (Å3) | 45.58 a |
| KT0 (GPa) | 236 a |
| K’T0 | 3.9 a |
| αKT(V0,T) (GPa/K) | 0.0083(3) |
| (∂KT/∂T)V (GPa/K) | −0.0031(31) |
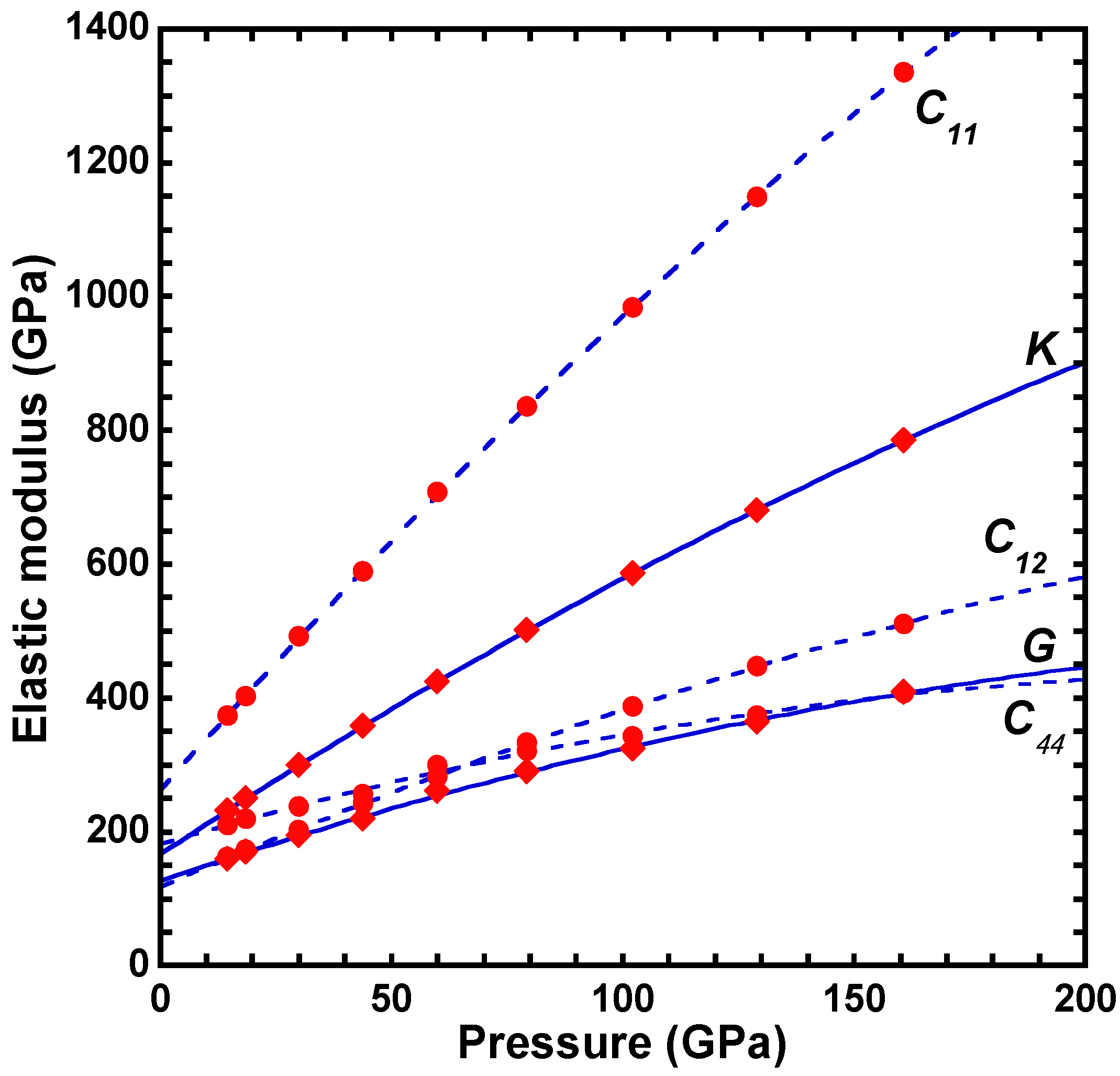
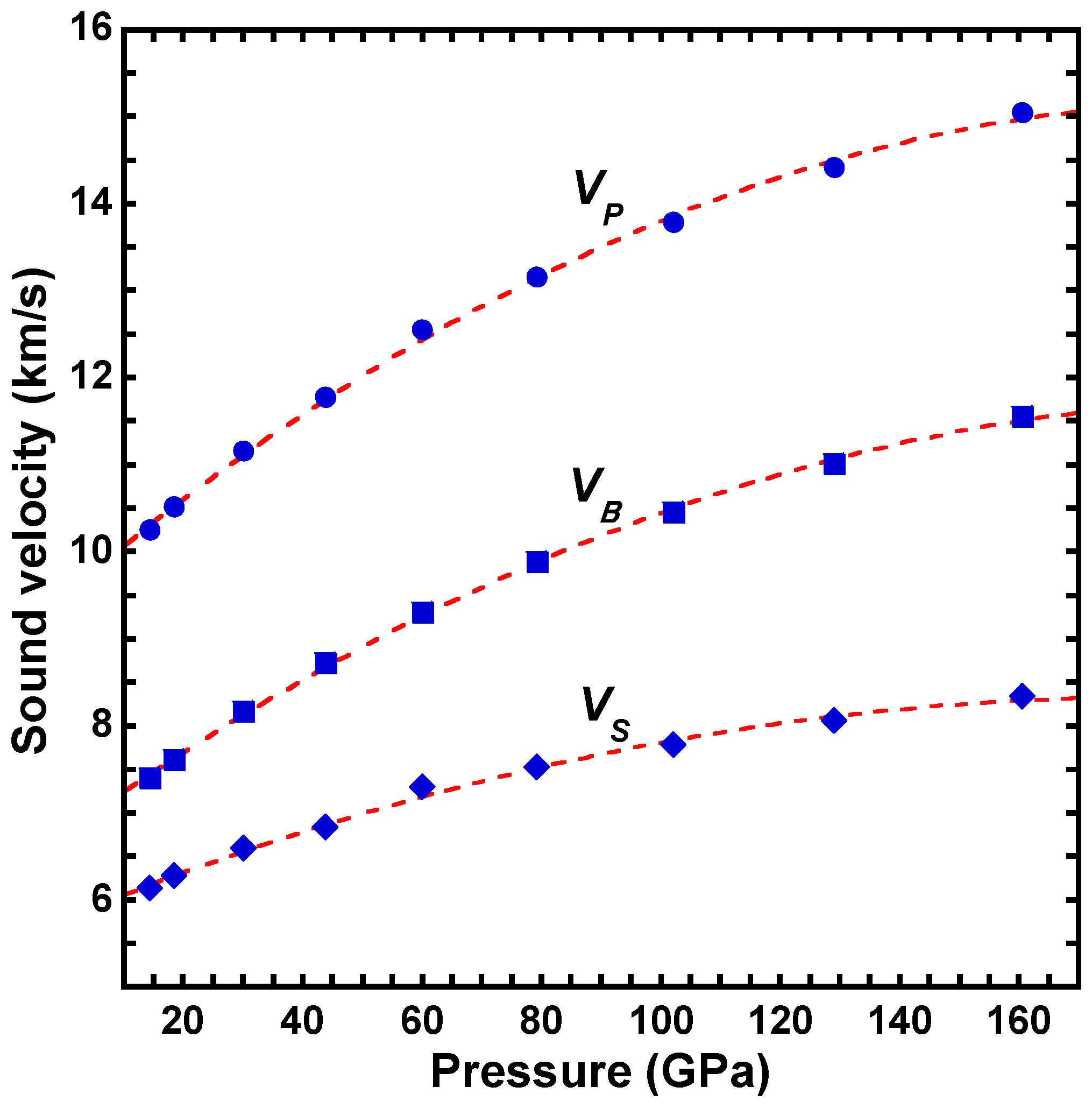
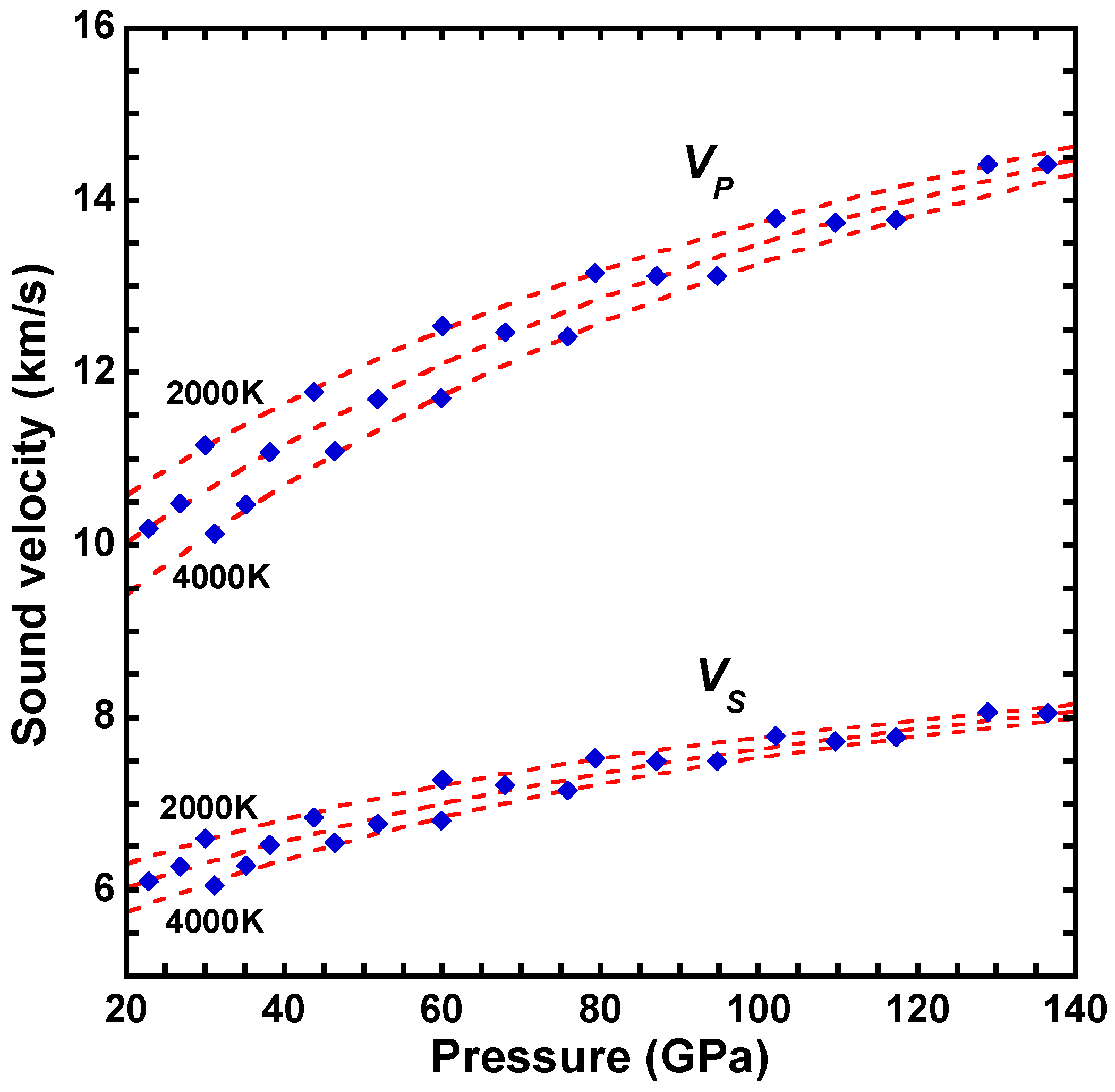
| a | b | c | d | |
|---|---|---|---|---|
| VP | 7.12(0.27) | −6.96(0.33) × 10−4 | 4.07(0.30) × 10−7 | 1.56(0.06) |
| VS | 4.65(0.15) | −3.20(0.02) × 10−4 | 1.75(0.17) × 10−6 | 0.74(0.04) |
4. Discussion
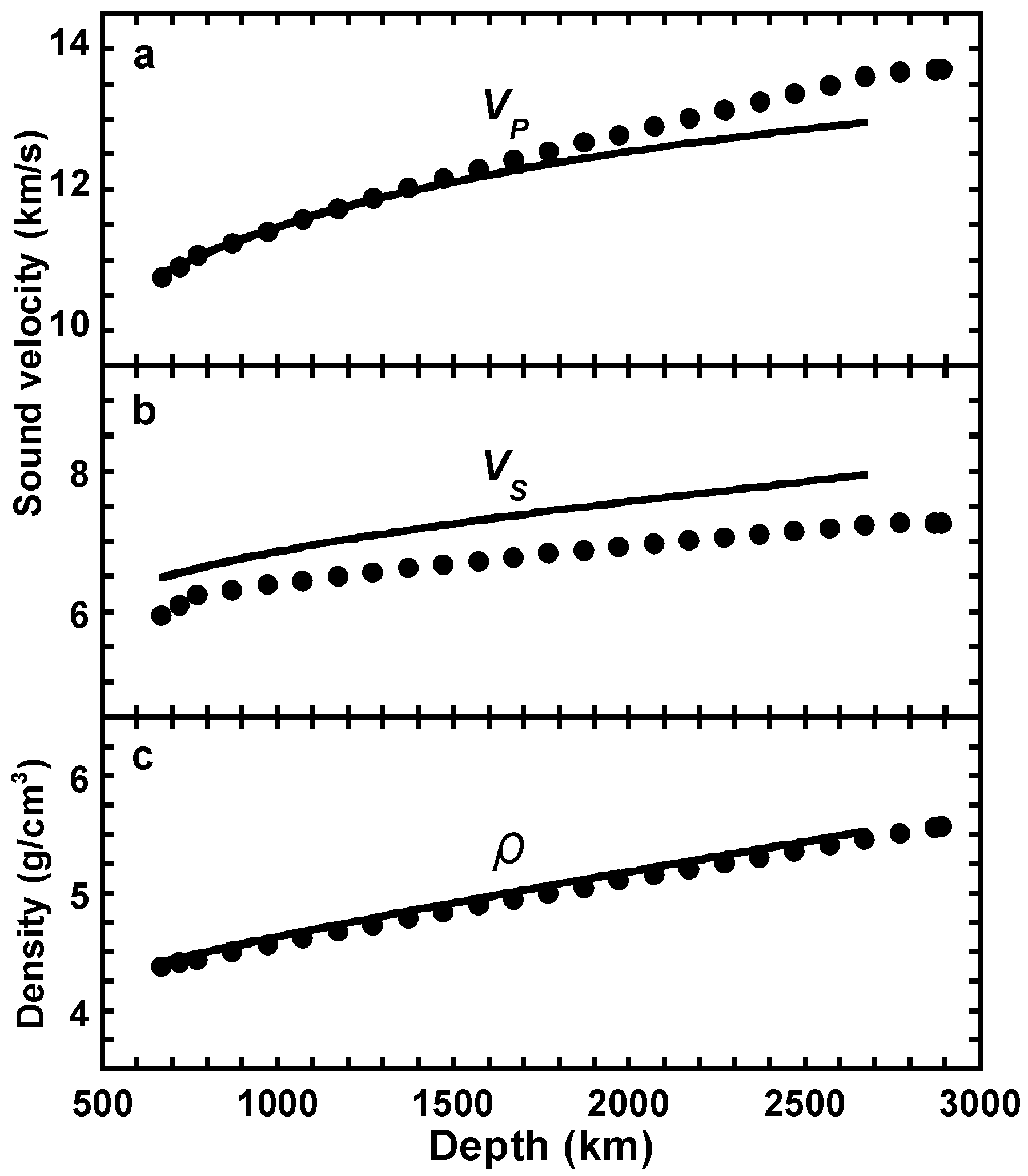
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Anderson, D.L. Composition of the Earth. Science 1989, 243, 367–370. [Google Scholar] [CrossRef] [PubMed]
- Irifune, T.; Ringwood, A.E. Phase Transitions in Primitive MORB and Pyrolite Compositions to 25 GPa and Some Geophysical Implications. In High-Pressure Research in Mineral Physics; Manghnanii, M.H., Syono, Y., Eds.; Terra Scientific Publishing Company, Tokyo/American Geophysical Union: Washington, DC, USA, 1987; pp. 231–242. [Google Scholar]
- Ono, S. Experimental constraints on the temperature profile in the lower mantle. Phys. Earth Planet. Inter. 2008, 170, 267–273. [Google Scholar] [CrossRef]
- Shim, S.H.; Jeanloz, R.; Duffy, T.S. Tetragonal structure of CaSiO3 perovskite above 20 GPa. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Ono, S.; Ohishi, Y.; Mibe, K. Phase transition of Ca-perovskite and stability of Al-bearing Mg-perovskite in the lower mantle. Am. Mineral. 2004, 89, 1480–1485. [Google Scholar]
- Caracas, R.; Wentzcovitch, R.; Price, G.D.; Brodholt, J. CaSiO3 perovskite at lower mantle pressures. Geophys. Res. Lett. 2005, 32, L06306. [Google Scholar] [CrossRef]
- Adams, D.J.; Oganov, A.R. Ab inito molecular dynamics study CaSiO3 perovskite at P-T conditions of Earth’s lower mantle. Phys. Rev. B 2006, 73, 184106. [Google Scholar] [CrossRef]
- Li, L.; Weidner, D.J.; Brodholt, J.; Alfè, D.; Price, G.D.; Caracas, R.; Wentzcovitch, R. Phase stability of CaSiO3 perovskite at high pressure and temperature: Insights from ab initio molecular dynamics. Phys. Earth Planet. Inter. 2006, 155, 260–268. [Google Scholar] [CrossRef]
- Karki, B.B.; Crain, J. First-principles determination of elastic properties of CaSiO3 perovskite at lower mantle pressures. Geophys. Res. Lett. 1998, 25, 2741–2744. [Google Scholar] [CrossRef]
- Stixrude, L.; Lithgow-Bertelloni, C.; Kiefer, B.; Fumagalli, P. Phase stability and shear softening in CaSiO3 perovskite at high pressure. Phys. Rev. B 2007, 75, 024108. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Ono, S.; Brodholt, J.P.; Alfè, D.; Alfredsson, M.; Price, G.D. Ab initio molecular dynamics simulations for thermal equation of state of B2-type NaCl. J. Appl. Phys. 2008, 86, 5801–5808. [Google Scholar] [CrossRef]
- Ono, S. First-principles molecular dynamics calculations of the equation of state for tantalum. Int. J. Mol. Sci. 2009, 10, 4342–4351. [Google Scholar] [CrossRef] [PubMed]
- Ono, S. Synergy Between First-Principles Computation and Experiment in Study of Earth Science. In Some Applications of Quantum Mechanics; Pahlavani, M.R., Ed.; InTech: Vienna, Austria, 2012; pp. 91–108. [Google Scholar]
- Mehl, M.J.; Osburn, J.E.; Papaconstantopoulos, D.A.; Klein, B.M. Structural properties of ordered high-melting-temperature intermetallic alloys from first-principles total-energy calculations. Phys. Rev. B 1990, 41, 10311–10323. [Google Scholar] [CrossRef]
- Shim, S.H.; Duffy, T.S. The stability and P-V-T equation of state of CaSiO3 perovskite in the Earth’s lower mantle. J. Geophys. Res. 2000, 105, 25955–25968. [Google Scholar] [CrossRef]
- Poirier, J.P. Introduction to the Physics of the Earth’s Interior; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Anderson, O.L. Equations of State of Solids for Geophysics and Ceramic Science; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Karki, B.B.; Stixrude, L. Seismic velocities of major silicate and oxide phases of the lower mantle. J. Geophys. Res. 1999, 104, 13025–13033. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ono, S. Elastic Properties of CaSiO3 Perovskite from ab initio Molecular Dynamics. Entropy 2013, 15, 4300-4309. https://doi.org/10.3390/e15104300
Ono S. Elastic Properties of CaSiO3 Perovskite from ab initio Molecular Dynamics. Entropy. 2013; 15(10):4300-4309. https://doi.org/10.3390/e15104300
Chicago/Turabian StyleOno, Shigeaki. 2013. "Elastic Properties of CaSiO3 Perovskite from ab initio Molecular Dynamics" Entropy 15, no. 10: 4300-4309. https://doi.org/10.3390/e15104300
APA StyleOno, S. (2013). Elastic Properties of CaSiO3 Perovskite from ab initio Molecular Dynamics. Entropy, 15(10), 4300-4309. https://doi.org/10.3390/e15104300




