Evaluating the Spectrum of Unlocked Injection Frequency Dividers in Pulling Mode
Abstract
:1. Introduction
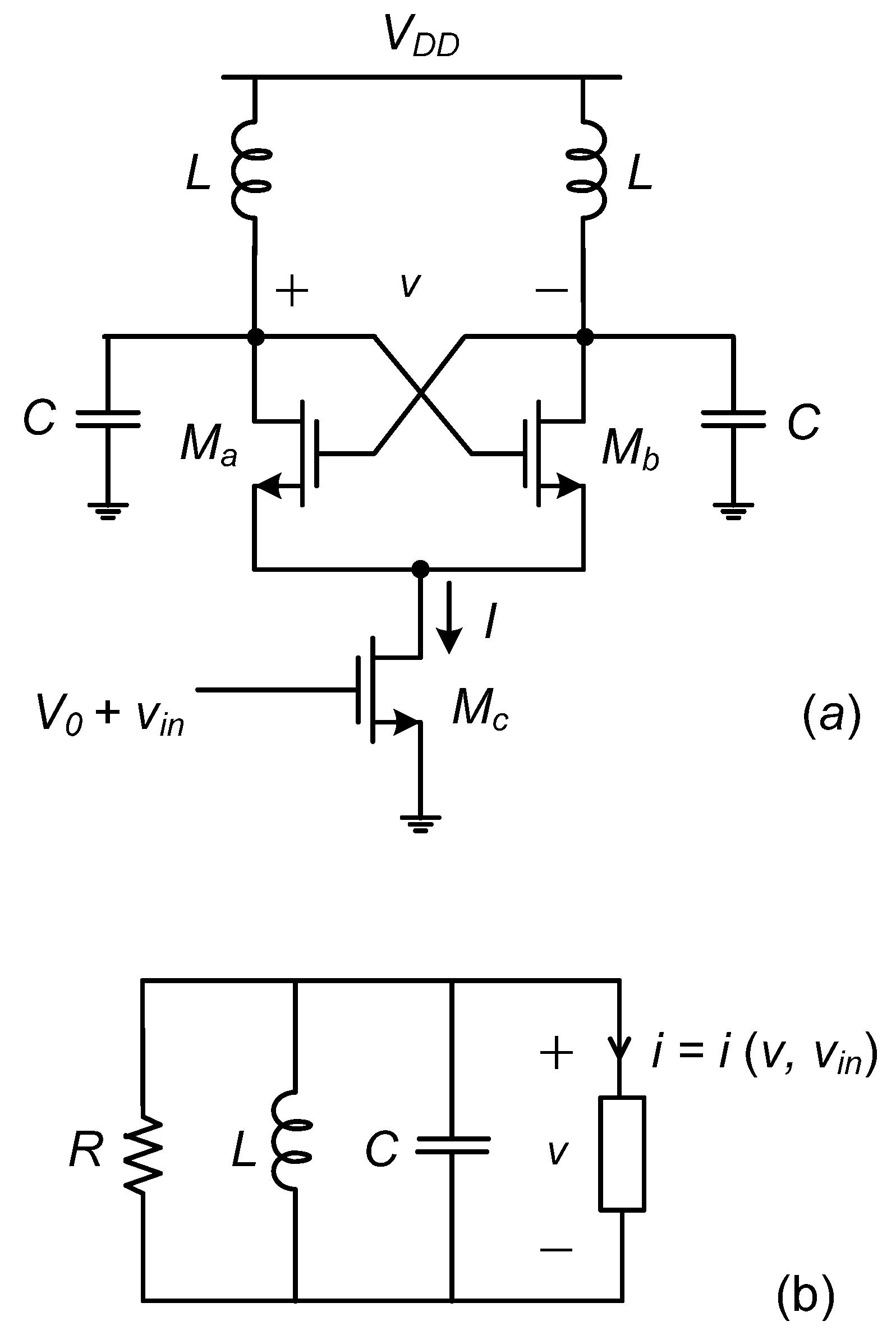
2. Nonlinear Model of Injection-Locked LC Frequency Dividers
3. Analytical Treatment of Periodic Pulling
3.1. Phase Modulation and Spectrum
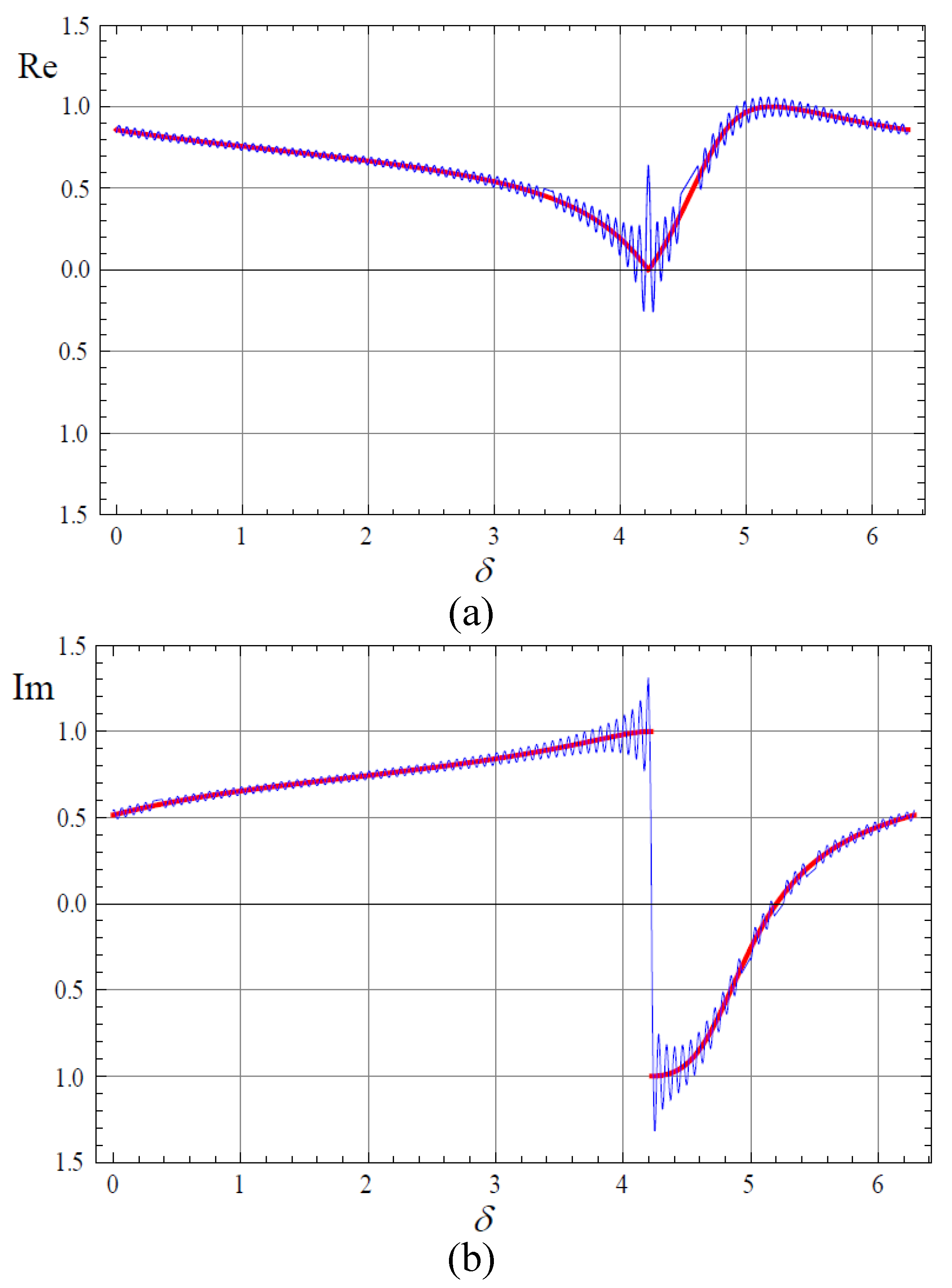
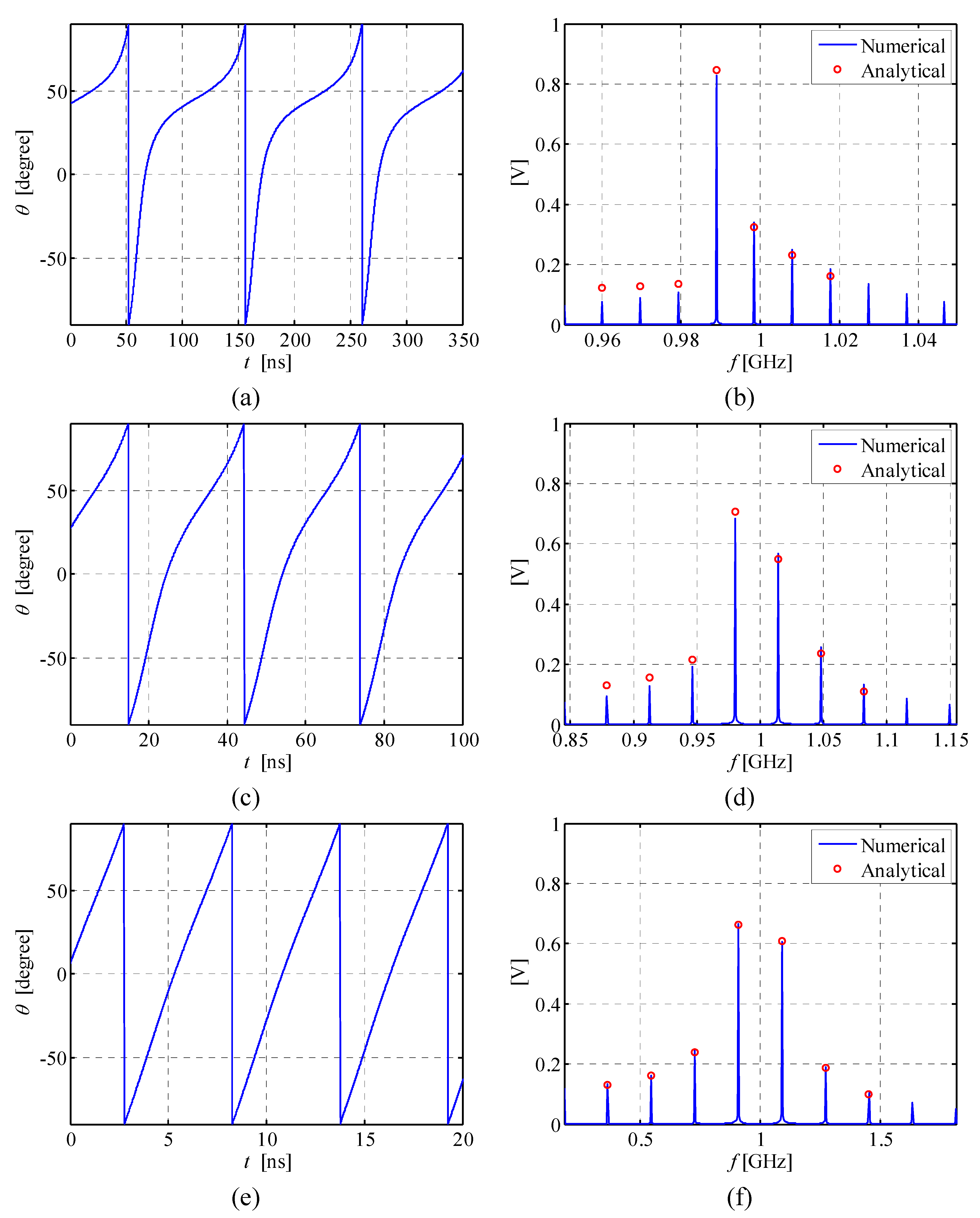
3.2. Amplitude Modulation and Spectrum
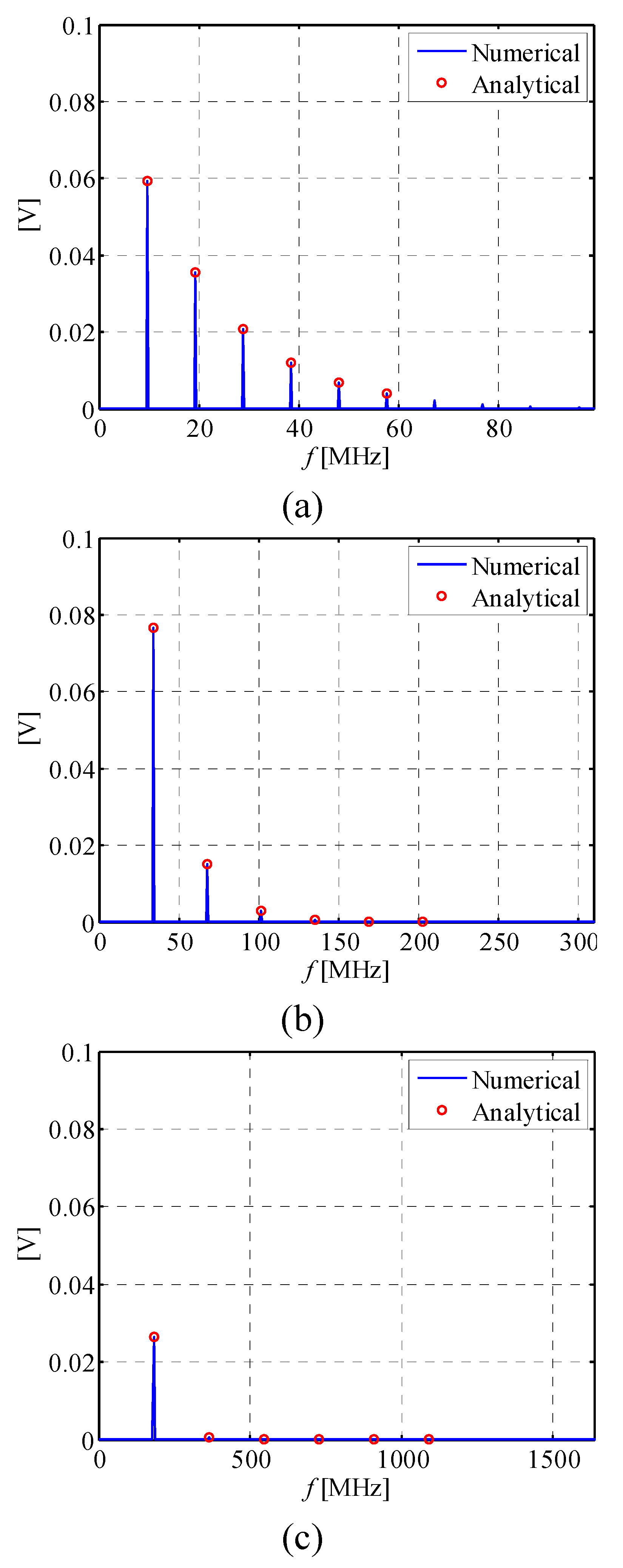
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Hayashi, C. Nonlinear Oscillations in Physical Systems; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Minorsky, N. Introduction to Non-Linear Mechanics; Edwards Brothers Inc.: Ann Arbor, MI, USA, 1947. [Google Scholar]
- Balanov, A.; Janson, N.; Postnov, D.; Sosnovtseva, O. Synchronization: From Simple to Complex; Springer-Verlag: Berlin/Heidelberg, Gemany, 2009. [Google Scholar]
- Khokhlov, R.V. A method of analysis in the theory of sinusoidal self-oscillations. IRE Trans. Circuit Theory 1960, 7, 398–413. [Google Scholar] [CrossRef]
- Schmackers, J.; Mathis, W. Entrainment of driven oscillators and the dynamic behavior of PLL’s. In Proceedings of the 2005 International Symposium on Nonlinear Theory and its Applications (NOLTA2005), Bruges, Belgium, 18–21 October 2005; pp. 521–524.
- Rjasin, P. Einstellungs-und Schwebungsprozesse bei der Mitnahme (Tuning or beat phenomena in entrainment). J. Tech. Phys. USSR 1935, 5, 195–214. (in Russian). [Google Scholar]
- Adler, R. A study of locking phenomena in oscillators. Proc. IRE Waves Electrons 1946, 34, 351–357. [Google Scholar] [CrossRef]
- Stover, H.L. Theoretical explanation of the output spectra of unlocked driven oscillators. Proc. IEEE 1966, 54, 310–311. [Google Scholar] [CrossRef]
- Armand, M. On the output spectrum of unlocked driven oscillators. Proc. IEEE 1969, 59, 798–799. [Google Scholar] [CrossRef]
- Kurokawa, K. Injection locking of microwave solid-state oscillators. Proc. IEEE 1973, 61, 1386–1410. [Google Scholar] [CrossRef]
- Koepke, M.E.; Hartley, D.M. Experimental verification of periodic pulling in a nonlinear electronic oscillator. Phys. Rev. A 1991, 44, 6877–6887. [Google Scholar] [CrossRef] [PubMed]
- Rohde, A.; Piel, A.; Klostermann, H. Simulation of the nonlinear dynamics of grid sheath oscillations in double plasma devices. Phys. Plasmas 1997, 4, 3933–3942. [Google Scholar] [CrossRef]
- Mettin, R.; Parlitz, U.; Lauterborn, W. Bifurcation structure of the driven van der Pol oscillator. Int. J. Bifurcat. Chaos 1993, 3, 1529–1555. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Hoffman, K.; Weckesser, W. The forced van der Pol equation I: The slow flow and its bifurcations. SIAM J. Appl.Dyn. Syst. 2003, 1, 1–35. [Google Scholar] [CrossRef]
- Shilnikov, A.; Shilnikov, L.; Turaev, D. On some mathematical topics in classical synchronization. A tutorial. Int. J. of Bifurcat. Chaos 2003, 14, 2143–2160. [Google Scholar] [CrossRef]
- Adler, R.L.; Konheim, A.G.; McAndrew, M.H. Topological entropy. Trans. Amer. Math. Soc. 1965, 114, 61–85. [Google Scholar] [CrossRef]
- Caneco, A.; Rocha, J.L.; Gracio, C. Topological entropy in the synchronization of piecewise linear and monotone maps. Coupled Duffing oscillators. Int. J. of Bifurcat. Chaos 2009, 11, 3855–3868. [Google Scholar] [CrossRef]
- Razavi, B. A study of injection pulling and locking in oscillators. IEEE J. Solid-State Circuits 2004, 39, 1415–1424. [Google Scholar] [CrossRef]
- Heidari, M.E.; Abidi, A.A. Behavioral models of frequency pulling in oscillator. In Proceedings of the IEEE International Behavioral Modeling and Simulation Workshop (BMAS 2007), San José, CA, USA, September, 2007; pp. 100–104.
- Maffezzoni, P.; D’Amore, D. Evaluating pulling effects in oscillators due to small-signal injection. IEEE Trans. Comput.-Aided Design Integr. Circuits Syst. 2009, 28, 22–31. [Google Scholar] [CrossRef]
- Ali, I.; Banerjee, A.; Mukherjee, A.; Biswas, B.N. Study of injection locking with amplitude perturbation and its effect on pulling of oscillator. IEEE Trans. Circuits Syst., I. Reg. Papers 2012, 59, 137–147. [Google Scholar] [CrossRef]
- Buonomo, A.; Lo Schiavo, A. Analytical approach to the study of injection-locked frequency dividers. IEEE Trans. Circuits Syst., I: Reg. Papers 2013, 60, 51–62. [Google Scholar] [CrossRef]
- Buonomo, A.; Lo Schiavo, A. A deep investigation of the synchronization mechanisms in LC-CMOS frequency dividers. IEEE Trans. Circuits Syst., I: Reg. Papers 2013. [Google Scholar] [CrossRef]
- Buonomo, A.; Lo Schiavo, A. Locking and pulling in injection-locked LC-CMOS dividers. J. Low Power Electron. 2013, 9, 221–228. [Google Scholar] [CrossRef]
- Bogolyubov, N.N.; Mitropol’skii, Y.A. Asymptotic Methods in the Theory of Non-Linear Oscillations; Gordon and Breach Publ., Inc.: New York, NY, USA, 1961. [Google Scholar]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Buonomo, A.; Kennedy, M.P.; Lo Schiavo, A. On the synchronization condition for superharmonic coupled QVCOs. IEEE Trans. Circuits Syst., I: Reg. Papers 2011, 58, 1637–1646. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Buonomo, A.; Lo Schiavo, A. Evaluating the Spectrum of Unlocked Injection Frequency Dividers in Pulling Mode. Entropy 2013, 15, 4026-4041. https://doi.org/10.3390/e15104026
Buonomo A, Lo Schiavo A. Evaluating the Spectrum of Unlocked Injection Frequency Dividers in Pulling Mode. Entropy. 2013; 15(10):4026-4041. https://doi.org/10.3390/e15104026
Chicago/Turabian StyleBuonomo, Antonio, and Alessandro Lo Schiavo. 2013. "Evaluating the Spectrum of Unlocked Injection Frequency Dividers in Pulling Mode" Entropy 15, no. 10: 4026-4041. https://doi.org/10.3390/e15104026
APA StyleBuonomo, A., & Lo Schiavo, A. (2013). Evaluating the Spectrum of Unlocked Injection Frequency Dividers in Pulling Mode. Entropy, 15(10), 4026-4041. https://doi.org/10.3390/e15104026



