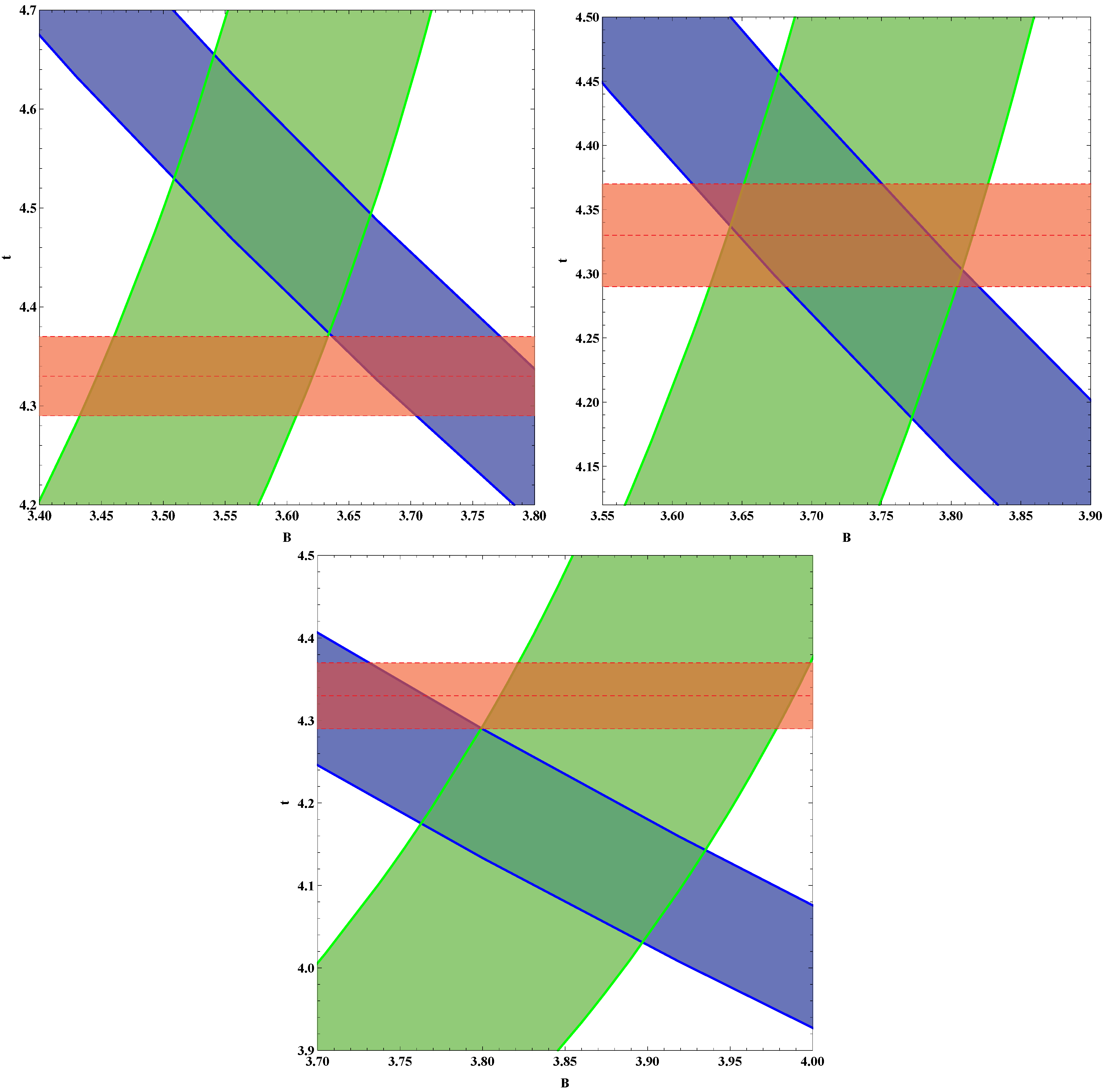1. Introduction
The recent astronomical measurements revealed that the current Universe is accelerating [
1,
2]. It is believed that the acceleration is caused by an unknown energy,
i.e., dark energy, and grasping the identity of dark energy is one of most fundamental problems in the modern cosmology [
3]. Many theoretical models for dark energy have been proposed ever since. Among them, the standard approach is to introduce a cosmological constant [
4,
5,
6,
7,
8,
9]. In spite of its simplicity and theoretical diversities, it confronts the extreme fine tuning problem. An attractive alternative is to consider that the acceleration is driven by a scalar field. The well known models include quintessence [
10,
11] phantom [
12], k-essence [
13,
14,
15] with the non-canonical kinetic term for the scalar field, and quintom [
16] models. In these models various aspects of dark energy can be well described in terms of dynamics of the scalar field and especially, the smallness of the cosmological constant is attributed to the decaying scalar energy density [
17].
On the other hand, dark matter plays a central role in the early Universe in the process of structure formation [
3]. Most of the dark matter is the cold dark matter (CDM) which is non-relativistic and non-baryonic. In particular, the CDM model with the cosmological constant Λ is established as a standard cosmological model, Λ-CDM [
3]. This model is in good agreements with the CMBR data [
18,
19,
20] as well as SN Ia data [
1,
2]. The special feature of Λ-CDM model is that it assumes the Universe with a zero spatial curvature.
Recently, the dark energy model based on a nonlinear sigma model [
21] with or without a cosmological constant was investigated. In this model the target space is noncompact four-dimensional de Sitter manifold and four scalar fields are introduced to account for this. It was found that an exponentially accelerating solution is possible even without the cosmological constant and that the model could describe dark energy interacting with stiff matter even without any matter present. The possibility of other kind of dark matter should be also addressed and it motivates to extend to the more general situation where matter is introduced separately. Therefore, in this paper, we consider more general case of the de Sitter nonlinear sigma model where the matter with the equation of state
and also an exponential potential term for the nonlinear sigma model are added to the action, and we investigate the cosmological consequences.
Recall that in spite of the dynamical explanation of the smallness of the current dark energy density contrary to the cosmological constant, the approaches of [
10,
11,
12,
13,
14,
15] have their own shortcomings. For quintessence model, it has the nice properties of tracking solution and scaling behavior, but it is somewhat difficult to match the equation of state to be close to
, and has its own fine-tuning problem [
22]. The phantom model gives favorable result with the equation of state, but it has the issue of quantum instability, even though it is classically stable. The k-essence model has the ghost problem coming from the higher derivative nature of the theory. We do not attempt to address these difficult issues with the introduction of the four scalar fields, but one advantage is the existence of the exact solution, which makes comparisons with Λ-CDM more direct. ( See Equations (
11) and (44).)
Let us mention other salient features of our investigation. The field content consists of a phantom and the triplet fields which are canonical scalar fields. Unlike the ordinary phantom model where Big Rip singularity is known to exist, we have an explicit solution which does not show such a behavior. As far as the exact cosmic solution is concerned, the potential is of a negative exponential form of the scalar field ϕ. This solution prolongs from the matter-dominated epoch to the dark energy epoch. Recall that in the pure phantom model, the negative kinetic energy prohibits the potential to assume a negative value. In our approach, the triplet of scalar fields provides enough compensating positive energy density such that the weak energy condition is not violated. This exact solution can be exploited to extract some numerical values that can be compared with current observations. In particular, we calculate the age of the Universe and compare with the observations. We find that with a fine-tuning of a couple of parameters, is consistent with the observation. This matter corresponds to an exotic cosmological fluid.
The paper is organized as follows. In Section II, we present a basic analysis of -CDM model paying attention to the exact cosmological solution and its stability analysis. In Section III, we consider the Einstein gravity coupled with the de Sitter nonlinear sigma model including an exponential potential and cosmological fluid with the equation of state , and discuss the cosmological evolution equations. In Section IV, the stability analysis is performed and various critical points are identified. In Section V, we present the exact cosmological solution for a negative exponential potential and calculate the current age of the Universe. We compare it with the observational data and -CDM model. Section VI includes conclusion and discussion.
2. ΛCDM Model
Let us first consider an action in which the Einstein gravity has a cosmological constant (c.c.) term with a matter term:
where
. Introducing the standard space-time metric via
leads to the following equations:
In these expressions,
is the equation of state parameter for the matter term, which satisfies
when
are assumed.
In order to check the stability, we introduce the following dimensionless quantities (for
)
From the above quantities, one obtains
and
as (
)
The critical points,
i.e., the solutions corresponding to
and the eigenvalues for the critical points [
23] are given by
From these eigenvalues we see that the matter dominant phase is unstable for
while c.c. dominant phase has a decaying mode,
i.e.,
being stable. (The existence of a zero eigenvalue (
) in Equation (
9) is originated from the fact that two variables
x and
y are connected by the relation
. Therefore in this case one can reduce to one−dimensional space [
24].) It is well-known that there exists the non-perturbative solution of Equations (
3)–(5) which connects these two critical points as
where
. This solution describes a smooth transition from matter-dominated power law expansion at early times into cosmological constant-dominated exponential acceleration at late times.
To check the stability of the above solutions Equation (
11), we consider the variation of Equations (
3)–(5), which yields
Then we find the solution for the above Equations (
12)–(14) as
where
,
C is an arbitrary constant and
. Note that
approaches
as
and both
and
decay, which implies that the solution (
11) is stable.
Introducing the dimensionless density parameters
and
, Equation (
3) becomes
Particularly for the solution (
11),
and
are given by
By using the experimental data,
i.e.,
,
and the solution
, we can evaluate the value
. From these values we find
and
for the dust-like matter (
) as
which are in agreement with the observational data [
25].
3. de Sitter Nonlinear Sigma Model with Potential
In this section, we extend the analysis performed in the case of
-CDM to the de Sitter nonlinear sigma model [
21] with a potential term. The cosmological fluid with the equation of state
is also added. The starting action is
where
,
λ is a dimensionless coupling constant and
. Here
is the metric of the de Sitter target space,
where
ξ is an arbitrary positive constant and
is the potential given by
with an arbitrary constant
γ and
. Among diverse possibilities, we have chosen exponential potential. A couple of reasons could be cited. The first one is that this potential is the prototype which gives rise to accelerating Universe and has interesting properties like scaling solution and attractor in the quintessence [
26] or phantom model [
23]. The second one is that it can yield non-perturbative solution of the type discussed in the previous section in our case for the negative potential with
. We regard the second and third terms of Equation (
19) as representing the dark energy sector. For the matter part, we assume a cosmological fluid of the perfect fluid form,
, which satisfies the continuity equation,
We first note that the following ansatz
solves the
field equations. The above ansatz first appeared in higher dimensional gravity theory in association with spontaneous compactification of the extra dimensions [
27,
28,
29,
30]. It was revived in four dimensions recently in describing the accelerating Universe with the de Sitter nonlinear sigma model [
21]. Note that it does not break the isotropy and homogeneity of the universe as long as we do not introduce the potential for the
σ fields. With this ansatz, the standard space-time metric Equation (
2), and
, the evolution equations, are given by
and the continuity equation implies
where
is a barotropic equation of state with
. We mention a couple of properties of the above evolution equations. The first one is that in spite of the
ϕ being a phantom, the presence of the second term in Equation (24) that comes from the spatial variations of
fields could prevent the Big Rip singularity from being developed; it is not guaranteed that
will stay always positive at late times when
is ignored. The other is that even in the
case, the weak energy condition could not be violated (in the ordinary phantom model with a negative potential, the weak energy condition is always violated because of
). This again is due to the the second terms in Equations (
23) and (24) coming from the spatial variations. In fact, we will show that for
there exists an exact cosmological solution of the type discussed in
-CDM case, which interpolates between matter-dominated and dark energy-dominated epochs.
4. Stability
To perform the stability analysis and figure out the energy dominance of the kinetic (
x), spatial (
y) and potential (
z) parts in Equation (
23), we first introduce the following dimensionless quantities,
Then the constraint Equation (
23) is given by
With
, we obtain
where
. The various critical points and their properties including the stabilities of the above equations are summarized in
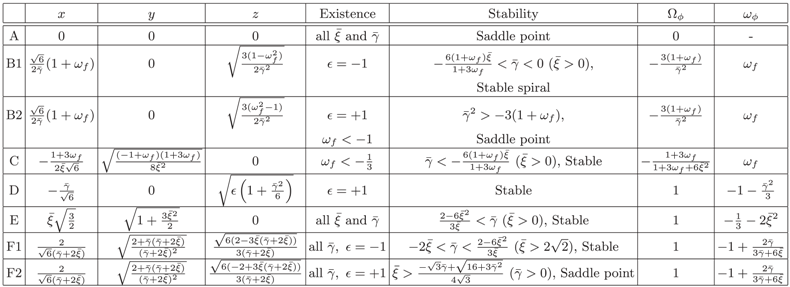
Table 1 with their eigenvalues being given as follows:
Note that all of the above eigenvalues of the critical points do not have any
ϵ-dependence even though the various critical points themselves carry its dependence.
Table 1.
The classification and the properties of the critical points.
Table 1.
The classification and the properties of the critical points.
In
Table 1, the second to fourth columns denote energy contents of the dark energy sector, the fifth column shows the conditions for the existence of the solutions of the critical Equations (
28)–(30). The critical points B and F are further divided for
. The sixth column is about the stability condition for each eigenvalue. In the seventh column,
is the density parameter for the dark energy, and the last column displays the equation of state for the dark energy. First, we note that the results of phases A, B2, D with
and
agree with those in the literature [
23], which correspond to the phantom with a positive potential. In particular, the system approaches the scalar-dominated solution D with non-relativistic dark matter
. The point F2 also corresponds to scalar-dominated solution but with a non-zero value of
y.
Let us focus on the
case from here on. Then, points E and F1 both give scalar-dominated solutions. Which solution will the system choose depends on the allowed parameters for the existence and stability conditions and on the initial conditions. For solution E,
and
approaches to
when
. On the other hand, for solution F, all
x,
y and
z contribute to the dark energy and
converges to
when
goes to infinity. In the next section, we present an explicit solution of Equations (
23)–(25), which prolongs from B1 at early times to E at late times.
5. Exact Cosmological Solution
In order to investigate the exact solution for Equations (
23)–(25), we first assume that
, which corresponds to
. Here
f is an arbitrary constant at this stage. In the case of
, from the above ansatz one can find an exact solution as follows:
where
C is an arbitrary constant and
and
are given by
with
,
. It is to be noticed that
C should be a negative value to preserve the weak energy condition. In this case, introducing a time scale defined by
, Equation (
40) and
reduce to
where
and
We note that for
the solution (44) behaves as
, which shows that it represents an expanding Universe with cosmological fluid
, whereas at late times, it represents an accelerating Universe with
. Now, let us check that the above solution indeed corresponds to the one that prolongs from B1 at early times to E at late times, as was mentioned in the previous section. To this end we first substitute the solutions (
41)–(44) into the dimensionless quantities
of Equation (
26). Then one can find
When choosing
, we see that at early times,
i.e.,
, the quantities
of Equations (
45)–(47) are given by
and at late times (
) they become
If we identify
, and substituting
into B1 and E of
Table 1, we exactly find the above values of
x,
y and
z. Therefore, we conclude that our solution corresponds to the phase B1 at early times and to the phase E at late times.
We now determine the allowed range of
for this exact solution by comparing with the current observational data. It turns out that the non-relativistic dark matter with
is not consistent with the current value of
. To carry out this in detail, we recall the density parameter of the scalar field given by (we set
)
where
with
and the Hubble parameter
We first comment on the dependence of
, and
H of Equations (
48) and (
49) on the initial conditions. The exact solutions, Equations (
43) and (44), show the dependence of
ϕ and
a on the initial conditions. However, the dependence of the quantities
and
z on the initial conditions are absent as can be seen in the expressions of Equations (
45)–(47). This may be due to the fact that our exact cosmological solution satisfies the condition
and is of a non-perturbative nature. The only remaining dependence is through the variable
, which we have set to zero without loss of generality. Therefore,
and
H of Equations (
48) and (
49) are insensitive to the initial conditions as far as the non-perturbative solutions Equations (
43) and (44) are concerned. This aspect is rather unexpected because there is a priori no reason why the quantities
x,
y and
z defined in Equation (
26) should not depend on the initial conditions of
ϕ and
a.
In the above two Equations (
48) and (
49), we treat
,
at
as input parameters to determine
and especially
. Since the observational data [
25]
and
are given with experimental uncertainty, these equations give permitted range of
. We use the strategy that we first pick up a specific value of
. Then, Equations (
48) and (
49) will give allowed ranges of
B for
and
respectively. We can plot these quantities in (
)-plane. If there exist intersecting region, then, this value of
is allowed. The results are displayed in
Figure 1. We find that for values of
and
, there does not exist a region intersected by the bands of
and
. Therefore, we conclude that the allowed value
consistent with the current observational data is given by
, which corresponds to an exotic cosmological fluid with non-vanishing pressure.
Figure 1.
The plot of on the (B, t)-plane for (left), (right), (lower). The red band is the current age with uncertainty .
Figure 1.
The plot of on the (B, t)-plane for (left), (right), (lower). The red band is the current age with uncertainty .
6. Conclusion
In this paper, we have investigated various cosmological consequences of the de Sitter nonlinear sigma model with the exponential potential and cosmological fluid term. It consists of a phantom and triplet scalar fields. We have displayed that the presence of the triplet σ fields with isotropic spatial dependence provides contrasting features to the phantom model without such fields. For example, the energy and pressure coming from the spatial variations could prevent the Big Rip singularity from being developed. In particular, we found an exact cosmological solution in the case of a negative potential. In this solution, the Universe undergoes a power law expansion at early times as in -CDM. But the difference is that unlike the -CDM we have a non-vanishing scalar energy contribution ( of B1 phase) even in the matter dominated epoch. At late times, a complete dark energy-dominance is achieved with and with a suitable choice of the parameter.
The Hubble parameter Equation (
49) is exactly the same as
H of
CDM in Equation (
11) when we identify the parameter as
. However, with this choice, one can check that the energy density
of cosmological fluid is different from the matter density
of Equation (
11) in
CDM, and is given by
. Note that for
,
is always greater than
. Also, the dark energy density from Equation (
48) approaches
asymptotically from below. These show that even if the scale factors in both cases behave exactly the same, there exist qualitative differences between the two approaches.
We also have shown that to be consistent with the observational data, the equation of state for the cosmological fluid has to be within the range
unlike
-CDM with a dust like matter. This range of
appears in the literature [
31,
32] corresponding to cosmic strings with
or domain walls with
. We notice that in
-CDM model, the dark matter has the perfect fluid form and admits a barotropic equation of state. In this case, the dark matter should be pressureless in order to be in accordance with the observational data. However, it is known [
33,
34] that the dark matter can also be described by an anisotropic fluid but only in the case of non-zero effective pressure or a polytropic equation of state [
35]. On the other hand, our exotic cosmological fluid not only satisfies a barotropic equation of state but also takes a perfect fluid form. In spite of this, it should have non-zero pressure to be in agreement with the observational data.
We conclude with the following remark. We found that with the evolution is exactly that of Λ-CDM. But this does not fit the observational data as was discussed, e.g., has to be in the range of 0.13 and 0.22 to give the observed age of the universe. We speculate that this feature of deviation from the Λ-CDM for general time-varying dark energy density holds in general. That is, in models where dark energy density varies, the dark matter with might have some difficulty in fitting the observations. Nevertheless, this does not imply that the dynamical dark energy models with non-zero equation of state dark matter must be excluded, and it remains to be seen whether the exotic cosmological fluid considered in this work could be related to the realistic dark matter candidates.