Impact of Interference in Coexisting Wireless Networks with Applications to Arbitrarily Varying Bidirectional Broadcast Channels
Abstract
:Notation
1. Introduction
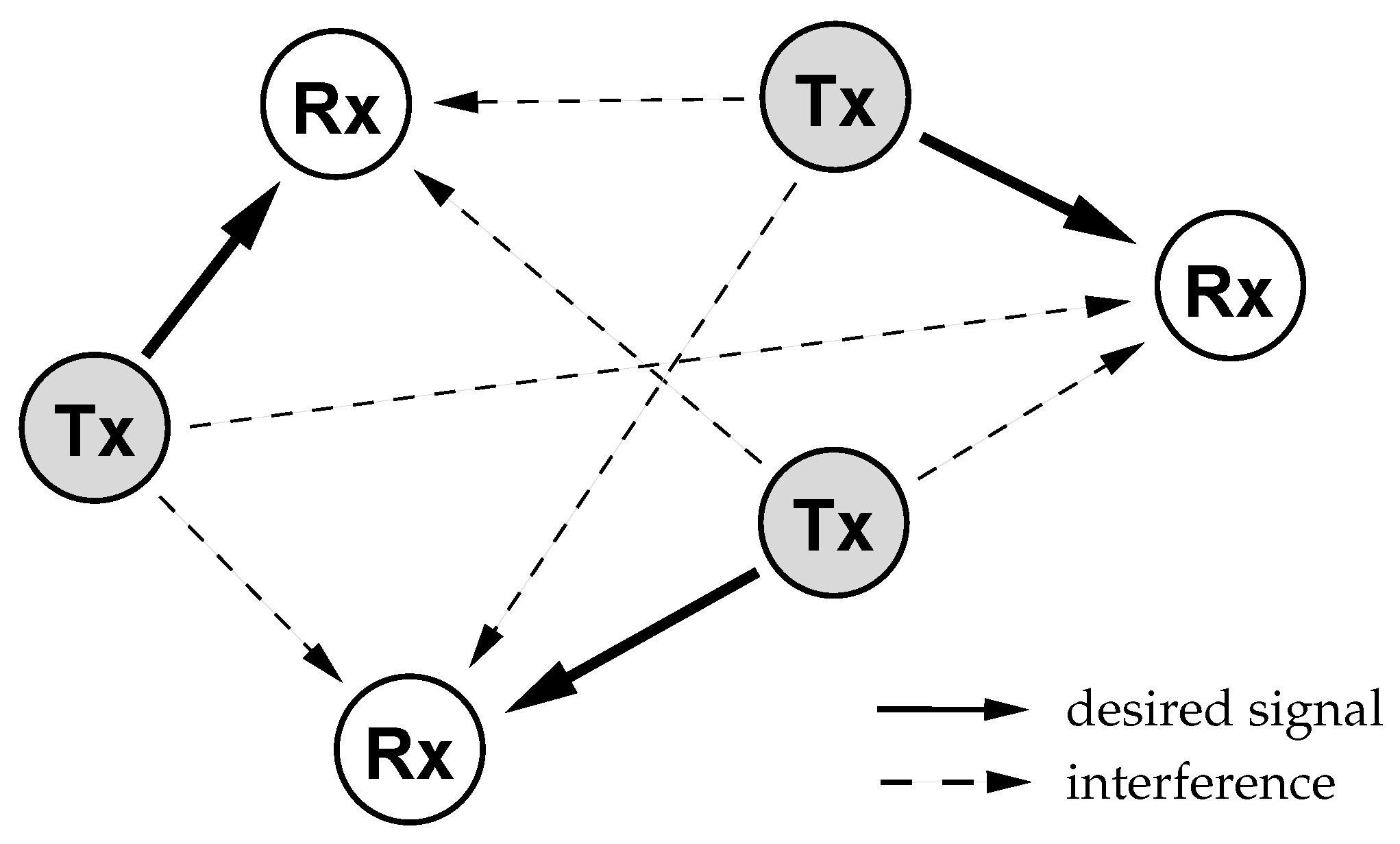
2. Preliminaries
3. Modeling of Communication in Coexisting Wireless Networks
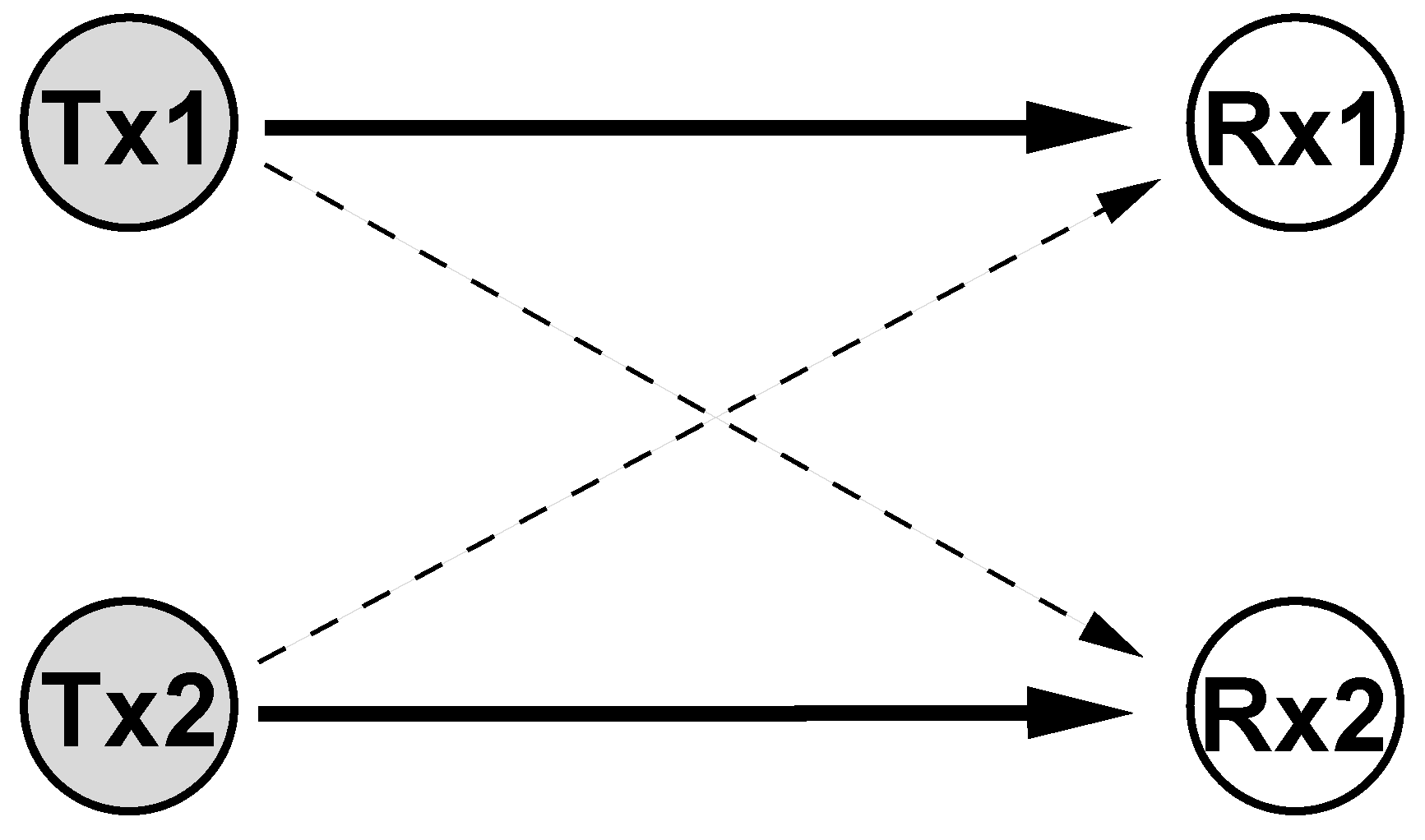
3.1. Impact of Coordination within Transmitter-Receiver Pair
3.1.1. No Additional Coordination
3.1.2. Encoder-Decoder Coordination Based on Common Randomness
3.1.3. Encoder-Decoder Coordination Based on Correlated Side Information
4. Bidirectional Relaying under Arbitrarily Varying Channels

4.1. Arbitrarily Varying Bidirectional Broadcast Channel
4.1.1. Input and State Constraints
4.1.2. Coordination Strategies
4.2. Encoder-Decoder Coordination Based on Common Randomness
4.2.1. Compound Bidirectional Broadcast Channel
4.2.2. Robustification
4.2.3. Converse
4.3. No Additional Coordination
4.3.1. Symmetrizability
4.3.2. Positive Rates
- (i)
- there exists an such that
- (ii)
- for each codeword with which satisfies for some , we have where are dummy random variables such that equals the joint type of .
4.3.3. Converse
4.3.4. Capacity Region
4.4. Unknown Varying Additive Interference
4.4.1. No Additional Coordination
4.4.2. Encoder-Decoder Coordination Based on Common Randomness
5. Discussion
Acknowledgments
References
- Blackwell, D.; Breiman, L.; Thomasian, A.J. The capacities of certain channel classes under random coding. Ann. Math. Stat. 1960, 31, 558–567. [Google Scholar] [CrossRef]
- Ahlswede, R. Elimination of correlation in random codes for arbitrarily varying channels. Z. Wahrscheinlichkeitstheorie verw. Gebiete 1978, 44, 159–175. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems, 2 ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Csiszár, I.; Narayan, P. The capacity of the arbitrarily varying channel revisited: Positivity, constraints. IEEE Trans. Inf. Theory 1988, 34, 181–193. [Google Scholar] [CrossRef]
- Csiszár, I.; Narayan, P. Arbitrarily varying channels with constrained inputs and states. IEEE Trans. Inf. Theory 1988, 34, 27–34. [Google Scholar] [CrossRef]
- MolavianJazi, E.; Bloch, M.; Laneman, J.N. Arbitrary jamming can preclude secure communication. In Proceedings of the Allerton Conference Communication, Control, Computing, Urbana-Champaign, IL, USA, 30 September–02 October 2009; pp. 1069–1075.
- Bjelaković, I.; Boche, H.; Sommerfeld, J. Strong secrecy in arbitrarily varying wiretap channels. In Proceedings of the IEEE Information Theory Workshop, Lausanne, Switzerland, 3–7 September 2012.
- Jahn, J.H. Coding of arbitrarily varying multiuser channels. IEEE Trans. Inf. Theory 1981, 27, 212–226. [Google Scholar] [CrossRef]
- Gubner, J.A. On the deterministic-code capacity of the multiple-access arbitrarily varying channel. IEEE Trans. Inf. Theory 1990, 36, 262–275. [Google Scholar] [CrossRef]
- Ahlswede, R.; Cai, N. Arbitrarily varying multiple-access channels part I—Ericson’s symmetrizability is adequate, gubner’s conjecture is true. IEEE Trans. Inf. Theory 1999, 45, 742–749. [Google Scholar] [CrossRef]
- Gubner, J.A. State constraints for the multiple-access arbitrarily varying channel. IEEE Trans. Inf. Theory 1991, 37, 27–35. [Google Scholar] [CrossRef]
- Gubner, J.A.; Hughes, B.L. Nonconvexity of the capacity region of the multiple-access arbitrarily varying channel subject to constraints. IEEE Trans. Inf. Theory 1995, 41, 3–13. [Google Scholar] [CrossRef]
- Wiese, M.; Boche, H.; Bjelaković, I.; Jungnickel, V. The compound multiple access channel with partially cooperating encoders. IEEE Trans. Inf. Theory 2011, 57, 3045–3066. [Google Scholar] [CrossRef]
- Wiese, M.; Boche, H. The arbitrarily varying multiple-access channel with conferencing encoders. In Proceedings of the IEEE International Symposium Information Theory, Saint Petersburg, Russia, 31 July–5 August 2011; pp. 993–997.
- Hof, E.; Bross, S.I. On the deterministic-code capacity of the two-user discrete memoryless arbitrarily varying general broadcast channel with degraded message sets. IEEE Trans. Inf. Theory 2006, 52, 5023–5044. [Google Scholar] [CrossRef]
- Rankov, B.; Wittneben, A. Spectral efficient protocols for half-duplex fading relay channels. IEEE J. Sel. Areas Commun. 2007, 25, 379–389. [Google Scholar] [CrossRef]
- Larsson, P.; Johansson, N.; Sunell, K.E. Coded bi-directional relaying. In Proceedings of the 5th Scandinavian Workshop on Ad Hoc Networks, Stockholm, Sweden, 3–4 May 2005; pp. 851–855.
- Wu, Y.; Chou, P.; Kung, S.Y. Information exchange in wireless networks with network coding and physical-layer broadcast. In Proceedings of the Conference Information Sciences and Systems, Baltimore, MD, USA, March 2005; pp. 1–6.
- Knopp, R. Two-way radio networks with a star topology. In Proceedings of the International Zurich Seminar on Communication, Zurich, Switzerland, February 2006; pp. 154–157.
- Oechtering, T.J.; Schnurr, C.; Bjelaković, I.; Boche, H. Broadcast capacity region of two-phase bidirectional relaying. IEEE Trans. Inf. Theory 2008, 54, 454–458. [Google Scholar] [CrossRef]
- Kim, S.J.; Mitran, P.; Tarokh, V. Performance bounds for bidirectional coded cooperation protocols. IEEE Trans. Inf. Theory 2008, 54, 5235–5241. [Google Scholar] [CrossRef]
- Kramer, G.; Shamai (Shitz), S. Capacity for classes of broadcast channels with receiver side information. In Proceedings of the IEEE Information Theory Workshop, Tahoe City, CA, USA, 2–6 September 2007; pp. 313–318.
- Xie, L.L. Network coding and random binning for multi-user channels. In Proceedings of the Canadian Workshop on Information Theory, 6–8 June 2007; pp. 85–88.
- Wyrembelski, R.F.; Oechtering, T.J.; Bjelaković, I.; Schnurr, C.; Boche, H. Capacity of Gaussian MIMO bidirectional broadcast channels. In Proceedings of the IEEE International Symposium Information Theory, Toronto, Canada, 6–11 July 2008; pp. 584–588.
- Oechtering, T.J.; Wyrembelski, R.F.; Boche, H. Multiantenna bidirectional broadcast channels–optimal transmit strategies. IEEE Trans. Signal Process. 2009, 57, 1948–1958. [Google Scholar] [CrossRef]
- Oechtering, T.J.; Jorswieck, E.A.; Wyrembelski, R.F.; Boche, H. On the optimal transmit strategy for the MIMO bidirectional broadcast channel. IEEE Trans. Commun. 2009, 57, 3817–3826. [Google Scholar] [CrossRef]
- Wyrembelski, R.F.; Bjelaković, I.; Oechtering, T.J.; Boche, H. Optimal coding strategies for bidirectional broadcast channels under channel uncertainty. IEEE Trans. Commun. 2010, 58, 2984–2994. [Google Scholar] [CrossRef]
- Wyrembelski, R.F.; Oechtering, T.J.; Boche, H.; Skoglund, M. Robust transmit strategies for multiantenna bidirectional broadcast channels. In Proceedings of the ITG Workshop Smart Antennas, Dresden, Germany, 7–8 March 2012; pp. 46–53.
- Kim, T.T.; Poor, H.V. Diversity-multiplexing trade-off in adaptive two-way relaying. IEEE Trans. Inf. Theory 2011, 57, 4235–4254. [Google Scholar] [CrossRef]
- Zhao, J.; Kuhn, M.; Wittneben, A.; Bauch, G. Optimum time-division in MIMO two-way decode-and-forward relaying systems. In Proceedings of the Asilomar Conf. Signals, Systems, Computers, Pacific Grove, CA, USA, 26–29 November 2008; pp. 1494–1500.
- Sezgin, A.; Khajehnejad, M.A.; Avestimehr, A.S.; Hassibi, B. Approximate capacity region of the two-pair bidirectional Gaussian relay network. In Proceedings of the IEEE International Symposium Information Theory, Seoul, Korea, 28 June–3 July 2009; pp. 2018–2022.
- Popovski, P.; Koike-Akino, T. Coded bidirectional relaying in wireless networks. In New Directions in Wireless Communications Research; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Zhang, R.; Liang, Y.C.; Chai, C.C.; Cui, S. Optimal beamforming for two-way multi-antenna relay channel with analogue network coding. IEEE J. Sel. Areas Commun. 2009, 27, 699–712. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Quek, T.Q.S.; Shin, H. Amplify-and-forward two-way relay networks: Error exponents and resource allocation. IEEE Trans. Commun. 2009, 58, 2653–2666. [Google Scholar] [CrossRef]
- Roemer, F.; Haardt, M. Tensor-based channel estimation and iterative refinements for two-way relaying with multiple antennas and spatial reuse. IEEE Trans. Signal Process. 2010, 58, 5720–5735. [Google Scholar] [CrossRef]
- Yilmaz, E.; Zakhour, R.; Gesbert, D.; Knopp, R. Multi-pair two-way relay channel with multiple Antenna relay station. In Proceedings of the IEEE International Conference Communication, Cape Town, South Africa, 23–27 May 2010; pp. 1–5.
- Schnurr, C.; Oechtering, T.J.; Stańczak, S. Achievable rates for the restricted half-duplex two-way relay channel. In Proceedings of the Asilomar Conference Signals, Systems, Computers, Pacific Grove, CA, USA, 4–7 November 2007; pp. 1468–1472.
- Gündüz, D.; Tuncel, E.; Nayak, J. Rate regions for the separated two-way relay channel. In Proceedings of the Allerton Conference Communication, Control, Computing, Urbana-Champaign, IL, USA, 23–26 September 2008; pp. 1333–1340.
- Zhong, P.; Vu, M. Compress-forward without Wyner-Ziv binning for the one-way and two-way relay channels. In Proceedings of the Allerton Conference Communication, Control, Computing, Urbana-Champaign, IL, USA, 28–30 September 2011; pp. 426–433.
- Ong, L.; Kellett, C.M.; Johnson, S.J. Functional-decode-forward for the general discrete memoryless two-way relay channel. In Proceedings of the IEEE International Conference Communication Systems, Singapore, 17–19 November 2010; pp. 351–355.
- Wilson, M.P.; Narayanan, K.; Pfister, H.D.; Sprintson, A. Joint physical layer coding and network coding for bidirectional relaying. IEEE Trans. Inf. Theory 2010, 56, 5641–5654. [Google Scholar] [CrossRef]
- Nam, W.; Chung, S.Y.; Lee, Y.H. Capacity of the gaussian two-way relay channel to within bit. IEEE Trans. Inf. Theory 2010, 56, 5488–5494. [Google Scholar] [CrossRef]
- Baik, I.J.; Chung, S.Y. Network coding for two-way relay channels using lattices. Telecommun. Rev. 2007, 17, 1009–1021. [Google Scholar]
- Nazer, B.; Gastpar, M. Compute-and-forward: Harnessing interference through structured codes. IEEE Trans. Inf. Theory 2011, 57, 6463–6486. [Google Scholar] [CrossRef]
- Song, Y.; Devroye, N. A lattice compress-and-forward scheme. In Proceedings of the IEEE Infomation Theory Workshop, Paraty, Brasil, 16–20 October 2011; pp. 110–114.
- Kim, S.J.; Smida, B.; Devroye, N. Lattice strategies for a multi-pair bi-directional relay network. In Proceedings of the IEEE International Symposium Infomation Theory, Saint Petersburg, Russia, 31 July–5 August 2011; pp. 2243–2247.
- Lim, S.H.; Kim, Y.H.; El Gamal, A.; Chung, S.Y. Layered noisy network coding. In Proceedings of the IEEE Wireless Network Coding Conference, Boston, MA, USA, 21 June 2010; pp. 1–6.
- Lim, S.H.; Kim, Y.H.; El Gamal, A.; Chung, S.Y. Noisy network coding. IEEE Trans. Inf. Theory 2011, 57, 3132–3152. [Google Scholar] [CrossRef]
- Kramer, G.; Hou, J. Short-message quantize-forward network coding. In Proceedings of the 8th International Workshop on Multi-Carrier Systems & Solutions, Herrsching, Germany, 3–4 May 2011; pp. 1–3.
- Kramer, G.; Hou, J. On message lengths for noisy network coding. In Proceedings of the IEEE Infomation Theory Workshop, Paraty, Brazil, 16–20 October 2011; pp. 430–431.
- Wyrembelski, R.F.; Bjelaković, I.; Boche, H. Coding strategies for bidirectional relaying for arbitrarily varying channels. In Proceedings of the IEEE Global Communication Conference, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6.
- Wyrembelski, R.F.; Bjelaković, I.; Boche, H. On the capacity of bidirectional relaying with unknown varying channels. In Proceedings of the IEEE Workshop Computational Advances Multi-Sensor Adaptive Processing, Aruba, Dutch Antilles, 13–16 December 2009; pp. 269–272.
- Wyrembelski, R.F.; Bjelaković, I.; Boche, H. List decoding for bidirectional broadcast channels with unknown varying channels. In Proceedings of the IEEE International Conference Communication, Cape Town, South Africa, 23–27 May 2010; pp. 1–6.
- Ahlswede, R.; Cai, N. Correlated sources help transmission over an arbitrarily varying channel. IEEE Trans. Inf. Theory 1997, 43, 1254–1255. [Google Scholar] [CrossRef]
- Ahlswede, R. Coloring hypergraphs: A new approach to multi-user source coding—II. J. Comb. Inform. Syst. Sci. 1980, 5, 220–268. [Google Scholar]
- Ahlswede, R. Arbitrarily varying channels with states sequence known to the sender. IEEE Trans. Inf. Theory 1986, 32, 621–629. [Google Scholar] [CrossRef]
- Ahlswede, R.; Wolfowitz, J. The structure of capacity functions for compound channels. In Proceedings of the International Symposium on Probability and Information Theory, McMaster University, Hamilton, Canada, April 1969; pp. 12–54.
- Csiszár, I.; Narayan, P. Capacity of the gaussian arbitrarily varying channel. IEEE Trans. Inf. Theory 1991, 37, 18–26. [Google Scholar] [CrossRef]
- Hughes, B.; Narayan, P. Gaussian arbitrarily varying channels. IEEE Trans. Inf. Theory 1987, 33, 267–284. [Google Scholar] [CrossRef]
- Lapidoth, A.; Narayan, P. Reliable communication under channel uncertainty. IEEE Trans. Inf. Theory 1998, 44, 2148–2177. [Google Scholar] [CrossRef]
- Yates, R.D. A framework for uplink power control in cellular radio systems. IEEE J. Sel. Areas Commun. 1995, 13, 1341–1347. [Google Scholar] [CrossRef]
- Boche, H.; Schubert, M. A unifying approach to interference modeling for wireless networks. IEEE Trans. Signal Process. 2010, 58, 3282–3297. [Google Scholar] [CrossRef]
- Boche, H.; Schubert, M. Concave and convex interference functions—General characterizations and applications. IEEE Trans. Signal Process. 2008, 56, 4951–4965. [Google Scholar] [CrossRef]
- Vucic, N.; Boche, H. Robust QoS-constrained optimization of downlink multiuser MISO systems. IEEE Trans. Signal Process. 2009, 57, 714–725. [Google Scholar] [CrossRef]
- Vucic, N.; Boche, H.; Shi, S. Robust transceiver optimization in downlink multiuser MIMO systems. IEEE Trans. Signal Process. 2009, 57, 3576–3587. [Google Scholar] [CrossRef]
- Jorswieck, E.A.; Boche, H. Majorization and matrix-monotone functions in wireless communications. 2007, 3, 553–701. [Google Scholar] [CrossRef]
- Boche, H.; Jorswieck, E.A. Outage probability of multiple antenna systems: Optimal transmission and impact of correlation. In Proceedings of the International Zurich Seminar on Communication, Zurich, Switzerland, 18–20 February 2004; pp. 116–119.
- Jorswieck, E.A.; Boche, H. Optimal transmission strategies and impact of correlation in multiantenna systems with different types of channel state information. IEEE Trans. Signal Process. 2004, 52, 3440–3453. [Google Scholar] [CrossRef]
- Jorswieck, E.A.; Boche, H. Channel capacity and capacity-range of beamforming in MIMO wireless systems under correlated fading with covariance feedback. IEEE Trans. Wireless Commun. 2004, 3, 1543–1553. [Google Scholar] [CrossRef]
- Pinsker, M.S. Information and Information Stability of Random Variables and Processes; Holden-Day: San Francisco, CA, USA, 1964. [Google Scholar]
Appendices
A. Additional Proofs
A.1. Proof of Lemma 1
A.2. Proof of Lemma 2
A.3. Proof of Lemma 3
A.4. Proof of Lemma 8
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wyrembelski, R.F.; Boche, H. Impact of Interference in Coexisting Wireless Networks with Applications to Arbitrarily Varying Bidirectional Broadcast Channels. Entropy 2012, 14, 1357-1398. https://doi.org/10.3390/e14081357
Wyrembelski RF, Boche H. Impact of Interference in Coexisting Wireless Networks with Applications to Arbitrarily Varying Bidirectional Broadcast Channels. Entropy. 2012; 14(8):1357-1398. https://doi.org/10.3390/e14081357
Chicago/Turabian StyleWyrembelski, Rafael F., and Holger Boche. 2012. "Impact of Interference in Coexisting Wireless Networks with Applications to Arbitrarily Varying Bidirectional Broadcast Channels" Entropy 14, no. 8: 1357-1398. https://doi.org/10.3390/e14081357
APA StyleWyrembelski, R. F., & Boche, H. (2012). Impact of Interference in Coexisting Wireless Networks with Applications to Arbitrarily Varying Bidirectional Broadcast Channels. Entropy, 14(8), 1357-1398. https://doi.org/10.3390/e14081357




