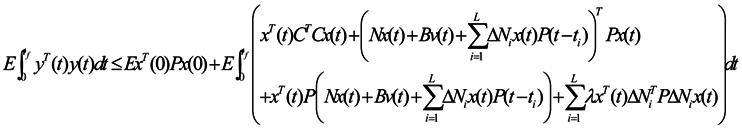On the Information Transmission Ability of Nonlinear Stochastic Dynamic Networks

Abstract

The major function of dynamic networks is to sense information from the environment and process the information to the downstream. Therefore how to measure the information transmission ability of a dynamic network is an important topic to evaluate network performance. However, the dynamic behavior of a dynamic network is complex and, despite knowledge of network components, interactions and noises, it is a challenge to measure the information transmission ability of a dynamic network, especially a nonlinear stochastic dynamic network. Based on nonlinear stochastic dynamic system theory, the information transmission ability can be investigated by solving a Hamilton-Jacobi inequality (HJI)-constrained optimization problem. To avoid difficulties associated with solving a complex HJI-constrained optimization problem for information transmission ability, the Takagi-Sugeno (T-S) fuzzy model is introduced to approximate the nonlinear stochastic dynamic network by interpolating several local linear stochastic dynamic networks so that a HJI-constrained optimization problem can be replaced by the linear matrix inequalities (LMIs)-constrained optimization problem. The LMI problem can then be efficiently solved for measuring information transmission ability. We found that a more stable (robust) dynamic network has less information transmission ability, and vice versa. Finally, an example of a biochemical network in cellular communication is given to illustrate the measurement of information transmission ability and to confirm the results by using Monte Carlo simulations.

1. Introduction

There exist many kinds of networks to process information in the real world. For example, signal transmission networks (signal transduction pathways) are one of the fastest information processing networks in biological networks. They enable cells to sense and transduce extracellular signals through inter- and intra-cellular communication. Signal transmission networks consist of interactions between signal proteins, where different external changes or events stimulate specific signaling networks. Typical external signal stimuli are hormones, pheromones, heat, cold, light, osmotic pressure, and ionic concentration changes [1]. Therefore, signal transmission networks can also be viewed as the information processing and transferring systems of cells [2]. Similarly, many communication networks like sensor networks or wireless sensor networks (WSNs) can be also considered as information processing and transferring systems [3,4,5].

For biological networks, many studies have investigated the properties of signal transduction pathway, such as amplification [6], specificity [7], adaptive ultrasensitivity [8,9], oscillation [9] and synchronization [10]. However, due to the complex behavior of dynamic networks, knowledge of components of dynamic networks and their interactions is often not enough to interpret the system behavior of dynamic networks. To the best of our knowledge, the first attempt to express the information transmission ability as a mathematic formula appeared in 1982 [11]. It focused on sensitivity amplification, which is defined as the ratio of the percent change in output response to the percent change in the input stimulus, i.e., the relative change of network output respect to a specific input. Further, a signal amplification is also defined as signal gain for a signaling network, where at least one maximum exists with respect to the ratio of inputs to outputs [12,13]. More recently, based on cascade mechanisms in electrical engineering systems, signal transmission ability is designated as the maximum of output to the maximum of input, i.e., Output_max/Input_max [14]. Obviously, the information transmission ability designed above is on a case-by-case basis, i.e., the measured results are affected by not only structure of the network, but also the input to the network.

In this study, we specifically investigate the information transmission ability of a dynamic network, which will be measured based on information and system theory from the viewpoint of input/output signal energy [15]. In accordance with system gain viewpoint, the ratio of output to input signal energy of a stochastic dynamic network is determined for all possible input signals. Then the maximum ratio is denoted as the information transmission ability, i.e., from the system (network) gain perspective [16,17,18,19,20]. This measure of information transmission ability is more dependent on the system characteristics of the studied dynamic network rather than the input signals. Like a low-pass filter, the filtering ability is more dependent on the systematic characteristics of the low-pass filter itself compared to the input signals. Based on the proposed information transmission ability, the measurement scheme needs to solve a corresponding nonlinear Hamilton-Jacobi inequality (HJI) for information transmission ability of nonlinear stochastic dynamic networks. At present, there are no analytic or numerical solutions for HJI directly, except for some simple cases. In this study, a T-S fuzzy system is employed to interpolate several local linear stochastic dynamic networks via a set of fuzzy bases to approximate a nonlinear stochastic dynamic network [21,22,23,24,25,26]. In this situation, HJIs can be replaced by a set of linear matrix inequalities (LMIs) [21,22,23,24,25,27]. Then, this allows the HJI-constrained optimization problem for nonlinear transmission ability measurement to be transformed into an equivalent LMIs-constrained optimization problem, which can be easily solved with the help of the LMI toolbox in Matlab [28].

Further, because the proposed method for information transmission ability is based on fuzzy local interpolation of nonlinear stochastic dynamic networks, the information transmission ability can be investigated from these fuzzy-interpolated local linear stochastic dynamic networks. With this method, we can gain insight into network information transmission from the linear system viewpoint. In the future, nonlinear stochastic dynamic networks may be characterized according to the proposed measurement, which is useful for development and application in network processing. Finally, a nonlinear biological network is given to illustrate the measure procedure of information transmission ability and to confirm the results of proposed measurement method by using Monte Carlo computer simulations.

2. On the Information Transmission Ability Measure of Linear Stochastic Dynamic Networks

Initially, for the convenience of illustration, we consider the following linear dynamic network:

$$\begin{array}{l}\frac{dx(t)}{dt}=Nx(t)+Bv(t)\\ y(t)=Cx(t)\end{array}$$

(1)

where x(t) denotes the state vector of the dynamic network, v(t) and y(t) denotes the input and output signal vectors, N denotes the network interaction matrix, and B and C denote the input and output coupling matrices, respectively, in the following:

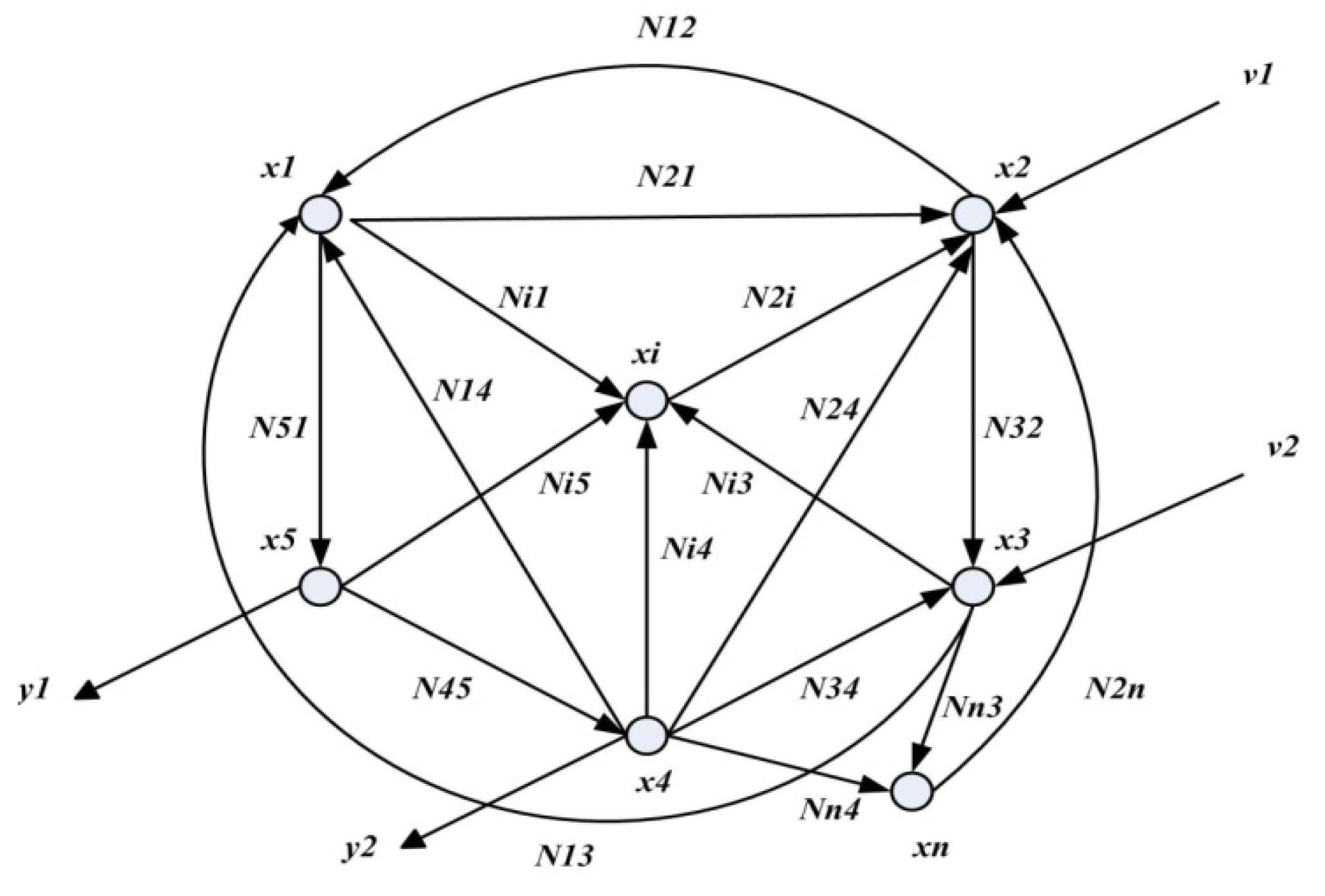
in which x_i(t) denotes the state of the ith node, and N_ii denotes the dynamic interaction from node j to node i in the linear dynamic network (see Figure 1).

Remark 1: 

In the molecular gene network [1,2], x(t) denotes the concentrations of n genes, v(t) denotes the molecular regulation from the upstream genes and environment, y(t) denotes the output molecules to the downstream genes, and N_ij denotes the regulation from the jth gene to the ith gene.

Suppose the linear dynamic network suffers from intrinsic parameter fluctuations so that N is perturbed by random fluctuation sources as N + ΔNn(t), where ΔN denotes the effect on the network due to random fluctuation source n(t), which is represented by white Gaussian noise with zero mean and unit variance to denote the stochastic part of fluctuation. That is, the stochastic part of fluctuation is absorbed by n(t) with dw(t) = n(t)dt, where w(t) is a standard Wiener process [16,17,18] (Brownian motion) and the change of linear dynamic network by the random fluctuation source n(t) is denoted by ΔN.

Figure 1. A simple linear dynamic network with $\dot{x}(t)=Nx(t)+Bv(t)$, $y(t)=Cx(t)$, where $B=\left[\begin{array}{ll}0& 0\\ 1& 0\\ 0& 1\\ ⋮& ⋮\\ 0& 0\end{array}\right]$

Figure 1. A simple linear dynamic network with $\dot{x}(t)=Nx(t)+Bv(t)$, $y(t)=Cx(t)$, where $B=\left[\begin{array}{ll}0& 0\\ 1& 0\\ 0& 1\\ ⋮& ⋮\\ 0& 0\end{array}\right]$

In the situation, the linear dynamic network in (1) is modified as follows:

$$\begin{array}{l}\frac{dx(t)}{dt}=(N+\Delta Nn(t))x(t)+Bv(t)\\ y(t)=Cx(t)\end{array}$$

(2)

In the conventional notation of engineering and system science, the linear stochastic dynamic network in (2) can be represented by the following Ito stochastic dynamic network [16]:

$$\begin{array}{l}dx(t)=Nx(t)dt+Bv(t)dt+\Delta Nx(t)dw(t)\\ y(t)=Cx(t)\end{array}$$

(3)

where dw(t) = n(t)dt, and w(t) denotes the corresponding Wiener process or Brownian motion of random parametric fluctuation in the linear stochastic dynamic network.

Remark 2: 

The random parametric fluctuation modeled as Wiener process in the Ito stochastic dynamic network (3) may be due to continuous thermal fluctuation, modeling error, time-varying characteristic or gene variation in biological networks. However, if the random parametric fluctuation is due to some discontinuous pathogen invasion, genetic mutations or impulsive stimuli, which may be accumulated in the dynamic network, it is more appropriate to be modeled as Poisson (jump) process [29]. In this situation, the linear stochastic dynamic network (3) can be modified as follows:

(4)

where is a weighted Poisson process. denotes a Poisson process with mean λt and variance λt. ΔN_i denotes the variation of N due to discontinuous changes P(t − t_i) occurring at t = t_i.

The focus of this study is on the measurement of information transmission ability of the stochastic dynamic network in (3). Since information transmission ability is a systematic property, it is not easy to investigate information transmission ability from the input/output data directly. Like a filter, the filtering ability is more dependent on systematic property itself of the filter rather than to input/output signals. Further, from the information transmission ability, we could get insight into the system characteristic of communication networks. The information transmission ability can be defined from the system gain viewpoint as follows [15]:

(5)

where v(t) and y(t) are the input and output signals of the linear stochastic dynamic network in (3), respectively. The physical meaning of information transmission ability is the maximum root mean square (RMS) energy ratio of output signal to input signal for all possible finite energy input signals within the time interval [0,t_f ], where L₂[0,t_f ] denoted the set of all possible finite energy signals in [0,t_f ]. The reason for employing the maximum RMS energy ratio of the output signal to all possible input signals is that input signals to stochastic dynamic network may change under different conditions, causing the signal RMS energy ratio to vary. Hence, information transmission ability should be based on the maximum effect of all the possible input signals on the output signals and exhibit greater dependency on the characteristics of the stochastic dynamic network, in accordance with the system gain viewpoint. Theoretically, the information transmission ability in (5) can be measured directly by testing all possible finite energy input signals to get the maximum RMS energy ratio. In general, the maximization problem described in (5) for measuring the information transmission ability of stochastic dynamic network cannot be solved directly because infinite finite-energy input signals need to be tested. It can only be solved indirectly by applying a systematic analysis method to the stochastic dynamic network in (3). In this study, we will solve the optimization problem in (5) for measuring the information transmission ability from the suboptimal perspective, i.e., minimize its upper bound to approach the optimal value I_o.

Let us denote the upper bound of information transmission ability as follows:

(6)

or:

(7)

for x(0) = 0. In (6) and (7), if I² is the upper bound of for every v(t) ∈ L₂[0,t_f] , then I² is also the upper bound of $I_o^2$ in (5), as every v(t) ∈ L₂[0,t_f] should include the input signal which leads to the maximum RMS energy ratio in (5). Therefore, we can find the upper bound I for the information transmission ability I_o, and then minimize the upper bound I to approach the information transmission ability I_o, i.e., the information transmission ability I_o is estimated by minimizing the upper bound I. Then we get the following result:

Theorem 1: 

For the linear stochastic dynamic network in (3), if a positive definite symmetric matrix P > 0 exists, satisfying the following Riccati-like inequality:

$$C^{T}C+N^{T}P+PN+\frac{1}{I^2}PB{B}^{T}P+\Delta N^{T}P\Delta N\le 0$$

(8)

then the information transmission ability I_o is bounded by I. Proof: See Appendix A.

The above theorem claims that if the Riccati-like inequality in (8) has a positive definite solution P > 0, then I is the upper bound of the information transmission ability I_o.

Remark 3: 

For the linear stochastic dynamic network with discontinuous parametric fluctuation (4), the Riccati-like inequality (8) in Theorem 1 can be modified as follows:

(9)

Therefore, if there exists a positive definite symmetric matrix P > 0 satisfied the Riccati-like inequality (9), then the information transmission ability I_o can also be bounded by I. Proof: See Appendix B.

In order to solve the Riccati-like inequality in (8) by the conventional LMI method, the positive definite symmetric matrix Q = P⁻¹ is multiplied at both sides of (8). The Riccati-like inequality in (8) can be described as:

$$Q{C}^{T}CQ+Q{N}^T+NQ+\frac{1}{I^2}B{B}^T+Q\Delta N^T{Q}^{-1}\Delta NQ\le 0$$

(10)

By the Schur complement method [15], the Riccati-like inequality in (10) is then equivalent to the following LMI:

(11)

If the LMI in (11) holds for Q > 0, the information transmission ability of linear stochastic dynamic network in (3) is less than I, i.e., I is the upper bound of the information transmission ability I_o in (5). Therefore, the information transmission ability of the stochastic dynamic network in (3) could be obtained by solving the following LMI-constrained optimization problem:

(12)

which can then be solved by decreasing I until no positive definite symmetric matrix Q is able to satisfy the inequality in (10) or (11).

Remark4: 

(i) The constrained optimization problem in (12) for information transmission ability measurement is known as an “eigenvalue problem” [15], which can be efficiently solved by the LMI toolbox in Matlab [28]. (ii) After substituting I_o for I in (8), we get:

$$C^{T}C+N^{T}P+PN+\frac{1}{I_o^2}PB{B}^{T}P+\Delta N^{T}P\Delta N\le 0$$

(13)

If I_o is smaller, the fourth term will be larger so that the eigenvalues of N would be in the far left hand complex domain, (i.e., with more negative real part or more stable) to let the inequality in (13) hold, i.e., if the stochastic dynamic network is more stable (robust), the information transmission ability is smaller (or the input signal is attenuated by the stochastic dynamic network). If I_o is larger, the eigenvalues of N would approach the imaginary axis (less stable) in order to amplify the input signal. If ΔN becomes larger in (13), I_o will become large, i.e., the network perturbation will lead to an overestimate of information transmission ability. Obviously, the information transmission ability is more dependent on the system characteristics N, B ,C, ΔN of stochastic dynamic network than on input signal v(t), just as a low-pass filter is more dependent on the low-pass characteristics (poles and zeros ) of the system than on the filtered noise.

3. On the Information Transmission Ability Measurement of Nonlinear Stochastic Dynamic Networks

In real world, many stochastic dynamic networks are nonlinear. In this situation, the linear stochastic dynamic network in (3) should be modified as:

$$\begin{array}{l}dx(t)=N(x(t))dt+B(x(t))v(t)dt+\Delta N(x(t))dw(t)\\ y(t)=C(x(t))\end{array}$$

(14)

where N(x(t)) and ΔN(x(t)) denote the nonlinear interaction and perturbation of the nonlinear stochastic dynamic network, respectively; B(x(t)) and C(x(t)) denote the nonlinear input and output couplings of the nonlinear stochastic dynamic network, respectively.

Consider the nonlinear stochastic dynamic network in (14). There exist many equilibrium points (phenotypes in nonlinear biological network). Suppose a stable equilibrium x_e is of interest. For convenience of analysis, the origin of the nonlinear stochastic dynamic network is shifted to the equilibrium point x_e to simplify the measuring procedure of information transmission ability of the nonlinear stochastic dynamic network. Let us denote $\tilde{x}=x(t)-x_e$, then the following shifted nonlinear stochastic dynamic network can be obtained as follows [17,18]:

$$\begin{array}{l}d\tilde{x}(t)=N(\tilde{x}(t)+x_e)dt+B(\tilde{x}(t)+x_e)v(t)dt+\Delta N(\tilde{x}(t)+x_e)dw(t)\\ y(t)=C(\tilde{x}(t)+x_e)\end{array}$$

(15)

That is, the origin $\tilde{x}(t)=0$ of the shifted nonlinear stochastic dynamic network in (15) is at the equilibrium x_e of the original nonlinear stochastic dynamic network in (14). Then, let us consider the information transmission ability of the nonlinear stochastic dynamic network in (15). According to the stochastic Lyapunov theory [17], we get the following result.

Theorem 2: 

If the following Hamilton Jacobi inequality (HJI) holds, for some positive Lyapunov function $V(\tilde{x}(t))>0$.

(16)

then the information transmission ability I_o of the nonlinear stochastic dynamic network in (14) or (15) is less than or equal to I. Proof: See Appendix C.

Since I is the upper bound of information transmission ability, the information transmission ability I_o can be obtained by solving the following HJI-constrained optimization problem:

(17)

It means to make I as small a value as possible without violating HJI with $V(\tilde{x}(t))>0$ in (16). After solving the information transmission ability I_o from the HJI-constrained optimization problem in (17) and substituting I_o for I in (16), we find:

(18)

From (18), it is seen that if the information transmission ability I_o is small, the third term in (18) will be relatively large. In this situation, the second term should be more negative (more stable) so that the HJI in (18) still holds, i.e., a more stable nonlinear stochastic dynamic network will lead to a less information transmission. On the other hand, if is less negative (less stable), then the information transmission ability I_o could be large enough to satisfy HJI in (18). It can be seen that a less stable nonlinear stochastic dynamic network will lead to a more information transmission. Further, the last term in (18) due to network perturbation will lead to an overestimate of I_o because a large $\Delta N(\tilde{x}(t))$ will make I_o large.

In general, it is still very difficult to solve HJI-constrained optimization problem in (17) for the measurement of information transmission ability of nonlinear stochastic dynamic network in (14) or (15). Recently, T-S fuzzy method has been employed to interpolate several local linear systems to efficiently approximate a nonlinear system via fuzzy bases [21,22,23,24]. Thus, in this study, the fuzzy interpolation method is employed to overcome the nonlinear HJI problem in (16) and to simplify the procedure of solving the HJI-constrained optimization problem in (17) for measuring the information transmission ability.

The T-S fuzzy dynamic model is described by fuzzy “If-then” rules and employed here to solve the HJI-constrained optimization problem in (17) for information transmission ability of nonlinear stochastic dynamic network in (14) or (15). The ith rule of fuzzy model for nonlinear stochastic dynamic network in (15) is proposed as follows [21,22,23,24]:

(19)

where i = 1,2,...L. ${\tilde{x}}_i(t)$ is the premise variable, F_ij is the fuzzy set, N_i, B_i, ΔN_i and C_i are local linear system matrices of the nonlinear stochastic dynamic network. L is the number of fuzzy rules, and l is the number of premise variables. If all state variables are used as premise variables then L = n. The physical meaning of fuzzy rule i in (19) is that if state variables ${\tilde{x}}_1(t),{\tilde{x}}_2(t),\text{...}{\tilde{x}}_{\mathrm{l}}(t)$ are with the local fuzzy set F_i1,F_i2F_il, then the nonlinear stochastic dynamic network in (15) could be represented by the linear stochastic dynamic network in the “then” part of (19). The fuzzy inference system of (19) can then be described as follows [21,22,23,24]:

(20)

where and , with $F_{ij}({\tilde{x}}_i(t))$ describing the grade of membership of ${\tilde{x}}_i(t)$ in F_ij and $m_i({\tilde{x}}_i(t))$, i = 1,2,...L are fuzzy bases. The denominator is applied to enable normalization so that the total sum of fuzzy bases . The physical meaning of fuzzy interference system in (20) is that L local linear stochastic dynamic networks are interpolated through nonlinear fuzzy bases $m_i({\tilde{x}}_i(t))$ to approximate the nonlinear stochastic dynamic network in (15). Aside from the fuzzy bases, other interpolation bases could also be employed to interpolate several linear stochastic dynamic networks to approximate a nonlinear stochastic dynamic network, for example, the global linearization method, which interpolates local linear systems at M vertices of a polytope to approximate a nonlinear system [15].

Remark 5: 

In applying a T–S fuzzy approach [24] to approximate a nonlinear system, the effect from fuzzy approximation errors and are usually omitted for concise representation. It is well known, the fuzzy approximation error is not only dependent on the complexity of nonlinear system but also dependent on the number of fuzzy rules L, i.e., $\epsilon (\tilde{x}(t))$ and $\Delta \epsilon (\tilde{x}(t))$ decrease as L increases. It has also been proven [30] that the fuzzy approximation errors would be bounded if the continuous functions $N(\tilde{x}(t))$ and $\Delta N(\tilde{x}(t))$ are defined on a compact set . The problems dealing with the effect of fuzzy approximation error can be acquisited in our previous researches [31,32,33].

By fuzzy approximation, the nonlinear stochastic dynamic network in (15) can be represented by the following fuzzy interpolated stochastic dynamic network:

(21)

There are many fuzzy system identification methods to determine the local system matrices N_i ,B_i,ΔN_i and C_i for fuzzy models [24], such as the fuzzy toolbox in Matlab. After that, we can get the following result.

Theorem 3: 

For the nonlinear stochastic dynamic network in (21), if the following Riccati-like inequalities exist a positive definite symmetric solution P > 0 :

$$C_i^T{C}_j+N_i^{T}P+P{N}_i+\frac{1}{I^2}P{B}_i{B}_i^{T}P+\Delta N_i^{T}P\Delta N_j\le 0,i=1,2,\text{...}L,j=1,2,\text{...}L$$

(22)

then the information transmission ability I_o is bounded by I. Proof: See Appendix D.

The Riccati-like inequalities in (22) can be considered as the local linearization of HJI in (16). In order to solve the above Riccati-like inequalities by the conventional LMI method, the positive definite matrix Q = P⁻¹ is multiplied at both sides of (22). Then the Riccati-like inequalities in (22) can be rewritten as:

$$Q{C}_i^T{C}_{j}Q+Q{N}_i^T+N_{i}Q+\frac{1}{I^2}{B}_i{B}_i^T+Q\Delta N_i^T{Q}^{-1}\Delta N_{j}Q\le 0,i=1,2,\text{...}L,j=1,2,\text{...}L$$

(23)

By the Schur complement method [15], the Riccati-like inequalities in (23) are then equivalent to the following LMIs:

(24)

If the LMIs in (24) hold for Q > 0, the information transmission ability I_o of the nonlinear stochastic dynamic network in (21) is less than or equal to I, i.e., I is the upper bound of the information transmission ability I_o. Therefore, the information transmission ability I_o of a nonlinear stochastic dynamic network could be obtained by solving the following LMIs-constrained optimization problem:

(25)

which can then be solved by decreasing I until no positive definite symmetric matrix Q is able to satisfy the LMIs in (24) or (25).

Remark 6: 

(i) Using the fuzzy approximation method, the HJI in (16) is interpolated by a set of Riccati-like inequalities in (22) or (23), i.e., the Riccati-like inequalities in (22) or (23) are an approximation of HJI with L local systems. Similarly, the LMIs-constrained optimization problem in (25), describing the information transmission ability measurement of a nonlinear stochastic dynamic network, is also an efficient approach based on a fuzzy interpolation method to replace the very difficult HJI-constrained optimization problem in (17). (ii) The LMIs-constrained optimization problem for the information transmission ability is known as an “eigenvalue problem” [15], which can be efficiently solved by the LMI toolbox in Matlab. (iii) After substituting I_o in (25) for I_o in (22), we get:

$$C_i^T{C}_j+N_i^{T}P+P{N}_i+\frac{1}{I_o^2}P{B}_i{B}_i^{T}P+\Delta N_i^{T}P\Delta N_j\le 0,i=1,2,\text{...}L,j=1,2,\text{...}L$$

(26)

If I_o is smaller, then the fourth term will be larger so that the eigenvalues of N_i would be in far left hand complex plane (i.e., with more negative real part or more stable (robust) for local linear networks) and the Riccati-like inequalities in (26) could still hold, i.e., more stable local linear stochastic dynamic networks will lead to small information transmission ability of nonlinear stochastic dynamic network in (21). If I_o is larger, the fourth term in (26) become smaller, meaning the eigenvalues of N_i would be closer to the imaginary axis (i.e., with smaller negative real part or less stable (robust)), i.e., less stable (robust) local linear stochastic dynamic networks will lead to a larger information transmission ability of nonlinear stochastic dynamic network in (21). Further, large network perturbation ΔN_i in local linear stochastic dynamic networks will lead to an overestimate of I_o.

Remark 7: 

If the fuzzy approximation errors $\epsilon (\tilde{x}(t))$ and $\Delta \epsilon (\tilde{x}(t))$ are considered in the measurement of information transmission ability, with the assumption that and , then the Riccati-like inequality in (26) should be modified as:

(27)

Obviously, the last term due to fuzzy approximation errors will lead to an overestimate of the information transmission ability, i.e., the large fuzzy approximation errors σ₁ and σ₂ will make I_o large.

Simulation Example

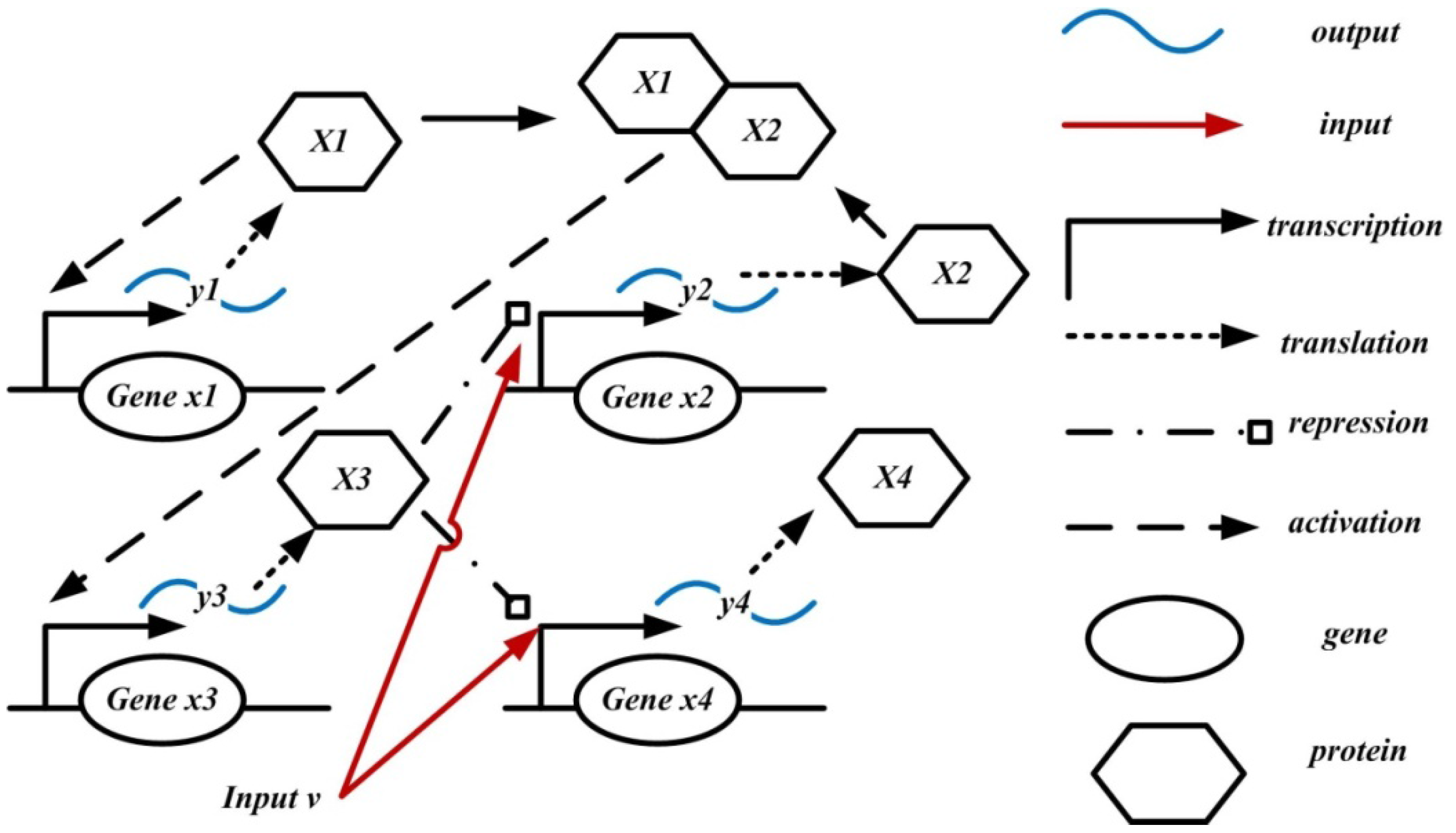
To demonstrate the procedure of our proposed measurement of information transmission ability, a nonlinear stochastic dynamic network example is given in the following for illustration. Consider a typical genetic regulatory network in Figure 2, that describing the gene, mRNA, and protein interactions [1,2].

Figure 2. Gene regulatory network comprising four genes x₁ – x₄, input v and outputs y₁ – y₄.

Figure 2. Gene regulatory network comprising four genes x₁ – x₄, input v and outputs y₁ – y₄.

These genes are regulated by other genes and then expressed through transcription and translation to obtain their products, i.e., proteins. Then, these proteins could be as the transcription factors (TFs) of other genes to regulate the expressions of other genes. If we consider only the mRNA abundances x₁(t), x₂(t), x₃(t) and x₄(t), we can obtain the following nonlinear stochastic gene network as follows [1,2]:

(28)

where λ₁, λ₂, λ₃, and λ₄ are the first-order rate constants of the degradation of x₁(t), x₂(t), x₃(t) and x₄(t), respectively. w₁ denotes the constant rate of expression of gene x₁(t), and the Hill term describes the formation of x₂(t), which is activated by x₄(t) with maximal rate V₂, dissociation constant Λ₂, and Hill coefficient n₄. The inhibition by x₃(t) is expressed by the term . The formation of x₃(t) is modeled with Hill expression that points to a threshold of the formation of x₃(t) depending on the concentrations of x₁(t) and x₂(t). V₃ and Λ₃ are the maximal rate and the dissociation constant, respectively, and n₁₂ is the Hill coefficient. The production of x₄(t) depends on the maximal rate V₄ and on the inhibition by x₃(t). The parameters are chosen as follows [1]:

From the simulation result of the nominal gene regulatory network (i.e., without considering the stochastic noise W(t) and input signal v(t)), the equilibrium point of the nominal gene regulatory network is at [x_e1, x_e2, x_e3, x_e4] = [1.0000, 0.5903, 1.0560, 0.5736]. Therefore, the shifted nonlinear stochastic gene network of (28) is obtained as follows:

(29)

By the fuzzy interpolation method in (19) or (20) with L = 81, and the parameters N_i, B_i, can be easily identified with the fuzzy toolbox in Matlab. By solving the LMIs-constrained optimization problem in (25), we obtain I_o = 0.199 and the corresponding positive definite symmetric matrix P = Q⁻¹ as follows:

(30)

To confirm the information transmission ability of the proposed measurement method, let the input signal v(t) be a zero mean white noise with unit variance. Then the information transmission ability I_o of the nonlinear stochastic gene network by Monte Carlo simulation with 1000 runs is estimated as follows:

(31)

Obviously, the information transmission ability estimated by the proposed method is larger than the result by unitary white noise input. There are three main reasons for this result: (i) The network perturbations in x₂(t), x₄(t) and fuzzy approximation errors will lead to an overestimate of I_o, (ii) The information transmission ability I_o in (5) is the worst-case output/input RMS energy ratio for all possible finite-energy input signals. Therefore, it may get a more conservative result than an arbitrary input signal. (iii) In general, we can get a conservative result by solving LMIs for Q = > 0 in (24) or (25) by LMI toolbox [28].

4. Conclusion

In order to measure the information transmission ability of nonlinear stochastic dynamic network by experiments, it is necessary to test a large number of input signals and compute the ratio of root mean square (RMS) energy ratio of the output to input signals. This process requires numerous experiments and is not a realistic method of obtaining data. Therefore, a method that is independent of the measurement output and input signals is required. According to the concept of a system gain, we proposed a new method to measure the information transmission ability of a nonlinear stochastic dynamic network, which is dependent on the system characteristics of the nonlinear stochastic dynamic network. We found that if a stochastic dynamic network is more stable (or robust); it will lead to small information transmission ability, and vice versa. Further, the network perturbation will lead to an overestimate of information transmission ability of stochastic dynamic networks.

In general, it is very difficult to solve HJI-constrained optimization problems to estimate the information transmission ability of nonlinear stochastic dynamic networks. In this study, based on fuzzy interpolation method, a set of LMIs are obtained to replace HJI at each local linear system, so that the HJI-constrained optimization problem for information transmission ability can be replaced by LMIs-constrained optimization problem, which can be efficiently solved with the help of the LMI toolbox in Matlab. From this simulation example, the measurement result of information transmission ability can be confirmed by the proposed method. In the future, the characterization of information transmission ability may have much potential application to many kinds of nonlinear stochastic dynamic networks.