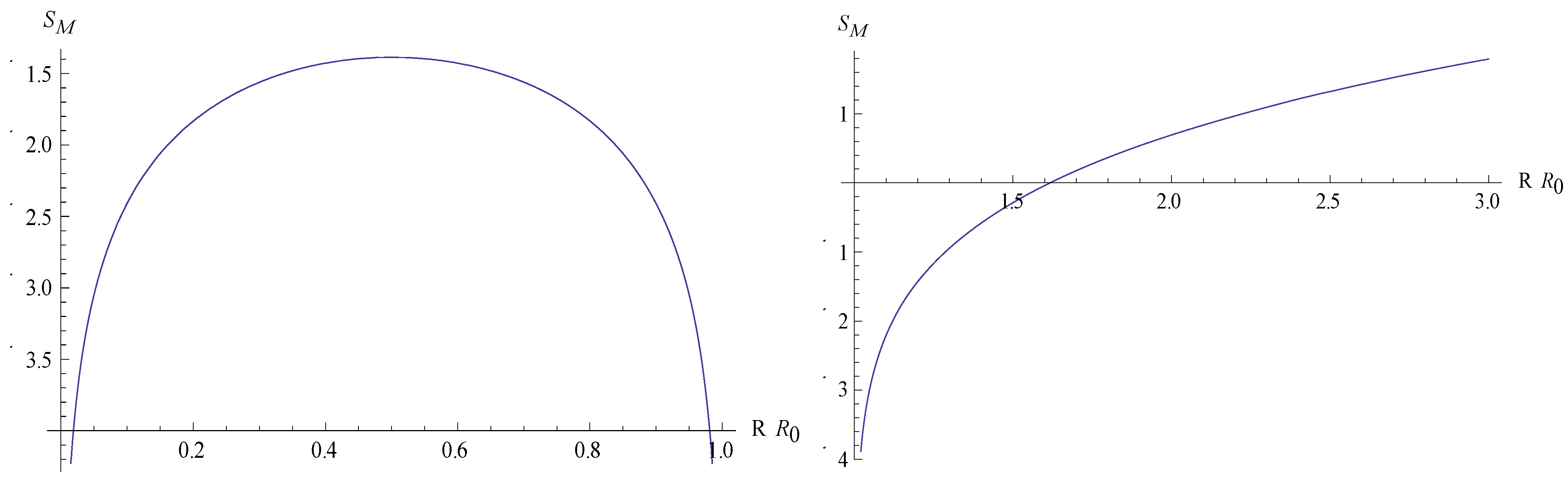1. Introduction
The arrow of time arises from the universe being far from equilibrium in a state of low entropy. The Second Law of Thermodynamics requires that the entropy of the universe does not decrease. Hence the universe must initially have been in a state of very low entropy. Callender [
1] has discussed this “Past Hypothesis”, writing: “The Boltzmann entropy of the entire universe was very low (compared to now) roughly 15 billion years ago. In particular, the entropy of this state was low enough to make subsequent entropy increase likely for many billions of years.” Then he notes: “When we look to cosmology for information about the actual Past State, we find early cosmological states that appear to be states of very high entropy, not very low entropy. Cosmology tells us that the early universe is an almost homogeneous isotropic state of approximately uniform temperature,
i.e. a very high entropy state.”
Observations favor that the spatial geometry of the universe is Euclidean. This means that with the topology R3 the universe has infinitely large spatial extension. Then the evolution of “the entropy within a surface co-moving with the Hubble flow” is representative of the evolution of “the entropy of the universe”.
A homogeneous universe with a perfect fluid expands adiabatically with constant entropy. Measurements of temperature variations in the cosmic microwave background has shown that 400,000 years after the Big Bang the universe was in a state very close to thermal equilibrium. Later attractive gravity made the original small mass concentrations larger, and created hot regions like stars. The temperature differences became much larger, and one might wonder if the thermodynamic entropy of the universe had become smaller in conflict with the Second Law of Thermodynamics. Maybe gravity saves the Past Hypothesis. Callender [
1] argues that this is far from obvious. In the present review we shall consider different aspects of this question.
2. Entropy Change during Gravitational Contraction
Let us first calculate the change of entropy of a gas in which gravity may be neglected, evolving away from equilibrium due to some external agent acting on it. The change of thermal entropy of a gas of
N molecules originally in thermal equilibrium at a temperature
T, then separated into two parts with temperatures
and
with constant thermal energy so that
, is:
where
is Boltzmann’s constant and
. This decrease of entropy due to evolution away from thermal equilibrium is a second order effect in
.
Next we shall make a Newtonian calculation of the effect of gravity upon the change of entropy of an expanding or contracting distribution of ideal gas, giving a further development of a simple model introduced by Wallace [
2]. The thermal entropy of an ideal gas with temperature
T and volume
V, consisting of
N molecules, is:
where C is a constant. The internal energy of the gas is equal to the kinetic energy
of the gas molecules. In the case of monoatomic molecules
. We consider a spherically symmetric distribution of
N molecules each with mass
inside a radius
R. The volume inside
R is
, and mass inside
R is
. Hence, the thermal entropy of the gas is:
where
is another constant. The surface with radius
is comoving with the matter. Hence, when the cloud expands or contracts so that the value of
changes, the mass
inside this surface is constant. The change of the thermal entropy when the radius
R changes, is:
The total mechanical energy of the gas molecules is equal to the sum of the kinetic and potential energy in the field of gravity of the cloud,
. Since the total energy is constant, the kinetic energy changes as
. In the case of contraction this is
a conversion of gravitational energy to thermal energy of the gas. Assuming that the gas is homogeneous the potential energy of the gas inside the radius
R is:
where G is Newton’s constant of gravity. Hence the change of kinetic energy of the gas molecules is
. The rate of change of the thermal entropy of the gas is:
which may be written explicitly as a function of
R as:
The thermal entropy is:
with
for
and
for
. The kinetic energy is:
Since
we have the conditions: if
then
, and there is expansion
i.e. motion upwards along the curve (b) in
Figure 1, and the entropy increases. If
then
, and there is contraction say from
along the right hand part of the curve (a). Again the entropy increases until it reaches a maximum at
. When the cloud contracts further its entropy decreases.
In terms of the energies the entropy has a maximum if . According to the virial theorem the gas is at dynamical equilibrium when this condition is fulfilled. One can show that if the kinetic energy of the gas is less than , then the cloud will collapse. In this case so that , and during the collapse giving . Hence the thermal entropy of the gas decreases due to the increasing temperature gradient in the gas although there is a conversion of gravitational energy to thermal energy.
The change of thermal entropy of matter that collapses to a star can be estimated in the following way [
2]. About 300,000 years after the Big Bang there was a nearly homogeneous cosmic plasma with density
baryons/m
3 and temperature
K. There are about
baryons in the Sun. The average density and temperature of the Sun are, respectively
and
. The entropy change
when the matter of the Sun changed from its state as a nearly homogeneous cosmic plasma 300,000 years after the Big Bang to a star, can be calculated from Equation (2). Using that
leads to:
Figure 1.
Thermal entropy (modulus an undetermined constant and in units of (3/2)Nk) as a function of R for a gas cloud contracting or expanding under the action of its own gravity. (a) Contraction. Here R < R0. Then the entropy first increases towards a maximum at R = R0/2, and then decreases. (b) Expansion. Here R > R0. The entropy of the gas increases.
Figure 1.
Thermal entropy (modulus an undetermined constant and in units of (3/2)Nk) as a function of R for a gas cloud contracting or expanding under the action of its own gravity. (a) Contraction. Here R < R0. Then the entropy first increases towards a maximum at R = R0/2, and then decreases. (b) Expansion. Here R > R0. The entropy of the gas increases.
This is roughly how much the thermal entropy of the matter decreases when matter that existed in the cosmic plasma 300,000 years after the Big Bang later is formed to a star due to gravity. However, in order to calculate the entropy change of the universe one also has to find the entropy change of the environment during the collapse. Due to the conversion of gravitational energy to thermal energy the temperature of the gas increases, leading to an increased rate of electromagnetic radiation from the gas. Following Wallace [
2] I will make a rough estimate of the accumulated entropy of the electromagnetic radiation emitted by the gas. The entropy of electromagnetic radiation with energy
E and temperature
T is:
Assuming that the collapsing mass has lost a tenth of its mass as radiation, the energy of the radiation is
. Wallace [
2] has calculated the entropy of this radiation for the case that it has the temperature
. The result is
. This is a factor
larger than the decrease in entropy of the star’s matter. Hence the entropy of the universe has increased during the formation of the star due to gravitational collapse.
If so that , then the kinetic energy of the molecules is sufficiently great that the cloud will expand, , and . In spite of the fact that in this case there is a conversion of thermal energy to gravitational energy, the thermal entropy of the gas will increase. This is due to the approach towards thermal equilibrium in this process.
We shall now see how Lorentz invariant vacuum energy (LIVE) which may be represented by a cosmological constant,
, in the gravitational field equations, modifies these results. In this case the Poisson equation for the gravitational potential
in a distribution of matter with density
takes the form [
3]:
Assuming a spherical matter distribution with constant density out to a boundary with radius
R, the potential inside the matter is:
with zero potential at:
which is outside the comoving volume with mass
. The potential energy of the mass distribution is:
The rate of change of the entropy of the gas is:
where the contribution of the vacuum energy to the rate of change of the entropy is:
Since
this shows that the contribution of LIVE to the rate of change of the entropy is to increase the entropy during expansion and decrease the entropy during contraction. Amarzguioui and Grøn [
4] have presented a relativistic calculation of the effect of gravitational contraction upon the cosmic entropy to first order in
. They perturbed a homogeneous FRW universe model and calculated the increase of temperature,
, due to conversion of gravitational energy to thermal energy. In this way they showed that during this process there would be a corresponding increase of thermal entropy:
Hence, due to the release of gravitational energy there is an increase of thermal entropy to first order in
. Comparing with eq.(1) it is clear that the evolution of a gas in which gravity may be neglected, and the evolution of a self gravitating gas, is very different as illustrated in
Figure 2.
Figure 2.
Evolution of a system (a) in which gravity may be neglected, and (b) in a self gravitating system where the box is much larger than the Jean’s length of the gas it contains.
Figure 2.
Evolution of a system (a) in which gravity may be neglected, and (b) in a self gravitating system where the box is much larger than the Jean’s length of the gas it contains.
The importance of gravity in connection with the Second Law has been discussed by several authors. One of the first of those discussions appeared in the remarkable book
The Physics of Time Asymmetry by P. C. W. Davies [
5]. He clearly expected the result of Amarzuioui and Grøn [
4] because already in 1974 he wrote: “gravitational condensation and collapse is itself a means of bringing about an increase of entropy.” And: “At first sight it appears paradoxical that an element of the cosmological fluid can start out in a quasi-equilibrium condition, and yet still increase in entropy at later epoch.” He further notes that this paradox is resolved because a self-gravitating system has no equilibrium configuration. Hence the origin of all thermodynamic irreversibility in the real universe depends ultimately on gravitation. In this connection Leubner [
6] writes: “In contrast to thermodynamic systems driven to a uniform distribution, the components of gravitating systems tend to clump, thus implying a gravitational arrow of time, which points in the direction of growing inhomogeneity”, and further: “Increasing inhomogeneity due to gravitational clumping reflects increasing gravitational entropy in a time evolving universe”.
3. Entropy of Black Holes and Cosmic Horizons
In 1974 Bekenstein [
7] conjectured that the black hole entropy is proportional to the area
of its event horizon divided by the square of the Planck length,
, and in the case of a Schwarzschild black hole Hawking [
8] deduced the proportionality constant:
where
is the Schwarzschild radius of the black hole, and
is the surface gravity at the horizon. This formula shows that the Bekenstein-Hawking entropy of a black hole is equal to the Boltzmann constant times one fourth of the spatial area of its event horizon in Planck units. A black hole with the mass of the Sun, for example has a Schwarzschild radius
and hence a Bekenstein-Hawking entropy
.
Damour [
9] has given a thorough discussion of the entropy of black holes, and I refer to this article for more references on this topic. Bekenstein’s black-hole entropy was viewed by him as a measure of the information about the interior of a black hole which is inaccessible to an external observer. Furthermore Bekenstein conjectured the validity of a
generalized version of the second law of thermodynamics, stating that the sum of the black-hole entropy (19) and of the ordinary entropy in the exterior of the black hole never decreases. However, even after Hawking’s deduction the challenge of interpreting
, in the same way as Boltzmann’s interpretation of thermal entropy, as the logarithm of the number of quantum micro-states of a macroscopic black hole, remained. The most striking “explanation” of black-hole entropy was obtained within the framework of string theory and was reviewed by Damour [
9] with many further references. A Boltzmann interpretation of the entropy of a black hole, related to general expected properties of quantum gravity, has recently been deduced in a model independent way by Saida [
10].
For a star with 3 Sun masses Equation (19) gives
. Wallace [
2] calculated that the entropy of a neutron star with this mass is
. So when a star collapses to a black hole in a hypernova explosion producing a gamma ray burst, the entropy increases by more than twenty five orders of magnitude.
Vaas [
11] noted that “The strongest ‘concentrations’ of gravity, black holes, are also the biggest accumulations of entropy. Physically speaking, gravitational collapse leads to the greatest possible amount of disorder. The entropy of a single black hole with the mass of a million suns (such as the one at the galactic centre, for example) is a hundred times higher than the entropy of all ordinary particles in the entire observable universe.”
We have seen that the entropy of black holes is extremely large. This may be an expression of the fact that classically we have lost all information of the matter that collapsed to a black hole since a black holes have at most three properties: mass, charge and angular momentum.
In spite of the quantum mechanical string theory interpretation of the entropy of black holes, one may wonder whether the large entropy of a black hole is a measure of the inhomogeneity of a gravitational field on a classical level. Then the entropy of a black hole might be related to the Weyl curvature of its gravitational field.
In 1977 Gibbons and Hawking [
12] suggested that one should associate an entropy with an event horizon proportional to its area, interpreted as an expression of the lack of information of an observer about the region which he cannot see. Similarly to the expression of the entropy associated with the event horizon of a black hole, the entropy associated with a cosmic event horizon with proper area
is:
This will be called the cosmic event horizon entropy, CEHE. In the case of a flat universe model the proper area of the event horizon is
. Here
is the scale factor is normalized so that its present value is 1, meaning that
a represents the distances of objects participating in the Hubble flow at an arbitrary time relative to their present distances. Furthermore
is the cosmic radial standard coordinate comoving with the Hubble flow, and:
its value at the event horizon, which exists only if this integral is finite. The definition (21) implies that the value of
decreases with time for all universe models. For universe models with an event horizon the CEHE is:
This shall now be applied to some important and simple classes of universe models in order to find the time evolution of CEHE in these models. A flat universe model dominated by a perfect fluid with equation of state
with constant value of
has scale factor:
where
is the point of time for which
, which may be taken to be the present time. Inserting the expression (24) into the integral (21) shows that there exists an event horizon only if
. This is just the condition that the universe model has accelerated expansion. In this case the coordinate distance to the event horizon is:
Hence the CEHE increases with time as for all flat, accelerating universe models with an event horizon dominated by a single cosmic fluid.
A flat LIVE-dominated universe model has scale factor:
In this universe model the coordinate distance to the event horizon is:
Hence, the CEHE is:
which is constant.
Davis, Davies and Lineweaver [
13] have investigated the change of CEHE with time in a spacetime with LIVE and radiation. Considering a universe model with flat 3-space the scale factor is:
where
and
are the present values of the density parameters of the radiation and LIVE, respectively. Furthermore
where the density of LIVE,
, is constant. With this scale factor the expression (21) for
is an elliptical integral. However Davis
et al. [
13] have investigated the evolution of CEHE in such universe models with different values of the spatial curvature and of
and
by performing numerical integrations of Friedmann’s equation for such a universe model. They found that the CEHE increases with time in a flat FRW-universe model with LIVE and radiation.
However, the entropy of the radiation inside the horizon decreases with time. The reason is that the entropy is proportional to the number of photons inside the horizon, and inside a surface that is comoving with the Hubble flow the number of photons and thus the entropy of the radiation is constant. This is in agreement with the fact that there is no heat in a homogeneous universe since there are no large scale temperature differences. Thus the universe expands adiabatically. But a comoving surface has a constant value of , and from the definition (21) follows that the radius of the event horizon, , decreases with time. There is a leakage of photons out of the event horizon.
For simplicity the mathematical expression of this will here be deduced only for a flat universe model. Then the volume inside the event horizon is
. As noted by Davis, Davies and Lineweaver [
13] the entropy of the radiation inside the event horizon is:
where
is the radiation constant. Since the radiation density fulfills
, it follows that:
which decreases with time. However, Davis, Davies and Lineweaver [
13] found that in all cases the sum of the CEHE and the radiation entropy increases with time.
4. The Weyl Curvature Hypothesis
A universe which obeys the Second Law of Thermodynamics must come from an initial state with very low entropy. In this context Wald [
14] has written that the claim that the entropy of the very early universe must have been extremely low appears to blatantly contradict the “standard model” of cosmology. From observations of the very small temperature fluctuations of the cosmic microwave radiation we see that the universe was very close to thermal equilibrium 400,000 years after the Big Bang, which seems to correspond to a state of nearly maximum entropy.
However that would be the case only in the absence of gravity. The situation changes dramatically when gravity is present. Then, for a sufficiently large system, the entropy can always be increased by clumping the system and using the binding energy that is thereby released to heat up the system. The state of maximum entropy will not correspond to a homogeneous distribution of matter, but rather to that of a black hole.
In an effort to incorporate the tendency of (attractive) gravity to produce inhomogeneities–and in the most extreme cases black holes–into a generalized Second Law of Thermodynamics, Penrose [
15] made some suggestions about how to define a quantity representing the entropy of a gravitational field. Such a quantity should vanish in the case of a homogeneous field and obtain a maximal value given by the Bekenstein-Hawking entropy (19) for the field of a black hole. In this connection Penrose formulated what is called the
Weyl curvature hypothesis, saying that the Weyl curvature should be small near the initial singularity of the universe. Wainwright and Anderson [
16] interpreted this hypothesis in terms of the ratio of the Weyl and Ricci curvature invariants:
According to their formulation of the Weyl curvature hypothesis
should vanish at the initial singularity of the universe. The physical content of the hypothesis is that the initial state of the universe is homogeneous and isotropic. Hence, the hypothesis need not be interpreted as a hypothesis about gravitational entropy. Neither need it refer to an unphysical initial singularity, but should instead be concerned with an initial state, say at the Planck time. A related attempt to implement Penrose’s suggestions was made in a paper by Mena and Tod [
17].
Wald [
14] asked: “What caused the very early universe to be in a very low entropy state?” and noted that there are basically two types of answers: (i) The initial state of the universe was random, but dynamical evolution caused at least the observable part of the universe to have very low entropy initially. (ii) The universe came into existence in a very special initial state. He then argued that the latter possibility is the more plausible one, and concluded that it will be more fruitful to seek an answer of the second type than to attempt to pursue dynamical explanations. In this connection Lebowitz [
18] wrote: ”It would certainly be nice to have a theory which would explain the “cosmological initial state”. Grøn and Hervik [
19,
20] tried to follow the path that Wald considered the most fruitful one, by investigating whether a quantum calculation of initial conditions for the universe based upon the Wheeler-DeWitt equation supports Penrose’s Weyl curvature hypothesis, according to which the Ricci part of the curvature dominates over the Weyl part at the initial singularity of the universe.
The vanishing of the Weyl curvature tensor at the initial singularity is a very special initial condition. Due to the evolution during the inflationary era, however, this condition may be relaxed. A much larger variety of initial conditions are consistent with the observed approximate homogeneity of the universe, as seen in the cosmic background radiation, in inflationary universe models than in models without inflation. A relevant question in this connection is: if a larger class of initial conditions leads to the same observable universe after a period of inflation, do inflationary processes lead to the production of entropy? After all, if entropy counts the number of microstates underlying a macrostate, and many more microstates lead to the same macrostate with inflation, then that should be the case. This topic will be further discussed in section 7 below.
It was shown by Grøn and Hervik [
19,
20] that according to the Einstein’s classical field equations
diverges at the initial singularity both in the case of the homogeneous, but anisotropic Bianchi type I universe models and the isotropic, but inhomogeneous Tolman-Lemaitre Bondi (LTB) universe models. This means that there are large anisotropies and inhomogeneities near the initial singularities in these universe models. Hence the classical behavior of
is not in agreement with the Weyl curvature hypothesis.
Consequently,
is not a suitable quantity to represent the entropy of a gravitational field. The reason for this failure may be that
is a local quantity. In the case of the LTB universe models Grøn and Hervik showed that:
where
is the average density and
the actual density. Near the initial singularity
will be rapidly fluctuating in space between negative and positive values.
If the entropy represents a large number of gravitational microstates corresponding to a certain gravitational field, it may more properly be represented by a non-local quantity proportional to
. Such a quantity may be finite at the initial singularity even if
diverges. Grøn and Hervik therefore considered the entity:
Here
is a constant which is determined below, and
is the invariant volume corresponding to a unit coordinate volume in coordinates co-moving with the cosmic fluid. The behavior of this quantity in LTB universe models with cold matter and LIVE represented by a cosmological constant
in Einstein’s field equations, is as follows [
19,
20]:
Expanding universe with large : In the initial epoch the dust dominates and is increasing linearly with . The universe is becoming more and more inhomogeneous. At late times dominates, and stops growing, evolving asymptotically towards a constant value. The universe inflates.
Expanding universe with small : Again the dust dominates initially. In this case increases forever, but with a decreasing rate and again approaches a constant value asymptotically.
Expanding universe with vanishing
: The quantity
again increases forever, this time approaching asymptotically a function
where
c and
b are constants and
if
and
if
. (The function
is defined in refs. [
19] and [
20].)
Recollapsing universe: Due to the dust term the final singularity will be more inhomogeneous than the initial singularity.
This shows that in the LTB universe the quantity behaves in accordance with the Weyl curvature hypothesis. It should be noted that the Schwarzschild spacetime is a special case of the general LTB models. It has and a vanishing Ricci tensor. Hence, the quantity diverges in the Schwarzschild spacetime. This is in some sense the maximal possible value of , the Weyl tensor is as large as possible, and the Ricci tensor is as small as possible. Thus if one wants to associate entropy with a gravitational field, then at the classical level it seems that the Schwarzschild spacetime has the largest possible value of such a gravitational entropy.
The unphysical divergence of is probably not a physical reality, but due to the lack of a quantum gravity theory. Even though the classical vacuum has vanishing Ricci tensor, a quantum field will fluctuate and cause the expectation value of the square of the Ricci tensor to be non-zero. Hence, there will probably be an upper bound on how large can be, even in a vacuum.
As to the Bianchi type I universe models Grøn and Hervik [
19,
20] showed that magnitude of
at the initial singularity is proportional to the inverse of the dust density. Furthermore in universe models with LIVE a large value of Λ means that
has a small value and a small value of Λ means that
has a large value. For a more general class of universe models dominated by a fluid with equation of state
it was shown that
increases as long as
.
5. The Weyl Curvature Hypothesis and Black Hole Entropy
Rudjord, Grøn and Hervik [
21] have investigated how far the black hole entropy can be accounted for by an entropy,
, due to the inhomogeneity of a gravitational field as suggested in the Weyl curvature hypothesis. This work was followed up by Romero, Thomas and Pérez [
22].
Considering the spacetime of a black hole we define a gravitational entropy current vector by the expression:
where
P2 is a quantity proportional to the Weyl curvature invariant. However, it cannot be given by eq.(32) since the Ricci curvature invariant vanishes in the Schwarzschild spacetime. So Rudjord
et al. [
21] replaced the Wainwright, Anderson expression (32) by:
where the denominator is the Kretschmann curvature scalar. They proved that
in all spacetimes with vanishing energy flux, which encompasses the spacetime outside the most general Kerr-Newman black hole and the isotropic and homogeneous Friedman universe models.
According to eq. (19) the entropy of a black hole is proportional to the area of the black hole horizon. Hence, the entropy can be described as a surface integral over the horizon, σ:
where
has been determined by demanding that the condition
as given in eq. (19) shall be valid for a Schwarzschild black hole. This means that according to the present theory all of the entropy of a Schwarzschild black hole is due to the inhomogeneity of the gravitational field. Writing eq. (37) as a volume integral by means of Gauss’ divergence theorem, the entropy density is:
We now consider static spherically symmetric spaces where the space time line element takes the form:
in curvature coordinates defined by the condition that the invariant area of a spherical surface with radius
r is
. In the Schwarzschild spacetime:
where
is the Schwarzschild radius, and:
giving
. Romero, Thomas and Pérez [
22] showed that
also for the Kerr spacetime. This is of course a rather obvious result, since the Weyl curvature scalar is equal to the Kretschmann curvature scalar in empty space in general. Hence,
in every empty region of an arbitrary spacetime. However in light of both the expressions (32) and (36) something more can be said about the Weyl entropy of a black hole. Considering a black hole as a limit in which space is empty, and the density profile has diverged to a Dirac delta function, the numerator of eq. (32) diverges, while at the same time, the denominator tends to zero. This shows the very strong way that black holes can be considered as the most inhomogeneous possible spacetimes. In this sense one may expect that there is maximal gravitational entropy in the Schwarzschild and Kerr spacetimes, and they can thus be considered to be the most inhomogeneous possible spacetimes.
The covariant expression for the entropy density is:
where
is the determinant of the matrix made of the spatial components
of the spatial metrical tensor. In the Schwarzschild spacetime the gravitational entropy density (33) is:
Rudjord, Grøn and Hervik [
21] then calculated the entropy of the horizons due to the inhomogeneity in the gravitational field of a Reissner-Nordström black hole based upon the expression (38). It turned out that it was less than the Bekenstein-Hawking entropy of a charged black hole. Hence either the gravitational field accounts for only a part of the entropy of a charged black hole, or the expression (38) does not catch up all of the gravitational entropy.
Further they calculated the gravitational contribution to the entropy of the black hole horizon of the Schwarzschild-de Sitter spacetime. This spacetime has two horizons, a black hole horizon and a cosmological horizon. Their radii are [
21]:
where
and
are defined in eq. (14). In the limit that the vacuum energy,
i.e. Λ vanishes, the black hole horizon has a radius
, and in the limit that the mass,
i.e. the Schwarzschild radius, vanishes there is de Sitter spacetime and the cosmological horizon has a radius
. The surface gravities of the horizons in the Schwarzschild-de Sitter spacetime are:
The corresponding entropies are:
Shankaranarayanan [
23] suggested that the entropy of the Schwarzschild-de Sitter spacetime is:
Rudjord, Grøn and Hervik [
21] found that the gravitational contribution according to the expression (38) to the black hole horizon in the Schwarzschild-de Sitter spacetime is:
This expression shows that the gravitational contribution to the black hole horizon entropy decreases with increasing value of Λ. The entropy of the cosmological horizon, , is given by eq.(48) with and replaced by and .
In the limit that
there is de Sitter spacetime with no black hole horizon, only a cosmological horizon with radius
and entropy:
In this limit
. There is no gravitational contribution to the entropy of the de Sitter horizon. This is the “opposite” limit to that of the Schwarzschild black hole limit representing a spacetime in which the gravitational field is homogeneous. This will be the case in all conformally flat spacetimes, for example in all the Friedmann-Robertson-Walker universe models. Hence the entropy of horizons in conformally flat spacetimes must be of nongravitational origin according to the theory based upon the Weyl curvature hypothesis. It should also be noted that Penrose has expressed a doubt as to whether the entropy
associated with the de Sitter horizon has any physical significance. He writes [
24]: “I am inclined to be sceptical about
representing a true entropy in any case, for at least two further reasons. In the first place if
really is a constant, so
is just a fixed number, then
does not give rise to any actually discernible physical degrees of freedom. Moreover, I am not aware of any clear physical argument to justify the entropy
, like the Bekenstein argument for black hole entropy.”
6. Is There a Maximal Entropy for the Universe?
Processes supporting the existence of life in the universe depend upon the possibility that the entropy has not yet reached a maximal value where all organized activity cease. But there still remains some ambiguity about how to best define the maximum entropy. This question was recently discussed by Egan [
25]. There are several conjectures as to what the maximal entropy may be [
26]. One is the so-called
Bekenstein bound [
27]. The maximum entropy of a system with radius
R and non-gravitational energy
E is:
The physical meaning is that the entropy lost into a black hole cannot be larger than the increase in the horizon entropy of the black hole. In the context of a flat FRW-universe the Bekenstein bound says that the maximal entropy inside a co-moving surface with standard coordinate radius
is:
where
is the density of the cosmic fluid and
a the scale factor. For a universe dominated by a cosmic fluid with equation of state
, the density changes during the expansion according to
where
is the present density. Hence the Bekenstein bound of the cosmic entropy is proportional to
. In the radiation dominated that lasts for about fifty thousand years after the Big Bang, the dominating fluid,
i.e. the radiation, had
. Hence
the Bekenstein maximum of entropy was constant during the radiation dominated era. For cosmic matter with
, for example cold dark matter with
, the Bekenstein bound increases with time, and for cosmic dark energy with
the Bekenstein bound of maximal entropy increases faster that in the matter dominated era.
Secondly the
Holographic bound [
28,
29] may be formulated by asserting that for a given volume
V, the state of maximal entropy is the one containing the largest black hole that fits inside
V, and this maximum is given by the finite area that encloses this volume. The maximum entropy is not proportional to the volume as one might have expected. As applied to the space inside the cosmological horizon in a FRW universe this gives the entropy bound:
In the present era of our universe which is dominated by dark energy, possibly in the form of LIVE, the holographic bound (52) increases exponentially fast in the future. Several versions of this bound have been discussed by Custadio and Horvath [
30]. However, as noted by Veneziano [
31], entropy in cosmology is extensive,
i.e. it grows like
, but the holographic entropy boundary grows like
. Therefore at sufficiently large
the holographic entropy boundary must be violated.
Frautschi [
32] identified the maximum entropy inside the particle horizon of a universe as the entropy that is produced if all matter inside the horizon collapses to a single black hole. Again as applied to a flat FRW universe this leads to:
For a universe dominated by a cosmic fluid with equation of state , this implies that . Hence, an era dominated by cold matter has approximately constant value for this upper bound on the entropy. The bound decreased in the radiation dominated era and increases in the present and future LIVE-dominated era.
Pavon and Radicella [
33] have recently discussed the question whether the entropy of the universe will tend to a maximum. They took as a point of departure that the dominating contribution to the entropy of the universe is that associated with a cosmological horizon, and represented for simplicity the horizon by the surface around an observer where the velocity of the Hubble flow is equal to the velocity of light. Hence the physical radius of the surface is equal to the Hubble radius,
. The area of this surface is
, and the entropy is:
The Hubble factor and hence the entropy is here assumed to be given as a function of the scale factor, , and differentiation of with respect to a is denoted by . According to the second law of thermodynamics the entropy of the universe does not decrease, . Then, if the entropy shall reach a maximum the condition must be obeyed for large values of a.
Let us look at the time evolution of
in the flat ΛCDM universe model which has:
where
and
are the present values of the density parameter of LIVE and dark matter, respectively. Hence
In this universe model, which is compatible with all cosmological observations so far, the entropy approaches the finite maximal value .
7. Entropy Change During the Inflationary Era
The importance of gravity for the establishment of an arrow of time in the universe was emphasized by Davies [
34] in an article titled
Inflation and the time asymmetry in the universe. He noted that when gravity is attractive, gravity tends to contract matter and, if possible, make black holes. In this case a smooth distribution of matter represents a small gravitational entropy.
However if gravity is repulsive so that gravity tends to smoothen the distribution of matter and energy, it seems natural to say that a state with an irregular mass distribution would be a low entropy state and a smooth state would be one of maximal entropy. Under attractive gravity an inhomogeneous clumped field has high entropy, but with the switch to repellent gravity it is redefined as low entropy. Concentrations of mass, i.e. curvature, try to smooth themselves out and the gravitational field tends towards uniformity.
This way of talking about gravitational entropy is in accordance with the Second Law, securing that gravitational entropy increases during a period dominated by repulsive gravity. However, it is in conflict with the definition of gravitational entropy defined as an expression of inhomogeneity of a gravitational field. A general agreement as to how one should define and describe mathematically the gravitational contribution to the cosmic entropy during a period dominated by repulsive gravity has not yet been obtained.
Before the Planck time, s, the universe was probably in a state of quantum gravitational fluctuations. Then it entered an inflationary era lasting for about s dominated by dark energy with a huge density, possibly in the form of LIVE. The universe then evolved exponentially fast toward a smooth and maximally symmetric de Sitter space which represents the equilibrium end state with maximal entropy when the evolution is dominated by a non-vanishing cosmological constant. This was an essentially adiabatic expansion with small changes of entropy.
At the end of the inflationary era the entropic situation changed abruptly. The vacuum energy was transformed to radiation and matter, gravity became attractive, and it became favorable for the Universe to grow clumpy. As pointed out by Veneziano [
31] in any inflationary scenario, most of the present entropy is the result of these dissipative processes. But not only did the entropy of the matter increase. Also the value of the maximum possible entropy increased–and much more than the actual entropy. Hence a large gap opened up between the actual entropy of the universe and the maximum possible entropy. According to Davies this accounts for all the observed macroscopic time asymmetry in the physical world and imprints an arrow of time on it.
Page [
35] has disputed this conclusion. He argues that because the de Sitter spacetime, the perturbed form of which is equal to the spacetime during most of the inflationary era, is time symmetric, then for every solution of Einstein’s equations which corresponds to decaying perturbations, there will be a time-reversed solution which describes growing perturbations. Page also noted that a sufficient, though not necessary condition for decaying perturbations is the absence of correlations in the perturbations in the region. Davies answered [
36]: The perturbations will only grow if they conspire to organize themselves over a large spatial region in a cooperative fashion. Hence, it is necessary to explain why it is reasonable for the universe to have been in a state with no correlations initially.
Davies then went on to give the following explanation. Due to repulsive gravitation de Sitter spacetime may be considered to be a state of equilibrium with maximal entropy. But quantum effects will cause fluctuations about the de Sitter background. Large fluctuations are much rarer than small fluctuations. At the minimum point of such a fluctuation the perturbations will be uncorrelated. A randomly chosen perturbed state will almost certainly be such a state of no correlations at the minimum of a fluctuation curve. This state is thus one in which the perturbations will decay rather than grow whichever direction of time is chosen as forward.
Hence inflation lowers the “Weyl-entropy” in a co-moving volume and expansion raises it, and it is not obvious which should dominate. We shall therefore calculate the “Weyl-entropy” change during the inflationary era in a plane-symmetric Bianchi type I universe dominated by LIVE, using given in eq. (34) and with given in eq. (38), as measures of gravitational entropy.
The line element of the LIVE-dominated, plane symmetric Bianchi type I universe is [
37]:
here:
The co-moving volume is:
For this spacetime the Ricci scalar, the Weyl scalar and the Kretschmann curvature scalar are, respectively:
Hence, the quantities
given in eq.(32) and
given in eq.(38) are, respectively:
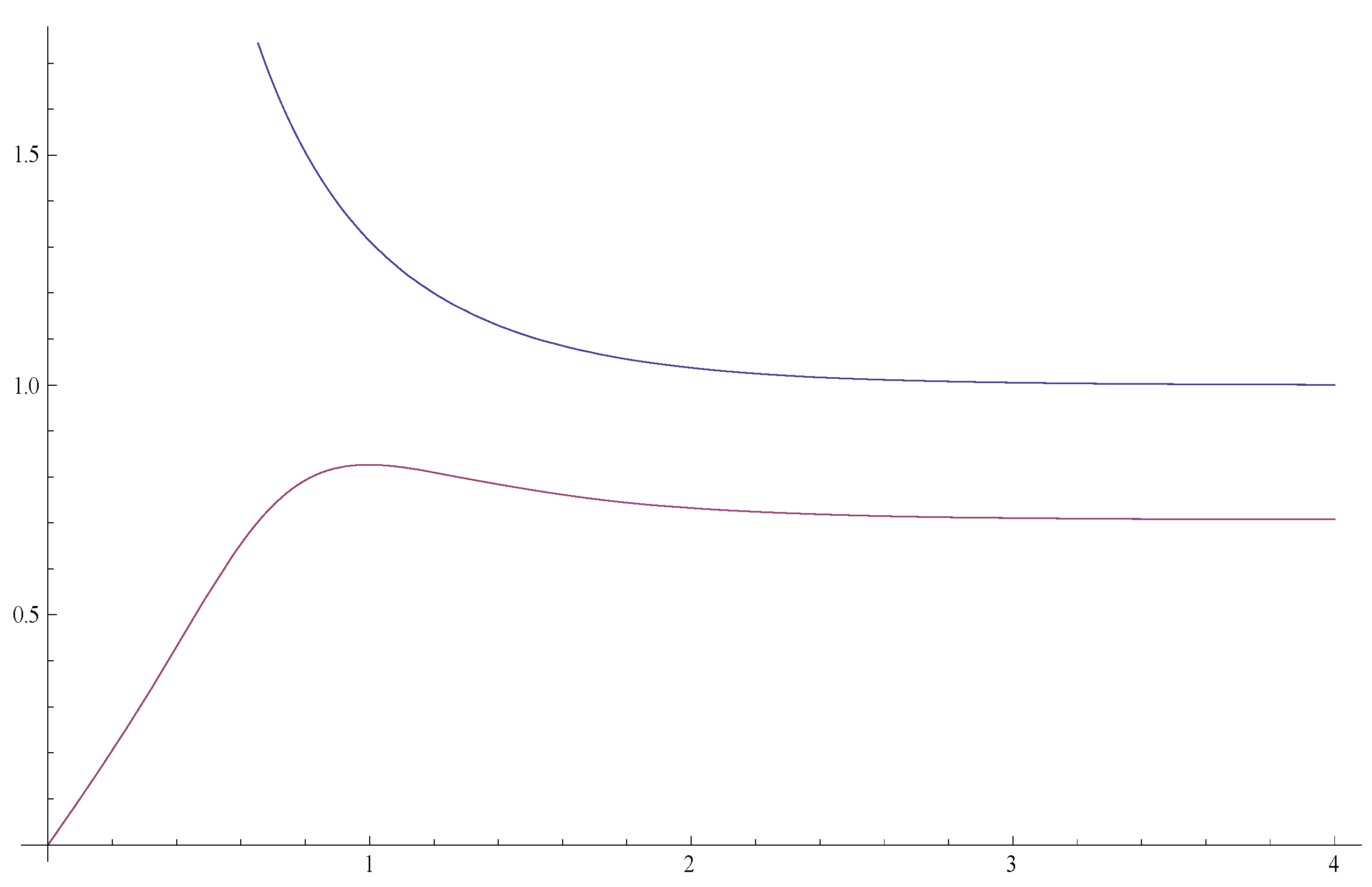
The time variations of these quantities at the beginning of the inflationary era are shown in
Figure 3.
Figure 3.
Time-variation of the candidate gravitational entropies (upper curve) and in a comoving volume during the beginning of the inflationary era.
Figure 3.
Time-variation of the candidate gravitational entropies (upper curve) and in a comoving volume during the beginning of the inflationary era.
We see that if or were a dominating form of entropy, then the entropy of the universe decreased during most part of the inflationary era except possibly during a transient initial period.
Davies [
36] further mentioned the problem of deciding whether the cosmic initial conditions are very inhomogeneous resembling a universe with primordial black holes or more homogeneous. If it was too inhomogeneous when it entered the inflationary era the inhomogeneities might not have been sufficiently inflated during the inflationary era to let the universe evolve towards the homogeneous state it was in 400,000 years after the Big Bang when the relative temperature deviations,
from homogeneity was of the order of magnitude 10
-5.
More research should be performed on the evolution of the cosmic entropy during the inflationary era. Even during an inflationary era, particularly a late phase lambda dominated one, even though the lambda term dominates the overall expansion, locally, gravity remains attractive, and so one should consider scenarios which are a mixture of repulsive gravity at large scales, and attractive at small ones.
8. The Entropy of the Universe
Frampton, Hsu, Kephart and Reeb [
38] have recently calculated the entropy within the observable part of the universe. This has been followed up by Egan and Lineweaver [
39]. They have presented still more accurate results and also include the entropy of the cosmological horizon.
The observable part of the universe is that part which is inside the event horizon, and has at the present time the magnitude
. Egan and Lineweaver found that the baryonic matter in the universe in the form of stars and interstellar gas and dust contributes with
. The microwave background radiation has an entropy
where
is the
Stefan-Boltzmann constant, and the present temperature of the radiation is
. This gives
. The entropy of the relic neutrinos is a factor 11/4 larger,
i.e. . Egan and Lineweaver [
39] have also estimated the entropy of relic gravitons,
. The entropy of the dark matter was found to be
. All of these entropy contributions are thermodynamic. Then come two contributions that may be due to inhomogeneous gravitational fields. The entropy of the stellar black holes with masses
where
is the mass of the Sun, is calculated to be
. The corresponding entropy of the supermassive black holes in the centers of the galaxies was found to be
. Hence these gravitational contributions to the entropy of the Universe are much larger than the thermodynamic contributions. Frampton [
40] has suggested that intermediate mass black holes in galactic haloes may contribute with even more entropy, up to
. The entropy of the cosmic event horizon is vast,
where
giving
. Since the spacetime of the universe model is conformally flat, all of this entropy is of non-gravitational origin according to the theory based upon the Weyl curvature hypothesis. The physical significance and origin of this dominating entropy is still not known.
The time evolution of the entropy of the universe was summarized briefly by Egan and Lineweaver [
39]. I will here neglect the evolution of the entropy associated with the cosmological horizon, as the physical significance of this is rather speculative and not well understood.
At the Planck time,
the universe may have fluctuated into an inflationary era dominated by vacuum energy and lasting for about
. During this era the universe became increasingly homogeneous. Then the thermodynamic entropy increased, but as shown above (see
Figure 3) the gravitational entropy based upon the Weyl curvature hypothesis decreased, and the sum of the two can be a decreasing function of time.
If this theory is correct, we have to modify the second law of thermodynamics. The usual formulation is then generally valid only when the dominating cosmic gravity is attractive. In that case the entropy of the universe cannot decrease, as we are used to. But the entropy of the universe may decrease if the processes determining the change of the entropy in the universe are dominated by repulsive gravity like in the inflationary era. Hence, if the arrow of time is due to gravitational entropy, then the arrow of time may have been directed along decreasing entropy in the inflationary era. As mentioned above there is no general agreement as to how the gravitational contribution to the cosmic entropy shall be defined.
At the end of the inflationary era the vacuum energy was transformed to radiation and matter with an enormous heating involved, and gravity became attractive. This produced an increase of thermodynamic entropy by many orders of magnitude, and the maximal value of the cosmic entropy increased so much that a vast entropy gap opened up, but the Weyl gravitational entropy remained low.
After about a hundred million years the first stars formed from collapsing clouds of hydrogen and helium, and shortly thereafter the first black holes formed. The entropy in stellar black holes increased rapidly during the galactic evolution. Subsequently the gravitational entropy increased further due to the formation of supermassive black holes in the centers of the galaxies. In a far away future the black holes may disappear due to Hawking radiation, and the asymptotic future of the entropy budget will then be radiation dominated. One may wonder whether the disappearance of black holes is an entropy increasing process according to the conventional description of the entropy of black holes and of the form of energy which is Hawking radiated from a black hole. Presumably it is so, and the entropy increase in Hawking evaporation has been estimated by Zurek [
41].
9. Conclusions
In this article we have considered four types of entropy: the usual thermal entropy as interpreted by Boltzmann, entropy of black holes, entropy of cosmological event horizons and entropy associated with the inhomogeneity of gravitational fields, as suggested by the Weyl curvature hypothesis. The generalized Second Law of Thermodynamics says that the sum of all these entropies in the universe cannot decrease.
The gravitational entropy given by the volume integral of the divergence of the square root of the ratio between the Weyl- and Kretschmann curvature scalars is in general different from the Bekenstein-Hawking entropy of the horizons in an arbitrary spacetime. However the Schwarzschild spacetime seems to be an exceptional case in which all of the horizon-entropy comes from the gravitational entropy due to the inhomogeneity of the gravitational field. On the other hand all conformally flat spacetimes have vanishing gravitational entropy. This is the case for all of the Friedmann universe models if local inhomogeneities are neglected. In particular there is no gravitational contribution to the entropy of the cosmological horizon of the de Sitter universe.
If the universe has evolved from an initial rather homogeneous state, the gravitational entropy was low at the beginning. Also a vast reduction of the gravitational entropy may have taken place in the inflationary era while the thermodynamical entropy increased. At the end of the inflationary era the universe was in a state with a high degree of homogeneity and nearly perfect thermal equilibrium. During the later condensation of matter and increment of local inhomogeneities the temperature differences increased, but due to release of gravitational energy which was transformed to thermal energy, the thermodynamical entropy increased also during these processes. Furthermore there was a great increase of gravitational entropy due to gravitational condensation with production of a large number of black holes in our universe.
Quantum calculations show that an inhomogeneous universe is more likely to be spontaneously created than a homogeneous one, and that a universe with a large cosmological constant is more likely to be created than a universe with a small cosmological constant.
As to the evolution of entropy in our expanding universe, it was noted by Wallace [
2] that although the early universe was at local thermal equilibrium, it was not at global thermal equilibrium because of the expansion of the universe and because it was highly uniform, and the process of becoming non-uniform is entropy-increasing when conversion of gravitational energy to thermal energy and emission of electromagnetic radiation is taken into account. However, the dominating entropy-increasing processes are the formation of black holes.