Expectation Values and Variance Based on Lp-Norms
Abstract
:1. Introduction
2. The Generalized Formal Scheme of Means Characterization
2.1. The Means Characterization Based on Optimization Methods
2.2. Formal Scheme of Means Characterization
3. The Concept of -Expectation Values
3.1. The Non-Euclidean Norm Operator
- (i)
- The non-Euclidean mean of is the Euclidean mean of
- (ii)
- Zero-mean of ,
- (iii)
- (iv)
- In the Euclidean case, degenerates to the identity operator .
- (v)
- Linear operations: .Hence, , which reads Equation (8).
- (vi)
- Non-additivity of : .
- (vii)
- Inverse of non-Euclidean norm operator, , ,
3.2. The Non-Euclidean -Mean Estimator and Its Expectation Value
3.3. Examples
3.3.1. Gas at Thermal Equilibrium
3.3.2. Plasma Out of Thermal Equilibrium
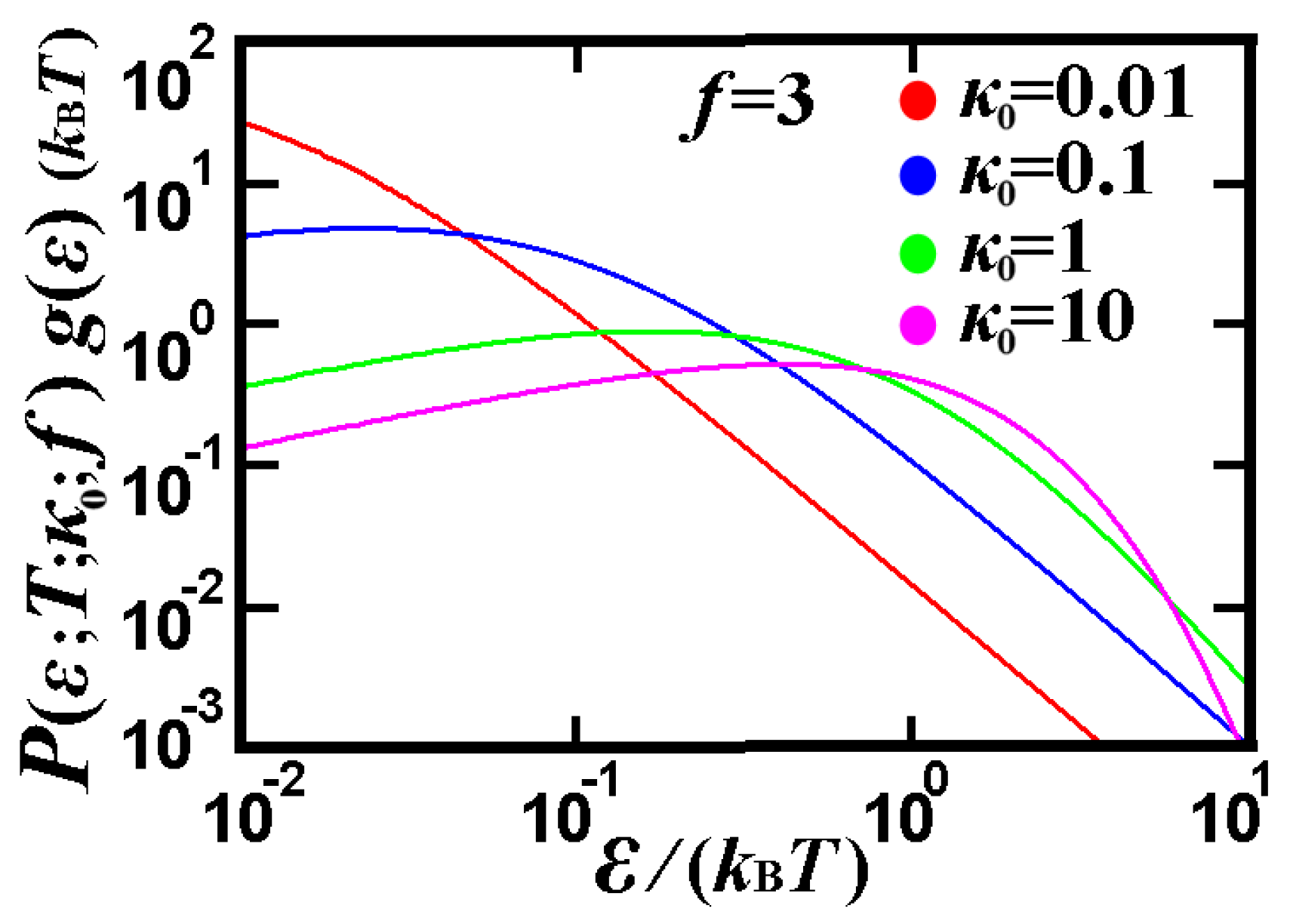
3.3.3. D-Dimensional Quantum Harmonic Oscillator in Thermal Equilibrium
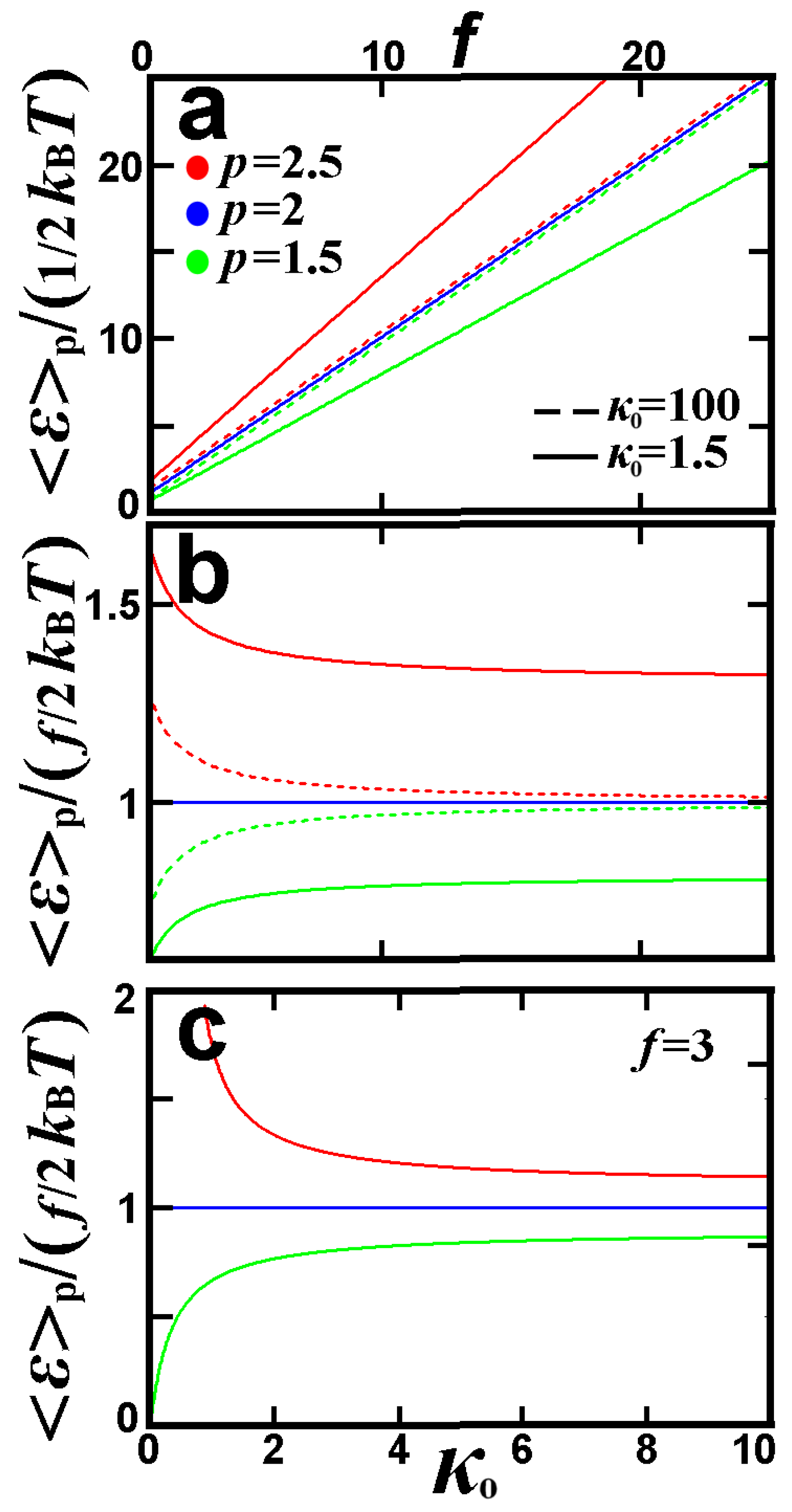
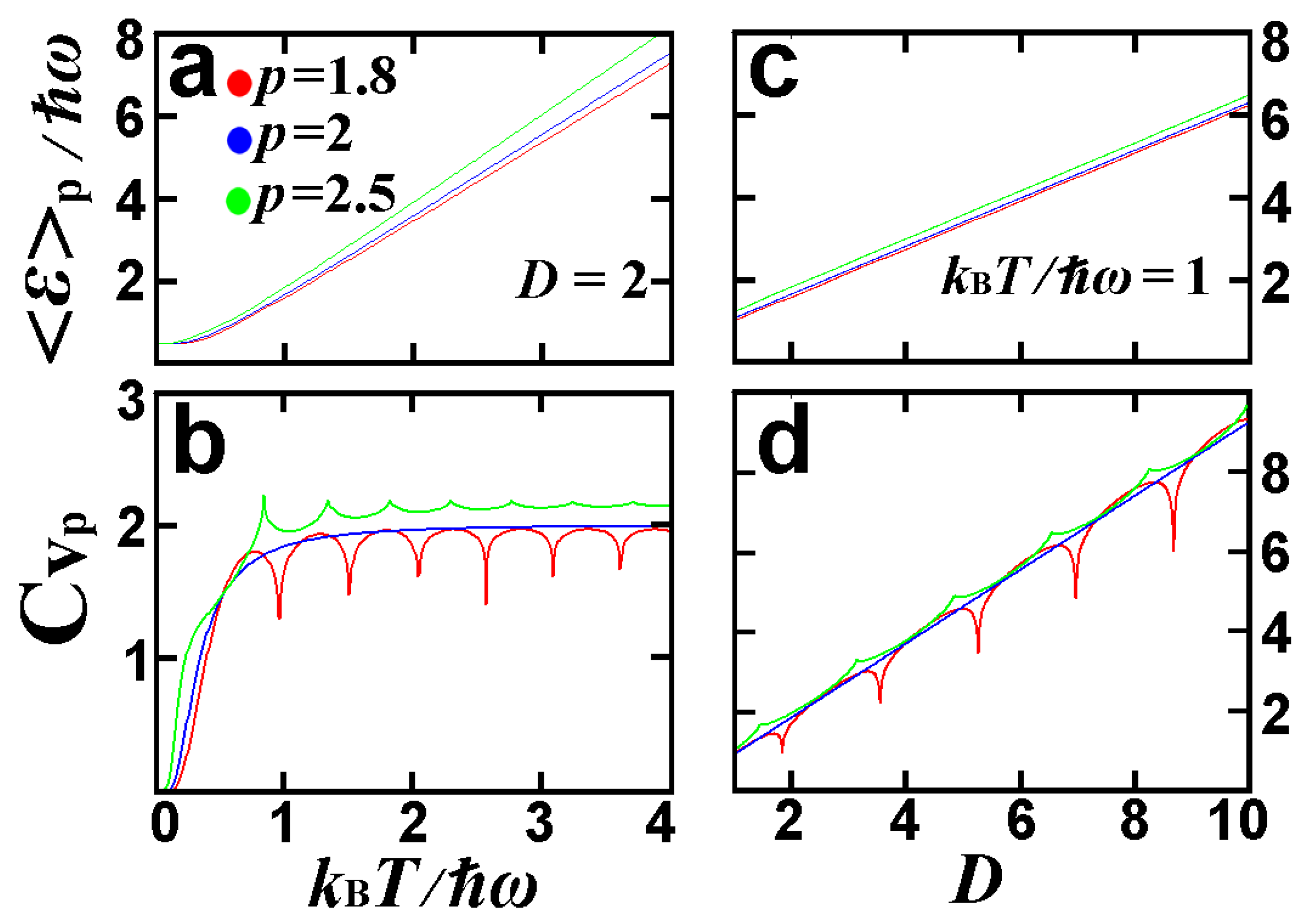
4. The Non-Euclidean -Variance of the -Expectation Value
4.1. Preliminaries: Formulations
4.2. Examples
4.2.1. Example 1: Gaussian distribution
4.2.2. Example 2: Generalized Gaussian distribution
4.3. Justification of the -Variance Expression
5. Further Analytical and Numerical Examples
5.1. Analytical Example: The Spectrum of the Means and Its Degeneration
5.2. Numerical Example: Earth’s Magnetic Field
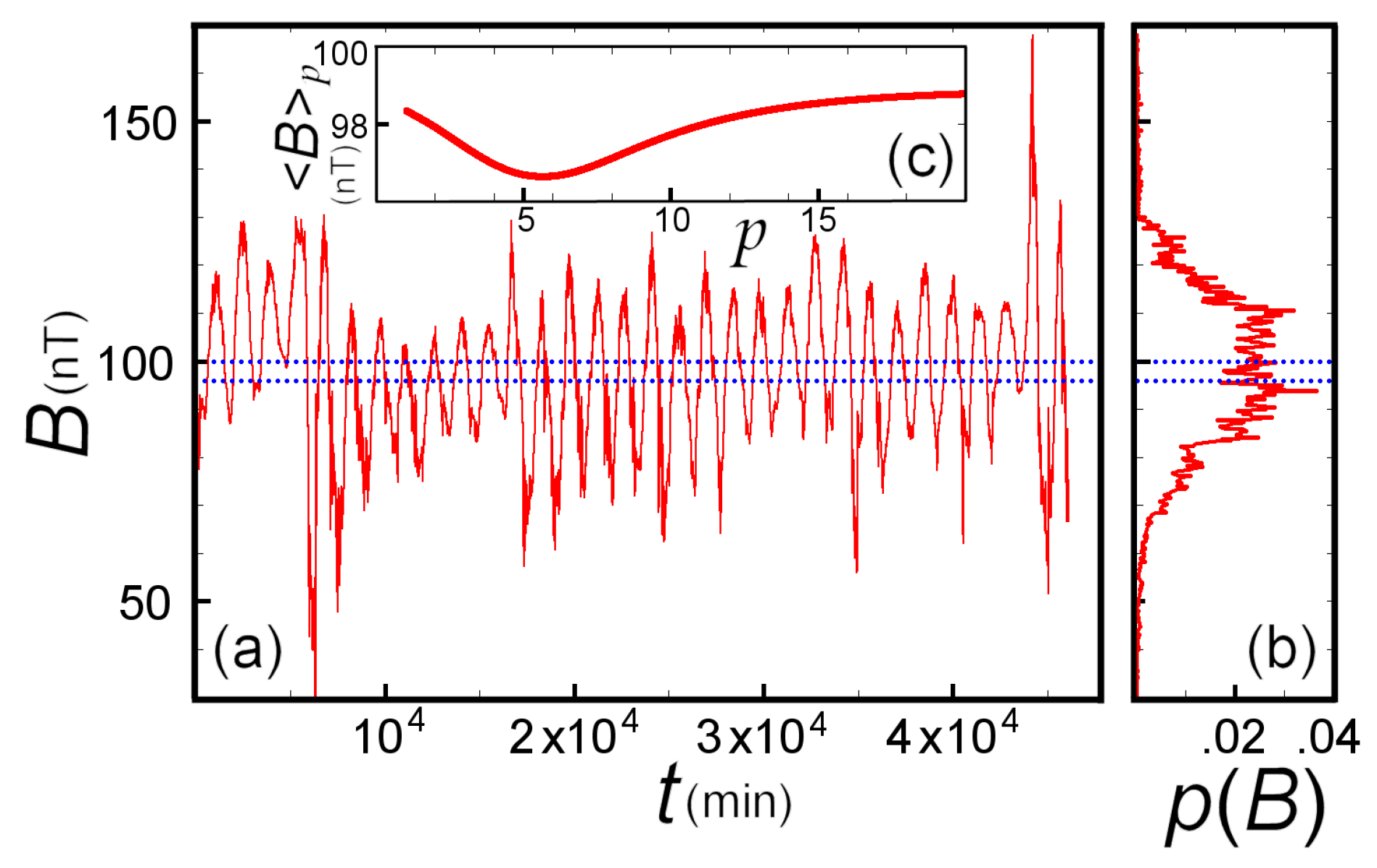
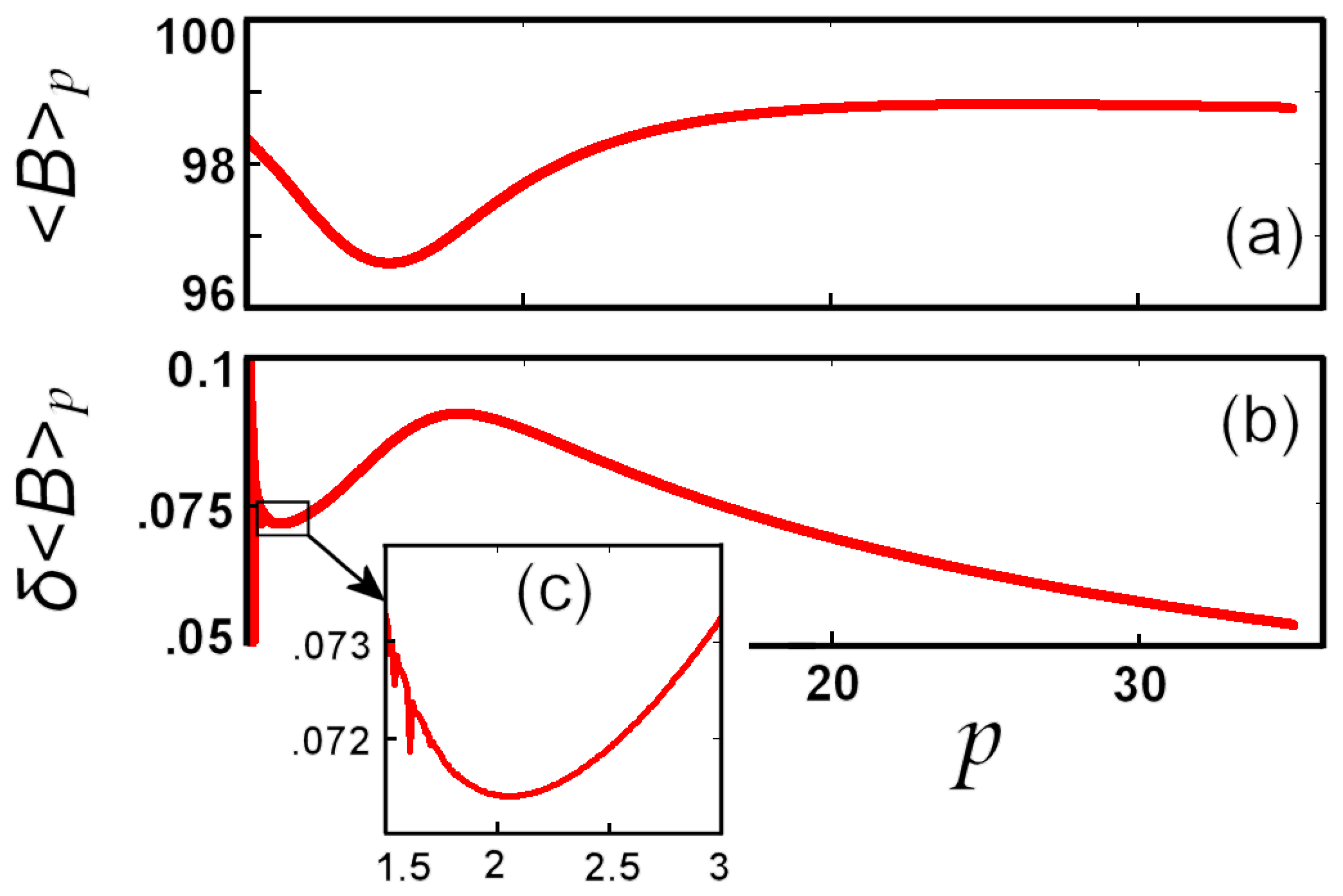
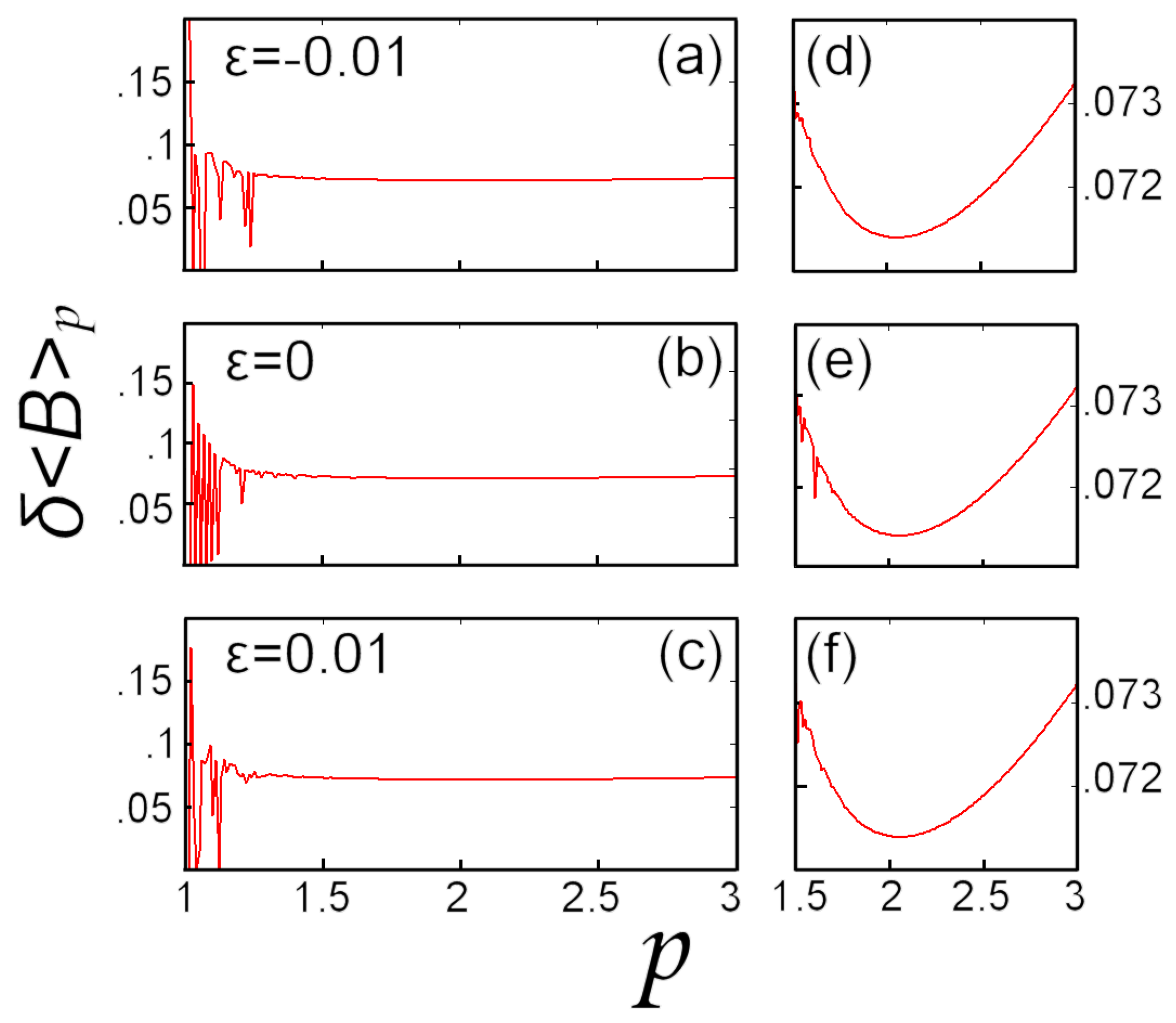
6. Conclusions
References
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Kolmogorov, A.N. Sur la notion de la moyenne (in French). Atti Accad. Naz. Lincei 1930, 12, 388–391. [Google Scholar]
- Nagumo, M. Uber eine Klasse der Mittelwerte (in German). Jpn. J. Math. 1930, 7, 71–79. [Google Scholar]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1934. [Google Scholar]
- Ben-Tal, A. On generalized means and generalized convex functions. J. Optimiz. 1977, 21, 1–13. [Google Scholar] [CrossRef]
- Páles, Z. On the characterization of quasi arithmetic means with weight function. Aequationes Math. 1987, 32, 171–194. [Google Scholar] [CrossRef]
- Livadiotis, G. Approach to block entropy modeling and optimization. Physica A 2008, 387, 2471–2494. [Google Scholar] [CrossRef]
- Bajraktarevic, M. Sur un equation fonctionelle aux valeurs moyens (in French). Glas. Mat.-Fiz. Astronom. 1958, 13, 243–248. [Google Scholar]
- Aczél, J.; Daroczy, Z. On Measures of Information and Their Characterization; Academy Press: New York, NY, USA, 1975. [Google Scholar]
- Norries, N. General means and statistical theory. Am. Stat. 1976, 30, 8–12. [Google Scholar]
- Kreps, D.M.; Porteus, E.L. Temporal resolution of uncertainty and dynamic choice theory. Econometrica 1978, 46, 185–200. [Google Scholar] [CrossRef]
- Flandrin, P. Separability, positivity, and minimum uncertainty in time-frequency energy distributions. J. Math. Phys. 1998, 39, 4016–4039. [Google Scholar] [CrossRef]
- Czachor, M.; Naudts, J. Thermostatistics based on Kolmogorov–Nagumo averages: Unifying framework for extensive and nonextensive generalizations. Phys. Lett. A 2002, 298, 369–374. [Google Scholar] [CrossRef]
- Dukkipati, A.; Narasimha-Murty, M.; Bhatnagar, S. Uniqueness of nonextensive entropy under Renyi’s recipe. Comp. Res. Rep. 2005, 511078. [Google Scholar]
- Tzafestas, S.G. Applied Control: Current Trends and Modern Methodologies; Electrical and Computer Engineering Series; Marcel Dekker, Inc.: New York, 1993. [Google Scholar]
- Koch, S.J.; Wang, M.D. Dynamic force spectroscopy of protein-DNA interactions by unzipping DNA. Phys. Rev. Lett. 2003, 91, 028103. [Google Scholar] [CrossRef] [PubMed]
- Still, S.; Kondor, I. Regularizing portfolio optimization. New J. Phys. 2010, 12, 075034. [Google Scholar] [CrossRef]
- Livadiotis, G. Approach to general methods for fitting and their sensitivity. Physica A 2007, 375, 518–536. [Google Scholar] [CrossRef]
- Bavaud, F. Aggregation invariance in general clustering approaches. Adv. Data Anal. Classif. 2009, 3, 205–225. [Google Scholar] [CrossRef]
- Gajek, L.; Kaluszka, M. Upper bounds for the L1-risk of the minimum L1-distance regression estimator. Ann. Inst. Stat. Math. 1992, 44, 737–744. [Google Scholar] [CrossRef]
- Huber, P. Robust Statistics; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Hampel, F.R.; Ronchetti, E.M.; Rousseeuw, P.J.; Stahel, W.A. Robust Statistics. The Approach Based on Influence Functions; John Willey & Sons: New York, NY, USA, 1986. [Google Scholar]
- Aczél, J. On mean values. Bull. Amer. Math. Soc. 1948, 54, 392–400. [Google Scholar] [CrossRef]
- Aczél, J. Lectures on Functional Equations and Their Applications; Academy Press: New York, NY, USA, 1966. [Google Scholar]
- Toader, G.; Toader, S. Means and generalized means. J. Inequal. Pure Appl. Math. 2007, 8, 45. [Google Scholar]
- Livadiotis, G.; McComas, D.J. Beyond kappa distributions: Exploiting Tsallis statistical mechanics in space plasmas. J. Geophys. Res. 2009, 114, A11105. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Livadiotis, G.; McComas, D.J. Invariant kappa distribution in space plasmas out of equilibrium. Astrophys. J. 2011, 741, 88. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Measure of the departure of the q-metastable stationary states from equilibrium. Phys. Scripta 2010, 82, 035003. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Exploring transitions of space plasmas out of equilibrium. Astrophys. J. 2010, 714, 971. [Google Scholar] [CrossRef]
- Melissinos, A.C. Experiments in Modern Physics; Academic Press Inc.: London, UK, 1966; pp. 438–464. [Google Scholar]
- Kantelhardt, J.; Zschiegner, S.A.; Koscielny-Bunde, E.; Bunde, A.; Havlin, S.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Attempt to distinguish electric signals of a dichotomous nature. Phys. Rev. E 2003, 68, 031106. [Google Scholar] [CrossRef]
- Hassani, H.; Thomakos, D. A review on singular spectrum analysis for economic and financial time series. Stat. Interface 2010, 3, 377–397. [Google Scholar] [CrossRef]
- Mahmoudvand, R.; Hassani, H. Two new confidence intervals for the coefficient of variation in a normal distribution. J. Appl. Stat. 2009, 36, 429–442. [Google Scholar] [CrossRef]
© 2012 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Livadiotis, G. Expectation Values and Variance Based on Lp-Norms. Entropy 2012, 14, 2375-2396. https://doi.org/10.3390/e14122375
Livadiotis G. Expectation Values and Variance Based on Lp-Norms. Entropy. 2012; 14(12):2375-2396. https://doi.org/10.3390/e14122375
Chicago/Turabian StyleLivadiotis, George. 2012. "Expectation Values and Variance Based on Lp-Norms" Entropy 14, no. 12: 2375-2396. https://doi.org/10.3390/e14122375
APA StyleLivadiotis, G. (2012). Expectation Values and Variance Based on Lp-Norms. Entropy, 14(12), 2375-2396. https://doi.org/10.3390/e14122375



