Violation of the Third Law of Black Hole Thermodynamics inHigher Curvature Gravity
Abstract
:1. Introduction
2. Black Hole Solution in the Einstein–GB-Λ System
2.1. Model
2.2. Solutions
2.3. Properties of the Solutions
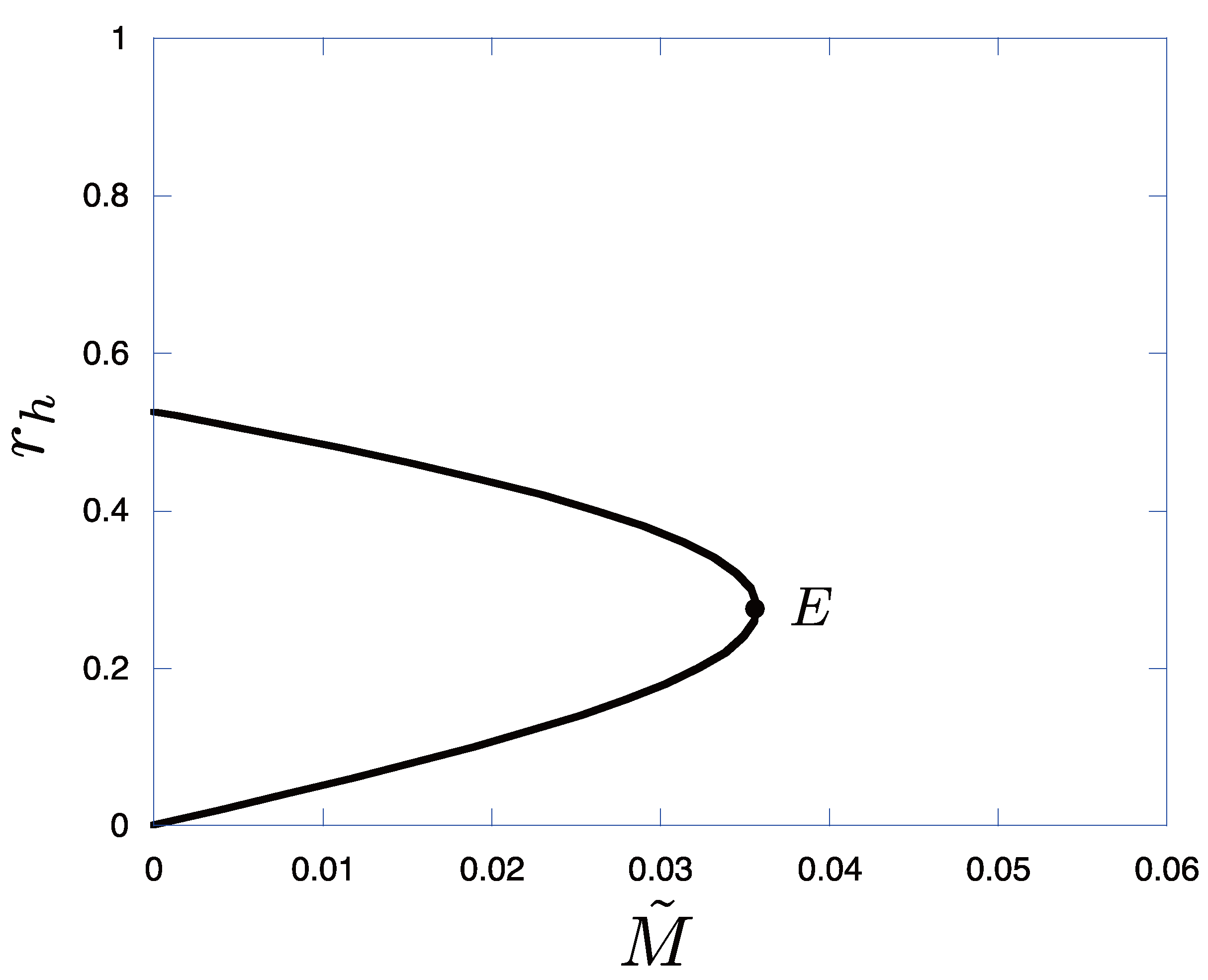
3. Equation of Motion of the Thin Dust Shell
4. Motion of the Shell in 6-dimensional Spacetime
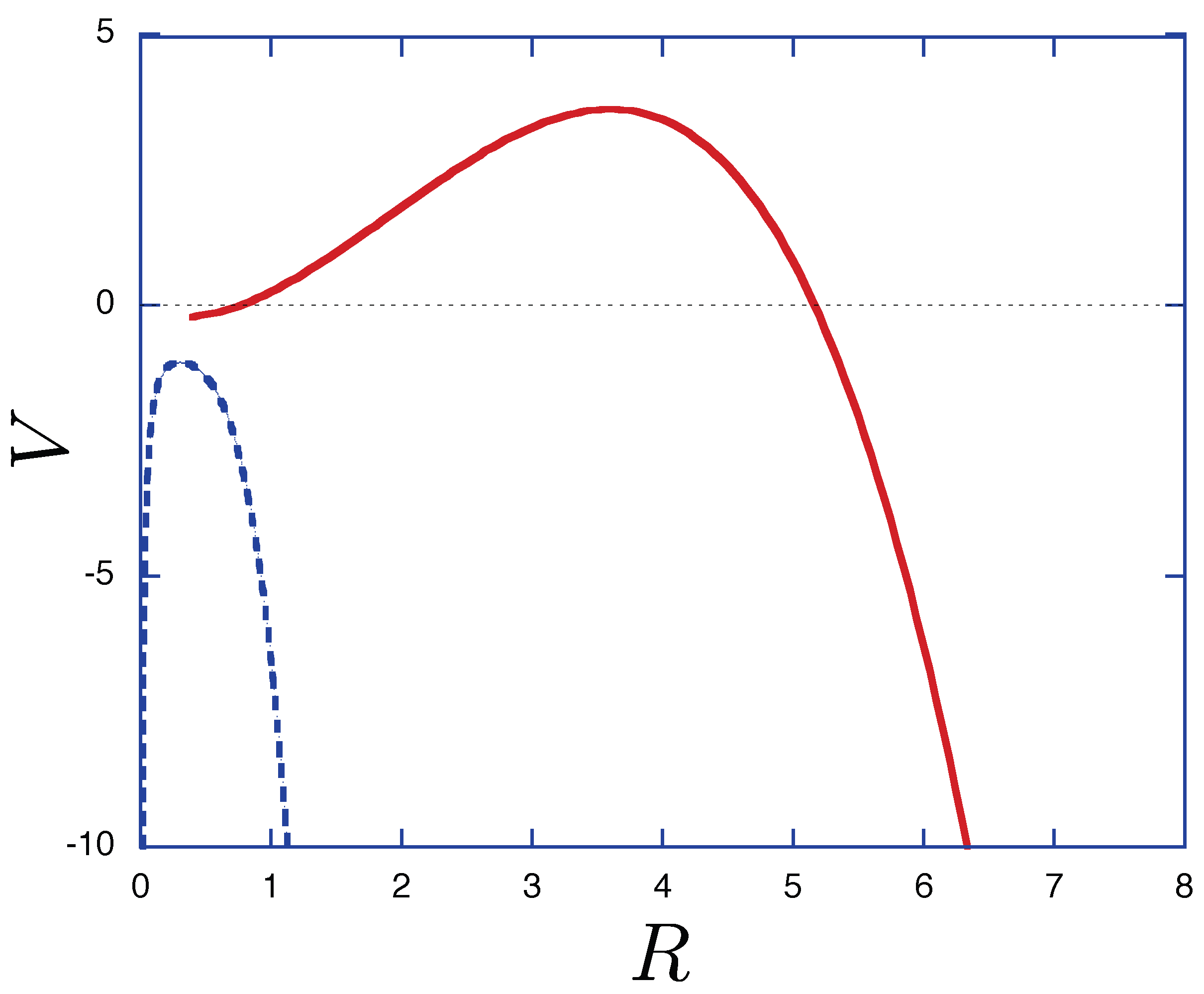
5. Conclusions
Acknowledgments
References
- Wald, R.M. Gravitation, thermodynamics and quantum theory. Class. Quantum Grav. 1999, 16, A177–A190. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Hawking, S.W. Black-hole evaporation. Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black-holes and the second law. Lett. Nuovo Cimento 1972, 4, 737–740. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Generalized second law of thermodynamics in black-hole physics. Phys. Rev. D 1974, 9, 3292–2200. [Google Scholar] [CrossRef]
- Unruh, W.G.; Wald, R.M. Acceleration radiation and the generalized second law of thermodynamics. Phys. Rev. D 1982, 25, 942–958. [Google Scholar] [CrossRef]
- Zurek, W.H.; Thorne, K.S. Statistical mechanical origin of the entropy of a rotating, charged black hole. Phys. Rev. Lett. 1985, 54, 2171–2175. [Google Scholar] [CrossRef] [PubMed]
- Frolov, V.P.; Page, D.N. Proof of the generalized second law for quasistationary semiclassical black holes. Phys. Rev. Lett. 1993, 71, 3902–3905. [Google Scholar] [CrossRef] [PubMed]
- Wald, R.M. “Nernst theorem" and black hole thermodynamics. Phys. Rev. D 1997, 56, 6467–6474. [Google Scholar] [CrossRef]
- Boulware, D.G. Naked singularities, thin shells, and the reissner-nordström metric. Phys. Rev. D 1973, 8, 2363–2368. [Google Scholar] [CrossRef]
- Wald, R.M. Gedanken experiments to destroy a black hole. Ann. Phys. 1974, 82, 548–556. [Google Scholar] [CrossRef]
- Israel, W. Third law of black-hole dynamics: A formulation and proof. Phys. Rev. Lett. 1986, 57, 397–399. [Google Scholar] [CrossRef] [PubMed]
- Racz, I. Does the third law of black hole thermodynamics really have a serious failure? Class. Quantum Grav. 2000, 17, 4353–4356. [Google Scholar] [CrossRef]
- Lue, A.; Weinberg, E.J. Gravitational properties of monopole spacetimes near the black hole threshold. Phys. Rev. D 2000, 61, 124003:1–124003:10. [Google Scholar] [CrossRef]
- Strominger, A.; Vafa, C. Microscopic origin of the Bekenstein-Hawking entropy. Phys. Lett. B 1996, 379, 99–104. [Google Scholar] [CrossRef]
- Maldacena, J.M.; Strominger, A. Statistical entropy of four-dimensional extremal black holes. Phys. Rev. Lett. 1996, 77, 428–429. [Google Scholar] [CrossRef] [PubMed]
- Maldacena, J.M. The large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–251. [Google Scholar]
- Witten, E. Anti-de sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar]
- Gross, D.J.; Sloan, J.H. The quartic effective action for the heterotic string. Nucl. Phys. B 1987, 291, 41–89. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O. Maximally symmetric cosmological solutions of higher-curvature string effective theories with dilatons. Phys. Lett. B 1996, 368, 198–201. [Google Scholar] [CrossRef]
- Zwieback, B. Curvature squared terms and string theories. Phys. Lett. B 1985, 156, 315–317. [Google Scholar] [CrossRef]
- Zumino, B. Gravity theories in more than four dimensions. Phys. Rep. 1986, 137, 109–114. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Boulware, D.G.; Deser, S. String-generated gravity models. Phys. Rev. Lett. 1985, 55, 2656–2660. [Google Scholar] [CrossRef] [PubMed]
- Torii, T.; Maeda, H. Spacetime structure of static solutions in Gauss-Bonnet gravity: Neutral case. Phys. Rev. D 2005, 71, 124002:1–124002:18. [Google Scholar] [CrossRef]
- Torii, T.; Maeda, H. Spacetime structure of static solutions in Gauss-Bonnet gravity: Charged case. Phys. Rev. D 2005, 72, 064007:1–064007:19. [Google Scholar] [CrossRef]
- Nozawa, M.; Maeda, H. Dynamical black holes with symmetry in Einstein-Gauss-Bonnet gravity. Class. Quantum Grav. 2008, 25, 055009:1–055009:21. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole entropy is the Noether charge. Phys. Rev. D 1993, 48, R3427–R3431. [Google Scholar] [CrossRef]
- Iyer, V.; Wald, R.M. Some properties of the Noether charge and a proposal for dynamical black hole entropy. Phys. Rev. D 1994, 50, 846–864. [Google Scholar] [CrossRef]
- Iyer, V.; Wald, R.M. Comparison of the Noether charge and Euclidean methods for computing the entropy of stationary black holes. Phys. Rev. D 1995, 52, 4430–4439. [Google Scholar] [CrossRef]
- Israel, W. Singular hypersurfaces and thin shells in general relativity. Nuovo Cimento B 1966, 44, 1–14. [Google Scholar] [CrossRef]
- Davis, S.C. Generalized Israel junction conditions for a Gauss-Bonnet brane world. Phys. Rev. D 2003, 67, 024030:1–024030:4. [Google Scholar] [CrossRef]
- Gravanis, E.; Willison, S. Israel conditions for the Gauss?Bonnet theory and the Friedmann equation on the brane universe. Phys. Lett. B 2003, 562, 118–126. [Google Scholar] [CrossRef]
- Cai, R.-G. Gauss-Bonnet black holes in AdS spaces. Phys. Rev. D 2002, 65, 084014:1–084014:9. [Google Scholar] [CrossRef]
- Tangherlini, F.R. Schwarzschild field in n dimensions and the dimensionality of space problem. Nouvo Cimento 1963, 27, 636–651. [Google Scholar] [CrossRef]
- Maeda, K.; Torii, T. Covariant gravitational equations on a brane world with a Gauss-Bonnet term. Phys. Rev. D 2004, 69, 024002:1–024002:11. [Google Scholar] [CrossRef]
Appendix
A. Asymptotic Motion of the Shell
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Torii, T. Violation of the Third Law of Black Hole Thermodynamics inHigher Curvature Gravity. Entropy 2012, 14, 2291-2301. https://doi.org/10.3390/e14112291
Torii T. Violation of the Third Law of Black Hole Thermodynamics inHigher Curvature Gravity. Entropy. 2012; 14(11):2291-2301. https://doi.org/10.3390/e14112291
Chicago/Turabian StyleTorii, Takashi. 2012. "Violation of the Third Law of Black Hole Thermodynamics inHigher Curvature Gravity" Entropy 14, no. 11: 2291-2301. https://doi.org/10.3390/e14112291
APA StyleTorii, T. (2012). Violation of the Third Law of Black Hole Thermodynamics inHigher Curvature Gravity. Entropy, 14(11), 2291-2301. https://doi.org/10.3390/e14112291



