k-Nearest Neighbor Based Consistent Entropy Estimation for Hyperspherical Distributions
Abstract
:1. Introduction
2. Construction of knn Entropy Estimators
2.1. Unbiasedness of
2.2. Consistency of
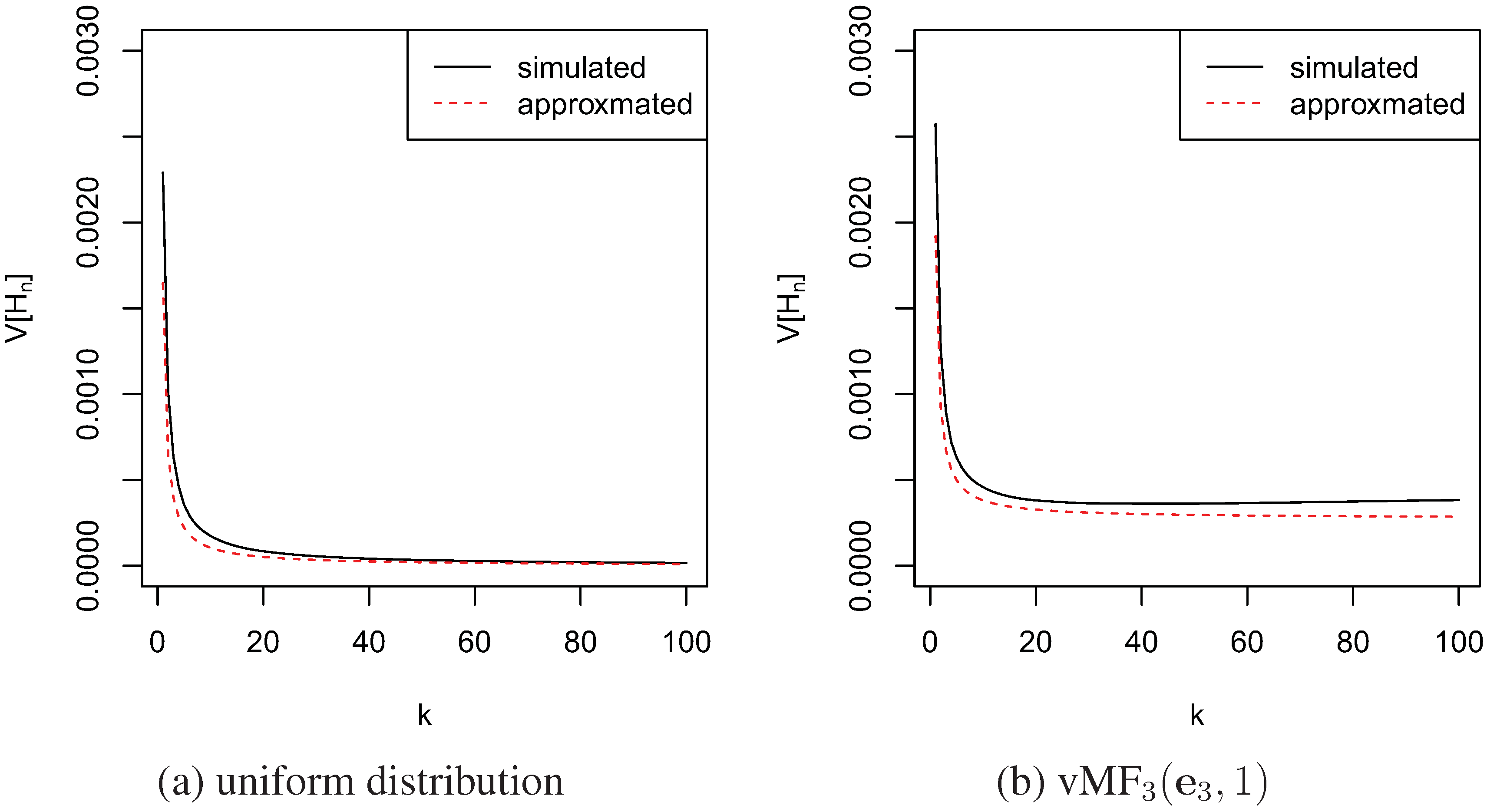
3. Estimation of Cross Entropy and KL-divergence
3.1. Estimation of Cross Entropy
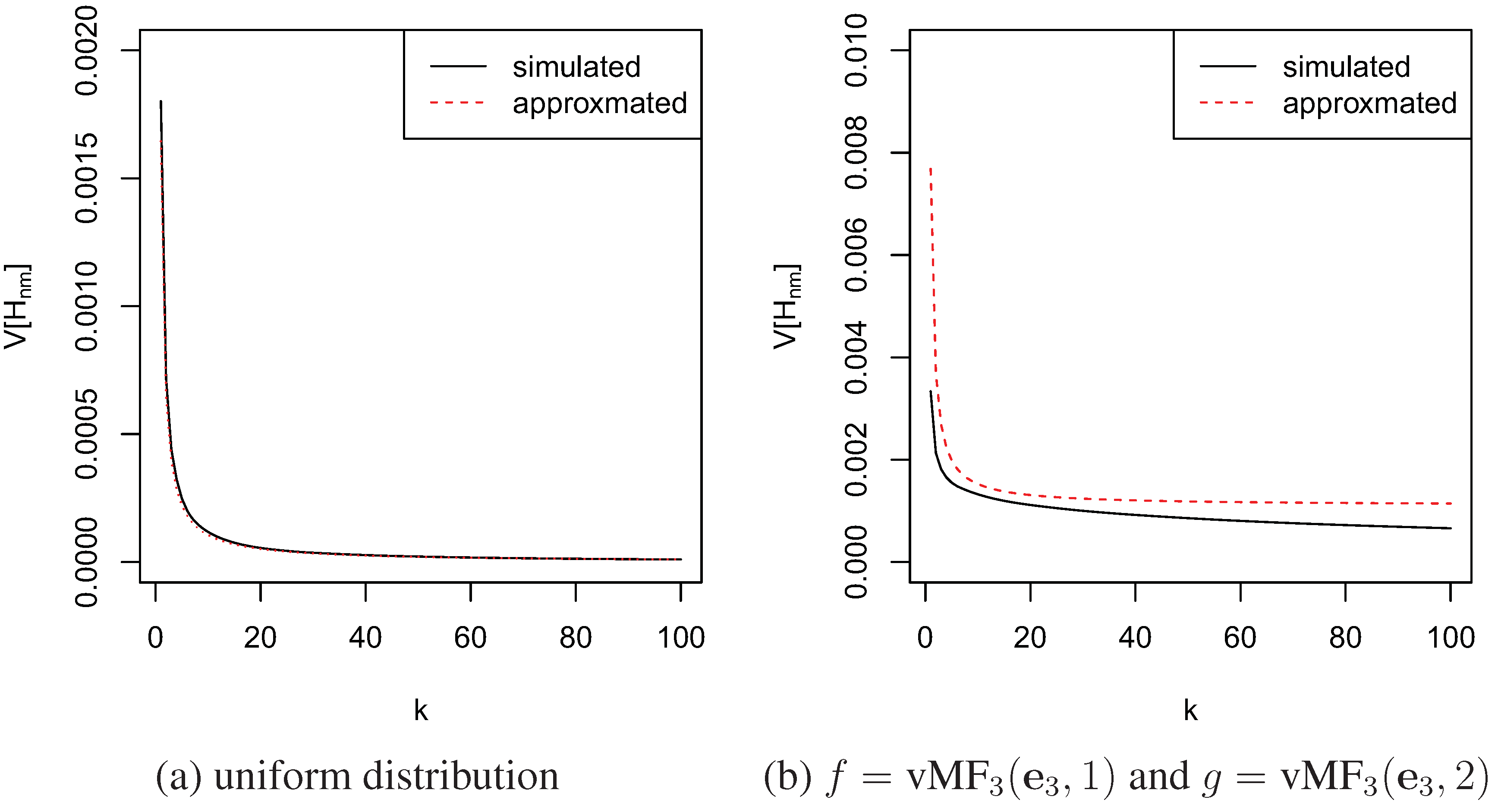
3.2. Estimation of KL-Divergence

4. Simulation Study
4.1. Bias and Standard Deviation

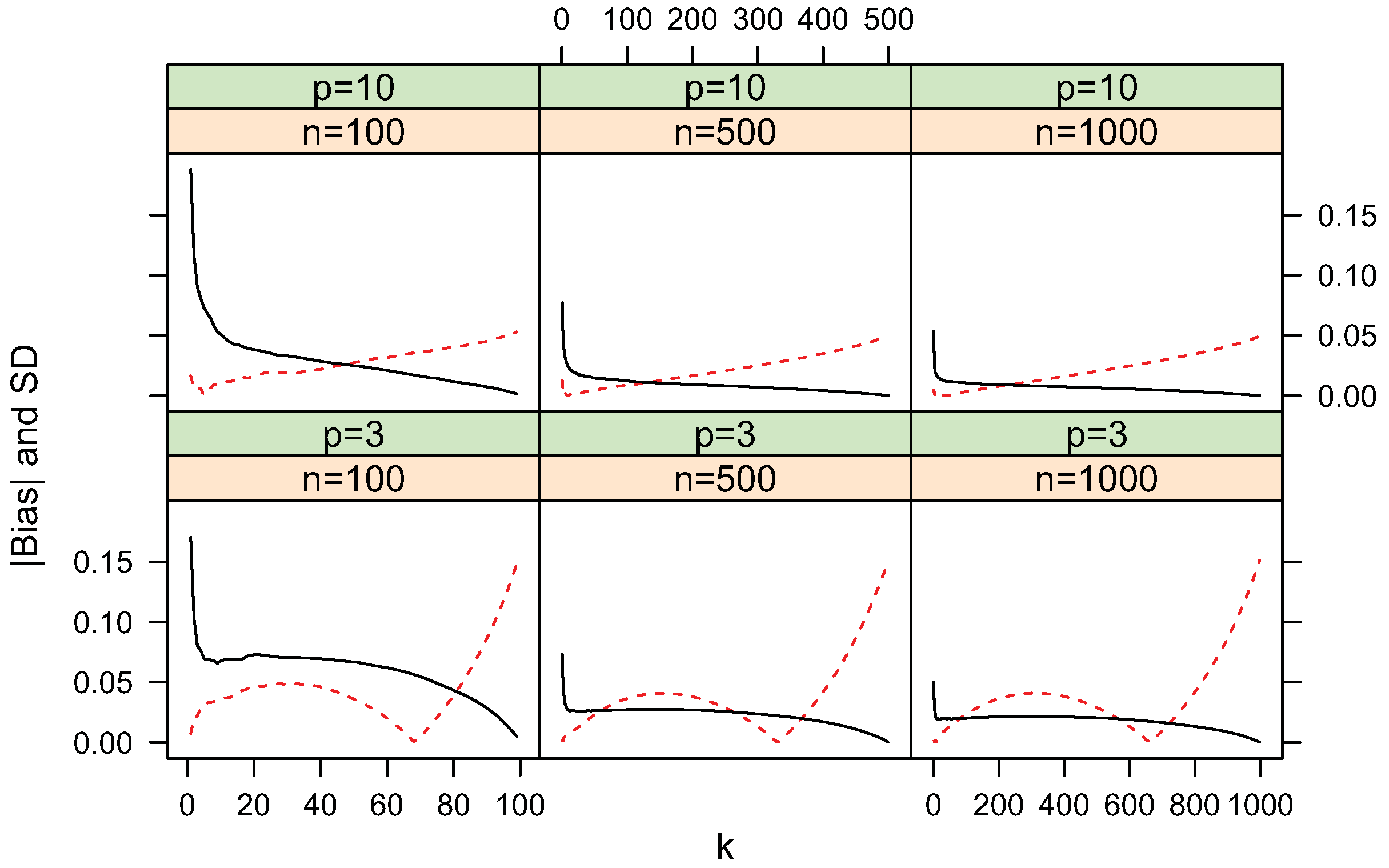
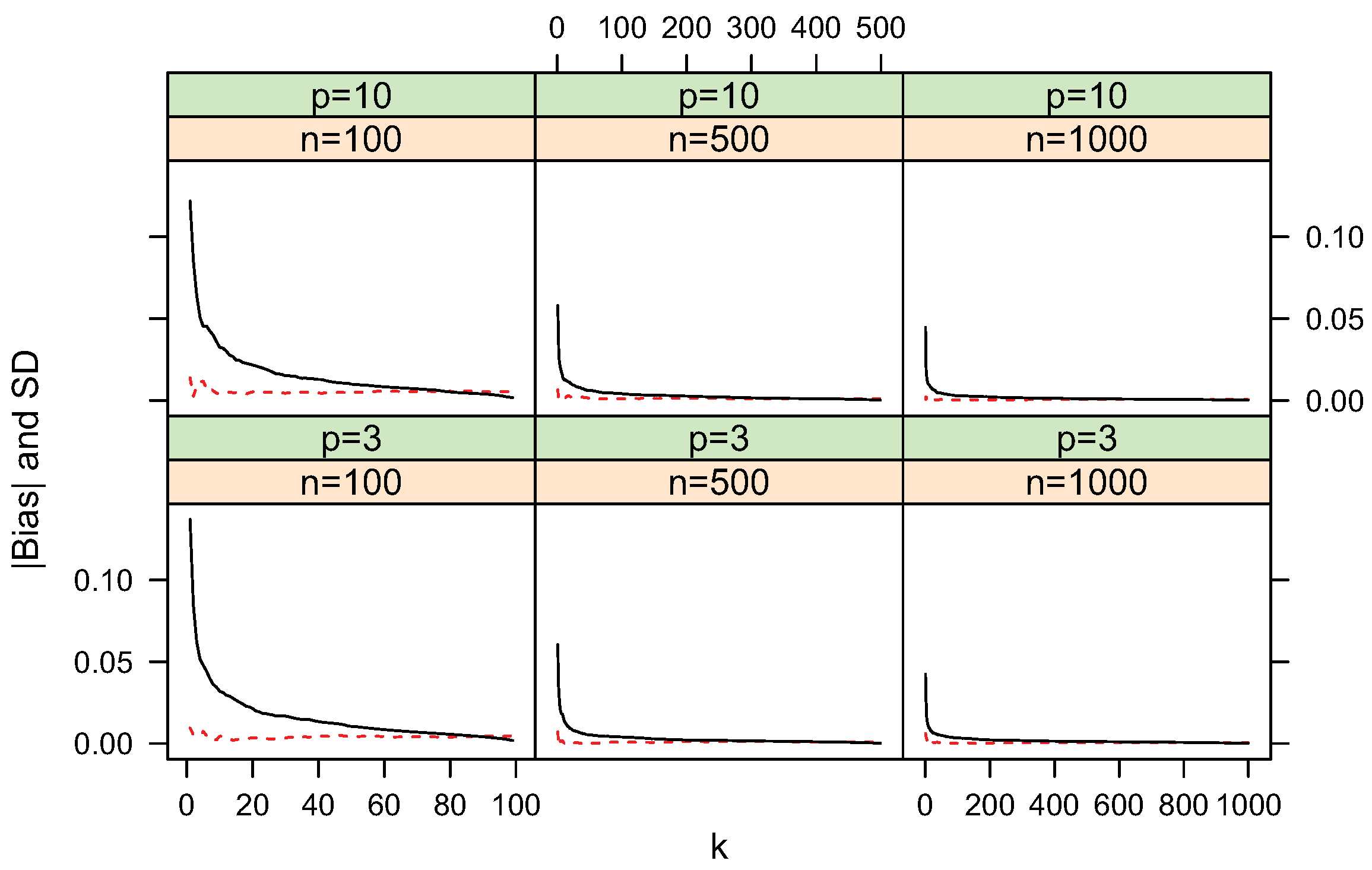
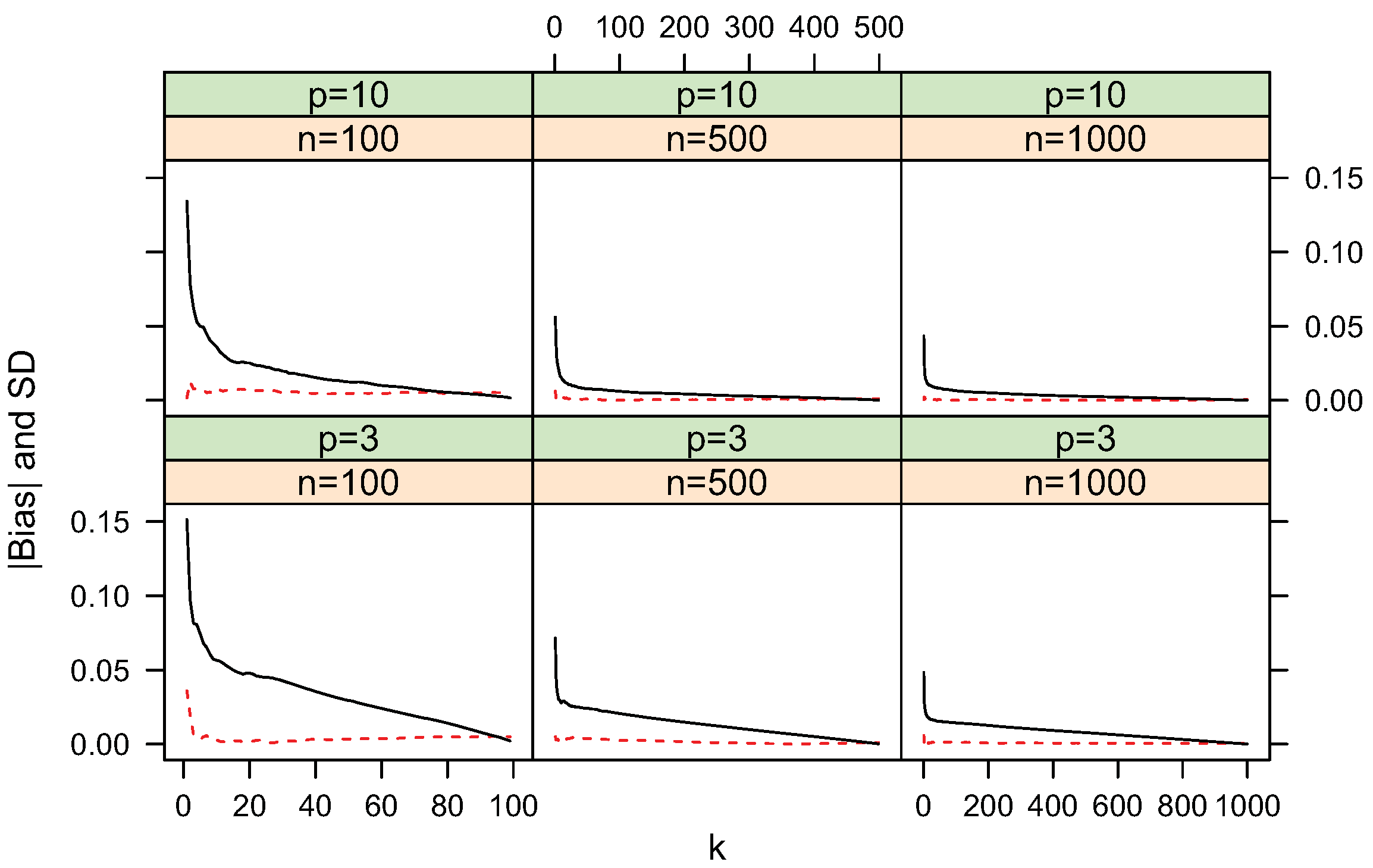
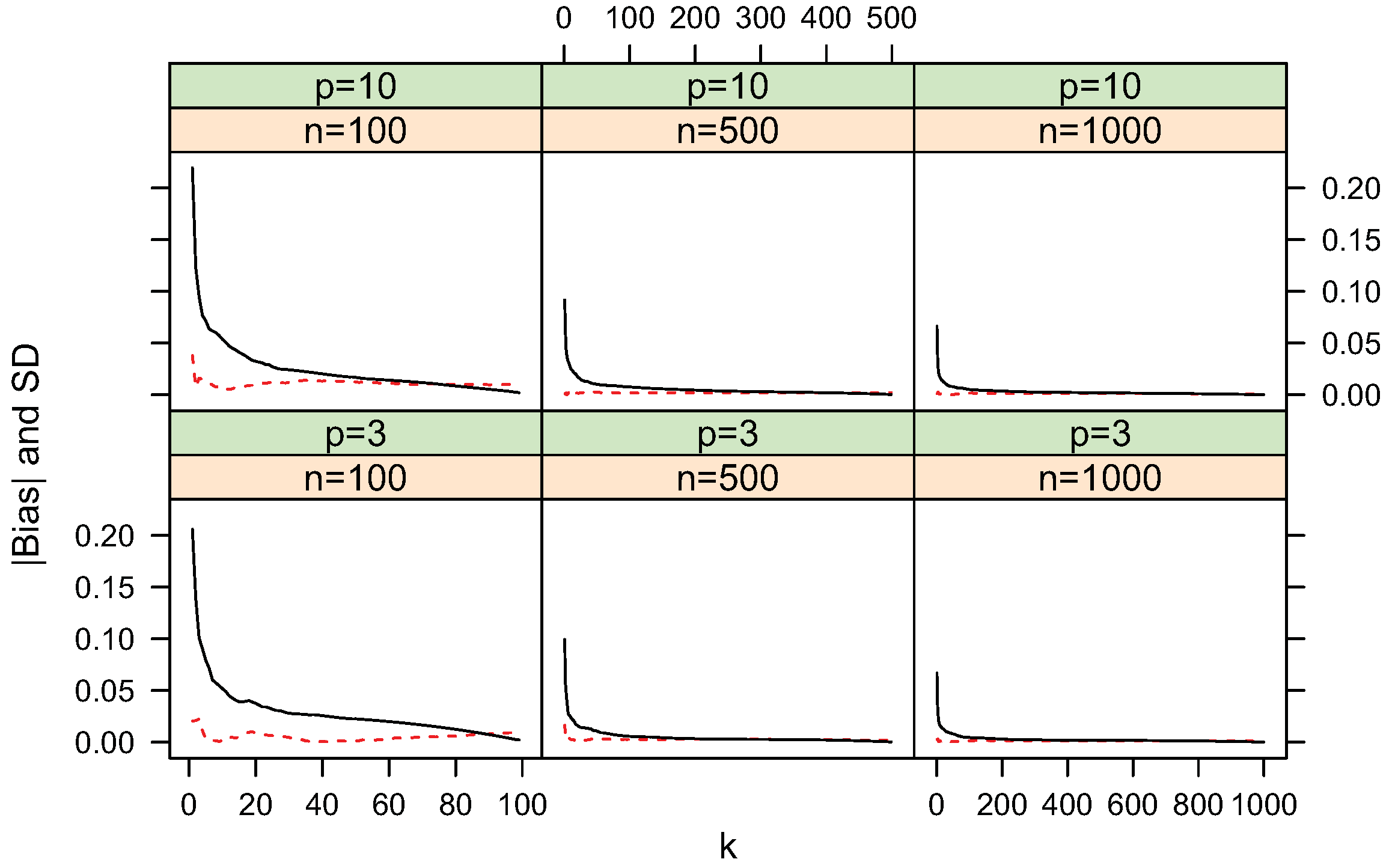
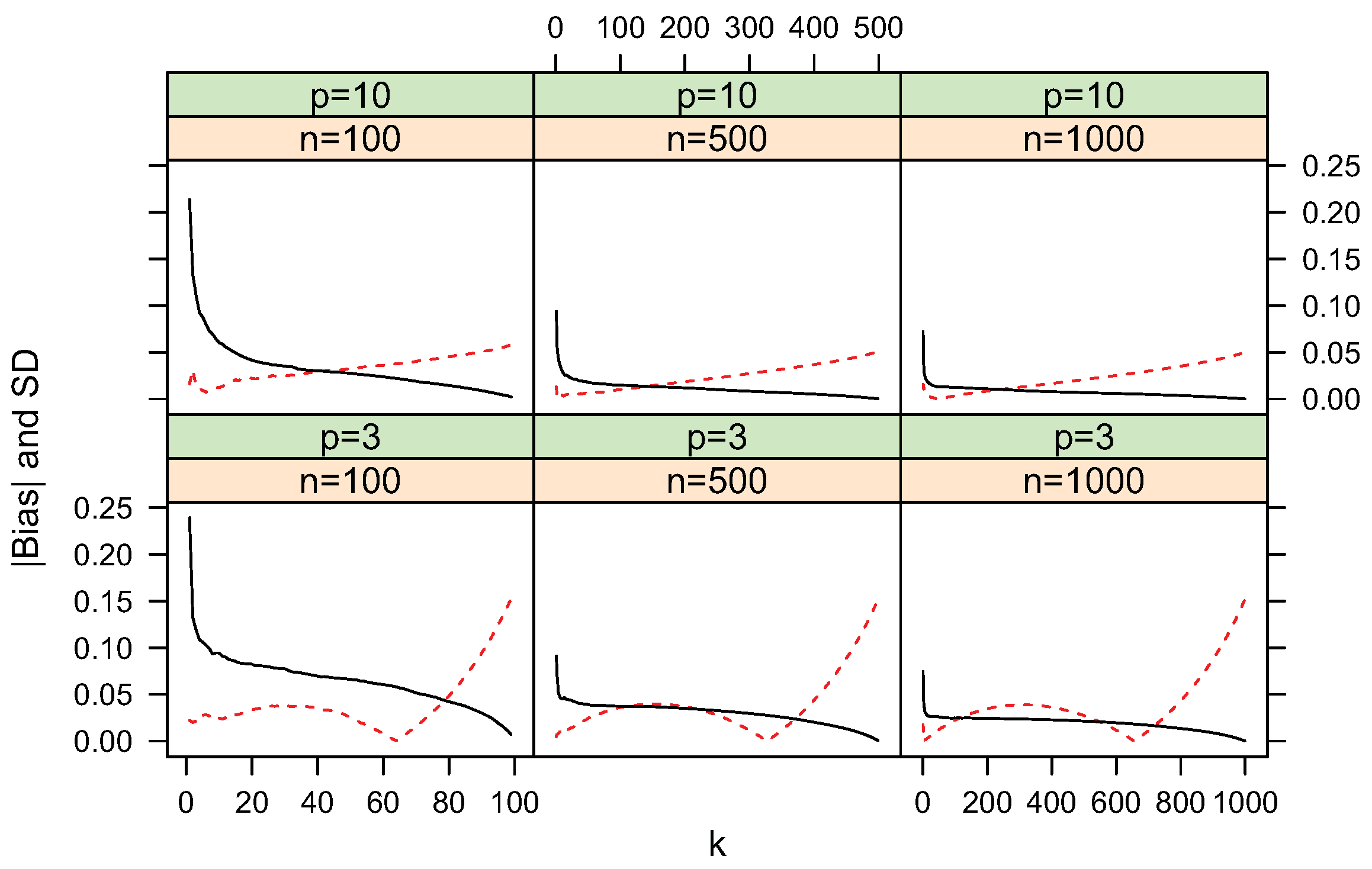
4.2. Convergence
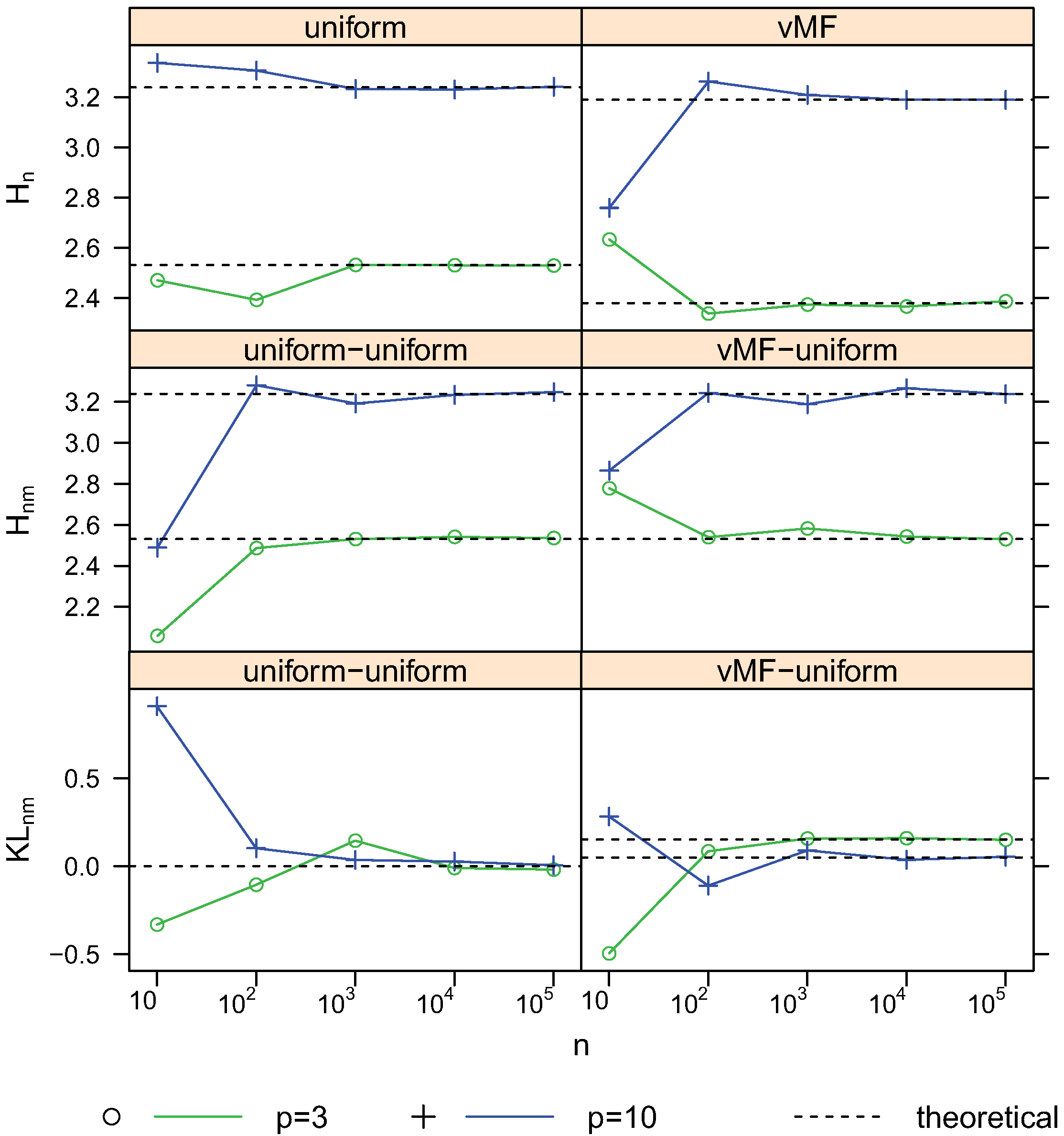
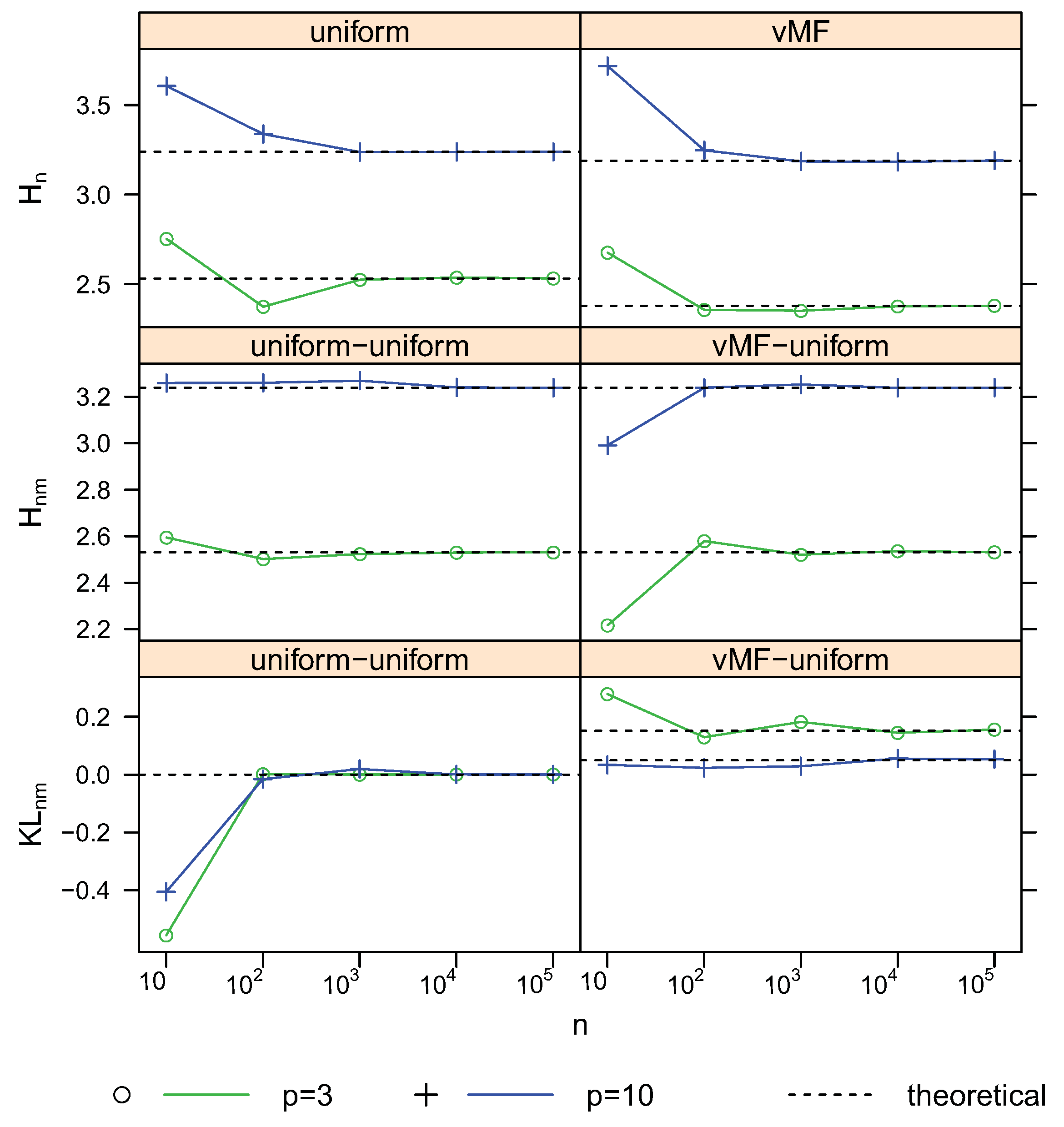
4.3. Comparison with the Moment-Recovered Construction
| Method | knn | MR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| p | n | k | bias | SD | RMSE | t | bias | SD | RMSE |
| Uniform: | |||||||||
| 3 | 100 | 99 | 0.00500 | 0.00147 | 0.00521 | 0.01 | 0.00523 | 0.01188 | 0.01298 |
| 3 | 500 | 499 | 0.00100 | 0.00013 | 0.00101 | 0.01 | 0.00107 | 0.00233 | 0.00257 |
| 3 | 1000 | 999 | 0.00050 | 0.00005 | 0.00050 | 0.01 | 0.00051 | 0.00120 | 0.00130 |
| 10 | 100 | 99 | 0.00503 | 0.00130 | 0.00520 | 0.01 | 0.00528 | 0.01331 | 0.01432 |
| 10 | 500 | 499 | 0.00100 | 0.00011 | 0.00101 | 0.01 | 0.00102 | 0.00264 | 0.00283 |
| 10 | 1000 | 999 | 0.00050 | 0.00004 | 0.00050 | 0.01 | 0.00052 | 0.00130 | 0.00140 |
| vMF: | |||||||||
| 3 | 100 | 71 | 0.01697 | 0.05142 | 0.05415 | 0.30 | 0.02929 | 0.04702 | 0.05540 |
| 3 | 500 | 337 | 0.00310 | 0.02336 | 0.02356 | 0.66 | 0.00969 | 0.02318 | 0.02512 |
| 3 | 1000 | 670 | 0.00145 | 0.01662 | 0.01668 | 0.74 | 0.00620 | 0.01658 | 0.01770 |
| 10 | 100 | 46 | 0.02395 | 0.02567 | 0.03511 | 0.12 | 0.02895 | 0.02363 | 0.03737 |
| 10 | 500 | 76 | 0.00702 | 0.01361 | 0.01531 | 0.40 | 0.01407 | 0.01247 | 0.01881 |
| 10 | 1000 | 90 | 0.00366 | 0.01026 | 0.01089 | 0.47 | 0.01115 | 0.00907 | 0.01437 |
5. Discussion and Conclusions
Acknowledgements and Disclaimer
References
- Mack, Y.; Rosenblatt, M. Multivariate k-nearest neighbor density estimates. J. Multivar. Anal. 1979, 9, 1–15. [Google Scholar] [CrossRef]
- Penrose, M.D.; Yukich, J.E. Laws of large numbers and nearest neighbor distances. In Advances in Directional and Linear Statistics; Wells, M.T., SenGupta, A., Eds.; Physica-Verlag: Heidelberg, Germany, 2011; pp. 189–199. [Google Scholar]
- Kozachenko, L.; Leonenko, N. On statistical estimation of entropy of a random vector. Probl. Inform. Transm. 1987, 23, 95–101. [Google Scholar]
- Singh, H.; Misra, N.; Hnizdo, V.; Fedorowicz, A.; Demchuk, E. Nearest neighbor estimates of entropy. Am. J. Math. Manag. Sci. 2003, 23, 301–321. [Google Scholar] [CrossRef]
- Leonenko, N.; Pronzato, L.; Savani, V. A class of Rényi information estimators for multidimensional densities. Ann. Stat. 2008, 36, 2153–2182, Correction: 2010, 38, 3837–3838. [Google Scholar] [CrossRef]
- Mnatsakanov, R.; Misra, N.; Li, S.; Harner, E. kn-Nearest neighbor estimators of entropy. Math. Meth. Stat. 2008, 17, 261–277. [Google Scholar] [CrossRef]
- Eggermont, P.P.; LaRiccia, V.N. Best asymptotic normality of the kernel density entropy estimator for smooth densities. IEEE Trans. Inf. Theor. 1999, 45, 1321–1326. [Google Scholar] [CrossRef]
- Li, S.; Mnatsakanov, R.; Fedorowicz, A.; Andrew, M.E. Entropy estimation of multimodal circular distributions. In Proceedings of Joint Statistical Meetings, Denver, CO, USA, 3–7 August 2008; pp. 1828–1835.
- Misra, N.; Singh, H.; Hnizdo, V. Nearest neighbor estimates of entropy for multivariate circular distributions. Entropy 2010, 12, 1125–1144. [Google Scholar] [CrossRef]
- Mnatsakanov, R.M.; Li, S.; Harner, E.J. Estimation of multivariate Shannon entropies using moments. Aust. N. Z. J. Stat. 2011, in press. [Google Scholar]
- Li, S. Concise formulas for the area and volume of a hyperspherical cap. Asian J. Math. Stat. 2011, 4, 66–70. [Google Scholar] [CrossRef]
- Gray, A. Tubes, 2nd ed.; Birkhäuser-Verlag: Basel, Switzerland, 2004. [Google Scholar]
- Yfantis, E.; Borgman, L. An extension of the von Mises distribution. Comm. Stat. Theor. Meth. 1982, 11, 1695–1076. [Google Scholar] [CrossRef]
- Gatto, R.; Jammalamadaka, R. The generalized von Mises distribution. Stat. Methodol. 2007, 4, 341–353. [Google Scholar] [CrossRef]
- Mardia, K.; Jupp, P. Directional Statistics; John Wiley & Sons, Ltd.: New York, NY, USA, 2000. [Google Scholar]
- Watamori, Y. Statistical inference of Langevin distribution for directional data. Hiroshima Math. J. 1995, 26, 25–74. [Google Scholar]
- Knutsson, H. Producing a continuous and distance preserving 5-D vector representation of 3-D orientation. In Proceedings of IEEE Computer Society Workshop on Computer Architecture for Pattern Analysis and Image Database Management, Miami Beach, FL, November 1985; pp. 175–182.
- Rieger, B.; van Vliet, L. Representing orientation in n-dimensional spaces. Lect. Notes Comput. Sci. 2003, 2756, 17–24. [Google Scholar]
- McGraw, T.; Vemuri, B.; Yezierski, R.; Mareci, T. Segmentation of high angular resolution diffusion MRI modeled as a field of von Mises-Fisher mixtures. Lect. Notes Comput. Sci. 2006, 3953, 463–475. [Google Scholar]
- Bhalerao, A.; Westin, C.F. Hyperspherical von Mises-Fisher mixture (HvMF) modelling of high angular resolution diffusion MRI. Lect. Notes Comput. Sci. 2007, 4791, 236–243. [Google Scholar]
- Özarslan, E.; Vemuri, B.C.; Mareci, T.H. Generalized scalar measures for diffusion MRI using trace, variance, and entropy. Magn. Reson. Med. Sci. 2005, 53, 866–876. [Google Scholar] [CrossRef] [PubMed]
- Leow, A.; Zhu, S.; McMahon, K.; de Zubicaray, G.; Wright, M.; Thompson, P. A study of information gain in high angular resolution diffusion imaging (HARDI). In Proceedings of 2008 MICCAI Workshop on Computational Diffusion MRI, New York, NY, USA, 10 September 2008.
- Loève, M. Probability Theory I, 4th ed.; Springer-Verlag: New York, NY, USA, 1977. [Google Scholar]
- Wang, Q.; Kulkarni, S.R.; Verdú, S. Divergence estimation for multidimensional densities via k-nearest-neighbor distances. IEEE Trans. Inf. Theor. 2009, 55, 2392–2405. [Google Scholar] [CrossRef]
* 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, S.; Mnatsakanov, R.M.; Andrew, M.E. k-Nearest Neighbor Based Consistent Entropy Estimation for Hyperspherical Distributions. Entropy 2011, 13, 650-667. https://doi.org/10.3390/e13030650
Li S, Mnatsakanov RM, Andrew ME. k-Nearest Neighbor Based Consistent Entropy Estimation for Hyperspherical Distributions. Entropy. 2011; 13(3):650-667. https://doi.org/10.3390/e13030650
Chicago/Turabian StyleLi, Shengqiao, Robert M. Mnatsakanov, and Michael E. Andrew. 2011. "k-Nearest Neighbor Based Consistent Entropy Estimation for Hyperspherical Distributions" Entropy 13, no. 3: 650-667. https://doi.org/10.3390/e13030650
APA StyleLi, S., Mnatsakanov, R. M., & Andrew, M. E. (2011). k-Nearest Neighbor Based Consistent Entropy Estimation for Hyperspherical Distributions. Entropy, 13(3), 650-667. https://doi.org/10.3390/e13030650




