1. Introduction
The study of radiative and magnetic field effects has important applications in physics and engineering. Hydromagnetic flow and heat transfer problems have received considerable attention, due to their applications in many industrial fields. The radiative flows of an electrically conducting fluid with high temperature in the presence of a magnetic field are encountered in various propulsion devices for satellites and interplanetary spacecraft, electrical power generation, astrophysical flows, solar power technology, space vehicle re-entry, nuclear engineering applications and other industrial areas. The unsteady flow past a moving plate in the presence of free convection and radiation was studied by Mansour [
1]. The effect of suction/injection on the flow and heat transfer for a continuous moving plate in a micro polar fluid in the presence of rendition was studied by El-Arabawy [
2]. Ibrahim
et al. [
3] studied radiative and thermal dispersion effects on non-Darcy natural convection with lateral mass flux for a non-Newtonian fluid from a vertical flat plate in a saturated porous medium. Dolapc and Pakdemirli [
4] studied approximate symmetries of creeping flow equations of a second grade fluid. Transient radiative hydromagnetic free convection flow past an impulsively started vertical plate with uniform heat and mass fluxes was studied by Ramachandra
et al. [
5,
6]. The magnetic field parameter has retarding effect on the velocity, temperature and concentration increase with increasing value of the magnetic field parameter. The time required to reach the steady state increases as radiation parameter increases [
5]. For small values of the radiation parameter, the velocity and temperature of the fluid sharply increase as the time increases. The local and average Nusselt number increase with increasing value of radiation parameter.
Thermal radiation effects on MHD flow past an impulsively started vertical plate in the presence of heat source/sink was investigated [
6]. Heat due to viscous dissipation was considered. As the radiation parameter increases, both the velocity and temperature increase, whereas the concentration decreases. An increase in the magnetic parameter decelerates the velocity. A rise in dissipative heat induces a substantial rise in both velocity and temperature. As the heat absorption/generation parameter increases, the velocity increases whereas the temperature decreases. An increase in the Schmidt number leads to a decrease in the velocity and concentration. Rani
et al. [
7] studied numerically the effects of radiation, magnetic field, variable viscosity and variable thermal conductivity on similarity solutions of mixed convection at a vertical flat plate embedded in a porous medium. In absence of a magnetic field, the parameter
C takes the value unity, and for increasing intensity of the magnetic field, the parameter takes values smaller than unity. Reduced flow can be expected for smaller values of
C or for increased intensity of the magnetic field as the Lorentz force (due to the magnetic field) obstructs the flow. When transfer of heat by radiation is neglected, the parameter
Rd that describes radiation takes zero value and when increasing intensity of thermal radiation, the parameter takes larger values. Solutions are found for the values 0, 0.5 and 10 of the parameter
Rd. Increasing values of the parameter
Rd can increase thermal boundary layer thickness. Shateyi [
8] investigated thermal radiation and buoyancy effects on heat and mass transfer over a semi-infinite stretching surface with suction and blowing. It was found that when the Grashof number increases, the fluid velocity also increases. However, this same effect was found to decrease both thermal and concentration boundary layers. The flow is appreciably influenced by thermal radiation. It was observed that increasing the thermal radiation parameter produces significant increase in the thermal conditions of the fluid temperature which induces more fluid in the boundary layer through buoyancy effect, causing the velocity of the fluid to increase. The hydrodynamic boundary layer and thermal boundary layer thicknesses increase as a result of increasing radiation. However, the concentration boundary layer thickness decreases as a result of increasing the thermal radiation parameter. It was also observed that increasing the Schmidt number, induces reduction in the distribution of concentration in the boundary layer. Natural convection of an electrically conducting and radiating fluid in the presence of an external magnetic field is numerically investigated by Akiyama and Chong [
9]. The two opposing side walls are differentially heated with a specified temperature difference, while the top and bottom walls are insulated. Basically three types of fluids are considered: opaque, transparent and participating fluids. The results are presented in the form of isotherms and streamline contours, mid-plane velocity profiles, and total heat transfer rates across the enclosure. The main conclusions are as follows: In case of the opaque fluid, the effect of an imposed magnetic field is to suppress the convection. If the fluid is not opaque in the absence of an external magnetic field, the flow structure and the temperature field in an enclosure are considerably affected by the radiation. In the framework of the same radiation environment, the thermo-fluid dynamics behavior of a radiating fluid is substantially altered together with the strength of the imposed magnetic field. For the transparent fluid, the effect of the magnetic field is as follows: in the mid-region apart from the adiabatic walls, the applied magnetic field affects the degree of tilting of a streamline axis appreciably. The radiation effect on a thermal field is localized near the adiabatic walls. Inversely, the thermal distribution in the mid-region is affected by the magnetic field rather than the radiation. In terms of the participating fluid, as the magnetic field becomes stronger, the unicellular flow originally turns into the flow with the inner core including two convective rolls. The overall flow in the enclosure is suppressed by the retarding effect of the Lorentz force. Nevertheless the axis of the resulting streamline is not slanted even in the presence of a strong magnetic field. On the other hand, the thermal distribution in the participating fluid is seriously affected by not only the external magnetic field but radiation, even in the region far from the insulated walls. In general terms, it was found that the main effect of the external magnetic field is to reduce the overall heat transfer rate across the enclosure. More specifically, regardless the fluid type, the distribution of conductive Nusselt number decreases for both hot and cold walls in accordance with the increase in the strength of the magnetic field. A similar trend is observed with the radiative Nusselt number distribution. As a consequence, the increase in Hartmann number leads to the decrease in the local Nusselt number distribution, thereby resulting in the decrease of the average Nusselt number.
Combined heat and mass transfer has attracted considerable attention due to its importance in various fields such as in engineering as well as geophysical applications. Comprehensive reviews of this area have been made by many researches, some of them are Nield and Bejan [
10] and Trevisan and Bejan [
11]. The efficient utilization of energy is the primary objective in the design of any thermodynamic system, which can be achieved by entropy generation minimization. Theoritical method of entropy generation has been used to treat external and internal irreversibilities. In thermosolutal convection, irreversibilities are mainly due to heat transfer, mass transfer and fluid flow. Second law analysis in heat transfer and thermal design was described in details by Bejan [
12,
13]. Generally speaking, the irreversibility phenomena, which are expressed by entropy generation, are related to heat transfer, mass transfer, viscous dissipation, chemical reactions, magnetic field,
etc. Magherbi
et al. [
14] numerically studied entropy generation in convective heat and mass transfer through an oriented square cavity for the case of aiding buoyancy forces. They showed that maximum value of entropy generation increases with thermal Grashof number and it was obtained at an inclination angle of the cavity α = 45° for Gr
T = 10
4. Entropy generation increases with the buoyancy forces that induce an augmentation of exchanged heat between the flow and the walls. Hidouri
et al. [
15] studied the influence of Soret effect on entropy generation in double diffusive convection for the case of a binary perfect gas mixture for both aiding and opposing buoyancy forces through a square cavity. They showed that entropy generation takes a minimum value for the case of opposing buoyancy forces with equal intensity (
i.e., N = −1) when thermal Grashof values Gr
T ≥ 10
5. In a similar way, the influence of Dufour effect on entropy generation in convective heat and mass transfer for a binary perfect gas mixture was numerically studied by Magherbi
et al. [
16]. They showed that entropy generation takes also a minimum value when N = −1 for values of thermal Grashof number Gr
T ≥ 10
4.
The purpose of this paper is to investigate radiative and magnetic effects on entropy generation in thermosolutal convection with heat and mass transfer flow in 2D approximation for both aiding and opposing buoyancy forces, which is in our knowledge, has not been studied yet. Thus, this study is a complementary study to those of Hidouri
et al. [
15] and Magherbi
et al. [
16]. In this case, the enclosure is subjected to an oriented magnetic field. Effects of the thermal Rayleigh number, the buoyancy ratio, the Hartmann number, the Radiation parameter and the inclination angle of the magnetic field on entropy generation in steady-unsteady states as well as on local irreversibility are studied.
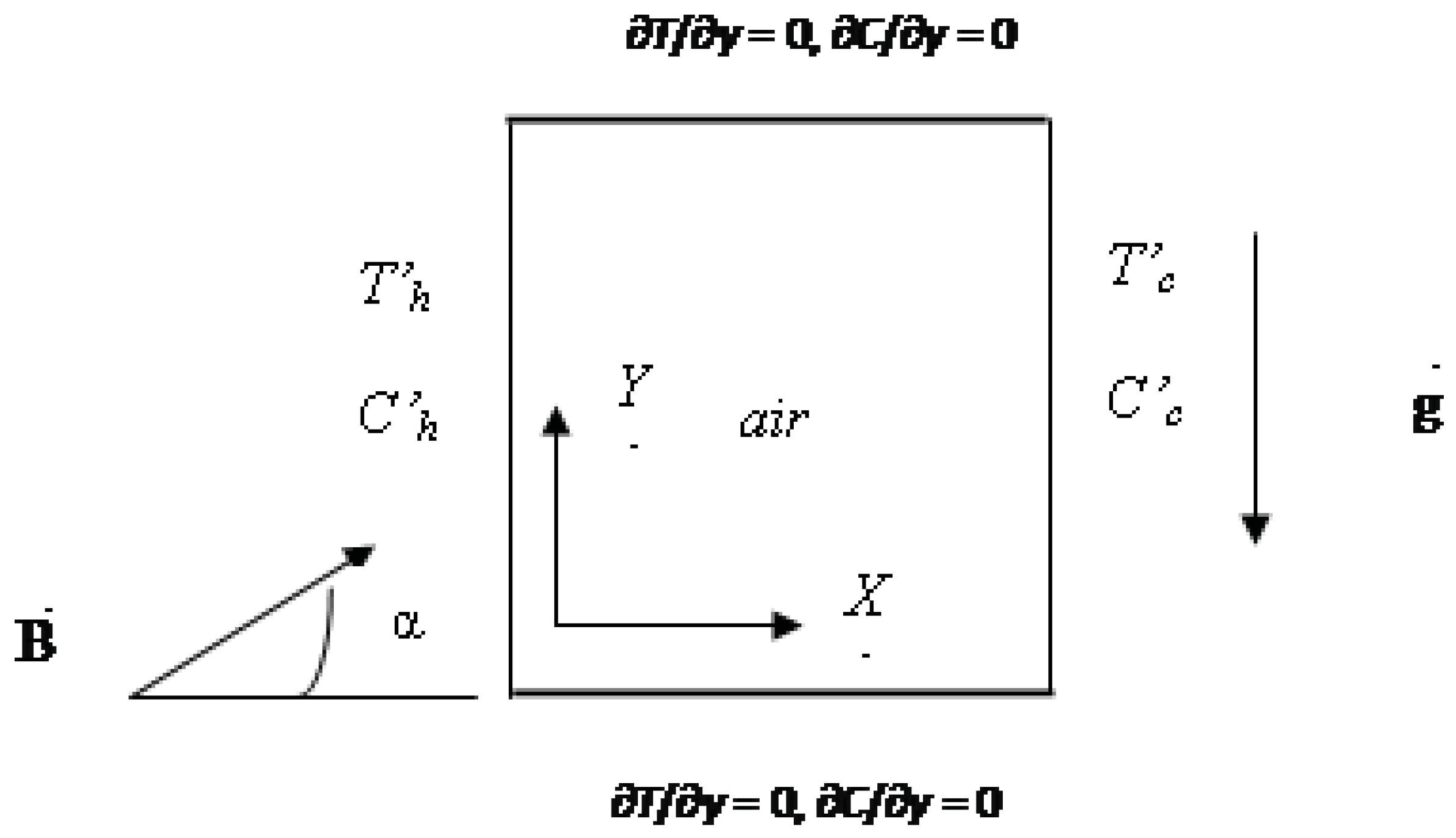
4. Results and Discussions
In this parametric study, the Prandtl number was fixed at 0.71. Thermal Rayleigh number, irreversibility distribution ratios and the inclination angle of the magnetic field are in the following ranges: 103 ≤ Ra ≤ 105; 10−7 ≤
≤ 10−4, 10−1 ≤
≤ 0.5; 10−5 ≤
≤ 10−2 and 0° ≤ α ≤ 180°, respectively.
and
are equal to 0 in natural convection regime.
In absence of both magnetic field and radiation effects,
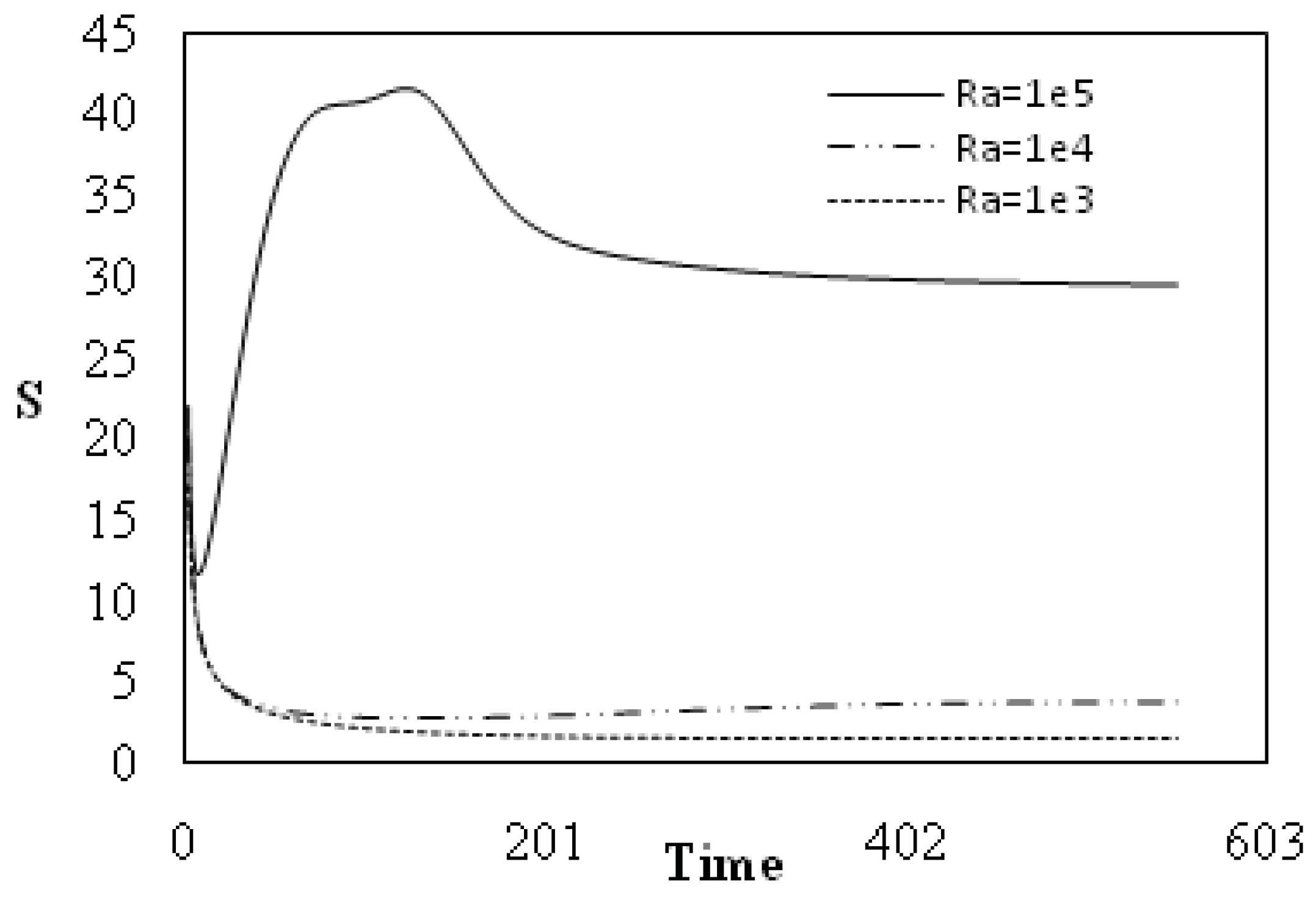
Figure 2 illustrates transient entropy generation for different values of thermal Rayleigh number. As it can be seen, for relatively lower and moderate thermal Rayleigh numbers (
i.e., 10
3 ≤ Ra ≤ 10
4, entropy generation quickly decreases from a maximum value at the beginning of the transient state), then asymptotically decreases towards a constant value in steady state, showing that the system evolves in the linear branch of thermodynamics for irreversible processes. On increasing the thermal Rayleigh number (
i.e., Ra ≥ 10
5), transient entropy generation exhibits an oscillatory behavior showing that the system is in a spiral approach corresponding to non linear branch of thermodynamics for irreversible processes. As time proceeds, entropy generation reaches a maximum then asymptotically decreases towards a constant value in steady state.
Figure 2.
Dimensionless total entropy generation versus time for: α = 0°; Ha = 0; N = 0; Nr = 0.
Figure 2.
Dimensionless total entropy generation versus time for: α = 0°; Ha = 0; N = 0; Nr = 0.
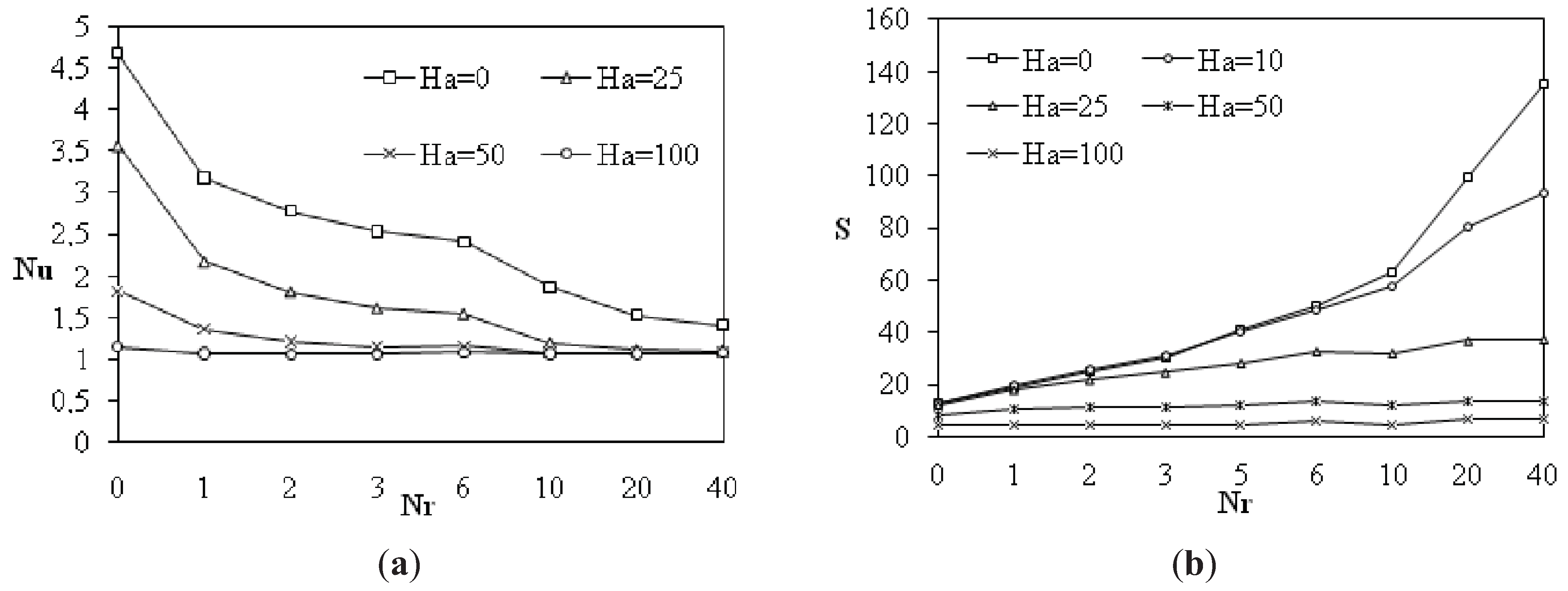
Influence of both magnetic and radiation effects on Nusselt number and entropy generation in steady state for Gr = 10
5 is illustrated in
Figure 3a and
Figure 3b. As it can be seen, magnetic and radiation parameters induce the decrease of heat transfer expressed by Nusselt number towards unity value. Thus radiation effect reduces Nusselt number and homogenizes the temperature inside the cavity by reducing the temperature gap between the two insulated walls. It enhances the heat transfer inside the cavity. Magnetic effect by Lorentz force suppresses the flow. The increase of heat transfer inside the enclosure induces the increase of entropy generation as illustrated in
Figure 3b. It is important to notice that the increase of Hartmann number considerably induces the decrease of entropy generation regardless the radiation parameter.
Figure 3.
Average Nusselt number (a) and Dimensionless total entropy generation (b) versus Radiation parameter for different Hartmann numbers: Ra = 105; N = 0.
Figure 3.
Average Nusselt number (a) and Dimensionless total entropy generation (b) versus Radiation parameter for different Hartmann numbers: Ra = 105; N = 0.
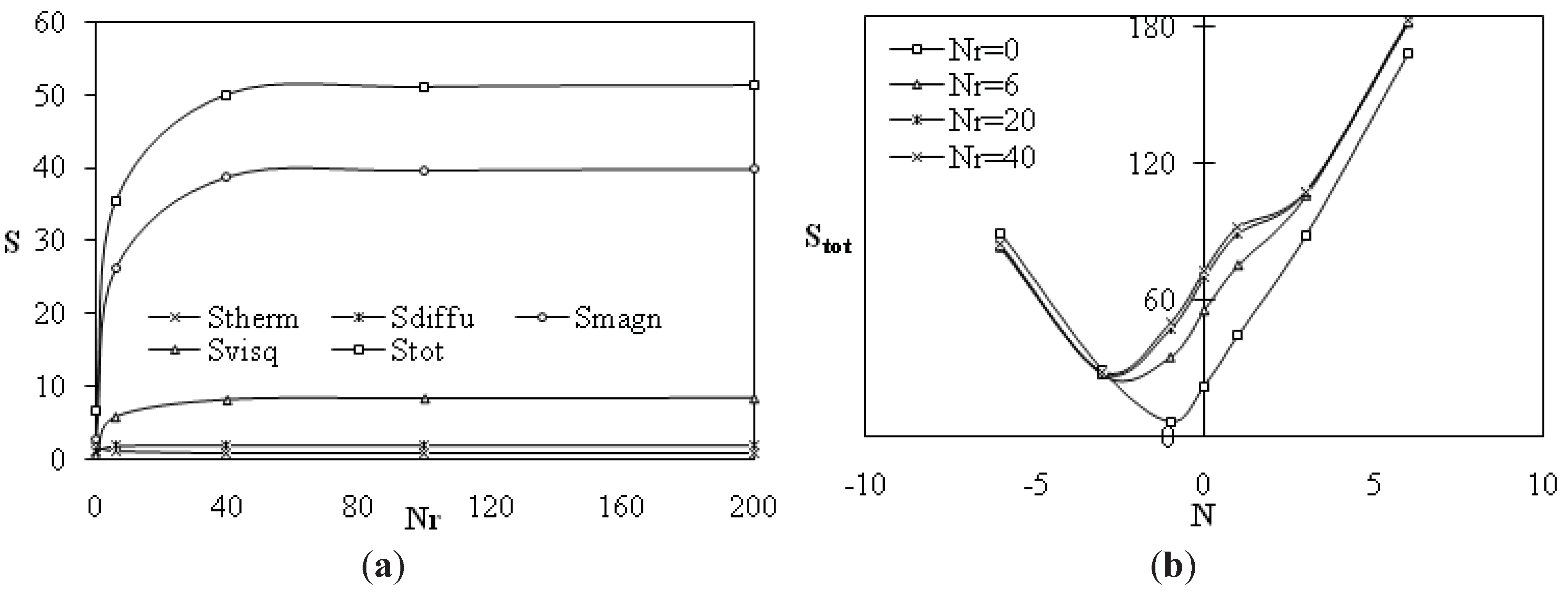
From
Figure 4a, entropy generation is mainly due to magnetic and viscous irreversibilities for the case where N = −1 and Ha = 25. This is due to the fact that both thermal and concentration gradients are at their minimum values, then entropy generation is induced by magnetic and viscous irreversibilities. A critical radiation parameter from which entropy generation takes a constant value is obtained and equal to 50. Minimum entropy generation considerably depends on both buoyancy ratio and radiation parameter. As it can be seen from
Figure 4b, this minimum is obtained at N = −1 and Nr = 0, this result is in good agreement with that obtained by Hidouri
et al. [
15] and Magherbi
et al. [
16]. As radiation parameter increases, buoyancy ratio corresponding to minimum entropy generation are shifted to values smaller than −1. In this case, this minimum is obtained at N = −2 and −3 for Nr = 6 and 40, respectively. It is important to notice that minimum entropy generation increases with radiation parameter, since radiation heat transfer increases inside the enclosure. Entropy generation amplitude is higher for the case of aiding buoyancy forces than that of opposing buoyancy forces since thermal, concentration and velocity gradients are more important when N ≻ 0.
Figure 4.
Dimensionless entropy generation versus radiation parameter for N = −1 and Ha = 25 (a) and versus buoyancy ratios for different radiation parameter values at Ha = 25 (b) Ra = 105; α = 0°.
Figure 4.
Dimensionless entropy generation versus radiation parameter for N = −1 and Ha = 25 (a) and versus buoyancy ratios for different radiation parameter values at Ha = 25 (b) Ra = 105; α = 0°.
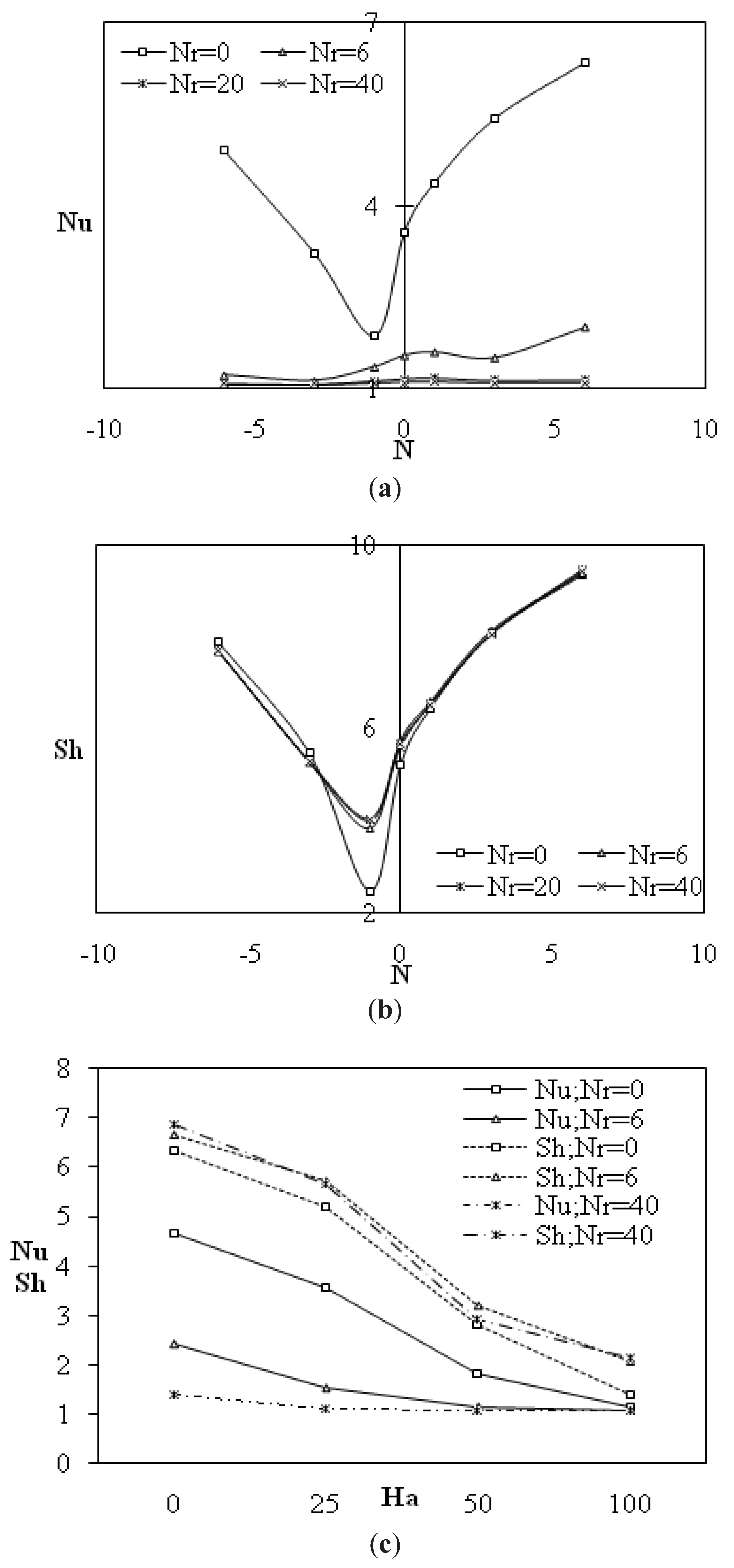
In order to illustrate the influence of magnetic, radiation and buoyancy ratio parameters on heat and mass transfer,
Figure 5a shows that radiation parameter enhances heat transfer inside the cavity and Nusselt number value tends towards zero value for Nr ≥ 20 indicating that all heat transfer is generated inside the enclosure. Inversely mass transfer, which is expressed by Sherwood number, has similar behaviour of entropy generation. In this case, Sherwood number is minimum for N = −1 where velocity, thermal and concentration gradients are at their minimum values. This minimum increases with radiation parameter showing that mass transfer increases with radiation effects. Sherwood number is higher for aiding buoyancy forces than that of opposing ones as indicated by
Figure 5b. Both heat and mass transfer decrease towards unity value for considerable Hartmann number value (
i.e., Ha ≥ 100) showing that magnetic field tends to stabilize the system regardless radiation parameter as indicated in
Figure 5c.
Figure 5.
Average Nusselt number (a) Average Sherwood number (b) versus buoyancy ratio for different radiation parameters (c) Nusselt and Sherwood numbers versus Hartmann number for different radiation parameters: Ra = 105; α = 0°.
Figure 5.
Average Nusselt number (a) Average Sherwood number (b) versus buoyancy ratio for different radiation parameters (c) Nusselt and Sherwood numbers versus Hartmann number for different radiation parameters: Ra = 105; α = 0°.
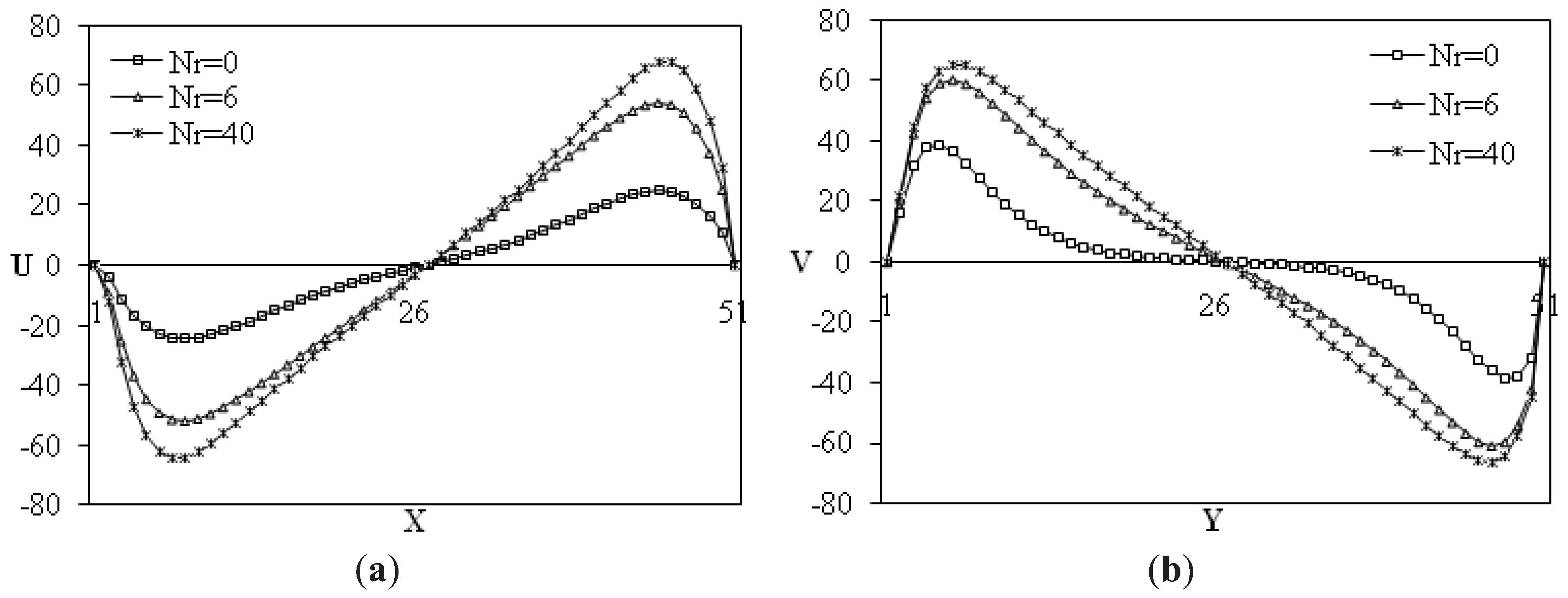
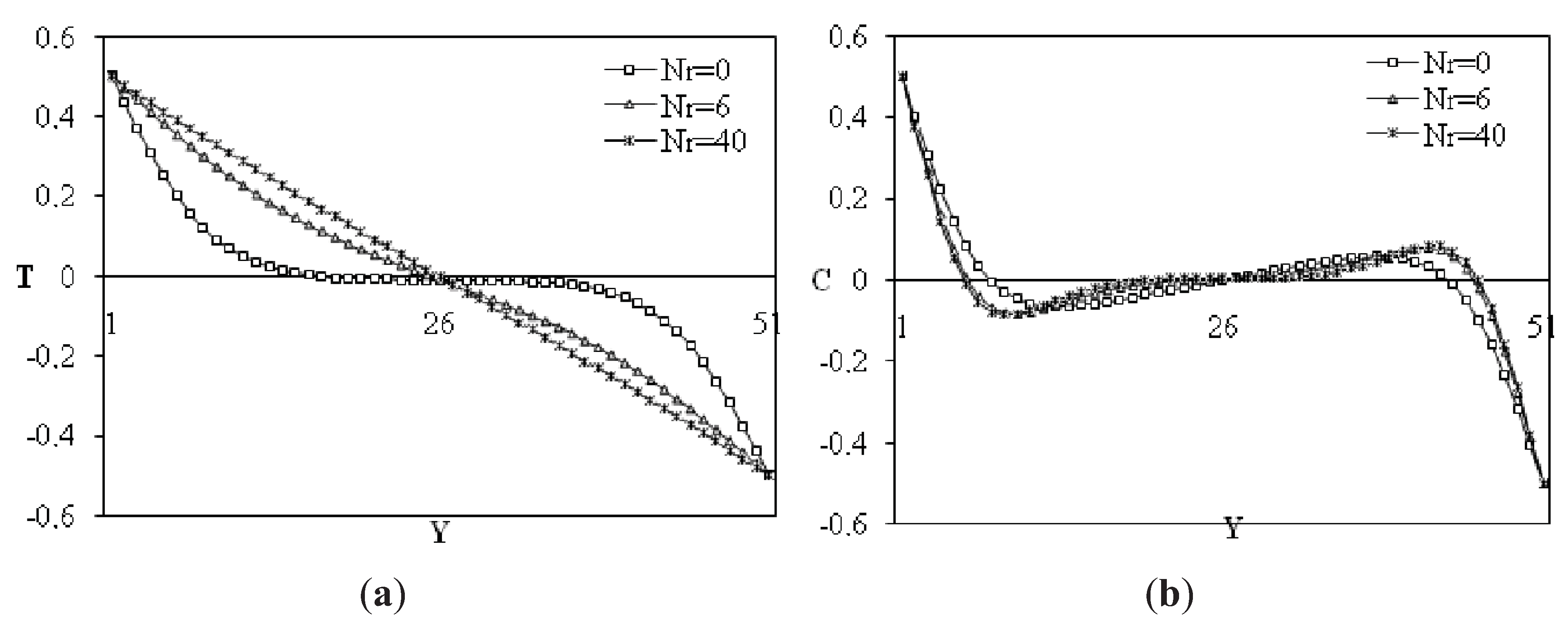
Figure 6 illustrates the effect of radiation parameter on velocity profiles, the horizontal velocity component decreases at the left half of the cavity and increases at the right half with increasing of radiation parameter. The opposite behaviour is observed for the vertical velocity component. Thus, velocity shows a centrosymetric trend. Similar results are obtained for temperature and concentration profiles. As radiation parameter increases temperature profiles tend to linearity (see
Figure 7). The influence of the magnetic field’s inclination angle is illustrated in
Figure 8, which indicated that the angle of 80° corresponds to maximum values of Nusselt and Sherwood numbers and for total entropy generation but minimum values are found for an angle around 135°.
Figure 6.
Midsection x-component velocity at y = 0.5 (a) and midsection y-component velocity at x = 0.5 (b) for different Radiation parameters: Ra = 105; α = 0°; Ha = 25; N = 0.
Figure 6.
Midsection x-component velocity at y = 0.5 (a) and midsection y-component velocity at x = 0.5 (b) for different Radiation parameters: Ra = 105; α = 0°; Ha = 25; N = 0.
Figure 7.
Midsection y-component temperature (a) and concentration (b) at y = 0.5 for different Radiation parameters Ra = 105; α = 0°; Ha = 25; N = 0.
Figure 7.
Midsection y-component temperature (a) and concentration (b) at y = 0.5 for different Radiation parameters Ra = 105; α = 0°; Ha = 25; N = 0.
Figure 8.
Average Nusselt number (a) Average Sherwood number (b) and Total entropy generation (c) versus inclination angle of magnetic field for different radiation parameters: Ra = 105; α = 0°; Ha = 25 and N = 0.
Figure 8.
Average Nusselt number (a) Average Sherwood number (b) and Total entropy generation (c) versus inclination angle of magnetic field for different radiation parameters: Ra = 105; α = 0°; Ha = 25 and N = 0.
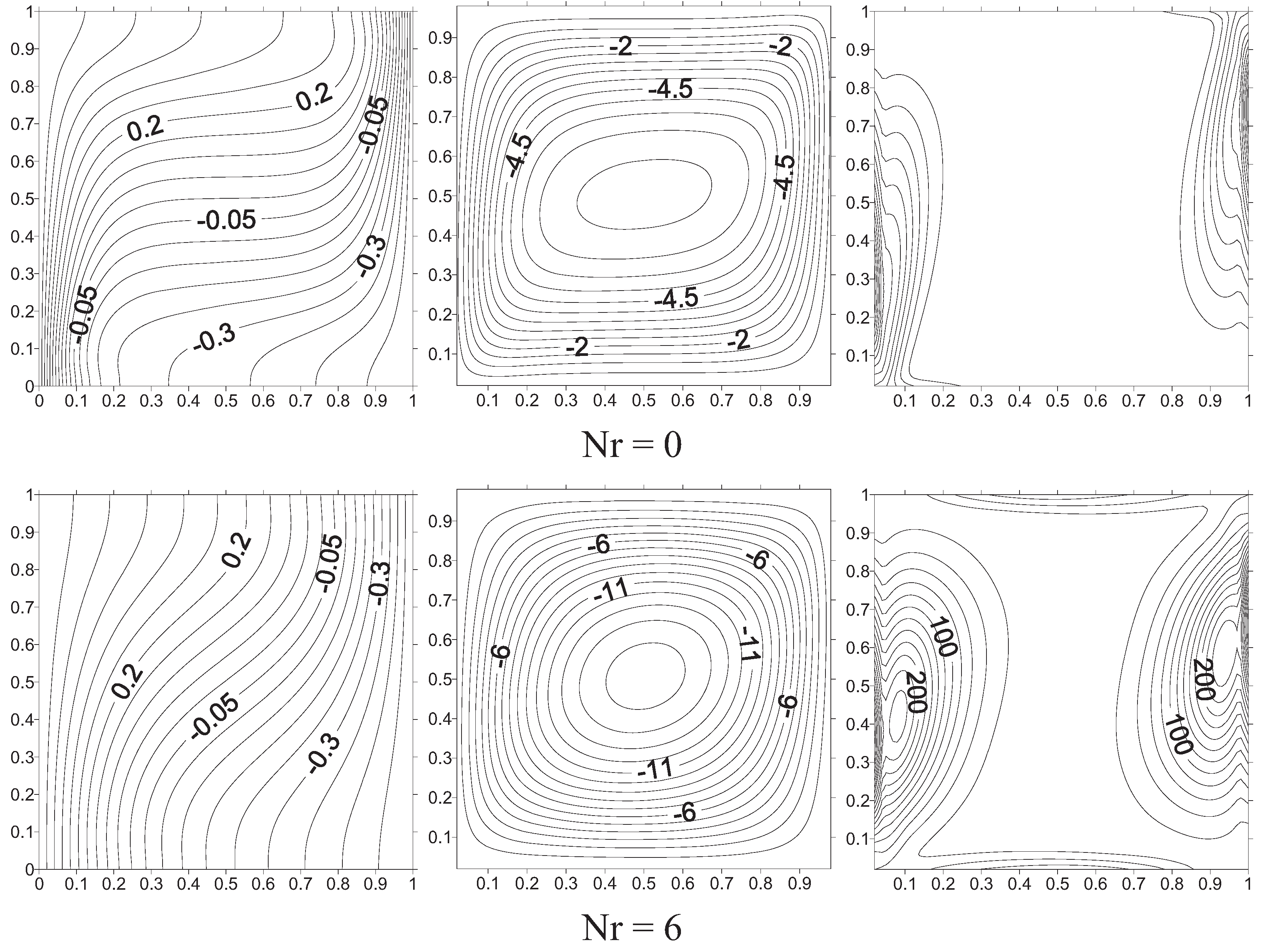
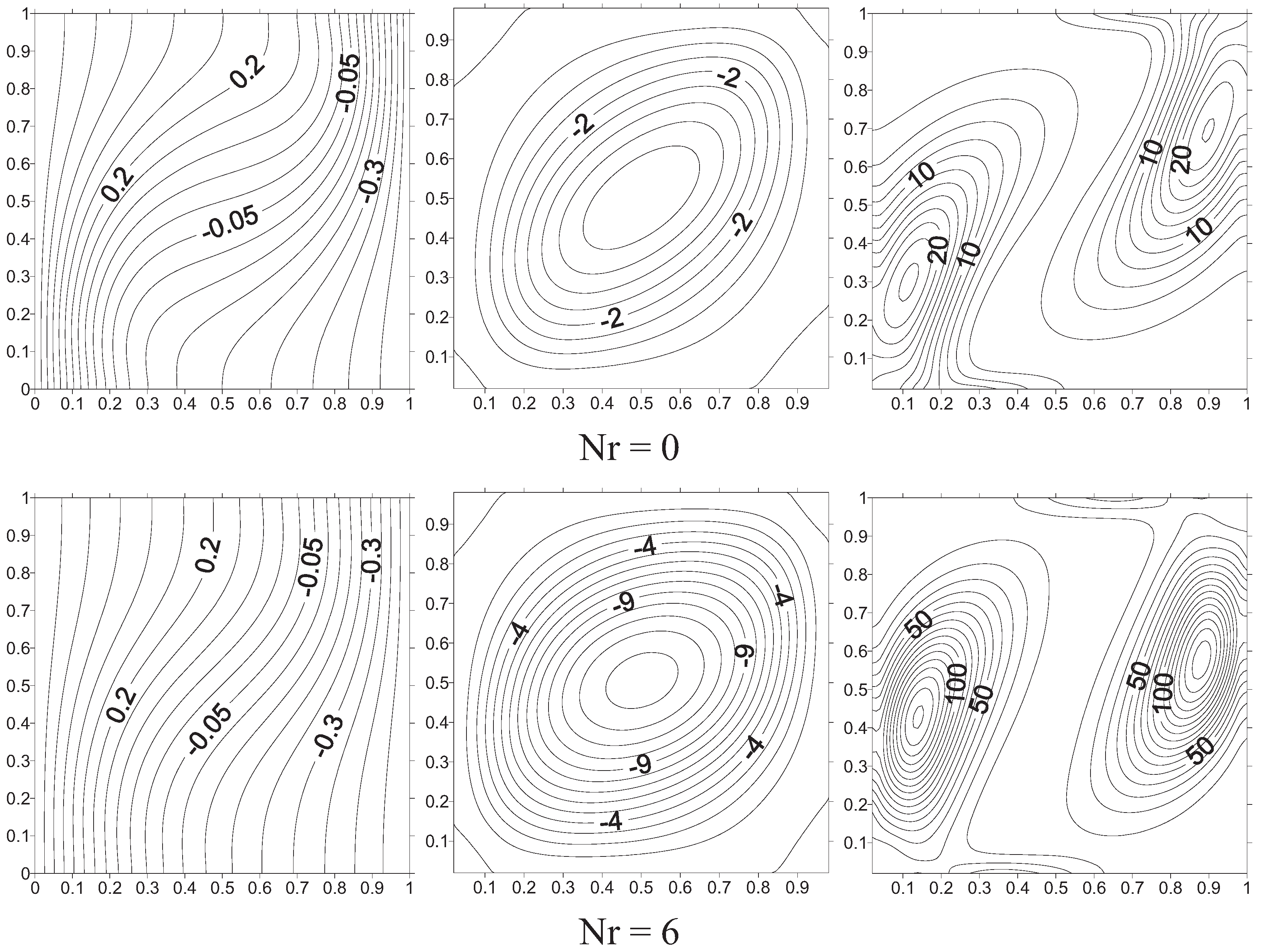
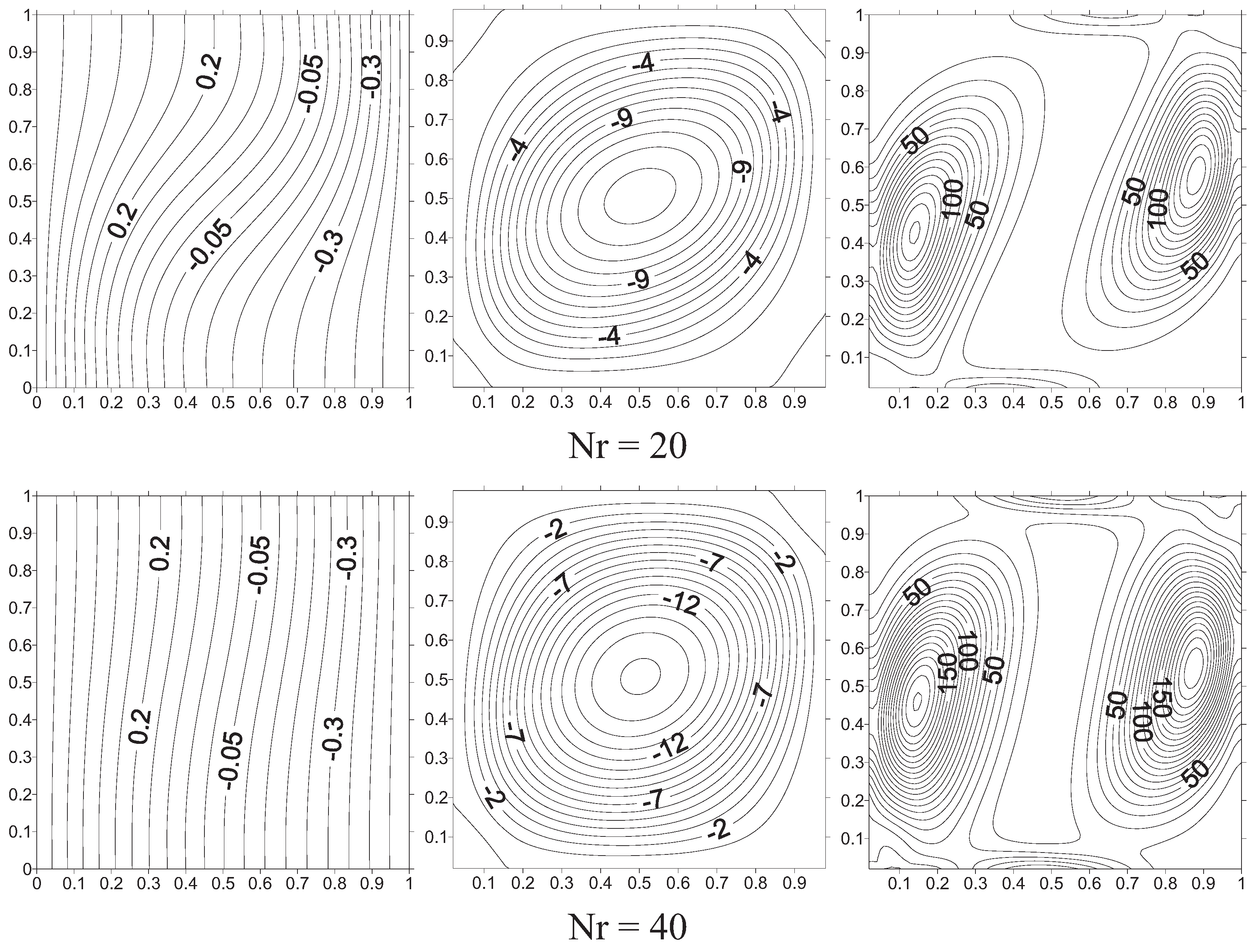
Figure 9,
Figure 10 and
Figure 11 illustrate isothermal lines, stream lines and irreversibility lines. In natural convection (
i.e., N = 0) and in absence of a magnetic effect (
i.e., Ha = 0),
Figure 9 shows that isothermal lines are confined through the bottom region of the heated wall and the upper region of the cooled wall, a two cells structure of the flow is observed and irreversibility is localized on the indicated regions. As radiation parameter increases, horizontal temperature through the active wall decreases as well as velocity gradients inducing a one cell structure for Nr ≥ 6. The irreversibility lines are dispersed along the active as well as the insulated walls with decreasing amplitude. Thus, increasing radiation effect induces homogenous behaviour of fluid flow as well as thermal gradients inside the cavity leading to decrease of local entropy generation. In presence of a magnetic field (
i.e., Ha = 25),
Figure 10 shows that both radiation and magnetic effects tend to stabilize the system even for relatively higher thermal Rayleigh number (
i.e., Ra ≥10
5).
Figure 11 shows the case where thermal and concentration gradients have the same amplitude and act in opposite way (
i.e., N = −1). In this case, isothermal lines are mainly parallel to active walls showing a quasi conduction mode with a unicellular structure and increasing two cells structure of entropy generation as radiation parameter enhances both heat and mass transfer inside the enclosure.
Figure 9.
Isothermal lines, Stream lines and Isentropic lines for Ha = 0; N = 0 and Ra = 105 with different radiation parameter at horizontal magnetic field.
Figure 9.
Isothermal lines, Stream lines and Isentropic lines for Ha = 0; N = 0 and Ra = 105 with different radiation parameter at horizontal magnetic field.
Figure 10.
Isothermal lines, Stream lines and Isentropic lines for Ha = 25; N = 0 and Ra = 105 with different radiation parameter at horizontal magnetic field.
Figure 10.
Isothermal lines, Stream lines and Isentropic lines for Ha = 25; N = 0 and Ra = 105 with different radiation parameter at horizontal magnetic field.
Figure 11.
Isothermal lines, Stream lines and Isentropic lines for Ha = 25; N = −1 and Ra = 105 with different radiation parameter at horizontal magnetic field.
Figure 11.
Isothermal lines, Stream lines and Isentropic lines for Ha = 25; N = −1 and Ra = 105 with different radiation parameter at horizontal magnetic field.