Entropy Generation Analysis of Desalination Technologies
Abstract
:1. Introduction
2. Derivation of Performance Parameters for Desalination
2.1. Work and Heat of Separation
2.2. Second Law Efficiency
2.3. Energetic Performance Parameters
3. Analysis of Entropy Generation Mechanisms in Desalination
3.1. Flashing
3.2. Flow through an Expansion Device without Phase Change
3.3. Pumping and Compressing
3.4. Isobaric Heat Transfer Process
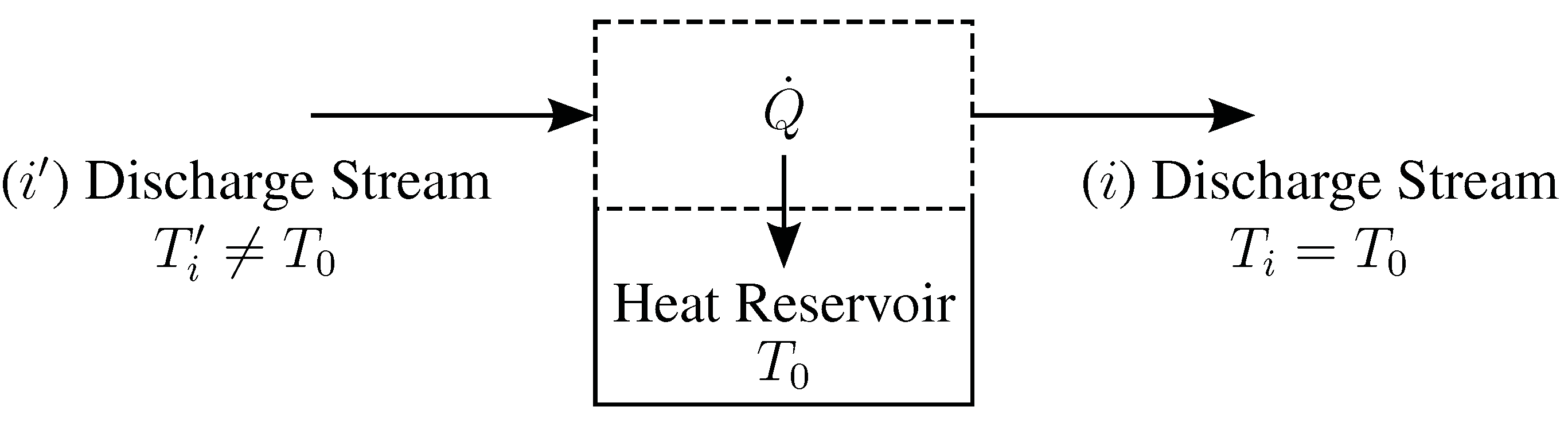
3.5. Thermal Disequilibrium of Discharge Streams
3.6. Chemical Disequilibrium of Brine Stream
4. Application of Entropy Generation Mechanisms to Seawater Desalination Technologies
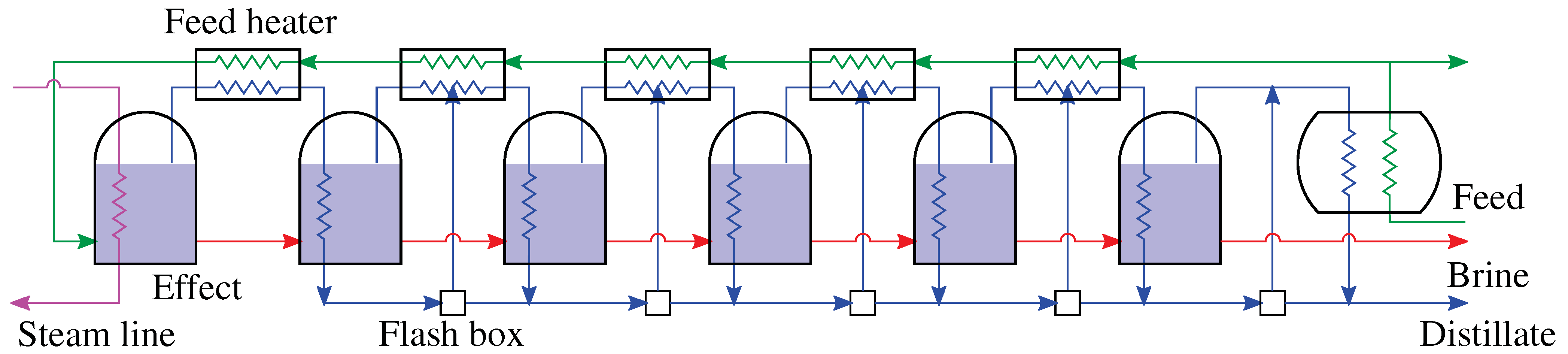
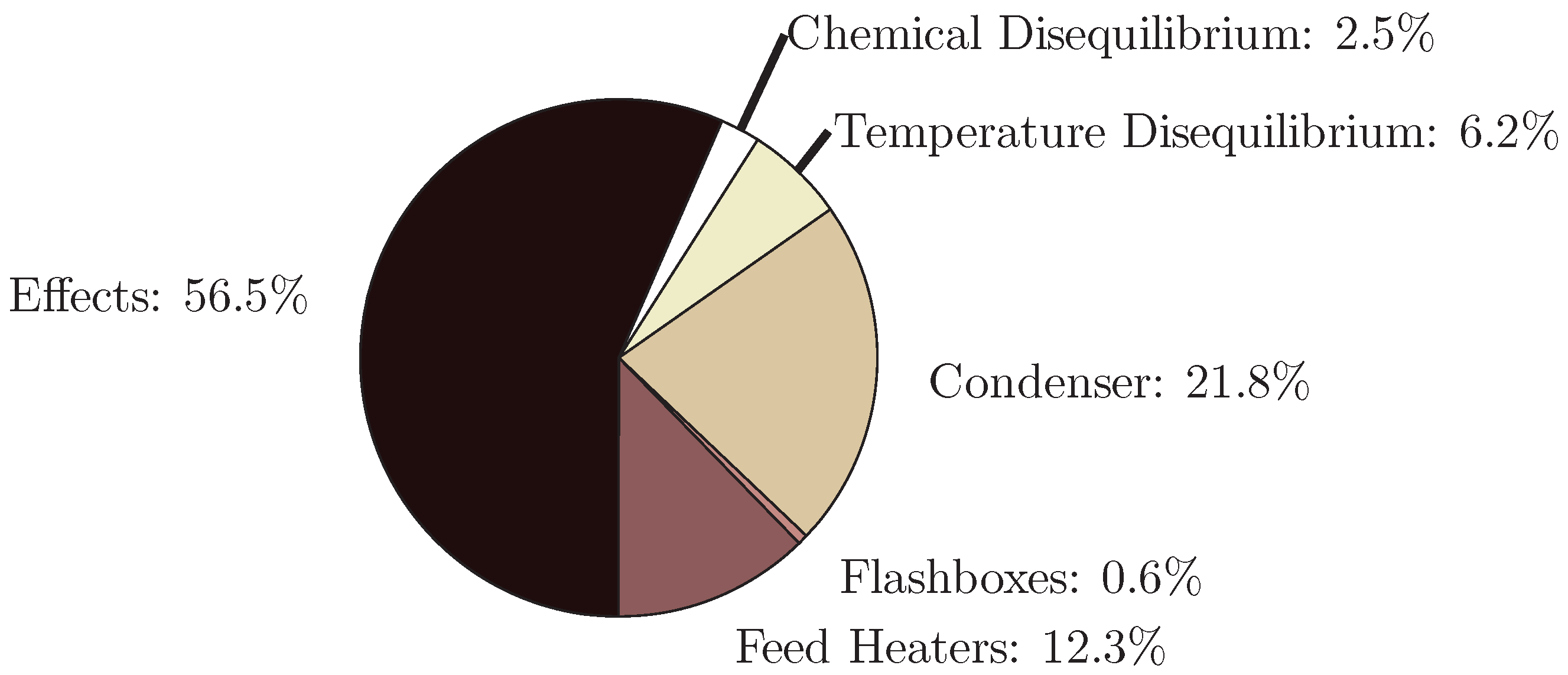
4.1. Multiple Effect Distillation
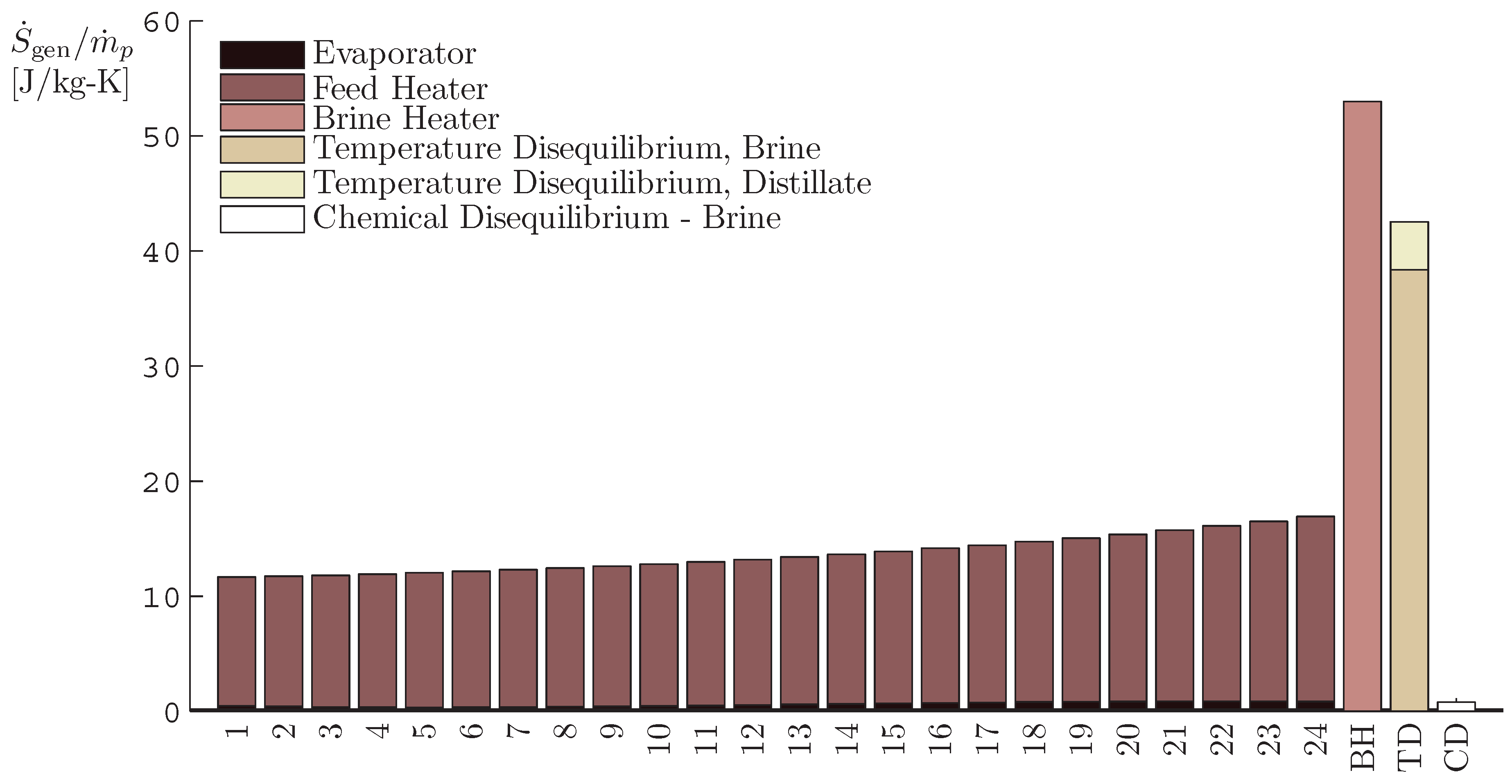
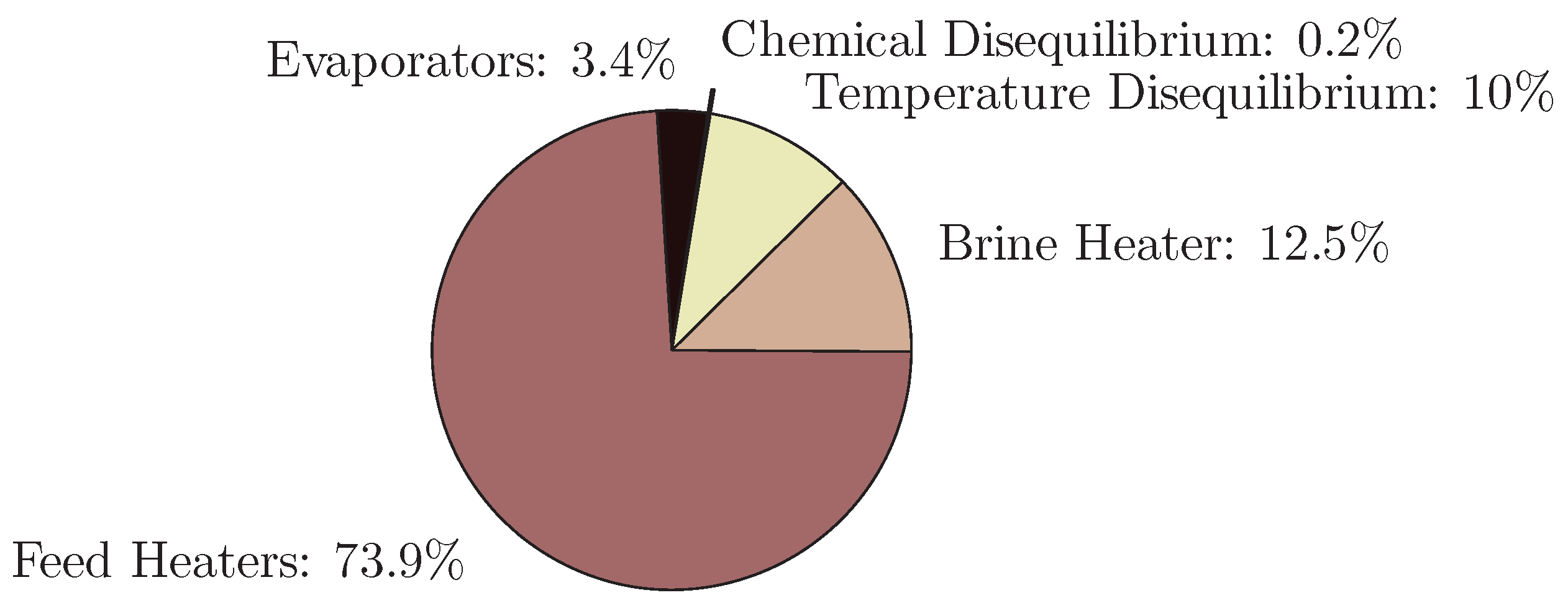
4.2. Multistage Flash
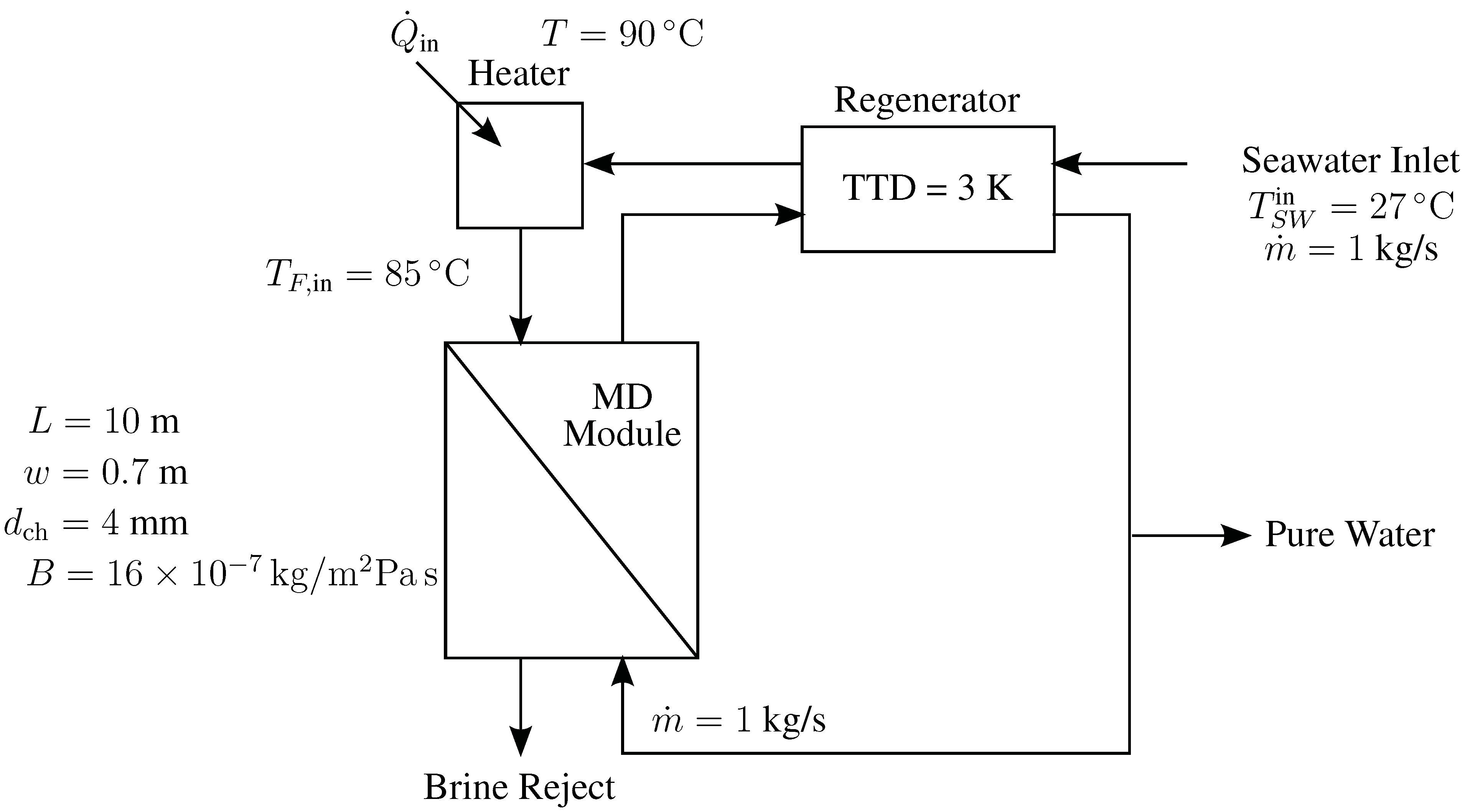
4.3. Direct Contact Membrane Distillation
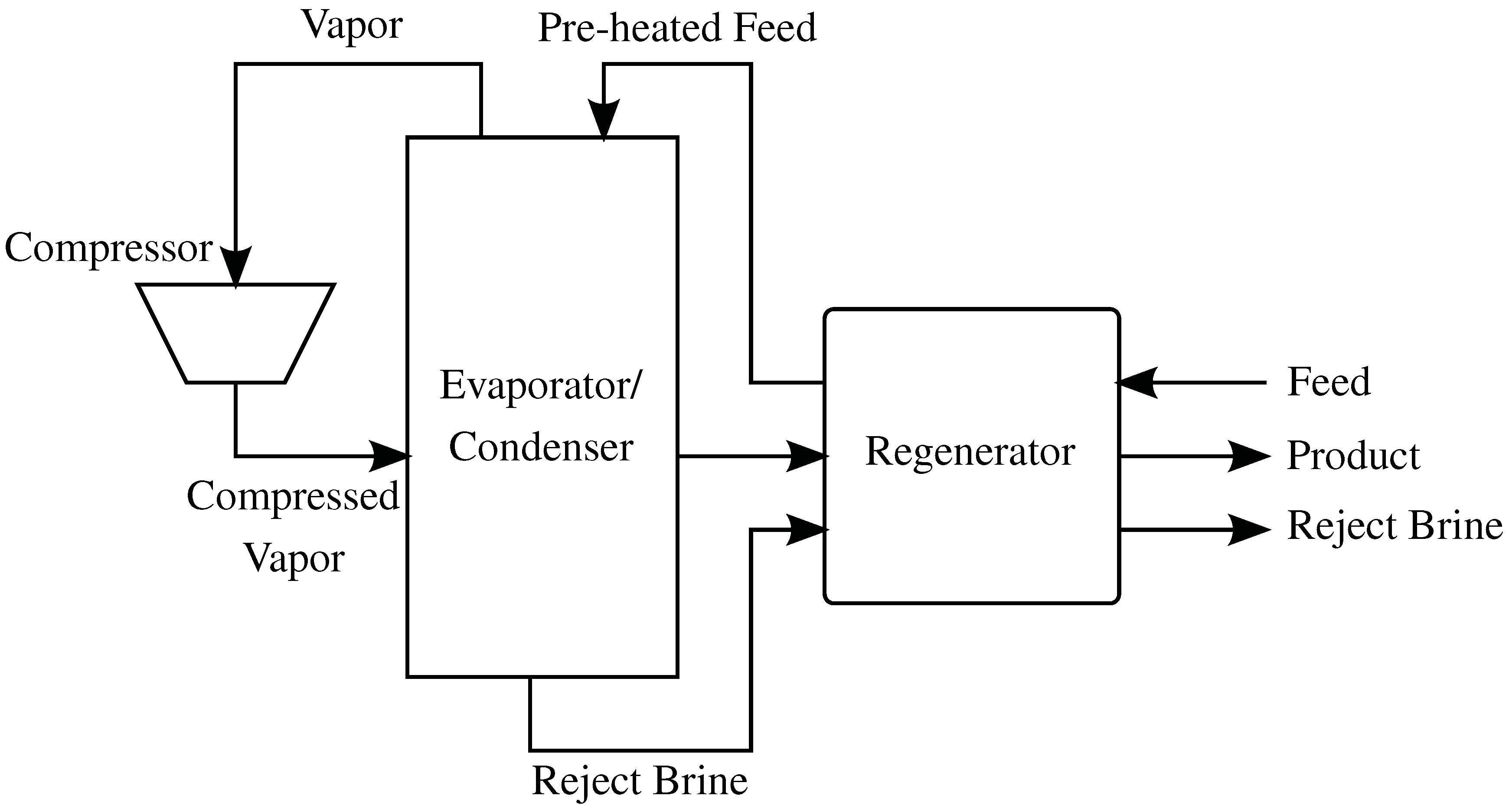
4.4. Mechanical Vapor Compression
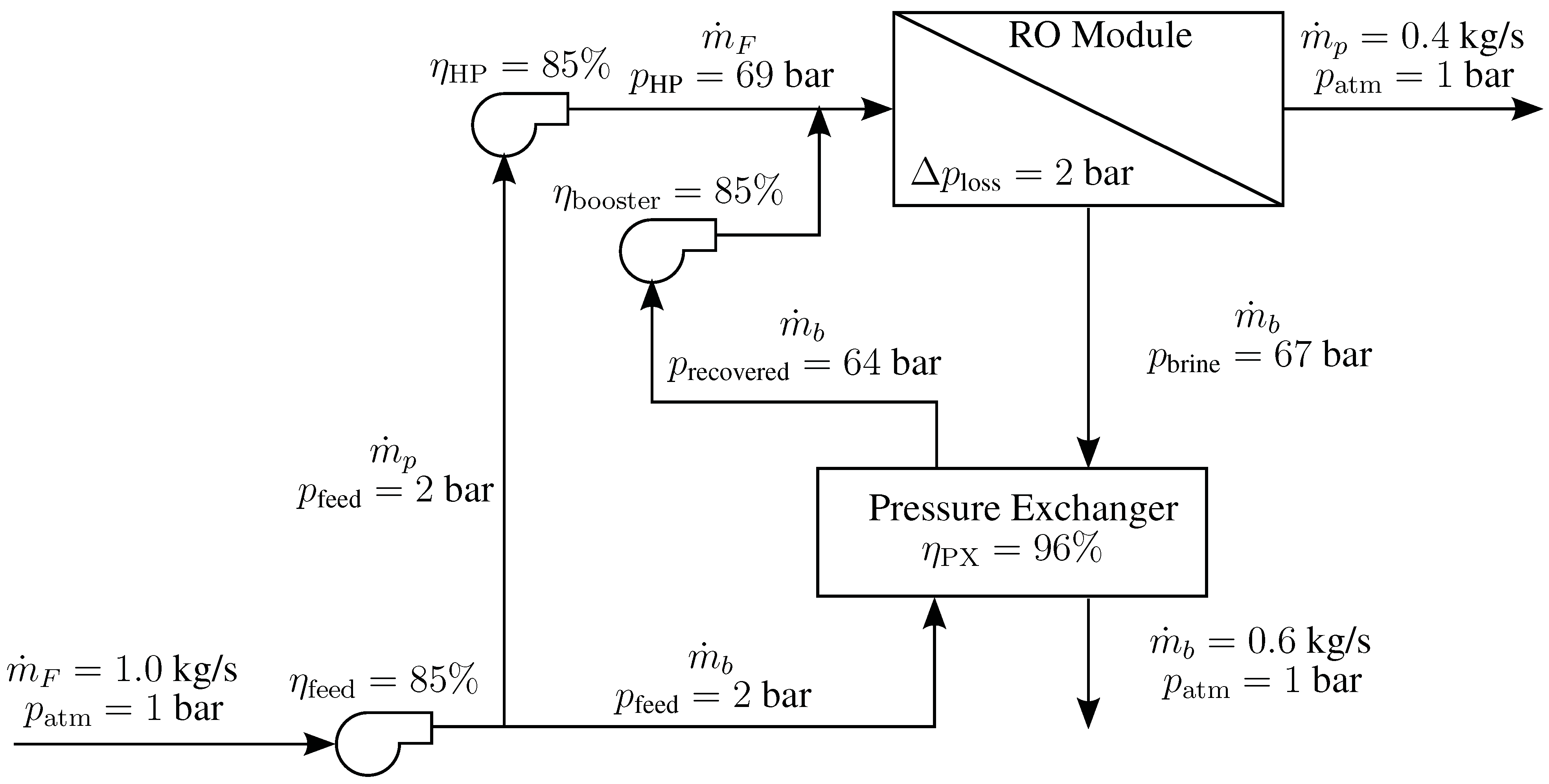
4.5. Reverse Osmosis
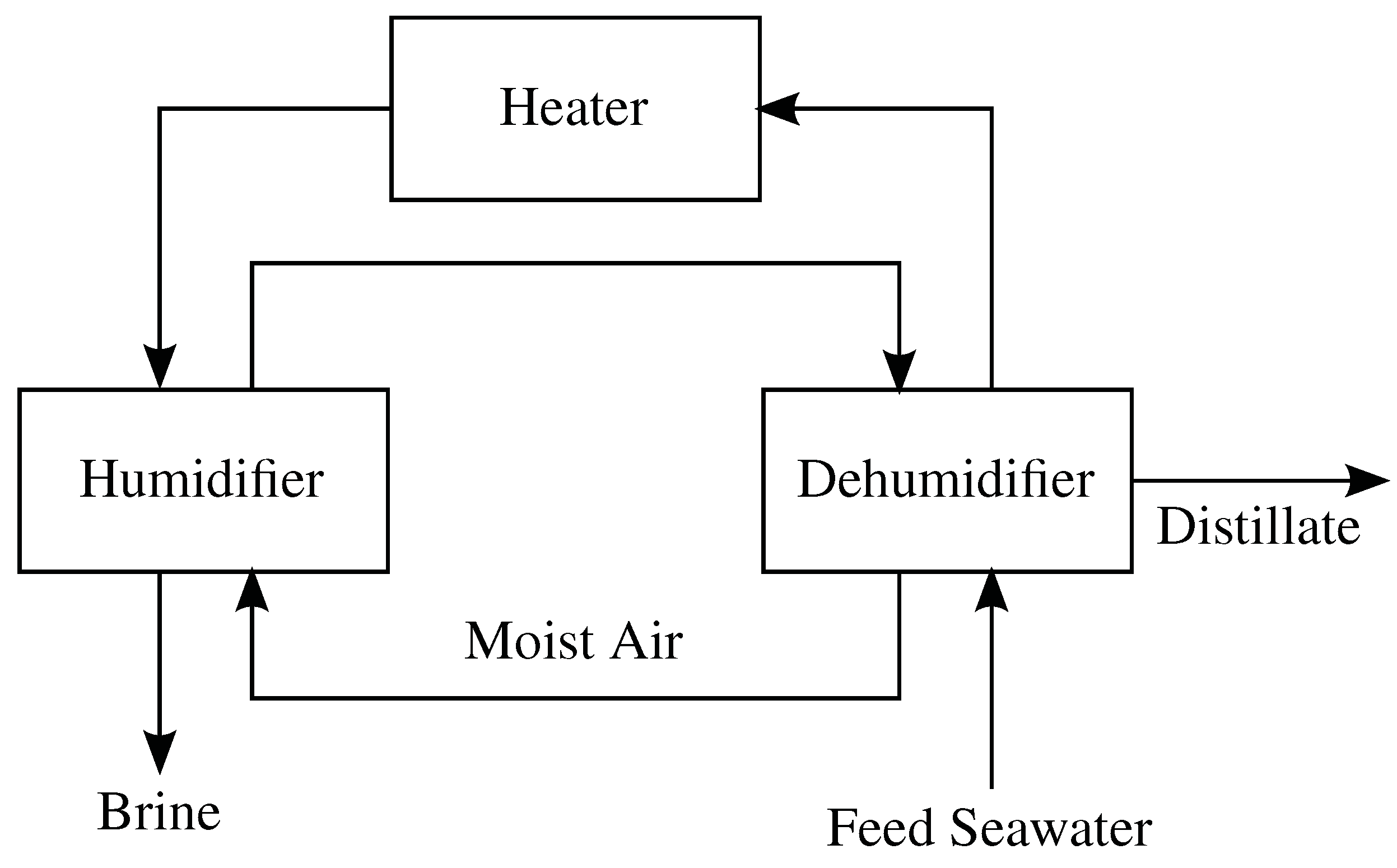
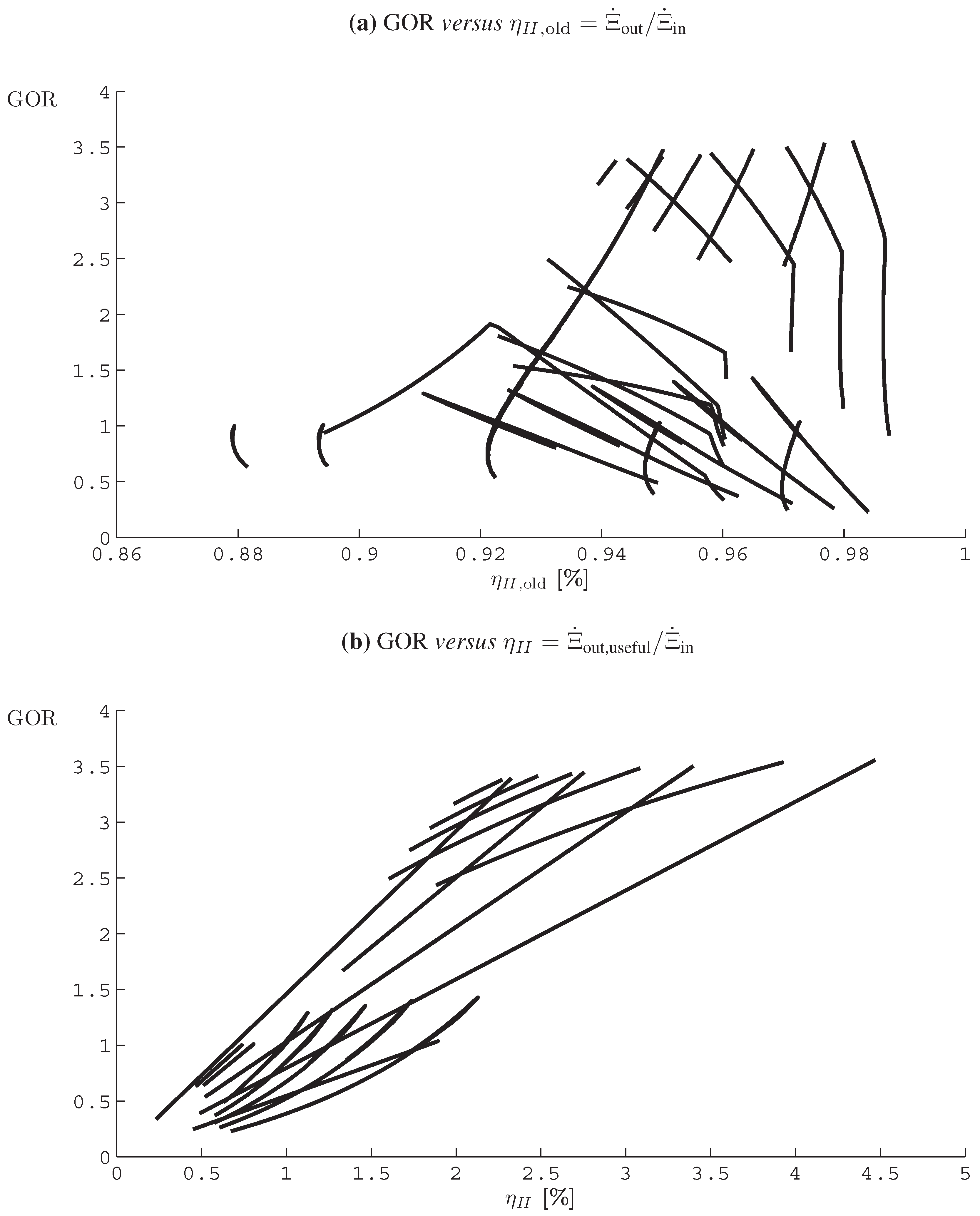
4.6. Humidification-Dehumidification
5. Conclusions
- A Second Law efficiency is developed for desalination systems and is defined as the useful work output divided by the total work input to the system. The useful work output of a desalination system is the minimum least work of separation, since the useful output of the system is pure water, not pure hot water. Minimum least work of separation is defined such that all input and output streams with exception of the product stream are in thermal, mechanical, and chemical equilibrium with the environment (total dead state). The product stream is in thermal and mechanical equilibrium with the environment (restricted dead state). The exergy input to the desalination systems analyzed is either in the form of work or heat. See Equation (16).
- When considering the work input to be the minimum least work of separation plus lost work due to entropy generation, it is essential to consider entropy generated not only due to irreversibilities in the separation process, but also due to temperature disequilibrium of the discharge and the irreversible mixing of the brine with the ambient seawater. See Equation (14).
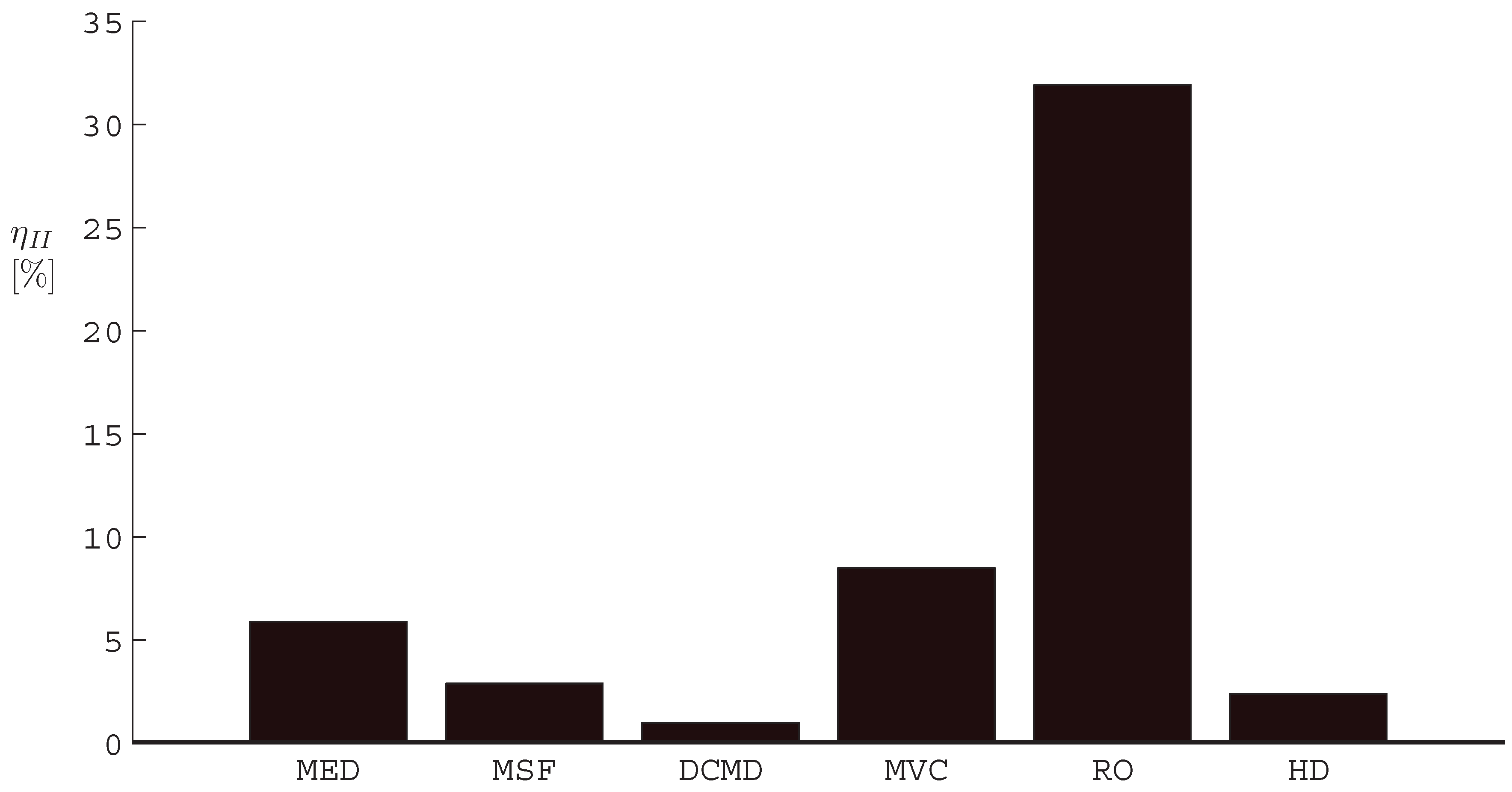
- The application of entropy generation analysis to various desalination technologies showed that thermal disequilibrium of the discharge streams results in a substantial portion of the entropy generated in thermal systems. Similarly, it was seen that entropy generation due to chemical disequilibrium is important only in systems with high recovery ratios. Depending on whether thermal or chemical disequilibrium is important, modifications to the systems can be implemented in order to capitalize on the potential differences between the discharge streams and the environment and reduce the required energy input.
Acknowledgments
Nomenclature
| Symbols | exergy destruction rate [kW] | ||
| B | membrane distillation coefficient [kg/m2-Pa-s] | exergy flow rate [kW] | |
| c | specific heat [kJ/kg-K] | specific exergy destruction [kJ/kg] | |
| specific heat at constant pressure [kJ/kg-K] | ρ | denisty [kg/m3] | |
| distillate from effect i [kg/s] | |||
| distillate from flashing in effect i [kg/s] | Subscripts | ||
| distillate from flashing in flash box i [kg/s] | atm | atmospheric | |
| flow channel depth [m] | b | brine | |
| g | specific Gibbs free energy [kJ/kg] | f | flashing |
| h | specific enthalpy [kJ/kg] | p | product |
| hfg | latent heat of vaporization [kJ/kg] | F | feed |
| hfg | latent heat of vaporization [kJ/kg] | i | state |
| L | length [m] | ref | reference |
| mass flow rate [kg/s] | s | steam | |
| n | number of effects or stages [-] | seawater | |
| p | pressure [kPa] | ||
| heat transfer [kW] | Superscripts | ||
| least heat of separation [kW] | HX | heat exchanger | |
| minimum least heat of separation [kW] | IF | incompressible fluid | |
| heat of separation [kW] | IG | ideal gas | |
| R | ideal gas constant [kJ/kg-K] | s | isentropic |
| r | recovery ratio [(kg/s product)/(kg/s feed)] | ′ | stream before exiting CV |
| entropy generation rate [kW/K] | |||
| s | specific entropy [kJ/kg-K] | Acronyms | |
| specific entropy generation per unit fluid [kJ/kg-K] | BH | brine heater | |
| specific entropy generation per unit water produced [kJ/kg-K] | CAOW | closed air open water | |
| T | temperature [K] | CD | chemical disequilibrium |
| ambient (dead state) temperature [K] | DCMD | direct contact membrane distillation | |
| temperature of heat reservoir [K] | ERI | Energy Recovery Inc. | |
| v | specific volume [m3/kg] | FF | forward feed |
| least work of separation [kW] | GOR | gained output ratio | |
| minimum least work of separation [kW] | HD | humidification-dehumidification | |
| work of separation [kW] | HP | high pressure | |
| w | width [m] | MED | multiple effect distillation |
| w | specific work [kJ/kg] | MSF | multistage flash |
| x | quality [kg/kg] | MVC | mechanical vapor compression |
| y | salinity [g/kg] | OT | once through |
| z | generalized compressibility [-] | PR | performance ratio |
| PX | pressure exchanger | ||
| Greek | RDS | restricted dead state | |
| Δ | change in a variable | RO | reverse osmosis |
| η | mole ratio of salt in seawater [-] | TD | temperature disequilibrium |
| isentropic efficiency of expander [-] | TDS | total dead state | |
| isentropic efficiency of pump/compressor [-] | WH | water heated | |
| Second Law/exergetic efficiency [-] |
References
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Smakhtin, V.; Revenga, C.; Döll, P. Taking into account environmental water requirements in global-scale water resources assessments. In Comprehensive Assessment Research Report 2; Comprehensive Assessment Secretariat, International Water Management Institute: Colombo, Sri Lanka, 2004. [Google Scholar]
- Shannon, M.A.; Bohn, P.W.; Elimelech, M.; Georgiadis, J.G.; Marinas, B.J.; Mayes, A.M. Science and technology for water purification in the coming decades. Nature 2008, 452, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Semiat, R. Energy issues in desalination processes. Environ. Sci. Tech. 2008, 42, 8193–8201. [Google Scholar] [CrossRef]
- Spiegler, K.S.; El-Sayed, Y.M. The energetics of desalination processes. Desalination 2001, 134, 109–128. [Google Scholar] [CrossRef]
- Mistry, K.H.; Lienhard V, J.H.; Zubair, S.M. Effect of entropy generation on the performance of humidification-dehumidification desalination cycles. Int. J. Therm. Sci. 2010, 49, 1837–1847. [Google Scholar] [CrossRef]
- Alasfour, F.; Darwish, M.; Amer, A.B. Thermal analysis of ME–TVC+MEE desalination systems. Desalination 2005, 174, 39–61. [Google Scholar] [CrossRef]
- Kahraman, N.; Cengel, Y.A. Exergy analysis of a MSF distillation plant. Energ. Convers. Manag. 2005, 46, 2625–2636. [Google Scholar] [CrossRef]
- Veza, J.M. Mechanical vapour compression desalination plants—A case study. Desalination 1995, 101, 1–10. [Google Scholar] [CrossRef]
- Cerci, Y. Exergy analysis of a reverse osmosis desalination plant in California. Desalination 2002, 142, 257–266. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Zubair, S.M.; Lienhard V, J.H. Second Law analysis of reverse osmosis desalination plants: An alternative design using pressure retarded osmosis. Energy 2011, in press. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Lienhard V, J.H.; Zubair, S.M. On exergy calculations of seawater with applications in desalination systems. Int. J. Therm. Sci. 2011, 50, 187–196. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Lienhard V, J.H.; Zubair, S.M. Thermophysical properties of seawater: A review of existing correlations and data. Desalination and Water Treatment 2010, 16, 354–380. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M. Themal Design and Optimization; John Wiley & Sons, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Wagner, W.; Pruss, A. The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef]
- Bejan, A. General criterion for rating heat-exchanger performance. Int. J. Heat. Mass Tran. 1978, 21, 655–658. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- El-Sayed, Y.M.; Silver, R.S. Principles of Desalination; Academic Press: New York, NY, USA, 1980; Volume A, Chapter Fundamentals of Distillation; pp. 55–109. [Google Scholar]
- Darwish, M.; Al-Juwayhel, F.; Abdulraheim, H.K. Multi-effect boiling systems from an energy viewpoint. Desalination 2006, 194, 22–39. [Google Scholar] [CrossRef]
- El-Dessouky, H.T.; Ettouney, H.M. Fundamentals of Salt Water Desalination; Elsevier: Amsterdamn, The Netherlands, 2002. [Google Scholar]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation. J. Membr. Sci. 1997, 124, 1–25. [Google Scholar] [CrossRef]
- Rodriguez-Maroto, J.; Martinez, L. Bulk and measured temperatures in direct contact membrane distillation. J. Membr. Sci. 2005, 250, 141–149. [Google Scholar] [CrossRef]
- Martinez-Diez, L.; Florido-Diaz, F.J. Desalination of brines by membrane distillation. Desalination 2001, 137, 267–273. [Google Scholar] [CrossRef]
- Song, L.; Li, B.; Sirkar, K.K.; Gilron, J.L. Direct contact membrane distillation-based desalination: Novel membranes, devices, larger-scale studies, and a model. Ind. Eng. Chem. Res. 2007, 46, 2307–2323. [Google Scholar] [CrossRef]
- Lee, H.; He, F.; Song, L.; Gilron, J.; Sirkar, K.K. Desalination with a cascade of cross-flow hollow fiber membrane distillation devices integrated with a heat exchanger. AIChE J. 2011, 57, 1780–1795. [Google Scholar] [CrossRef]
- Bui, V.; Vu, L.; Nguyen, M. Modelling the simultaneous heat and mass transfer of direct contact membrane distillation in hollow fibre modules. J. Membr. Sci. 2010, 353, 85–93. [Google Scholar] [CrossRef]
- Lienhard IV, J.H.; Lienhard V, J.H. A Heat Transfer Textbook, 4th ed.; Dover Publications: Mineola, NY, USA, 2011. [Google Scholar]
- Fath, H.E.; Elsherbiny, S.M.; Hassan, A.A.; Rommel, M.; Wieghaus, M.; Koschikowski, J.; Vatansever, M. PV and thermally driven small-scale, stand-alone solar desalination systems with very low maintenance needs. Desalination 2008, 225, 58–69. [Google Scholar] [CrossRef]
- Banat, F.; Jwaied, N.; Rommel, M.; Koschikowski, J.; Wieghaus, M. Desalination by a “compact SMADES” autonomous solar-powered membrane distillation unit. Desalination 2007, 217, 29–37. [Google Scholar] [CrossRef]
- Aly, S.E. Gas turbine total energy vapour compression desalination system. Energ. Convers. Manag. 1999, 40, 729–741. [Google Scholar] [CrossRef]
- Nafey, A.; Fath, H.; Mabrouk, A. Thermoeconomic design of a multi-effect evaporation mechanical vapor compression (MEE-MVC) desalination process. Desalination 2008, 230, 1–15. [Google Scholar] [CrossRef]
- Lara, J.; Noyes, G.; Holtzapple, M. An investigation of high operating temperatures in mechanical vapor-compression desalination. Desalination 2008, 227, 217–232, Issue 1 First Oxford and Nottingham Water and Membranes Research Event, Oxford, UK, 2–4 July 2006. [Google Scholar] [CrossRef]
- Lukic, N.; Diezel, L.; Fröba, A.; Leipertz, A. Economical aspects of the improvement of a mechanical vapour compression desalination plant by dropwise condensation. Desalination 2010, 264, 173–178. [Google Scholar] [CrossRef]
- Energy Recovery Inc. ERI Power Model. Available online: http://www.energyrecovery.com/index.cfm/0/0/56-Power-Model.html (accessed on 22 August 2011).
- Energy Recovery Inc. Technology Overview. Available online: http://www.energyrecovery.com/index.cfm/0/0/33-Overview.html (accessed on 22 August 2011).
- Elimelech, M.; Phillip, W.A. The future of seawater desalination: Energy, technology, and the environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef] [PubMed]
- Desalitech Ltd. Doing away with RO energy-recovery devices. Desalination and Water Reuse 2010, 20, 26–28. [Google Scholar]
- Mistry, K.H.; Mitsos, A.; Lienhard V, J.H. Optimal operating conditions and configurations for humidification-dehumidification desalination cycles. Int. J. Therm. Sci. 2011, 50, 779–789. [Google Scholar] [CrossRef]
- Mistry, K.H.; Narayan, G.P.; Mitsos, A.; Lienhard V, J.H. Optimization of multi-pressure humidification-dehumidification desalination using thermal vapor compression and hybridization. In Proceedings of the 21st National & 10th ISHMT-ASME Heat and Mass Transfer Conference, IIT Madras, India, 27–30 December 2011. No. ISHMT_USA_15.
- Mistry, K.H. Second Law Analysis and Optimization of Humidification-Dehumidification Desalination Cycles. Master’s thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2010. [Google Scholar]
- Narayan, G.P.; Sharqawy, M.H.; Lienhard V, J.H.; Zubair, S.M. Thermodynamic analysis of humidification dehumidification desalination cycles. Desalination and Water Treatment 2010, 16, 339–353. [Google Scholar] [CrossRef]
- Narayan, G.P.; Sharqawy, M.H.; Summers, E.K.; Lienhard V, J.H.; Zubair, S.M.; Antar, M. The potential of solar-driven humidification-dehumidification desalination for small-scale decentralized water production. Renew. Sustain. Energ. Rev. 2010, 14, 1187–1201. [Google Scholar] [CrossRef]
- Narayan, G.P.; Mistry, K.H.; Sharqawy, M.H.; Zubair, S.M.; Lienhard V, J.H. Energy effectiveness of simultaneous heat and mass exchange devices. Front. Heat Mass Trans. 2010, 1, 1–13. [Google Scholar] [CrossRef]
- Hyland, R.W.; Wexler, A. Formulations for the thermodynamic properties of dry air from 173.15 K to 473.15 K, and of saturated moist air from 173.15 K to 372.15 K, at pressures to 5 MPa. ASHRAE Trans. 1983b, Part 2A (RP-216), 520–535. [Google Scholar] [PubMed]
- Cooper, J.R. Revised release on the IAPWS industrial formulation 1997 for the thermodynamic properties of water and steam. In Proceedings of the Annual Meeting of the International Association for the Properties of Water and Steam, Lucerne, Switzerland, August 2007; pp. 1–48.
Appendices
A. Least Work of Separation as a Function of Recovery Ratio
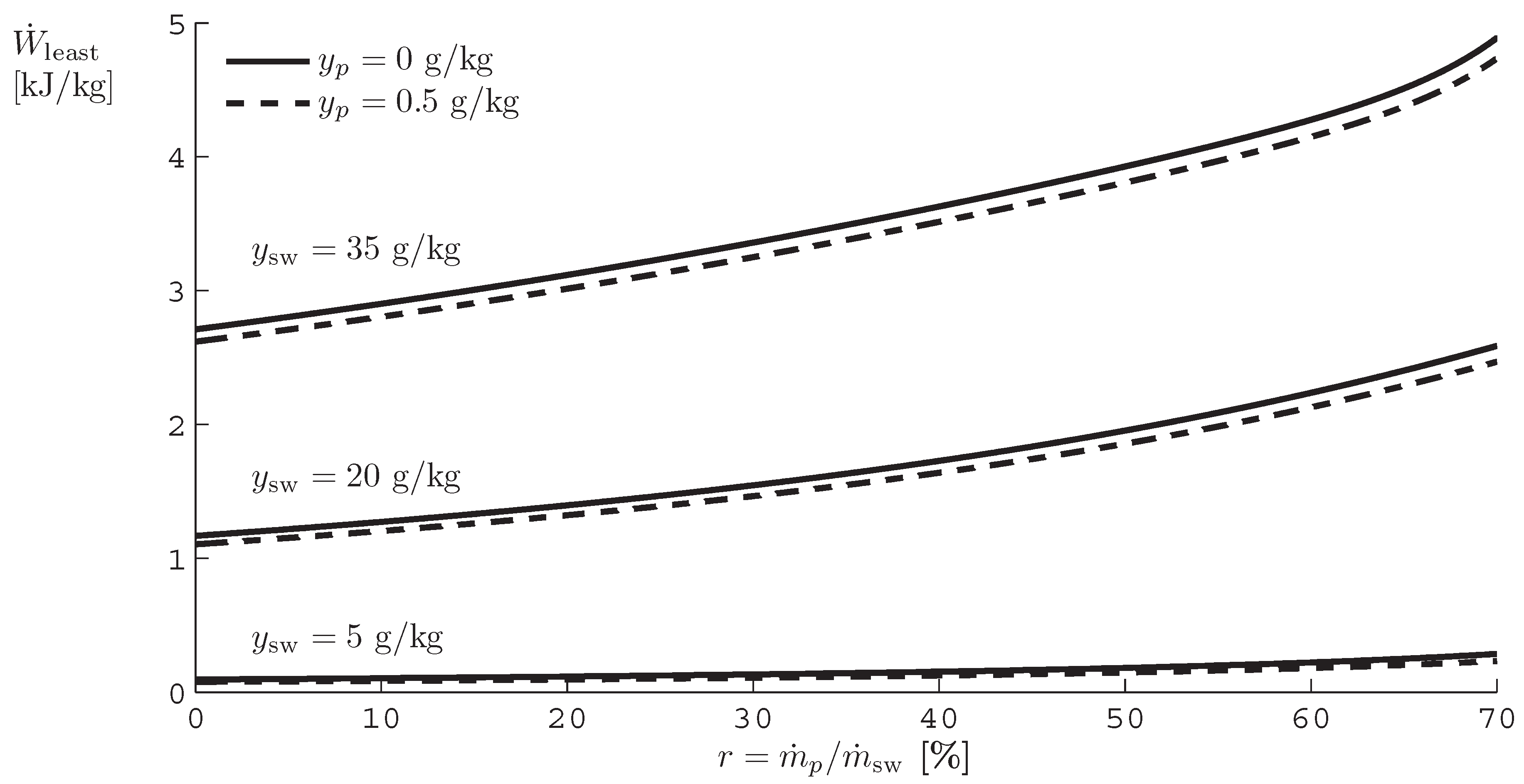
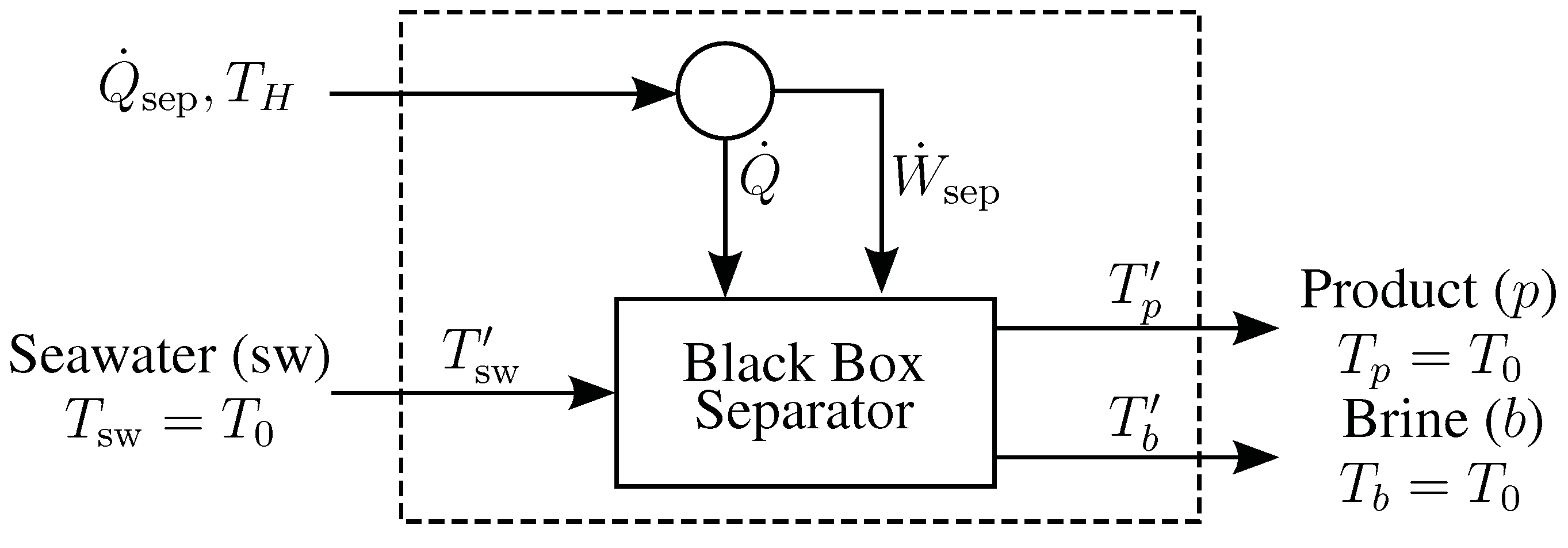
B. Derivation of Entropy Generation Equations
B.1. Incompressible Fluid and Ideal Gas Approximations
B.2. Flashing
B.3. Flow Through an Expansion Device Without Phase Change (Expanders, Pipes, Throttles, Membranes, etc.)
B.4. Pumping and Compressing
B.5. Approximately Isobaric Heat Transfer Process

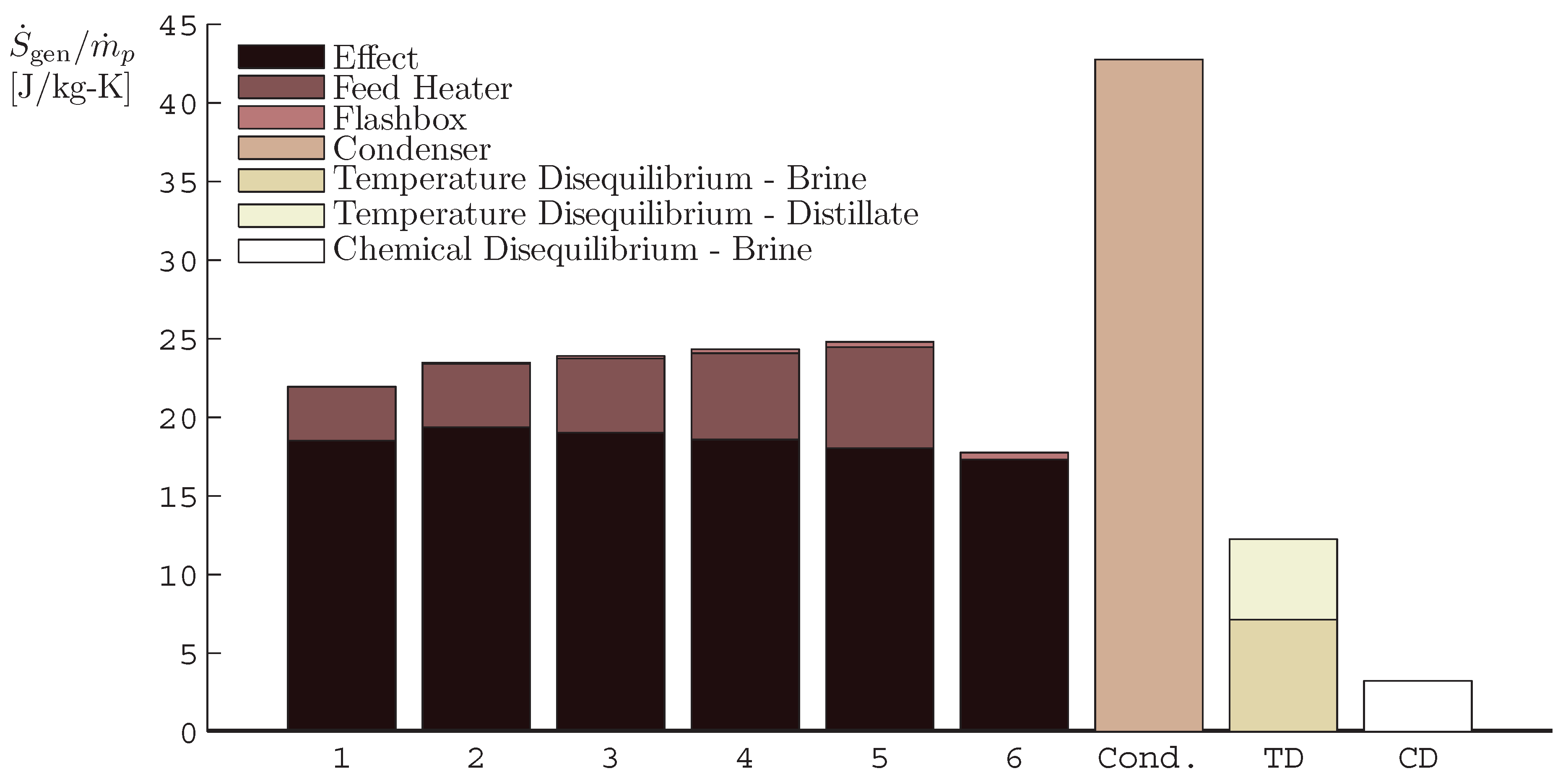


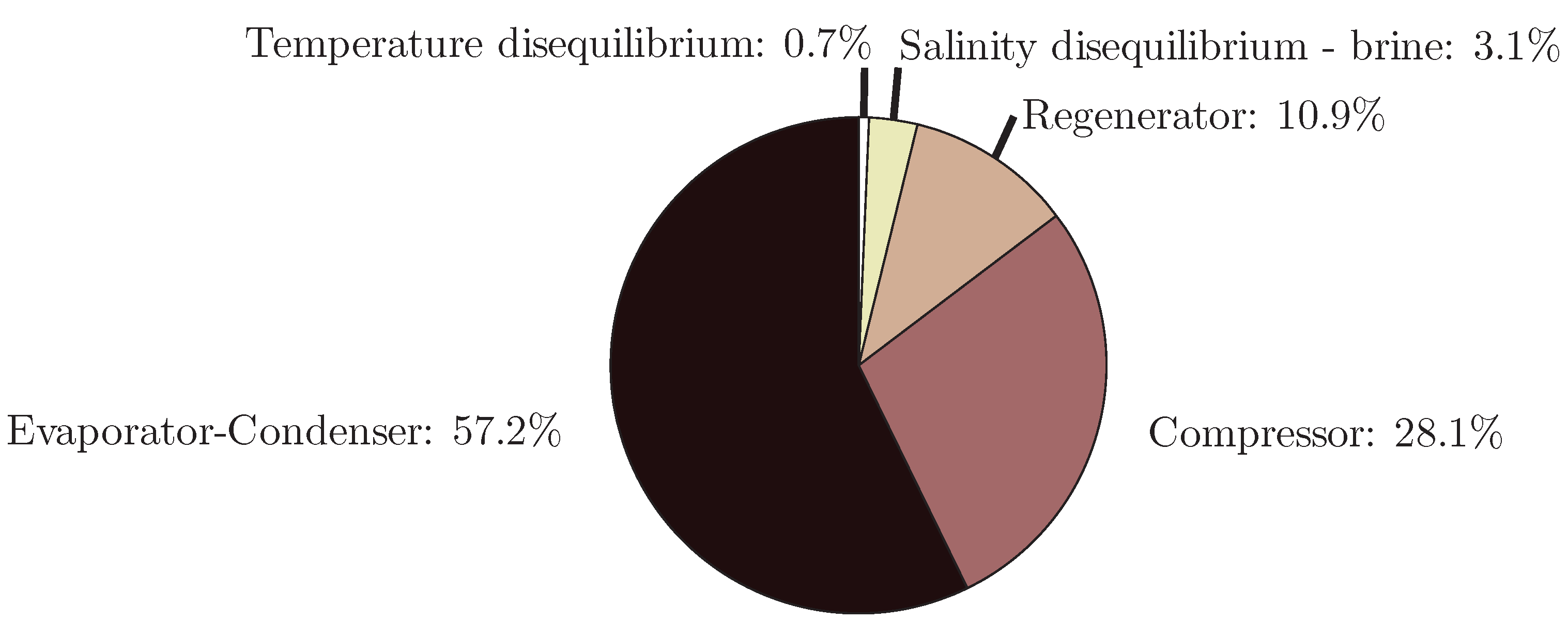
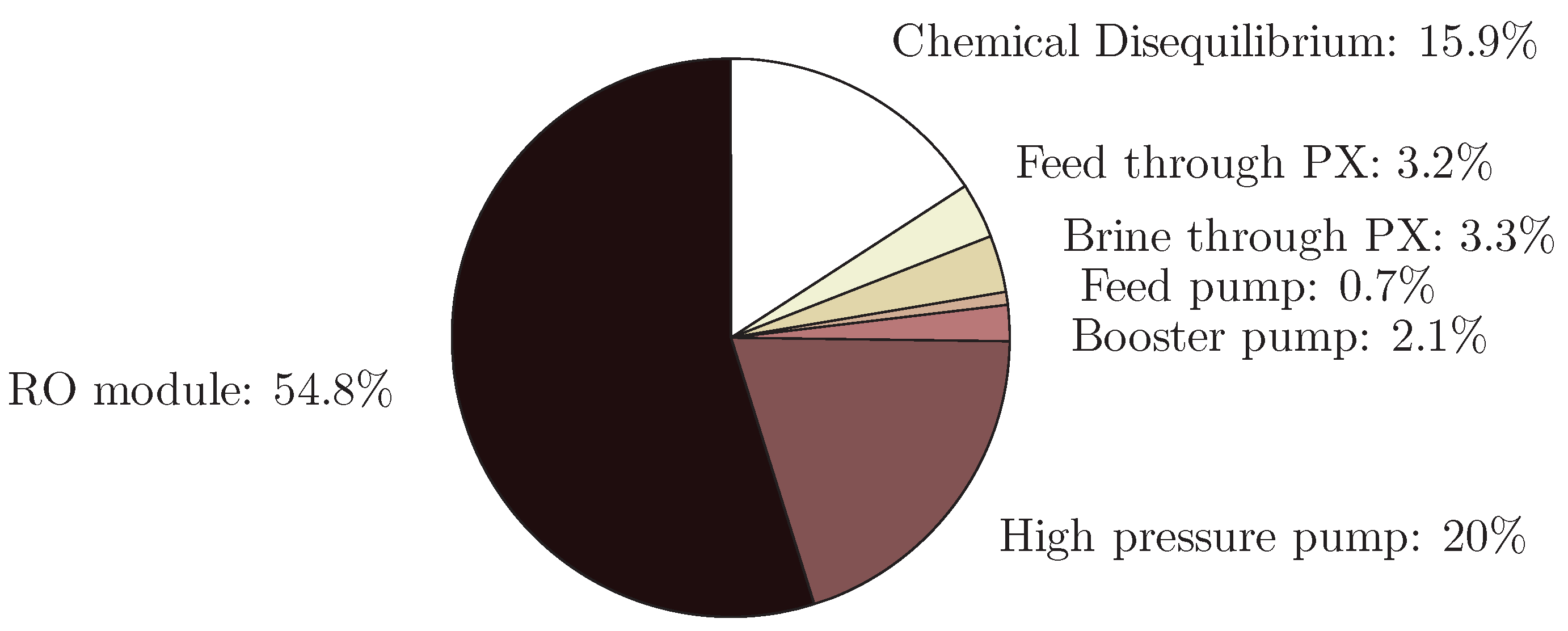
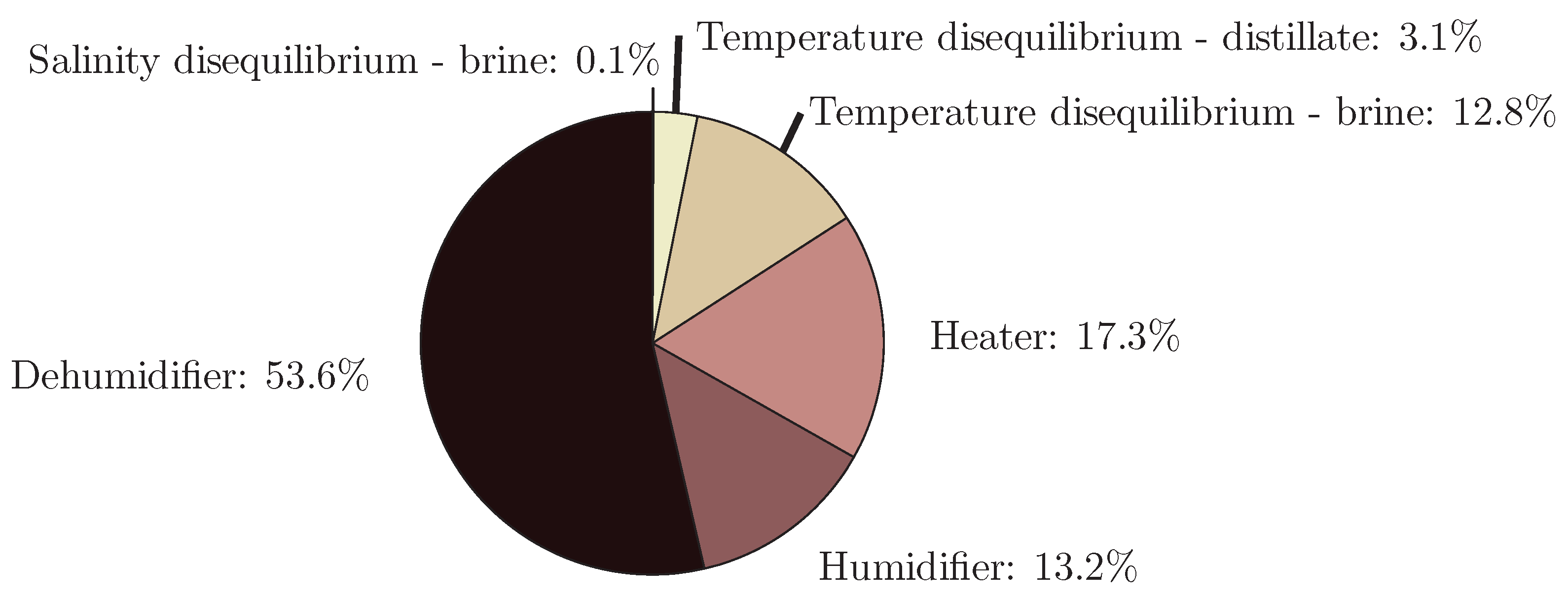
| Pure water and vapor constants, kPa | |||
| c | 4.18 kJ/kg-K | 2590 kJ/kg | |
| 1.95 kJ/kg-K | 209 kJ/kg | ||
| R | 0.462 kJ/kg-K | 8.07 kJ/kg-K | |
| v | m3/kg | 0.704 kJ/kg-K | |
| Seawater constants, 50 °C, 35,000 ppm | |||
| c | 4.01 kJ/kg-K | 200 kJ/kg | |
| v | m3/kg | 0.672 kJ/kg-K | |
| Output | Model Value | |
| Performance ratio | PR | 4.2 |
| Gained output ratio | GOR | 4.6 |
| Top brine temperature | [°C] | 109 |
| Steam flow rate | [kg/s] | 91.1 |
| Max salinity | [g/kg] | 47.3 |
| Input | Value |
| Seawater inlet temperature | 25 °C |
| Seawater inlet salinity | 35 g/kg |
| Product water salinity | 0 g/kg |
| Discharged brine salinity | 58.33 g/kg |
| Top brine temperature | 60 °C |
| Pinch: evaporator-condenser | 2.5 K |
| Recovery ratio | 40% |
| Isentropic compressor efficiency | 70% |
| Compressor inlet pressure | 19.4 kPa |
| Output | Value |
| Specific electricity consumption | 8.84 kWh/m3 |
| Discharged brine temperature | 27.2 °C |
| Product water temperature | 29.7 °C |
| Compression ratio | 1.15 |
| Second Law efficiency, | 8.5% |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Mistry, K.H.; McGovern, R.K.; Thiel, G.P.; Summers, E.K.; Zubair, S.M.; Lienhard, J.H., V. Entropy Generation Analysis of Desalination Technologies. Entropy 2011, 13, 1829-1864. https://doi.org/10.3390/e13101829
Mistry KH, McGovern RK, Thiel GP, Summers EK, Zubair SM, Lienhard JH V. Entropy Generation Analysis of Desalination Technologies. Entropy. 2011; 13(10):1829-1864. https://doi.org/10.3390/e13101829
Chicago/Turabian StyleMistry, Karan H., Ronan K. McGovern, Gregory P. Thiel, Edward K. Summers, Syed M. Zubair, and John H. Lienhard, V. 2011. "Entropy Generation Analysis of Desalination Technologies" Entropy 13, no. 10: 1829-1864. https://doi.org/10.3390/e13101829
APA StyleMistry, K. H., McGovern, R. K., Thiel, G. P., Summers, E. K., Zubair, S. M., & Lienhard, J. H., V. (2011). Entropy Generation Analysis of Desalination Technologies. Entropy, 13(10), 1829-1864. https://doi.org/10.3390/e13101829





