Projective Power Entropy and Maximum Tsallis Entropy Distributions

Abstract

We discuss a one-parameter family of generalized cross entropy between two distributions with the power index, called the projective power entropy. The cross entropy is essentially reduced to the Tsallis entropy if two distributions are taken to be equal. Statistical and probabilistic properties associated with the projective power entropy are extensively investigated including a characterization problem of which conditions uniquely determine the projective power entropy up to the power index. A close relation of the entropy with the Lebesgue space $L_p$ and the dual $L_q$ is explored, in which the escort distribution associates with an interesting property. When we consider maximum Tsallis entropy distributions under the constraints of the mean vector and variance matrix, the model becomes a multivariate q-Gaussian model with elliptical contours, including a Gaussian and t-distribution model. We discuss the statistical estimation by minimization of the empirical loss associated with the projective power entropy. It is shown that the minimum loss estimator for the mean vector and variance matrix under the maximum entropy model are the sample mean vector and the sample variance matrix. The escort distribution of the maximum entropy distribution plays the key role for the derivation.

1. Introduction

In the classical statistical physics and the information theory the close relation with Boltzmann-Shannon entropy has been well established to offer elementary and clear understandings. The Kullback-Leibler divergence is directly connected with maximum likelihood, which is one of the most basic ideas in statistics. Tsallis opened new perspectives for the power entropy to elucidate non-equilibrium states in statistical physics, and these give the strong influence on the research for non-extensive and chaotic phenomenon, cf. [1,2]. There are proposed several generalized versions of entropy and divergence, cf. [3,4,5,6,7]. We consider generalized entropy and divergence defined on the space of density functions with finite mass,

$$\begin{array}{c}\hfill \mathcal{F}=\left\{f:\int f(x)dx<\infty ,f(x)\ge 0 \text{for almost everywhere} x\right\}\end{array}$$

in a framework of information geometry originated by Amari, cf. [8,9].

A functional $D:\mathcal{F}\times \mathcal{F}\mapsto [0,\infty )$ is called a divergence if $D(g,f)\ge 0$ with equality if and only if $g=f$. It is shown in [10,11] that any divergence associates with a Riemannian metric and a pair of conjugate connections in a manifold modeled in $\mathcal{F}$ under mild conditions.

We begin with the original form of power cross entropy [12] with the index β of $\mathbb{R}$ defined by

$$\begin{array}{c}\hfill C_{\beta }^{\left(\mathrm{o}\right)}(g,f)=-\frac{1}{\beta }\int g\left(x\right)\{f{\left(x\right)}^{\beta }-1\}dx+\frac{1}{1+\beta }\int f{\left(x\right)}^{1+\beta }dx\end{array}$$

for all g and f in $\mathcal{F}$, and so the power (diagonal) entropy

$$\begin{array}{c}\hfill H_{\beta }^{\left(\mathrm{o}\right)}\left(f\right)=C_{\beta }^{\left(\mathrm{o}\right)}(f,f)=-\frac{1}{\beta (\beta +1)}\int f{\left(x\right)}^{1+\beta }dx+\frac{1}{\beta }\int f\left(x\right)dx\end{array}$$

See [13,14] for the information geometry and statistical applications for the independent component analysis and pattern recognition. Note that this is defined in the continuous case for probability density functions, but can be reduced to a discrete case, see Tsallis [2] for the extensive discussion on statistical physics. In fact, the Tsallis entropy

$$\begin{array}{c}\hfill S_q\left(f\right)=\frac{1}{q-1}\left\{1-\int f{\left(x\right)}^{q}dx\right\}\end{array}$$

for a probability density function $f\left(x\right)$ is proportional to the power entropy to a constant with $q{H}_{\beta }^{\left(\mathrm{o}\right)}\left(g\right)-1$, where $q=1+\beta$. The power divergence is given by

$$\begin{array}{c}\hfill D_{\beta }^{\left(\mathrm{o}\right)}(g,f)=C_{\beta }^{\left(\mathrm{o}\right)}(g,f)-H_{\beta }^{\left(\mathrm{o}\right)}\left(g\right)\end{array}$$

as, in general, defined by the difference of the cross entropy and the diagonal entropy.

In this paper we focus on the projective power cross entropy defined by

$$\begin{array}{c}\hfill C_{\gamma }(g,f)=-\frac{1}{\gamma (1+\gamma )}\frac{\int g\left(x\right)f{\left(x\right)}^{\gamma }dx}{{\left\{\int f{\left(x\right)}^{1+\gamma }dx\right\}}^{\frac{\gamma }{1+\gamma }}}\end{array}$$

(1)

and so the projective power entropy is

$$\begin{array}{c}\hfill H_{\gamma }\left(f\right)=-\frac{1}{\gamma (1+\gamma )}{\left\{\int f{\left(x\right)}^{1+\gamma }dx\right\}}^{\frac{1}{1+\gamma }}\end{array}$$

(2)

The log expression for $C_{\gamma }(g,f)$ is defined by

$$\begin{array}{c}\hfill C_{\gamma }^{\log }(g,f)=-\frac{1}{\gamma }log\{-\gamma (1+\gamma )C_{\gamma }(g,f)\}\end{array}$$

See [15,16] for the derivation of $C_{\gamma }^{\log }$, and detailed discussion on the relation between $C_{\beta }^{\left(\mathrm{o}\right)}(g,f)$ and $C_{\gamma }(g,f)$. The projective power cross entropy $C_{\gamma }(g,f)$ satisfies the linearity with respect to g and the projective invariance, that is $C_{\gamma }(g,\lambda f)=C_{\gamma }(g,f)$ for any constant $\lambda >0$. Note that $H_{\gamma }\left(f\right)$ has a one-to-one correspondence with $S_q\left(f\right)$ as given by

$$\begin{array}{c}\hfill H_{\gamma }\left(f\right)=-\frac{1}{q(q-1)}{\{1-(q-1)S_q\left(f\right)\}}^{\frac{1}{q}}\end{array}$$

where $q=1+\gamma$. The projective power divergence is

$$\begin{array}{c}\hfill D_{\gamma }(g,f)=C_{\gamma }(g,f)-H_{\gamma }\left(g\right)\end{array}$$

(3)

which will be discussed on a close relation with the H$\ddot{\mathrm{o}}$lder’s inequality. The divergence defined by $C_{\gamma }(g,f)$ satisfies

$$\begin{array}{c}\hfill D_{\gamma }^{\log }(g,f)=C_{\gamma }^{\log }(g,f)-C_{\gamma }^{\log }(g,g)\ge 0\end{array}$$

for all γ of $\mathbb{R}$ if there exist integrals in $D_{\gamma }^{\log }(g,f)$. The nonnegativity leads to

$$\begin{array}{c}\hfill D_{\gamma }(g,f)\ge 0\end{array}$$

(4)

We remark that the existence range of the power index γ for $C_{\gamma }(g,f)$ and $H_{\gamma }\left(f\right)$ depends on the sample space on which f and g are defined. If the sample space is compact, both $C_{\gamma }(g,f)$ and $H_{\gamma }$ are well-defined for all $\gamma \in \mathbb{R}$. If the sample space is not compact, $C_{\gamma }(g,f)$ is defined for $\gamma \ge 0$ and $H_{\gamma }\left(f\right)$ is for $\gamma >-1$. More precisely we will explore the case that the sample space is ${\mathbb{R}}^d$ in a subsequent discussion together with moment conditions. Typically we observe that

$$\begin{array}{c}\hfill \underset{\gamma \to 0}{lim}{D}_{\gamma }(g,f)=D_0(g,f)\end{array}$$

(5)

where $D_0(g,f)$ denotes the Kullback-Leibler divergence,

$$\begin{array}{c}\hfill D_0(g,f)=\int g\left(x\right)log\frac{g\left(x\right)}{f\left(x\right)}dx\end{array}$$

(6)

See Appendix 1 for the derivation of (5).

Let $\{x_1,\cdots ,x_n\}$ be a random sample from a distribution with the probability density function $g\left(x\right)$. A statistical model $\left\{f\right(x,\theta ):\theta \in \Theta \}$ with parameter θ is assumed to sufficiently approximate the underlying density function $g\left(x\right)$, where Θ is a parameter space. Then the loss function associated with the projective power entropy $C_{\gamma }(g,f(·,\theta ))$ based on the sample is given by

$$\begin{array}{c}\hfill L_{\gamma }\left(\theta \right)=-\frac{1}{\gamma (1+\gamma )}\frac{1}{n}\sum _{i=1}^n{k}_{\gamma }\left(\theta \right)f{(x_i,\theta )}^{\gamma }\end{array}$$

in which we call

$$\begin{array}{c}\hfill {\widehat{\theta }}_{\gamma }\equiv \underset{\theta \in \Theta }{\mathrm{argmin}}{L}_{\gamma }\left(\theta \right)\end{array}$$

(7)

the γ-estimator, where

$$\begin{array}{c}\hfill k_{\gamma }\left(\theta \right)={\left\{\int f{(x,\theta )}^{1+\gamma }dx\right\}}^{-\frac{\gamma }{1+\gamma }}\end{array}$$

We note that

$$\begin{array}{c}\hfill {\mathbb{E}}_g\left\{L_{\gamma }\left(\theta \right)\right\}=C_{\gamma }(g,f(·,\theta ))\end{array}$$

where ${\mathbb{E}}_g$ denotes the statistical expectation with respect to g. It is observed that the 0-estimator is nothing but the maximum likelihood estimator (MLE) since the loss $L_{\gamma }\left(\theta \right)$ converges to the minus log-likelihood function,

$$\begin{array}{c}\hfill L_0\left(\theta \right)=-\frac{1}{n}\sum _{i=1}^{n}logf(x_i,\theta )\end{array}$$

in the sense that

$$\begin{array}{c}\hfill \underset{\gamma \to 0}{lim}\left\{L_{\gamma }\left(\theta \right)+\frac{1}{\gamma (1+\gamma )}\right\}=L_0\left(\theta \right)\end{array}$$

If the underlying density function $g\left(x\right)$ belongs to a Gaussian model with mean μ and variance ${\sigma }^2$, then the MLEs for μ and ${\sigma }^2$ are the sample mean and sample variance. The reverse statement is shown in [17,18]. We will extend this theory to a case of the γ-estimator under γ-model.

In Section 2 we discuss characterization of the projective power entropy. In Section 3 the maximum entropy distribution with the Tsallis entropy $S_q$ with $q=1+\gamma$ under the constraints of mean vector μ and variance matrix Σ is considered. We discuss the model of maximum entropy distributions, called the γ-model, in which 0-model and 2-model equal Gaussian and Wigner models, respectively. Then we show that the γ-estimators for μ and Σ under the γ-model are the sample mean and sample variance. Section 4 gives concluding remarks and further comments.

2. Projective Invariance

Let us look at a close relation of $\mathcal{F}$ with Lebesgue’s space

$$\begin{array}{c}\hfill L_p=\left\{{f\left(x\right):\int |f\left(x\right)|}^{p}dx<\infty \right\}\end{array}$$

where $p\ge 1$ and the $L_p$-norm ${\parallel \parallel }_p$ is defined by

$$\begin{array}{c}\hfill {\parallel f\parallel }_p={\left\{{\int |f\left(x\right)|}^{p}dx\right\}}^{\frac{1}{p}}\end{array}$$

Let q be the conjugate index of p satisfying $1/p+1/q=1$, in which p and q can be expressed as functions of the parameter $\gamma >0$ such that $p=1+{\gamma }^{-1}$ and $q=1+\gamma$. We note that this q is equal to the index q in Tsallis entropy $S_q$ in the relation $q=1+\gamma$. For any probability density function $f\left(x\right)$ we define the escort distribution with the probability density function,

$$\begin{array}{c}\hfill e_q\left(f\left(x\right)\right)=\frac{f{\left(x\right)}^q}{\int f{\left(y\right)}^{q}dy}\end{array}$$

cf. [2] for extensive discussion. We discuss an interesting relation of the projective cross entropy (1) with the escort distribution. By the definition of the escort distribution,

$$\begin{array}{c}\hfill C_{\gamma }(g,f)=-\frac{1}{\gamma (1+\gamma )}\int {\left\{e_q\left(f\left(x\right)\right)\right\}}^{\frac{1}{p}}g\left(x\right)dx\end{array}$$

(8)

We note that $e_q{\left(f\right)}^{\frac{1}{p}}$ is in the unit sphere of $L_p$ in the representation. The projective power diagonal entropy (2) is proportional to the $L_q$-norm, that is,

$$\begin{array}{c}\hfill H_{\gamma }\left(f\right)=-\frac{1}{\gamma (1+\gamma )}{\parallel f\parallel }_q\end{array}$$

from which the H$\ddot{\mathrm{o}}$lder’s inequality

$$\begin{array}{c}\hfill \int g\left(x\right)f{\left(x\right)}^{\gamma }dx\le {\parallel g\parallel }_q{\parallel f^{\gamma }\parallel }_p\end{array}$$

(9)

claims that $C_{\gamma }(g,f)\ge H_{\gamma }\left(g\right)$, or equivalently

$$\begin{array}{c}\hfill D_{\gamma }(g,f)\ge 0\end{array}$$

(10)

for all f and g in $\mathcal{F}$, which is also led by $C_{\gamma }^{\left(\mathrm{o}\right)}(g,f)\ge H_{\gamma }^{\left(\mathrm{o}\right)}\left(g\right)$. The equality in (10) holds if and only if $f\left(x\right)=\lambda g\left(x\right)$ for almost everywhere x, where λ is a positive constant. The power transform suggests an interplay between the space $L_p$ and $L_q$ by the relation,

$$\begin{array}{c}\hfill \parallel f^{\gamma }{\parallel }_p={{\parallel f\parallel }_q}^{\gamma }\end{array}$$

Taking the limit of γ to 0 in the H$\ddot{\mathrm{o}}$lder’s inequality (9) yields that

$$\begin{array}{c}\hfill \int g(x)logf(x)dx\le \int g(x)logg(x)dx\end{array}$$

since

$$\begin{array}{c}\hfill \underset{\gamma \to 0}{lim}\int g\left(x\right)\frac{f{\left(x\right)}^{\gamma }-1}{\gamma }dx=\int g\left(x\right)logf\left(x\right)dx\end{array}$$

and

$$\begin{array}{c}\hfill \underset{\gamma \to 0}{lim}\frac{\parallel f^{\gamma }{\parallel }_p{\parallel g\parallel }_q-1}{\gamma }=\int g\left(x\right)logg\left(x\right)dx\end{array}$$

(11)

This limit regarding p associates with another space rather than the $L_{\infty }$ space, which is nothing but the space of all density functions with finite Boltzmann-Shannon entropy, say $L_{\log }$. The power index γ reparameterizes the Lebesgue space $L_p$ and the dual space $L_q$ with the relation $p=1+{\gamma }^{-1}$, however, to take the power transform $f{\left(x\right)}^{\gamma }$ is totally different from the ordinary discussion of the Lebesgue space, so that the duality converges to $(L_{\log },L_1)$ as observed in (11). In information geometry the pair $(L_{\log },L_1)$ corresponds to that of mixture and exponential connections, cf. [9]. See also another one-parameterization of $L_p$ space [19].

We now discuss a problem of the uniqueness for $C_{\gamma }(g,f)$ as given in the following theorem. A general discussion on the characterization is given in [16], however, the derivation is rather complicated. Here we assume a key condition that a cross entropy $\Gamma (g,f)$ is linear in g to give an elementary proof. The Riesz representation theorem suggests

$$\begin{array}{c}\hfill \Gamma (g,f)=c(f)\int g(x)\psi (f(x))dx\end{array}$$

where $c\left(f\right)$ is a constant that depends on f. Thus we observe the following theorem when we make a specific form for $c\left(f\right)$ to guarantee the scale invariance.

Theorem 1.. Define a functional $\Gamma :\mathcal{F}\times \mathcal{F}\mapsto \mathbb{R}$ by

$$\begin{array}{c}\hfill \Gamma (g,f)=\phi \left(\int \rho (f(x))dx\right)\int g\left(x\right)\psi \left(f\left(x\right)\right)dx\end{array}$$

(12)

where φ, ρ and ψ are differentiable and monotonic functions. Assume that

(i). $\Gamma (g,g)={min}_{f\in \mathcal{F}}\Gamma (g,f)$ for all $g\in \mathcal{F}$,

and that

(ii). $\Gamma (g,f)=\Gamma (g,\lambda f)$ for all $\lambda >0$ and all $g,f\in \mathcal{F}.$

Then there exists γ such that $\Gamma (g,f)=C_{\gamma }(g,f)$ up to a constant factor, where $C_{\gamma }(g,f)$ is the projective power cross entropy defined by (1).

Proof.. The requirement (ii) means that

$$\begin{array}{c}\hfill \frac{\partial }{\partial \lambda }\left\{\phi \left(\int \rho (\lambda f(x))dx\right)\int \psi \left(\lambda f\left(x\right)\right)g\left(x\right)dx\right\}=0\end{array}$$

which implies that, if f is absolutely continuous and g is the Dirac measure at $x_0$, then

$$\begin{array}{c}\hfill \frac{\dot{\psi }\left(\lambda f\left(x_0\right)\right)}{\psi \left(\lambda f\left(x_0\right)\right)}\lambda f\left(x_0\right)=c\left(\lambda \right)\end{array}$$

where

$$\begin{array}{c}\hfill c\left(\lambda \right)=-\frac{\lambda \dot{\phi }\left(\int \rho \left(\lambda f\right(x\left)\right)dx\right)\int \dot{\rho }\left(\lambda f\left(x\right)\right)f\left(x\right)dx}{\phi \left(\int \rho \left(\lambda f\right(x\left)\right)dx\right)}\end{array}$$

Since we can take an arbitrary value $f\left(x_0\right)$ for any fixed λ,

$$\begin{array}{c}\hfill \frac{\dot{\psi }\left(t\right)}{\psi \left(t\right)}=c\left(\lambda \right)t^{-1}\end{array}$$

which is uniquely solved as $\psi \left(t\right)=t^{\gamma }$ where $\gamma =c\left(\lambda \right)$. Next let us consider a case of a finite discrete space, $\{x_i:1\le i\le m\}$. Then, since $\psi \left(f\right)=f^{\gamma }$, we can write

$$\begin{array}{c}\hfill \Gamma (g,f)=\phi \left(\sum _{i=1}^m\rho \left(f_i\right)\right)\sum _{i=1}^m{g}_i{f}_i^{\gamma }\end{array}$$

where $f_i=f\left(x_i\right)$ and $g_i=g\left(x_i\right)$. The requirement (i) leads that $(\partial /\partial f_j)\Gamma (g,f){|}_{f=g}=0$ for all $j,1\le j\le m$, which implies that

$$\begin{array}{c}\hfill \dot{\rho }\left(g_j\right)=-\gamma c(g_1,\cdots ,g_m)g_j^{\gamma }\end{array}$$

(13)

where

$$\begin{array}{c}\hfill c(g_1,\cdots ,g_m)=\frac{\phi \left({\sum }_{i=1}^m\rho \left(g_i\right)\right)}{{\sum }_{i=1}^m{g}_i^{1+\gamma }\dot{\phi }\left({\sum }_{i=1}^m\rho \left(g_i\right)\right)}\end{array}$$

(14)

It follows from (13) that $c(g_1,\cdots ,g_m)$ must be a constant in $g_1,\cdots ,g_m$, say C, so that we solve (13) as $\rho \left(g_j\right)=-\gamma C{g}_j^{1+\gamma }/(1+\gamma )$. Therefore, Equation (14) is written by

$$\begin{array}{c}\hfill \frac{\dot{\phi }\left(t\right)}{\phi \left(t\right)}=-\frac{\gamma }{1+\gamma }{t}^{-1}\end{array}$$

which leads to $\phi \left(t\right)=t^{-\frac{\gamma }{1+\gamma }}$. We conclude that $\Gamma (g,f)\propto C_{\gamma }(g,f)$, which completes the proof.☐

Remark 1.. The proof above is essentially applicable for the case that the integral (11) is given by the summation just for a binary distributions. In this sense the statement of Theorem 1 is not tight, however, statistical inference is discussed in a unified manner such that the distribution is either continuous or discrete. In a subsequent discussion we focus on the case for continuous distributions defined on ${\mathbb{R}}^d$.

Remark 2. We see the multiplicative decomposition for $C_{\gamma }(g,f)$ for statistical independence. In fact, if f and g are decomposed as $f=f_1\otimes f_2,g=g_1\otimes g_2$ in the same partition, then

$$\begin{array}{c}\hfill C_{\gamma }(g,f)=C_{\gamma }(g_1,f_1)C_{\gamma }(g_2,f_2)\end{array}$$

This property is also elemental, but we do not assume this decomposability as the requirement in Theorem 1.

3. Model of Maximum Entropy Distributions

We will elucidate a dualistic structure between the maximum entropy model on $H_{\gamma }$, defined in (2) and the minimum cross entropy estimator on $C_{\gamma }$, defined in (1). Before the discussion we overview the classical case in which the maximum likelihood estimation nicely makes good performance under the maximum entropy model on the Boltzmann-Shannon entropy, that is, a Gaussian model if we consider the mean and variance constraint. We will use conventional notations that X denotes random variable with value x. Let $\{x_1,\cdots ,x_n\}$ be a random sample from a Gaussian distribution with the density function

$$\begin{array}{c}\hfill f_0(x,\mu ,\Sigma )=det{(2\pi \Sigma )}^{-\frac{1}{2}}exp\{-\frac{1}{2}{(x-\mu )}^{\mathrm{T}}{\Sigma }^{-1}(x-\mu )\}\end{array}$$

The Gaussian density function is written by a canonical form

$$\begin{array}{c}\hfill {\left(2\pi \right)}^{-\frac{d}{2}}exp\left\{-\frac{1}{2}{(x-\mu )}^{\mathrm{T}}\Xi (x-\mu )+\frac{1}{2}logdet(\Xi )\right\}\end{array}$$

(15)

where Ξ is called the canonical parameter defined by ${\Sigma }^{-1}$. The differentiation of (15) on μ and Ξ yields

$$\begin{array}{c}\hfill {\mathbb{E}}_{f_0(·,\mu ,\Sigma )}\left(X\right)=\mu \mathrm{and}{\mathbb{V}}_{f_0(·,\mu ,\Sigma )}\left(X\right)=\Sigma \end{array}$$

where ${\mathbb{E}}_f$ and ${\mathbb{V}}_f$ denote the expectation vector and variance matrix with respect to a probability density function $f\left(x\right)$, respectively.

The maximum likelihood estimator is given by

$$\begin{array}{c}\hfill ({\widehat{\mu }}_0,{\widehat{\Sigma }}_0)=(\overline{x},S)\end{array}$$

(16)

where $\overline{x}$ and S are the sample mean vector and the sample variance matrix,

$$\begin{array}{c}\hfill \overline{x}=\frac{1}{n}\sum _{i=1}^n{x}_i,S=\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x}){(x_i-\overline{x})}^{\mathrm{T}}\end{array}$$

(17)

This is because the minus log-likelihood function is

$$\begin{array}{c}\hfill L_0(\mu ,\Sigma )=-\frac{1}{n}\sum _{i=1}^{n}log{f}_0(x_i,\mu ,\Sigma )\end{array}$$

which is written by

$$\begin{array}{c}\hfill \frac{1}{2}\mathrm{trace}(S\left(\mu \right)\Xi )-\frac{1}{2}logdet(\Xi )\end{array}$$

apart from a constant, where

$$\begin{array}{c}\hfill S\left(\mu \right)=\frac{1}{n}\sum _{i=1}^n(x_i-\mu ){(x_i-\mu )}^{\mathrm{T}}\end{array}$$

(18)

Hence the estimating system is

$$\begin{array}{c}\hfill \left[\begin{array}{c}{\displaystyle \frac{\partial }{\partial \mu }{L}_0(\mu ,\Sigma )}\\ {\displaystyle \frac{\partial }{\partial \Xi }{L}_0(\mu ,\Sigma )}\end{array}\right]=\left[\begin{array}{c}\Xi (\overline{x}-\mu )\\ {\displaystyle \frac{1}{2}\{S\left(\mu \right)-\Sigma \}}\end{array}\right]=\left[\begin{array}{c}0\\ \mathrm{O}\end{array}\right]\end{array}$$

which concludes the Expression (16) of the MLE since $S\left(\mu \right)=S+(\overline{x}-\mu ){(\overline{x}-\mu )}^{\mathrm{T}}$. Alternatively, we have another route to show (16) as follows. The Kullback-Leibler divergence defined in (6) is given by

$$\begin{array}{ccc}\hfill & & D_0(f_0(·,\mu ,\Sigma ),f_0(·,{\mu }_1,{\Sigma }_1))\hfill \end{array}$$

$$\begin{array}{ccc}\hfill & =& \frac{1}{2}{(\mu -{\mu }_1)}^{\mathrm{T}}{\Sigma }_1^{-1}(\mu -{\mu }_1)+\frac{1}{2}\mathrm{trace}\left\{(\Sigma -{\Sigma }_1){\Sigma }_1^{-1}\right\}-\frac{1}{2}logdet(\Sigma {\Sigma }_1^{-1})\hfill \end{array}$$

Thus, we observe that

$$\begin{array}{c}\hfill L_0(\mu ,\Sigma )-L_0(\overline{x},S)=D_0(f_0(·,\overline{x},S),f_0(·,\mu ,\Sigma ))\end{array}$$

(19)

which is nonnegative with equality if and only if $(\mu ,\Sigma )=(\overline{x},S)$. This implies (16).

Under mild regularity conditions the reverse statement holds, that is, the MLE for a location and scatter model satisfies (16) if and only if the model is Gaussian, cf. [17,18]. However, even if we do not assume anything for the underling distribution $g\left(x\right)$, the statistics $\overline{x}$ and S are asymptotically consistent for

$$\begin{array}{c}\hfill {\mu }_g={\mathbb{E}}_g\left(X\right)\mathrm{and}{\Sigma }_g={\mathbb{V}}_g\left(X\right)\end{array}$$

This is a direct result from the strong law of large numbers, and the central limit theorem leads to the asymptotic normality for these two statistics. In this sense, $(\overline{x},S)$ is also a nonparametric estimator for $({\mu }_g,{\Sigma }_g)$.

We explore a close relation of the statistical model and the estimation method. We consider a maximum entropy distribution with the γ-entropy $H_{\gamma }$ over the space of d-dimensional distributions with a common mean and variance,

$$\begin{array}{c}\hfill {\mathcal{F}}_{(\mu ,\Sigma )}=\{f\in \mathcal{F}:\int f\left(x\right)dx=1,{\mathbb{E}}_f\left(x\right)=\mu ,{\mathbb{V}}_f\left(x\right)=\Sigma \}\end{array}$$

(20)

Then we define a distribution with a probability density function written by

$$\begin{array}{c}\hfill f_{\gamma }(x,\mu ,\Sigma )=\frac{c_{\gamma }}{det{(2\pi \Sigma )}^{\frac{1}{2}}}{{\left\{1-\frac{\gamma }{2+d\gamma +2\gamma }{(x-\mu )}^{\mathrm{T}}{\Sigma }^{-1}(x-\mu )\right\}}_{+}}^{\frac{1}{\gamma }}\end{array}$$

(21)

where ${\left(\right)}_{+}$ denotes a positive part and $c_{\gamma }$ is the normalizing factor,

$$\begin{array}{c}\hfill c_{\gamma }=\left\{\begin{array}{cc}{\left(\frac{2\gamma }{2+d\gamma +2\gamma }\right)}^{\frac{d}{2}}\frac{\Gamma (1+\frac{d}{2}+\frac{1}{\gamma })}{\Gamma (1+\frac{1}{\gamma })}\hfill & \mathrm{if} \gamma >0\hfill \\ {\left(-\frac{2\gamma }{2+d\gamma +2\gamma }\right)}^{\frac{d}{2}}\frac{\Gamma (-\frac{1}{\gamma })}{\Gamma (-\frac{1}{\gamma }-\frac{d}{2})}\hfill & \mathrm{if} -\frac{2}{d+2}<\gamma <0\hfill \end{array}\right.\end{array}$$

(22)

See the derivation for $c_{\gamma }$ in Appendix 2. If the dimension d equals 1, then $f_{\gamma }(x,\mu ,\Sigma )$ is a q-Gaussian distribution with $q=\gamma +1$. We remark that

$$\begin{array}{c}\hfill \underset{\gamma \uparrow 0}{lim}{c}_{\gamma }=\underset{\gamma \downarrow 0}{lim}{c}_{\gamma }=1\end{array}$$

in which $f_{\gamma }(x,\mu ,\Sigma )$ is reduced to a d-variate Gaussian density when $\gamma =0$. The support of $f_{\gamma }(·,\mu ,\Sigma )$ becomes an ellipsoid defined as

$$\begin{array}{c}\hfill \left\{x\in {\mathbb{R}}^d:{(x-\mu )}^{\mathrm{T}}{\Sigma }^{-1}(x-\mu )\le \frac{2+d\gamma +2\gamma }{\gamma }\right\}\end{array}$$

if $\gamma >0$. On the other hand, if $-\frac{2}{d+2}<\gamma <0$, the density function (21) is written as

$$\begin{array}{c}\hfill f_{\gamma }(x,\mu ,\Sigma )=det{(\pi \tau \Sigma )}^{-\frac{1}{2}}\frac{\Gamma (-\frac{1}{\gamma })}{\Gamma (-\frac{1}{\gamma }-\frac{d}{2})}{\left\{1+\frac{1}{\tau }{(x-\mu )}^{\mathrm{T}}{\Sigma }^{-1}(x-\mu )\right\}}^{\frac{1}{\gamma }}\end{array}$$

(23)

where

$$\begin{array}{c}\hfill \tau =-\frac{2+(d+2)\gamma }{\gamma }\end{array}$$

The d-variate t-distribution is defined by

$$\begin{array}{c}\hfill g_{\nu }(x,\mu ,P)=det{\left(\pi \nu P\right)}^{-\frac{1}{2}}\frac{\Gamma \left(\frac{\nu +d}{2}\right)}{\Gamma \left(\frac{\nu }{2}\right)}{\left\{1+\frac{1}{\nu }{(x-\mu )}^{\mathrm{T}}{P}^{-1}(x-\mu )\right\}}^{-\frac{\nu +d}{2}}\end{array}$$

(24)

cf. [20] for the extensive discussion. Assume that

$$\begin{array}{c}\hfill \frac{\nu +d}{2}=-\frac{1}{\gamma }\mathrm{and}\nu P=\tau \Sigma \end{array}$$

Then we observe from (23) and (24) that

$$\begin{array}{c}\hfill f_{\gamma }(x,\mu ,\Sigma )=g_{\nu }(x,\mu ,P)\end{array}$$

Accordingly, the density function $f_{\gamma }(x,\mu ,\Sigma )$ with $-\frac{2}{d+2}<\gamma <0$ is a t-distribution. The distribution has elliptical contours on the Euclidean space ${\mathbb{R}}^d$ for any $\gamma >-\frac{2}{d+2}$, as shown in Figure 1 for typical cases of γ.

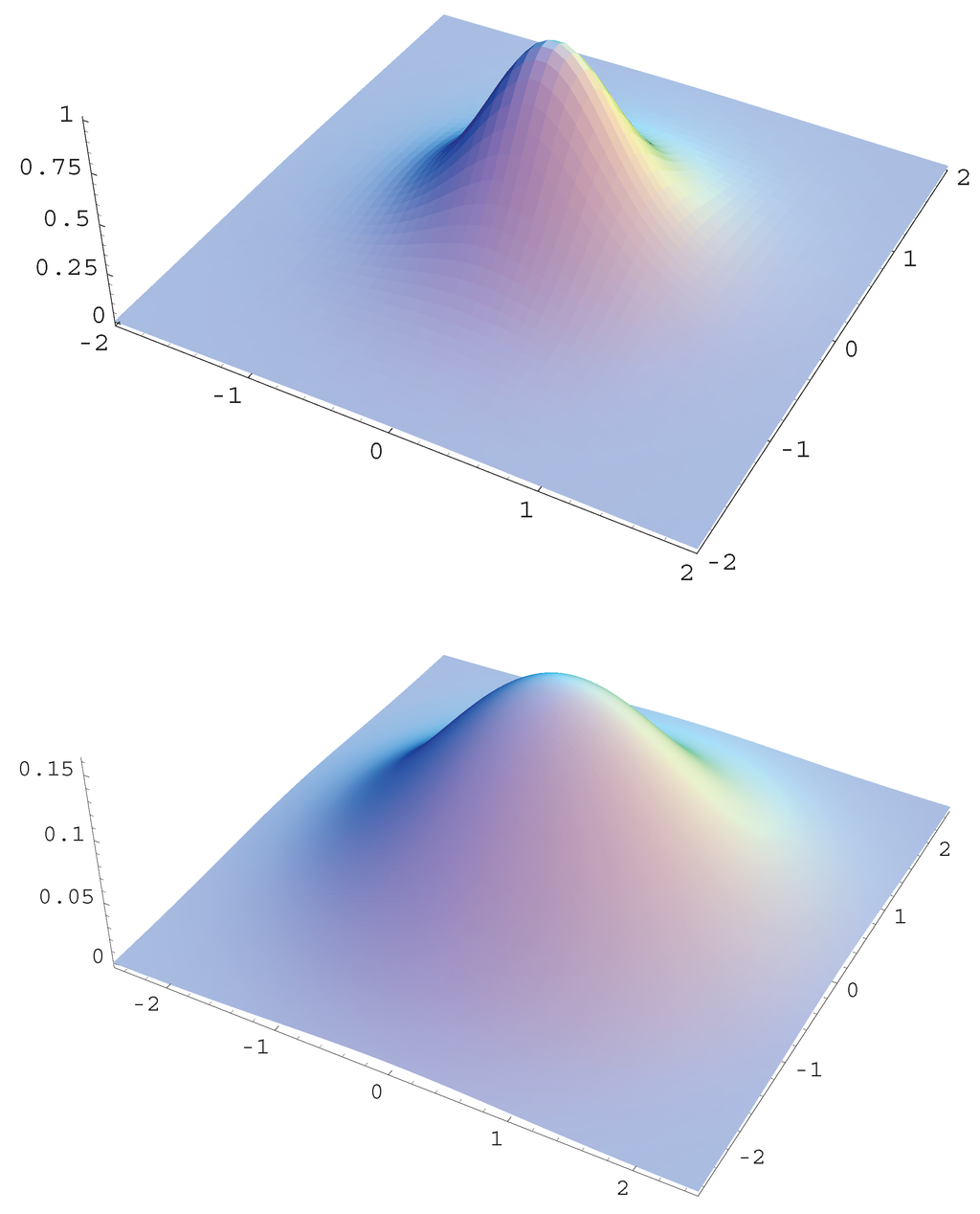
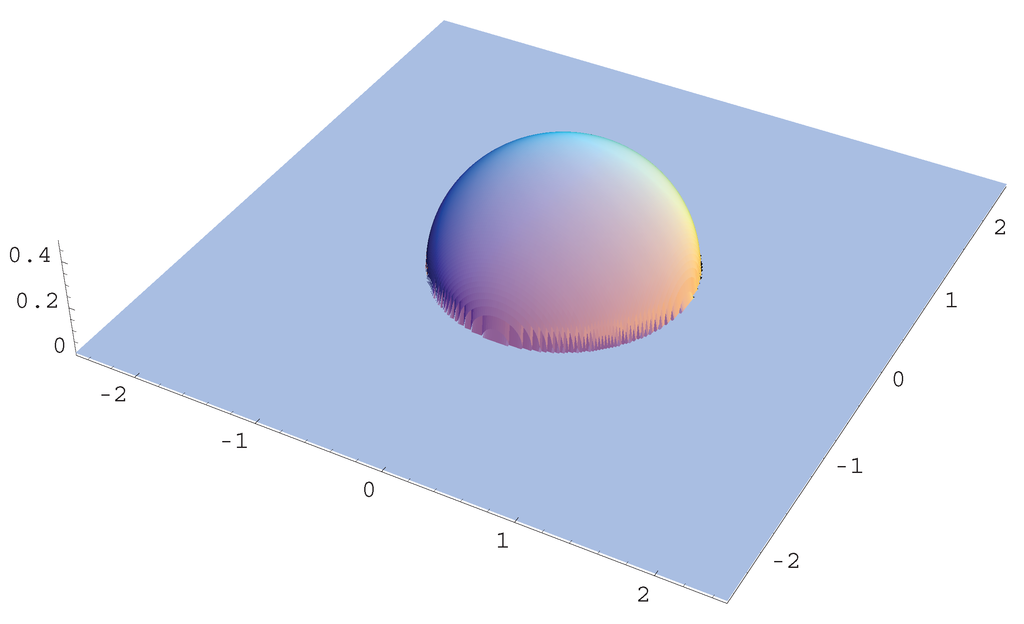
Figure 1. t-distribution $(\gamma =-0.4)$, Gaussian $(\gamma =0)$ and Wigner $(\gamma =2)$ distributions.

Let

$$\begin{array}{c}\hfill M_{\gamma }=\left\{f_{\gamma }(x,\mu ,\Sigma ):\mu \in {\mathbb{R}}^d,\Sigma \in {\mathcal{S}}_d\right\}\end{array}$$

(25)

which we call γ-model, where ${\mathcal{S}}_d$ denotes the space of all symmetric, positive-definite matrices of order d. We confirm the mean and variance of the γ-model as follows.

Lemma. Under the model $M_{\gamma }$ defined in (25) with the index $\gamma >-\frac{2}{d+2}$,

$$\begin{array}{c}\hfill {\mathbb{E}}_{f_{\gamma }(·,\mu ,\Sigma )}\left(X\right)=\mu \mathrm{and}{\mathbb{V}}_{f_{\gamma }(·,\mu ,\Sigma )}\left(X\right)=\Sigma \end{array}$$

Proof. We need to consider a family of escort distributions. In the model $M_{\gamma }$ we can define the escort distribution as

$$\begin{array}{c}\hfill e_q\left(f_{\gamma }(x,\mu ,\Sigma )\right)=\frac{c_{\gamma }^{*}}{det{(\Sigma )}^{\frac{1}{2}}}{\left\{1-\frac{\gamma }{2+d\gamma +2\gamma }{(x-\mu )}^{\mathrm{T}}{\Sigma }^{-1}(x-\mu )\right\}}_{+}^{\frac{1+\gamma }{\gamma }}\end{array}$$

(26)

where $q=1+\gamma$ and $c_{\gamma }^{*}$ is the normalizing factor. Hence,

$$\begin{array}{c}\hfill e_q\left(f_{\gamma }(x,\mu ,\Sigma )\right)=c_{\gamma }^{*}{\left\{det{(\Sigma )}^{-\frac{1}{2}\frac{\gamma }{1+\gamma }}-\frac{\gamma }{2+d\gamma +2\gamma }{(x-\mu )}^{\mathrm{T}}\{det{(\Sigma )}^{-\frac{1}{2}\frac{\gamma }{1+\gamma }}{\Sigma }^{-1}\}(x-\mu )\right\}}_{+}^{\frac{1+\gamma }{\gamma }}\end{array}$$

(27)

Here we define alternative parameter ${\Xi }_{\gamma }$ to the original parameter Σ by the transform

$$\begin{array}{c}\hfill {\Xi }_{\gamma }=det{(\Sigma )}^{-\frac{1}{2}\frac{\gamma }{1+\gamma }}{\Sigma }^{-1}\end{array}$$

(28)

and so that the inverse transform is given by

$$\begin{array}{c}\hfill \Sigma =det{\left({\Xi }_{\gamma }\right)}^{\frac{\gamma }{d\gamma +2\gamma +2}}{\Xi }_{\gamma }^{-1}\end{array}$$

(29)

noting that $det\left({\Xi }_{\gamma }\right)=det{(\Sigma )}^{-\frac{1}{2}\frac{d\gamma +2\gamma +2}{1+\gamma }}$. Thus, we get a canonical form of (26) as

$$\begin{array}{c}\hfill e_q\left(f_{\gamma }(x,\mu ,\Sigma )\right)=c_{\gamma }^{*}{\left\{det{\left({\Xi }_{\gamma }\right)}^{\frac{\gamma }{2+d\gamma +2\gamma }}-\frac{\gamma }{2+d\gamma +2\gamma }{(x-\mu )}^{\mathrm{T}}{\Xi }_{\gamma }(x-\mu )\right\}}_{+}^{\frac{1+\gamma }{\gamma }}\end{array}$$

(30)

By analogy of the discussion for an exponential family we have the following expression for the braced term in (30) as

$$\begin{array}{c}\hfill -\frac{2\gamma }{2+d\gamma +2\gamma }\left\{\frac{1}{2}\mathrm{trace}\left(x{x}^{\mathrm{T}}{\Xi }_{\gamma }\right)-{\mu }^{\mathrm{T}}{\Xi }_{\gamma }x+\frac{1}{2}{\mu }^{\mathrm{T}}{\Xi }_{\gamma }\mu -\frac{2+d\gamma +2\gamma }{2\gamma }det{\left({\Xi }_{\gamma }\right)}^{\frac{\gamma }{d\gamma +2\gamma +2}}\right\}\end{array}$$

(31)

A property of the escort distribution suggests moment formulae for the distribution (25) as follows: We have an identity

$$\begin{array}{c}\hfill \frac{\partial }{\partial \mu }\int c_{\gamma }^{*}{\left\{det{\left({\Xi }_{\gamma }\right)}^{\frac{\gamma }{d\gamma +2\gamma +2}}-\frac{\gamma }{2+d\gamma +2\gamma }{(x-\mu )}^{\mathrm{T}}{\Xi }_{\gamma }(x-\mu )\right\}}_{+}^{\frac{1+\gamma }{\gamma }}dx=0\end{array}$$

which implies that

$$\begin{array}{c}\hfill \int {\left\{det{\left({\Xi }_{\gamma }\right)}^{\frac{\gamma }{d\gamma +2\gamma +2}}-\frac{\gamma }{2+d\gamma +2\gamma }{(x-\mu )}^{\mathrm{T}}{\Xi }_{\gamma }(x-\mu )\right\}}_{+}^{\frac{1}{\gamma }}{\Xi }_{\gamma }(x-\mu )dx=0\end{array}$$

which concludes that

$$\begin{array}{c}\hfill {\mathbb{E}}_{f_{\gamma }(·,\mu ,\Sigma )}\left(X\right)=\mu \end{array}$$

Similarly,

$$\begin{array}{c}\hfill \frac{\partial }{\partial {\Xi }_{\gamma }}\int c_{\gamma }^{*}{\left\{det{\left({\Xi }_{\gamma }\right)}^{\frac{\gamma }{d\gamma +2\gamma +2}}-\frac{\gamma }{2+d\gamma +2\gamma }{(x-\mu )}^{\mathrm{T}}{\Xi }_{\gamma }(x-\mu )\right\}}_{+}^{\frac{1+\gamma }{\gamma }}dx=0\end{array}$$

which is

$$\begin{array}{ccc}\hfill & & \int c_{\gamma }^{*}{\left\{det{\left({\Xi }_{\gamma }\right)}^{\frac{\gamma }{d\gamma +2\gamma +2}}-\frac{\gamma }{2+d\gamma +2\gamma }{(x-\mu )}^{\mathrm{T}}{\Xi }_{\gamma }(x-\mu )\right\}}_{+}^{\frac{1}{\gamma }}\hfill \end{array}$$

$$\begin{array}{ccc}& \times & \left\{\frac{\gamma }{d\gamma +2\gamma +2}det{\left({\Xi }_{\gamma }\right)}^{\frac{\gamma }{d\gamma +2\gamma +2}}{\Xi }_{\gamma }^{-1}-\frac{\gamma }{2+d\gamma +2\gamma }(x-\mu ){(x-\mu )}^{\mathrm{T}}\right\}dx=0\hfill \end{array}$$

(32)

which concludes that

$$\begin{array}{c}\hfill {\mathbb{V}}_{f_{\gamma }(·,\mu ,\Sigma )}\left(X\right)=\Sigma \end{array}$$

because of the relation of ${\Xi }_{\gamma }$ and Σ as observed in (29). The proof is complete.  ☐

Remark 3. The canonical form (30) of the escort distribution (26) plays an important role on the proof of Lemma. Basically we can write the canonical form of (21), however it is not known any link to distributional properties like a case of exponential family.

Remark 4. In Equation (31) the function

$$\begin{array}{c}\hfill \phi (\Xi )=\frac{1}{2\omega }det{(\Xi )}^{\omega }\end{array}$$

(33)

is viewed as a potential function in the Fenchel convex duality, where

$$\begin{array}{c}\hfill \omega =\frac{\gamma }{2+d\gamma +2\gamma }\end{array}$$

cf. [21,22] for the covariance structure model.

From Lemma we observe that $f_{\gamma }(·,\mu ,\Sigma )\in \mathcal{F}(\mu ,\Sigma )$. Next we show that the distribution with density $f_{\gamma }(·,\mu ,\Sigma )$ maximizes the γ-entropy $H_{\gamma }$ over the space $\mathcal{F}(\mu ,\Sigma )$, where $H_{\gamma }$ is defined in (2).

Theorem 2.

(i). If $-\frac{2}{d+2}<\gamma \le 0$, then

$$\begin{array}{c}\hfill f_{\gamma }(·,\mu ,\Sigma )=\underset{f\in {\mathcal{F}}_{(\mu ,\Sigma )}}{\mathrm{argmax}}{H}_{\gamma }\left(f\right)\end{array}$$

(34)

where ${\mathcal{F}}_{(\mu ,\Sigma )}$ is defined in (20).

(ii). If $\gamma >0$, then

$$\begin{array}{c}\hfill f_{\gamma }(·,\mu ,\Sigma )=\underset{f\in {{\mathcal{F}}_{(\mu ,\Sigma )}}^{\left(\gamma \right)}}{\mathrm{argmax}}{H}_{\gamma }\left(f\right)\end{array}$$

(35)

where

$$\begin{array}{c}\hfill {{\mathcal{F}}_{(\mu ,\Sigma )}}^{\left(\gamma \right)}=\{f\in {\mathcal{F}}_{(\mu ,\Sigma )}:f\left(x\right)=0 \text{for almost everywhere} x\in B(\mu ,\Sigma )\}\end{array}$$

with $B(\mu ,\Sigma )$ being $\{x\in {\mathbb{R}}^d:{(x-\mu )}^{\mathrm{T}}{\Sigma }^{-1}(x-\mu )>\frac{2+d\gamma +2\gamma }{\gamma }\}$.

Proof. By the definition of ${\mathcal{F}}_{(\mu ,\Sigma )}$, we see from Lemma that $f_{\gamma }(·,\mu ,\Sigma )\in {\mathcal{F}}_{(\mu ,\Sigma )}$ for any $\gamma \in (-\frac{2}{d+2},0)$. This leads to

$$\begin{array}{c}\hfill {\mathbb{E}}_{f_{\gamma }(·,\mu ,\Sigma )}\left\{f_{\gamma }{(X,\mu ,\Sigma )}^{\gamma }\right\}={\mathbb{E}}_f\left\{f_{\gamma }{(X,\mu ,\Sigma )}^{\gamma }\right\}\end{array}$$

for any f in ${\mathcal{F}}_{(\mu ,\Sigma )}$, which implies that

$$\begin{array}{c}\hfill H_{\gamma }\left(f_{\gamma }(·,\mu ,\Sigma )\right)=C_{\gamma }(f,f_{\gamma }(·,\mu ,\Sigma ))\end{array}$$

Hence

$$\begin{array}{c}\hfill H_{\gamma }\left(f_{\gamma }(·,\mu ,\Sigma )\right)-H_{\gamma }\left(f\right)=D_{\gamma }(f,f_{\gamma }(·,\mu ,\Sigma ))\end{array}$$

(36)

which is nonnegative as discussed in (4). This concludes (34). Similarly, we observe that (36) holds for any $\gamma >0$ and any f in ${{\mathcal{F}}_{(\mu ,\Sigma )}}^{\left(\gamma \right)}$ since the support of f includes that of $f(·,\mu ,\Sigma )$. This concludes (35). ☐

We would like to elucidate a similar structure for the statistical inference by the minimum projective cross entropy in which the data set $\{x_1,\cdots ,x_n\}$ is assumed to follow the model $M_{\gamma }$. We recall (8) from the relation of the projective cross entropy with the escort distribution

$$\begin{array}{c}\hfill C_{\gamma }(g,f)=-\frac{1}{\gamma (1+\gamma )}\int e_q{\left(f\left(x\right)\right)}^{\frac{\gamma }{1+\gamma }}g\left(x\right)dx\end{array}$$

When we have got data $\{x_1,\cdots ,x_n\}$ to be fitted to the model $M_{\gamma }$, the loss function is

$$\begin{array}{c}\hfill L_{\gamma }(\mu ,\Sigma )=-\frac{1}{\gamma (1+\gamma )}\frac{1}{n}\sum _{i=1}^n{e}_q{\left(f_{\gamma }(x_i,\mu ,\Sigma )\right)}^{\frac{\gamma }{1+\gamma }}\end{array}$$

where $f_{\gamma }(x,\mu ,\Sigma )$ defined in (21). The γ-estimator is defined by

$$\begin{array}{c}\hfill ({\widehat{\mu }}_{\gamma },{\widehat{\Sigma }}_{\gamma })=\underset{(\mu ,\Sigma )}{\mathrm{argmin}}{L}_{\gamma }(\mu ,\Sigma )\end{array}$$

see the general definition (7). It follows from the canonical form defined in (30) with the canonical parameter ${\Xi }_{\gamma }$ defined in (28) that

$$\begin{array}{c}\hfill L_{\gamma }(\mu ,\Sigma )=-\frac{1}{\gamma (1+\gamma )}{\left(c_{\gamma }^{*}\right)}^{\frac{\gamma }{\gamma +1}}\left[det{\left({\Xi }_{\gamma }\right)}^{\omega }-\omega \{\mathrm{trace}\left({\Xi }_{\gamma }S\right)+{(\mu -\overline{x})}^{\mathrm{T}}{\Xi }_{\gamma }(\mu -\overline{x})\}\right]\end{array}$$

(37)

where $(\overline{x},S)$ and ω are defined in (17) and (33), and $c_{\gamma }^{*}$ is the normalizing factor defined in (27). Here we note that if $\gamma >0$, then the parameter $(\mu ,\Sigma )$ must be assumed to be in ${\Theta }_n$, where

$$\begin{array}{c}\hfill {\Theta }_n=\{(\mu ,\Sigma )\in {\mathbb{R}}^d\times {\mathcal{S}}_d:{(x_i-\mu )}^{\mathrm{T}}{\Sigma }^{-1}(x_i-\mu )<{\omega }^{-1}(\forall i=1,\cdots ,n)\}\end{array}$$

(38)

We note that $L_{\gamma }(\mu ,\Sigma )=C_{\gamma }(f(·,\overline{x},S),f(·,\mu ,\Sigma ))$ and $L_{\gamma }(\overline{x},S)=H_{\gamma }\left(f(·,\overline{x},S)\right)$ since

$$\begin{array}{c}\hfill {\mathbb{E}}_{f(·,\overline{x},S)}\left(X\right)=\overline{x},\mathrm{and}{\mathbb{V}}_{f(·,\overline{x},S)}\left(X\right)=S\end{array}$$

Accordingly, we observe the argument similar to (19) for the MLE. The projective divergence $D_{\gamma }$ defined in (3) equals the difference of the γ-loss functions as

$$\begin{array}{c}\hfill L_{\gamma }(\mu ,\Sigma )-L_{\gamma }(\overline{x},S)=D_{\gamma }(f_{\gamma }(·,\overline{x},S),f_{\gamma }(·,\mu ,\Sigma )),\end{array}$$

(39)

which is nonnegative with equality if and only if $(\mu ,\Sigma )=(\overline{x},S)$. See the discussion after equation (10). In this way, we can summarize the above discussion as follows:

Theorem 3. Let $\{x_1,\cdots ,x_n\}$ be a random sample from a γ-model defined in (21). Then the γ-estimator defined in (7) for $(\mu ,\Sigma )$ is $(\overline{x},S)$, where $(\overline{x},S)$ is defined in (17).

Proof. Let us give another proof. The estimating system is given by

$$\begin{array}{c}\hfill \left[\begin{array}{c}{\displaystyle \frac{\partial }{\partial \mu }{L}_{\gamma }(\mu ,\Sigma )}\\ {\displaystyle \frac{\partial }{\partial {\Xi }_{\gamma }}{L}_{\gamma }(\mu ,\Sigma )}\end{array}\right]=\left[\begin{array}{c}{\Xi }_{\gamma }(\overline{x}-\mu )\\ \omega \{det{\left({\Xi }_{\gamma }\right)}^{\omega }{\Xi }_{\gamma }^{-1}-S\left(\mu \right)\}\end{array}\right]=\left[\begin{array}{c}0\\ \mathrm{O}\end{array}\right]\end{array}$$

(40)

which is equivalent to

$$\begin{array}{c}\hfill \left[\begin{array}{c}\mu -\overline{x}\\ \Sigma -S\left(\mu \right)\end{array}\right]=\left[\begin{array}{c}0\\ \mathrm{O}\end{array}\right]\end{array}$$

because of the relation of ${\Xi }_{\gamma }$ into Σ as given in (29). Thus, we also attain the conclusion $({\widehat{\mu }}_{\gamma },{\widehat{\Sigma }}_{\gamma })=\left(\overline{x},S\right).$ In this way, we obtain the solution of the equation system defined by (40) via the parameter ${\Xi }_{\gamma }$ using the relation of the escort distribution with the loss function (37). ☐

Remark 5. Consider the location model $\left\{f_{\gamma }(·,\mu ,\Sigma )\right\}$ with the location parameter μ, where Σ is known in Theorem 3. Then we easily see that the γ-estimator for μ is $\overline{x}$. What about the reverse statement? We observe that if the γ-estimator for μ is $\overline{x}$ with the sample size $n\ge 3$, then the model is the γ-model, $\{f_{\gamma }(·,\mu ,\Sigma )$ with the known Σ. The proof is parallel to that of Theorem 2 given in [17]. In fact, we conclude that the model density function $f\left(x\right)$ satisfies that

$$\begin{array}{c}\hfill {\left\{f(x-\mu )\right\}}^{\gamma }=a+b{(x-\mu )}^{\mathrm{T}}{\Sigma }^{-1}(x-\mu )\end{array}$$

where a and b are constants.

Remark 6. If we look at jointly Theorem 2 and 3, then

$$\begin{array}{c}\hfill \underset{(\mu ,\Sigma )\in {\mathbb{R}}^d\times {\mathbb{S}}_d}{min}{L}_{\gamma }(\mu ,\Sigma )=\underset{f\in \mathcal{F}(\overline{x},S)}{max}{H}_{\gamma }\left(f\right)\end{array}$$

(41)

since $L_{\gamma }(\overline{x},S)=H_{\gamma }\left(f_{\gamma }(·,\overline{x},S)\right)$. Both sides of (41) associate with inequalities (39) and (36) on γ-divergence in separate discussion.

Remark 7. The derivation of the γ-estimator in Theorem 3 is provided by the canonical parameter ${\Xi }_{\gamma }$ of the escort distribution as given in (28). Here we directly calculate the gradient of the loss with respect to Σ as follows:

$$\begin{array}{ccc}\hfill \frac{\partial }{\partial \Sigma }{L}_{\gamma }(\mu ,\Sigma )& =& -\frac{1}{2{(1+\gamma )}^2}det{(\Sigma )}^{-\frac{1}{2}\frac{\gamma }{1+\gamma }}(1-\omega \mathrm{trace}\left\{S\left(\mu \right){\Sigma }^{-1}\right\}){\Sigma }^{-1}\hfill \\ \hfill & & +\frac{\gamma }{(1+\gamma )}\omega det{(\Sigma )}^{-\frac{1}{2}\frac{\gamma }{1+\gamma }}{\Sigma }^{-1}S\left(\mu \right){\Sigma }^{-1}\hfill \\ \hfill & =& -\frac{1}{2{(1+\gamma )}^2}det{(\Sigma )}^{-\frac{1}{2}\frac{\gamma }{1+\gamma }}\hfill \\ \hfill & & \times \left[(1-\omega \mathrm{trace}\left\{S\left(\mu \right){\Sigma }^{-1}\right\}){\Sigma }^{-1}-\frac{1+\gamma }{1+\frac{1}{2}d\gamma +\gamma }{\Sigma }^{-1}S\left(\mu \right){\Sigma }^{-1}\right]\hfill \end{array}$$

Therefore we observe that if we put $\mu =\overline{x}$ and $\Sigma =\alpha S\left(\overline{x}\right)$, then

$$\begin{array}{ccc}\hfill & & \frac{\partial }{\partial \Sigma }{L}_{\gamma }(\overline{x},\alpha S\left(\overline{x}\right))=-\frac{1}{2}\frac{\gamma }{1+\gamma }det{\left(\alpha S\left(\overline{x}\right)\right)}^{-\frac{1}{2}\frac{\gamma }{1+\gamma }}{\left(\alpha S\left(\overline{x}\right)\right)}^{-1}\hfill \end{array}$$

$$\begin{array}{ccc}& & \times \left[(1-\omega \mathrm{trace}\left\{S\left(\overline{x}\right){\left(\alpha S\left(\overline{x}\right)\right)}^{-1}\right\})\alpha S\left(\overline{x}\right)-\frac{1+\gamma }{1+\frac{1}{2}d\gamma +\gamma }S\left(\overline{x}\right)\right]{\left(\alpha S\left(\overline{x}\right)\right)}^{-1}\hfill \end{array}$$

(42)

The bracketed term of (42) is given by

$$\begin{array}{cc}& \left[\alpha (1-\omega \mathrm{trace}\left\{S\left(\overline{x}\right){\left(\alpha S\left(\overline{x}\right)\right)}^{-1}\right\})-\frac{1+\gamma }{1+\frac{1}{2}d\gamma +\gamma }\right]S\left(\overline{x}\right)\hfill \\ =& \left(\alpha -\frac{d\gamma }{2+d\gamma +2\gamma }-\frac{1+\gamma }{1+\frac{1}{2}d\gamma +\gamma }\right)S\left(\overline{x}\right)\hfill \end{array}$$

which concludes that if $\alpha =1$, then $(\partial /\partial \Sigma )L_{\gamma }(\overline{x},\alpha S\left(\overline{x}\right))=0$. This is a direct proof for Theorem 3, but it would accompany with a heuristic discussion for the substitution of $(\mu ,\Sigma )$ into $(\overline{x},\alpha S\left(\overline{x}\right))$.

4. Concluding Remarks

We explored the elegant property (39), the empirical Pythagoras relation between the γ-model and γ-estimator, in the sense that (39) directly shows Theorem 3 without any differential calculus. Another elegant expression is in the minimax game between Nature and a decision maker, see [23]. Consider the space $\mathcal{F}(\mu ,\Sigma )$ defined in (20). The intersection of the γ-model (21) and $\mathcal{F}(\mu ,\Sigma )$ is a singleton $\left\{f_{\gamma }(·,\mu ,\Sigma )\right\}$, which is the minimax solution of

$$\begin{array}{c}\hfill \underset{g\in \mathcal{F}(\mu ,\Sigma )}{max}\underset{f\in \mathcal{F}}{min}{C}_{\gamma }(g,f)=C_{\gamma }(f_{\gamma }(·,\mu ,\Sigma ),f_{\gamma }(·,\mu ,\Sigma ))\end{array}$$

Consider different indices γ and ${\gamma }^{*}$ which specify the γ-model and ${\gamma }^{*}$-estimator, respectively. Basically the ${\gamma }^{*}$-estimator is consistent under the γ-model for any choice of γ and ${\gamma }^{*}$. If we specifically fix $\gamma =0$ for the model, that is, a Gaussian model, then the ${\gamma }^{*}$-estimator is shown to be qualitatively robust for any ${\gamma }^{*}>0$, see [16]. The degree of robustness is proportional to the value of ${\gamma }^{*}$ with a trade for the efficiency. The ${\gamma }^{*}$-estimator for $(\mu ,\Sigma )$ of the Gaussian model is given by the solution of

$$\begin{array}{ccc}\hfill \mu & =& \frac{{\sum }_{i=1}^n{f}_0{(x_i,\mu ,\Sigma )}^{\gamma *}{x}_i}{{\sum }_{i=1}^n{f}_0{(x_i,\mu ,\Sigma )}^{\gamma *}}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \Sigma & =& (1+{\gamma }^{*})\frac{{\sum }_{i=1}^n{f}_0{(x_i,\mu ,\Sigma )}^{\gamma *}(x_i-\mu ){(x_i-\mu )}^{\mathrm{T}}}{{\sum }_{i=1}^n{f}_0{(x_i,\mu ,\Sigma )}^{\gamma *}}\hfill \end{array}$$

The weight function $f_0{(x_i,\mu ,\Sigma )}^{\gamma *}$ for the i-th observation $x_i$ becomes almost 0 when $x_i$ is an outlier. Alternatively, the classical robust method employs ${\gamma }^{*}=0$, that is, the MLE for the misspecified model $\gamma <0$ or t-distribution model, see [24,25]. Thus, the different indices γ and ${\gamma }^{*}$ work robust statistics in a dualistic manner.

This property is an extension of that associated between the exponential model and MLE, however, it is fragile in the sense that (19) does not hold if the indices in the γ-model and ${\gamma }^{*}$-estimator are slightly different. In practice, we find some difficulties for a numerical task for solving the MLE under the γ-model with $\gamma >0$ because the support of the density depends on the parameter and the index γ. We discussed statistical and probabilistic properties on the model and estimation associated with the specific cross entropy. A part of properties discussed still holds for any cross entropy in a much wider class, which is investigated from the point of the Fenchel duality in [13,26].