The Nonadditive Entropy Sq and Its Applications in Physics and Elsewhere: Some Remarks
Abstract
:1. Introduction
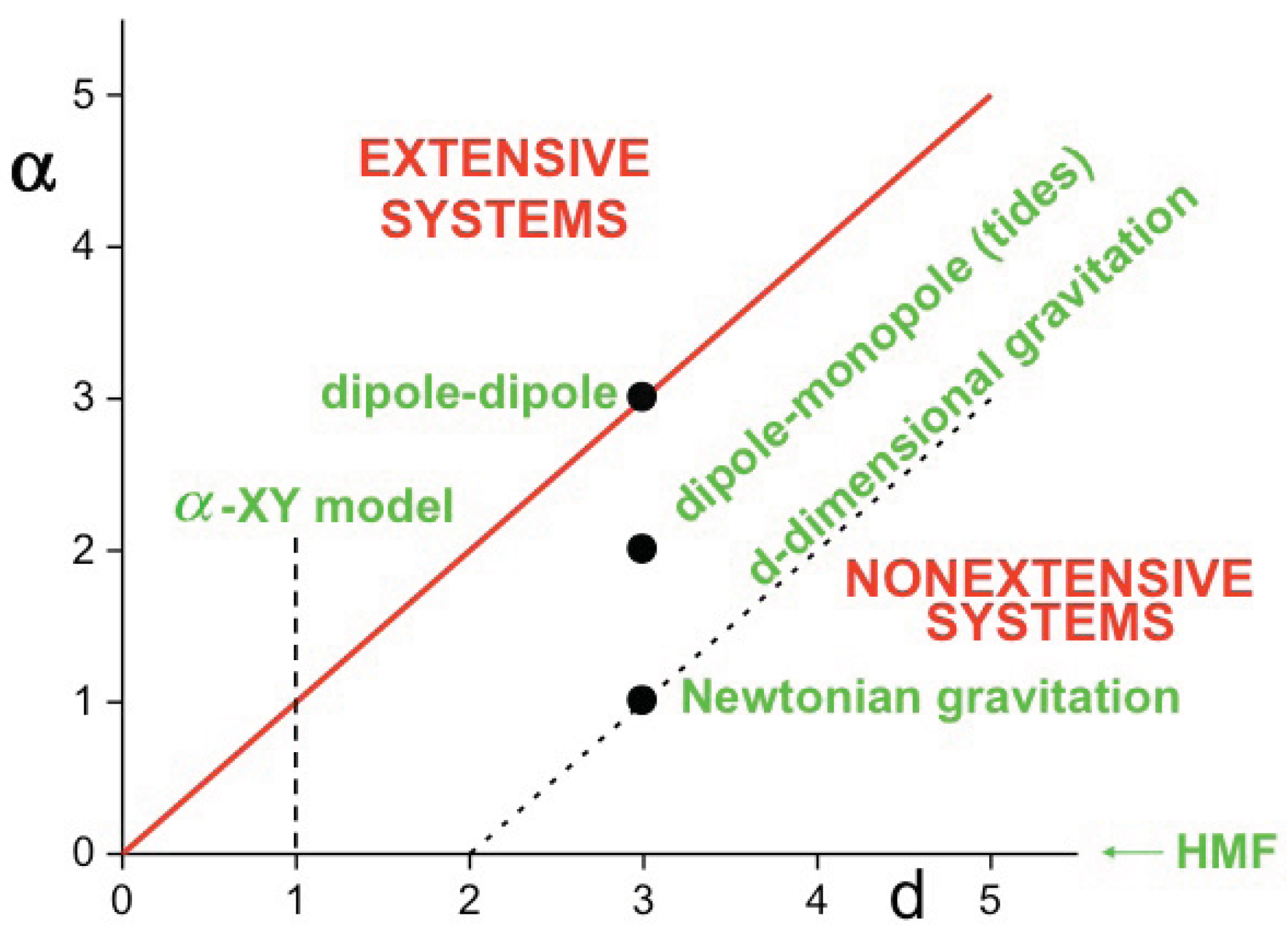
2. Additivity versus Extensivity
3. Probability Distributions that Are Attractors in the Sense of the Central Limit Theorem
4. Remarks on Paradigmatic Low-Dimensional Nonlinear Dynamical Systems Near the Edge of Chaos
4.1. One-Dimensional Dissipative Unimodal Maps
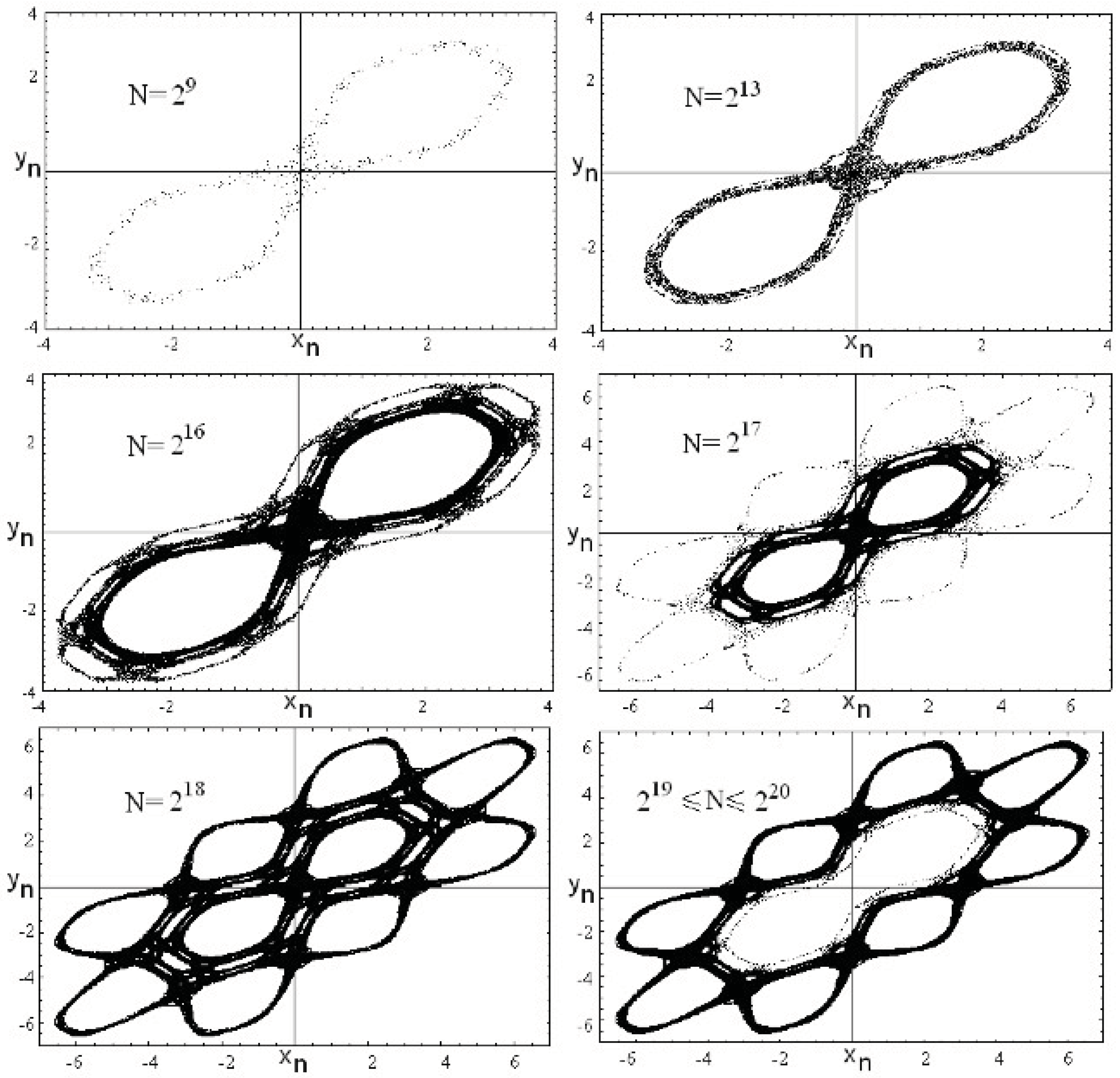
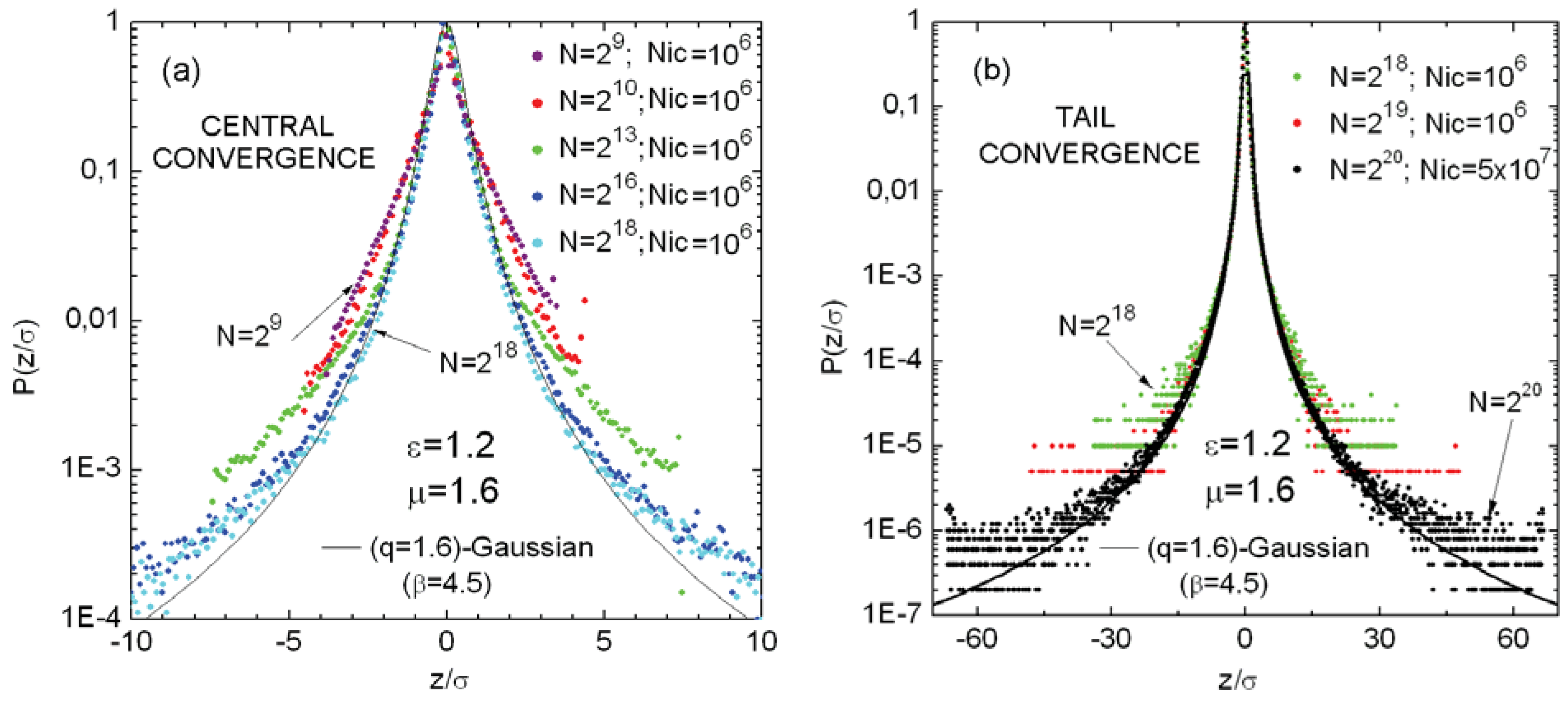
4.2. Two-Dimensional Conservative Maps
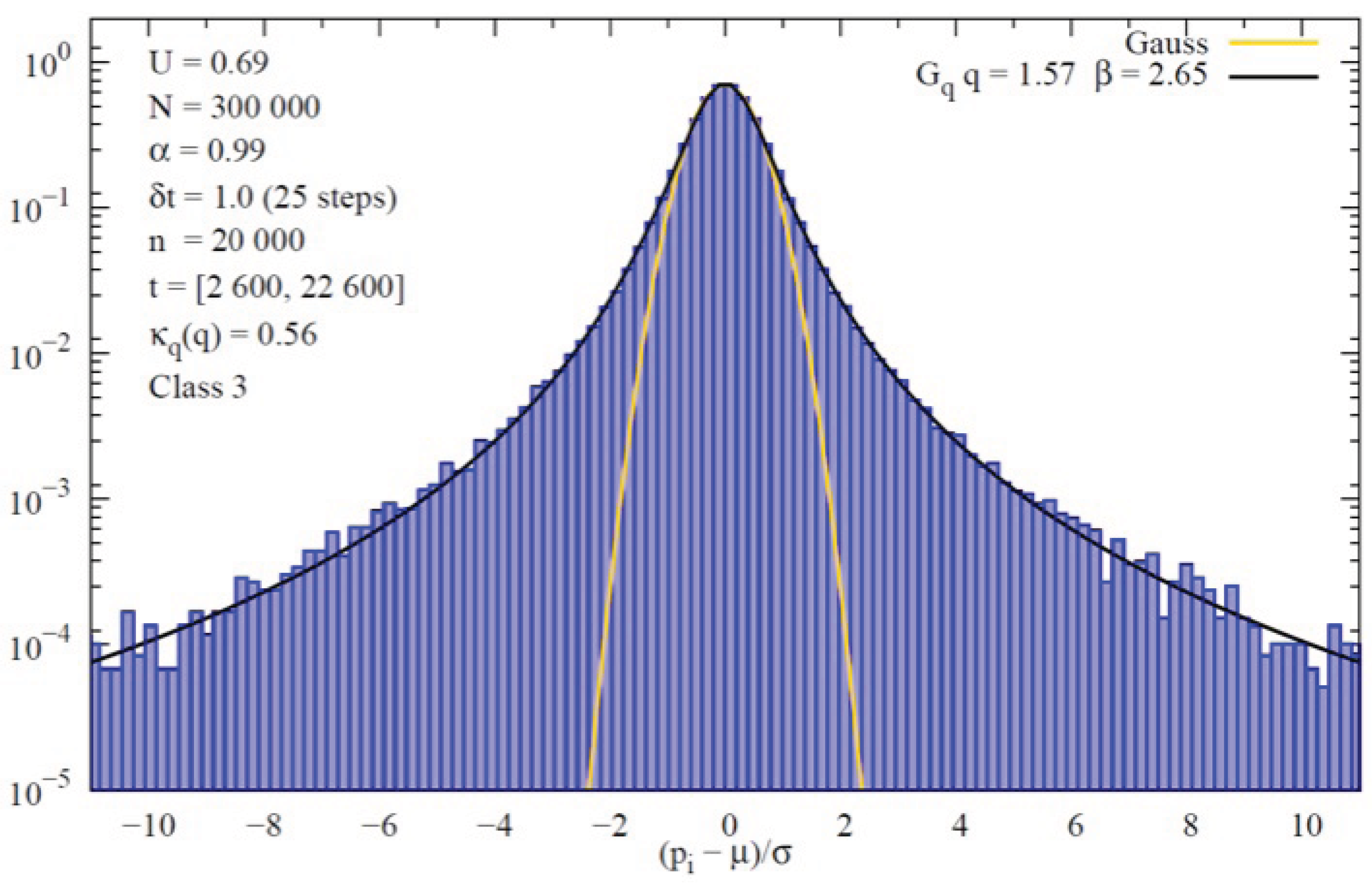
5. Remarks on Paradigmatic Long-Range-Interacting Many-Body Classical Hamiltonian Systems
6. Applications
- (i)
- The velocity distribution of (cells of) Hydra viridissima follows a q-Gaussian probability distribution function (PDF) with [101,102]. Anomalous diffusion has been independently measured as well [101,102], and an exponent has been observed (where the squared space scales with time t like ). Therefore, within the error bars, the prediction [54] is verified in this system.
- (ii)
- The velocity distribution of (cells of) Dictyostelium discoideum is well fitted by a q-Gaussian PDF with in the vegetative state, and with in the starved state [103].
- (iii)
- (iv)
- The velocity distribution of cold atoms in a dissipative optical lattice was predicted [105] to be a q-Gaussian with , where and are parameters related to the optical lattice potential. This prediction was verified three years later, both in the laboratory and with quantum Monte Carlo techniques [106,107].
- (v)
- (vi)
- The velocity distribution in a driven-dissipative 2D dusty plasma was found to be of the q-Gaussian form, with and at temperatures of and respectively [110].
- (vii)
- The spatial (Monte Carlo) distributions of a trapped ion cooled by various classical buffer gases at was verified to be of the q-Gaussian form, with q increasing from close to unity to about 1.9 when the mass of the molecules of the buffer increases from that of to about 200 [111].
- (viii)
- The distributions of price returns and stock volumes at the New York and NASDAQ stock exchanges are well fitted by q-Gaussians and q-exponentials respectively [112,113,114,115]. The volatility smiles that are obtained within this approach also are well fitted. The distributions of interoccurrence times between losses in financial markets are consistently well described by universal q-exponentials, which enables a simple analytical expression for the risk function [116].
- (ix)
- The Bak–Sneppen model of biological evolution exhibits a time-dependence of the spread of damage which is well approached by a q-exponential with [117].
- (x)
- (xi)
- The distributions of returns in the coherent noise model are well fitted with q-Gaussians where q is analytically obtained through , τ being the exponent associated with the distribution of sizes of the events [120].
- (xii)
- (xiii)
- The distributions of angles in the model approaches as time evolves towards a q-Gaussian form with [123].
- (xiv)
- (xv)
- The relaxation in various paradigmatic spin-glass substances through neutron spin echo experiments is well reproduced by q-exponential forms with [126].
- (xvi)
- The fluctuating time dependence of the width of the ozone layer over Buenos Aires (and, presumably, around the Earth) yields a q-triplet with [127].
- (xvii)
- (xviii)
- (xix)
- The tissue radiation response follows a q-exponential form [137].
- (xx)
- (xxi)
- Experimental and simulated molecular spectra due to the rotational population in plasmas are frequently interpreted as two Boltzmann distributions corresponding to two different temperatures. These fittings involve three fitting parameters, namely the two temperatures and the relative proportion of each of the Boltzmann weights. It has been shown [141] that equally good fittings can be obtained with a single q-exponential weight, which has only two fitting parameters, namely q and a single temperature.
- (xxii)
- High energy physics has been since more than one decade handled with q-statistics [142,143,144,145]. During the last decade various phenomena, such as the flux of cosmic rays and others, have been shown to exhibit relevant nonextensive aspects [146,147,148,149]. The distributions of transverse momenta of hadronic jets outcoming from proton-proton collisions (as well as others) have been shown to exhibit q-exponentials with . These results have been obtained at the LHC detectors CMS, ATLAS and ALICE [150,151,152,153,154,155,156,157], as well as at SPS and RHIC in Brookhaven [158,159]. Predictions for the rapidities in such experiments have been advanced as well [160].
- (xxiii)
- (xxiv)
- (xxv)
- (xxvi)
- Nonlinear generalizations of the Schroedinger, the Klein–Gordon and the Dirac equations have been implemented which admit q-plane wave solutions as free particles, i.e., solutions of the type [194], with the energy given by and the momentum given by , . The nonlinear Schroedinger equation yields (), and the nonlinear Klein-Gordon and Dirac equations yield the Einstein relation ().
- (xxvii)
7. Final Remarks
Acknowledgments
References and Notes
- We should, however, always have in mind that we cannot use the continuous expression (3) for states involving too narrow continuous distributions. Indeed, only expressions such as (1) and (4) can guarantee the non-negativeness of a well defined entropy, whose lowest admissible value is zero (corresponding to the system being at its fundamental state, where all information is available). This feature reflects, of course, the fact that nature ultimately is quantum rather than classical. A well known consequence of this question is the fact that classical specific heats do not vanish in the T → 0 limit, in contrast with the quantum ones, which always do.
- The Cases (5) and (6) can be unified by imposing the generic constraint 〈E(x)〉 = constant. The distribution which maximizes SBG is then given by , which corresponds of course to the celebrated BG distribution for thermal equilibrium at a temperature T given by T = 1/(βk).
- This is sometimes referred to as the Boltzmann program. Boltzmann died in 1906 without accomplishing it.
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Curado, E.M.F.; Tsallis, C. Generalized statistical mechanics: connection with thermodynamics. J. Phys. A 1991, 24, L69–L72, Corrigenda: 24, 3187 (1991) and 25, 1019 (1992). [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Physica A 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Tsallis, C. Nonextensive Entropy—Interdisciplinary Applications; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Tsallis, C.; Brigatti, E. Nonextensive statistical mechanics: A brief introduction. Continuum. Mech. Therm. 2004, 16, 223–235. [Google Scholar] [CrossRef]
- Boon, J.P.; Tsallis, C. Nonextensive statistical mechanics: New trends, new perspectives. Europhys. News 2005, 36, 6. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics—Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tsallis, C. Entropy. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: Berlin, Germany, 2009; Volume 11, ISBN 978-0-387-75888-6. [Google Scholar]
- Tsallis, C. On the nonuniversality of the mathematical connection between the Clausius thermodynamic entropy and the probabilities of the microscopic configurations. In Concepts and Recent Advances in Generalized Information Measures and Statistics; Kowalski, A.M., Rossignoli, R., Curado, E.M.F., Eds.; Bentham Science Publishers: Sharjah, United Arab Emirates, 2011; in press. [Google Scholar]
- Havrda and Charvat [211] were apparently the first to ever introduce—for possible cybernetic purposes—the entropic form of Equation (7), though with a different prefactor, adapted to binary variables. Vajda [212] further studied this form, quoting Havrda and Charvat. Daroczy [213] rediscovered this form (he quotes neither Havrda-Charvat nor Vajda). Lindhard and Nielsen [214] rediscovered this form (they quote none of the predecessors) through the property of entropic composability. Sharma and Mittal [215] introduced a two-parameter form which reproduces both Sq and Renyi entropy [216,217] as particular cases. Aczel and Daroczy [218] quote Havrda-Charvat and Vajda, but not Lindhard-Nielsen. Wehrl [219] mentions the form of Sq in page 247, quotes Daroczy, but ignores Havrda-Charvat, Vajda, Lindhard-Nielsen, and Sharma-Mittal. Myself I rediscovered this form in 1985 with the aim of generalizing Boltzmann–Gibbs statistical mechanics, but quote none of the predecessors in my 1988 paper [4]. Indeed, I started knowing the whole story quite a few years later thanks to S.R.A. Salinas and R.N. Silver, who were the first to provide me with the corresponding informations. Such rediscoveries can by no means be considered as particularly surprising. Indeed, this happens in science more frequently than usually realized. This point is lengthily and colorfully developed by Stigler [220]. In page 284, a most interesting example is described, namely that of the celebrated normal distribution. It was first introduced by Abraham De Moivre in 1733, then by Pierre Simon de Laplace in 1774, then by Robert Adrain in 1808, and finally by Carl Friedrich Gauss in 1809, nothing less than 76 years after its first publication! This distribution is universally called Gaussian because of the remarkable insights of Gauss concerning the theory of errors, applicable in all experimental sciences. A less glamorous illustration of the same phenomenon, but nevertheless interesting in the present context, is that of Renyi entropy [216,217]. According to Csiszar [221], the Renyi entropy had already been essentially introduced by Schutzenberger [222].
- Penrose, O. Foundations of Statistical Mechanics: A Deductive Treatment; Dover Publications: Mineola, NY, USA, 1970; p. 167. [Google Scholar]
- This expression can be rewritten as Sq(A + B) = Sq(A) + Sq(B) + Sq(A)Sq(B), which shows that there are two different manners to approach the BG limit. One of them is the obvious (q − 1) → 0 limit for fixed k, the other one being k → ∞ for fixed q. Since in thermal equilibrium, as well as in other relevant many-body stationary states, k is always accompanied by T in the form kT, we may say that k → ∞ is somehow equivalent to k → ∞. This consistently reflects the fact that all thermal statistics are expected to merge with the classic BG one at very high temperature. This is indeed what happens with Fermi-Dirac statistics, Bose-Einstein statistics, and q-statistics as well. In addition to this, we can make another generic remark concerning, this time, the four independent physical universal constants of contemporary physics, which can be chosen to be the velocity of light c, Newton constant G, Planck constant h, and Boltzmann constant kB (the elementary electron charge qe can be seen as an appropriate combination of these ones, through the hyperfine structure universal pure number). All units used in all natural sciences can be uniquely expressed in terms of powers of these four constants. If we start from basic Newtonian mechanics (which corresponds to (1/c, G, h, 1/kB) = (0, 0, 0, 0)), Maxwell electromagnetism and special relativity require to allow for 1/c ≠ 0, gravitation requires to allow for G ≠ 0, quantum mechanics requires to allow for h ≠ 0, general relativity requires to simultaneously allow for G ≠ 0 and 1/c ≠ 0, Dirac equation requires to simultaneously allow for 1/c ≠ 0 and h ≠ 0, and so on (e.g., quantum gravity is assumed to require for (1/c, h, G) ≠ (0,0,0)). Standard BG statistics at any finite temperature requires to allow for 1/kB ≠ 0 (and consistently, the totally elusive statistical mechanics of quantum gravity would in principle require (1/c, h, G, 1/kB) ≠ (0,0,0,0)). But, as we have seen above, in the context of q-statistics, 1/kB ≠ 0 can be alternatively seen as (q − 1) ≠ 0. A curious difference nevertheless is noticed: whereas all four universal constants 1/c, h, G and 1/kB are non-negative, the quantity (1 − q)/kB has no such restriction, both positive and negative values being mathematically admissible. It would certainly be very interesting to know whether this fact has any relevant physical interpretation!
- Tsallis, C. Nonextensive statistical mechanics: Construction and physical interpretation. In Nonextensive Entropy—Interdisciplinary Applications; Gell-Mann, M., Tsallis, C., Eds.; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Tsallis, C.; Gell-Mann, M.; Sato, Y. Asymptotically scale-invariant occupancy of phase space makes the entropy Sq extensive. Proc. Natl. Acad. Sci. USA 2005, 102, 15377–15382. [Google Scholar] [CrossRef] [PubMed]
- Caruso, F.; Tsallis, C. Nonadditive entropy reconciles the area law in quantum systems with classical thermodynamics. Phys. Rev. E 2008, 78, 021101:1–021101:6. [Google Scholar] [CrossRef] [PubMed]
- Saguia, A.; Sarandy, M.S. Nonadditive entropy for random quantum spin-S chains. Phys. Lett. A 2010, 374, 3384:1–3384:5. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S. When do generalised entropies apply? How phase space volume determines entropy. arXiv, 2011; arXiv:1104.2064v1. [Google Scholar]
- Aranha, R.F.; Soares, I.D.; Tonini, E.V. Mass-energy radiative transfer and momentum extraction by gravitational wave emission in the collision of two black holes. Phys. Rev. D 2010, 81, 104005:1–104005:14. [Google Scholar] [CrossRef]
- For example, Renyi entropy is additive for all values of q.
- Kuhn, T.S. The Structure of Scientific Revolutions, 3rd ed.; University of Chicago Press: Chicago, IL, USA, 1996. [Google Scholar]
- Anteneodo, C.; Tsallis, C. Breakdown of the exponential sensitivity to the initial conditions: Role of the range of the interaction. Phys. Rev. Lett. 1998, 80, 5313–5316. [Google Scholar] [CrossRef]
- To be more explicit, equals ez (∀z) if q = 1, vanishes for z ≤ −1/(1 − q) and equals [1 + (1 − q)z] for z > −1/(1 − q) if q < 1, and equals [1 + (1 − q)z] for all z <1 /(q − 1) (value at which it blows up to infinity) if q > 1.
- If x is a d-dimensional real vector, normalizability mandates that converges, hence . If, in addition to that, the system has a density of states φ(x) which diverges like xδ for x → ∞ (a quite frequent case), then normalizability mandates that converges, hence . Similarly, the finiteness of the first moment mandates that converges, hence .
- Since long known in plasma physics under the name suprathermal or κ distributions [223,224] if q > 1, and equal to the Student’s t-distributions [225] for special rational values of q > 1. They are also occasionally referred to as generalized Lorentzians [226].
- If x is a d-dimensional real vector, normalizability mandates that converges, hence . If, in addition to that, the system has a density of states φ(x) which diverges like xδ for x → ∞ (a quite frequent case), then normalizability mandates converges, hence . Similarly, the finiteness of the second moment mandates that converges, hence .
- Bologna, M.; Tsallis, C.; Grigolini, P. Anomalous diffusion associated with nonlinear fractional derivative Fokker-Planck-like equation: Exact time-dependent solutions. Phys. Rev. E 2000, 62, 2213–2218. [Google Scholar] [CrossRef]
- Tsallis, C. Nonextensive statistical mechanics, anomalous diffusion and central limit theorems. Milan J. Math. 2005, 73, 145–176. [Google Scholar] [CrossRef]
- Tsallis, C.; Queiros, S.M.D. Nonextensive statistical mechanics and central limit theorems I—Convolution of independent random variables and q-product. AIP Conf. Proc. 2007, 965, 8–20. [Google Scholar]
- Queiros, S.M.D.; Tsallis, C. Nonextensive statistical mechanics and central limit theorems II—Convolution of q-independent random variables. AIP Conf. Proc. 2007, 965, 21–23. [Google Scholar]
- Umarov, S.; Tsallis, C.; Steinberg, S. On a q-central limit theorem consistent with nonextensive statistical mechanics. Milan J. Math. 2008, 76, 307–328. [Google Scholar] [CrossRef]
- Umarov, S.; Tsallis, C.; Gell-Mann, M.; Steinberg, S. Generalization of symmetric α-stable Lévy distributions for q > 1. J. Math. Phys. 2010, 51, 033502. [Google Scholar] [CrossRef] [PubMed]
- Nelson, K.P.; Umarov, S. Nonlinear statistical coupling. Physica A 2010, 389, 2157–2163. [Google Scholar] [CrossRef]
- Hilhorst, H.J. Central limit theorems for correlated variables: some critical remarks. Braz. J. Phys. 2009, 39, 371–379. [Google Scholar] [CrossRef]
- Hilhorst, H.J. Note on a q-modified central limit theorem. J. Stat. Mech. 2010, 2010, P10023. [Google Scholar] [CrossRef]
- Jauregui, M.; Tsallis, C. q-generalization of the inverse Fourier transform. Phys. Lett. A 2011, 375, 2085:1–2085:6. [Google Scholar] [CrossRef]
- Jauregui, M.; Tsallis, C. New representations of π and Dirac delta using the nonextensive-statistical-mechanics q-exponential function. J. Math. Phys. 2010, 51, 063304:1–063304:13. [Google Scholar] [CrossRef]
- Jauregui, M.; Tsallis, C.; Curado, E.M.F. q-Moments raise the degeneracy associated with the inversion of the q-Fourier transform. J. Stat. Mech. 2011, in press. [Google Scholar] [CrossRef]
- Budde, C.; Prato, D.; Re, M. Superdiffusion in decoupled continuous time random walks. Phys. Lett. A 2001, 283, 309:1–309:9. [Google Scholar] [CrossRef]
- Tsallis, C.; Plastino, A.R.; Alvarez-Estrada, R.F. Escort mean values and the characterization of power-law-decaying probability densities. J. Math. Phys. 2009, 50, 043303. [Google Scholar] [CrossRef]
- Rodriguez, A.; Tsallis, C. A generalization of the cumulant expansion. Application to a scale-invariant probabilistic model. J. Math. Phys. 2010, 51, 073301. [Google Scholar] [CrossRef]
- Vignat, C.; Plastino, A. Central limit theorem and deformed exponentials. J. Phys. A 2007, 40, F969. [Google Scholar] [CrossRef]
- Vignat, C.; Plastino, A. Geometry of the central limit theorem in the nonextensive case. Phys. Lett. A 2009, 373, 1713–1718. [Google Scholar] [CrossRef]
- Hahn, M.G.; Jiang, X.X.; Umarov, S. On q-Gaussians and exchangeability. J. Phys. A 2010, 43, 165208:1–165208:14. [Google Scholar] [CrossRef]
- Rodriguez, A.; Schwammle, V.; Tsallis, C. Strictly and asymptotically scale-invariant probabilistic models of N correlated binary random variables having q–Gaussians as N → ∞ limiting distributions. J. Stat. Mech. Theory Exp. 2008, 2008, P09006. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S.; Tsallis, C. Limit distributions of scale-invariant probabilistic models of correlated random variables with the q-Gaussian as an explicit example. Eur. Phys. J. B 2009, 72, 263–268. [Google Scholar] [CrossRef]
- Moyano, L.G.; Tsallis, C.; Gell-Mann, M. Numerical indications of a q-generalised central limit theorem. Europhys. Lett. 2006, 73, 813–819. [Google Scholar] [CrossRef]
- Thistleton, W.J.; Marsh, J.A.; Nelson, K.P.; Tsallis, C. q-Gaussian approximants mimic non-extensive statistical-mechanical expectation for many-body probabilistic model with long-range correlations. Cent. Eur. J. Phys. 2009, 7, 387–394. [Google Scholar] [CrossRef]
- Marsh, J.A.; Fuentes, M.A.; Moyano, L.G.; Tsallis, C. Influence of global correlations on central limit theorems and entropic extensivity. Physica A 2006, 372, 183–202. [Google Scholar] [CrossRef]
- Hilhorst, H.J.; Schehr, G. A note on q-Gaussians and non-Gaussians in statistical mechanics. J. Stat. Mech. 2007, 2007, P06003. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Non-extensive statistical mechanics and generalized Fokker-Planck equation. Physica A 1995, 222, 347–354. [Google Scholar] [CrossRef]
- Tsallis, C.; Bukman, D.J. Anomalous diffusion in the presence of external forces: Exact time-dependent solutions and their thermostatistical basis. Phys. Rev. E 1996, 54, R2197–R2200. [Google Scholar] [CrossRef]
- Borland, L. Ito-Langevin equations within generalized thermostatistics. Phys. Lett. A 1998, 245, 67–72. [Google Scholar] [CrossRef]
- Fuentes, M.A.; Caceres, M.O. Computing the non-linear anomalous diffusion equation from first principles. Phys. Lett. A 2008, 372, 1236–1239, To compare with the present paper, it must be done q → 2 − q. [Google Scholar] [CrossRef]
- Anteneodo, C.; Tsallis, C. Multiplicative noise: A mechanism leading to nonextensive statistical mechanics. J. Math. Phys. 2003, 44, 5194–5203. [Google Scholar] [CrossRef]
- Mariz, A.M.; Tsallis, C. Long memory constitutes a unified mesoscopic mechanism for nonextensive statistical mechanics. arXiv, 2011; arXiv:1106.3100v1. [Google Scholar]
- We are using an analogy with dependence on time (instead of dependence on N) regarding the entropy production index qentropy production as a function of the indices associated with successive directions for the sensitivity to initial conditions (see Equation (26) in [60]).
- Ananos, G.F.J.; Baldovin, F.; Tsallis, C. Anomalous sensitivity to initial conditions and entropy production in standard maps: Nonextensive approach. Eur. Phys. J. B 2005, 46, 409–417. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. From Gibbs microcanonical ensemble to Tsallis generalized canonical distribution. Phys. Lett. A 1994, 193, 140–143. [Google Scholar] [CrossRef]
- Mendes, R.S.; Tsallis, C. Renormalization group approach to nonextensive statistical mechanics. Phys. Lett. A 2001, 285, 273–278. [Google Scholar] [CrossRef]
- Malacarne, L.C.; Mendes, R.S.; Pedron, I.T.; Lenzi, E.K. N-dimensional nonlinear Fokker-Planck equation with time-dependent coefficients. Phys. Rev. E 2002, 65, 052101. [Google Scholar] [CrossRef] [PubMed]
- Almeida, M.P. Thermodynamical entropy (and its additivity) within generalized thermodynamics. Physica A 2003, 325, 426–438. [Google Scholar] [CrossRef]
- da Silva, P.C.; da Silva, L.R.; Lenzi, E.K.; Mendes, R.S.; Malacarne, L.C. Anomalous diffusion and anisotropic nonlinear Fokker-Planck equation. Physica A 2004, 342, 161–166. [Google Scholar] [CrossRef]
- Tsallis, C. Nonadditive entropy and nonextensive statistical mechanics—An overview after 20 years. Braz. J. Phys. 2009, 39, 337–356. [Google Scholar] [CrossRef]
- Burlaga, L.F.; Vinas, A.F. Triangle for the entropic index q of non-extensive statistical mechanics observed by Voyager 1 in the distant heliosphere. Physica A 2005, 356, 375–375. [Google Scholar] [CrossRef]
- Tsallis, C.; Plastino, A.R.; Zheng, W.-M. Power-law sensitivity to initial conditions—New entropic representation. Chaos, Solitons and Fractals 1997, 8, 885–891. [Google Scholar] [CrossRef]
- Baldovin, F.; Robledo, A. Sensitivity to initial conditions at bifurcations in one-dimensional nonlinear maps: Rigorous nonextensive solutions. Europhys. Lett. 2002, 60, 518–524. [Google Scholar] [CrossRef]
- Baldovin, F.; Robledo, A. Universal renormalization-group dynamics at the onset of chaos in logistic maps and nonextensive statistical mechanics. Phys. Rev. E 2002, 66, R045104. [Google Scholar] [CrossRef] [PubMed]
- Baldovin, F.; Robledo, A. Nonextensive Pesin identity. Exact renormalization group analytical results for the dynamics at the edge of chaos of the logistic map. Phys. Rev. E 2004, 69, 045202(R). [Google Scholar] [CrossRef] [PubMed]
- Mayoral, E.; Robledo, A. Tsallis’ q index and Mori’s q phase transitions at edge of chaos. Phys. Rev. E 2005, 72, 026209. [Google Scholar] [CrossRef] [PubMed]
- Robledo, A. Incidence of nonextensive thermodynamics in temporal scaling at Feigenbaum points. Physica A 2006, 370, 449–460. [Google Scholar] [CrossRef]
- Lyra, M.L.; Tsallis, C. Nonextensivity and multifractality in low-dimensional dissipative systems. Phys. Rev. Lett. 1998, 80, 53. [Google Scholar] [CrossRef]
- Anania, G.; Politi, A. Dynamical behavior at the onset of chaos. Europhys. Lett. 1988, 7, 119–124. [Google Scholar] [CrossRef]
- The qsen = 1 limit can not be found in this expression, but in a more general one, conjecturally something like [10] with [αmin − f(αmin)] → 0.
- Grassberger, P. Temporal scaling at Feigenbaum points and nonextensive thermodynamics. Phys. Rev. Lett. 2005, 95, 140601. [Google Scholar] [CrossRef] [PubMed]
- Robledo, A.; Moyano, L.G. q-deformed statistical-mechanical property in the dynamics of trajectories en route to the Feigenbaum attractor. Phys. Rev. E 2008, 77, 032613. [Google Scholar] [CrossRef] [PubMed]
- These two references concern the approach to the multifractal attractor as a function of time. However, [77] contains a general criticism concerning also the time evolution within the attractor. This is rebutted in [73] (see also [227]).
- Tirnakli, U.; Beck, C.; Tsallis, C. Central limit behavior of deterministic dynamical systems. Phys. Rev. E 2007, 75, 040106(R). [Google Scholar] [CrossRef] [PubMed]
- Tirnakli, U.; Tsallis, C.; Beck, C. A closer look on the time-average attractor at the edge of chaos of the logistic map. Phys. Rev. E 2009, 79, 056209:1–056209:6. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C.; Tirnakli, U. Nonadditive entropy and nonextensive statistical mechanics—Some central concepts and recent applications. J. Phys. Conf. Ser. 2010, 201, 012001:1–012001:15. [Google Scholar] [CrossRef]
- Also this result is, like the relaxation one, criticized by Grassberger [228].
- Fuentes, M.A.; Robledo, A. Stationary distributions of sums of marginally chaotic variables as renormalization group fixed points. J. Phys. Conf. Ser. 2010, 201, 012002:1–012002:7. [Google Scholar] [CrossRef]
- Fuentes, M.A.; Robledo, A. Renormalization group structure for sums of variables generated by incipiently chaotic maps. J. Stat. Mech. 2010, 2010, P01001. [Google Scholar] [CrossRef]
- Fuentes, M.A.; Sato, Y.; Tsallis, C. Sensitivity to initial conditions, entropy production, and escape rate at the onset of chaos. Phys. Lett. A 2011, 375, 2988–2991. [Google Scholar] [CrossRef]
- Tirnakli, U.; Tsallis, C.; Lyra, M.L. Circular-like maps: Sensitivity to the initial conditions, multifractality and nonextensivity. Eur. Phys. J. B 1999, 11, 309–315. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, G.; Tsallis, C. Nonextensivity at the edge of chaos of a new universality class of one-dimensional unimodal dissipative maps. Eur. Phys. J. B 2009, 67, 577:1–577:17. [Google Scholar] [CrossRef]
- Casati, G.; Tsallis, C.; Baldovin, F. Linear instability and statistical laws of physics. Europhys. Lett. 2005, 72, 355–361. [Google Scholar] [CrossRef]
- Ruiz, G.; Bountis, T.; Tsallis, C. Time-evolving statistics of chaotic orbits of conservative maps in the context of the Central Limit Theorem. Int. J. Bifurc. Chaos 2011, in press. [Google Scholar] [CrossRef]
- A detailed analysis of this question demands to separately focus on cases where the divergence in the BG partition function comes from the dynamical variables themselves (e.g., the hydrogen atom, or gravitation), or comes from coupling constants slowly decaying with distance (e.g., the α-XY model).
- Campa, A.; Giansanti, A.; Moroni, D.; Tsallis, C. Classical spin systems with long-range interactions: Universal reduction of mixing. Phys. Lett. A 2001, 286, 251–256. [Google Scholar] [CrossRef]
- Cabral, B.J.C.; Tsallis, C. Metastability and weak mixing in classical long-range many-rotator system. Phys. Rev. E 2002, 66, 065101(R). [Google Scholar] [CrossRef] [PubMed]
- Cirto, L.J.L.; de Assis, V.R.V.; Tsallis, C. Non-Gaussian Behaviour in a Long-Range Hamiltonian System. In Proceedings of the XXXIV National Meeting of Condensed Matter Physics, Iguassu, Brazil, 2011; Available online: http://www.sbf1.sbfisica.org.br/eventos/enf/2011/prog/ trabalhos.asp?sesId=110 (accessed on 21 September 2011).
- Leo, M.; Leo, R.A.; Tempesta, P. Thermostatistics in the neighborhood of the π-mode solution for the Fermi-Pasta-Ulam β system: From weak to strong chaos. J. Stat. Mech. 2010, P04021:1–P04021:15. [Google Scholar]
- Antonopoulos, C.G.; Bountis, T.C.; Basios, V. Quasi-stationary chaotic states in multi-dimensional Hamiltonian systems. Physica A 2011, 390, 3290–3307. [Google Scholar] [CrossRef]
- Miritello, G.; Pluchino, A.; Rapisarda, A. Central limit behavior in the Kuramoto model at the ‘edge of chaos’. Physica A 2009, 388, 4818–4826. [Google Scholar] [CrossRef]
- Penson, K.A.; Gorska, K. Exact and explicit probabilities densities for one-sided Lévy stable distributions. Phys. Rev. Lett. 2010, 105, 210604. [Google Scholar] [CrossRef] [PubMed]
- Gorska, K.; Penson, K.A. Lévy stable two-sided distributions: Exact and explicit densities for asymmetric case. Phys. Rev. E 2011, 83, 061125. [Google Scholar] [CrossRef] [PubMed]
- Group of Statistical Physics. Available online: http://tsallis.cat.cbpf.br/biblio.htm (accessed on 21 September 2011).
- Upadhyaya, A.; Rieu, J.-P.; Glazier, J.A.; Sawada, Y. Anomalous diffusion and non-Gaussian velocity distribution of Hydra cells in cellular aggregates. Physica A 2001, 293, 549–558. [Google Scholar] [CrossRef]
- Thurner, S.; Wick, N.; Hanel, R.; Sedivy, R.; Huber, L.A. Anomalous diffusion on dynamical networks: A model for epithelial cell migration. Physica A 2003, 320, 475–484. [Google Scholar] [CrossRef]
- Reynolds, A.M. Can spontaneous cell movements be modelled as Lévy walks? Physica A 2010, 389, 273–277. [Google Scholar] [CrossRef]
- Daniels, K.E.; Beck, C.; Bodenschatz, E. Defect turbulence and generalized statistical mechanics. Physica D 2004, 193, 208–217. [Google Scholar] [CrossRef]
- Lutz, E. Anomalous diffusion and Tsallis statistics in an optical lattice. Phys. Rev. A 2003, 67, 051402(R). [Google Scholar] [CrossRef]
- Douglas, P.; Bergamini, S.; Renzoni, F. Tunable Tsallis distributions in dissipative optical lattices. Phys. Rev. Lett. 2006, 96, 110601. [Google Scholar] [CrossRef] [PubMed]
- Bagci, G.B.; Tirnakli, U. Self-organization in dissipative optical lattices. Chaos 2009, 19, 033113:1–033113:9. [Google Scholar] [CrossRef] [PubMed]
- Arevalo, R.; Garcimartin, A.; Maza, D. Anomalous diffusion in silo drainage. Eur. Phys. J. E 2007, 23, 191–198. [Google Scholar] [CrossRef] [PubMed]
- Arevalo, R.; Garcimartin, A.; Maza, D. A non-standard statistical approach to the silo discharge. Eur. Phys. J. Spec. Top. 2007, 143, 191–197. [Google Scholar] [CrossRef]
- Liu, B.; Goree, J. Superdiffusion and non-Gaussian statistics in a driven-dissipative 2D dusty plasma. Phys. Rev. Lett. 2008, 100, 055003:1–055003:9. [Google Scholar] [CrossRef] [PubMed]
- DeVoe, R.G. Power-law distributions for a trapped ion interacting with a classical buffer gas. Phys. Rev. Lett. 2009, 102, 063001. [Google Scholar] [CrossRef] [PubMed]
- Borland, L. Closed form option pricing formulas based on a non-Gaussian stock price model with statistical feedback. Phys. Rev. Lett. 2002, 89, 098701. [Google Scholar] [CrossRef] [PubMed]
- Borland, L. A theory of non-gaussian option pricing. Quant. Finance 2002, 2, 415–4431. [Google Scholar]
- Osorio, R.; Borland, L.; Tsallis, C. Distributions of high-frequency stock-market observables. In Nonextensive Entropy—Interdisciplinary Applications; Gell-Mann, M., Tsallis, C., Eds.; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Queiros, S.M.D. On non-Gaussianity and dependence in financial in time series: A nonextensive approach. Quant. Finance 2005, 5, 475–485. [Google Scholar] [CrossRef]
- Ludescher, J.; Tsallis, C.; Bunde, A. Universal behaviour of interoccurrence times between losses in financial markets: An analytical description. Europhys. Lett. 2011, 95, 68002. [Google Scholar] [CrossRef]
- Tamarit, F.A.; Cannas, S.A.; Tsallis, C. Sensitivity to initial conditions in the Bak-Sneppen model of biological evolution. Eur. Phys. J. B 1998, 1, 545–548. [Google Scholar] [CrossRef]
- Bakar, B.; Tirnakli, U. Analysis of self-organized criticality in Ehrenfest’s dog-flea model. Phys. Rev. E 2009, 79, 040103(R):1–040103(R):5. [Google Scholar] [CrossRef] [PubMed]
- Bakar, B.; Tirnakli, U. Return distributions in dog-flea model revisited. Physica A 2010, 389, 3382–3386. [Google Scholar] [CrossRef]
- Celikoglu, A.; Tirnakli, U.; Queiros, S.M.D. Analysis of return distributions in the coherent noise model. Phys. Rev. E 2010, 82, 021124. [Google Scholar] [CrossRef] [PubMed]
- Caruso, F.; Pluchino, A.; Latora, V.; Vinciguerra, S.; Rapisarda, A. Analysis of self-organized criticality in the Olami-Feder-Christensen model and in real earthquakes. Phys. Rev. E 2007, 75, 055101(R). [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.Q.; Tirnakli, U.; Wang, L.; Chen, T.L. Self organized criticality in a modified Olami-Feder-Christensen model. Eur. Phys. J. B 2011, 82, 83–89. [Google Scholar] [CrossRef]
- Moyano, L.G.; Anteneodo, C. Diffusive anomalies in a long-range Hamiltonian system. Phys. Rev. E 2006, 74, 021118. [Google Scholar] [CrossRef] [PubMed]
- Boghosian, B.M. Thermodynamic description of the relaxation of two-dimensional turbulence using Tsallis statistics. Phys. Rev. E 1996, 53, 4754–4763. [Google Scholar] [CrossRef]
- Anteneodo, C.; Tsallis, C. Two-dimensional turbulence in pure-electron plasma: A nonextensive thermostatistical description. J. Mol. Liquids 1997, 71, 255–267. [Google Scholar] [CrossRef]
- Pickup, R.M.; Cywinski, R.; Pappas, C.; Farago, B.; Fouquet, P. Generalized spin glass relaxation. Phys. Rev. Lett. 2009, 102, 097202:1–097202:4. [Google Scholar] [CrossRef] [PubMed]
- Ferri, G.L.; Reynoso Savio, M.F.; Plastino, A. Tsallis q-triplet and the ozone layer. Physica A 2010, 389, 1829–1833. [Google Scholar] [CrossRef]
- Borges, E.P.; Tsallis, C.; Ananos, G.F.J.; Oliveira, P.M.C. Nonequilibrium probabilistic dynamics at the logistic map edge of chaos. Phys. Rev. Lett. 2002, 89, 254103:1–254103:8. [Google Scholar] [CrossRef] [PubMed]
- Ananos, G.F.J.; Tsallis, C. Ensemble averages and nonextensivity at the edge of chaos of one-dimensional maps. Phys. Rev. Lett. 2004, 93, 020601:1–020601:5. [Google Scholar] [CrossRef] [PubMed]
- Pluchino, A.; Rapisarda, A.; Tsallis, C. Nonergodicity and central limit behavior in long-range Hamiltonians. Europhys. Lett. 2007, 80, 26002:1–26002:6. [Google Scholar] [CrossRef]
- Pluchino, A.; Rapisarda, A.; Tsallis, C. A closer look at the indications of q-generalized Central Limit Theorem behavior in quasi-stationary states of the HMF model. Physica A 2008, 387, 3121:1–3121:11. [Google Scholar] [CrossRef]
- Afsar, O.; Tirnakli, U. Probability densities for the sums of iterates of the sine-circle map in the vicinity of the quasi-periodic edge of chaos. Phys. Rev. E 2010, 82, 046210:1–046210:7. [Google Scholar] [CrossRef] [PubMed]
- White, D.R.; Kejzar, N.; Tsallis, C.; Farmer, D.; White, S. A generative model for feedback networks. Phys. Rev. E 2006, 73, 016119:1–016119:8. [Google Scholar] [CrossRef] [PubMed]
- Soares, D.J.B.; Tsallis, C.; Mariz, A.M.; da Silva, L.R. Preferential attachment growth model and nonextensive statistical mechanics. Europhys. Lett. 2005, 70, 70–76. [Google Scholar] [CrossRef]
- Thurner, S.; Tsallis, C. Nonextensive aspects of self-organized scale-free gas-like networks. Europhys. Lett. 2005, 72, 197:1–197:7. [Google Scholar] [CrossRef]
- Thurner, S.; Kyriakopoulos, F.; Tsallis, C. Unified model for network dynamics exhibiting nonextensive statistics. Phys. Rev. E 2007, 76, 036111. [Google Scholar] [CrossRef] [PubMed]
- Sotolongo-Grau, O.; Rodriguez-Perez, D.; Antoranz, J.C.; Sotolongo-Costa, O. Tissue radiation response with maximum Tsallis entropy. Phys. Rev. Lett. 2010, 105, 158105. [Google Scholar] [CrossRef] [PubMed]
- Andrade, J.S., Jr.; da Silva, G.F.T.; Moreira, A.A.; Nobre, F.D.; Curado, E.M.F. Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett. 2010, 105, 260601:1–260601:4. [Google Scholar] [CrossRef] [PubMed]
- Levin, Y.; Pakter, R. Comment on: Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett. 2011, 107, 088901. [Google Scholar] [CrossRef] [PubMed]
- Andrade, J.S., Jr.; da Silva, G.F.T.; Moreira, A.A.; Nobre, F.D.; Curado, E.M.F. Reply to the Comment by Levin and Pakter. Phys. Rev. Lett. 2011, 107, 088902. [Google Scholar] [CrossRef]
- Reis, J.L., Jr.; Amorim, J.; Dal Pino, A., Jr. Occupancy of rotational population in molecular spectra based on nonextensive statistics. Phys. Rev. E 2011, 83, 017401:1–017401:4. [Google Scholar] [CrossRef] [PubMed]
- Kaniadakis, G.; Lavagno, A.; Quarati, P. Generalized statistics and solar neutrinos. Phys. Lett. B 1996, 369, 308:1–308:4. [Google Scholar] [CrossRef]
- Alberico, W.M.; Lavagno, A.; Quarati, P. Non-extensive statistics, fluctuations and correlations in high energy nuclear collisions. Eur. Phys. J. C 2000, 12, 499–506. [Google Scholar] [CrossRef]
- Bediaga, I.; Curado, E.M.F.; Miranda, J. A nonextensive thermodynamical equilibrium approach in e+e− → hadrons. Physica A 2000, 286, 156–163. [Google Scholar] [CrossRef]
- Beck, C. Non-extensive statistical mechanics and particle spectra in elementary interactions. Physica A 2000, 286, 164–180. [Google Scholar] [CrossRef]
- Tsallis, C.; Anjos, J.C.; Borges, E.P. Fluxes of cosmic rays: A delicately balanced stationary state. Phys. Lett. A 2003, 310, 372–376. [Google Scholar] [CrossRef]
- Beck, C. Generalized statistical mechanics of cosmic rays. Physica A 2003, 331, 173:1–173:10. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Power laws in elementary and heavy-ion collisions - A story of fluctuations and nonextensivity? Eur. Phys. J. A 2009, 40, 299:1–299:14. [Google Scholar] [CrossRef]
- Biro, T.S.; Purcsel, G.; Urmossy, K. Non-extensive approach to quark matter. Eur. Phys. J. A 2009, 40, 325–340. [Google Scholar] [CrossRef]
- CMS Collaboration. Transverse-momentum and pseudorapidity distributions of charged hadrons in pp collisions at = 0.9 and 2.36 TeV. J. High Energy Phys. 2010, 02, 041. [Google Scholar]
- CMS Collaboration. Transverse-momentum and pseudorapidity distributions of charged hadrons in pp collisions at = 7 TeV. Phys. Rev. Lett. 2010, 105, 022002. [Google Scholar]
- d’Enterria, D.; Engel, R.; Pierog, T.; Ostapchenko, S.; Werner, K. Constraints from the first LHC data on hadronic event generators for ultra-high energy cosmic-ray physics. arXiv, 2011; arXiv:1101.5596v3. [Google Scholar]
- CMS Collaboration. Strange particle production in pp collisions at = 0.9 and 7 TeV. J. High Energy Phys. 2011, 05, 064. [Google Scholar]
- ALICE Collaboration. Transverse momentum spectra of charged particles in proton-proton collisions = 900 GeV with ALICE at the LHC. Phys. Lett. B 2010, 693, 53–68. [Google Scholar]
- ALICE Collaboration. Strange particle production in proton-proton collisions at = 0.9 TeV with ALICE at the LHC. Eur. Phys. J. C 2011, 71, 1594:1–1594:34. [Google Scholar]
- Tawfik, A. Antiproton-to-proton ratios for ALICE heavy-ion collisions. Nucl. Phys. A 2011, 859, 63–72. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Charged-particle multiplicities in pp interactions measured with the ATLAS detector at the LHC. New J. Phys. 2011, 13, 053033:1–053033:24. [Google Scholar]
- Adare, A.; Afanasiey, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Aoki, K.; Aphecetche, L.; Armendariz, R.; et al. Measurement of neutral mesons in p+p collisions at = 200 GeV and scaling properties of hadron production. arXiv, 2010; arXiv:1005.3674v1. [Google Scholar]
- Shao, M.; Yi, L.; Tang, Z.B.; Chen, H.F.; Li, C.; Xu, Z.B. Examination of the species and beam energy dependence of particle spectra using Tsallis statistics. J. Phys. G 2010, 37, 085104. [Google Scholar] [CrossRef]
- Wibig, T. The non-extensivity parameter of a thermodynamical model of hadronic interactions at LHC energies. J. Phys. G Nucl. Part. Phys. 2010, 37, 115009:1–115009:4. [Google Scholar] [CrossRef]
- Du, J. Test of nonextensive statistical mechanics by solar sound speeds. Europhys. Lett. 2006, 75, 861–867. [Google Scholar] [CrossRef]
- Carvalho, J.C.; Silva, R.; do Nascimento, J.D.; de Medeiros, J.R. Power law statistics and stellar rotational velocities in the Pleiades. Europhys. Lett. 2008, 84, 59001. [Google Scholar] [CrossRef]
- Cho, J.; Lazarian, A. Simulations of electron magnetohydrodynamic turbulence. Astrophys. J. 2009, 701, 236–252. [Google Scholar] [CrossRef]
- Esquivel, A.; Lazarian, A. Tsallis statistics as a tool for studying interstellar turbulence. Astrophys. J. 2010, 710, 125–132. [Google Scholar] [CrossRef]
- Moret, M.A.; de Senna, V.; Zebende, G.F.; Vaveliuk, P. X-ray binary systems and nonextensivity. Physica A 2010, 389, 854–858. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Beyond kappa distributions: Exploiting Tsallis Statistical Mechanics in space plasmas. J. Geophys. Res. Space Phys. 2009, 114, A11105. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Exploring transitions of space plasmas out of equilibrium. Astrophys. J. 2010, 714, 971. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Measure of the departure of the q-metastable stationary states from equilibrium. Phys. Scr. 2010, 82, 035003. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Non-Equilibrium Stationary States in the Heliosphere and the Influence of Pick-Up Ions. Pickup Ions Throughout the Heliosphere and Beyond. In Proceedings of the 9th Annual International Astrophysics Conference, Maui, HI, USA, 14–19 March 2010; Volume 1302, pp. 70–76.
- Livadiotis, G.; McComas, D.J.; Dayeh, M.A.; Funsten, H.O.; Schwadron, N.A. First sky map of the inner heliosheath temperature using IBEX spectra. Astrophys. J. 2011, 734, 1. [Google Scholar] [CrossRef]
- Tofflemire, B.M.; Burkhart, B.; Lazarian, A. Interstellar sonic and Alfvenic Mach numbers and the Tsallis distribution. Astrophys. J. 2011, 736, 60. [Google Scholar] [CrossRef]
- Betzler, A.S.; Borges, E.P. Nonextensive distributions of rotation periods and diameters of asteroids Alberto. Earth Planet. Astrophys. 2011. preprint, 1107.5084 [astro-ph.EP]. [Google Scholar]
- Burlaga, L.F.; Vinas, A.F.; Ness, N.F.; Acuna, M.H. Tsallis statistics of the magnetic field in the heliosheath. Astrophys. J. 2006, 644, L83. [Google Scholar] [CrossRef]
- Burlaga, L.F.; Ness, N.F. Compressible “turbulence" observed in the heliosheath by Voyager 2. Astrophys. J. 2009, 703, 311. [Google Scholar] [CrossRef]
- Kalimeri, M.; Papadimitriou, C.; Balasis, G.; Eftaxias, K. Dynamical complexity detection in pre-seismic emissions using nonadditive Tsallis entropy. Physica A 2008, 387, 1161–1172. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Kalimeri, M.; Eftaxias, K. Nonextensivity and universality in the earthquake preparation process. Phys. Rev. E 2008, 77, 036101. [Google Scholar] [CrossRef] [PubMed]
- Contoyiannis, Y.F.; Eftaxias, K. Tsallis and Levy statistics in the preparation of an earthquake. Nonlinear Process. Geophys. 2008, 15, 1, 379. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Dynamical complexity in Dst time series using non-extensive Tsallis entropy. Geophys. Res. Lett. 2008, 35, L14102. [Google Scholar] [CrossRef]
- Vallianatos, F. A non-extensive approach to risk assessment. Nat. Hazards Earth Syst. Sci. 2009, 9, 211–216. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Investigating dynamical complexity in the magnetosphere using various entropy measures. J. Geophys. Res. Space Phys. 2009, 114, A00D06. [Google Scholar] [CrossRef]
- Balasis, G.; Eftaxias, K. A study of non-extensivity in the Earth’s magnetosphere. Eur. Phys. J. Spec. Top. 2009, 174, 219–225. [Google Scholar] [CrossRef]
- Eftaxias, K.; Athanasopoulou, L.; Balasis, G.; Kalimeri, M.; Nikolopoulos, S.; Contoyiannis, Y.; Kopanas, J.; Antonopoulos, G.; Nomicos, C. Unfolding the procedure of characterizing recorded ultra low frequency, kHZ and MHz electromagetic anomalies prior to the L’Aquila earthquake as pre-seismic ones. Part I. Nat. Hazards Earth Syst. Sci. 2009, 9, 1953–1971. [Google Scholar] [CrossRef]
- Eftaxias, K.; Balasis, G.; Contoyiannis, Y.; Papadimitriou, C.; Kalimeri, M.; Athanasopoulou, L.; Nikolopoulos, S.; Kopanas, J.; Antonopoulos, G.; Nomicos, C. Unfolding the procedure of characterizing recorded ultra low frequency, kHZ and MHz electromagnetic anomalies prior to the L’Aquila earthquake as pre-seismic ones - Part 2. Nat. Hazards Earth Syst. Sci. 2009, 10, 275–294. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. Is plate tectonics a case of non-extensive thermodynamics? Physica A 2010, 389, 4989–4993. [Google Scholar] [CrossRef]
- Eftaxias, K. Footprints of nonextensive Tsallis statistics, selfaffinity and universality in the preparation of the L’Aquila earthquake hidden in a pre-seismic EM emission. Physica A 2010, 389, 133–140. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Anastasiadis, A.; Eftaxias, K. Investigating magnetospheric dynamics using various complexity measures. AIP Conf. Proc. 2010, 1320, 65–71. [Google Scholar]
- Vallianatos, F. A non-extensive statistical physics approach to the polarity reversals of the geomagnetic field. Physica A 2011, 390, 1773–1778. [Google Scholar] [CrossRef]
- Vallianatos, F.; Kokinou, E.; Sammonds, P. Non-extensive statistical physics approach to fault population distribution. A case study from the Southern Hellenic Arc (Central Crete). Acta Geophys. 2011, 59, 770:1–770:15. [Google Scholar] [CrossRef]
- Vallianatos, F.; Triantis, D.; Sammonds, P. Non-extensivity of the isothermal depolarization relaxation currents in uniaxial compressed rocks. Europhys. Lett. 2011, 94, 68008. [Google Scholar] [CrossRef]
- Balasis, G.; Papadimitriou, C.; Daglis, I.A.; Anastasiadis, A.; Athanasopoulou, L.; Eftaxias, K. Signatures of discrete scale invariance in D(st) time series. Geophys. Res. Lett. 2011, 38, L13103:1–L13103:6. [Google Scholar] [CrossRef]
- Pavlos, G.P.; Iliopoulos, A.C.; Tsoutsouras, V.G.; Sarafopoulos, D.V.; Sfiris, D.S.; Karakatsanis, L.P.; Pavlos, E.G. First and second order non-equilibrium phase transition and evidence for non-extensive Tsallis statistics in Earth’s magnetosphere. Physica A 2011, 390, 2819–2839. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Minadakis, G.; Eftaxias, K. Analysis of electromagnetic pre-seismic emissions using Fisher Information and Tsallis entropy. Physica A 2011, in press. [Google Scholar] [CrossRef]
- Karakatsanis, L.P.; Pavlos, G.P.; Sfiris, D.S. Universality of first and second order phase transition in solar activity. Evidence for non-extensive Tsallis statistics. Int. J. Bifurc. Chaos 2011, in press. [Google Scholar]
- Nobre, F.D.; Rego-Monteiro, M.A.; Tsallis, C. Nonlinear generalizations of relativistic and quantum equations with a common type of solution. Phys. Rev. Lett. 2011, 106, 140601:1–140601:4. [Google Scholar] [CrossRef] [PubMed]
- Thurner, S. Nonextensive statistical mechanics and complex networks. Europhysics News 2005, 36, 218–220. [Google Scholar] [CrossRef]
- de Meneses, M.D.S.; da Cunha, S.D.; Soares, D.J.B.; da Silva, L.R. Preferential attachment scale-free growth model with random fitness and connection with Tsallis statistics. Prog. Theor. Phys. Suppl. 2006, 162, 131–137. [Google Scholar] [CrossRef]
- Nobre, F.D.; Tsallis, C. Infinite-range Ising ferromagnet: thermodynamic limit within generalized statistical mechanics. Physica A 1995, 213, 337–356, Erratum: 1995, 216, 369. [Google Scholar] [CrossRef]
- Caride, A.O.; Tsallis, C.; Zanette, S.I. Criticality of the anisotropic quantum Heisenberg model on a self-dual hierarchical lattice. Phys. Rev. Lett. 1983, 51, 145; 1983, 51, 145–147. [Google Scholar]
- Lucena, L.S.; da Silva, L.R.; Tsallis, C. Departure from Boltzmann-Gibbs statistics makes the hydrogen-atom specific heat a computable quantity. Phys. Rev. E 1995, 51, 6247–6249. [Google Scholar] [CrossRef]
- Oliveira-Neto, N.M.; Curado, E.M.F.; Nobre, F.D.; Rego-Monteiro, M.A. Approach to equilibrium of the hydrogen atom at low temperature. Physica A 2007, 374, 251–262. [Google Scholar] [CrossRef]
- Oliveira-Neto, N.M.; Curado, E.M.F.; Nobre, F.D.; Rego-Monteiro, M.A. A simple model to describe the low-temperature behaviour of some atoms and molecules: An application to the hydrogen atom. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 1975–1989. [Google Scholar] [CrossRef]
- Anteneodo, C.; Plastino, A.R. Maximum entropy approach to stretched exponential probability distributions. J. Phys. A 1999, 32, 1089–1097. [Google Scholar] [CrossRef]
- Curado, E.M.F. General aspects of the thermodynamical formalism. Braz. J. Phys. 1999, 29, 36–45. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E.G.D. Superstatistics. Physica A 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Tsallis, C.; Souza, A.M.C. Constructing a statistical mechanics for Beck-Cohen superstatistics. Phys. Rev. E 2003, 67, 026106:1–026106:5. [Google Scholar] [CrossRef] [PubMed]
- Curado, E.M.F.; Nobre, F.D. On the stability of analytic entropic forms. Physica A 2004, 335, 94–106. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S. A comprehensive classification of complex statistical systems and an axiomatic derivation of their entropy and distribution functions. Europhys. Lett. 2011, 93, 20006. [Google Scholar] [CrossRef]
- Tempesta, P. Group entropies, correlation laws, and zeta functions. Phys. Rev. E 2011, 84, 021121:1–021121:10. [Google Scholar] [CrossRef] [PubMed]
- Hanel, R.; Thurner, S.; Gell-Mann, M. Generalized entropies and the transformation group of superstatistics. Proc. Nat. Acad. Sci. USA 2011, 108. [Google Scholar] [CrossRef]
- dos Santos, B.C.C.; Tsallis, C. Time evolution towards q-Gaussian stationary states through unified Itô-Stratonovich stochastic equation. Phys. Rev. E 2010, 82, 061119. [Google Scholar] [CrossRef] [PubMed]
- Havrda, J.; Charvat, F. Concept of structural α-entropy. Kybernetika 1967, 3, 30–35. [Google Scholar]
- Vajda, I. Axioms of α-entropy of generalized probability distribution. Kybernetika 1968, 4, 105–112. [Google Scholar]
- Daroczy, Z. Generalized information measures. Inf. Control 1970, 16, 36–51. [Google Scholar] [CrossRef]
- Lindhard, J.; Nielsen, V. Det Kongelige Danske Videnskabernes Selskab Matematisk-fysiske Meddelelser (Denmark). Studies in Statistical Mechanics 1971, 38, 1–42. [Google Scholar]
- Sharma, B.D.; Mittal, D.P. New non-additive measures of entropy for discrete probability distributions. J. Math. Sci. 1975, 10, 28–40. [Google Scholar]
- Renyi, A. On measures of information and entropy. In Proceedings of the 4th Berkeley Symposium, (Los Angeles, California, USA), 20 June–30 July 1960; University of California Press: Berkeley, Los Angeles, 1961; Volume 1, p. 547. [Google Scholar]
- Renyi, A. Probability Theory; North-Holland: Amsterdam, The Netherlands, 1970; (and references therein.). [Google Scholar]
- Aczel, J.; Daroczy, Z. On measures of information and their characterization. In Mathematics in Science and Engineering; Bellman, R., Ed.; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221. [Google Scholar] [CrossRef]
- Stigler, S.M. Statistics on the Table—The History of Statistical Concepts and Methods; Harvard University Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Csiszar, I. Information measures: A critical survey. In Transactions of the Seventh Prague Conference on Information Theory, Statistical Decision Functions, Random Processes, and the European Meeting of Statisticians, 1974; Reidel: Dordrecht, The Netherlands, 1978; p. 73. [Google Scholar]
- Schutzenberger, P.-M. Contributions aux applications statistiques de la theorie de l’ information. Publ. Inst. Statist. Univ. Paris 1954, 3, 3. [Google Scholar]
- Vasyliunas, V.M. A survey of low-energy electron waves. J. Geophys. Res. 1968, 73, 2839. [Google Scholar] [CrossRef]
- Rios, L.A.; Galvão, R.M.O. Self-modulation of linearly polarized electromagnetic waves in non-Maxwellian plasmas. Phys. Plasmas 2010, 17, 042116:1–042116:8. [Google Scholar] [CrossRef]
- Souza, A.M.C.; Tsallis, C. Student’s t- and r-distributions: Unified derivation from an entropic variational principle. Physica A 1997, 236, 52–57. [Google Scholar] [CrossRef]
- Treumann, R.A. Generalized-Lorentziann path integrals. Phys. Rev. E 1998, 57, 5150–5153. [Google Scholar] [CrossRef]
- Tsallis, C. Comment on “Temporal scaling at Feigenbaum points and nonextensive thermodynamics" by P. Grassberger. arXiv, 2005; arXiv:cond-mat/0511213v1. [Google Scholar]
- Grassberger, P. Proposed central limit behavior in deterministic dynamical systems. Phys. Rev. E 2009, 79, 057201. [Google Scholar] [CrossRef] [PubMed]

© 2011 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Tsallis, C. The Nonadditive Entropy Sq and Its Applications in Physics and Elsewhere: Some Remarks. Entropy 2011, 13, 1765-1804. https://doi.org/10.3390/e13101765
Tsallis C. The Nonadditive Entropy Sq and Its Applications in Physics and Elsewhere: Some Remarks. Entropy. 2011; 13(10):1765-1804. https://doi.org/10.3390/e13101765
Chicago/Turabian StyleTsallis, Constantino. 2011. "The Nonadditive Entropy Sq and Its Applications in Physics and Elsewhere: Some Remarks" Entropy 13, no. 10: 1765-1804. https://doi.org/10.3390/e13101765
APA StyleTsallis, C. (2011). The Nonadditive Entropy Sq and Its Applications in Physics and Elsewhere: Some Remarks. Entropy, 13(10), 1765-1804. https://doi.org/10.3390/e13101765



