1. Introduction
A common view of Gibbs’ paradox, that the straightforward formula for the statistical mechanical entropy was not properly extensive, was nicely resolved by recognizing the indistinguishability of atoms. (I will defer to others regarding what should really be called Gibbs paradox.) However, understanding the entropy of distinguishable particles is not so transparent. A recent attempt to understand this subtlety has led to an interesting, and radical departure from the conventional wisdom regarding the basic statistical mechanical formulation of entropy [
1,
2].
The conventional wisdom is that entropy in a microcanonical ensemble is
where Ω is the number of states with energy in a narrow range, E to E+dE, that is accessible to the system. While the symbol Ω has been used by many [
3,
4,
5,
6,
7,
8,
9,
10,
11], W, [
12,
13,
14,
15,
16], C [
17], M [
18], and Γ [
19,
20,
21] have also been used. These authors, not all of whom would have been pleased to be described merely as textbook writers, defined their respective symbols as the number of states [
3,
4,
5,
6,
7,
8,
9,
12,
13,
14,
15,
16] or, the classical equivalent, the volume in phase space [
10,
11,
19,
20,
21]. A notable exception was Planck [
22] who used the symbol W and called it Wahrscheinlichkeit (probability). Apparently Planck was responsible for the inscription
on Boltzmann’s tombstone and crediting the formula to Boltzmann even though Boltzmann seems not to have published it [
2]. Although Planck described W as probability, the examples in his book give values of W that exceed unity [
22]. Early on, Fowler [
17] devoted several pages to a critique of calling W a probability and also to Boltzmann’s concept of entropy. Later, Wannier [
18] wrote “By an unfortunate choice of language most books refer to this number as a probability even though it is a number larger than 1.” While agreeing with Wannier’s criticism, my perhaps less than exhaustive research has not turned up the other books to which he alluded.
As every reader of this journal undoubtedly knows, entropy is often alternatively defined [
4,
23] in terms of probability
where P
i is the probability of the i
th state and the sum goes over all the Ω states accessible to the system. Equation (3) has its origins with Gibbs [
24]. It is not limited to the microcanonical ensemble. However, when it is applied to a microcanonical ensemble, P
i = 1/ Ω for each state by Gibbs equal
a priori postulate, and Equation (3) reduces to Equation (1). Of course, Gibbs predated quantum mechanics, so his writing involved S = −k <ln P> and continuous variables in phase space. When applied to classical distinguishable ideal monatomic gases, Gibbs’ entropy has the well known form
which contains the volume dependent entropic term that will be defined in this paper as
where V is the volume, N is the number of distinguishable particles and the subscript G is for Gibbs. Equation (5) is the notorious, non-extensive part of the entropy that gives rise to a common view of Gibbs paradox. As is well known, this part of the classical entropy of indistinguishable particles becomes Nk ln(V/N) upon insertion of a factor of 1/N! in the classical partition function to take into account the permutation of unphysical labels. This commonly accepted procedure was criticized as
ad hoc [
1], but a formal derivation has since been presented [
25]. Of course, as is well known [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20], extensivity and a ln(V/N) term follow from the fundamental quantum statistical mechanics of indistinguishable particles.
More recently, it has been argued that Equation (5) is incorrect for classical, distinguishable particles [
1,
2]. As was emphasized, Equation (1) is then also incorrect because Equation (1) implies Equation (5) and falsifying Equation (5) falsifies Equation (1). Instead, it has been proposed that statistical mechanics should return to the writings of Boltzmann and make Equation (2) the fundamental equation and number of states Ω should be replaced by probability W [
2]. A major result of that proposal is that Equation (5) is replaced by
for classical, distinguishable particles, where the subscript S is for Swendsen. In this proposal, non-extensivity and Gibbs paradox disappear even for distinguishable particles, so Gibbs paradox could be considered as Gibbs mistakenly not paying enough attention to Boltzmann.
In this paper I argue that S
G in Equation (5) is correct for classical, distinguishable particles. If my argument is accepted, then it dispels the objection [
1,
2] to the conventional Equation (1), even though it abandons extensitivity, which many feel should be postulational. My argument would not, of course, preclude an alternative fundamental definition of entropy in a microcanonical ensemble, especially for non-equilibrium processes [
27].
I furthermore argue that S
S in Equation (6) is incorrect when one takes distinguishability to its logical limit. Since the proposal [
1] to use probability W along the lines of Equation (2) leads to Equation (6), my argument therefore implies that the recent attempt to follow Boltzmann’s writings to provide a fundamental definition of entropy [
2] is also untenable.
It should be noted that my position has previously been included in a more extensive critique [
25] of the first paper of Swendsen on the entropy of distinguishable particles [
1]. However, the reader of those two papers [
1,
25] may be perplexed because Equation (5) was attributed to Boltzmann [
1] and I followed suit [
25]. In a subsequent paper Swendsen [
2] presented evidence that the historical record should be corrected with respect to Boltzmann, and this correction is consistent with Fowler’s discussion [
17]. (It may be noted that this would entail correcting the current presentation on Wikipedia which ascribes Equation (1) to Boltzmann. It also runs counter to the textbook name of Maxwell-Boltzmann statistics that describes distinguishable modes by not including the 1/N! factor.) In agreement with Swendsen [
2], Fowler [
17] and Planck [
22], I am inclined to agree that there should be a change in names in [
1,
25]. In [
25] the S
BCD that corresponded to Equation (5) above carried the subscripts BCD for Boltzmann Classical Distinguishable and those subscripts should be changed to GCD for Gibbs Classical Distinguishable. In [
25] the entropy that corresponded to Equation (6) above carried the subscripts SCD for Swendsen Classical Distinguishable and now Boltzmann’s name could be attached to that, although that may be taking too great liberty as Boltzmann apparently never wrote that equation [
2]. In this paper I use S
S instead of S
B in Equation (6).
Although most busy scientists would be inclined to accept the well established conventional wisdom of Equation (1), readers of this issue of Entropy would not be so inclined to blindly accept the conventional wisdom. Also, since typical laboratory gases are generally composed of a few types of atoms, and the atoms within each type are indistinguishable, statistical mechanicians have not been much concerned with systems of truly distinguishable particles where each particle is different. However, Swendsen has made the important points that particles in computer simulations are clearly distinguishable [
1] and that colloidal particles, such as in homogenized milk, are likely to be distinguishable [
2]. Another example is the class of branched, saturated, hydrocarbon polymers C
nH
2n+2 in which each molecule with the same value of n has the same mass but the locations of the multiple branches distinguish the different isomers; furthermore, the number of molecules in this class exceeds Avogadro’s number for values of n of order 100. Because only one counter-example can disprove conventional wisdom, it is therefore appropriate to spend some thought provoking effort to try to understand the statistical mechanics of distinguishable particles.
2. Definitions
I assume that truly distinguishable particles can be assigned distinct names. For a system of N distinguishable particles, for convenience I will simply assign the numeric names 1, 2, …, N. If the particles are distinguishable, there must be, at least in principle, some way to isolate each one. In my first two examples below I will define a semi-permeable membrane M
i for each particle i such that M
i provides a barrier to particle i but is transparent to all other particles. In my third sample below only two semi-permeable membranes will be required. The difficulty of physically realizing these semi-permeable membranes for a real colloidal system such as homogenized milk [
2] should not be allowed to preclude gedanken experiments any more than the impossibility of performing completely reversible processes should not be allowed to prevent us from using thermodynamics.
Furthermore, in the examples below it will be assumed that the system is ideal in the usual sense that the interactions between particles and walls, while allowing equilibrium to be attained, are negligible and that there is no change in the average energy of particles in the system, so we can continue to ignore the translational kinetic energy EK term in Equation (4). Each Yi term in Equation (4) depends upon the mass of the ith particle as well as contributions to the entropy from internal degrees of freedom of the particles. For particles to be truly distinguishable, Yi would generally be different for each particle. The example of hydrocarbon isomers noted above shows that this difference is not necessarily due to a difference in mass, but different Yi could be due to vibrational frequencies, although if the difference only involves modes with energies large compared to kT, the differences in Yi may be made as small as one pleases. Most importantly, any such differences in Yi will remain constant for the examples given below because they involve the same particles and no changes in temperature or average energies. Therefore, it is appropriate to focus on the translational volume terms, as in Equations (5) and (6), instead of the total entropy in Equation (4).
3. Example 1
Consider state
α created by placing particles 1, …, N/2 in a container of volume V and particles (N/2) + 1, …, N in another container, also of volume V. Consider the αβ process that creates state β by breaking a partition between the two containers to allow all N particles to move freely within one container of volume 2V. What has changed? Clearly, the density of particles has not changed and that would guarantee that the translational volume entropy would not change if the particles were indistinguishable. However, for distinguishable particles there are three reasons that the entropy should increase. (i) There is less information regarding the whereabouts of each named particle in state β than in state α, so if there is the usual connection between missing information and entropy [
26,
27,
28], then entropy should be greater in the β state. (ii) Reforming the original α state could be done by recompressing each particle i into its original volume using the M
i semi-permeable membrane. This takes external work w done
on the system. To maintain the same energy, heat q = w would have to flow
out of the system isothermally and that would decrease the thermodynamic entropy of the system by
minus q/T. (iii) Starting from state α, one could use the M
i semi-permeable membranes to extract work w during quasistatic expansions for each particle i [
25]. For these three reasons, the entropy should increase for process αβ. The traditional Gibbs Equation (5) does this nicely,
However, Equation (6) gives
and so it fails this test.
Incidentally, not so many years ago it was customary to use the expression “entropy of mixing” to describe this αβ process, but Ben-Naim [
29] has taught us that this is a misleading term; rather, each particle has been allowed to expand into a larger volume (accompanied by ‘assimilation’ if the particles are identical). The primary case discussed by Ben-Naim was that of allowing two different kinds of gases, each of which was composed of indistinguishable particles, to expand into the volume initially occupied by the other. The difference in the present example involving distinguishable particles is that there are N different gases, each of which has only one particle, and each of which expands during the αβ process. However, the increase in entropy is exactly the same conceptually and the result in Equation (7c) is identical. This is consistent with Ben-Naim’s discussion involving the ‘mixing’ of a single A particle with a gas of B particles [
29].
4. Example 2
While Example 1 strongly favors Equation (5) over Equation (6), Example 2 proves more challenging and it recovers deeper insights into the meaning of entropy. A new state γ is created from state β in Example 1 by inserting a partition into the 2V volume to again provide two volumes V as in state α in Example 1. It is clear that there should be no change in entropy in process βγ and ΔS
Sβγ is obviously zero. However, if state γ is assumed to be the same as state α, then it would appear that ΔS
Gβγ = −ΔS
Gαβ < 0. The fallacy behind this incorrect result is the assumption that state γ is the same as state α. State α was prepared knowing precisely which distinguishable particles were in each subvolume, but there is no such knowledge about state γ, so from the information point of view it is clear that states α and γ are not equivalent [
26,
27,
28]. Independent of the information perspective, sorting the particles in state γ back to state α can be accomplished with the semi-permeable membranes M
i, but this requires the expenditure of free energy by the sorter, which should indeed reduce the entropy of the particles.
The challenge that this example poses to the traditional Gibbs interpretation is to explain why Equation (5) should not be applied straightforwardly. It is convenient to consider one particle at a time, noting that for each particle S
G = k ln (volume) in Equation (5), where the volume in state α is V and it is 2V in state β. What is the volume available to a particular distinguishable particle in state γ? Clearly, it is V if it is known to be in either subvolume, but it is not known to the experimenter who inserted the partition or to any other observer which subvolume a particular distinguishable particle is in, so the missing information is still k ln 2V. This suggests that application of Equation (5) to state γ should use the volume 2V. This answer will likely be uncomfortable to many, as it was to me, because it implies that the definition of entropy depends upon observers. Surely, the system ‘knows’ which subvolume the particle is in after the partition is inserted! However, the concept of entropy has always been divorced from what the system ‘knows’. In general, any system of classical gases, indistinguishable or distinguishable, ‘knows’ precisely the position of all its particles in phase space, so entropy would never increase even in a free expansion if it is defined by what the system ‘knows’. The idea that the microscopic state of the system determines the entropy is therefore not a valid counterargument to the argument presented here, namely, that the effective volume to use for state γ in Equation (5) is 2V, not V. This is consistent with the perspective that entropy is the missing information about the system that observers do not know, but could in principle obtain [
27,
28]. It may also be noted that the information interpretation of entropy is often faulted as being subjective [
30] (but see [
27] for a different perspective on the objectivity/subjectivity issue). In our case the information is objective in the sense it could not be obtained for observers as a class without the expenditure of free energy to obtain it.
At the risk of further complicating the issue, it may also be interesting to consider a way to determine which subvolume each of the particles is in after the partition is inserted. After such a determination, it would be known that there is a state with essentially half the particles 1ʹ, 2ʹ, …, N
2ʹ in one subvolume and particles N
2+1ʹ, …, Nʹ in the other subvolume, where the primes indicate a permutation of the original numbering scheme to account for the probable outcome that it is a different set of particles in each subvolume. Although this state, which we will call state δ, is different than state α, the entropy of states δ and α should clearly be the same. The idea for identifying the locations of the particles is to use the M
i membranes. If sweeping the M
i membrane through one of the subvolumes encounters no pressure, then particle i is in the other subvolume. If the sweep encounters pressure, one stops the sweep and returns M
i to its original position quasistatically, so no work is done on the system and particle i has been identified to be in that subvolume. Unlike the use of the semi-permeable membranes to reproduce state α precisely, this process requires no net work on the system of particles. However, it does produce information to the observer. Supposing that there is a connection of entropy to missing information [
26,
27,
28], this gives a decrease in the observer’s evaluation of the entropy of the system. How entropy of this system can be reduced with no exchange of heat or work is reminiscent of the nontrivial Maxwell demon paradox [
31]. Generally, the demon (observer) is supposed to have to expend free energy to accomplish the determination of the subvolume locations of the particles in state δ and this pays for the increase in the free energy (decrease in entropy) of the system.
5. Example 3
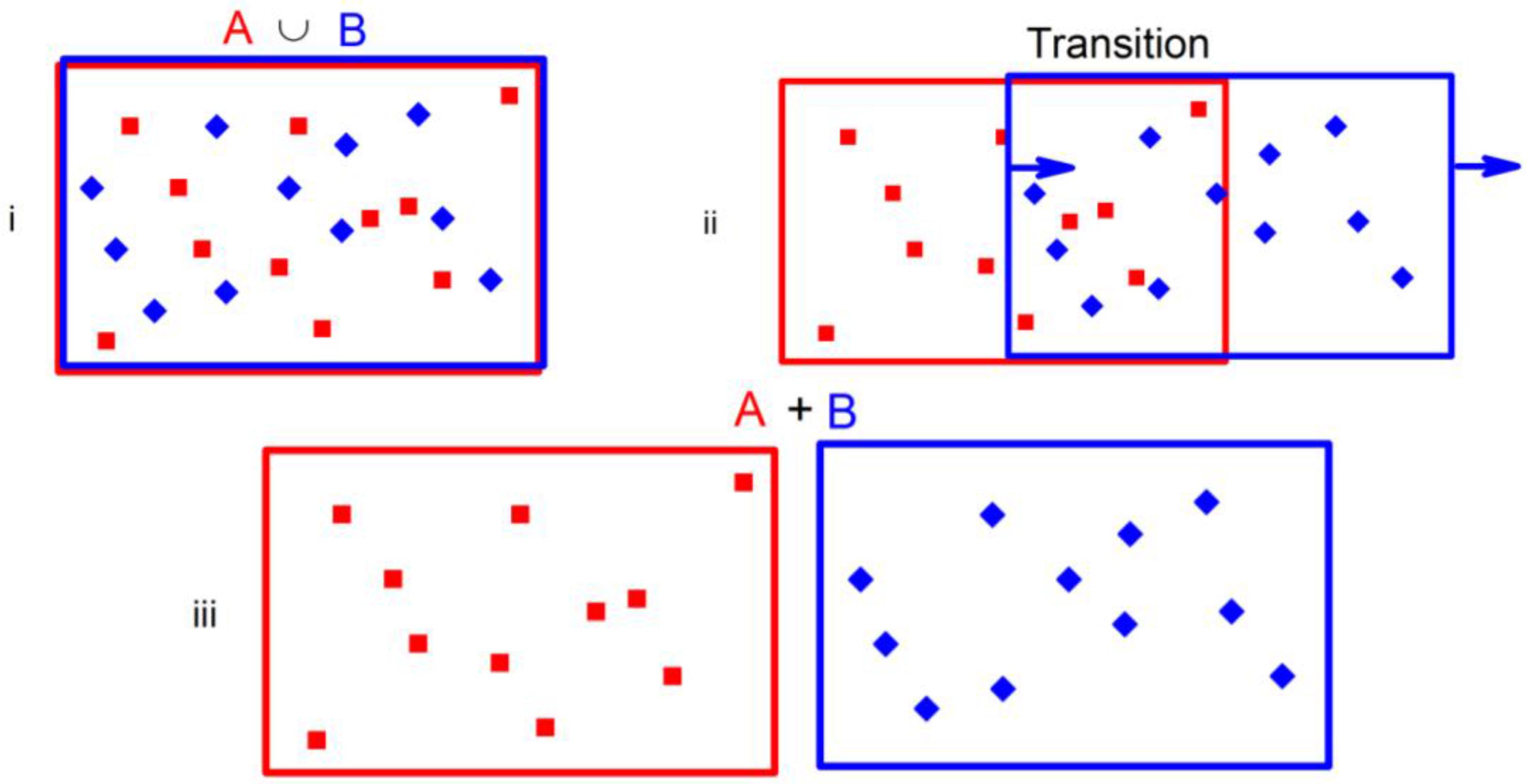
For a rather easier example, let us start with the classical Gibbs method, illustrated in
Figure 1, for separating two non-interacting gases of types A (red squares) and B (blue diamonds). This example also uses semi-permeable membranes that will form the walls of the containers, but only two types are required. One A
B wall (blue) is permeable to the type A (red) particles and impermeable to the type B (blue) particles. The other
AB wall (red) is permeable to type B particles and impermeable to type A particles. Starting with the merged A∪Β state in
Figure 1(i) with N
A A particles and N
B B particles in the same volume V, the A
B blue walled container is moved quasistatically as indicated in
Figure 1(ii). Negligible work is done (
i.e., the same amount as slowly moving any container), so w = 0. The containers are maintained at constant temperature, so dU = 0. Therefore, TdS = dU + w = 0 and the final separated state A + B, which has N
A A particles in volume V and N
B B particles also in a separate volume V, has the same entropy S
A+B as the initial entropy S
A∪Β of the A∪Β state.
Equation (9) applies equally whether each particle of type A (B, respectively) is indistinguishable from other A type particles or whether each is distinguishable, not only from B (A, respectively) particles but also from all other A (B, respectively) particles. For distinguishable particles, let us designate the A type particles to be the set of those with names 1, …, N/2 and those with names N/2+1, …, N will be the set of B type particles, where NA = NB = N/2 keeps the math simple. Of course, with N distinguishable particles, there are many more ways to designate the A and B types, but only one way will suffice for our example as all others with NA=NB are equivalent. As with the usual case where particles within each type are indistinguishable, for distinguishable particles we also need semi-permeable walls. Let us consider an AB (AB, respectively) wall that is impermeable to distinguishable particles of type A (B, respectively) and permeable (impermeable, respectively) to particles of type B (A, respectively). If one has all N Mi membranes from examples 1 and 2, then an AB wall can be constructed using Mi with i = 1, …, N/2 in series, but having all Mi membranes, while sufficient, is not necessary for having AB and AB walls.
Figure 1.
(i) The union of A type particles (red squares) and B type particles (blue diamonds) in a common volume V. Within each type, the particles are indistinguishable in traditional discussions; they are distinguishable in the novel discussion in this paper. (ii) Procedure to separate the A and B particles using red (blue) walls that are impermeable to A (B) particles and permeable to B (A) particles (respectively). (iii) The sum of separate gases of A and B particles, each contained in the same volume V in all three panels.
Figure 1.
(i) The union of A type particles (red squares) and B type particles (blue diamonds) in a common volume V. Within each type, the particles are indistinguishable in traditional discussions; they are distinguishable in the novel discussion in this paper. (ii) Procedure to separate the A and B particles using red (blue) walls that are impermeable to A (B) particles and permeable to B (A) particles (respectively). (iii) The sum of separate gases of A and B particles, each contained in the same volume V in all three panels.
Let us first insert the Gibbs entropy S
G in Equation (5) into the two sides of Equation (9).
Clearly, the Gibbs entropies in Equations (10a) and (10b) satisfy Equation (9). Next, let us insert the entropy S
S in Equation (6) into the two sides of Equation (9).
Clearly, S
S does not satisfy Equation (9), having a discrepancy of Nk ln 2. I attribute the root cause to Equation (6) being the proper formula only when all the particles are indistinguishable. Then there can be no Gibbs separation process so it is not surprising that Equation (9) is not valid. In case there is any distinguishability between subsets of the particles, the right hand side of Equation (9) should be used to calculate S
A∪Β of the mixture. For example, when there are M mutually distinguishable subsets, each consisting of N/M indistinguishable particles, Equation (9) gives S
A∪Β = Nk ln(MV/N). In the limit of complete indistinguishability, S
A∪Β = Nk ln(V/N) as required. In the limit of complete distinguishability, M = N and S
A∪Β = Nk ln V and S
G is recovered.
6. General Summary
In the first two examples above the Gibbs entropy of the system of distinguishable classical particles increases from state α to state β, it then remains the same in β and γ, and then it decreases to be the same in state δ as it was in state α. In typical laboratory practice, one never deals with states α and δ because it is too laborious to identify the different distinguishable particles. Therefore, when one begins with two containers of homogenized milk, each with particles distinguishable only in principle, one does not begin with state α, but with state γ. Pouring the two containers together to make state β does not change the entropy, nor does it change upon subsequent repartitioning that again takes one back to state γ. For the βγ process, Equation (6) works quite nicely. That is because Equation (6) is valid for indistinguishable particles, and for computing changes in the entropy the particles can essentially be treated as indistinguishable in the βγ process.
However, if one cares seriously about the distinguishability of particles, then it is necessary to consider states α and δ, and then Equation (5) is the preferred equation. While understanding the βγ process for a system of such distinguishable particles is more subtle in the context of Equation (5), involving fundamental concepts of entropy, the αβ process can not be understood at all using Equation (6). Although obtaining the α state is impractical in the laboratory, it should not be neglected when considering questions of principle such as the fundamental definition of entropy in Equation (1) versus Equation (2). Finally, Example 3 above clearly shows that Equation (5) works well for distinguishable particles and Equation (6) does not. These examples, as well as others that do not involve semi-permeable membranes [
25], have led me to reject the assertion [
1,
2] that statistical mechanics should reject Equation (1) and the conventional wisdom attributable to Gibbs. I also suggest that a common view of Gibbs paradox is well treated within the existing paradigm of Equations (1) and (5) when the subtleties of the entropy of distinguishable particles are fully considered and appreciated.