Autocatalytic Sets and the Origin of Life
Abstract
:1. The Origin of Life
1.1. An RNA world
1.2. Prebiotic metabolism
1.3. From RNA to proteins and DNA
1.4. A scenario for the origin of life
2. Autocatalytic Sets
- Reflexively autocatalytic (RA) if every reaction in is catalyzed by at least one molecule involved in any of the reactions in ;
- F-generated (F) if every reactant in can be constructed from a small “food set” F by successive applications of reactions from ;
- Reflexively autocatalytic and F-generated (RAF) if it is both RA and F.
- Formalized the notion of a catalytic reaction system (CRS) and autocatalytic (RAF) sets;
- Introduced a polynomial-time algorithm for determining if any CRS has within it an RAF set, and if so, finding such self-sustaining subsystems (including ones that are minimal);
- Showed that only a linear growth rate (with system size) in catalytic activity is sufficient for RAF sets to appear with high probability in random instances of a simple catalytic reaction system based on polymer cleavage and ligation reactions (the original model of [26]).
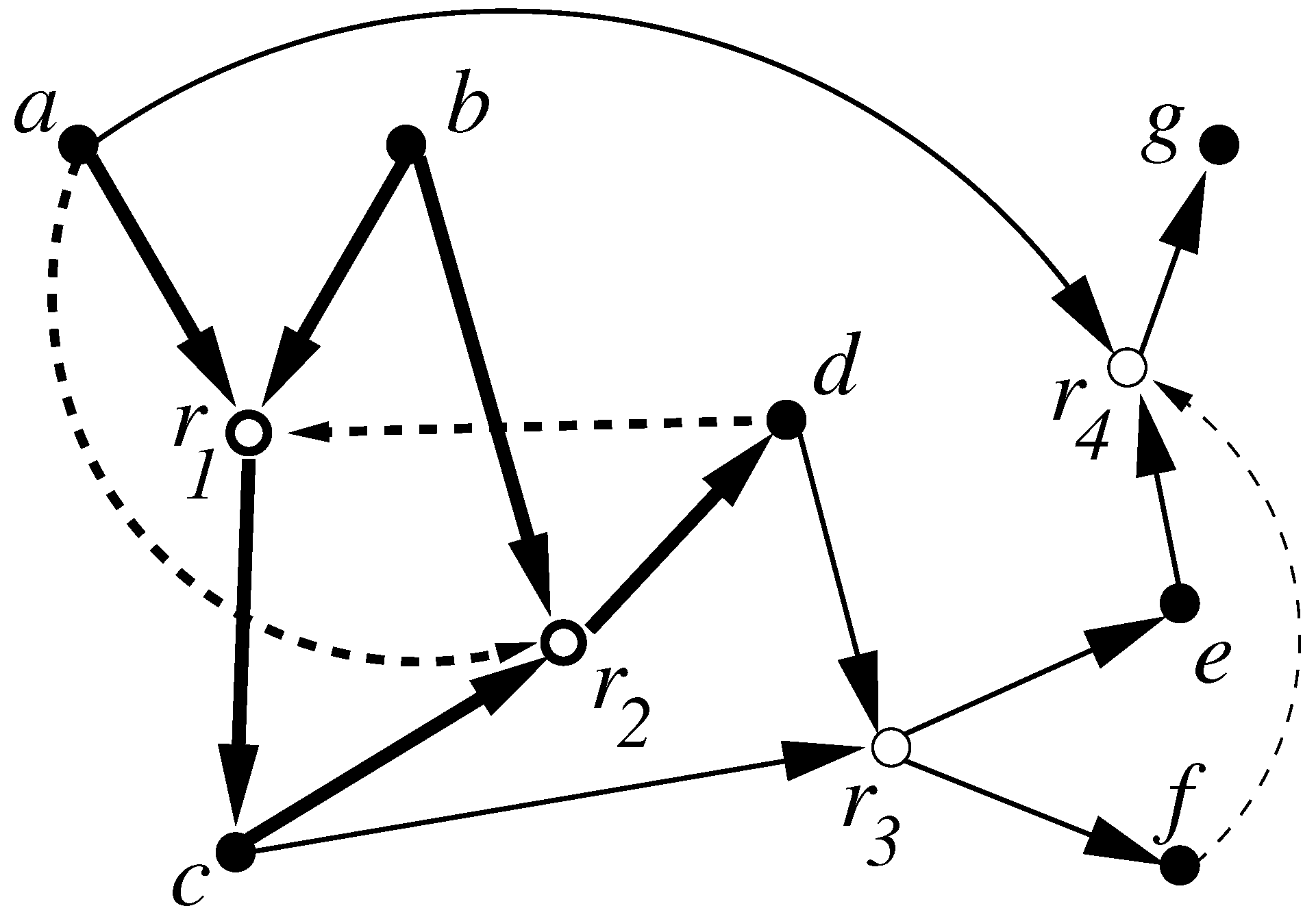
- Allowing some reactions to proceed without any catalysis;
- Ensuring that at least some reaction products in the RAF are not contained in the food set F [39];
- Ensuring that not all reactions are only catalyzed by molecules in F. In this case some of the catalysts must arise by either (i) being built up from F by a series of reactions, each of which was catalyzed by a molecule that has already been produced (starting from F)—this concept of a ‘constructively auto-catalytic and F-generated’ system was formalized and explored in [39]; or (ii) by being produced initially in trace quantities from non-catalyzed reactions (i.e. at much lower rates) which helps to establish an RAF for which the molecules’ production is possible via catalyzed reactions.
3. Autocatalytic Sets and the Origin of Life
4. Summary and Outlook
5. Acknowledgments
References
- Gilbert, W. The RNA world. Nature 1986, 319, 618. [Google Scholar] [CrossRef]
- Joyce, G.F. RNA evolution and the origins of life. Nature 1989, 338, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Joyce, G.F. The antiquity of RNA-based evolution. Nature 2002, 418, 214–221. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.M.; Szathmáry, E. The Origins of Life; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Fenchel, T. Origin and Early Evolution of Life; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Penny, D. An interpretive review of the origin of life research. Biol. Phil. 2005, 20, 633–671. [Google Scholar] [CrossRef]
- Anastasi, C.; Buchet, F.F.; Crowe, M.A.; Parkes, A.L.; Powner, M.W.; Smith, J.M.; Sutherland, J.D. RNA: Prebiotic product, or biotic invention? Chem. Biodivers. 2007, 4, 721–739. [Google Scholar] [CrossRef] [PubMed]
- Oparin, A.I. The Origins of Life on Earth; Oliver and Boyd: Edinburgh, Scotland, 1957. [Google Scholar]
- Miller, S.L. A production of amino acids under possible primitive Earth conditions. Science 1953, 117, 528–529. [Google Scholar] [CrossRef] [PubMed]
- Oró, J. Mechanism of synthesis of adenine from hydrogen cyanide under possible primitive Earth conditions. Nature 1961, 191, 1193–1194. [Google Scholar] [CrossRef] [PubMed]
- Morowitz, H.J.; Kostelnik, J.D.; Yang, J.; Cody, G.D. The origin of intermediary metabolism. Proc. Natl. Acad. Sci. USA 2000, 97, 7704–7708. [Google Scholar] [CrossRef] [PubMed]
- Smith, E.; Morowitz, H.J. Universality in intermediary metabolism. Proc. Natl. Acad. Sci. USA 2004, 101, 13168–13173. [Google Scholar] [CrossRef] [PubMed]
- Wächterhäuser, G. Evolution of the first metabolic cycles. Proc. Natl. Acad. Sci. USA 1990, 87, 200–204. [Google Scholar] [CrossRef]
- Wächterhäuser, G. On the chemistry and evolution of the pioneer organism. Chem. Biodivers. 2007, 4, 584–602. [Google Scholar] [CrossRef] [PubMed]
- Ross, D.S. The viability of a nonenzymatic reductive citric acid cycle—Kinetics and thermochemistry. Origins Life Evol. Biosphere 2007, 37, 61–65. [Google Scholar] [CrossRef] [PubMed]
- Orgel, L.E. The implausibility of metabolic cycles on the prebiotic earth. PLoS Biology 2008, 6, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Kalapos, M.P. The energetics of the reductive citric acid cycle in the pyrite-pulled surface metabolism in the early stage of evolution. J. Theor. Biol. 2007, 248, 251–258. [Google Scholar] [CrossRef] [PubMed]
- Powner, M.W.; Gerland, B.; Sutherland, J.D. Synthesis of activated pyrimidine ribonucleotides in prebiotically plausible conditions. Nature 2009, 459, 239–242. [Google Scholar] [CrossRef] [PubMed]
- Lane, N. Life Ascending: The Ten Great Inventions of Evolution; W. W. Norton & Company: New York, NY, USA, 2009. [Google Scholar]
- Eigen, M.; Schuster, P. The hypercycle: A principle of natural self-organization. Part A: Emergence of the hyperccyle. Naturwissenschaften 1977, 64, 541–565. [Google Scholar] [CrossRef] [PubMed]
- Eigen, M.; Schuster, P. The Hypercycle; Springer-Verlag: Berlin, Germany, 1979. [Google Scholar]
- Smith, J.M. Hypercycles and the origin of life. Nature 1979, 280, 445–446. [Google Scholar] [CrossRef] [PubMed]
- Poole, A.M.; Jeffares, D.C.; Penny, D. Prokaryotes, the new kids on the block. BioEssays 1999, 21, 880–889. [Google Scholar] [CrossRef]
- Dyson, F.J. A model for the origin of life. J. Mol. Evol. 1982, 18, 344–350. [Google Scholar] [CrossRef] [PubMed]
- Dyson, F.J. Origins of Life; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Kauffman, S.A. Autocatalytic sets of proteins. J. Theor. Biol. 1986, 119, 1–24. [Google Scholar] [CrossRef]
- Kauffman, S.A. The Origins of Order; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Sharov, A.A. Genetic gradualism and the extraterrestrial origin of life. J. Cosmol. 2010, 5, 833–842. [Google Scholar]
- Lifson, S. On the crucial stages in the origin of animate matter. J. Mol. Evol. 1997, 44, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S.A. Question 1: Origin of life and the living state. Origins Life Evol. Biosphere 2007, 37, 315–322. [Google Scholar] [CrossRef] [PubMed]
- Sievers, D.; von Kiedrowski, G. Self-replication of complementary nucleotide-based oligomers. Nature 1994, 369, 221–224. [Google Scholar] [CrossRef] [PubMed]
- Ashkenasy, G.; Jegasia, R.; Yadav, M.; Ghadiri, M.R. Design of a directed molecular network. PNAS 2004, 101, 10872–10877. [Google Scholar] [CrossRef] [PubMed]
- Hayden, E.J.; von Kieddrowski, G.; Lehman, N. Systems chemistry on ribozyme self-construction: Evidence for anabolic autocatalysis in a recombination network. Angew. Chem. Int. Ed. 2008, 120, 8552–8556. [Google Scholar] [CrossRef]
- Lee, D.H.; Severin, K.; Ghadiri, M.R. Autocatalytic networks: The transition from molecular self-replication to molecular ecosystems. Curr. Opin. Chem. Biol. 1997, 1, 491–496. [Google Scholar] [CrossRef]
- Martin, W.; Russel, M.J. On the origins of cells: A hypothesis for the evolutionary transition from abiotic geochemistry to chemoautotrophic prokaryotes, and from prokaryotes to nucleated cells. Phil. Trans. Roy. Soc. B-Biol. Sci. 2003, 358, 59–85. [Google Scholar] [CrossRef] [PubMed]
- Martin, W.; Russel, M.J. On the origin of biochemistry at an alkaline hydrothermal vent. Phil. Trans. Roy. Soc. B-Biol. Sci. 2007, 362, 1887–1925. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. Detecting autocatalytic, self-sustaining sets in chemical reaction systems. J. Theor. Biol. 2004, 227, 451–461. [Google Scholar] [CrossRef] [PubMed]
- Steel, M. The emergence of a self-catalysing structure in abstract origin-of-life models. Appl. Math. Lett. 2000, 3, 91–95. [Google Scholar] [CrossRef]
- Mossel, E.; Steel, M. Random biochemical networks: The probability of self-sustaining autocatalysis. J. Theor. Biol. 2005, 233, 327–336. [Google Scholar] [CrossRef] [PubMed]
- Sharov, A.A. Self-reproducing systems: Structure, niche relations and evolution. BioSystems 1991, 25, 237–249. [Google Scholar] [CrossRef]
- Sharov, A.A. Coenzyme autocatalytic network on the surface of oil microspheres as a model for the origin of life. Int. J. Mol. Sci. 2009, 10, 1838–1852. [Google Scholar] [CrossRef] [PubMed]
- Letelier, J.C.; Soto-Andrade, J.; Abarzúa, F.G.; Cornish-Bowden, A.; Cárdenas, M.L. Organizational invariance and metabolic closure: Analysis in terms of (M;R) systems. J. Theor. Biol. 2006, 238, 949–961. [Google Scholar] [CrossRef] [PubMed]
- Cornish-Bowden, A.; Cárdenas, M.L.; Letelier, J.C.; Soto-Andrade, J. Beyond reductionism: Metabolic circularity as a guiding vision for a real biology of systems. Proteomics 2007, 7, 839–845. [Google Scholar] [CrossRef] [PubMed]
- Gánti, T. Biogenesis itself. J. Theor. Biol. 1997, 187, 583–593. [Google Scholar] [CrossRef] [PubMed]
- Segré, D.; Lancet, D. A statistical chemistry approach to the origin of life. Chemtracts—Biochem. Mol. Biol. 1999, 12, 382–397. [Google Scholar]
- Bartsev, S.I.; Mezhevikin, V.V. On initial steps of chemical prebiotic evolution: Triggering autocatalytic reaction of oligomerization. Adv. Space Res. 2008, 42, 2008–2013. [Google Scholar] [CrossRef]
- Crossfire, 2009. Beilstein and Gmelin Databases. Available online: http://www.info.crossfiredatabases.com (accessed on 20 March 2010).
- Bishop, K.J.M.; Klajn, R.; Grzybowski, B.A. The core and most useful molecules in organic chemistry. Angewandte Chemie Int. Ed. 2006, 118, 5474–5480. [Google Scholar] [CrossRef]
- Grzybowski, B.A.; Bishop, K.J.M.; Kowalczyk, B.; Wilmer, C.E. The ’wired’ universe of organic chemistry. Nat. Chem. 2009, 1, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Stankiewicz, J.; Eckhardt, L.H. Chembiogenesis 2005 and systems chemistry workshop. Angewandte Chemie Int. Ed. 2006, 45, 342–344. [Google Scholar] [CrossRef]
- Ludlow, R.F.; Otto, S. Systems chemistry. Chem. Soc. Rev. 2008, 37, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Kun, A.; Papp, B.; Szathmáry, E. Computational identification of obligatorily autocatalytic replicators embedded in metabolic network. Genome Biol. 2008, 9, R51. [Google Scholar] [CrossRef] [PubMed]
- Jeffery, C.J. Moonlighting proteins. Trends Biochem. Sci. 1999, 24, 8–11. [Google Scholar] [CrossRef]
- Jeffery, C.J. Moonlighting proteins: Old proteins learning new tricks. Trends Genet. 2003, 19, 415–417. [Google Scholar] [CrossRef]
- Tokuriki, N.; Tawfik, D.S. Protein dynamism and evolvability. Science 2009, 324, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Segré, D.; Ben-Eli, D.; Deamer, D.W.; Lancet, D. The lipid world. Origins Life Evol. Biosphere. 2001, 31, 119–145. [Google Scholar] [CrossRef]
- Hordijk, W.; Fontanari, J.F. Catalytic reaction sets, decay, and the preservation of information. In KIMAS’03 (IEEE International Conference on Integration of Knowledge Intensive Multi-Agent Systems), Cambridge, MA, USA, 2–4 October 2003; pp. 133–138.
- Benkö, G.; Centler, F.; Dittrich, P.; Flamm, C.; Stadler, B.; Stadler, P.F. A topological approach to chemical organizations. Artif. Life 2009, 15, 71–88. [Google Scholar] [CrossRef] [PubMed]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Hordijk, W.; Hein, J.; Steel, M. Autocatalytic Sets and the Origin of Life. Entropy 2010, 12, 1733-1742. https://doi.org/10.3390/e12071733
Hordijk W, Hein J, Steel M. Autocatalytic Sets and the Origin of Life. Entropy. 2010; 12(7):1733-1742. https://doi.org/10.3390/e12071733
Chicago/Turabian StyleHordijk, Wim, Jotun Hein, and Mike Steel. 2010. "Autocatalytic Sets and the Origin of Life" Entropy 12, no. 7: 1733-1742. https://doi.org/10.3390/e12071733
APA StyleHordijk, W., Hein, J., & Steel, M. (2010). Autocatalytic Sets and the Origin of Life. Entropy, 12(7), 1733-1742. https://doi.org/10.3390/e12071733



