Abstract
The origin of life is one of the most fundamental, but also one of the most difficult problems in science. Despite differences between various proposed scenarios, one common element seems to be the emergence of an autocatalytic set or cycle at some stage. However, there is still disagreement as to how likely it is that such self-sustaining sets could arise “spontaneously”. This disagreement is largely caused by the lack of formal models. Here, we briefly review some of the criticism against and evidence in favor of autocatalytic sets, and then make a case for their plausibility based on a formal framework that was introduced and studied in our previous work.
1. The Origin of Life
The origin of life (OoL) remains an elusive problem, although much progress has been made in recent years. Having gone from a problem considered ‘beyond science’ to ‘solvable in principle but maybe not in practice’, many researchers now believe it will be solved in the next few decades. In fact, there are currently several OoL scenarios, but all still have some difficulties and lacunae. Although often quite different in their details, one common element which most of these scenarios have is the appearance of an autocatalytic set or cycle at some stage.
1.1. An RNA world
All life as we know it depends on a delicate interplay between DNA and proteins. However, this DNA-protein machinery seems too complex to have arisen all at once. So there appears to be a “chicken-and-egg” problem: which came first, the chicken (protein, phenotype), or the egg (DNA, genotype)?
The most widely accepted resolution of this problem is that of an RNA world [,,] preceding DNA and proteins, i.e., a collection of (self-)replicating RNA molecules, using template complementarity plus the ability to perform and catalyze their own (or each others) synthesis as a way of achieving reproduction and self-sustainability. The possibility of an RNA world has some experimental support, and is now generally considered to have been an important step in the origin of life [,]. However, an RNA world “spontaneously” generating proteins and DNA is not straightforward, and is certainly not (yet) proven beyond any doubt. Moreover, and perhaps more importantly, the initial appearance of an RNA world itself is still mostly an open question [,,,].
1.2. Prebiotic metabolism
The idea of a “primordial soup” [] spontaneously generating the basic building blocks for life sounded attractive after some initial experiments along these lines [,], but has been much debated since then and criticized as not being capable of creating these building blocks in sufficiently large concentrations. So, there must have been something more sustainable to get anything like an RNA world started.
A basic element underlying all metabolism (and therefore believed to be of very ancient origins) is the citric acid (or Krebs) cycle. This is a chemical reaction network involving a cyclic sequence of 11 substrates and reactions. It turns out that this cycle can (and does) also operate in reverse, known as the reductive citric acid cycle. In fact, in chemoautotrophs (such as eubacteria and archea), this (reverse) cycle “is the central starting point on the route to all biochemicals” [].
Furthermore, even though most of the catalysis in this metabolic cycle is now performed by enzymes (proteins), it is claimed that many of them could initially have been performed by simple molecules (e.g., co-factors) that are likely to have been present on the early earth. And so, it is argued, the reductive citric acid cycle (or similar metabolic cycles) could very well have provided an intermediate step from prebiotic chemistry to organic molecules such as RNA [,,,]. This claim is still highly debated [,], but there is experimental evidence that suggests that simple (auto)catalytic reaction networks could indeed have produced the necessary building blocks for an RNA world [,].
1.3. From RNA to proteins and DNA
Given the existence of an RNA world, some of these RNA molecules likely started encoding for and synthesizing small proteins. These newly created proteins, being much more efficient, would then have started to take over some of the catalysis required for RNA replication. This opened up the way for creating longer strands of RNA, which in turn enabled encoding for more complex proteins. Furthermore, with proteins, the synthesis and replication of DNA molecules became possible. DNA, being much more stable than RNA, is able to encode for an even larger number of proteins, eventually taking over the role of information carriers from RNA [,,].
Arguably, some sort of self-sustaining or self- reinforcing cycle, such as a hypercycle [,,] or Darwin-Eigen cycle [,] seems necessary for this RNA to DNA transition to succeed. Such cycles can be seen as special instances of autocatalytic sets in general. In fact, autocatalytic sets arising in a mixture of interacting chemicals which can be both substrates and/or catalysts, were originally proposed as an alternative solution to the “chicken-and-egg” problem [,,,,].
A collectively autocatalytic set is a set of molecules and catalyzed reactions where each molecule is created by at least one reaction from this set, and each reaction is catalyzed by at least one molecule from the set. It has been claimed that in sufficiently complex chemical reaction systems, autocatalytic sets will arise almost inevitably [,]. This was later disputed [] by pointing out that this requires an (unrealistic) exponential growth in catalytic activity with increasing system size. Despite this criticism, the original claim (including its disputed argument) still seems to persist []. However, there is evidence that simple autocatalytic sets can actually be constructed experimentally [,,]. This evidence, together with our own results reviewed below, make it at least plausible that autocatalytic sets indeed played a role in the emergence of proteins and DNA from an RNA world [].
1.4. A scenario for the origin of life
Summarizing the above story, a plausible scenario for the origin of life that is gaining more support recently is as follows [,,,]:
None of these steps have (yet) been proven beyond any doubt, but as argued above, they are certainly possible and there is actual evidence (theoretical and/or experimental) to support them.
(In)organic chemistry ⇒ Prebiotic metabolism ⇒ RNA world ⇒ Proteins ⇒ DNA
2. Autocatalytic Sets
Autocatalytic cycles and sets seem to play an important role in more than one of the steps in the above OoL scenario, and are a necessary, although not sufficient, condition for life. Autocatalytic sets are defined more formally in [] as follows. Given a network of catalyzed chemical reactions, a (sub)set of such reactions is called:
- Reflexively autocatalytic (RA) if every reaction in is catalyzed by at least one molecule involved in any of the reactions in ;
- F-generated (F) if every reactant in can be constructed from a small “food set” F by successive applications of reactions from ;
- Reflexively autocatalytic and F-generated (RAF) if it is both RA and F.
This formal RAF framework was introduced and analyzed (both theoretically and computationally) in our previous work [,,]. In particular, we:
- Formalized the notion of a catalytic reaction system (CRS) and autocatalytic (RAF) sets;
- Introduced a polynomial-time algorithm for determining if any CRS has within it an RAF set, and if so, finding such self-sustaining subsystems (including ones that are minimal);
- Showed that only a linear growth rate (with system size) in catalytic activity is sufficient for RAF sets to appear with high probability in random instances of a simple catalytic reaction system based on polymer cleavage and ligation reactions (the original model of []).
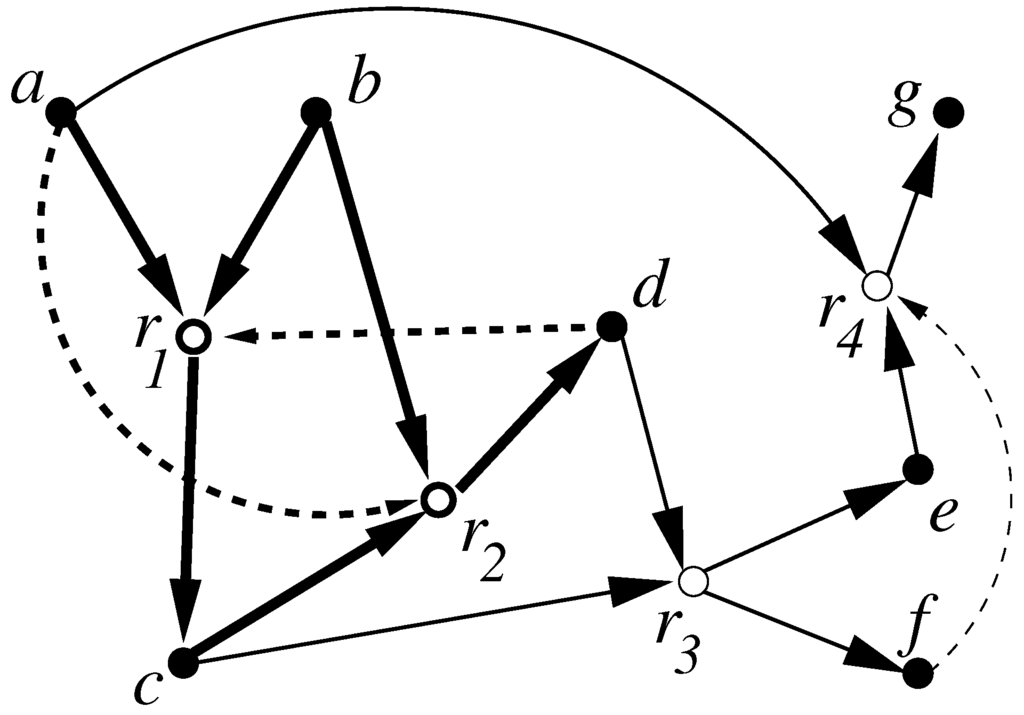
Figure 1.
A simple example of a catalytic reaction system (CRS) with seven molecule types (solid nodes) and four reactions (open nodes). The food set is . Solid arrows indicate reactants going into and products coming out of a reaction, dashed arrows indicate catalysis. The subset (shown with bold arrows) is RAF: (1) The molecules involved in are , reaction is catalyzed by d, and by a, so is reflexively autocatalytic (RA). (2) The reactants in are either already in the food set (a and b) or can be created from it through (c), so is also F-generated (F). The RAF algorithm applied to this CRS would return the set .
Next to the above basic three requirements in an RAF we can easily build in additional assumptions to incorporate greater biochemical realism and to exclude trivial situations. Some such assumptions are:
- Allowing some reactions to proceed without any catalysis;
- Ensuring that at least some reaction products in the RAF are not contained in the food set F [];
- Ensuring that not all reactions are only catalyzed by molecules in F. In this case some of the catalysts must arise by either (i) being built up from F by a series of reactions, each of which was catalyzed by a molecule that has already been produced (starting from F)—this concept of a ‘constructively auto-catalytic and F-generated’ system was formalized and explored in []; or (ii) by being produced initially in trace quantities from non-catalyzed reactions (i.e. at much lower rates) which helps to establish an RAF for which the molecules’ production is possible via catalyzed reactions.
It is also possible to express the RAF model within other mathematical frameworks—in particular, it can be rephrased within the context of Petri nets, a model that Sharov has used to study self-reproducing systems in biology in an early paper [] (see also []). The concept of an RAF also shares some similarities with Rosen’s category-theoretic approach to metabolic closure [,]. Other mathematically-based models of autocatalysis have been proposed in, e.g., [,,].
3. Autocatalytic Sets and the Origin of Life
The RAF framework is important and relevant to the origin of life in several ways. First, it places the notion of autocatalytic sets in a formal framework which can be (and has been) used and studied both analytically and computationally. This is a necessary first step when attempting to say anything about the plausibility of their appearance. As mentioned, other formal models have been introduced and studied previously, but many of these either already assumed the existence of one or more autocatalytic sets or cycles (such as the hypercycle [,,] or the Chemoton model []), or their claims were based on flawed arguments (such as Kauffman’s original claim [], as pointed out in []). Some claims (especially those arguing against the plausibility of autocatalytic sets) seem to lack any mathematical support at all []. So, having a mathematically sound model and computationally efficient method available to study the probability of the emergence of autocatalytic sets is an important step forward in itself.
Second, our RAF framework includes an efficient algorithm for finding autocatalytic sets in general reaction networks, which allows us to study their appearance both in model systems and in real (bio)chemical networks (such an algorithm was not provided with any of the other mentioned mathematical models of autocatalytic sets). In [], we introduced a polynomial time algorithm for finding RAF sets, and applied it to Kauffman’s model of binary polymers with ligation and cleavage reactions [,]. The average running time of the algorithm was shown to be sub-quadratic (in the size of the reaction network). Therefore, it provides an efficient tool to study real (bio)chemical networks as well.
For example, recently the Beilstein database [] of all known organic compounds and reactions was studied [,], showing that there is a core set (a strongly connected component) that contains only 4% of the compounds, but which together give rise to 78% of all known organic molecules in just a few reactions (three steps on average). These studies, however, did not take catalysis into account. It would be useful to apply the RAF algorithm to this same database of organic molecules and reactions, including the catalysis, and perform a similar analysis for the occurrence of RAF sets. In [] the size of the reaction set studied was about 7 million reactions. The largest networks analyzed with the RAF algorithm in [] were about 5 million catalyzed reactions, i.e., of the same order of magnitude as the Beilstein database. So, it is clearly possible to analyze this largest known real chemical reaction set with the RAF algorithm (which we hope to undertake in future work). Such an analysis could, for example, result in the identification of other possible candidates for prebiotic metabolism (like the reverse citric acid cycle), or provide useful directions for setting up chemical experiments to create autocatalytic sets in vitro, which is currently still one of the major challenges in systems chemistry [,].
As another example, complete metabolic networks of several organisms (mostly bacteria) were analyzed recently to find autocatalytically replicating molecules []. However, although highly original in its setup, the algorithmic method used in that study is not as mathematically complete as the RAF framework, and mainly finds individual molecules (as opposed to complete RAF sets). Therefore, this provides another setting where the RAF algorithm can be applied to analyze the occurrence of autocatalytic sets, which we indeed expect to do in the future. This could help in answering many questions about the appearance, size distribution, and structure of autocatalytic sets in real (evolved) biochemical networks.
Finally, and perhaps most importantly, the RAF framework has provided strong support for the claim that autocatalytic sets indeed have a high probability of occurrence, even with very moderate levels of catalysis. Our computational results in [] indicate that only a linear growth in catalytic activity (with system size) is necessary for RAF sets to appear with high likelihood in Kauffman’s binary polymer model. This was subsequently verified analytically []. The level of catalysis necessary for RAF sets to occur in our simulations is between 1 and 2 reactions per molecule (on average), a number which is (bio)chemically quite realistic, especially for proteins [,,]. This is in stark contrast to the exponential growth required in Kauffman’s original argument, and therefore re-instates his claim that in “sufficiently complex chemical reaction systems” autocatalytic sets will arise almost inevitably. Moreover, we have provided a formal way of quantifying “sufficiently complex”, in terms of the level of catalysis required. These results, combined with existing experimental evidence, make autocatalytic sets a serious and plausible candidate for consideration in origin of life scenarios.
It is important, though, to stress that the existence of an RAF, while necessary for the emergence of self-sustaining life, is far from sufficient for it for at least three reasons. Firstly, the approach ignores the concentration and stoichiometry of reactants, the possibility of degrading side reactions or the presence of molecules that inhibit other reactions, or complex catalysis in which a catalyst may remain bound at the end of the reaction to some of the products. However, as with the Petri net formalism [], some of these extensions can be built into the model—for example inhibition in an RAF has already been modeled by a slightly more general definition of RAF in []. Secondly, the approach does not address (let alone solve) the ‘containment problem’ that requires reactions to be physically contained by some boundary or membrane so the reactants do not diffuse and reduce their concentrations. This is, of course, a problem faced by nearly all attempts to explain the origin of early life, and is not specific to the autocatalytic set, or metabolism first, point of view. Moreover, several proposed theories already exist to try to solve this ’containment problem’, for example by considering reactions that take place on the surface of some (inorganic, possibly catalytic) substance [,,], or reactions contained inside tiny, naturally occurring compartmental structures in e.g., ocean-floor thermal vents [,], or even through the formation of self-organizing lipid membranes []. And thirdly, the RAF approach does not directly address the problem of heredity in prebiotic systems, and the role of natural selection. But here too, this issue arises in all approaches to early-life models, and is obviously directly related to the containment problem.
While it will be interesting and worthwhile to extend the RAF approach to handle some of these complexities, we see the basic necessity (rather than sufficiency) of RAFs in early life research as the justification for searching for such subsets in biochemical systems: The RAF concept is a simple, testable and searchable combinatorial criterion, and while few RAFs would furnish a viable basis for early life, restricting attention to them severely limits the possible candidates one needs to examine in trying to identify the origins of primitive biochemistry.
4. Summary and Outlook
Autocatalytic sets (in various forms) appear to have played an important role in the origin of life. However, the likelihood of their “spontaneous” occurrence has been debated for a long time and has not been resolved so far, partly due to a lack of mathematical models that can be analyzed formally. We hope to have made an important contribution towards filling this gap by the introduction and formal analysis of a mathematical framework of autocatalytic (RAF) sets. This framework includes an efficient algorithm for finding RAF sets in general catalytic reaction systems, and has provided strong support for a high likelihood of their occurrence even with very moderate levels of catalysis. The RAF framework currently still requires more chemical realism, but it nonetheless provides a promising first step towards a more formal study of autocatalytic sets in general. The next steps would be (1) to include dynamics into the models in the form of reaction kinetics and the evolution of reaction sets (for example by using a genetic algorithm to evolve reaction sets []), and (2) to use the RAF framework to analyze real (bio)chemical networks as discussed above (e.g., the Beilstein database and bacterial metabolic networks). For a different but somewhat related (topological) approach to formally analyzing the appearance of structure and organization in chemical reaction systems, see e.g., []. We expect that such formal models and analyses will eventually shed more light on the possibility and plausibility of the various origin of life scenarios, and that they will also be helpful in actually constructing autocatalytic sets experimentally.
5. Acknowledgments
We thank the two anonymous referees for their helpful comments. The third author thanks the Royal Society of New Zealand for funding under its James Cook Fellowship scheme.
References
- Gilbert, W. The RNA world. Nature 1986, 319, 618. [Google Scholar] [CrossRef]
- Joyce, G.F. RNA evolution and the origins of life. Nature 1989, 338, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Joyce, G.F. The antiquity of RNA-based evolution. Nature 2002, 418, 214–221. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.M.; Szathmáry, E. The Origins of Life; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Fenchel, T. Origin and Early Evolution of Life; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Penny, D. An interpretive review of the origin of life research. Biol. Phil. 2005, 20, 633–671. [Google Scholar] [CrossRef]
- Anastasi, C.; Buchet, F.F.; Crowe, M.A.; Parkes, A.L.; Powner, M.W.; Smith, J.M.; Sutherland, J.D. RNA: Prebiotic product, or biotic invention? Chem. Biodivers. 2007, 4, 721–739. [Google Scholar] [CrossRef] [PubMed]
- Oparin, A.I. The Origins of Life on Earth; Oliver and Boyd: Edinburgh, Scotland, 1957. [Google Scholar]
- Miller, S.L. A production of amino acids under possible primitive Earth conditions. Science 1953, 117, 528–529. [Google Scholar] [CrossRef] [PubMed]
- Oró, J. Mechanism of synthesis of adenine from hydrogen cyanide under possible primitive Earth conditions. Nature 1961, 191, 1193–1194. [Google Scholar] [CrossRef] [PubMed]
- Morowitz, H.J.; Kostelnik, J.D.; Yang, J.; Cody, G.D. The origin of intermediary metabolism. Proc. Natl. Acad. Sci. USA 2000, 97, 7704–7708. [Google Scholar] [CrossRef] [PubMed]
- Smith, E.; Morowitz, H.J. Universality in intermediary metabolism. Proc. Natl. Acad. Sci. USA 2004, 101, 13168–13173. [Google Scholar] [CrossRef] [PubMed]
- Wächterhäuser, G. Evolution of the first metabolic cycles. Proc. Natl. Acad. Sci. USA 1990, 87, 200–204. [Google Scholar] [CrossRef]
- Wächterhäuser, G. On the chemistry and evolution of the pioneer organism. Chem. Biodivers. 2007, 4, 584–602. [Google Scholar] [CrossRef] [PubMed]
- Ross, D.S. The viability of a nonenzymatic reductive citric acid cycle—Kinetics and thermochemistry. Origins Life Evol. Biosphere 2007, 37, 61–65. [Google Scholar] [CrossRef] [PubMed]
- Orgel, L.E. The implausibility of metabolic cycles on the prebiotic earth. PLoS Biology 2008, 6, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Kalapos, M.P. The energetics of the reductive citric acid cycle in the pyrite-pulled surface metabolism in the early stage of evolution. J. Theor. Biol. 2007, 248, 251–258. [Google Scholar] [CrossRef] [PubMed]
- Powner, M.W.; Gerland, B.; Sutherland, J.D. Synthesis of activated pyrimidine ribonucleotides in prebiotically plausible conditions. Nature 2009, 459, 239–242. [Google Scholar] [CrossRef] [PubMed]
- Lane, N. Life Ascending: The Ten Great Inventions of Evolution; W. W. Norton & Company: New York, NY, USA, 2009. [Google Scholar]
- Eigen, M.; Schuster, P. The hypercycle: A principle of natural self-organization. Part A: Emergence of the hyperccyle. Naturwissenschaften 1977, 64, 541–565. [Google Scholar] [CrossRef] [PubMed]
- Eigen, M.; Schuster, P. The Hypercycle; Springer-Verlag: Berlin, Germany, 1979. [Google Scholar]
- Smith, J.M. Hypercycles and the origin of life. Nature 1979, 280, 445–446. [Google Scholar] [CrossRef] [PubMed]
- Poole, A.M.; Jeffares, D.C.; Penny, D. Prokaryotes, the new kids on the block. BioEssays 1999, 21, 880–889. [Google Scholar] [CrossRef]
- Dyson, F.J. A model for the origin of life. J. Mol. Evol. 1982, 18, 344–350. [Google Scholar] [CrossRef] [PubMed]
- Dyson, F.J. Origins of Life; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Kauffman, S.A. Autocatalytic sets of proteins. J. Theor. Biol. 1986, 119, 1–24. [Google Scholar] [CrossRef]
- Kauffman, S.A. The Origins of Order; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Sharov, A.A. Genetic gradualism and the extraterrestrial origin of life. J. Cosmol. 2010, 5, 833–842. [Google Scholar]
- Lifson, S. On the crucial stages in the origin of animate matter. J. Mol. Evol. 1997, 44, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S.A. Question 1: Origin of life and the living state. Origins Life Evol. Biosphere 2007, 37, 315–322. [Google Scholar] [CrossRef] [PubMed]
- Sievers, D.; von Kiedrowski, G. Self-replication of complementary nucleotide-based oligomers. Nature 1994, 369, 221–224. [Google Scholar] [CrossRef] [PubMed]
- Ashkenasy, G.; Jegasia, R.; Yadav, M.; Ghadiri, M.R. Design of a directed molecular network. PNAS 2004, 101, 10872–10877. [Google Scholar] [CrossRef] [PubMed]
- Hayden, E.J.; von Kieddrowski, G.; Lehman, N. Systems chemistry on ribozyme self-construction: Evidence for anabolic autocatalysis in a recombination network. Angew. Chem. Int. Ed. 2008, 120, 8552–8556. [Google Scholar] [CrossRef]
- Lee, D.H.; Severin, K.; Ghadiri, M.R. Autocatalytic networks: The transition from molecular self-replication to molecular ecosystems. Curr. Opin. Chem. Biol. 1997, 1, 491–496. [Google Scholar] [CrossRef]
- Martin, W.; Russel, M.J. On the origins of cells: A hypothesis for the evolutionary transition from abiotic geochemistry to chemoautotrophic prokaryotes, and from prokaryotes to nucleated cells. Phil. Trans. Roy. Soc. B-Biol. Sci. 2003, 358, 59–85. [Google Scholar] [CrossRef] [PubMed]
- Martin, W.; Russel, M.J. On the origin of biochemistry at an alkaline hydrothermal vent. Phil. Trans. Roy. Soc. B-Biol. Sci. 2007, 362, 1887–1925. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. Detecting autocatalytic, self-sustaining sets in chemical reaction systems. J. Theor. Biol. 2004, 227, 451–461. [Google Scholar] [CrossRef] [PubMed]
- Steel, M. The emergence of a self-catalysing structure in abstract origin-of-life models. Appl. Math. Lett. 2000, 3, 91–95. [Google Scholar] [CrossRef]
- Mossel, E.; Steel, M. Random biochemical networks: The probability of self-sustaining autocatalysis. J. Theor. Biol. 2005, 233, 327–336. [Google Scholar] [CrossRef] [PubMed]
- Sharov, A.A. Self-reproducing systems: Structure, niche relations and evolution. BioSystems 1991, 25, 237–249. [Google Scholar] [CrossRef]
- Sharov, A.A. Coenzyme autocatalytic network on the surface of oil microspheres as a model for the origin of life. Int. J. Mol. Sci. 2009, 10, 1838–1852. [Google Scholar] [CrossRef] [PubMed]
- Letelier, J.C.; Soto-Andrade, J.; Abarzúa, F.G.; Cornish-Bowden, A.; Cárdenas, M.L. Organizational invariance and metabolic closure: Analysis in terms of (M;R) systems. J. Theor. Biol. 2006, 238, 949–961. [Google Scholar] [CrossRef] [PubMed]
- Cornish-Bowden, A.; Cárdenas, M.L.; Letelier, J.C.; Soto-Andrade, J. Beyond reductionism: Metabolic circularity as a guiding vision for a real biology of systems. Proteomics 2007, 7, 839–845. [Google Scholar] [CrossRef] [PubMed]
- Gánti, T. Biogenesis itself. J. Theor. Biol. 1997, 187, 583–593. [Google Scholar] [CrossRef] [PubMed]
- Segré, D.; Lancet, D. A statistical chemistry approach to the origin of life. Chemtracts—Biochem. Mol. Biol. 1999, 12, 382–397. [Google Scholar]
- Bartsev, S.I.; Mezhevikin, V.V. On initial steps of chemical prebiotic evolution: Triggering autocatalytic reaction of oligomerization. Adv. Space Res. 2008, 42, 2008–2013. [Google Scholar] [CrossRef]
- Crossfire, 2009. Beilstein and Gmelin Databases. Available online: http://www.info.crossfiredatabases.com (accessed on 20 March 2010).
- Bishop, K.J.M.; Klajn, R.; Grzybowski, B.A. The core and most useful molecules in organic chemistry. Angewandte Chemie Int. Ed. 2006, 118, 5474–5480. [Google Scholar] [CrossRef]
- Grzybowski, B.A.; Bishop, K.J.M.; Kowalczyk, B.; Wilmer, C.E. The ’wired’ universe of organic chemistry. Nat. Chem. 2009, 1, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Stankiewicz, J.; Eckhardt, L.H. Chembiogenesis 2005 and systems chemistry workshop. Angewandte Chemie Int. Ed. 2006, 45, 342–344. [Google Scholar] [CrossRef]
- Ludlow, R.F.; Otto, S. Systems chemistry. Chem. Soc. Rev. 2008, 37, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Kun, A.; Papp, B.; Szathmáry, E. Computational identification of obligatorily autocatalytic replicators embedded in metabolic network. Genome Biol. 2008, 9, R51. [Google Scholar] [CrossRef] [PubMed]
- Jeffery, C.J. Moonlighting proteins. Trends Biochem. Sci. 1999, 24, 8–11. [Google Scholar] [CrossRef]
- Jeffery, C.J. Moonlighting proteins: Old proteins learning new tricks. Trends Genet. 2003, 19, 415–417. [Google Scholar] [CrossRef]
- Tokuriki, N.; Tawfik, D.S. Protein dynamism and evolvability. Science 2009, 324, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Segré, D.; Ben-Eli, D.; Deamer, D.W.; Lancet, D. The lipid world. Origins Life Evol. Biosphere. 2001, 31, 119–145. [Google Scholar] [CrossRef]
- Hordijk, W.; Fontanari, J.F. Catalytic reaction sets, decay, and the preservation of information. In KIMAS’03 (IEEE International Conference on Integration of Knowledge Intensive Multi-Agent Systems), Cambridge, MA, USA, 2–4 October 2003; pp. 133–138.
- Benkö, G.; Centler, F.; Dittrich, P.; Flamm, C.; Stadler, B.; Stadler, P.F. A topological approach to chemical organizations. Artif. Life 2009, 15, 71–88. [Google Scholar] [CrossRef] [PubMed]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.