Measurement Back-Action in Quantum Point-Contact Charge Sensing
Abstract
:1. Introduction
2. Charge Detection with a Quantum Point Contact

3. Photonic Back-Action in an InAs Double Dot
3.1. Back-action in quantum-dot systems
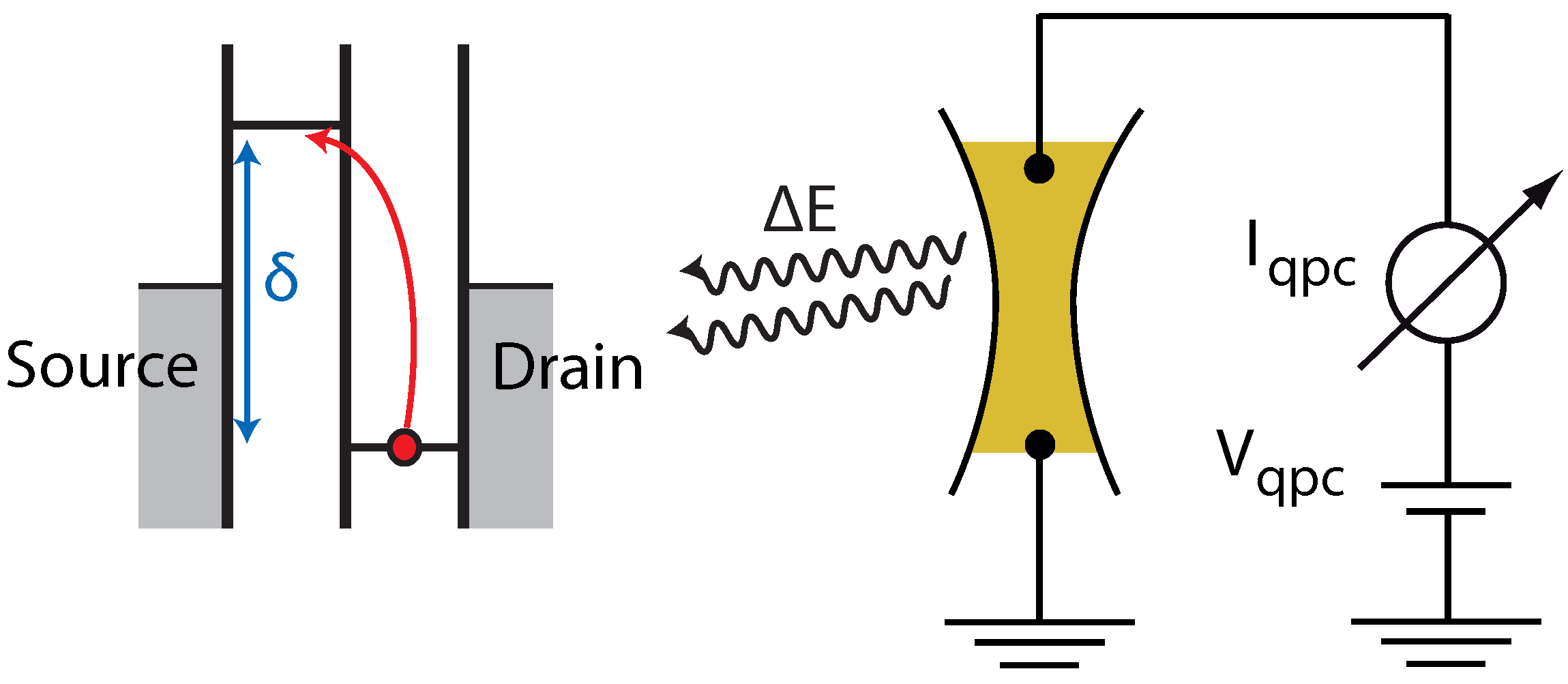
3.2. Sample and measurement description
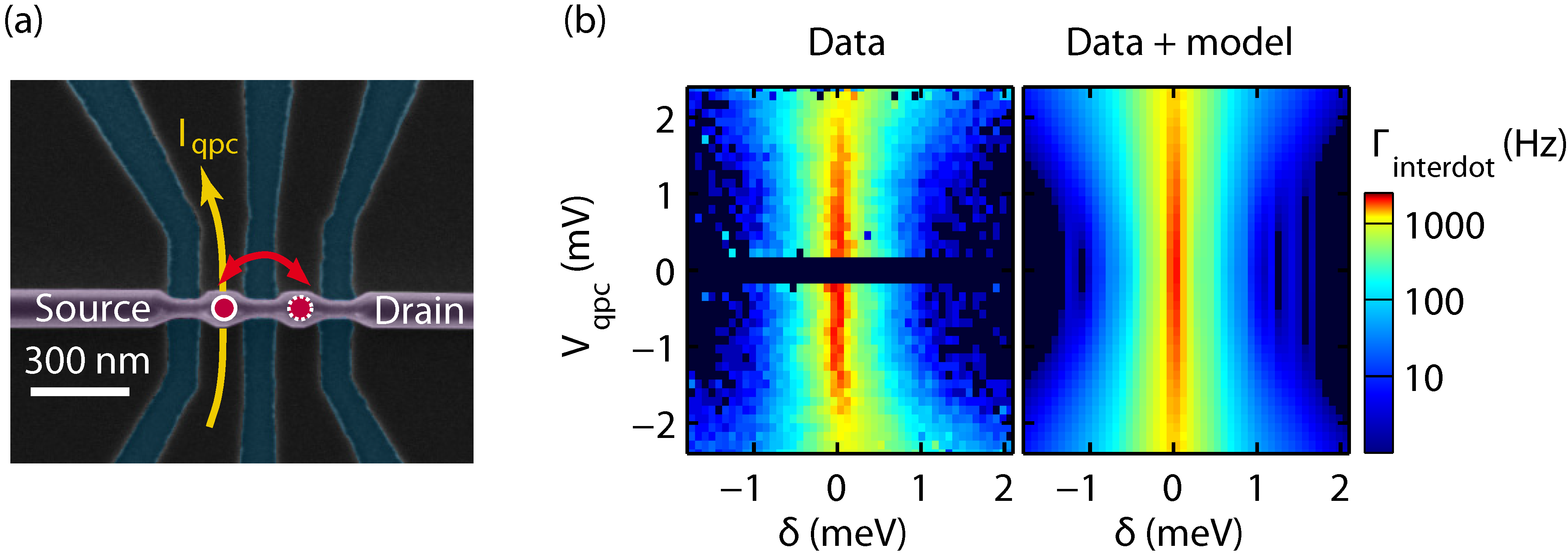
3.3. Model based on QPC shot-noise
4. Charge Readout with Cross-Correlation Techniques
4.1. Noise limitation of charge readout
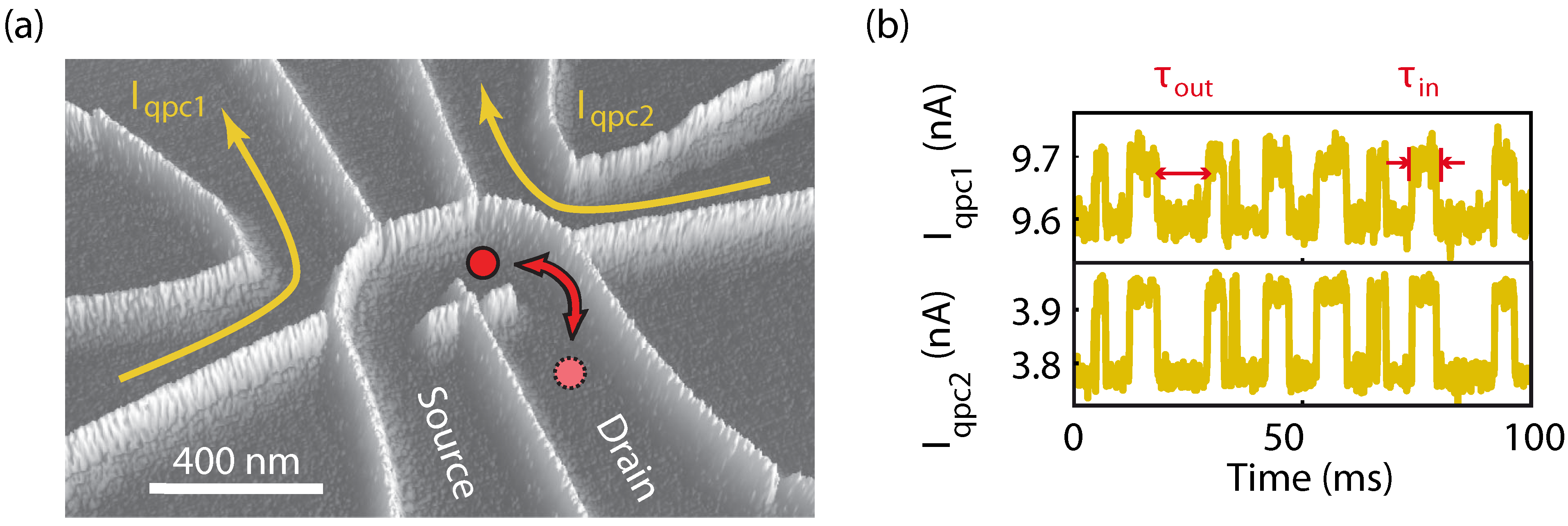
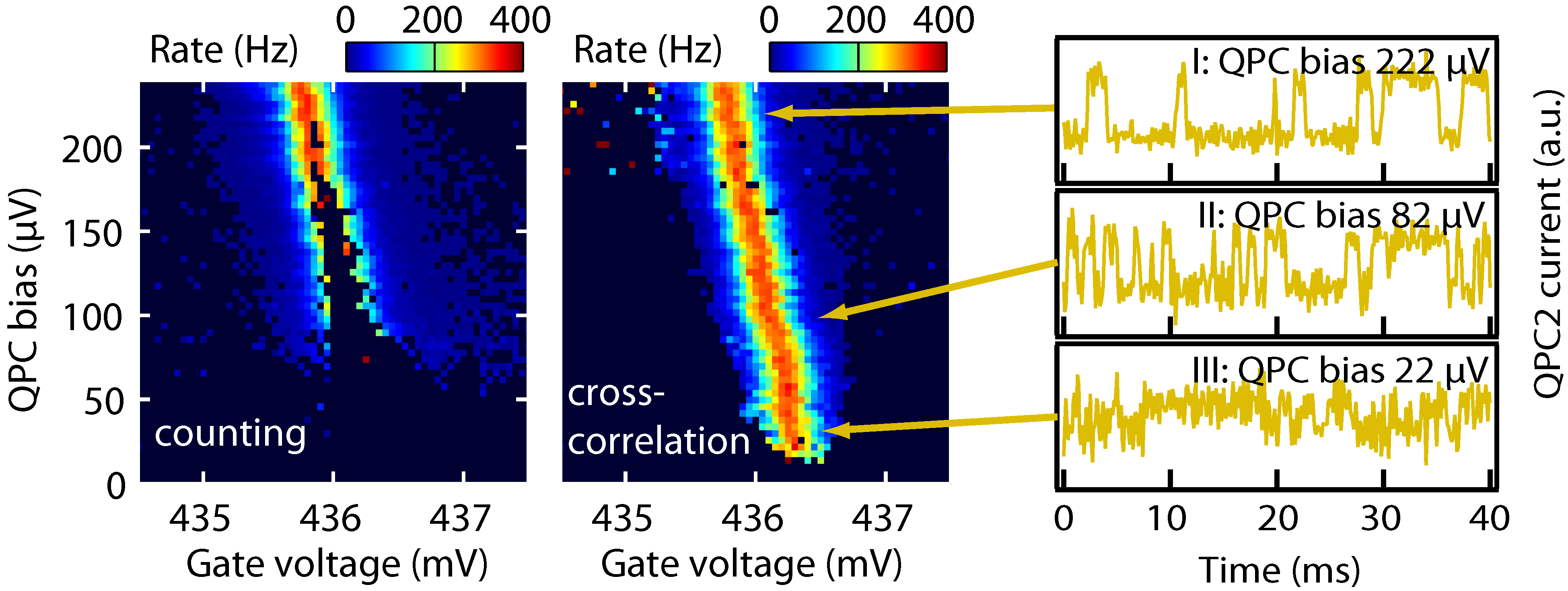
4.2. Cross-correlation analysis
5. Conclusions
Acknowledgments
References
- Kouwenhoven, L.P.; Marcus, C.M.; McEuen, P.M.; Tarucha, S.; Westervelt, R.M.; Wingreen, N.S. Electron transport in quantum dots. In Mesoscopic Electron Transport; Sohn, L.L., Kouwenhoven, L.P., Schön, G., Eds.; NATO ASI Ser. E 345; Kluwer: Dordrecht, the Netherlands, 1997; pp. 105–214. [Google Scholar]
- Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120. [Google Scholar] [CrossRef]
- Petta, J.R.; Johnson, A.C.; Taylor, J.M.; Laird, E.A.; Yacoby, A.; Lukin, M.D.; Marcus, C.M.; Hanson, M.P.; Gossard, A.C. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 2005, 309, 2180–2184. [Google Scholar] [CrossRef]
- Koppens, F.H.L.; Buizert, C.; Tielrooij, K.J.; Vink, I.T.; Nowack, K.C.; Meunier, T.; Kouwenhoven, L.P.; Vandersypen, L.M.K. Driven coherent oscillations of a single electron spin in a quantum dot. Nature (London) 2006, 442, 766–771. [Google Scholar] [CrossRef]
- Ono, K.; Austing, D.G.; Tokura, Y.; Tarucha, S. Current rectification by pauli exclusion in a weakly coupled double quantum dot system. Science 2002, 297, 1313–1317. [Google Scholar] [CrossRef]
- Field, M.; Smith, C.G.; Pepper, M.; Ritchie, D.A.; Frost, J.E.F.; Jones, G.A.C.; Hasko, D.G. Measurements of coulomb blockade with a noninvasive voltage probe. Phys. Rev. Lett. 1993, 70, 1311–1314. [Google Scholar] [CrossRef]
- Elzerman, J.M.; Hanson, R.; van Beveren, L.H.W.; Witkamp, B.; Vandersypen, L.M.K.; Kouwenhoven, L.P. Single-shot read-out of an individual electron spin in a quantum dot. Nature (London) 2004, 430, 431. [Google Scholar] [CrossRef]
- Barthel, C.; Reilly, D.J.; Marcus, C.M.; Hanson, M.P.; Gossard, A.C. Rapid single-shot measurement of a singlet-triplet qubit. Phys. Rev. Lett. 2009, 103, 160503. [Google Scholar] [CrossRef]
- Onac, E.; Balestro, F.; Willems van Beveren, L.H.; Hartmann, U.; Nazarov, Y.V.; Kouwenhoven, L.P. Using a quantum dot as a high-frequency shot noise detector. Phys. Rev. Lett. 2006, 96, 176601. [Google Scholar] [CrossRef]
- Gustavsson, S.; Studer, M.; Leturcq, R.; Ihn, T.; Ensslin, K.; Driscoll, D.C.; Gossard, A.C. Frequency-selective single-photon detection using a double quantum dot. Phys. Rev. Lett. 2007, 99, 206804. [Google Scholar] [CrossRef]
- Buks, E.; Schuster, R.; Heiblum, M.; Mahalu, D.; Umansky, V. Dephasing in electron interference by a ’which-path’ detector. Nature (London) 1998, 391, 871–874. [Google Scholar]
- Büttiker, M. Quantized transmission of a saddle-point constriction. Phys. Rev. B 1990, 41, 7906–7909. [Google Scholar] [CrossRef]
- Vandersypen, L.M.K.; Elzerman, J.M.; Schouten, R.N.; Willems van Beveren, L.H.; Hanson, R.; Kouwenhoven, L.P. Real-time detection of single-electron tunneling using a quantum point contact. Appl. Phys. Lett. 2004, 85, 4394–4396. [Google Scholar] [CrossRef]
- Schleser, R.; Ruh, E.; Ihn, T.; Ensslin, K.; Driscoll, D.C.; Gossard, A.C. Time-resolved detection of individual electrons in a quantum dot. Appl. Phys. Lett. 2004, 85, 2005. [Google Scholar] [CrossRef]
- Gustavsson, S.; Leturcq, R.; Simovic, B.; Schleser, R.; Ihn, T.; Studerus, P.; Ensslin, K.; Driscoll, D.C.; Gossard, A.C. Counting statistics of single electron transport in a quantum dot. Phys. Rev. Lett. 2006, 96, 076605. [Google Scholar] [CrossRef]
- Gustavsson, S.; Shorubalko, I.; Leturcq, R.; Ihn, T.; Ensslin, K.; Schön, S. Detecting terahertz current fluctuations in a quantum point contact using a nanowire quantum dot. Phys. Rev. B 2008, 78, 035324. [Google Scholar] [CrossRef]
- Khrapai, V.S.; Ludwig, S.; Kotthaus, J.P.; Tranitz, H.P.; Wegscheider, W. Double-dot quantum ratchet driven by an independently biased quantum point contact. Phys. Rev. Lett. 2006, 97, 176803. [Google Scholar] [CrossRef]
- Gasser, U.; Gustavsson, S.; Küng, B.; Ensslin, K.; Ihn, T.; Driscoll, D.C.; Gossard, A.C. Statistical electron excitation in a double quantum dot induced by two independent quantum point contacts. Phys. Rev. B 2009, 79, 035303. [Google Scholar] [CrossRef]
- Küng, B.; Gustavsson, S.; Choi, T.; Shorubalko, I.; Ihn, T.; Schön, S.; Hassler, F.; Blatter, G.; Ensslin, K. Noise-induced spectral shift measured in a double quantum dot. Phys. Rev. B 2009, 80, 115315. [Google Scholar] [CrossRef]
- Harbusch, D.; Taubert, D.; Tranitz, H.; Wegscheider, W.; Ludwig, S. Phonon-mediated vs. coulombic back-action in quantum dot circuits. 2009. arXiv:0910.4093v2. arXiv.org e-Print archive http://lanl.arxiv.org/abs/0910.4093v2 (accessed 24 June 2010).
- Taubert, D.; Pioro-Ladrière, M.; Schröer, D.; Harbusch, D.; Sachrajda, A.S.; Ludwig, S. Telegraph noise in coupled quantum dot circuits induced by a quantum point contact. Phys. Rev. Lett. 2008, 100, 176805. [Google Scholar] [CrossRef]
- Shorubalko, I.; Leturcq, R.; Pfund, A.; Tyndall, D.; Krischek, R.; Schön, S.; Ensslin, K. Self-aligned charge read-out for inAs nanowire quantum dots. Nano Lett. 2008, 8, 382–385. [Google Scholar] [CrossRef]
- Platero, G.; Aguado, R. Photon-assisted transport in semiconductor nanostructures. Phys. Rep. 2004, 395, 96–123. [Google Scholar] [CrossRef]
- Fujisawa, T.; Tarucha, S. Multiple Photon assisted tunneling between two coupled quantum dots. Jpn. J. Appl. Phys. 1997, 36, 4000–4003. [Google Scholar] [CrossRef]
- Devoret, M.H.; Esteve, D.; Grabert, H.; Ingold, G.L.; Pothier, H.; Urbina, C. Effect of the electromagnetic environment on the Coulomb blockade in ultrasmall tunnel junctions. Phys. Rev. Lett. 1990, 64, 1824–1827. [Google Scholar] [CrossRef]
- Aguado, R.; Kouwenhoven, L.P. Double quantum dots as detectors of high-frequency quantum noise in mesoscopic conductors. Phys. Rev. Lett. 2000, 84, 1986–1989. [Google Scholar] [CrossRef]
- Lesovik, G.B.; Loosen, R. On the detection of finite-frequency current fluctuations. JETP Lett. 1997, 65, 295–299. [Google Scholar] [CrossRef]
- Khlus, V.A. Current and voltage fluctuations in microjunctions between normal metals and superconductors. Sov. Phys. JETP 1987, 66, 1243–1249. [Google Scholar]
- Lesovik, G.B. Excess quantum noise in 2D ballistic point contacts. JETP Lett. 1989, 49, 592–594. [Google Scholar]
- Reilly, D.J.; Marcus, C.M.; Hanson, M.P.; Gossard, A.C. Fast single-charge sensing with a rf quantum point contact. Appl. Phys. Lett. 2007, 91, 162101. [Google Scholar] [CrossRef]
- Vink, I.T.; Nooitgedagt, T.; Schouten, R.N.; Vandersypen, L.M.K.; Wegscheider, W. Cryogenic amplifier for fast real-time detection of single-electron tunneling. Appl. Phys. Lett. 2007, 91, 123512. [Google Scholar] [CrossRef]
- Choi, T.; Shorubalko, I.; Gustavsson, S.; Schön, S.; Ensslin, K. Correlated counting of single electrons in a nanowire double quantum dot. New J. Phys. 2009, 11, 013005. [Google Scholar] [CrossRef]
- Küng, B.; Pfäffli, O.; Gustavsson, S.; Ihn, T.; Ensslin, K.; Reinwald, M.; Wegscheider, W. Time-resolved charge detection with cross-correlation techniques. Phys. Rev. B 2009, 79, 035314. [Google Scholar] [CrossRef]
- Machlup, S. Noise in semiconductors: Spectrum of a two-parameter random signal. J. Appl. Phys. 1954, 25, 341–343. [Google Scholar] [CrossRef]
- Jordan, A.N.; Büttiker, M. Continuous quantum measurement with independent detector cross correlations. Phys. Rev. Lett. 2005, 95, 220401. [Google Scholar] [CrossRef] [PubMed]
- Korotkov, A.N. Persistent Rabi oscillations probed via low-frequency noise correlation. 2010. arXiv:1004.0220v1. arXiv.org e-Print archive http://arxiv4.library.cornell.edu/abs/1004.0220/ (accessed 24 June 2010).
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Küng, B.; Gustavsson, S.; Choi, T.; Shorubalko, I.; Pfäffli, O.; Hassler, F.; Blatter, G.; Reinwald, M.; Wegscheider, W.; Schön, S.; et al. Measurement Back-Action in Quantum Point-Contact Charge Sensing. Entropy 2010, 12, 1721-1732. https://doi.org/10.3390/e12071721
Küng B, Gustavsson S, Choi T, Shorubalko I, Pfäffli O, Hassler F, Blatter G, Reinwald M, Wegscheider W, Schön S, et al. Measurement Back-Action in Quantum Point-Contact Charge Sensing. Entropy. 2010; 12(7):1721-1732. https://doi.org/10.3390/e12071721
Chicago/Turabian StyleKüng, Bruno, Simon Gustavsson, Theodore Choi, Ivan Shorubalko, Oliver Pfäffli, Fabian Hassler, Gianni Blatter, Matthias Reinwald, Werner Wegscheider, Silke Schön, and et al. 2010. "Measurement Back-Action in Quantum Point-Contact Charge Sensing" Entropy 12, no. 7: 1721-1732. https://doi.org/10.3390/e12071721
APA StyleKüng, B., Gustavsson, S., Choi, T., Shorubalko, I., Pfäffli, O., Hassler, F., Blatter, G., Reinwald, M., Wegscheider, W., Schön, S., Ihn, T., & Ensslin, K. (2010). Measurement Back-Action in Quantum Point-Contact Charge Sensing. Entropy, 12(7), 1721-1732. https://doi.org/10.3390/e12071721



