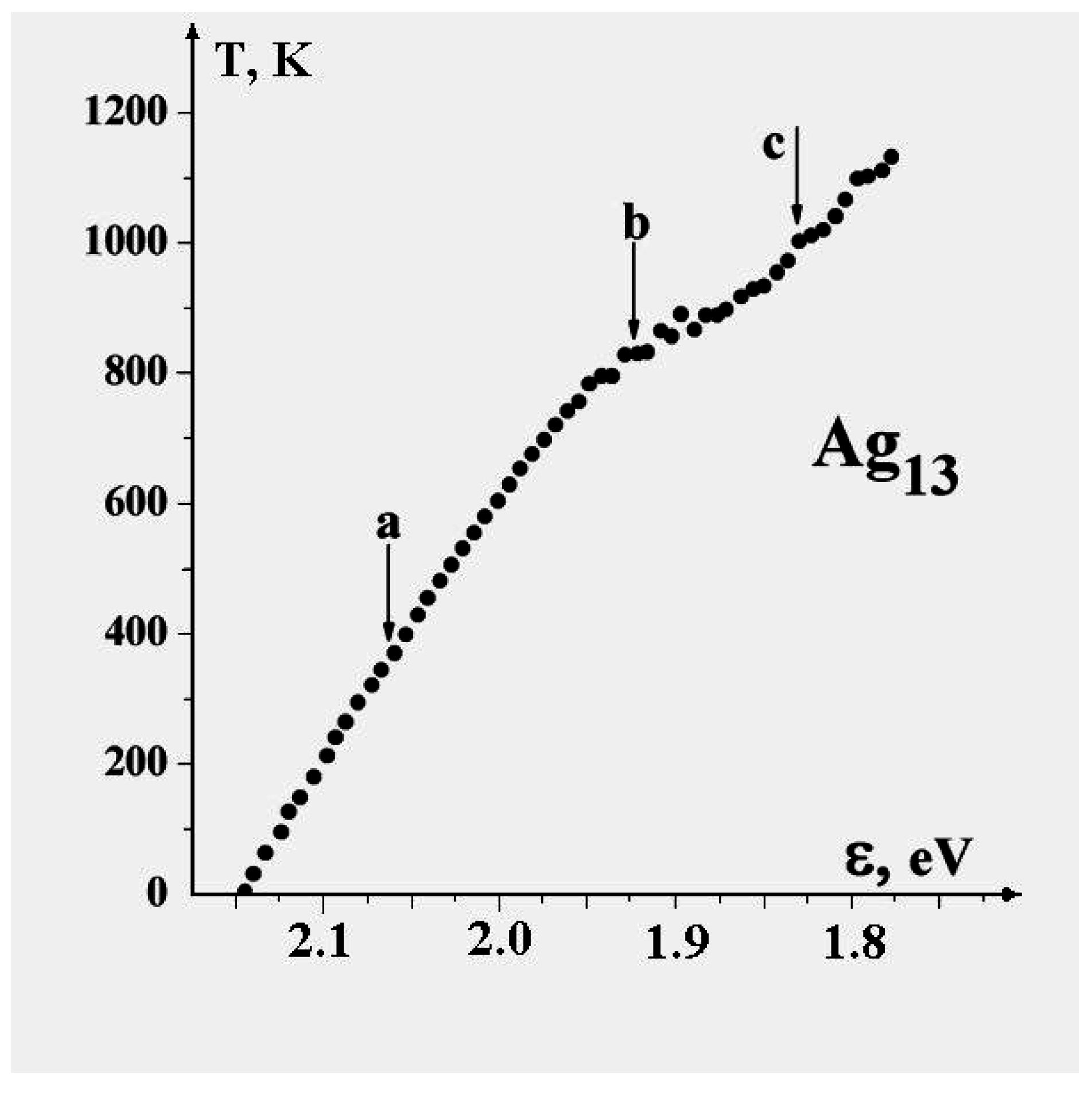
1. Introduction
Simulations established that small clusters can exhibit bands of temperature and pressure within which two, or more than two, phases may coexist in dynamic, as well as thermodynamic, equilibrium [
1,
2,
3,
4,
5,
6,
7,
8,
9,
12,
13]. The reason is simply that for systems comprised of small numbers of particles, the free energy difference between favored and unfavored phases, under conditions near but not at those of equal chemical potentials, can be small enough that observable amounts of the unfavored phase are present in observable quantities under equilibrium conditions. The situation is precisely analogous to the simultaneous coexistence of structural isomers. In contrast, systems made of large numbers of particles, e.g.,
ca.
, have vast differences in the free energies between favored and unfavored phases even if the conditions are barely away from equal chemical potentials. Hence thermodynamically unfavored phases cannot be present in observable amounts so macroscopic systems exhibit sharp phase changes, while small systems exhibit coexistence analogous to that of chemical isomers. For small systems, the actual limits of coexistence are set at the conditions at which the local free energy minimum disappears for that phase. More strictly, the unfavored form disappears under the conditions at which the local minimum of the potential energy surface of the system system cannot sustain a zero-point quantum state for that form.
Experiments have demonstrated the coexistence of solid and liquid phases over finite bands of temperature, e.g., [
14,
16] and of liquid and vapor phases [
15]. (In these experiments, being done in beams, the pressure is ill-defined and may be considered nearly zero.) Moreover the role of the energy and entropy changes in the transition have also been subject to study from various points of view [
17,
18,
19]. Most of the examinations of entropy and energy behavior with phase changes of clusters have dealt with issues such as the temperature dependence of the melting region and the occurrence of especially stable solid structures, the “magic numbers” which result from shell-closings, either of geometric or electronic structure [
20]. However one aspect of the phase changes of clusters that has not been investigated extensively is the question of the observability of coexisting phases, and specifically of the conditions under which such coexistence can actually be seen in experiments. That such ranges exist was demonstrated both in early simulations and in the experiments cited above. However, apart from one early discussion based on a continuum-capillarity model [
21], the conditions and constraints that allow the coexistence ranges to be wide enough to be detectable had not been identified until very recently [
22,
23].
The essential conclusion of the study so far of observability of coexisting phases over ranges of temperature and pressure is derived from a heuristic criterion, that the minority phase must be at least ten percent of the total composition. From this, one can derive the relation that the ratio of the temperature range
to the melting temperature
within which that condition is met is
(The numerical value of the constant is determined by the choice of the heuristic criterion limiting the coexistence range.) That relation was initially based on the assumption that the cluster could be described by a single potential surface, a model valid for dielectric species whose electronic excitation energies are large compared with the energy required to melt the cluster. That is not a valid assumption for many metal clusters, for which there are low-lying electronic excitations. Many clusters of metal atoms, moreover, exhibit metal-insulator transitions as functions of cluster size, so one can even suspect that there might be very sharp changes in the phase coexistence and melting behavior with size of cluster, for systems that exhibit such behavior. The goal of this work is to compare, at least in a limited way, the behavior of clusters of dielectric and metal atoms, with respect to their melting and freezing behavior, and specifically with regard to their observable coexistence regions, both of size and of temperature range. The previous results just cited already indicated why it seems that the coexistence range of Lennard-Jones or rare gas cluster sizes goes up only to about 100 atoms, while metal clusters apparently can show coexistence at considerably larger sizes. And, of course, metal clusters melt at much higher temperatures than do rare gas clusters.
To carry out our analysis and comparison of the two kinds of systems, we define an aggregate state of a cluster as the set of configurational states, the states associated with local minima on the multidimensional internal energy surface or surfaces, that lie within a relatively narrow energy band [
2]. The aggregate state may be a single isomer, a set of solid isomeric states, a liquid or some other form in which multiple minima are dynamically accessible to the system. For a typical excited state occupied at moderately high temperature, the ratio
g of its statistical weight to that of the ground state is much greater than 1, while at low temperatures or energies,
g is likely to be much closer to 1.
We carry out our analysis using 13-atom clusters as the vehicle for the study, both dielectric and metal. Virtually all such clusters have as their lowest-energy structure an icosahedron, twelve atoms at the vertices, surrounding a central atom. The archetype for dielectric clusters is the system in which the atoms interact pairwise, through the well-known Lennard-Jones potential, a 6th-power attraction and a 12th-power repulsion [
24,
25]. Such clusters have long been known to have a number of locally stable structures [
26,
27,
28]. It is convenient to think of these as local minima on an energy surface with all the
or 33 independent structural coordinates as the independent variables and the electronic energy of each configuration as the dependent variable. This is, of course, just the Born-Oppenheimer approximation, separating electronic and nuclear energies. The minima and saddles can be found by a number of algorithms, of which the first systematic one was the quenching procedure introduced by Stillinger and Weber [
29,
30,
31]. Other, even more efficient methods now enable one to locate stationary points on such multidimensional surfaces [
32,
33,
34]. A second separation also proves very useful, that between local vibrational equilibration and the slower configurational equilibration. The validity of this second kind of separation has been well-established, e.g., [
35], and provides a basis for describing the evolving motion of a system in terms of the kinetics of well-to-well passages in time, for example in terms of a master equation [
34,
36,
37]. The physical justification for this is simply that the time spent by the cluster in the vicinity of almost every local minimum is significantly longer than the time required for the vibrations to equilibrate and define an effective temperature in the vicinity of each local minimum.
2. Dielectric Cluster Behavior
The 13-atom cluster with atoms bound by Lennard-Jones interactions provides a particularly simple model for studying properties of dielectric clusters. Its elementary configurational excitations, from the closed-shell icosahedral global energy minimum, begin with the simple promotion of one particle from the icosahedral shell to the surface. The promoted particle is relatively free to move about on the surface, and presumably the vacancy it leaves also has significant but lower mobility. One can estimate the barrier between stable configurations simply by counting the number of nearest-neighbor contacts in the initial, final and transition state. Thus, when a particle promoted to the surface moves from one face of the icosahedron to another, it moves from a site with three contacts to another with three contacts, through a transition state with only two contacts. Hence the height of the energy barrier for the passage is essentially equal to the energy of a single contact,
i.e., the dissociation energy of one pair of these atoms.
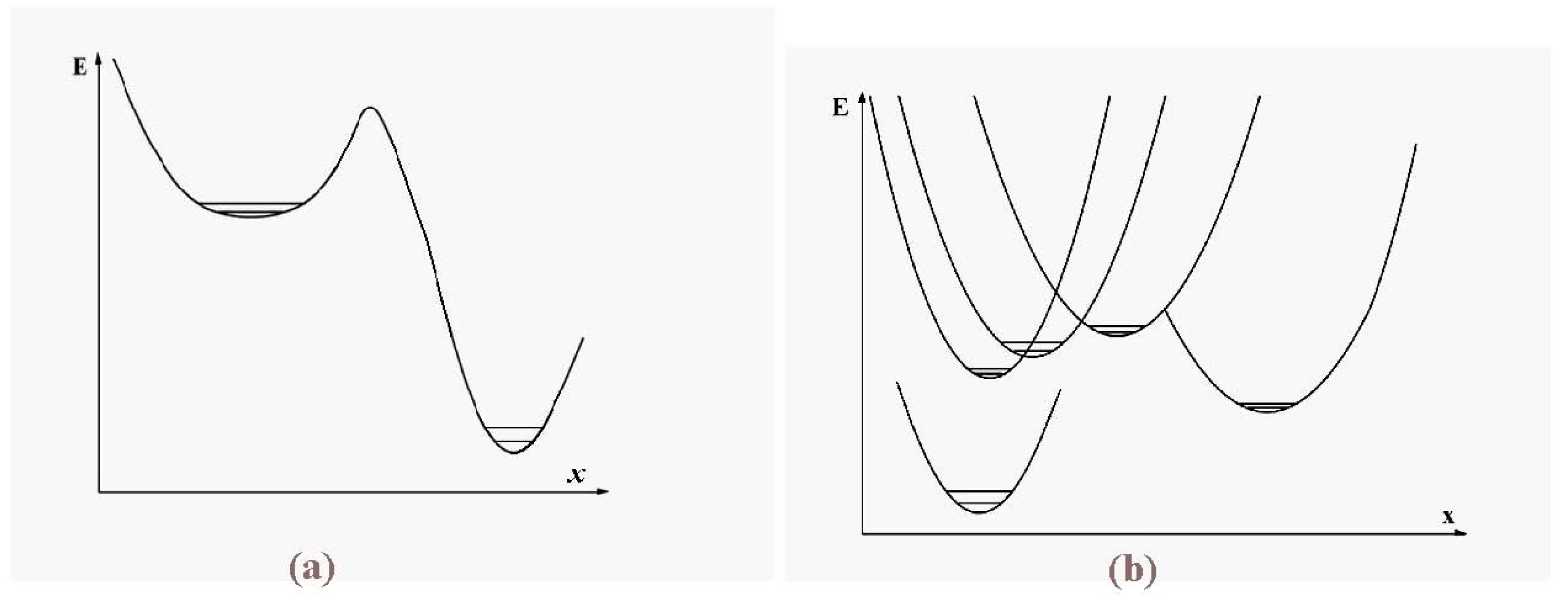
Figure 1 illustrates the promotion process.
Figure 1.
Configurational excitation of a cluster of 13 atoms bound by short-range pair interactions.
Figure 1.
Configurational excitation of a cluster of 13 atoms bound by short-range pair interactions.
There are of course many other locally stable structures of a cluster of 13 atoms. The current estimate is 1,509 geometrically distinct structures, each of which has roughly 13! permutational forms [
34]. (The number is of course actually less than 13! because of symmetries of many of the structures, which allows some permutations to be achieved by rigid-body rotations.)
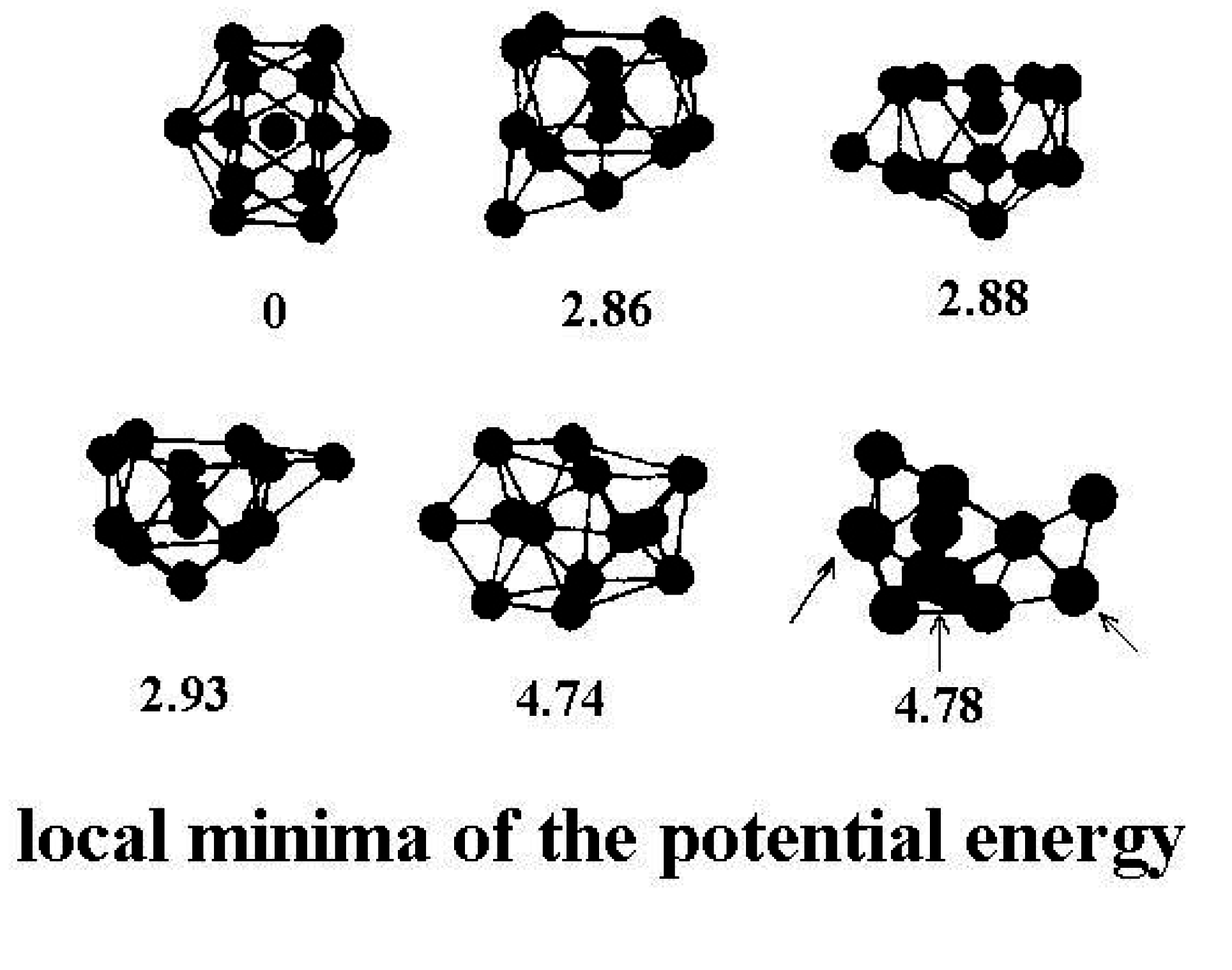
Figure 2 shows a few of the stable structures and their energies for this 13-particle system [
38].
Figure 2.
Structures of the lowest configurationally stable states for the 13-particle Lennard-Jones cluster at zero temperature [
38].
Figure 2.
Structures of the lowest configurationally stable states for the 13-particle Lennard-Jones cluster at zero temperature [
38].
At energies at which only one or perhaps two particles are promoted to the cluster’s surface, the dominant motion is of course that of the promoted particles around the surface. This has lower barriers for passage than exchange or motion within the icosahedral shell. In that sense, the promoted structure of
Figure 1 can be considered liquid-like, at least in a restricted way. Several structures, including some shown in
Figure 2, are accessible at relatively low energies and temperatures.
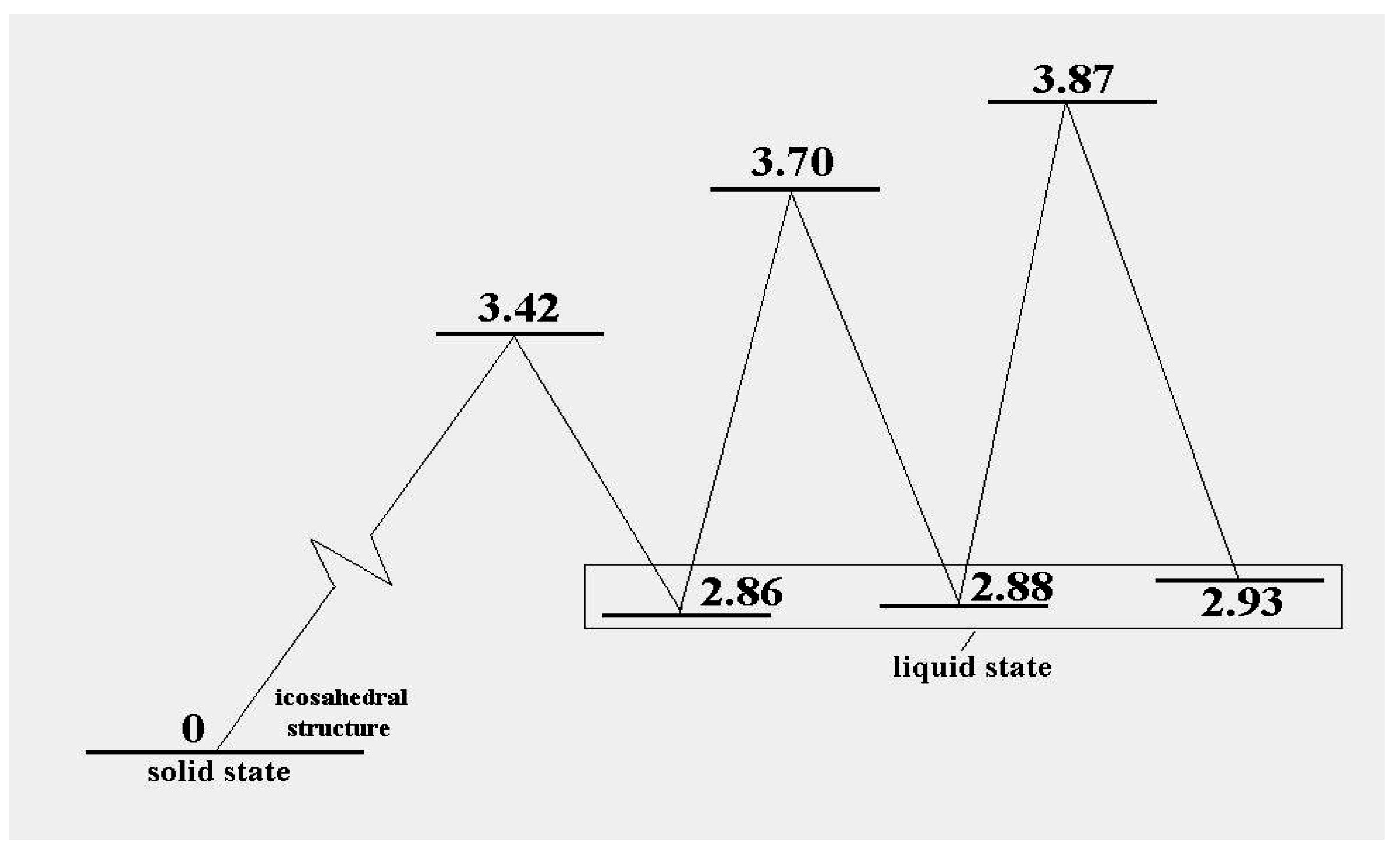
Figure 3 shows the energy pattern linking some of these with the icosahedral global minimum.
Figure 3.
The excitation energies and barrier energies for the lowest configuration excitations of the 13-atom Lennard-Jones cluster, according to [
38].
Figure 3.
The excitation energies and barrier energies for the lowest configuration excitations of the 13-atom Lennard-Jones cluster, according to [
38].
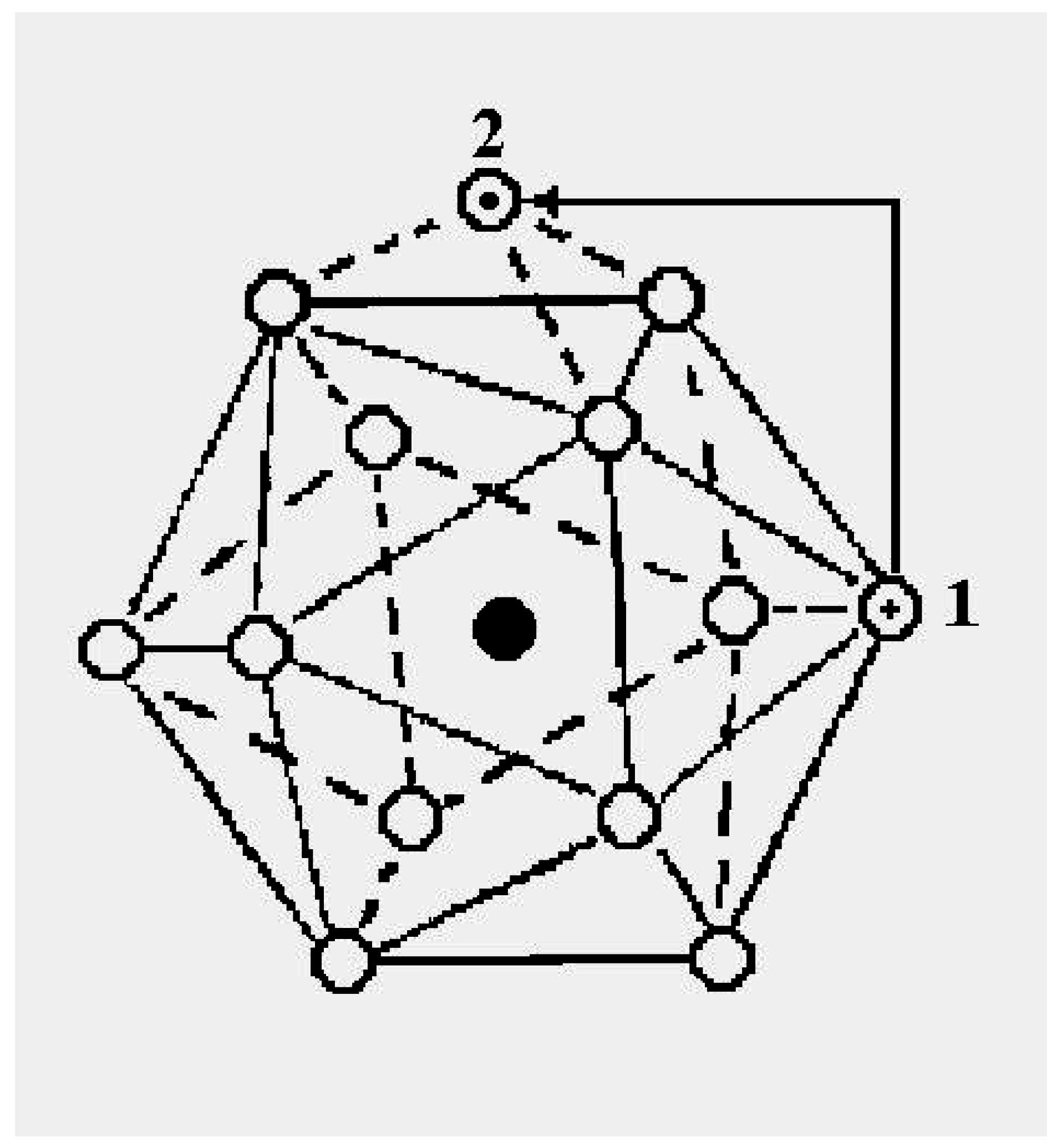
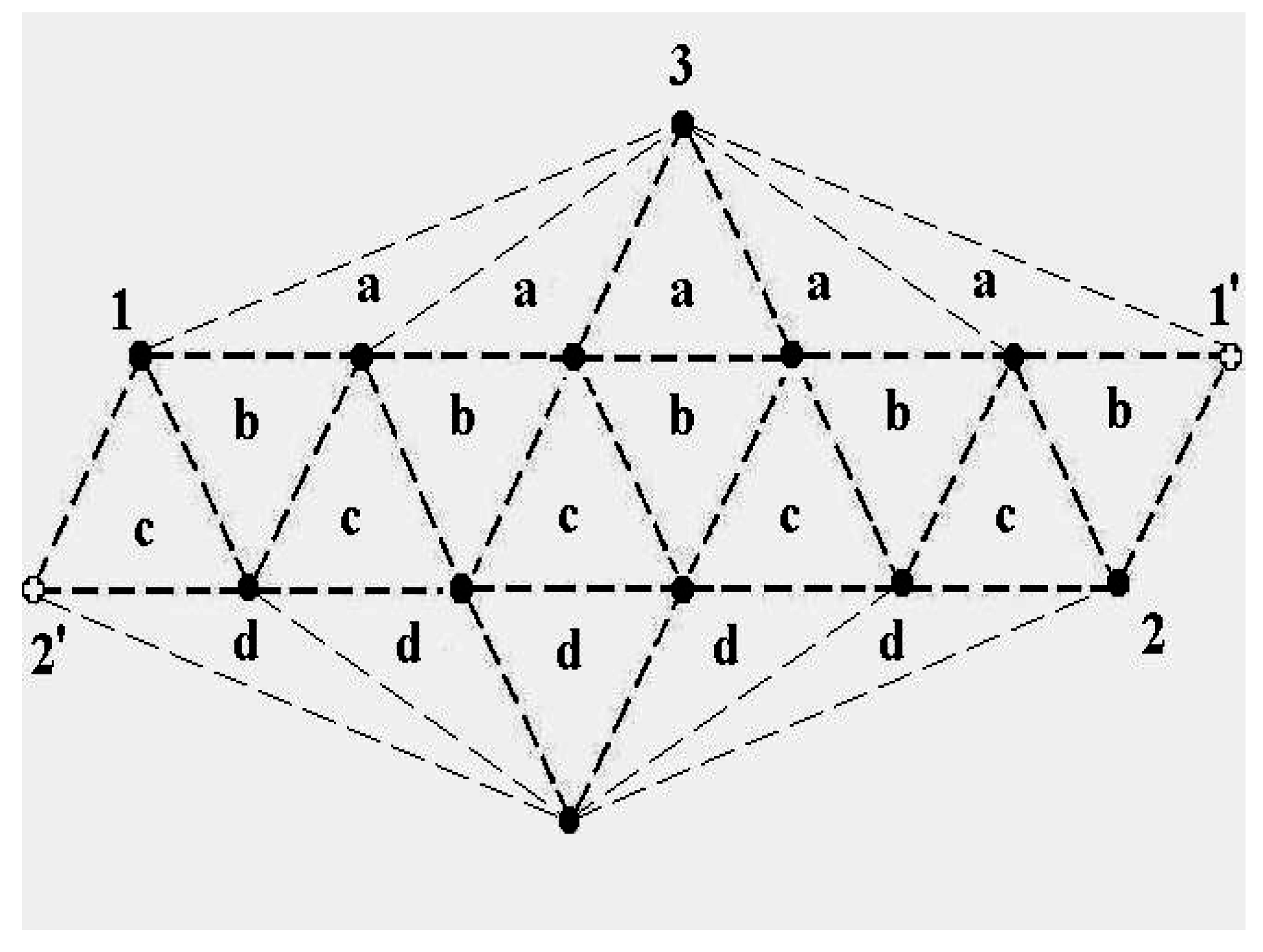
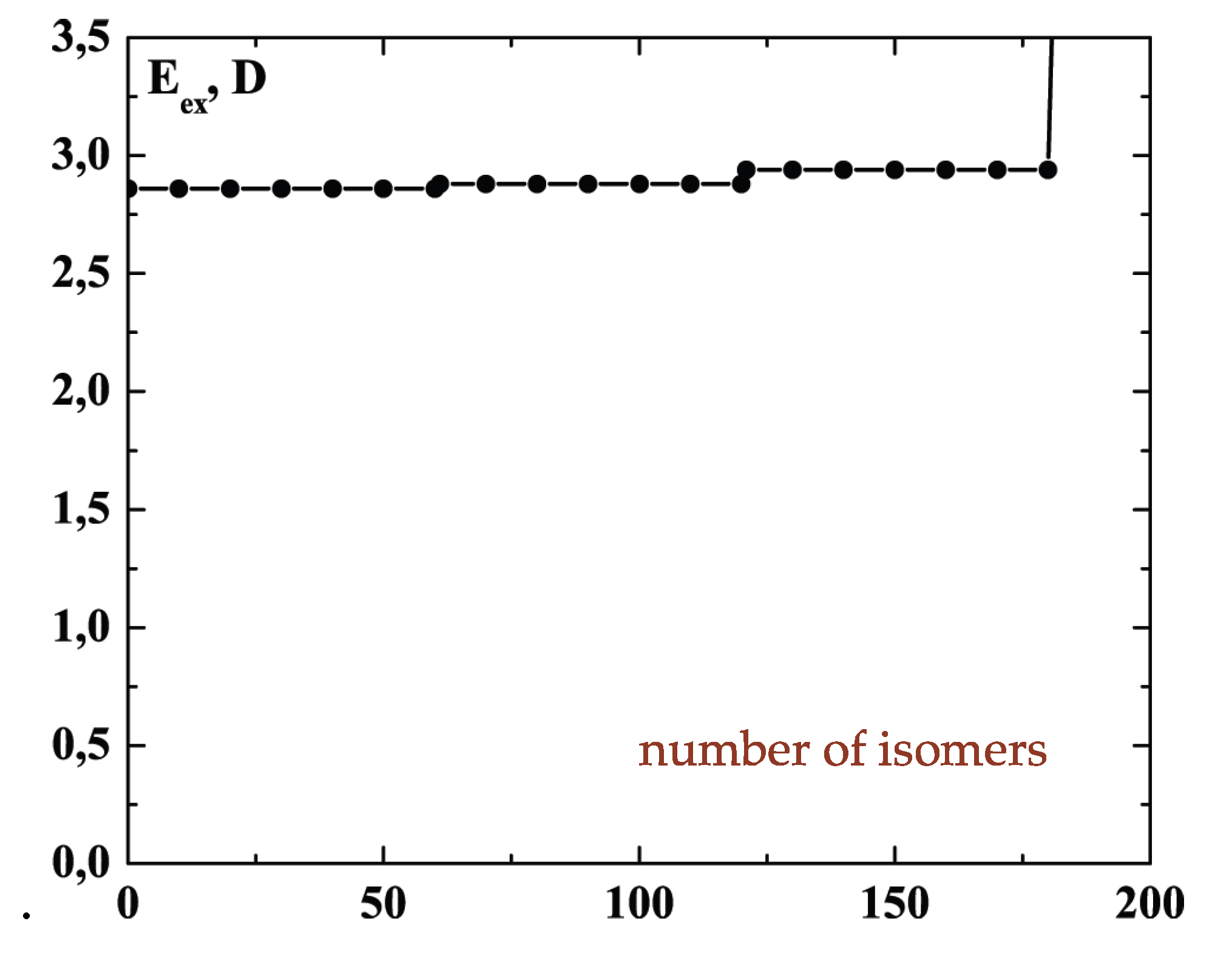
The schematic representation of
Figure 4 illustrates the relations among the single-particle excitations of the 13-atom cluster. We suppose that atom 3 moves to the cluster surface; there are then four kinds of transitions corresponding to the different triangular faces on which atom 3 may rest. The excitation energy to positions “a” is
(in terms of the pair dissociation energy
D) and to positions “b”, “c” and “d”, just
, at the level of this schema. As we see in
Figure 3, the precise energies of positions “b”, “c” and “d” are 2.86D, 2.88D and 2.93D.
To get a simple picture of the solid-liquid phase transition in the 13-atom dielectric cluster, we first use the separation of configurational and vibrational degrees of freedom [
39]. However we can assume here (but not generally) that the vibrations are harmonic for both solid and liquid (but of course with different frequencies). Taking the excitation energy in accordance with
Figure 3 to be
and the transition entropy
to be equal to that at zero temperature,
(
is the statistical weight for configurational excited states of
Figure 1b), we obtain a value for the hypothetical cluster melting point
of a harmonic model,
This differs from the more realistic value found in a variety of simulations. This difference reveals the role of anharmonicity in the phase transitions of clusters.
Let us now introduce the average anharmonicity parameter as
where
K is the average total kinetic energy of cluster atoms, and
is the total excitation energy of cluster atoms from the state at zero temperature. So defined,
η falls below 0.5 if the vibrations are softer than harmonic as most stretching modes are, and is greater than 0.5 if they are stiffer, as often occurs in bending modes. It is useful to think of a cluster as a member of a microcanonical ensemble if it does not exchange energy with an environment,
i.e., it is under adiabatic conditions, and as a member of a canonical ensemble under isothermal conditions, e.g., if this cluster is in a thermostat. In this analysis we assume that the time for energy exchange and equilibration among neighboring atoms is brief compared with the time that a cluster resides in each aggregate state. This allows us to introduce the concept of vibrational temperatures of the cluster atoms that are different for the solid and liquid states when the cluster is in a microcanonical ensemble but of course is the thermostat temperature when the cluster is in a canonical ensemble.
Figure 4.
A schematic representation of the single-particle excitations of a 13-atom cluster with short-range interparticle forces. When this schema is converted into an energy space surface structure, positions 1 and 1’ and also the positions 2 and 2’ are joined, and the cluster surface consists of 20 equilateral triangles.
Figure 4.
A schematic representation of the single-particle excitations of a 13-atom cluster with short-range interparticle forces. When this schema is converted into an energy space surface structure, positions 1 and 1’ and also the positions 2 and 2’ are joined, and the cluster surface consists of 20 equilateral triangles.
Figure 5a shows the dependence of the anharmonic parameter (3) of the 13-atom Lennard-Jones cluster on the excitation energy
when cluster is under microcanonical conditions. This dependence is given for a range of effective temperatures in which the solid and liquid phases coexist. At
the probabilities for the cluster to be in the solid and liquid states are equal. The dependence of
Figure 5a was obtained [
40,
41] on the basis of computer simulation [
6] for an isolated 13-atom Lennard-Jones cluster. The higher temperature of the solid form, due to its lower average potential energy, is compensated in this case by its smaller anharmonic parameter, so that
within the accuracy limits.
Figure 5b also shows the anharmonic parameters (3) as temperature functions separately for the solid and liquid cluster states [
22]. These are also derived from the data of computer simulations [
6,
7] for the Lennard-Jones cluster under microcanonical and canonical conditions. It follows from
Figure 5 that atomic motion in the cluster is close to harmonic with
for an unexcited cluster,
i.e.,
, but the role of anharmonicity of atomic motion in the cluster becomes very significant when the system is excited.
Figure 5b exhibits the stronger deviation from harmonic motion for the liquid aggregate state.
Figure 5.
(a) The dependence on the excitation energy of the anharmonic parameter (3)for an isolated Lennard-Jones cluster of 13 atoms [
40,
41] obtained from computer simulation [
6]; (b), the temperature dependence of the anharmonic parameter (3) for the solid and liquid states [
2,
43] obtained on the basis of the results of computer simulation [
6].
Figure 5.
(a) The dependence on the excitation energy of the anharmonic parameter (3)for an isolated Lennard-Jones cluster of 13 atoms [
40,
41] obtained from computer simulation [
6]; (b), the temperature dependence of the anharmonic parameter (3) for the solid and liquid states [
2,
43] obtained on the basis of the results of computer simulation [
6].
One of the best parameters for determining the cluster’s melting point
from computer simulations by the method of molecular dynamics is the root mean square of the interparticle distance fluctuation that is introduced as
where
is a distance between atoms
i and
j. So defined, the parameter
δ takes into account the correlations in atomic positions [
6,
9,
42]. It is a variant on the parameter of the “Lindemann criterion” [
44]. This original formulation used the displacement of each particle from its equilibrium position as the key quantity. Later, two groups used the interparticle distances rather than displacements from equilibrium [
4,
5,
9]. There is, it turns out, some advantage to the latter [
45]. For the solid state, in which atoms are fixed in lattice sites, the value of this parameter is typically smaller than
, considerably smaller than that for the liquid state with its mobile atoms. This parameter corresponds to a time scale in which atomic transitions between sites for the solid cluster state are improbable, while these transitions for the liquid cluster state are effective.
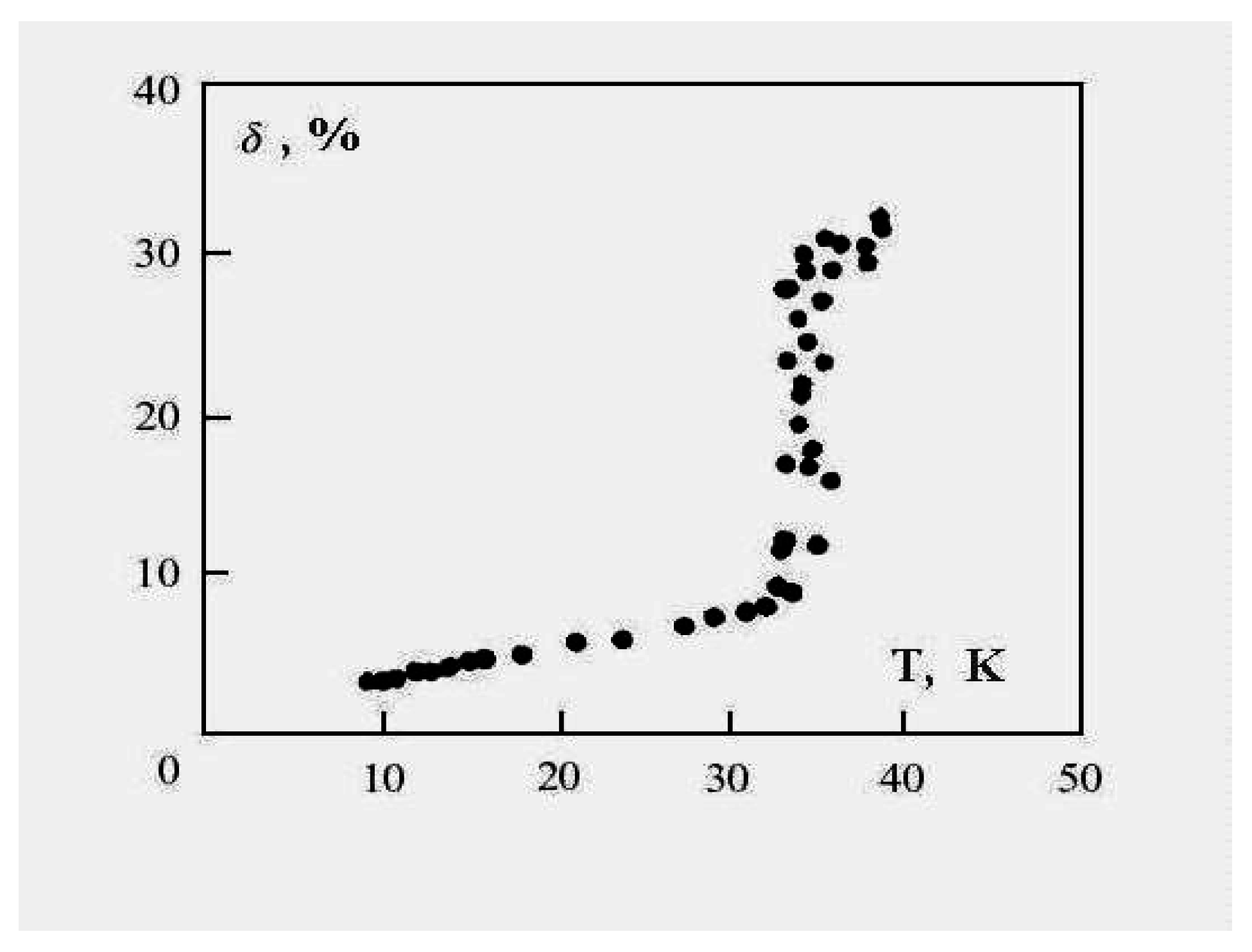
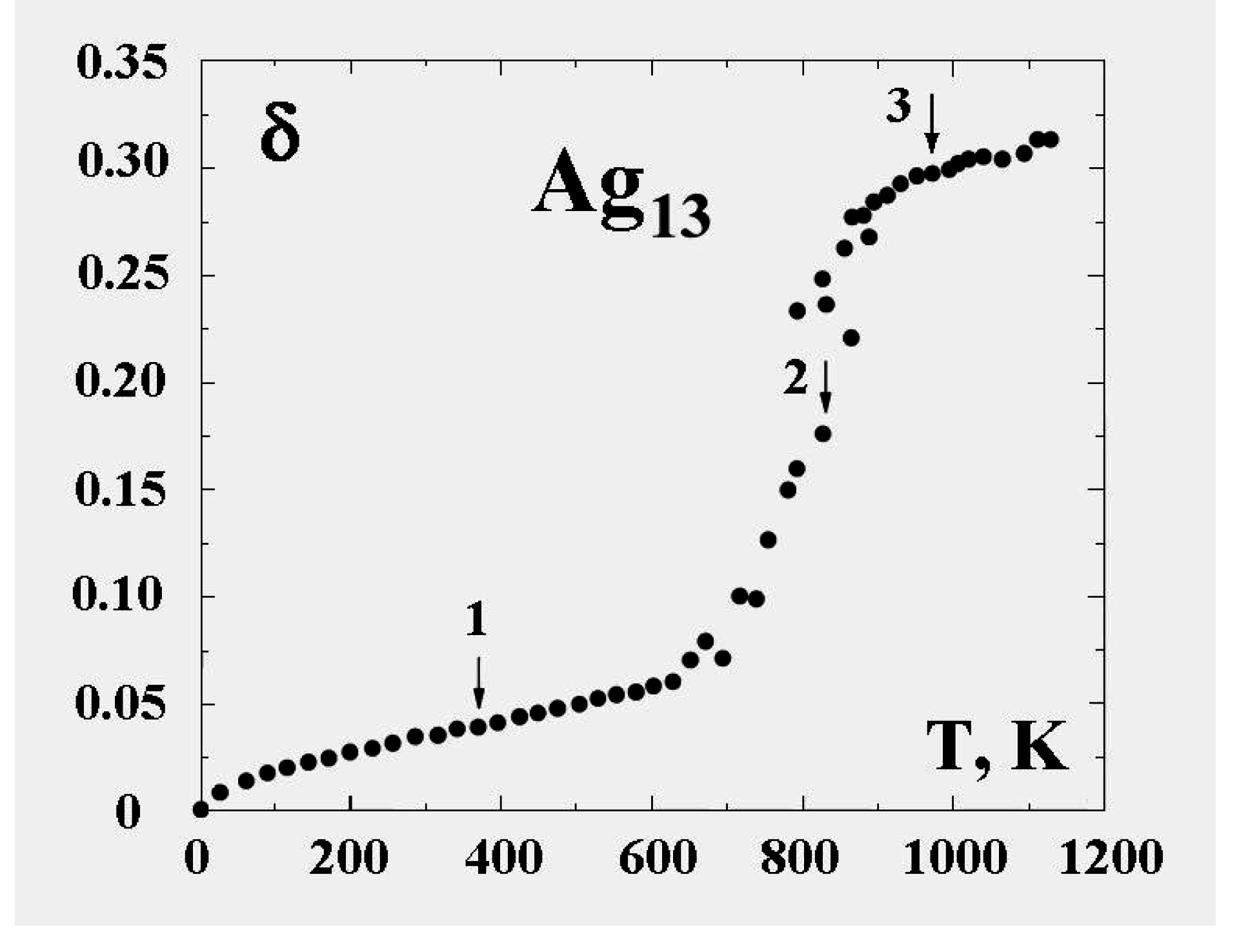
Figure 6 demonstrates this for the 13-atom Lennard-Jones cluster with the argon pair interaction parameters. One can see that the parameter
δ has a jump in the vicinity of the cluster melting point, and the point of inflection of this jump may be used as the definition of the melting point. But because the “jump” clearly takes place over a finite temperature interval, the meaning of the cluster’s melting point becomes one of one’s choice of definition, e.g., the point of inflection of this curve, or the point of equal chemical potentials of the two phase-like forms. Often, the term “melting point” of a cluster is taken to be the condition at which the free energies of the two phases are equal.
Figure 6.
The square of the length of fluctuations of the bond length defined by formula (
4) averaged over a long period for the 13-atom Lennard-Jones “argon" cluster [
6].
Figure 6.
The square of the length of fluctuations of the bond length defined by formula (
4) averaged over a long period for the 13-atom Lennard-Jones “argon" cluster [
6].
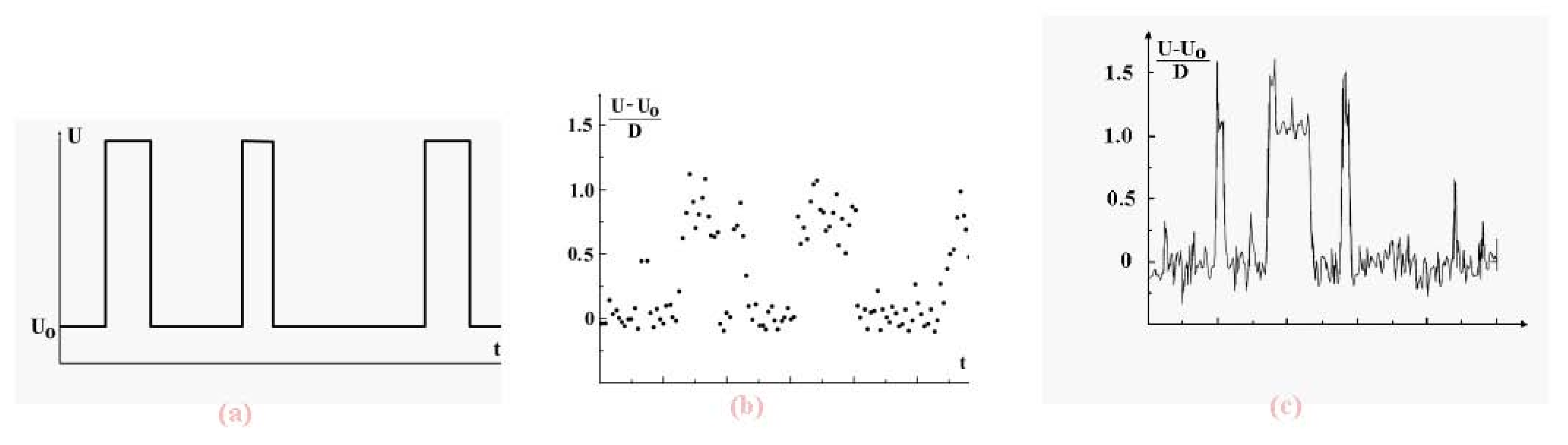
We now examine the dynamic coexistence of phases in the Lennard-Jones cluster when, part of the time, a cluster is found in the solid aggregate state, and the rest, in the liquid aggregate state. The character of phase coexistence is demonstrated in
Figure 7 which shows the time evolution of the atomic potential energy. The data are based on short-time average values of that potential energy. Indeed, let us ignore fluctuations and determine the potential energy
U of interacting atoms in a cluster on the basis of the relation
Figure 7.
Evolution in time of the total potential energy of cluster atoms with short-time fluctuations averaged (a), for the 13-atom Lennard-Jones cluster under isothermal conditions [
7] (b) and under adiabatic conditions [
8] at the excitation energy of 10.8D (the melting point,
i.e., the point of equal chemical potentials, corresponds to the excitation energy of 13.8D) (c). The data (b) and (c) results from computer simulations, time is measured in arbitrary units.
Figure 7.
Evolution in time of the total potential energy of cluster atoms with short-time fluctuations averaged (a), for the 13-atom Lennard-Jones cluster under isothermal conditions [
7] (b) and under adiabatic conditions [
8] at the excitation energy of 10.8D (the melting point,
i.e., the point of equal chemical potentials, corresponds to the excitation energy of 13.8D) (c). The data (b) and (c) results from computer simulations, time is measured in arbitrary units.
where
K is the total kinetic energy of the atoms, and
is the excitation energy from the state of zero temperature. For an isolated cluster, when it is under microcanonical conditions, we have, using the definition (3) of the anharmonic parameter,
Under canonical conditions,
i.e., if the cluster is in a thermostat, the temperature of the atoms
T is fixed, as is their total mean kinetic energy
, where
v is a number of vibrational degrees of freedom. In this case the mean potential energy of cluster atoms is given by
We see that in both cases, canonical and microcanonical, the potential energy of cluster atoms in the liquid state is higher than that in the solid, and evolution of the total atomic potential energy has the form given in
Figure 7a when the cluster is below the melting point (which we take as the point of equal chemical potentials). There, the probability that the cluster be liquid is lower than that of being a solid. In reality, fluctuations complicate this picture, as shown in the computer simulation results of
Figure 7b and
Figure 7c [
7,
8] These figures demonstrate the dynamic character of equilibrium phase coexistence in clusters.
Our analysis of the cluster phase transition assumes the two-state approximation,
i.e., that just two aggregate phase-like states coexist [
10,
11,
40,
42]. However this assumption does not follow from general considerations. In systems of small numbers of particles, the free energies of two–or more than two–phases may differ and yet be close enough that unfavored forms may be present in observable amounts [
22]. This is precisely the origin of the absence of sharp, bulk-like phase transitions in small clusters. The coexistence phenomenon first appeared clearly in computer simulations which exhibited the bimodal character of the atomic parameters over finite ranges [
3,
4,
5]. Using these results and comparing the results of computer simulations under various conditions, one can find the parameters for the model of two aggregate states. In particular, for the 13-atom Lennard-Jones cluster the excitation energy of the excited aggregate state (the liquid state) in the range of coexistence is [
2,
40,
41]
We note the limited accuracy of this value and its difference from that at zero temperature (
) that is given in
Figure 3.
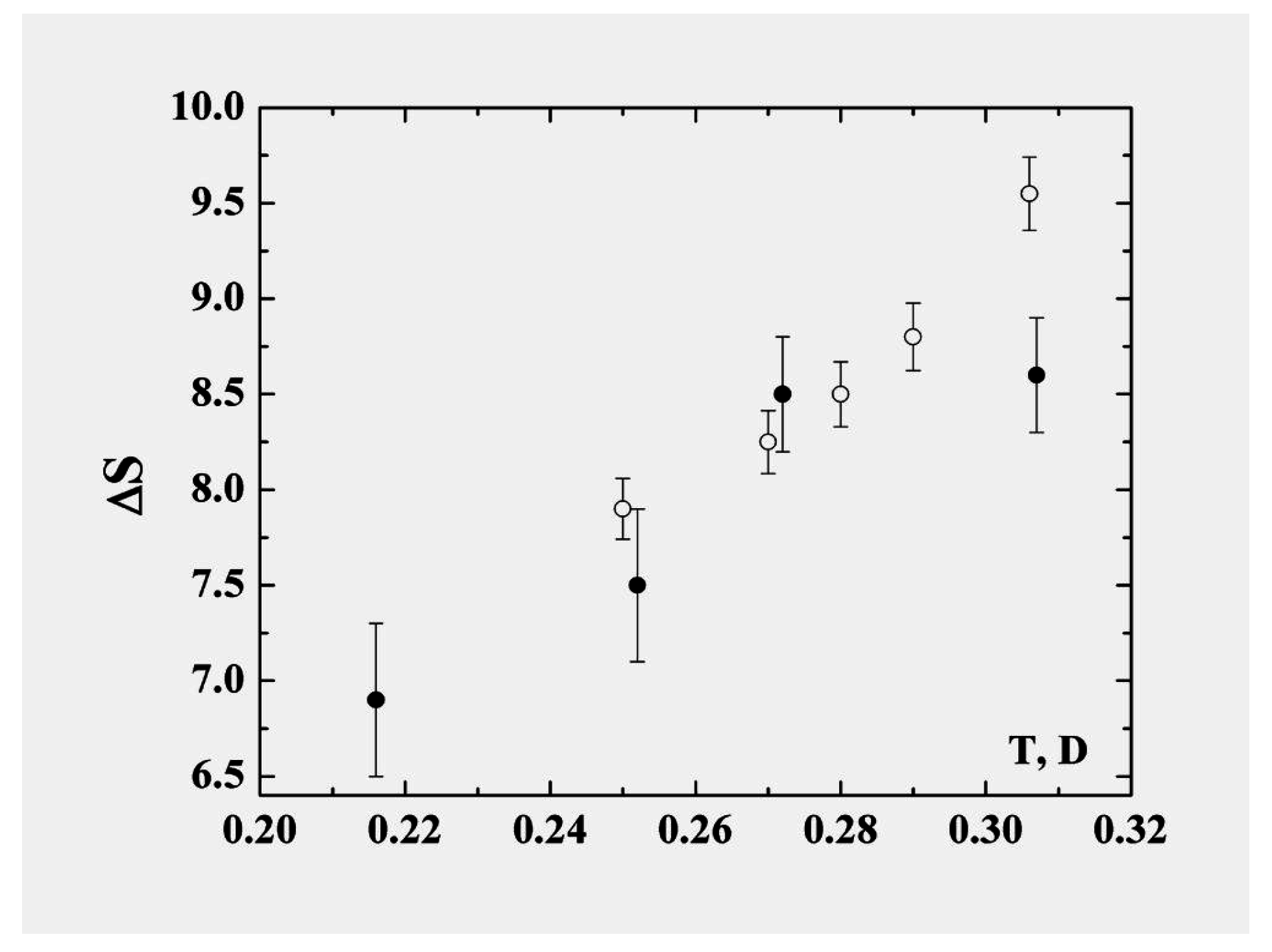
In describing the cluster within the framework of the model of two aggregate states in the coexistence phase range, we recognize that the liquid state is “looser” in the sense that the particles are not confined to specific sites and also that the accessible volume in phase space is larger and increases faster with temperature than for the solid. The liquid is therefore characterized by parameters with stronger temperature dependence than those of the solid state. Consequently some parameters of the cluster vary within the coexistence range; the character of this variation may be expressed through the anharmonicity parameter. In particular, in contrast to the phase transitions in macroscopic atomic systems with their extremely narrow—virtually infinitesimal—ranges of equilibrium coexistence, within which the entropy jump varies very little, the entropy jump at the phase transition of clusters varies significantly within the range of phase coexistence. The largest contribution to the variation of the entropy is determined by thermal motion of atoms in the liquid aggregate state. The entropy jump for the 13-atom Lennard-Jones cluster under isothermal conditions is given in
Figure 8 [
22,
23]. These values are obtained on the basis of probabilities that a cluster is located in the liquid or solid states; these, in turn, emerge from molecular dynamics simulations of this cluster under adiabatic [
6] and isothermal [
7] conditions.
Figure 8.
The entropy jump at melting of the 13-atom Lennard-Jones cluster [
22,
23]. Closed circles are obtained from the results of computer simulation of the isolated 13-atom Lennard-Jones cluster [
6], and open circles correspond to the isothermal 13-atom Lennard-Jones cluster [
7].
Figure 8.
The entropy jump at melting of the 13-atom Lennard-Jones cluster [
22,
23]. Closed circles are obtained from the results of computer simulation of the isolated 13-atom Lennard-Jones cluster [
6], and open circles correspond to the isothermal 13-atom Lennard-Jones cluster [
7].
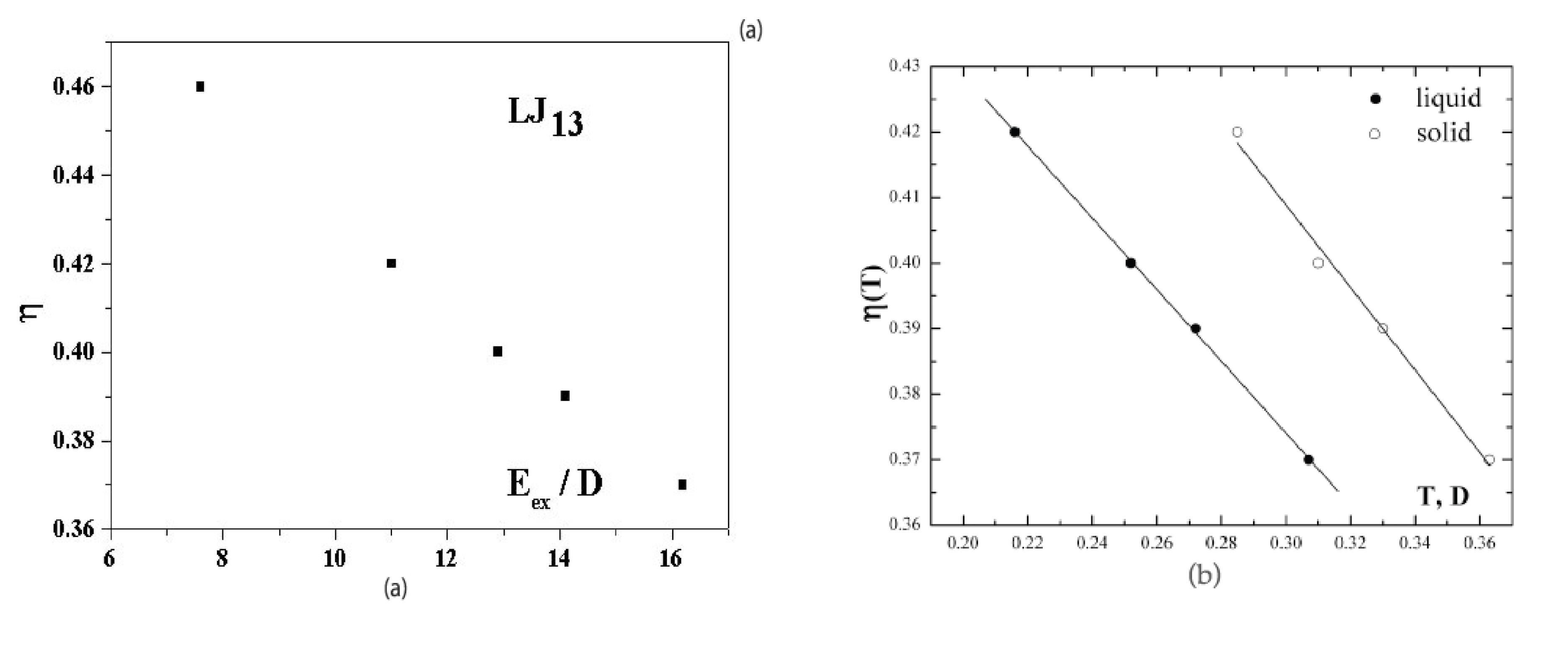
In particular, taking the entropy jump at the melting point to be
and using the energy change in the phase transition in accordance with formula (
8), we obtain, instead of formula (
2) for the melting point of the 13-atom Lennard-Jones cluster,
. This is one half of that given by formula (
2) which ignores the anharmonic character of atom oscillations. This demonstrates that the anharmonic character of atomic motion in the cluster is very important for its properties. In this operation we nevertheless do not take into account the temperature dependence of the entropy jump.
We can also find the range of observable phase coexistence for the 13-atom Lennard-Jones cluster. Let us introduce the probabilities
and
for cluster to be in the solid and liquid aggregate states, respectively, and the ratio of these probabilities is
For definiteness, we arbitrarily take the range of observable phase coexistence to be [
23]
On the other hand, this ratio for an isothermal cluster is
Taking
at the melting point and the transition energy according to formula (
8), we find that the relation (9) is fulfilled in the temperature range
. To account for the temperature dependence of the entropy jump, we take, according to
Figure 8,
. Then the relation (9) leads to a narrower coexistence range, that is
.
Note that in the analysis of the phase transitions of dielectric clusters, we generally used the Lennard-Jones interaction potential [
24,
25] as the pair interaction potential between atoms, and the most of cluster simulations are based on Lennard-Jones clusters. But the only real systems which correspond closely to this description for dielectric clusters are clusters of inert gases, and even macroscopic condensed inert gases are not described accurately by the Lennard-Jones interaction potential [
2,
46,
47]. A short-range interaction potential or a truncated Lennard-Jones potential in which interaction between nearest neighbors dominates, is more suitable for this purpose. Hence, the analysis of the Lennard-Jones systems must be recognized as only a model with respect to real condensed inert gases. Nevertheless, comparison of various characteristics of the phase transition for the Lennard-Jones clusters gives an overall semiquantitative understanding of this phenomenon despite its model character.
Thus, we can get considerable insight into the nature of the cluster phase transition on the basis of computer simulations of 13-atom Lennard-Jones clusters by molecular dynamics. This experience allows us to use a partially-traditional thermodynamic description of the cluster, but the real behavior of clusters is richer than that of macroscopic systems of the same composition, whose properties we traditionally derive from direct application of traditional thermodynamics of macroscopic systems. The principal difference between small clusters and macroscopic atomic systems is a simple consequence of the difference between large and small numbers, with the most dramatic result (to date) being the phase coexistence of clusters over finite bands of temperature and pressure, thus seeming to violate the Gibbs phase rule. This leads to other peculiarities of the cluster phase transitions. Many of these properties reveal themselves in the analysis of the 13-atom cluster with pair interactions between atoms, explicitly for the Lennard-Jones interaction. We refer to this cluster for several reasons. First, this cluster has a completed atomic shell, and the statistical weight of configurational excited states is more than that for the ground state, which allows this cluster to locate in a specific excited configurational state with the probability of one, if it has a suitable specific excitation energy. Second, there are molecular dynamics simulations that reveal detailed information about this cluster. Third, because this cluster is small, the lower configurational excitations are separated by large energy gaps from the ground state and from configurationally excited states at still higher energies. Fourth, fluctuations are relatively small for this cluster, and the properties of the solid and liquid aggregate states may be analyzed separately in the range of phase coexistence.
The discussion of the 13-atom cluster has, thus far, identified melting with promotion of a single particle from the icosahedral shell to the cluster surface. The mobilities of both the promoted “floater" particle and the vacancy in the icosahedral shell are sufficient to allow liquid-like mobility and other liquid-like properties. One might ask whether some kind of phase-transition-like phenomenon might occur when the system has enough energy or a high enough temperature that more particles could be promoted. None of the simulations cited show anything but smooth behavior in caloric curves or other properties, so it seems that the passage to states of higher excitation is smooth for the 13-particle cluster. However larger clusters do exhibit such successive transitions. Lennard-Jones clusters of more than about 45 particles show a clear phase-like form with a liquid-like surface layer and a solid core, in a temperature band between those of the solid and liquid. In fact there are three different coexistence bands for the 55-atom cluster: at the lowest temperatures of coexisting phases, e.g., about 33 K, the solid coexists with the surface-melted phase. Then, around 35 K, the solid, the surface-melted and the fully liquid phases coexist. Then there is a range in which only the surface-melted and liquid phases coexist, and above about 40K, only the liquid is stable [
13,
48,
49,
50,
51,
52,
53]. By examining such systems, we learn the limitations of using only a cluster of a single size, and a magic number size at that, as the basis of drawing general conclusions. We might well see phases with high surface mobility and solid cores in clusters with half or fewer of the surface sites occupied. Another kind of phase that has been conjectured but not yet observed, either in experiments or simulations, would appear in systems whose liquid form has a higher density that the solid, e.g., gallium or water. In clusters of these substances, one might see a phase with a liquid core and solid outer shell, like partly-frozen ice cubes.