Exergy as a Tool for Ecosystem Health Assessment
Abstract
:1. Introduction
2. Other Goal Functions
| Goal Functions | References |
|---|---|
| Multiple systems | |
| Maximum useful power or energy flow | [26,27] |
| Minimum specific dissipation | [28,29] |
| Minimum entropy | [30] |
| Maximum retention time | [31] |
| Ecological systems | |
| Maximum ascendency | [32] |
| Maximum cycling | [33] |
| Maximum biomass | [34] |
| Maximum persistent organic matter | [35,36] |
| Maximum emergy | [37] |
| Maximum exergy stored | [1] |
| Maximum exergy dissipation | [38] |
| Maximum indirect effects | [40] |
| Minimum empower to exergy ratio | [41] |
| Minimum specific dissipation (or minimum specific entropy production) | [62, 100] |
| Maximum Structural Information | [44] |
| Economic systems | |
| Maximum profit | Various authors |
3. Definition
4. Natural History of Exergy
5. Exergy Calculations
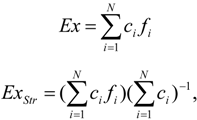
- -
- They break away from the “classical” exergy function, losing, in particular, the property of being pure thermodynamic measures of work and energy (they do not reflect the real capacity of work)
- -
- The calculation of the weighting factors is highly speculative and it is not universally accepted, particularly by biologists.
| Group | Exergy conversion factor | Group | Exergy conversion factor |
|---|---|---|---|
| Minimal cell | 5.8 | Brachiopoda | 109 |
| Bacteria | 8.5–12 | Seedless vascular plants | 158 |
| Archaea | 13.8 | Rotifera | 163 |
| Yeasts | 18 | Insecta | 167–446 |
| Alga | 15–298 | Chironomida | 300 |
| Cyanobacteria | 15 | Moss | 174 |
| Dynophyta | 18 | Crustaceans | 230–300 |
| Green microalgae | 20 | Cladocera | 232 |
| Diatoms | 66 | Copepoda | 240 |
| Macrophyta (alga) | 67–298 | Amphipoda | 290 |
| Rhodophyta | 92 | Mollusca | 297–450 |
| Protozoa | 31-97 | Bivalves | 297 |
| Amoeba | 38 | Gastropoda | 312–450 |
| Gastrotricha | 97 | Gymnosperm | 314 |
| Fungi | 61 | Macrophytes (Phanerogam) | 356–520 |
| Nemertina | 76 | Flowering plants | 393–543 |
| Worms | 91–133 | Fish | 499–800 |
| Cnidaria | 91 | Amphibia | 688 |
| Plathelminthes | 120 | Reptilia | 833 |
| Oligochaeta | 130 | Aves | 980 |
| Nematoda | 133 | Mammalia | 2127 |
| Sponges | 98 | Homo sapiens | 2173 |
6. Applications of Exergy to Specific Problems of Theoretical Ecology
- Increased input gives proportional increase of exergy and power;
- Additional links only affect power and exergy when they increase the overall network throughflow, thus the connection placement is important;
- Food chain prolongation has a positive effect on the power and exergy of the network;
- Reduction of loss of exergy to the environment or as detritus yields a higher power and exergy of the network;
- Faster cycling—detritus is decomposed faster or the transfer rates between two tropic levels are increased—implies higher power and exergy;
- Input of additional exergy or energy recycling flows has more effect the earlier in the food chain the addition takes place.
7. Applications of Exergy to Specific Problems of Aquatic Ecology
8. Exergy as Indicator of Ecosystem Health
9. Exergy and Other Indices and Goal Functions Relations
| Parameter | Exergy, Eco-Exergy, Exergy Index | Structural exergy, Specific Eco-Exergy, Specific Exergy Index | Reference |
|---|---|---|---|
| Total Biomass | Positive | [89,58,92,105,56] | |
| Phytoplankton biomass | Negative | Negative | [99,58,92,105,56] |
| Zooplankton biomass | Positive | Positive | [58,92,105,90] |
| Secchi Disk Transparency | Positive | Positive | [99,91] |
| Bacterial biomass | Positive | Negative | [92,105] |
| Fish biomass | Positive | [58,91] | |
| Benthic biomass | Positive | [60,92,105] | |
| Biodiversity as species richness | Positive | Positive | [57,88,92,105,90] |
| Biodiversity as heterogeneity | Positive | [57,88,92,105] | |
| Shannon–Wiener Index | Positive | Positive | [24,87] |
| Margalef Index | Positive | Positive | [24] |
| Pielou evenness | Positive | Positive | [24] |
| Ratio of zooplankton biomass to phytoplankton biomass | Positive | Positive | [92,105,90,91] |
| Trophic State | Positive | Negative | [89,56,90] |
| Carlson’s Trophic State Index | Negative | Negative | [99] |
| Zooplankton buffer capacity | Positive | [58,90] | |
| Ecological Evaluation Index | Positive | Positive | [18] |
| Fisher Information | Negative | [106] | |
| Emergy | Positive | Positive | [56,107,108] |
| Ascendancy | Positive | Positive | [77,23,109,110,64] |
10. Development of New Ecosystem Health Indices on The Basis of Exergy
11. Use of Exergy for Lake Baikal Ecosystem State Assessment
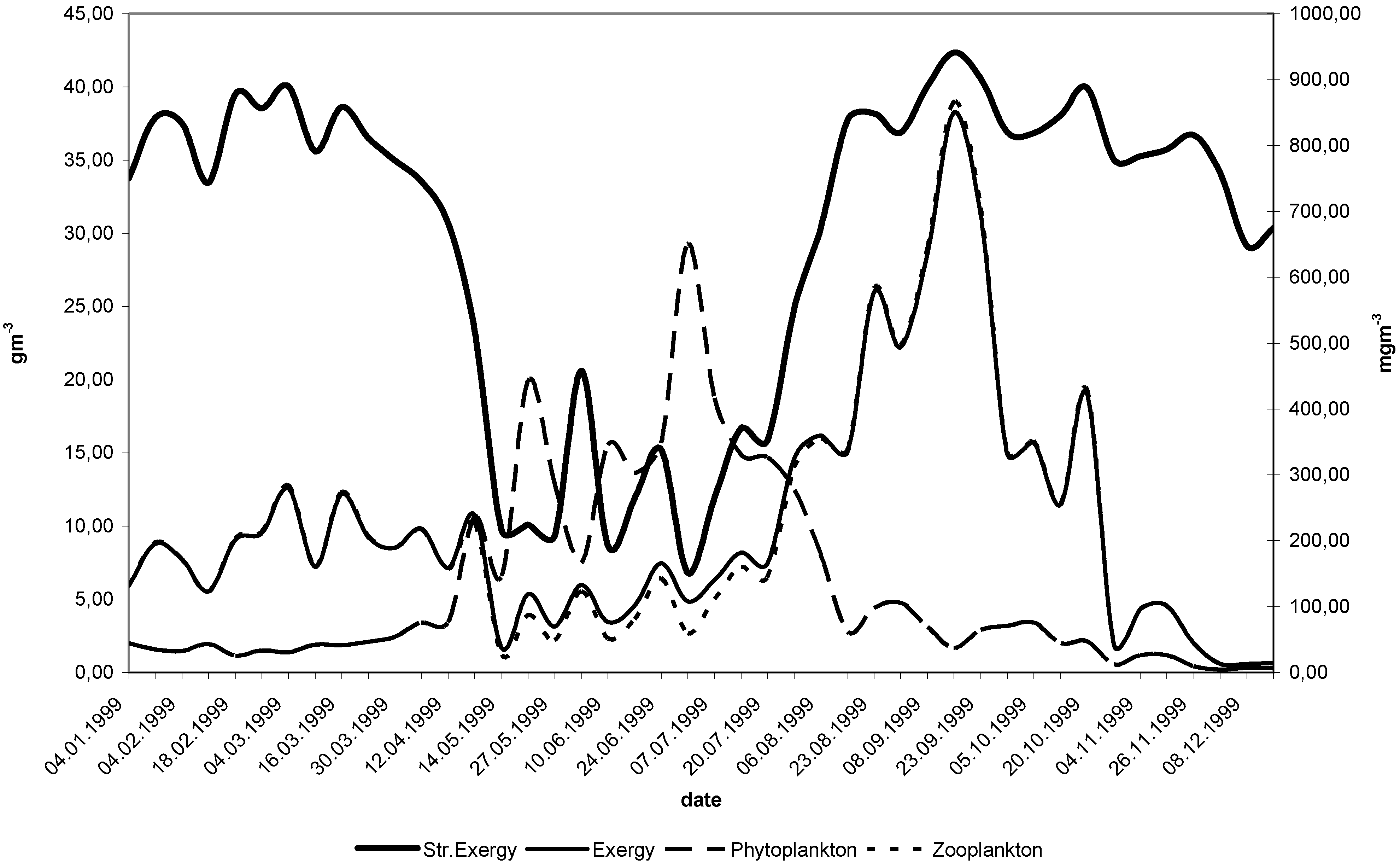
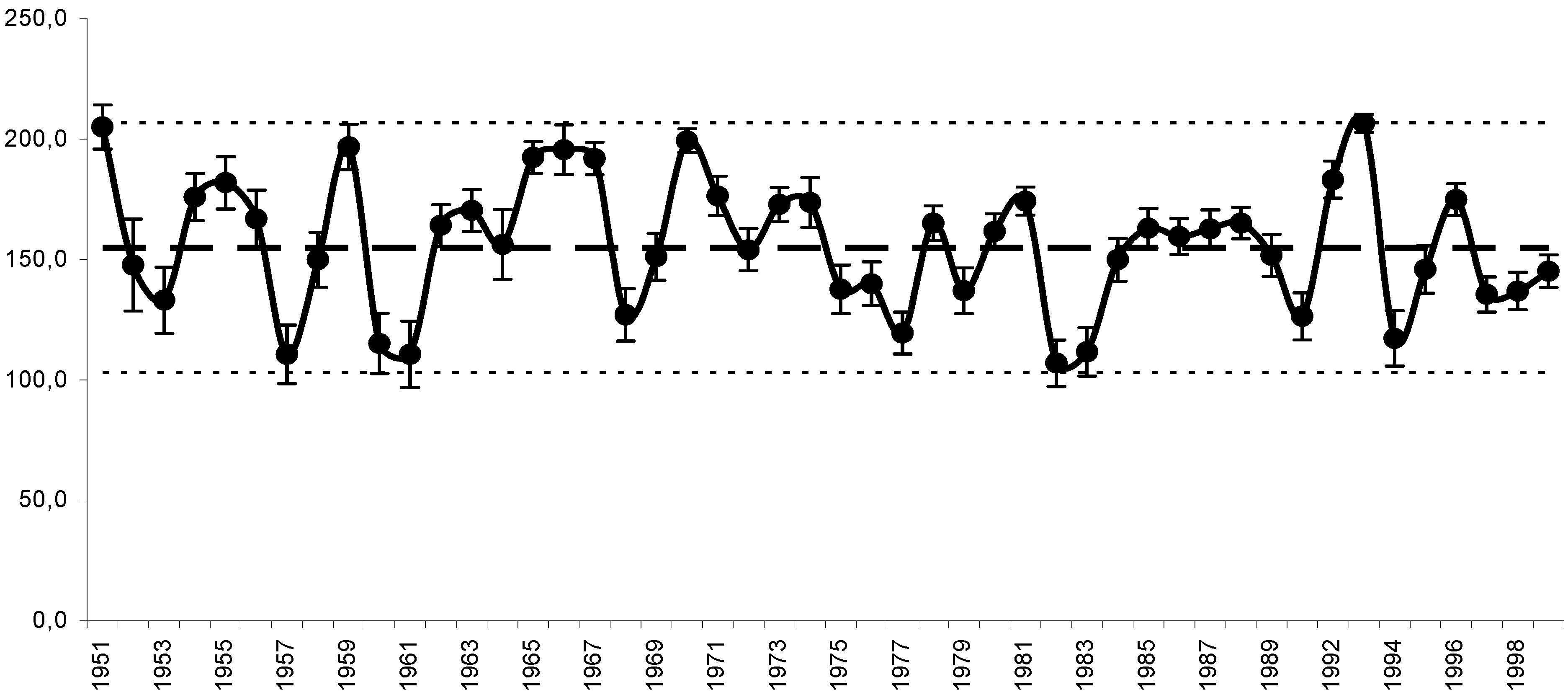
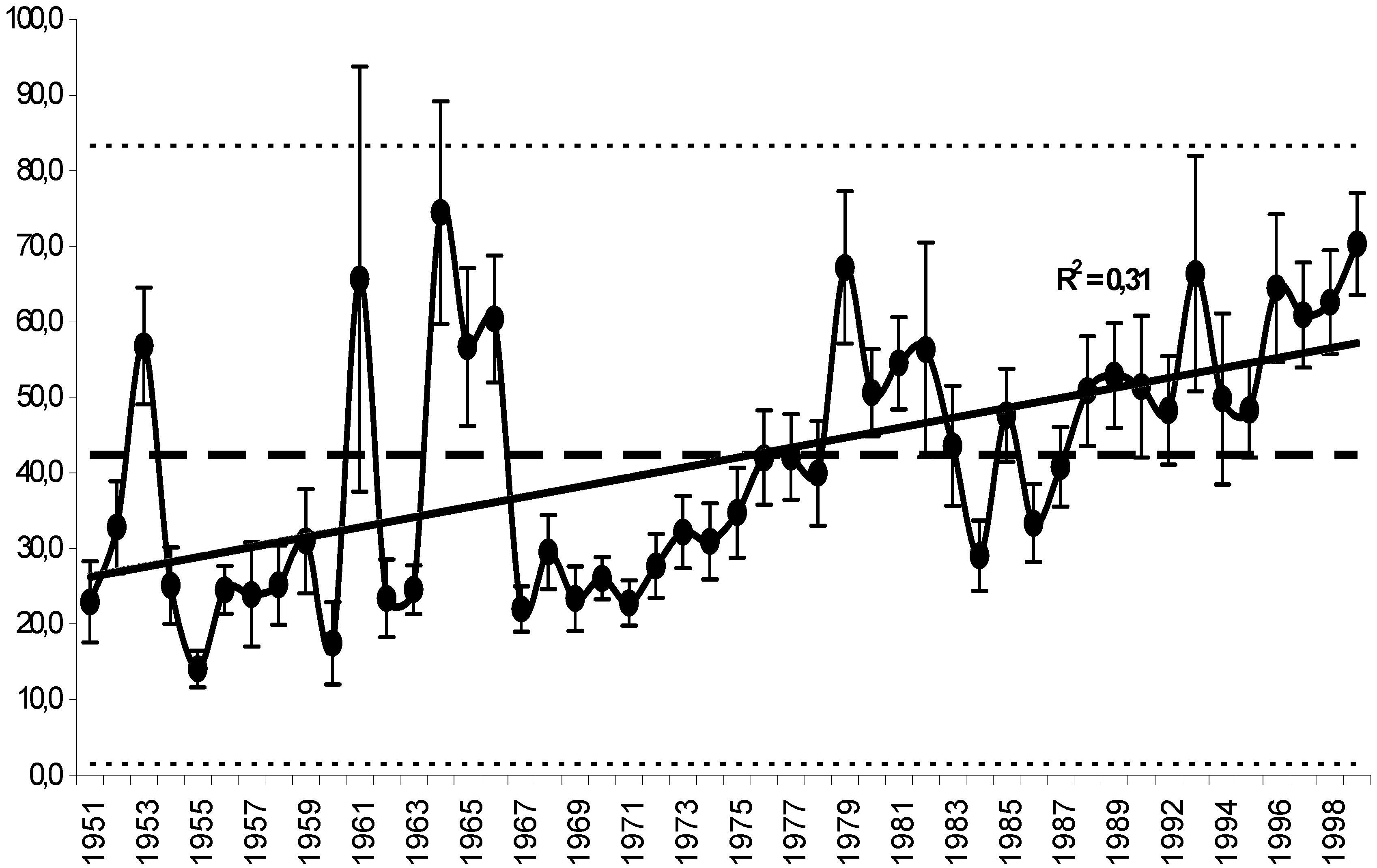
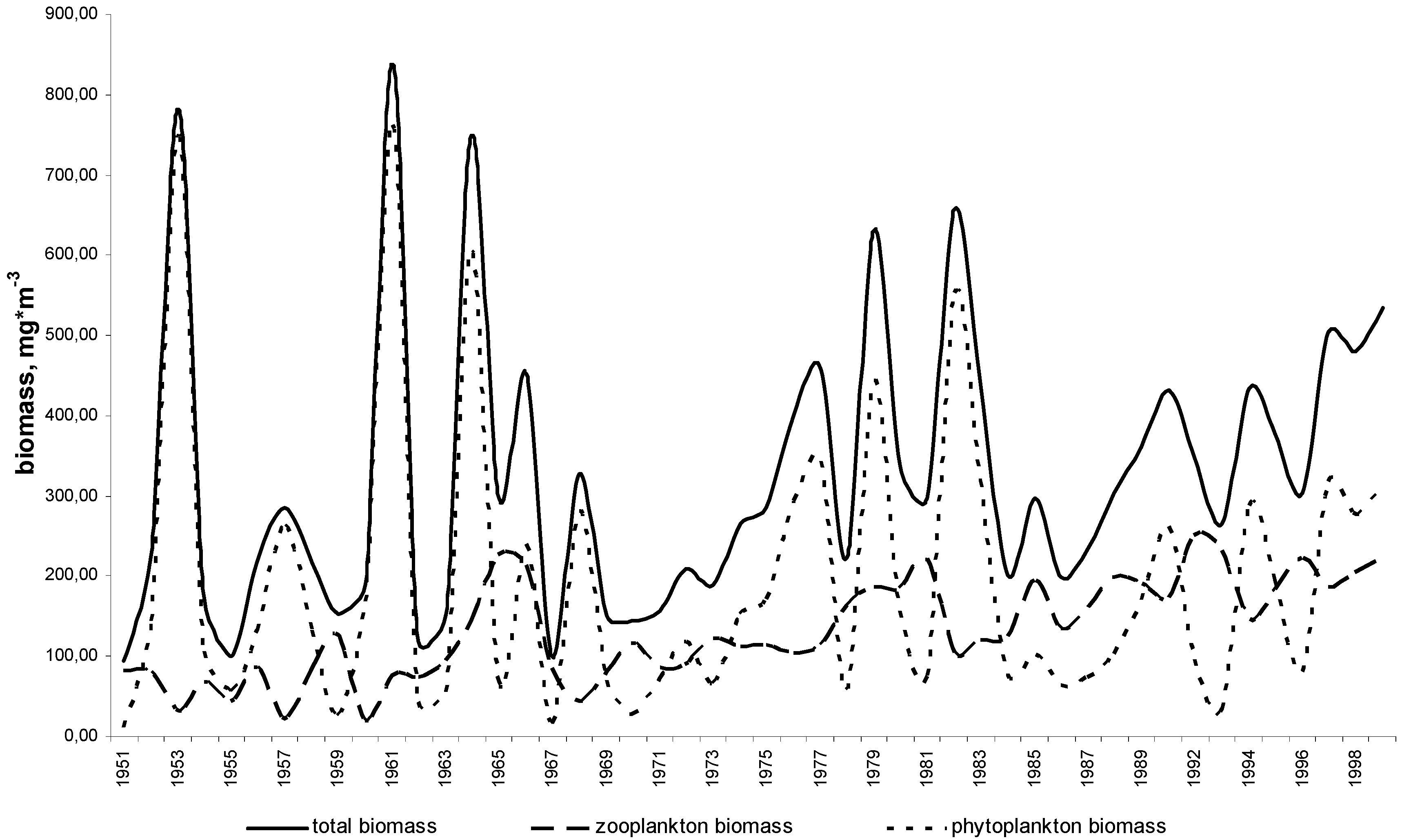
12. Conclusion
Acknowledgments
References
- Mejer, H.F.; Jorgensen, S.E. Energy and ecological buffer capacity. In State of the Art of Ecol. Modell. Environmental Sciences and Applications; Jorgensen, S.E., Ed.; International Society for Ecological Modelling: Copenhagen, Denmark, 1979; pp. 829–846. [Google Scholar]
- Holling, C.S. The resilience of terrestrial ecosystems: local surprise and global change. In Sustainable Development of the Biosphere; Cambridge University Press: Cambridge, UK, 1986; pp. 292–317. [Google Scholar]
- Jørgensen, S.E. Parameters, ecological constraints and exergy. Ecol. Modell. 1992, 62, 163–170. [Google Scholar] [CrossRef]
- Susani, L.; Pulselli, F.M.; Jørgensen, S.E.; Bastianoni, S. Comparison between technological and ecological exergy. Ecol. Modell. 2006, 193, 447–456. [Google Scholar] [CrossRef]
- Odum, H.T. Environmental Accounting: Emergy and Environmental Decision Making; John Wiley and Sons: New York, NY, USA, 1996; p. 384. [Google Scholar]
- Gattie, D.K.; Kellam, N.N.; Turk, H.J. Informing ecological engineering through ecological network analysis, ecological modelling, and concepts of systems and engineering ecology. Ecol. Modell. 2007, 208, 25–40. [Google Scholar] [CrossRef]
- Hellström, D.; Kärrman, E. Exergy analysis and nutrient flows of various sewerage systems. WOSTBE 1997, 35, 135–144. [Google Scholar] [CrossRef]
- Spiegelman, E.; Spiegelman, G.B.; Spiegelman, J. Money as social exergy. J. Bioecon. 2007, 9, 265–277. [Google Scholar] [CrossRef]
- Verdesca, D.; Federici, M.; Torsello, L.; Basosi, R. Exergy-economic accounting for sea-coastal systems: A novel approach. Ecol. Modell. 2006, 193, 132–139. [Google Scholar] [CrossRef]
- Yang, L.; Hu, S.; Chen, D.; Zhang, D. Exergy analysis on eco-industrial systems. SCBCFQ 2006, 49, 281–288. [Google Scholar] [CrossRef]
- Kanoglu, M.; Dincer, I.; Gengel, Y.A. Exergy for better environment and sustainability. Environ. Dev. Sustain. 2008, 11, 971–988. [Google Scholar] [CrossRef]
- Chen, B.; Chen, G.Q. Emergy-based energy and material metabolism of the yellow River basin. CNSNS 2009, 14, 923–934. [Google Scholar] [CrossRef]
- Ayres, R.U. Integrated assessment of the grand nutrient cycles. Environ. Model. Assess. 1997, 2, 107–128. [Google Scholar] [CrossRef]
- Hansell, R.; Bass, B. Holling’s figure-eight model: A technical reevaluation in relation to climate change and biodiversity. Environ. Monit. Assess. 1998, 49, 157–168. [Google Scholar] [CrossRef]
- Koehler, A. Water use in LCA: Managing the planet’s freshwater resources. Int. J. Life Cycle Assessment 2008, 13, 451–455. [Google Scholar] [CrossRef]
- Bösch, M.; Hellweg, S.; Huijbregts, M.; Frischknecht, R. Applying cumulative exergy demand indicators to the ecoevent database. Int. J. Life Cycle Assessment 2007, 12, 181–190. [Google Scholar] [CrossRef]
- Dewulf, J.; Bösch, M.B.; De Meester, B.; Van der Vorst, G.; Van Langenhove, H.; Hellweg, S.; Huijbredts, M.A.J. Cumulative exergy extraction from the natural environment: A comprehensive life cycle impact assessment method for resource accounting. ESTHAG 2007, 41, 8477–8483. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, G.A. Forest growth in the light of the thermodynamic theory of ecological systems. Ecol. Modell. 2008, 216, 102–106. [Google Scholar] [CrossRef]
- Fath, B.C.; Patten, B.C.; Choi, J.S. Complementarity of ecological goal functions. J. theor. Biol. 2001, 208, 493–506. [Google Scholar] [CrossRef] [PubMed]
- Beck, T.B.; Quigley, M.F.; Martin, J.F. Emergy evaluation of food production in urban residential landscapes. Urban Ecosystems 2001, 5, 187–207. [Google Scholar] [CrossRef]
- Brown, M.T.; Cohen, M.J.; Bardi, E.; Ingwersen, W.W. Species diversity in the Florida Everglades, USA: A system approach to calculating biodiversity. Aquat. Sci. 2006, 68, 254–277. [Google Scholar] [CrossRef]
- Brown, M.T.; Vivas, M.B. Landscape development intensity index. Environ. Monit. Assess. 2005, 101, 289–309. [Google Scholar] [CrossRef] [PubMed]
- Mandal, S.; Ray, S.; Roy, S.K. Study of biocomplexity in an aquatic ecosystem through ascendency. Bio. Systems 2009, 95, 30–34. [Google Scholar] [CrossRef] [PubMed]
- Patricio, J.; Ulanovicz, R.; Pardal, M.A.; Marques, J.C. Ascedency as ecological indicator for environmental quality assessment at the ecosystem level: a case study. Hydrobiologia 2006, 555, 19–30. [Google Scholar] [CrossRef]
- Bendoricchio, G.; Jørgensen, S.E. Exergy as goal function of ecosystem dynamic. Ecol. Modell. 1997, 102, 5–15. [Google Scholar] [CrossRef]
- Lotka, A.J. Contribution to the energetics of evolution. PNASA6 1922, 8, 147–151. [Google Scholar] [CrossRef] [PubMed]
- Odum, H.T.; Pinkerton, R.C. Time's speed regulator: the optimum efficiency for maximum power output in physical and biological systems. Am. Sci. 1955, 43, 331–343. [Google Scholar]
- Onsager, L. Reciprocal relations in irreversible processes. PRESCM 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Prigogine, I. Moderation et transformations irreversibles des systemes ouverts. Bulletin de la Classe des Sciences 1945, 31, 600–606. [Google Scholar]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley: New York, NY, USA, 1971; p. 430. [Google Scholar]
- Cheslak, E.F.; Lamarra, V.A. The residence time of energy as a measure of ecological organization. In Energy and Ecological Modelling; Mitsch, W.J., Bossermann, R.W., Klopatek, J.M., Eds.; Elsevier: Amsterdam, Netherlands, 1981; pp. 591–600. [Google Scholar]
- Ulanowicz, R.E. Growth and Development: Ecosystems Phenomenology; Springer: New York, NY, USA, 1986; p. 203. [Google Scholar]
- Morowitz, H.J. Energy Flow in Biology; Academic Press: New York, USA, 1968; p. 120. [Google Scholar]
- Margalef, R. Perspectives in Ecological theory; University Press: Chicago, IL, USA, 1968; p. 122. [Google Scholar]
- Whittaker, R.H.; Woodwell, G.M. Evolution of natural communities. In Ecosystem Structure and Function; Wiens, J.A., Ed.; Oregon State University Press: Corvallis, OR, USA, 1971; pp. 137–159. [Google Scholar]
- O'Neill, R.V.; Hanes, W.F.; Ausmus, B.S.; Richle, D.E. A theoretical basis for ecosystem analysis with particular reference to element cycling. In Mineral Cycling in South-Eastern Ecosystems; Howell, F.G., Gentry, J.B., Smith, M.H., Eds.; Athens University Press: Athens, GA, USA, 1975; pp. 28–40. [Google Scholar]
- Odum, H.T. System Ecology; Wiley: New York, NY, USA, 1983; p. 644. [Google Scholar]
- Schneider, E.D.; Kay, J.J. Complexity and thermodynamics. Towards a new ecology. Futures 1994, 26, 626–647. [Google Scholar] [CrossRef]
- Patten, B.C. Network integration of ecological extremal principles: Exergy, emergy, power, ascendancy and indirect effects. Ecol. Modell. 1995, 79, 75–84. [Google Scholar] [CrossRef]
- Bastianoni, S.; Marchettini, N. Emergy/exergy ratio as a measure of the level of organization of systems. Ecol. Modell. 1997, 99, 33–40. [Google Scholar] [CrossRef]
- Wall, G. Exergy, ecology and democracy. In Proceedings of the International Conference on Energy Systems and Ecology; Szargut, J., Morris, D.R., Steward, F.R., Eds.; ENSEC ’93: Krakow, Poland, 1993; pp. 111–121. [Google Scholar]
- Sengupta, A. Chaos, nonlinearity, complexity: A unified perspective. StudFuzz 2006, 206, 270–352. [Google Scholar]
- Ludovisi, A. Exergy vs. information in ecological successions: Interpreting community changes by a classical thermodynamic approach. Ecol. Modell. 2009, 220, 1566–1577. [Google Scholar] [CrossRef]
- Svirezhev, Y.M. Thermodynamics and ecology. Ecol. Modell. 2000, 132, 11–22. [Google Scholar] [CrossRef]
- Svirezhev, Y.M.; Steinborn, W.H. Exergy of solar radiation: Information approach. Ecol. Modell. 2001, 145, 101–110. [Google Scholar] [CrossRef]
- Park, Y.S.; Lek, S.; Scardi, M.; Verdonschot, P.F.M.; Jørgensen, S.E. Patterning exergy of benthic macroinvertebrate communities using self-organizing maps. Ecol. Modell. 2006, 195, 105–113. [Google Scholar] [CrossRef]
- Coffaro, G.; Bocci, M.; Bendoricchio, G. Application of structural dynamic approach to estimate space variability of primary producers in shallow marine water. Ecol. Modell. 1997, 102, 97–114. [Google Scholar] [CrossRef]
- Jørgensen, S.E. Review and comparison of goal functions in system ecology. Vie Milieu 1994, 44, 11–20. [Google Scholar]
- Jørgensen, S.E. State-of-the-art of Ecological Modelling with emphasis on development of structural dynamic models. Ecol. Modell. 1999, 120, 75–96. [Google Scholar] [CrossRef]
- Jørgensen, S.E. Integration of Ecosystem Theories: A Pattern, 3rd ed.; Kluwer Academic Publisher: Dordrecht, The Netherlands, 2002; p. 428. [Google Scholar]
- Jørgensen, S.E.; Svirezhev, Y.M. Towards a Thermodynamic Theory for Ecological Systems; Elsevier: Amsterdam, The Netherlands, 2004; p. 366. [Google Scholar]
- Fath, B.D.; Jørgensen, S.E.; Patten, B.C.; Straškraba, M. Ecosystem growth and development. Bio. Systems 2004, 77, 213–228. [Google Scholar] [CrossRef] [PubMed]
- Jørgensen, S.E.; Bendoricchio, G. Fundamentals of Ecological Modelling, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2001; p. 530. [Google Scholar]
- Austoni, M.; Giordani, G.; Viaroli, P.; Zaldivar, J.N. Application of specific exergy to macrophytes as an integrated index of environmental quality for coastal lagoons. Ecol. Indic. 2007, 7, 229–238. [Google Scholar] [CrossRef]
- Xu, F.L. Exergy and structural exergy as Ecol. Indic. for the development state of the Lake Chaohu ecosystem. Ecol. Modell. 1997, 99, 41–49. [Google Scholar] [CrossRef]
- Marques, J.C.; Pardal, M.A.; Nielsen, S.N.; Jørgensen, S.E. Analysis of the properties of exergy and biodiversity along an estuarine gradient of eutrophication. Ecol. Modell. 1997, 102, 155–167. [Google Scholar] [CrossRef]
- Marques, J.C.; Nielsen, S.N.; Pardal, M.A.; Jørgensen, S.E. Impact of eutrophication and river management within a framework of ecosystem theories. Ecol. Modell. 2003, 166, 147–168. [Google Scholar] [CrossRef]
- Silow, E.A. The use of two lumped models for the analysis of consequences of external influences on the lake Baikal ecosystem. Ecol. Modell. 1999, 121, 103–113. [Google Scholar] [CrossRef]
- Fonseca, J.C.; Marques, A.M.; Madeira, V.M.C.; Jørgensen, S.E. Nuclear DNA in the determination of weighing factors to estimate exergy from organism biomass. Ecol. Modell. 2000, 126, 179–189. [Google Scholar] [CrossRef]
- Fonseca, J.C.; Pardal, M.A.; Azeiteiro, U.M.; Marques, J.C. Estimation of ecological exergy using weighing parameters determined from DNA contents of organisms—A case study. Hydrobiologia 2002, 475/476, 79–90. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Ladegaard, N.; Debeljak, M.; Marques, J.C. Calculations of exergy for organisms. Ecol. Modell. 2005, 185, 165–175. [Google Scholar] [CrossRef]
- Ludovisi, A. Use of thermodynamic indices as Ecological indicators of the development state of lake ecosystems: Specific dissipation. Ecol. Indic. 2006, 6, 30–42. [Google Scholar] [CrossRef]
- Libralato, S.; Torricelli, P.; Pranovi, F. Exergy as ecosystem indicator: An application to the recovery process of marine benthic communities. Ecol. Modell. 2006, 192, 571–585. [Google Scholar] [CrossRef]
- Vassallo, P.; Fabiano, M.; Vezzulli, L.; Sandulli, R.; Marques, J.C.; Jørgensen, S.E. Assessing the health of coastal marine ecosystems: Aholistic approach based on sediment micro and meio-benthic measures. Ecol. Indic. 2006, 6, 525–542. [Google Scholar] [CrossRef]
- Jørgensen, S.E. Description of aquatic ecosystem’s development by eco-exergy and exergy destruction. Ecol. Modell. 2006, 204, 22–28. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Patten, B.C.; Straškraba, M. Ecosystem emerging: 3. Openness. Ecol. Modell. 1999, 117, 41–64. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Patten, B.C.; Straškraba, M. Ecosystem emerging: 4. Growth. Ecol. Modell. 2000, 126, 249–284. [Google Scholar] [CrossRef]
- Patten, B.C.; Straškraba, M.; Jørgensen, S.E. 1997. Ecosystems emerging: 1. Conservation. Ecol. Modell. 1997, 96, 221–284. [Google Scholar] [CrossRef]
- Straškraba, M.; Jørgensen, S.E.; Patten, B.C. Ecosystem emerging: 2. Dissipation. Ecol. Modell. 1999, 117, 3–39. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Verdonschot, P.; Lek, S. Explanation of the observed structure of functional feeding groups of aquatic macro-invertebrates by an ecological model and maximum exergy principle. Ecol. Modell. 2002, 158, 223–231. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Marques, J.; Nielsen, S.N. Structural changes in an estuary, described by models and using exergy as orientor. Ecol. Modell. 2002, 158, 233–240. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Ray, S.; Berec, L.; Straškraba, M. Improved calibration of eutrophication model by use of the size variation due to succession. Ecol. Modell. 2002, 158, 269–277. [Google Scholar] [CrossRef]
- Jørgensen, S.E. Explanation of ecological rules and observation by application of ecosystem theory and ecological models. Ecol. Modell. 2002, 158, 241–248. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Padisak, J. Does the intermediate disturbance hypothesis comply with thermodynamics? Ecol. Modell. 1996, 323, 9–21. [Google Scholar] [CrossRef]
- Pykh, Y.A.; Kennedy, E.T.; Grant, W.E. An overview of system analysis methods in delineating environmental quality indices. Ecol. Modell. 2000, 130, 25–38. [Google Scholar] [CrossRef]
- Nielsen, S.N. Thermodynamics of an ecosystem interpreted as a hierarchy of embedded systems. Ecol. Modell. 2000, 135, 279–289. [Google Scholar] [CrossRef]
- Mandal, S.; Ray, S.; Ray, S.; Jørgensen, S.E. Investigation of thermodynamic properties in an ecological model developing from ordered to chaotic states. Ecol. Modell. 2007, 204, 40–46. [Google Scholar] [CrossRef]
- Gaucherel, C. Influence of spatial patterns on ecological applications of extremal principles. Ecol. Modell. 2006, 193, 531–542. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Fath, D.B. Modelling the selective adaptation of Darwin’s Finches. Ecol. Modell. 2004, 176, 409–418. [Google Scholar] [CrossRef]
- Jørgensen, S.E. Evolution and exergy. Ecol. Modell. 2006, 203, 490–494. [Google Scholar] [CrossRef]
- Ray, S.; Berec, L.; Straškraba, M.; Jørgensen, S.E. Optimization of exergy and implications of body sizes of phytoplankton and zooplankton in an aquatic ecosystem model. Ecol. Modell. 2001, 140, 219–234. [Google Scholar] [CrossRef]
- Zhang, J.; Jørgensen, S.E.; Tan, C.O.; Beklioglu, M. A structurally dynamic modelling—Lake Mogan, Turkey as a case study. Ecol. Modell. 2003, 164, 103–120. [Google Scholar] [CrossRef]
- Zhang, J.; Jørgensen, S.E.; Beklioglu, M.; Ince, O. Hysteresis in vegetation shift—Lake Mogan prognoses. Ecol. Modell. 2003, 164, 227–238. [Google Scholar] [CrossRef]
- Windhorst, W.; Colijn, F.; Kabuta, S.; Laane, R.P.W.M.; Lenhart, H.-J. Defining a good ecological status of coastal waters—A case study for the Elbe plume. In Managing European Coasts: Past, Present, and Future; Vermaat, J.E., Salomons, W., Bouwer, L., Eds.; Springer-Verlag: Berlin, Germany, 2005; pp. 59–74. [Google Scholar]
- Nielsen, S.N. Examination and optimization of different exergy forms in macrophyte societies. Ecol. Modell. 1997, 102, 115–127. [Google Scholar] [CrossRef]
- Leguerrier, D.; Degre, D.; Niquil, N. Network analysis and inter-ecosystem comparison of two intertidal mudflat food webs (Brouage Mudflat and Aiguillon Cove, SW France). Estuarine Coastal Shelf Sci. 2007, 74, 403–418. [Google Scholar] [CrossRef]
- Zhang, F.J.; Tong, C.F.; Xie, Z.F.; Lu, J.J. Different Ecological indicators used in a re-colonization field study of benthic communities and its compliance with ecosystem theories. Estuarine Coastal Shelf Sci. 2009, 81, 463–469. [Google Scholar]
- Pranovi, F.; da Ponte, F.; Torricelli, P. Historical changes in the structure and functioning of the benthic community in the lagoon of Venice. Estuarine Coastal Shelf Sci. 2008, 76, 753–764. [Google Scholar] [CrossRef]
- Silow, E.A. The changes of ecosystem goal functions in stressed aquatic communities. JLAKES 1998, 10, 421–435. [Google Scholar]
- Xu, F.L.; Jørgensen, S.E.; Tao, S. Ecological indicators for assessing freshwater ecosystem health. Ecol. Modell. 1999, 116, 77–106. [Google Scholar] [CrossRef]
- Xu, F.L.; Jørgensen, S.E.; Tao, S.; Li, B.G. Modelling the effects of ecological engineering on ecosystem health of a shallow eutrophic Chinese Lake (Lake Chao). Ecol. Modell. 1999, 117, 239–260. [Google Scholar] [CrossRef]
- Silow, E.A.; Oh, I.H. Aquatic ecosystem assessment using exergy. Ecol. Indic. 2004, 4, 189–198. [Google Scholar] [CrossRef]
- Jørgensen, S.E. Application of holistic thermodynamic indicators. Ecol. Indic. 2006, 6, 24–29. [Google Scholar] [CrossRef]
- Ye, C.; Xu, Q.; Kong, H.; Shen, Z.; Yan, C. Eutrophication conditions and ecological status in typical bays of Lake Taihu in China. Environ. Monit. Assess. 2007, 135, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.L.; Dawson, R.W.; Tao, S.; Cao, J.; Li, B.G. A method for ecosystem health assessment: An Ecological Modeling Method (EMM) and its application. Hydrobiologia 2001, 443, 159–175. [Google Scholar] [CrossRef]
- Marques, J.C.; Nielsen, S.N.; Pardal, M.A.; Jørgensen, S.E. Impact of eutrophication and river management within a framework of ecosystem theories. Ecol. Modell. 2003, 166, 147–168. [Google Scholar] [CrossRef]
- Nunneri, C.; Lenhart, H.J.; Burkhard, B.; Windhorst, W. Ecological risk as a tool for evaluating the effects of offshore wind farm construction in the North Sea. Reg. Environ. Change 2008, 8, 31–43. [Google Scholar] [CrossRef]
- Xu, F.L.; Lam, K.C.; Zhao, Z.Y.; Zhan, W.; Chen, Y.D.; Tao, S. Marine coastal ecosystem health assessment: A case study of the Tolo Harbour, Hong Kong, China. Ecol. Modell. 2004, 173, 355–370. [Google Scholar] [CrossRef]
- Ludovisi, A.; Poletti, A. Use of thermodynamic indices as Ecological indicators of the development state of lake ecosystems. 2. Exergy and specific exergy indices. Ecol. Modell. 2003, 159, 223–238. [Google Scholar] [CrossRef]
- Ludovisi, A.; Pandolfi, P.; Taticchi, M.I. The strategy of ecosystem development: Specific dissipation as an indicator of ecosystem maturity. J. Theor. Biol. 2005, 235, 33–43. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.L.; Zhao, Z.Y.; Zhan, W.; Zhao, S.S.; Dawson, R.W.; Tao, S. An ecosystem health index methodology (EHIM) for lake ecosystem health assessment. Ecol. Modell. 2005, 188, 327–339. [Google Scholar] [CrossRef]
- Ulgiati, S.; Raugei, M.; Bargigli, S. Overcoming the inadequacy of single-criterion approaches to Life Cycle Assessment. Ecol. Modell. 2006, 190, 432–442. [Google Scholar] [CrossRef]
- Zhu, W.B.; Qiu, H.J.; Chang, X.; Cheng, X. The concept of agricultural prroductivity on ecosystem scale and its measurement. ASC 2006, 5, 707–712. [Google Scholar]
- Müller, F.; Burkhard, B. An ecosystem based framework to link landscape structures, functions and services. In Multifunctional Land Use; Mander, Ü., Wiggering, H., Helming, K., Eds.; Springer: Berlin, Germany, 2007; pp. 37–63. [Google Scholar]
- Silow, E.A. Possibility of using goal functions for estimation of “health” of ecological aquatic systems: exergy. Siberian Ecol. J. 2006, 3, 269–284. [Google Scholar]
- Fath, B.D.; Cabezas, H. Exergy and fisher Information as ecological indices. Ecol. Modell. 2004, 174, 25–35. [Google Scholar] [CrossRef]
- Hau, J.L.; Bakshi, B.R. Promises and problems of emergy analysis. Ecol. Modell. 2004, 178, 215–225. [Google Scholar] [CrossRef]
- Tiezzi, E.; Bastianoni, S.; Marchettini, N. Environmental cost and steady state: The problem of adiabaticity in the emergy value. Ecol. Modell. 1996, 90, 33–37. [Google Scholar] [CrossRef]
- Nielsen, S.N.; Ulanowicz, R.E. On the consistency between thermodynamical and network approaches to ecosystems. Ecol. Modell. 2000, 132, 23–31. [Google Scholar] [CrossRef]
- Ulanowicz, R.E.; Jørgensen, S.E.; Fath, B.D. Exergy, Information and aggradation: An ecosystem reconciliation. Ecol. Modell. 2006, 198, 520–524. [Google Scholar] [CrossRef]
- Svirezhev, Y.M. Nonlinearities in mathematical ecology: Phenomena and models. Would we live in Volterra’s world? Ecol. Modell. 2008, 216, 89–101. [Google Scholar] [CrossRef]
- Fietz, S.; Kobanova, G.; Izmest’eva, L.; Nicklisch, A. Regional, vertical and seasonal distribution of phytoplankton and photosynthetic pigments in Lake Baikal. J. Plankton Res. 2005, 27, 793–810. [Google Scholar] [CrossRef]
- Hampton, S.E.; Izmest’eva, L.R.; Moore, M.V.; Katz, S.L.; Dennis, B.; Silow, E.A. Sixty years of environmental change in the in the world’s largest freshwater lake—Lake Baikal, Siberia. Global Change Biol. 2008, 14, 1947–1958. [Google Scholar] [CrossRef]
- Moore, M.V.; Hampton, S.E.; Izmest’eva, L.R.; Silow, E.A.; Peshkova, E.V.; Pavlov, B.K. Climate Change and the World’s “Sacred Sea”—Lake Baikal, Siberia. BioScience. 2009, 59, 405–417. [Google Scholar] [CrossRef]
- Pislegina, E.V.; Silow, E.A. Long-term dynamics of Baikal zooplankton and climate change. In Presented at Materials of World Lake 13, Wuhan, China, 1–5 November 2009; Available online: http://lake.baikal.ru/ru/library/publication.html?action=show&id=639 (accessed on 5 November 2009).
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Silow, E.A.; Mokry, A.V. Exergy as a Tool for Ecosystem Health Assessment. Entropy 2010, 12, 902-925. https://doi.org/10.3390/e12040902
Silow EA, Mokry AV. Exergy as a Tool for Ecosystem Health Assessment. Entropy. 2010; 12(4):902-925. https://doi.org/10.3390/e12040902
Chicago/Turabian StyleSilow, Eugene A., and Andrew V. Mokry. 2010. "Exergy as a Tool for Ecosystem Health Assessment" Entropy 12, no. 4: 902-925. https://doi.org/10.3390/e12040902
APA StyleSilow, E. A., & Mokry, A. V. (2010). Exergy as a Tool for Ecosystem Health Assessment. Entropy, 12(4), 902-925. https://doi.org/10.3390/e12040902




