Imprecise Shannon’s Entropy and Multi Attribute Decision Making
Abstract
:1. Introduction
| Criterion 1 | Criterion 2 | … | Criterion n | |
|---|---|---|---|---|
| Alternative 1 | X11 | X12 | … | X1n |
| Alternative 2 | X21 | X22 | … | X2n |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| Alternative m | Xm1 | Xm2 | … | Xmn |
| W1 | W2 | … | Wn |
2. Interval Shannon’s Entropy
2.1. Method
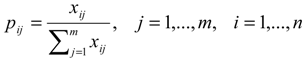
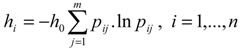 , where h0 is the entropy constant and is equal to (ln m)-1, and pij .ln pij is defined as 0 if pij = 0.
, where h0 is the entropy constant and is equal to (ln m)-1, and pij .ln pij is defined as 0 if pij = 0. 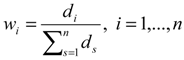 as the degree of importance of attribute i.
as the degree of importance of attribute i. | Criterion 1 | Criterion 2 | … | Criterion n | |
|---|---|---|---|---|
| Alternative 1 | [] | [ ] | ... | [ ] |
| Alternative 2 | [] | [] | ... | [] |
| ⋮ | ⋮ | ⋮ | ⋮ | |
| Alternative m | [] | [] | ... | [] |
| [] | [] | ... | [] |
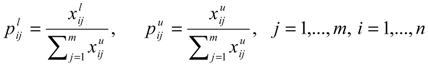
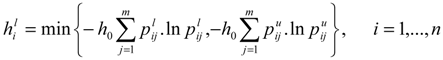
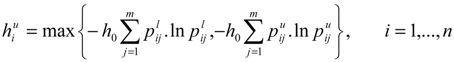
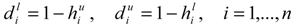
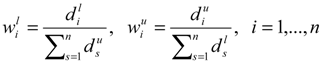 as the lower and upper bound of interval weight of attribute i.
as the lower and upper bound of interval weight of attribute i.  is held.
is held.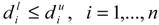 . So
. So 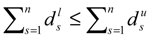 and
and 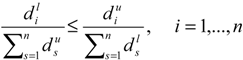 . Therefore
. Therefore  .
.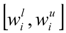 as the weight of i’th criterion obtained from interval entropy method. Notice that if all of the alternatives have deterministic data, then we have and also . So we have and therefore , then (the basic entropy weight). It means if all of the alternatives have deterministic data, then the interval entropy weight leads to the usual entropy weight. As a result, the entropy weight in the case of interval data as the proposed method is well defined, but if at least one of the numbers is interval, all weights will be in the interval form, even for the criteria with crisp data. The reason is that the final entropy weight is dependent on the degree of diversification (di) of all criteria based upon the forth step of the entropy method (
as the weight of i’th criterion obtained from interval entropy method. Notice that if all of the alternatives have deterministic data, then we have and also . So we have and therefore , then (the basic entropy weight). It means if all of the alternatives have deterministic data, then the interval entropy weight leads to the usual entropy weight. As a result, the entropy weight in the case of interval data as the proposed method is well defined, but if at least one of the numbers is interval, all weights will be in the interval form, even for the criteria with crisp data. The reason is that the final entropy weight is dependent on the degree of diversification (di) of all criteria based upon the forth step of the entropy method ( 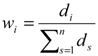 ). So, if a criterion is in the interval form, its degree of diversification will be obtained in the interval form too. Therefore, the weight of crisp criteria will alter based on the alteration of the degree of diversification of an interval criterion in its interval degree of diversification.
). So, if a criterion is in the interval form, its degree of diversification will be obtained in the interval form too. Therefore, the weight of crisp criteria will alter based on the alteration of the degree of diversification of an interval criterion in its interval degree of diversification.2.2. Comparing interval weights
 where m (D), m (E) are the mid-points of interval numbers D and E, and w (D), w (E) are the half-width of D and E. A(≺) may be interpreted as the ‘‘first interval to be inferior to the second interval’’. This procedure states that between two interval numbers with the same mid-point, the less uncertain interval will be the best choice for both of maximization and minimization purposes.
where m (D), m (E) are the mid-points of interval numbers D and E, and w (D), w (E) are the half-width of D and E. A(≺) may be interpreted as the ‘‘first interval to be inferior to the second interval’’. This procedure states that between two interval numbers with the same mid-point, the less uncertain interval will be the best choice for both of maximization and minimization purposes. 2.3. A numerical example
| C1 | C2 | C3 | C4 | |
|---|---|---|---|---|
| A1 | 1451 | [2551,3118] | [40,50] | [153,187] |
| A2 | 843 | [3742,4573] | [63,77] | [459,561] |
| A3 | 1125 | [3312,4049] | [48,58] | [153,187] |
| A4 | 55 | [5309,6488] | [72,88] | [347,426] |
| A5 | 356 | [3709,4534] | [59,71] | [151,189] |
| A6 | 391 | [4884,5969] | [72,88] | [388,474] |
| C1 | C2 | C3 | C4 |
|---|---|---|---|
| 0.343905 | [0.088491,0.108578] | [0.092623,0.115778] | [0.06442,0.343905] |
| 0.199703 | [0.130293,0.159066] | [0.145396,0.178244] | [0.193756,0.199703] |
| 0.266601 | [0.115092,0.140608] | [0.110932,0.134626] | [0.06442,0.266601] |
| 0.012884 | [0.184582,0.225841] | [0.166397,0.203554] | [0.146184,0.012884] |
| 0.084242 | [0.129207,0.15798] | [0.136241,0.164243] | [0.063429,0.084242] |
| 0.092666 | [0.169924,0.207926] | [0.166397,0.203554] | [0.163528,0.092666] |
| C1 | C2 | C3 | C4 | |
|---|---|---|---|---|
| Entropy | 0.851761 | [0.896549,0.984209] | [0.900264,0.988816] | [0.794438,0.851761] |
| Degree of Diversification | 0.148239 | [0.015791,0.103451] | [0.011184,0.099736] | [0.148239,0.205562] |
| Weight | [0.266143,0.458301] | [0.028352,0.319835] | [0.020079,0.308348] | [0.266143,0.635525] |
| Mid-point | 0.362222 | 0.174093 | 0.164213 | 0.450834 |
| Half-width | 0.096079 | 0.145742 | 0.144135 | 0.184691 |
| Rank | 2 | 3 | 4 | 1 |
3. Fuzzy Shannon’s Entropy
3.1. Fuzzy Shannon’s entropy based on α-level sets
| Criterion 1 | Criterion 2 | … | Criterion n | |
|---|---|---|---|---|
| Alternative 1 | ... | |||
| Alternative 2 | ... | |||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| Alternative m | ... | |||
| ... |
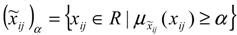 .
. 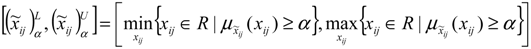
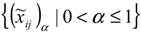 , which are all intervals. Now by using the proposed method in the previous section, we can obtain an interval weight for each α-level set. We name the entropy weight for the i’th fuzzy criterion in α-level as
, which are all intervals. Now by using the proposed method in the previous section, we can obtain an interval weight for each α-level set. We name the entropy weight for the i’th fuzzy criterion in α-level as 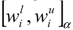 . Now by using every interval ranking method, we can rank all fuzzy criteria in every α-level set. In what follows, we find the weights for the criteria of a real MADM problem.
. Now by using every interval ranking method, we can rank all fuzzy criteria in every α-level set. In what follows, we find the weights for the criteria of a real MADM problem.3.2. Empirical example
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | |
|---|---|---|---|---|---|---|---|
| C1 | (3.400, 5.400, 7.400) | (3.799, 5.800, 7.800) | (4.333, 6.333, 8.266) | (6.199, 8.199, 9.600) | (2.599, 4.599, 6.599) | (5.266, 7.266, 9.066) | (6.733, 8.733, 9.866) |
| C2 | (1.799, 3.799, 5.800) | (3.799, 5.800, 7.800) | (5.533, 7.533, 9.266) | (7, 9,10) | (3, 5,7) | (5.533, 7.533, 9.266) | (3.799, 5.800, 7.800) |
| C3 | (3.799, 5.800, 7.733) | (3.799, 5.800, 7.733) | (3.799, 5.800, 7.733) | (6.333, 8.333, 9.600) | (3.799, 5.800, 7.733) | (5.266, 7.266, 9) | (5.133, 7.133, 8.866) |
| C4 | (4.066, 6.066, 8.066) | (5.800, 7.800, 9.333) | (5.800, 7.800, 9.333) | (5.800, 7.800, 9.333) | (1.933, 3.933, 5.933) | (5.800, 7.800, 9.333) | (4.066, 6.066, 8.066) |
| C5 | (4.599, 6.599, 8.533) | (5.266, 7.266, 8.933) | (5.266, 7.266, 8.933) | (5.266, 7.266, 8.933) | (3.133, 5.133, 7) | (5.266, 7.266, 8.933) | (4.599, 6.599, 8.533) |
| C6 | (2.866, 4.866, 6.866) | (4.866, 6.866, 8.666) | (5.400, 7.400, 9.066) | (5.533, 7.533, 9.199) | (3.400, 5.400, 7.400) | (6.733, 8.733, 9.866) | (3.799, 5.800, 7.733) |
| C7 | (2.466, 4.466, 6.466) | (4.866, 6.866, 8.666) | (4.866, 6.866, 8.666) | (5.533, 7.533, 9.133) | (4.466, 6.466, 8.399) | (6.466, 8.466, 9.600) | (3.400, 5.400, 7.333) |
| C8 | (4.466, 6.466, 8.199) | (4.466, 6.466, 8.199) | (4.466, 6.466, 8.199) | (4.466, 6.466, 8.199) | (2.599, 4.599, 6.599) | (2.599, 4.599, 6.599) | (4.466, 6.466, 8.199) |
| C9 | (2.333, 4.333, 6.333) | (5.133, 7.133, 8.866) | (5.133, 7.133, 8.866) | (5.133, 7.133, 8.866) | (2.866, 4.866, 6.866) | (2.866, 4.866, 6.866) | (5.133, 7.133, 8.866) |
| C10 | (5.533, 7.533, 9.199) | (3.400, 5.400, 7.400) | (3.533, 5.533, 7.466) | (2.266, 4.199, 6.133) | (3.933, 5.933, 7.933) | (3.799, 5.800, 7.800) | (3.799, 5.800, 7.800) |
| C11 | (2.466, 4.466, 6.466) | (4.066, 6.066, 8.066) | (5.400, 7.400, 9) | (5.133, 7.133, 8.866) | (6.733, 8.733, 9.866) | (6.599, 8.600, 9.800) | (3, 5,7) |
| C12 | (2.133, 4.066, 6.066) | (4.333, 6.333, 8.266) | (6.866, 8.866, 9.933) | (7, 9,10) | (3.799, 5.800, 7.733) | (5.266, 7.266, 9) | (5.266, 7.266, 9) |
| C13 | (3.400, 5.400, 7.400) | (5.400, 7.400, 9.199) | (5.800, 7.800, 9.399) | (2.200, 4.066, 6.066) | (0.866, 2.466, 4.466) | (6.733, 8.733, 9.866) | (2.866, 4.866, 6.866) |
| C14 | (5.133, 7.133, 8.866) | (3.400, 5.400, 7.400) | (3.533, 5.533, 7.466) | (2.133, 3.933, 5.866) | (2.733, 4.733, 6.666) | (5.133, 7.133, 8.866) | (3.533, 5.533, 7.533) |
| C15 | (4.599, 6.599, 8.533) | (2.733, 4.733, 6.733) | (4.199, 6.199, 8.199) | (2.333, 4.333, 6.333) | (1.133, 2.866, 4.866) | (6.333, 8.333, 9.666) | (1.533, 3.400, 5.400) |
| C16 | (3.666, 5.666, 7.666) | (5, 7,8.800) | (4.066, 6.066, 7.933) | (2.200, 4.199, 6.199) | (1.666, 3.400, 5.333) | (5.400, 7.400, 9.066) | (3.266, 5.266, 7.266) |
| α = 0.1 | α = 0.3 | α = 0.5 | |||||
| [] | Rank | [] | Rank | [] | Rank | ||
| C1 | [0.001106, 2.678872] | 9 | [0.001686, 1.798292] | 9 | [0.002775, 1.114091] | 9 | |
| C2 | [0.001769, 2.870533] | 8 | [0.002652, 1.936326] | 8 | [0.0043, 1.210006] | 7 | |
| C3 | [0.000477, 2.64328] | 11 | [0.000737, 1.764269] | 12 | [0.001227, 1.081136] | 14 | |
| C4 | [0.001264, 2.626005] | 13 | [0.00187, 1.762589] | 13 | [0.002994, 1.092323] | 11 | |
| C5 | [0.000371, 2.536726] | 15 | [0.000538, 1.689477] | 16 | [0.000844, 1.031383] | 16 | |
| C6 | [0.0009, 2.634344] | 12 | [0.001372, 1.764558] | 11 | [0.002255, 1.089002] | 13 | |
| C7 | [0.000914, 2.664014] | 10 | [0.00138, 1.7839] | 10 | [0.002252, 1.100421] | 10 | |
| C8 | [0.000553, 2.9384] | 7 | [0.00083, 1.96164] | 7 | [0.001347, 1.202042] | 8 | |
| C9 | [0.001173, 2.944939] | 6 | [0.001726, 1.976302] | 6 | [0.002749, 1.222171] | 6 | |
| C10 | [0.000727, 3.095741] | 5 | [0.001058, 2.073005] | 5 | [0.001672, 1.274704] | 5 | |
| C11 | [0.001338, 2.606493] | 14 | [0.002036, 1.751892] | 14 | [0.003342, 1.08908] | 12 | |
| C12 | [0.00143, 2.525463] | 16 | [0.002167, 1.698879] | 15 | [0.003546, 1.058105] | 15 | |
| C13 | [0.003731, 3.214919] | 3 | [0.005511, 2.198219] | 2 | [0.008824, 1.405822] | 2 | |
| C14 | [0.001095, 3.147682] | 4 | [0.001593, 2.112584] | 4 | [0.002515, 1.304852] | 4 | |
| C15 | [0.003194, 3.582455] | 1 | [0.004714, 2.438022] | 1 | [0.007556, 1.544431] | 1 | |
| C16 | [0.001725, 3.227949] | 2 | [0.002508, 2.17573] | 3 | [0.003956, 1.354434] | 3 | |
| α = 0.7 | α = 0.9 | ||||||
| [] | Rank | [] | Rank | ||||
| C1 | [0.005295, 0.592758] | 9 | [0.015317, 0.205936] | 9 | |||
| C2 | [0.0081, 0.655912] | 6 | [0.023193, 0.244052] | 4 | |||
| C3 | [0.002364, 0.560752] | 15 | [0.0069, 0.175001] | 15 | |||
| C4 | [0.005568, 0.58199] | 11 | [0.01574, 0.203552] | 10 | |||
| C5 | [0.001542, 0.530417] | 16 | [0.004288, 0.159366] | 16 | |||
| C6 | [0.004295, 0.574551] | 13 | [0.012403, 0.193142] | 13 | |||
| C7 | [0.004264, 0.579997] | 12 | [0.012259, 0.194217] | 12 | |||
| C8 | [0.002542, 0.622921] | 8 | [0.007297, 0.193332] | 14 | |||
| C9 | [0.005095, 0.646322] | 7 | [0.014376, 0.218216] | 7 | |||
| C10 | [0.003077, 0.663629] | 5 | [0.008639, 0.208405] | 11 | |||
| C11 | [0.006354, 0.584896] | 10 | [0.018306, 0.211323] | 7 | |||
| C12 | [0.006723, 0.570882] | 14 | [0.019317, 0.209957] | 8 | |||
| C13 | [0.016453, 0.798981] | 2 | [0.046753, 0.345504] | 1 | |||
| C14 | [0.004628, 0.686627] | 4 | [0.012987, 0.226037] | 5 | |||
| C15 | [0.014128, 0.858899] | 1 | [0.040333, 0.346101] | 2 | |||
| C16 | [0.007276, 0.725392] | 3 | [0.020421, 0.256179] | 3 | |||
4. Conclusions
Acknowledgements
References
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: NewYork, NY, USA, 1980. [Google Scholar]
- Chu, A.T.W.; Kalaba, R.E.; Spingarn, K. A comparison of two methods for determining the weights of belonging to fuzzy sets. J. Optimiz. Theor. App. 1979, 27, 531–538. [Google Scholar] [CrossRef]
- Hwang, C.L.; Lin, M.J. Group Decision Making under Multiple Criteria: Methods and Applications; Springer: Berlin, Germany, 1987. [Google Scholar]
- Choo, E.U.; Wedley, W.C. Optimal criterion weights in repetitive multicriteria decision-making. J. Oper. Res. Soc. 1985, 36, 983–992. [Google Scholar] [CrossRef]
- Fan, Z.P. Complicated multiple attribute decision making: Theory and applications. Ph.D Dissertation, Northeastern University, Shenyang, China, 1996. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Islam, S.; Roy, T.K. A new fuzzy multi-objective programming: Entropy based geometric programming and its application of transportation problems. Eur. J. Oper. Res. 2006, 173, 387–404. [Google Scholar] [CrossRef]
- Güneralpa, B.; Gertnera, G.; Mendozaa, G.; Anderson, A. Evaluating probabilistic data with a possibilistic criterion in land-restoration decision-making: Effects on the precision of results. Fuzzy Set Syst. 2007, 158, 1546–1560. [Google Scholar] [CrossRef]
- Sengupta, A.; Pal, T.K. On comparing interval numbers. Eur. J. Oper. Res. 2000, 127, 28–43. [Google Scholar] [CrossRef]
- Chanas, S.; Zielisnski, P. Ranking fuzzy interval numbers in the setting of random sets—further results. Inform. Sci. 1999, 117, 191–200. [Google Scholar] [CrossRef]
- Delgado, M.; Vila, M.A.; Voxman, W. A fuzziness measure for fuzzy numbers: Applications. Fuzzy Set Syst. 1998, 93, 125–135. [Google Scholar] [CrossRef]
- Delgado, M.; Vila, M.A.; Voxman, W. On a canonical representation of fuzzy numbers. Fuzzy Set Syst. 1998, 94, 205–216. [Google Scholar] [CrossRef]
- Moore, R.E. Method and Application of Interval Analysis; SIAM: Philadelphia, PA, USA, 1979. [Google Scholar]
- Sengupta, A.; Pal, T.K. A-index for ordering interval numbers. In Proceeding of the Indian Science Congress 1997; Delhi University: Delhi, India, 1997. [Google Scholar]
- Wang, T.C.; Chang, T.H. Application of TOPSIS in evaluating initial training aircraft under a fuzzy environment. Expert Syst. Appl. 2007, 33, 870–880. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lotfi, F.H.; Fallahnejad, R. Imprecise Shannon’s Entropy and Multi Attribute Decision Making. Entropy 2010, 12, 53-62. https://doi.org/10.3390/e12010053
Lotfi FH, Fallahnejad R. Imprecise Shannon’s Entropy and Multi Attribute Decision Making. Entropy. 2010; 12(1):53-62. https://doi.org/10.3390/e12010053
Chicago/Turabian StyleLotfi, Farhad Hosseinzadeh, and Reza Fallahnejad. 2010. "Imprecise Shannon’s Entropy and Multi Attribute Decision Making" Entropy 12, no. 1: 53-62. https://doi.org/10.3390/e12010053
APA StyleLotfi, F. H., & Fallahnejad, R. (2010). Imprecise Shannon’s Entropy and Multi Attribute Decision Making. Entropy, 12(1), 53-62. https://doi.org/10.3390/e12010053




