Fisher Information and Semiclassical Treatments
Abstract
:1. Introduction
2. Background Notions
2.1. HO’s coherent states
2.2. HO-expressions
2.3. Husimi probability distribution
2.4. Wehrl entropy
3. Fisher’s Information Measure
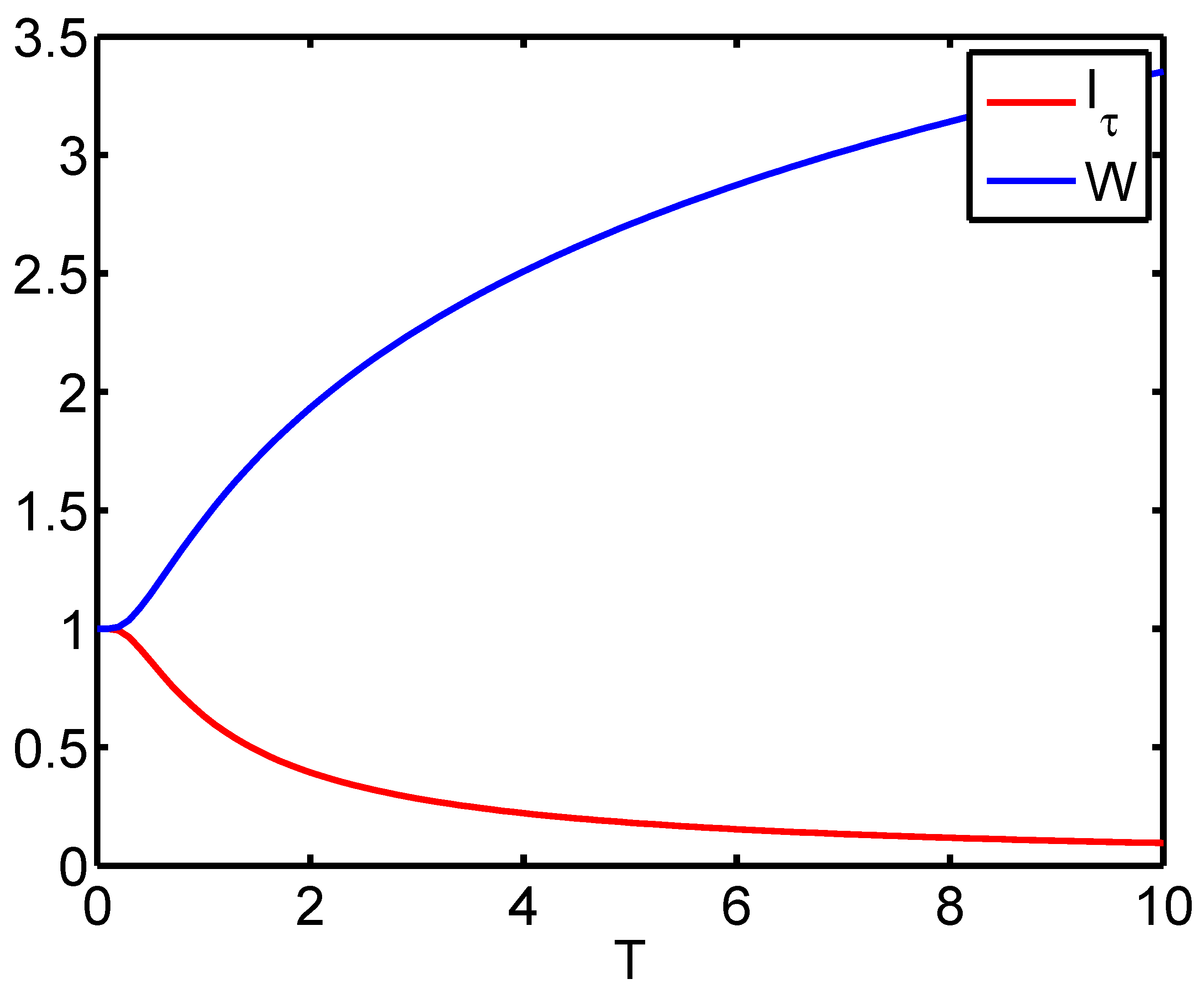
4. Fisher, Thermodynamics’ Third Law, and Thermodynamic Quantities
5. HO-Semiclassical Fisher’s Measure
5.1. MaxEnt approach
5.2. Delocalization
5.3. Second moment of the Husimi distribution
6. Thermodynamics-Like Relations
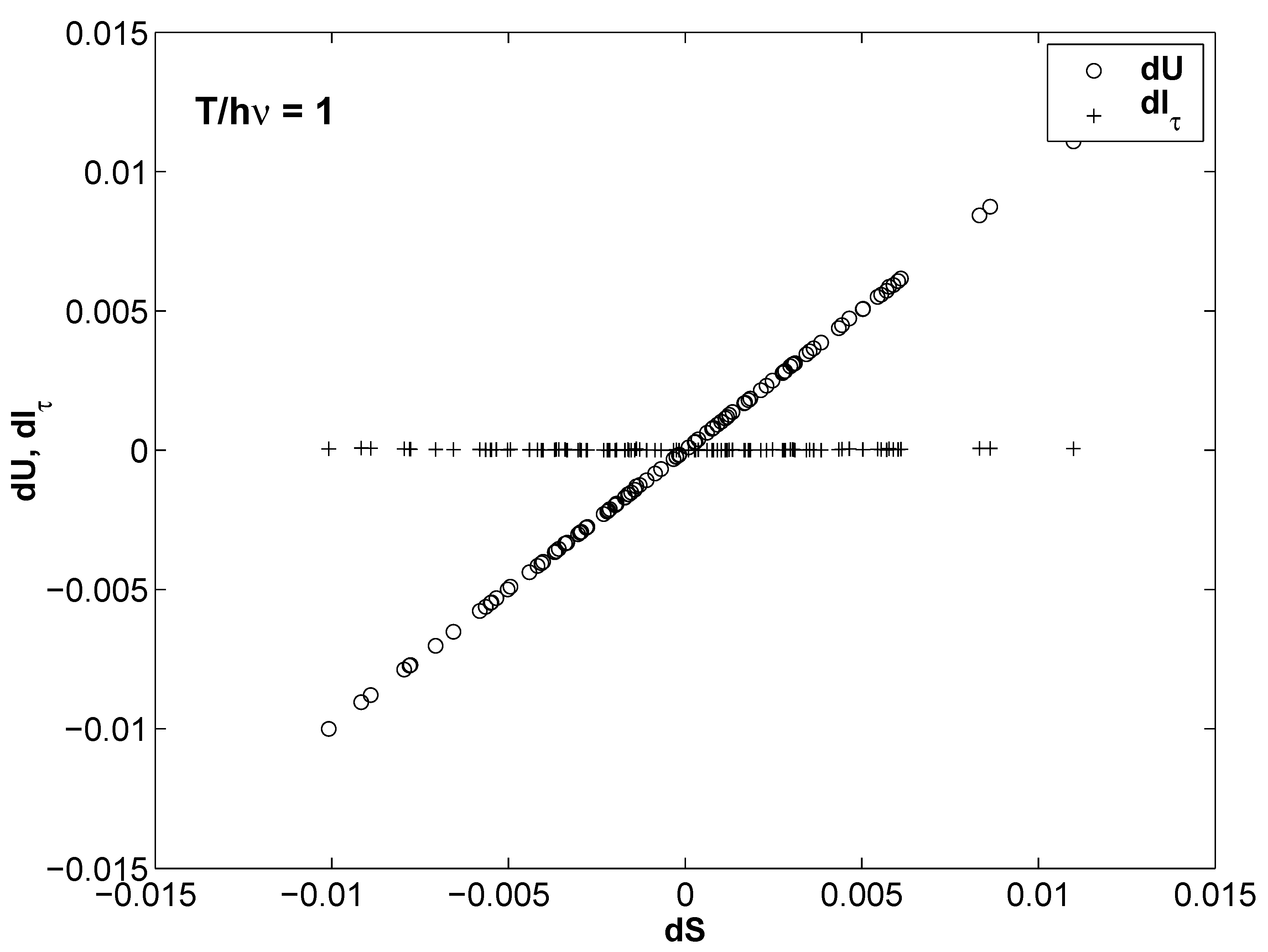
- part of it originates from excitation energy and
- the remaining is accounted for by phase space delocalization.
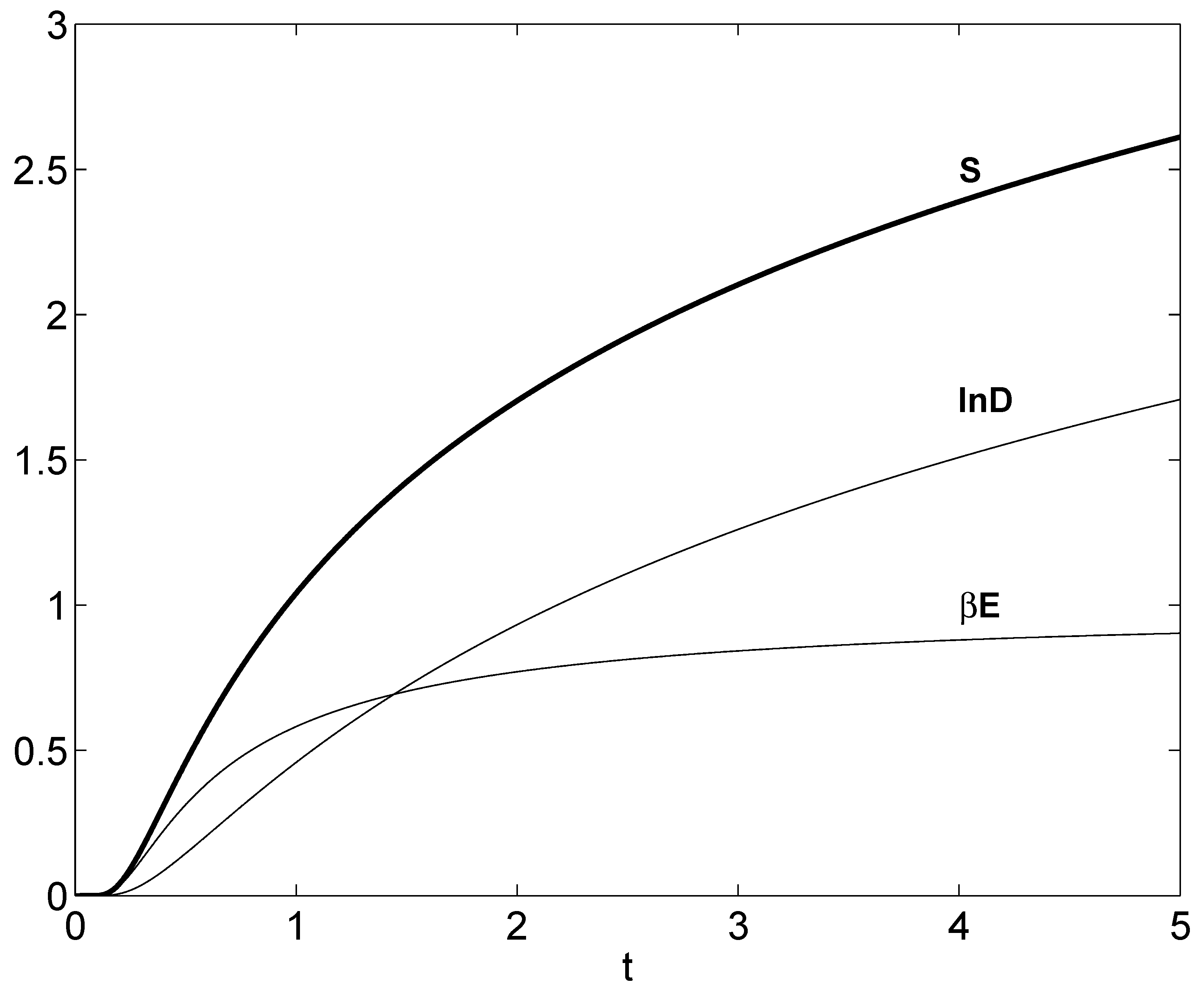
7. On Thermal Uncertainties
- from the excitation energy, that supplies a contribution and
- from the delocalization factor D.
8. Degrees of Purity Relations
8.1. Semiclassical purity
8.2. Quantal purity
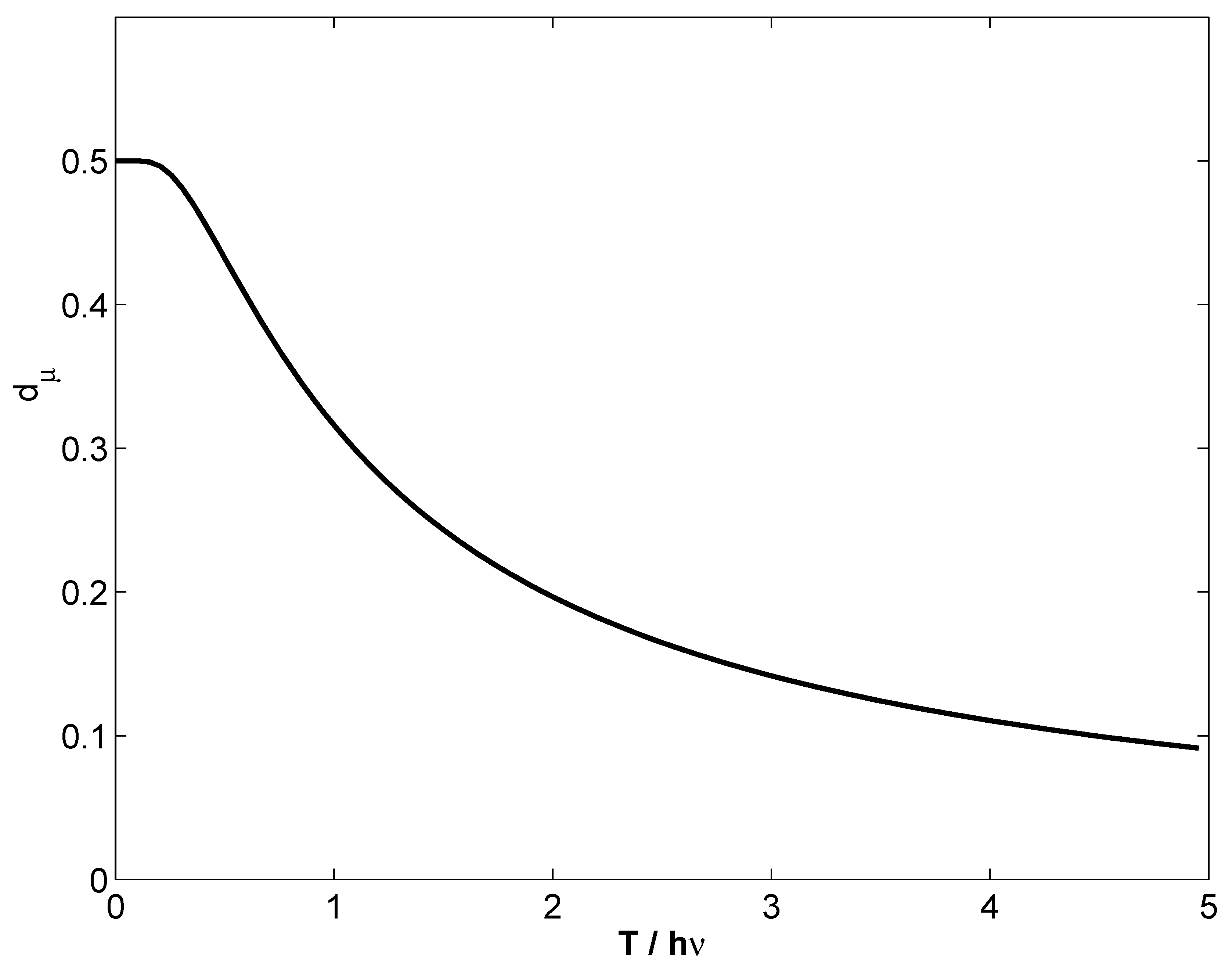
9. Conclusions
- a connection between Wehrl’s entropy and (cf. Equation (25)),
- an interpretation of as the HO’s ground state occupation probability (cf. Equation (26)),
- an interpretation of proportional to the HO’s specific heat (cf. Equation (30)),
- the possibility of expressing the HO’s entropy as a sum of two terms, one for each of the above FIM realizations (cf. Equation (31)),
- a new form of Heisenberg’s uncertainty relations in Fisher terms (cf. Equation (73)),
- that efficient -estimation can be achieved with at all temperatures, as the minimum Cramer–Rao value is always reached (cf. Equation (24)).
- established that the semiclassical Fisher measure contains all relevant statistical quantum information,
- shown that the Husimi distributions are MaxEnt ones, with the semiclassical excitation energy as the only constraint,
- complemented the Lieb bound on the Wehrl entropy using ,
- observed in detailed fashion how delocalization becomes the counterpart of energy fluctuations,
- written down the difference between the semiclassical and quantal entropy also in terms,
- provided a relation between energy excitation and degree of delocalization,
- shown that the derivative of twice the uncertainty function with respect to is the Planck constant ℏ,
- established a semiclassical uncertainty relation in terms of the semiclassical purity , and
- expressed both and the quantal degree of purity in terms of .
Acknowledgements
References and Notes
- Frieden, B.R. Science from Fisher Information, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [Green Version]
- Wootters, W.K. The acquisition of information from quantum measurements. PhD Dissertation, University of Texas, Austin, TX, USA, 1980. [Google Scholar] [Green Version]
- Frieden, B.R.; Soffer, B.H. Lagrangians of physics and the game of Fisher-information transfer. Phys. Rev. E 1995, 52, 2274–2286. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A.R.; Plastino, A. Rènyi entropies and Fisher informations as measures of nonextensivity in a Tsallis setting. Physica A 1998, 258, 446–457. [Google Scholar] [CrossRef]
- Frieden, B.R.; Plastino, A.; Plastino, A.R.; Soffer, H. Fisher-based thermodynamics: Its Legendre transformations and concavity properties. Phys. Rev. E 1999, 60, 48–53. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A.; Plastino, A.R.; Casas, M. How fundamental is the character of thermal uncertainty relations? Phys. Lett. A 2002, 302, 156–162. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Symmetries of the Fokker-Planck equation and the Fisher-Frieden arrow of time. Phys. Rev. E 1996, 54, 4423–4426. [Google Scholar] [CrossRef]
- Plastino, A.; Plastino, A.R.; Miller, H.G. On the relationship between the Fisher-Frieden-Soffer arrow of time, and the behaviour of the Boltzmann and Kullback entropies. Phys. Lett. A 1997, 235, 129–134. [Google Scholar] [CrossRef]
- Anderson, A.; Halliwell, J.J. Information-theoretic measure of uncertainty due to quantum and thermal fluctuations. Phys. Rev. D 1993, 48, 2753–2765. [Google Scholar] [CrossRef]
- Dimassi, M.; Sjoestrand, J. Spectral Asymptotics in the Semiclassical Limit; Cambridge Univesity Press: Cambridge, UK, 1999. [Google Scholar] [Green Version]
- Brack, M.; Bhaduri, R.K. Semiclassical Physics; Addison-Wesley: Boston, MA, USA, 1997. [Google Scholar] [Green Version]
- Wehrl, A. On the relation between classical and quantum entropy. Rep. Math. Phys. 1979, 16, 353–358. [Google Scholar] [CrossRef]
- Lieb, E.H. Proof of an entropy conjecture of wehrl. Commun. Math. Phys. 1978, 62, 35–41. [Google Scholar] [CrossRef]
- Schnack, J. Thermodynamics of the harmonic oscillator using coherent states. Europhys. Lett. 1999, 45, 647–652. [Google Scholar] [CrossRef]
- Klauder, J.R.; Skagerstam, B.S. Coherent States; World Scientific: Singapore, 1985. [Google Scholar] [Green Version]
- Pathria, R.K. Statistical Mechanics; Pergamon Press: Exeter, UK, 1993. [Google Scholar] [Green Version]
- Pennini, F.; Plastino, A. Heisenberg–Fisher thermal uncertainty measure. Phys. Rev. E 2004, 69, 057101:1–57101:4. [Google Scholar] [CrossRef]
- Wigner, E.P. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Wlodarz, J.J. Entropy and wigner distribution functions revisited. Int. J. Theor. Phys. 2003, 42, 1075–1084. [Google Scholar] [CrossRef]
- Husimi, K. Some formal properties of the density matrix. Proc. Phys. Math. Soc. JPN 1940, 22, 264–283. [Google Scholar]
- O’ Connel, R.F.; Wigner, E.P. Some properties of a non-negative quantum-mechanical distribution function. Phys. Lett. A 1981, 85, 121–126. [Google Scholar] [CrossRef]
- Mizrahi, S.S. Quantum mechanics in the Gaussian wave-packet phase space representation. Physica A 1984, 127, 241–264. [Google Scholar] [CrossRef]
- Mizrahi, S.S. Quantum mechanics in the Gaussian wave-packet phase space representation II: Dynamics. Physica A 1986, 135, 237–250. [Google Scholar] [CrossRef]
- Mizrahi, S.S. Quantum mechanics in the gaussian wave-packet phase space representation III: From phase space probability functions to wave-functions. Physica A 1988, 150, 541–554. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A. Escort Husimi distributions, Fisher information and nonextensivity. Phys. Lett. A 2004, 326, 20–26. [Google Scholar] [CrossRef]
- Cramer, H. Mathematical Methods of Statistics; Princeton University Press: Princeton, NJ, USA, 1946. [Google Scholar] [Green Version]
- Rao, C.R. Information and accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc. 1945, 37, 81–91. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics I. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Jaynes, E.T. Papers on Probability, Statistics and Statistical Physics; Rosenkrantz, R.D., Ed.; Kluwer Academic Publishers: Norwell, MA, USA, 1987. [Google Scholar] [Green Version]
- Katz, A. Principles of Statistical Mechanics: The Information Theory Approach; Freeman and Co.: San Francisco, CA, USA, 1967. [Google Scholar] [Green Version]
- Sugita, A.; Aiba, H. Second moment of the Husimi distribution as a measure of complexity of quantum states. Phys. Rev. E 2002, 65, 36205:1–36205:10. [Google Scholar] [CrossRef]
- Mandelbrot, B. The role of sufficiency and of estimation in thermodynamics. Ann. Math. Stat. 1962, 33, 1021–1038. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A. Power-law distributions and Fisher’s information measure. Physica A 2004, 334, 132–138. [Google Scholar] [CrossRef]
- Dodonov, V.V. Purity- and entropy-bounded uncertainty relations for mixed quantum states. J. Opt. B Quantum Semiclass. Opt. 2002, 4, S98–S108. [Google Scholar] [CrossRef]
- Munro, W.J.; James, D.F.V.; White, A.G.; Kwiat, P.G. Maximizing the entanglement of two mixed qubits. Phys. Rev. A 2003, 64, 30302:1–30302:4. [Google Scholar] [CrossRef]
- Fano, U. Description of states in quantum mechanics by density matrix and pperator techniques. Rev. Mod. Phys. 1957, 29, 74–93. [Google Scholar] [CrossRef]
- Batle, J.; Plastino, A.R.; Casas, M.; Plastino, A. Conditional q-entropies and quantum separability: A numerical exploration. J. Phys. A Math. Gen. 2002, 35, 10311–11324. [Google Scholar] [CrossRef]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of bose-einstein condensation in a dilute atomic vapor. Science 1995, 269, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Davis, K.B.; Mewes, M.-O.; Andrews, M.R.; van Druten, N.J.; Durfee, D.S.; Kurn, D.M.; Ketterle, W. Bose-einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 1995, 75, 3969–3973. [Google Scholar] [CrossRef] [PubMed]
- Bradley, C.C.; Sackett, C.A.; Hulet, R.G. Bose-einstein condensation of lithium: Observation of limited condensate number. Phys. Rev. Lett. 1997, 78, 985–989. [Google Scholar] [CrossRef]
- Curilef, S.; Pennini, F.; Plastino, A.; Ferri, G.L. Fisher information, delocalization and the semiclassical description of molecular rotation. J. Phys. A Math. Theor. 2007, 40, 5127–5140. [Google Scholar] [CrossRef]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Pennini, F.; Ferri, G.; Plastino, A. Fisher Information and Semiclassical Treatments. Entropy 2009, 11, 972-992. https://doi.org/10.3390/e11040972
Pennini F, Ferri G, Plastino A. Fisher Information and Semiclassical Treatments. Entropy. 2009; 11(4):972-992. https://doi.org/10.3390/e11040972
Chicago/Turabian StylePennini, Flavia, Gustavo Ferri, and Angelo Plastino. 2009. "Fisher Information and Semiclassical Treatments" Entropy 11, no. 4: 972-992. https://doi.org/10.3390/e11040972
APA StylePennini, F., Ferri, G., & Plastino, A. (2009). Fisher Information and Semiclassical Treatments. Entropy, 11(4), 972-992. https://doi.org/10.3390/e11040972




