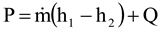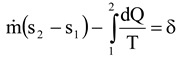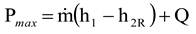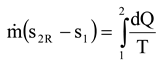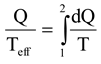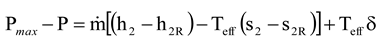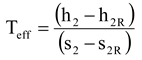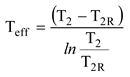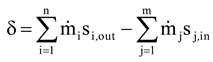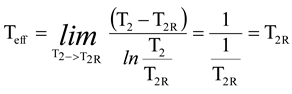1. Introduction
Exergy is usually defined as the maximum work output attainable in the natural environment, or the minimum work input necessary to realize the reverse process [
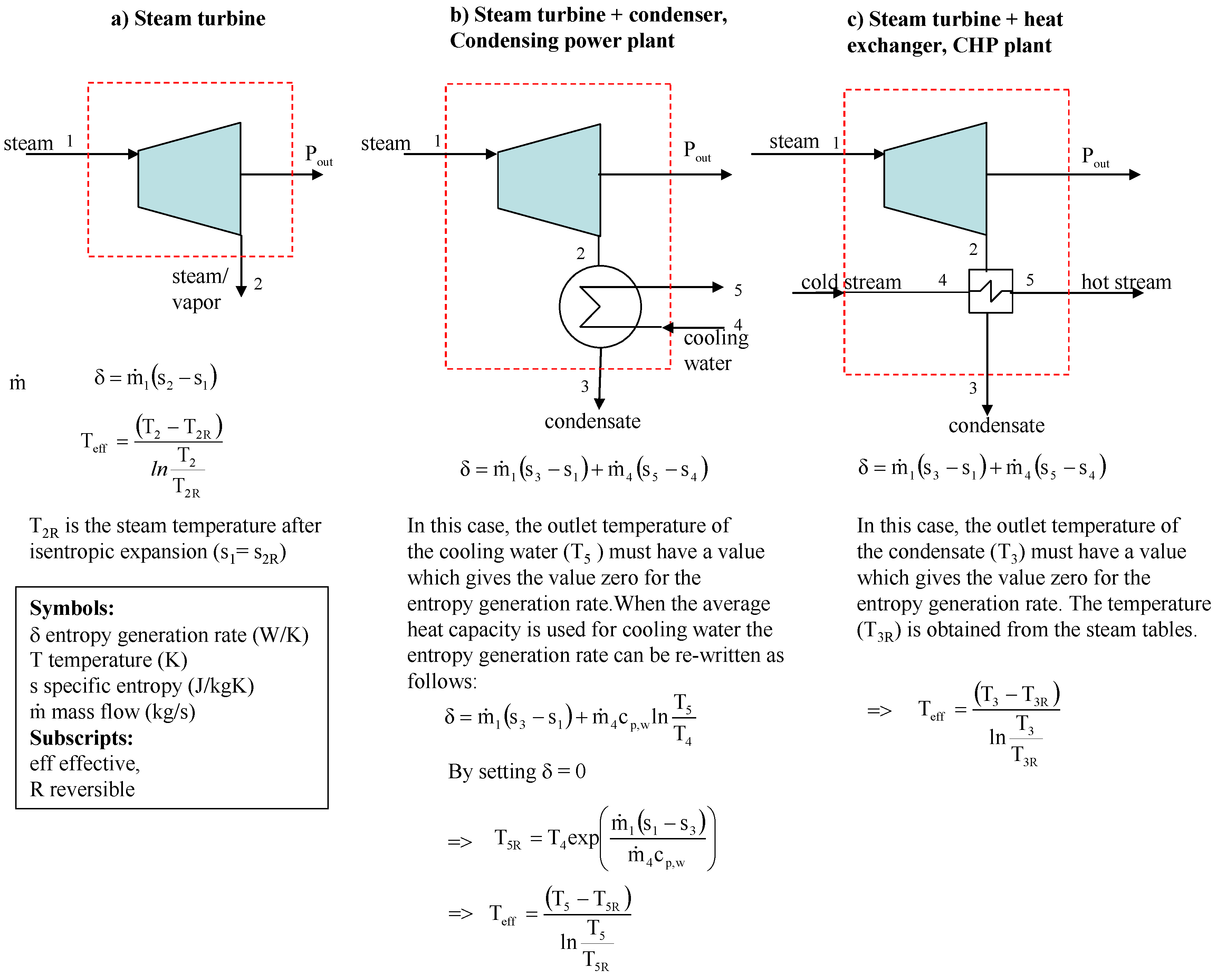
1]. All real processes generate entropy, and loss of exergy is determined by means of the Gouy-Stodola law:
where T
o is the real environmental temperature outside the system boundaries and δ the entropy generation rate. Equation (1) also expresses the improvement potential of the system.
If the system only exchanges heat at the real environmental temperature To, Equation (1) gives the exact improvement potential of the system. However, most industrial processes emit or absorb heat at a temperature level other than the real environmental temperature. It is easy to show that in these cases, Equation (1) does not give the real improvement potential of the system if the real environmental temperature To is used.
The first aim of this paper is to show through simple steam turbine example cases that the previous statement is true. The second aim of the paper is to define a so-called effective temperature Teff to calculate the real power loss of the system in all cases from Equation (1). From now on, the loss term in Equation (1) is always called power loss (Ploss) to distinguish it from exergy loss (Eloss), which is usually calculated using the real environmental temperature.
One of the simplest processes in which entropy generation occurs is steam or gas expansion in a turbine. Calculation of the power loss in a turbine using the Gouy-Stodola law has been studied in [
1,
2,
3,
4,
5,
6,
7]. With the exception of Bejan [
7], all of the authors have used the real environmental temperature T
o to calculate the power loss. Bejan states that the temperature in Equation (1) falls somewhere between T
out,rev and T
out,real when the power loss is calculated in steam expansion. However, Bejan does not state what the exact temperature in Equation (1) should then be. Lampinen and Wiksten have presented in Reference [
8] an in-depth analysis of the determination of the correct temperature in Equation (1) to calculate the real power loss.
In this paper, we will apply the ideas of Lampinen and Wiksten to calculate the real power loss from Equation (1) for the following example systems; i) steam expansion in a turbine, ii) steam expansion in a condensing turbine + condenser, and iii) steam expansion in a backpressure turbine + heat exchanger. The condensing turbine + condenser represents a condensing power plant in which the main goal is to maximize power generation. The backpressure turbine + heat exchanger represents an industrial CHP plant (combined heat and power plant) in which the primary goal is usually to produce heat, with electricity being obtained as a by-product. The paper also discusses the contradiction which arises when the real environmental temperature To is applied to industrial processes in the exergy analysis.
3. Results and Discussion
Figure 2 shows an example of the calculation of the power loss for steam expansion in a condensing and a backpressure turbine. It is obvious that the power loss for steam expansion in a turbine must be the enthalpy difference h
2–h
2R, which is 59.45 kJ/kg and 87.94 kJ/kg for the condensing and the backpressure turbine in the example case, respectively.
Figure 2.
Example of the calculation of the power loss for steam expansion in a condensing and a backpressure turbine.
Figure 2.
Example of the calculation of the power loss for steam expansion in a condensing and a backpressure turbine.
If a real environmental temperature of 20 °C is used, the power/exergy loss (see definitions in the Introduction) always becomes 56.95 kJ/kg, which is not the same as the difference h
2–h
2R. However, the turbine example shows that the Gouy-Stodola law gives the correct power loss when the entropy generation rate is multiplied by the effective temperature defined using Equation (3). This simple example already reveals that it is not always correct to use the real environmental temperature with the Gouy-Stodola law. The example calculations in
Figure 3 show in more detail when it is correct to use the Gouy-Stodola law for steam turbine calculations.
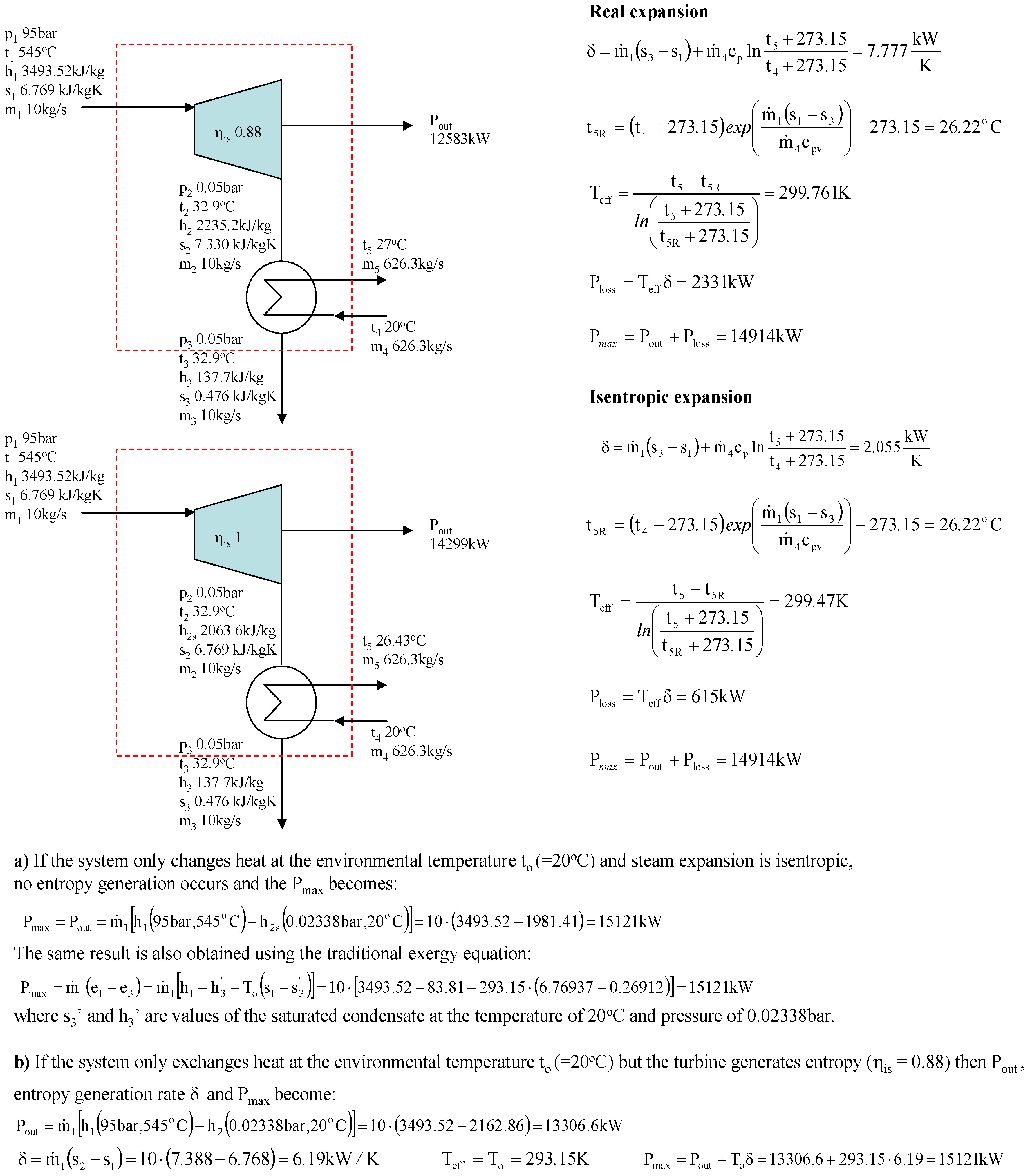
Figure 3 shows two steam turbine + condenser systems. In real expansion, the turbine and the condenser generate entropy. In isentropic expansion, only the condenser generates entropy, but steam expansion in the turbine is isentropic. The most important observation in
Figure 3 is that the sum of P
out + P
loss (real power production + power loss) becomes the same for both expansion cases when effective temperatures are used. The sum of P
out + P
loss gives the maximum power production of the system when no entropy generation occurs (i.e., a reversible system). As
Figure 3 shows, the entropy generation rate reduces in isentropic expansion, which leads to lower power loss (improvement potential of the system) and greater power production. In the case of isentropic expansion, the power loss can only be reduced in a heat exchanger and the improvement potential is 615 kW.
On the basis of
Figure 3, it is obvious that the P
loss reveals the real improvement potential of the system, and the sum of P
out + P
loss must always be the same for the system. However, this is not valid if the real environmental temperature (20 °C in
Figure 3) is used instead of the effective temperature. For real expansion the sum of P
out + P
loss would be 14,863 kW (12,583 kW + 293.15 K × 7,777 kW/K), if the real environmental temperature was used. For isentropic expansion the corresponding sum would be 13,185 kW (12,583 kW + 293.15K × 2.055 kW/K).
Figure 3.
Example of the calculation of the power loss for a steam turbine + condenser system.
Figure 3.
Example of the calculation of the power loss for a steam turbine + condenser system.
In theory, the maximum power production would be achieved if the system only exchanged heat at the environmental temperature and the process was reversible. It is obvious that this is not possible, but the theoretical maximum power production can be defined using the classic exergy equation, as the example calculation in
Figure 3 shows (point a below turbines). The example calculation (point b below turbines) in
Figure 3 also shows that it is correct to use the real environmental temperature with the Gouy-Stodola law if the system only exchanges heat with the environment at this temperature (i.e., P
max = P
out + P
loss). Because several processes may exchange heat at much higher or lower temperatures than the real environmental temperature, the use of the environmental temperature with the Gouy-Stodola law may cause a significant error in the determination of the power loss. In the cases of this study, the error already becomes considerable for a CHP plant (see steam expansion for a backpressure turbine in
Figure 2).
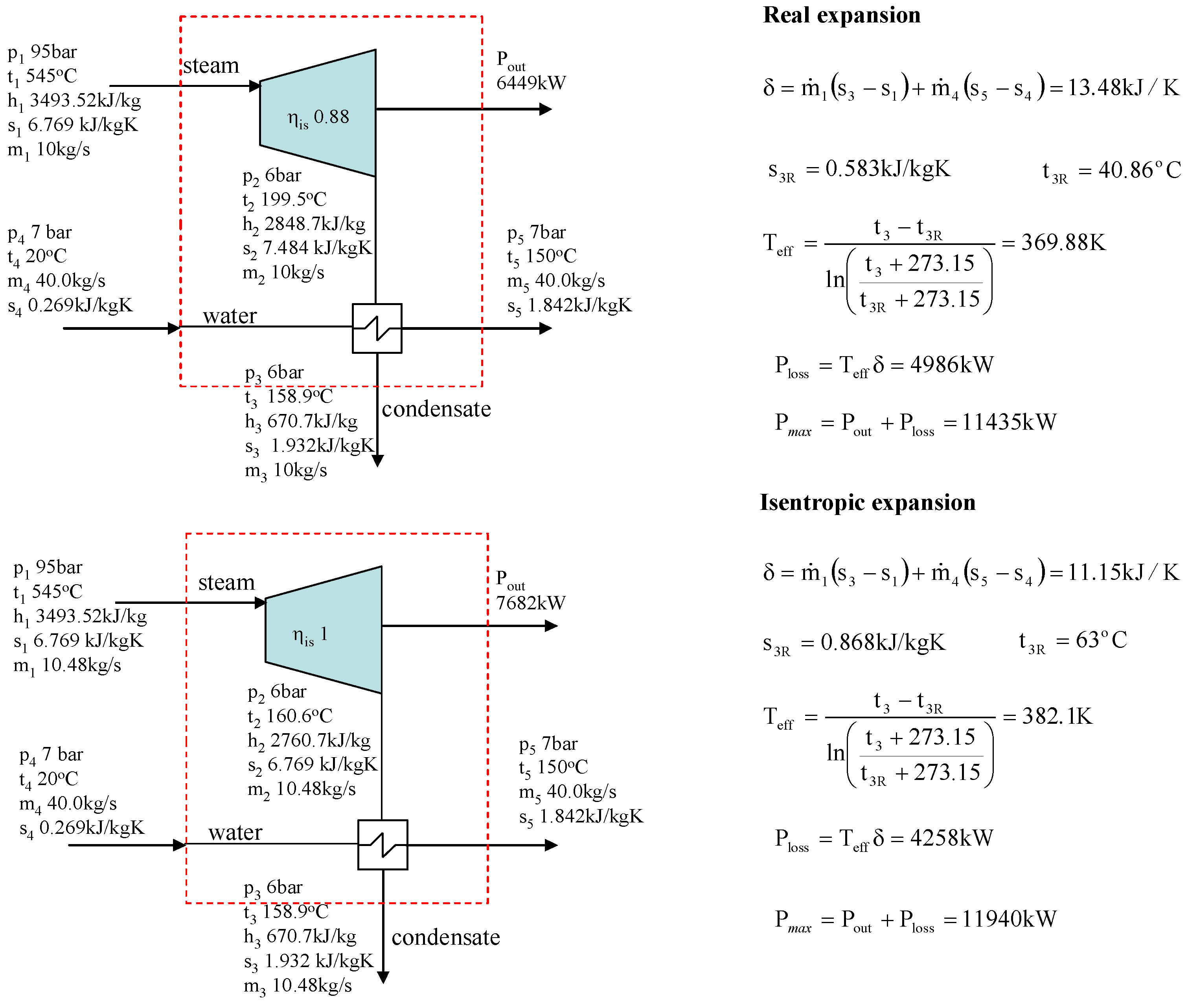
Figure 4 shows the calculation of the power loss for a backpressure turbine/CHP plant. Example calculations show that the sum of P
out + P
loss is not the same if the isentropic efficiency of the turbine changes (0.88 and 1 in
Figure 4). The result is different compared with the condensing turbine, where the isentropic efficiency has no influence on the sum of P
out + P
loss.
Figure 4.
Example of the calculation of the power loss for a backpressure steam turbine + heat exchanger system.
Figure 4.
Example of the calculation of the power loss for a backpressure steam turbine + heat exchanger system.
However, the results in
Figure 4 behave consistently. In the case of a backpressure turbine/CHP plant, the water flow must be heated from 20 °C to 150 °C. If the isentropic efficiency improves and the steam still expands to a pressure of 6 bar, the turbine produces more power. Due to increased power production the heat content of the outlet steam is not great enough to heat the entire water flow to the desired final temperature. To heat the entire water flow to a temperature of the 150 °C the steam mass flow m
1 must be increased, in which case the isentropic efficiency improves (see isentropic expansion in
Figure 4). Otherwise the energy balance is not valid. If the isentropic efficiency improves and the steam flow is not increased, the backpressure in isentropic expansion must be higher than 6 bar to be able to heat the water flow. In
Figure 4, the turbine with an isentropic efficiency of 1 represents the best possible turbine which generates no entropy. It is, of course, not possible to have a turbine like this in reality. In general, it is very questionable to use the real environmental temperature for the exergy analysis of the CHP plant because the primary function of the plant is to produce heat and not power.
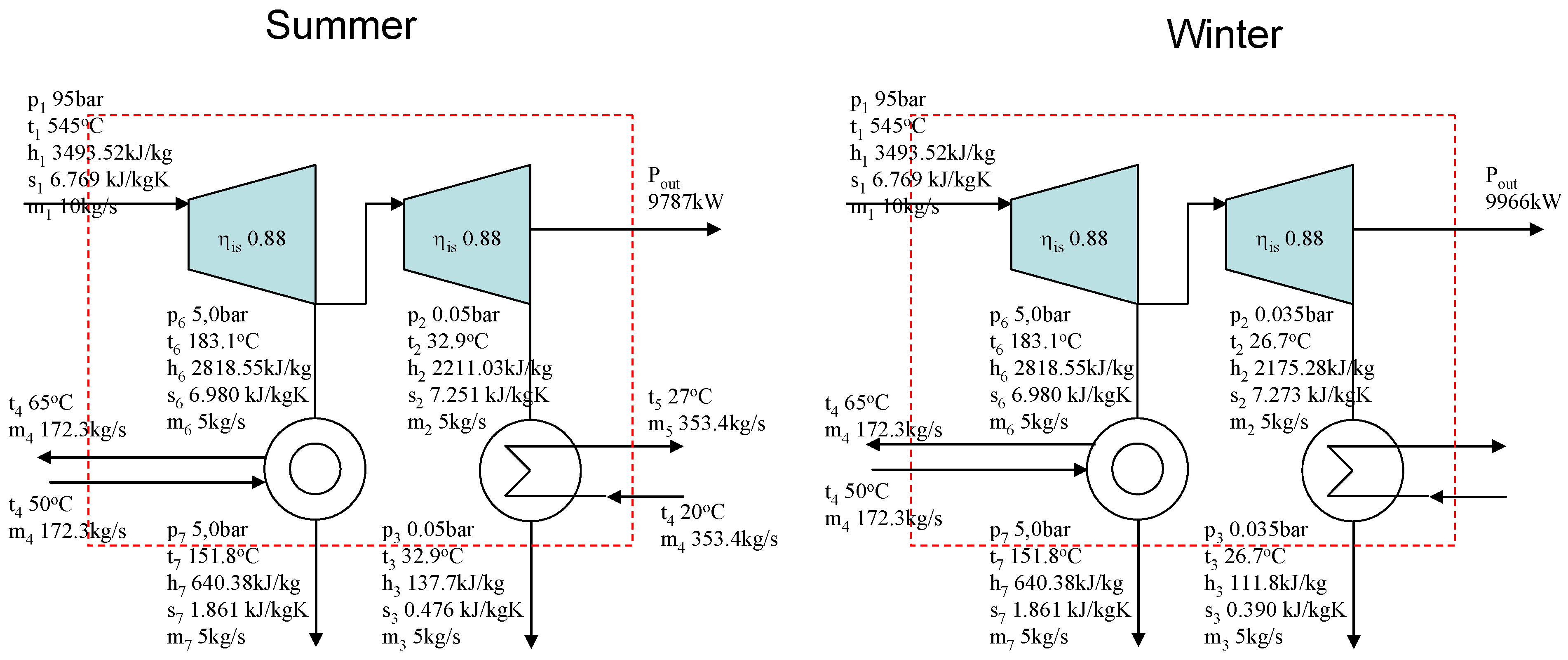
Figure 5 illustrates a simple industrial process, independent of the ambient temperature, and an industrial CHP plant with a condensing turbine. The left-hand side describes summer and the right-hand side winter. The only difference between summer and winter is the temperature of the cooling water used in the condenser. In the summer the temperature of the water is 20 °C and in the winter 4 °C. The operation and steam use of the industrial process remains unchanged throughout the year. Because of the cooler cooling water in winter, the pressure after the condensing turbine becomes lower and the power production of the turbine increases. Therefore the actual power loss caused by the steam demand of the process is greater in the winter than in the summer, 3,216 kW and 3,038 kW respectively.
Figure 5.
An industrial process with CHP plant. Summer on the left, winter on the right.
Figure 5.
An industrial process with CHP plant. Summer on the left, winter on the right.
However, if we try to estimate the power loss caused by the industrial process using the Gouy-Stodola law, it gives results that are just the opposite to the example calculation in
Figure 5. The entropy generation of the process is the same in the winter and summer. The only change is in the environmental temperature. Therefore the Gouy-Stodola law gives results where the power losses increase when the environmental temperature increases. This is an obvious contradiction compared with the example in
Figure 5.
4. Conclusions
The power/exergy loss of the system is usually calculated by multiplying the entropy generation rate by the real environmental temperature (the Gouy-Stodola law). The calculated power loss should also be the improvement potential of the system, and the sum of the power loss and real power production should be the maximum power production of the system.
Turbine example calculations (
Figure 3) show that it is correct to use the real environmental temperature with the Gouy-Stodola law if the system exchanges heat with the environment only at this temperature. The classic concept of exergy is based on this assumption. However, most industrial processes operate at temperatures higher or lower than the real environmental temperature. In this paper, the maximum power production is achieved when the system is reversible, but it does not have to exchange heat at the real environmental temperature. In these cases, the example calculations show that the sum of the power loss and real power production does not give the correct maximum power production for a reversible system if the real environmental temperature is used with the Gouy-Stodola law (
Figure 2 and
Figure 3). Especially in the case of CHP plant, the errors become significant if the real environmental temperature is used. The paper also shows through turbine examples that the correct power loss can be calculated if the effective temperature defined using Equation (3) is used instead of the real environmental temperature.
In addition, the example calculations reveal that calculation of the effective temperature depends on the system. In the case of adiabatic systems, one must know what flow temperature can be changed to define a reversible system and then the effective temperature (see condensing turbine vs. backpressure turbine).
In this paper, the Gouy-Stodola law has been used by multiplying the entropy generation rate by the effective temperature to calculate the real loss of power caused by the irreversibility of the system. It is obvious that the loss of power is zero if no entropy generation occurs and therefore the design of engineering systems should be based on minimisation of entropy generation, as Bejan states. The minimisation of entropy generation is equivalent to the minimisation of exergy/power losses and is an adequate tool to analyse thermodynamic systems from the viewpoint of the Second Law [
7]. In many cases, it is more convenient to calculate the improvement potential in energy units such as Watts or Joules, and therefore the entropy generation rate must be multiplied by an appropriate temperature. The concept of exergy is a useful tool if the theoretical maximum work available from the machine is to be analysed.