1. Introduction
By holding
K + 2 variables constant, one controls the macroscopic state of a thermodynamic system.
K equates with the number of components and at least one of the variables must be extensive. This axiom applies to solids, liquids, and gases at equilibrium [
2]. In spite of the simplicity, a system's state point is not infinitely sharp. If it were, there would be no uncertainty in any quantities related to the control variables. Their measurements would afford zero thermodynamic information. This turns out to be
almost the case as discussed in several classics [
3,
4,
5]. In
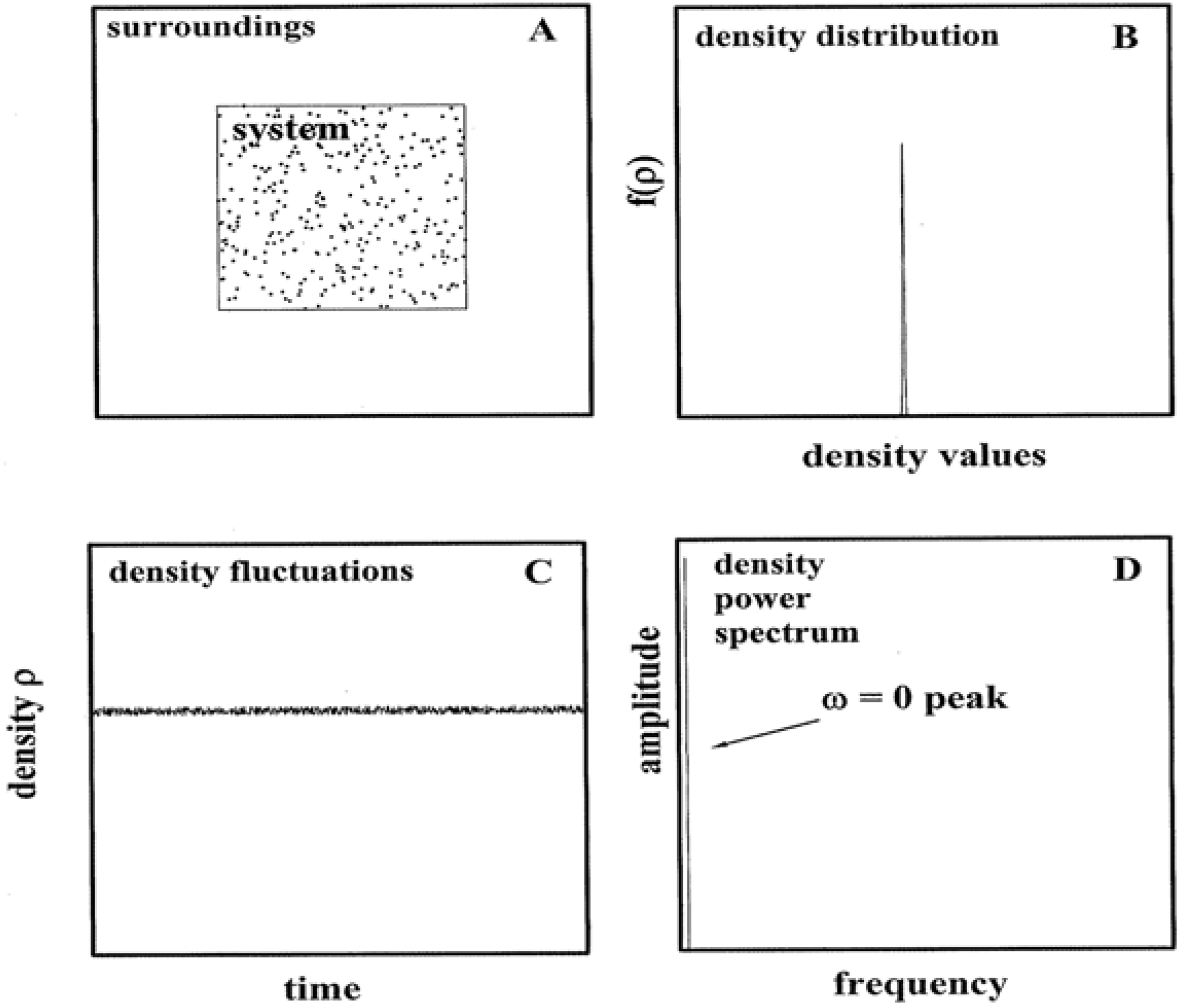
Figure 1, the minor impact of fluctuations is summarized.
Panel A shows a closed,
K = 1 gas in equilibrium with its surroundings. In the limit of ideal behavior, the density ρ is realized as:
where
N,
V,
p, and
T are accessible macroscopic variables: particle number, volume, pressure, and temperature, respectively [
6]. k
B is the Boltzmann entropy constant. Because of energy exchanges between the system and surroundings,
ρ necessarily fluctuates about an average. It can be shown that the ratio between the density standard deviation σ
ρ and the average <
ρ > is [
3,
4,
5]:
κ
T is the isothermal compressibility:
which reduces to 1/
p for ideal behavior. In this simplest of examples, the Equation 2 ratio is especially compact, namely:
Substitutions based on typical gas conditions make the crucial point. If, say, < ρ > were to equal 1023 particles/m3 (i.e., p ≈ 400 Pascals at room temperature), then σρ / < ρ > ≈ 3 × 10-12 and σρ ≈ 3 × 1011 particles/m3. Three standard deviations of the number density (σρ) would correspond to c. 1012 particles/m3. Repeated laboratory measurements of ρ for a 1 m3 volume would manifest a narrow distribution about the average. More than 99% of the readings would fall in the range 1023 +/− 1012 particles/m3. A probability density plot based on the measurements would yield a near δ-function as in Panel B; higher density conditions only sharpen the function. If alternatively the ρ-time dependence were monitored, a recording as in Panel C would obtain. Here the particle density is shown to fluctuate about the average in a noisy fashion. A Fourier synthesis (or transform) would identify a zero-frequency (ω) component as the dominant one. The power spectrum in Panel D based on the Fourier analysis would evidence a single peak at ω = 0. Given the slight impact of energy exchanges between the system and surroundings, the amplitude is featureless and nearly zero for ω > 0.
Figure 1.
Equilibrium Systems and Fluctuations. Panel A depicts a gas in equilibrium with its surroundings. Panel B shows the probability function that would obtain from repeated density measurements. Panel C illustrates the density behavior over time. Panel D shows the Fourier spectrum of the density behavior.
Figure 1.
Equilibrium Systems and Fluctuations. Panel A depicts a gas in equilibrium with its surroundings. Panel B shows the probability function that would obtain from repeated density measurements. Panel C illustrates the density behavior over time. Panel D shows the Fourier spectrum of the density behavior.
The
Figure 1 message is that while the role of fluctuations is not visible in state equations such as Equation 1, it is a typically (
i.e., when
ρ and V are appreciable) a very minor one. Thus
ρ quantified via Equation 1 and similar can be viewed as the overwhelmingly most probable value. Parallel arguments can be constructed for other state quantities such as the pressure
p, chemical potential
μ, and entropy
S. The sources of non-ideality, namely interactions between the particles, do not alter the message. The exception would be when the state point falls in the neighborhood of a phase boundary.
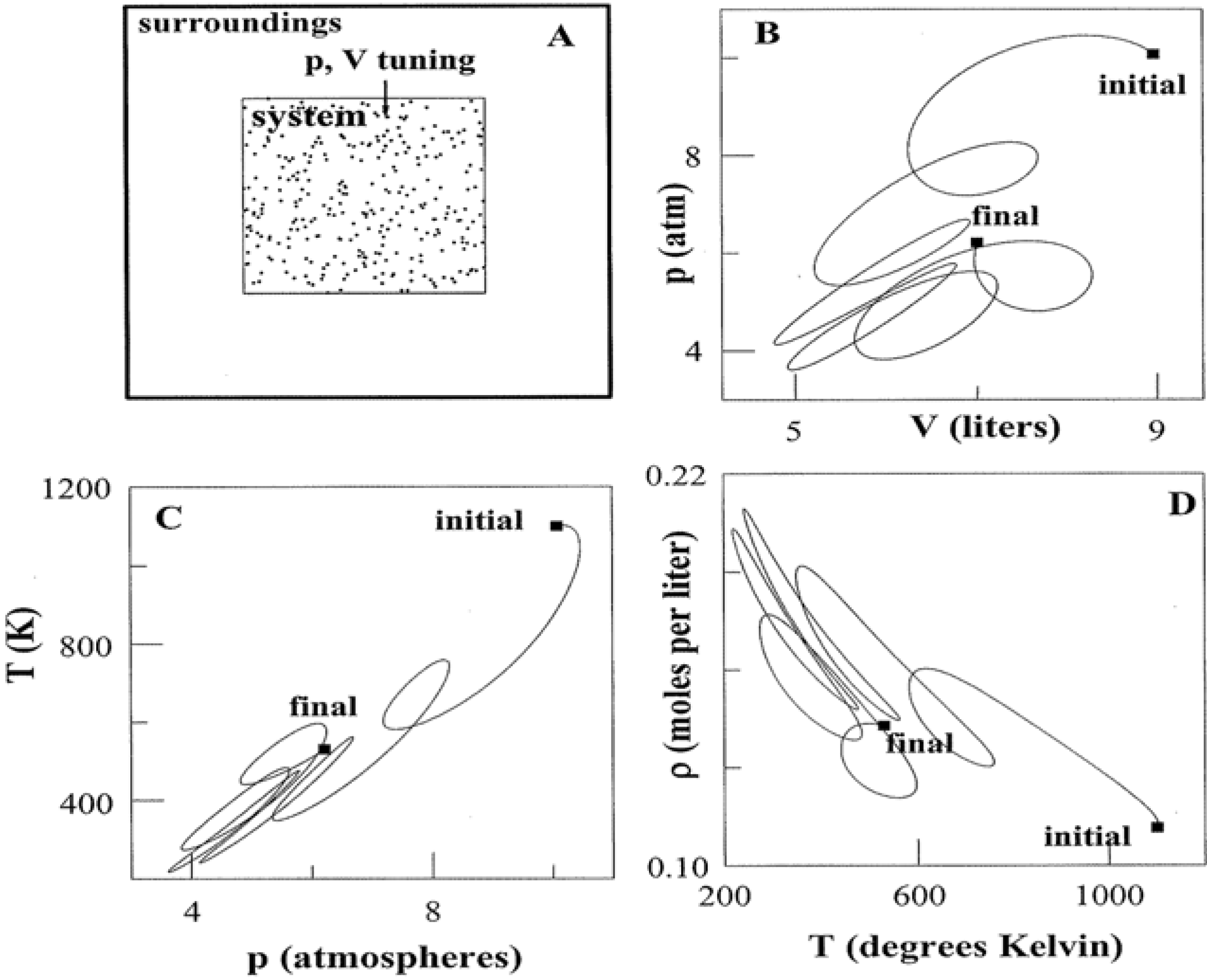
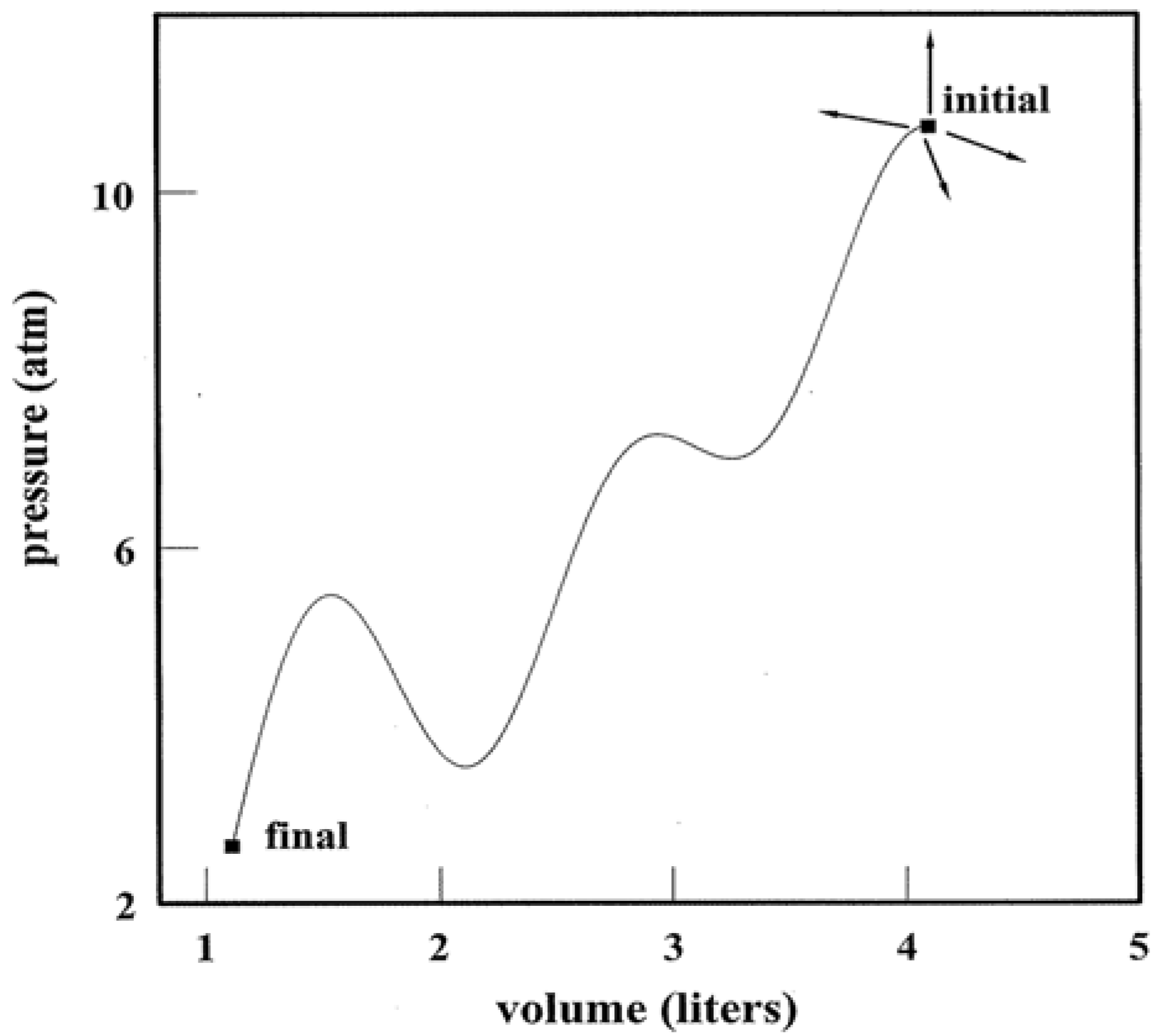
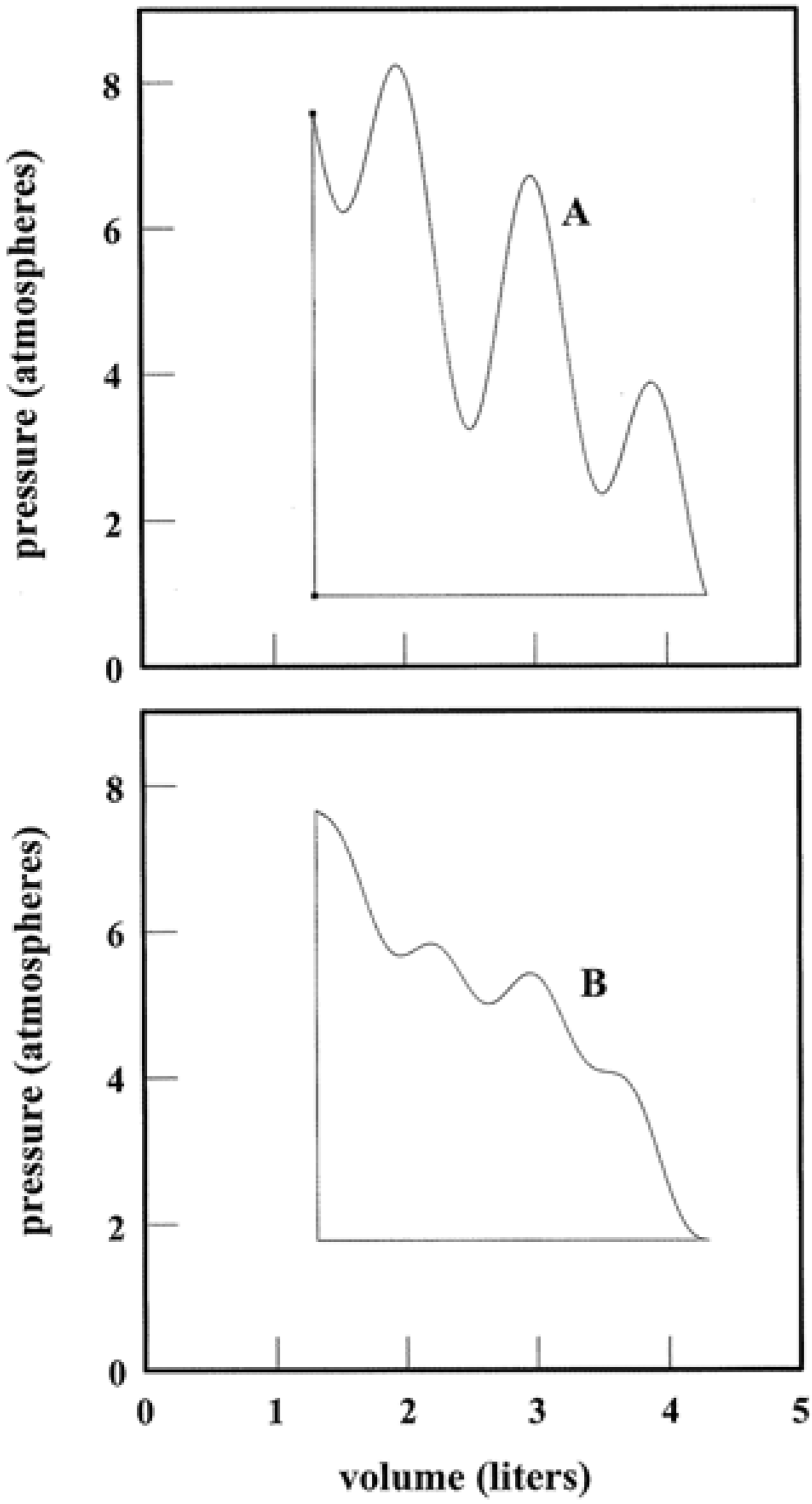
An individual state point poses little uncertainty regarding thermodynamic quantities. Multiple connected points paint an altogether different picture. This is the subject of
Figure 2. If control variables such as
p and
V are tuned, a system is directed along a pathway that threads nearest neighbor state points. The pathway can be elementary as in isothermal, adiabatic, and isochoric transformations where
T,
S, and
V, respectively, are constant. Yet the path need not be a proper function at all as in Panel B. Tuning
p and
V accesses an infinitude of states that link the initial to the final. Whether simple or complicated, a pathway allows for alternative representations using variables such as
T, ρ (Panels C and D) and more. Thermodynamic pathways form a time-honored subject [
7]. They continue to warrant study as model algorithms and computational programs. At a root level, thermodynamic pathways characterize step-wise parallel programming on the part of a system and its surroundings. The algorithms are executed via simultaneous tuning of variables tied to the work and heat exchanges.
Figure 2.
Systems and Variable Tuning. Panel A shows a system in which pressure and volume are tuned in parallel with work and heat exchanges. Panel B illustrates one of infinite possible pathways that connect the initial and final states. Panels C and D present alternative representations of the pathway. For simplicity, the system has been taken to be 1.00 mole of a monatomic ideal gas. The use of liter and atmosphere units follows the practice of classic thermodynamic texts [
2,
6,
7].
Figure 2.
Systems and Variable Tuning. Panel A shows a system in which pressure and volume are tuned in parallel with work and heat exchanges. Panel B illustrates one of infinite possible pathways that connect the initial and final states. Panels C and D present alternative representations of the pathway. For simplicity, the system has been taken to be 1.00 mole of a monatomic ideal gas. The use of liter and atmosphere units follows the practice of classic thermodynamic texts [
2,
6,
7].
Information is the lifeblood of programs and algorithms. It is an imbedded feature of all thermodynamic pathways. The scenarios are much in contrast with individual state points such as in
Figure 1 where a measurement traps very little information. Information in connection with thermodynamic pathways was explored by the author in a previous work [
1]. It was shown how a locus of nearest neighbor state points predicates a type of probability space. Objective queries of the system offer information in amounts significantly greater than for any single point. The amounts depend intricately on the pathway structure, measurement resolution, and system composition.
This paper takes another step by examining the spectral entropy allied with a pathway. This quantity also proves connected with collections of nearest neighbor states. Importantly, the spectral entropy identifies novel distinctions between ideal and non-ideal gases. It connects as well with the constraints placed by the first and second laws of thermodynamics. A pathway's spectral entropy highlights the optimum programming strategies for heat → work conversions. One notes the spectral entropy to provide a powerful tool in diverse fields. To cite only a few, it has found judicious applications in speech recognition algorithms, genome analysis, and particle motion research [
8,
9,
10]. To the author's knowledge, the present study examines a first link between the spectral entropy and thermodynamic pathways. While thermodynamics enjoys a highly-developed infrastructure, new theoretical and experimental tools continue to be discovered [
11]. Moreover, topics that are closely related to spectral entropy include heat engines, system fluctuations, and non-ideal gases. These have been well represented the past few years in this journal [
12,
13,
14,
15,
16].
2. Thermodynamic Pathways, Information, and Spectral Entropy
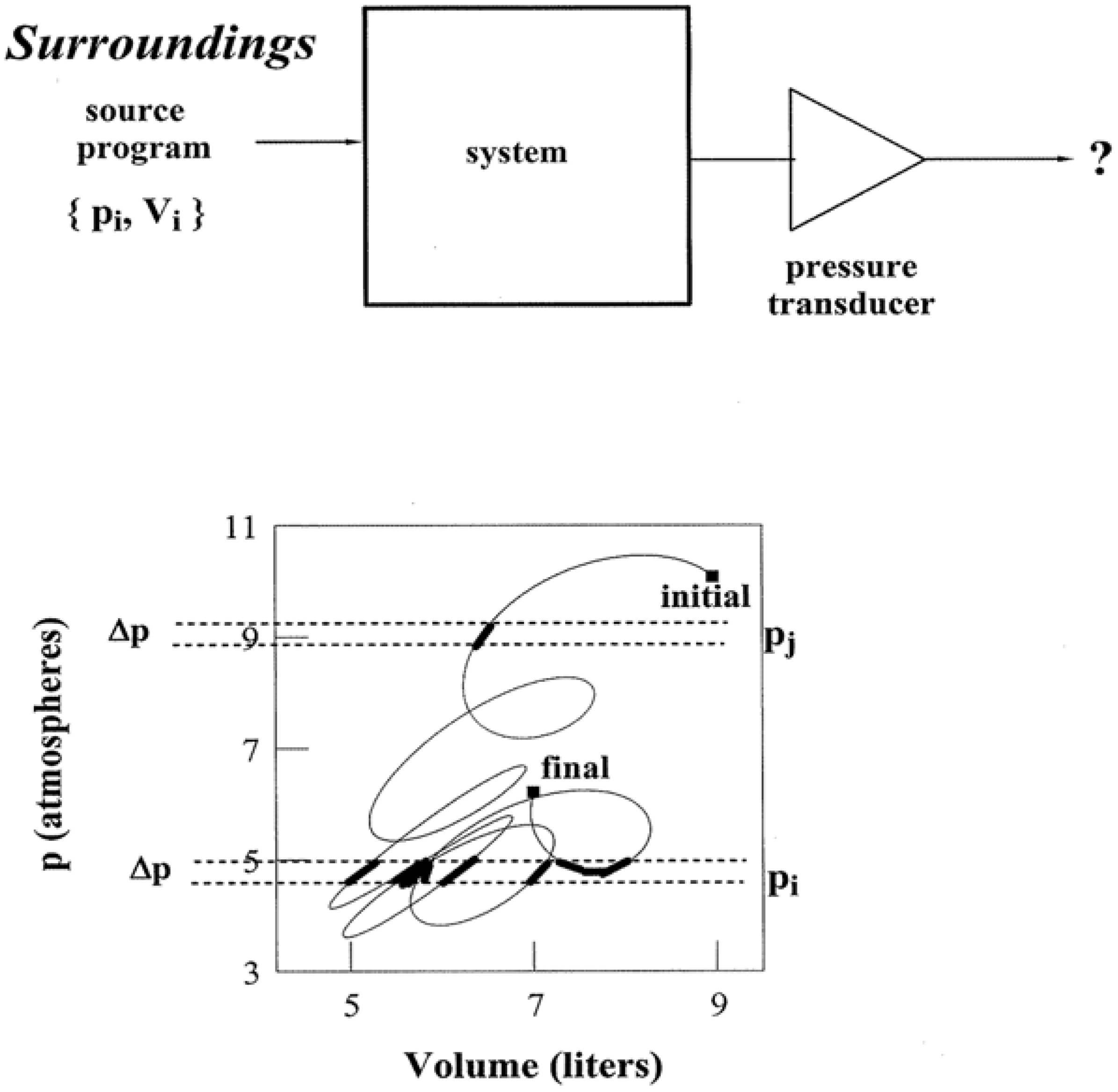
Figure 3 illustrates how information is expressed by a pathway. For simplicity, the system is taken to be a closed one composed of 1.00 mole of a monatomic ideal gas. Let the system be transformed along a path in the
pV plane that matches the one illustrated in
Figure 2. Transformations do not occur by themselves. Thus the upper portion of
Figure 3 schematically depicts the requisite parallel and serial programming by way of an entry {
pi,Vi} sequence. In effect, ordered pairs of
pi, Vi enable the system to be stepped precisely along a chosen pathway. There is more than one input program which can accomplish the task. The
K + 2 criterion for specifying state points allows other control variable pairs and sequences to be equally effective: {
pi,Ti}, {
ρi,Vi}, and so forth.
The pathway in
Figure 3 is clearly reversible. This means that the closed system maintains equilibrium with the surroundings at all stages. A non-equilibrium condition would indeed not correspond to any single point in the
pV,
Tρ, or other variable plane. Pathways articulate the initial, final, and intermediate states. Then if the equation of state is known, the differences between the numerous functions of state can be quantified: entropy
S, free energy
G, internal energy
U, and more. Quantities that instead hinge on the pathway structure details can also obtain: work received
Wrec and heat received
Qrec.
Reversible pathways yield many thermodynamic quantities. They are devoid of temporal data, however, on account of their equilibrium nature. All of the states are spelled out via an input program, but they lack qualifiers on their time and duration of access. Therefore if an objective experimenter who is knowledgeable of the state point locus, but ignorant of temporal details, inquires “Does the system pressure
p at present fall in the following range?”:
the answer would be uncertain in advance of measurement via a suitable transducer (represented by a triangle in
Figure 3) such as a McLeod gauge. In taking the pathway states to be equally probable, the likelihood of an affirmative answer—the conversion of uncertainty “?” to “yes” in
Figure 3, depends on the number of states that meet the above criterion. Note how for the pathway appearing in the lower half of
Figure 3, the likelihood of
p meeting the condition in (5) is greater than for:
As indicated by the enhanced blackening of pathway segments, there are about eight times the quantity of state points that meet the condition in (5) as compared with (6).
Figure 3.
Pathways and Information. The upper portion schematically illustrates how a control variable sequence {pi,Vi} operates as a thermodynamic algorithm for pathway traversal: ordered pairs pi, Vi enable the system to be stepped precisely through a succession of state points. Measurements via a transducer (triangle symbol) such as a McLeod gauge reduce uncertainty ? and trap information about the system, i.e., convert “?” to “yes” or “no”. The amount of information depends on the number and distribution of pathway state points.
Figure 3.
Pathways and Information. The upper portion schematically illustrates how a control variable sequence {pi,Vi} operates as a thermodynamic algorithm for pathway traversal: ordered pairs pi, Vi enable the system to be stepped precisely through a succession of state points. Measurements via a transducer (triangle symbol) such as a McLeod gauge reduce uncertainty ? and trap information about the system, i.e., convert “?” to “yes” or “no”. The amount of information depends on the number and distribution of pathway state points.
It was shown in previous research how to quantify the likelihood of “yes”
versus “no” answers to state queries [
1]. The procedure involved computing the pathway length over the states that meet the query conditions via line integrals. The pieces are summed and weighed against the total pathway length. The results include sets of probability values and surprisals: {
probi } and {−log
2probi }, respectively. The expectation value of the surprisals quantifies the pathway information
IY in bits:
where the subscript
Y denotes the thermodynamic quantity queried such as
Y ↔
p in
Figure 3.
IY is enhanced if the number of terms in Equation 7 is increased. This would be brought about by augmenting the pathway, or by extending the measurements at higher resolution—narrower Δ
p.
IY would be further enhanced if the probability terms proved equal (or nearly so) in value; this applies typically to pathways that evince complex structures.
IY is zero for certain quantities for certain pathways: isobaric, isothermal, and adiabatic pathways are absent in
Y ↔
p,
T, and
S information, respectively. All closed systems pose zero information regarding the particle number:
IY↔N = 0.
The spectral entropy
SY is an immediate by-product of information. There indeed exists
SY computable for every pathway state property,
i.e.,
Y ↔
p,
V,
T,
U,
G,
S,
etc. Unlike information,
SY does not stem from yes/no queries and measurements with thermometers, pressure gauges, and so forth. Its significance arises instead because of the contact made with the algorithmic structure. Most notably,
SY quantifies the symmetry, or lack of it, imbedded in a pathway.
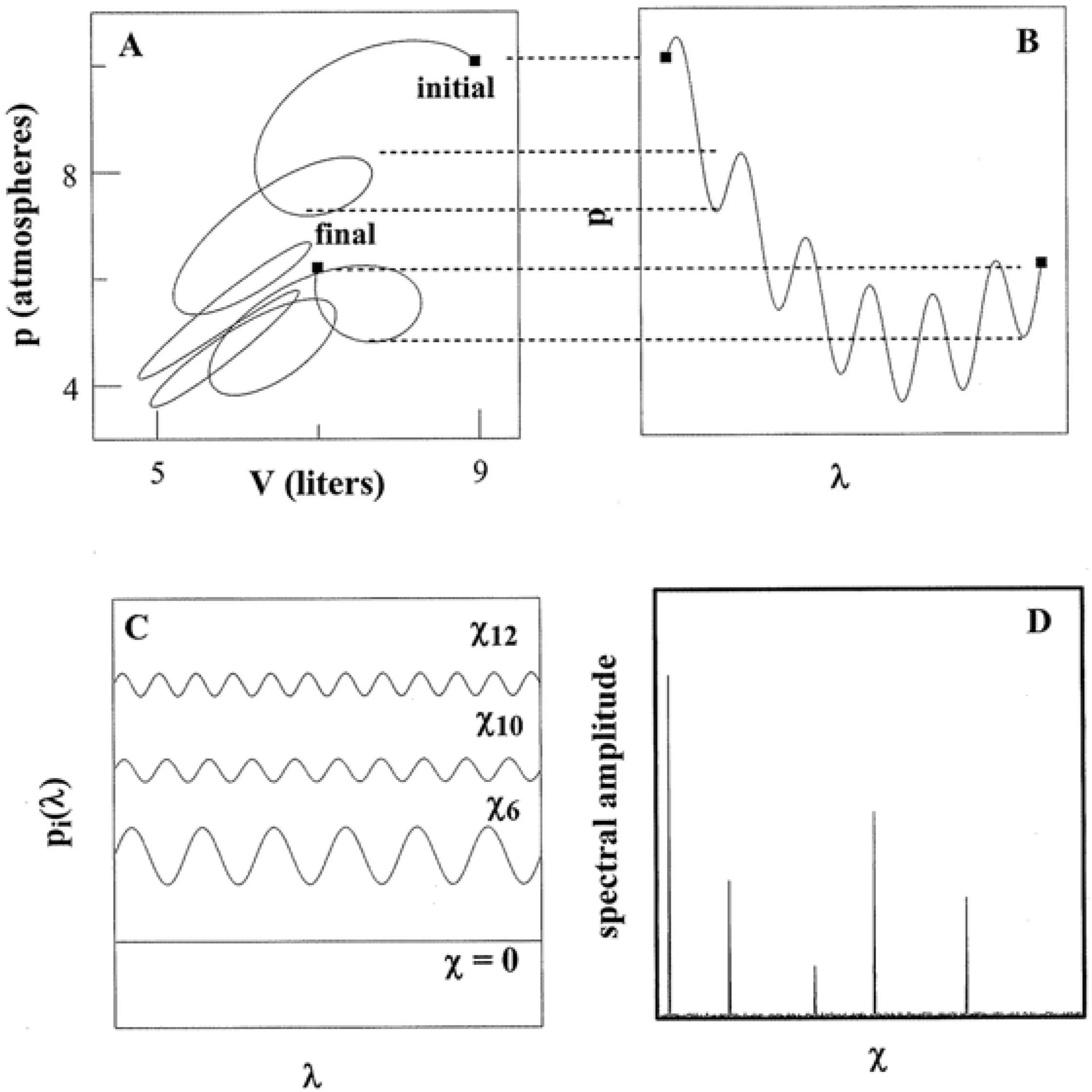
Figure 4, for example, shows how
SY originates for
Y ↔
p, the pressure tuning of a system with commentary as follows.
Whether simple or complex, a thermodynamic pathway always admits a parametric representation. In such a way, dimensionless
λ operates as an independent variable common to all state quantities. Panels A and B in
Figure 4 show the pressure behavior over the same path charted in
Figure 3. There is a one-to-one correspondence of
λ to each state point as indicated by the dotted lines. This correspondence holds for
V and all other quantities
T,
S,
etc., traversed by the path.
As is universally appreciated, algorithms and programs can be executed multiple times. Thus to quantify
SY, a thermodynamic pathway is regarded as expressing a state space period of 2
L. The periodicity allows each λ-dependent function to be written as a Fourier series [
17]. For instance, the pressure function of
Figure 4 can be re-expressed as:
where:
The arguments of the trigonometric functions define “frequencies”:
The quotation marks emphasize that the
χn have nothing to do with time as with ω in
Figure 1. The χ
n rather identify the density of the pathway kinks governed by the program. The pathway of Panel A demonstrates twists and turns in both pressure and volume. Their Fourier representations accordingly necessitate multiple terms with diverse
χn. By contrast, an isobaric or isochoric pathway demonstrates constant
p or
V, respectively. In such cases,
p(
λ) or
V(
λ) require only a single term in their Fourier expressions at
χo = 0. Each representation is equivalent to that for a single state point.
Figure 4.
Pathways and Spectral Entropy. Panels A and B show how a pathway admits a parametric representation. The representation can be expressed as a Fourier sum of trigonometric functions such as shown as in Panel C. The weight coefficients compose a power spectrum as in Panel D.
Figure 4.
Pathways and Spectral Entropy. Panels A and B show how a pathway admits a parametric representation. The representation can be expressed as a Fourier sum of trigonometric functions such as shown as in Panel C. The weight coefficients compose a power spectrum as in Panel D.
The coefficients
an,
bn determine the degree to which each Fourier term contributes. The modulus quantity:
then identifies the amplitude allied with each χ
n. A plot of
An versus χ
n realizes a power spectrum as in Panel D. At infinite resolution (infinitesimal Δ
p), Equations 8 and 9 converge to integrals which predicate an infinite number of spectral terms. A finite-step pathway is, of course, much closer to experimental reality.
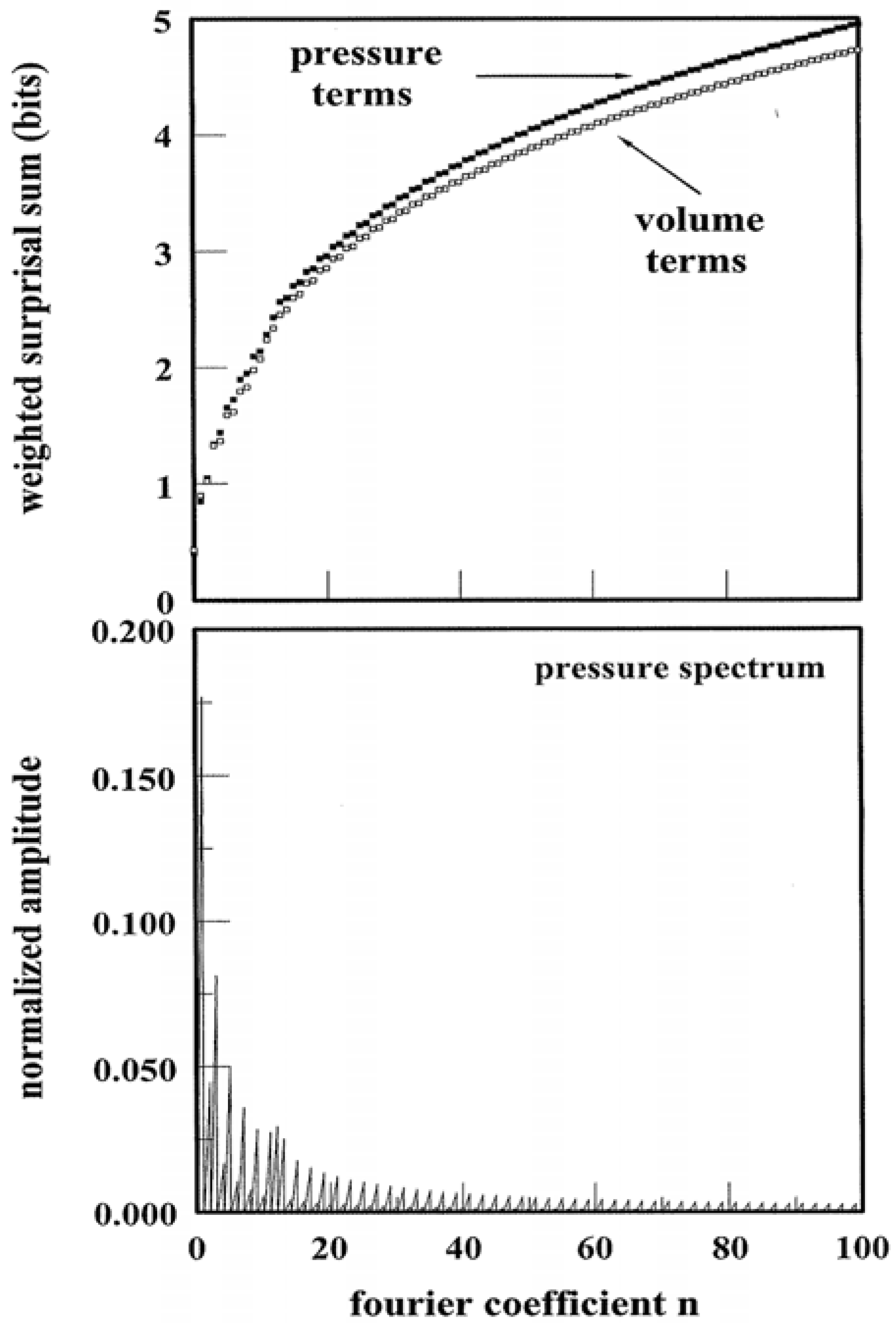
Figure 5 illustrates an example of the spectral entropy
SY↔p that results from pressure tuning of a system: The calculation follows from the pathway of
Figure 4 that is, in turn, described by the (arbitrarily chosen) parametric function:
λ is dimensionless while
B equates with the unit pressure, here assigned to be 1.00 atmosphere. The Fourier representation has been computed using Equations 8 and 9 and its normalized power spectrum is contained in the lower panel of
Figure 5. In calculating the spectrum, the
An have been rescaled by factor
ξ so that:
Clearly the spectrum reflects a non-trivial component distribution that is heavily weighted at low
χn. SY↔p follows straightaway, viz.
The summation is dictated by the number of Fourier components: 100 are more than sufficient given the typical pathway bias toward low χ
n and finite resolution. The logarithmic terms of Equation 14 are analogous to information surprisal quantities [
18]. Each term is weighted by a normalized amplitude which is analogous to a probability term. The results of the weighted summation appear in the upper panel of
Figure 5. The results for
SY↔V have been included for comparison. One observes that different thermodynamic quantities of the identical pathway need not express the same spectral entropy. The “bit” units are applicable in the same way as information. For this single, arbitrarily-chosen pathway—there are infinite possible—it requires approximately 5 bits to encode the amplitude terms in the
p,
V power spectra.
Figure 5.
Power Spectra and Weighted Surprisal Sums. The lower panel illustrates the normalized power spectrum based on p(λ) of
Figure 4. The upper panel illustrates the weighted sum of surprisals for pressure and volume pathway variables.
Figure 5.
Power Spectra and Weighted Surprisal Sums. The lower panel illustrates the normalized power spectrum based on p(λ) of
Figure 4. The upper panel illustrates the weighted sum of surprisals for pressure and volume pathway variables.
3. Applications and Discussion
The spectral entropy has been employed in diverse research [
8,
9,
10]. Concerning thermodynamic pathways,
SY contributes insights in four respects. The first concerns the properties that distinguish ideal from non-ideal gases. As is well known, the former demonstrates signature features beginning with Equation 1. Additional ones include that the internal energy
U and enthalpy
H depend solely on
N and
T [
6,
7]. For a monatomic ideal gas:
and:
It follows that for ideal systems, the heat capacities
CV, Cp are independent of volume and temperature:
and:
Other response functions such as the coefficient of thermal expansion
αp and isothermal compressibility
κT (Equation 3) are equally simple:
and
κT = 1/
p. A non-ideal system requires more complicated mathematics for the state relations. The van der Waals equation is a well-established, elementary model for interacting gases [
6,
7,
16]:
where
a and
b scale, respectively, with the attractive and repulsive forces between the particles. Note that conventional notation is being used in Equation 20 and beyond. The van der Waals
a and
b coefficients are not to be confused with the Fourier weight coefficients of Equations 9 and 11. Then with Equation 20, or similar non-ideal equation of state operative, the representations of potentials
U and
H are no longer so compact. In the van der Waals case:
while:
CV for a van der Waals system is equivalent to that appearing in Equation 17.
Cp does not demonstrate the same economy, however:
where:
The take-home points are as follows. There are established properties that distinguish ideal from non-ideal gases. To the list need to be added three additional:
(1) Ideal and non-ideal samples alike express SY↔T = 0 for isothermal pathways. Yet only an ideal gas expresses zero SY↔U and SY↔H for isothermal pathways.
(2) All pathways—no exceptions—for a closed ideal system express zero SY↔CV and SY↔Cp. In sharp contrast, only highly select ones demonstrate zero SY↔Cp for non-ideal systems. This is because Cp depends non-trivially on p, T, V, a, and b as in Equations 23, 24, and 25.
(3) If a system is ideal, its isothermal and isobaric pathways pose zero SY↔αp and SY↔κT, respectively. Matters are more complicated for a non-ideal system. Zero SY↔αp and SY↔κT can only be demonstrated by highly rarefied pathways. This is because κp and αT depend intricately on p, T, and V, and case-specific a and b. The zero SY↔αp and SY↔κT pathways programmed for an argon sample would not apply to neon.
The above can be demonstrated via numerous equations of state, not simply the van der Waals, that address the effects of interparticle forces. Even so, real materials conduct themselves ideally at sufficiently low densities and high temperatures. Hence the features 1–3 are universal in their application. The second and third are especially striking. To construct a pathway with fixed heat capacity is trivial for an ideal gas–any and all pathways will do. To engineer likewise for a non-ideal material, however, incurs infinitely greater programming costs. Regarding (3), to ascertain a system’s thermodynamic properties, knowledge of
either CV or
Cp along a pathway that threads a range of
p and
T is required [
6]. Usually
Cp is experimentally more accessible via the specific heat
cp:
where
m is the system mass. Equation 26 plus Feature (2) inform the experimenter, however, that the accessibility of
Cp obtains at the price of greater pathway complexity for a non-ideal system. One way of quantifying the complexity is via
SY↔Cp.
Along related lines, knowledge of
both αp and
κT is required at
all points in a region of state space in order to realize the thermodynamic quantities U, G, S,
etc. [
6]. From Feature (3), one learns that it is impossible to measure
αp or
κT for
one state of a non-ideal system and thereby automatically know the values for points along the intersecting isotherms and isobars in the state space. As with
Cp, the complexity of
αp and
κT is non-trivial for real systems, yet it is directly quantified by
SY↔αp and
SY↔κT.
The second insight relates pathway spectral entropy to the first law of thermodynamics. This law holds that the internal energy change Δ
U of any system equates with the work and heat received:
with special cases applying to isochoric (
Wrec = 0) and adiabatic (
Qrec = 0 ) transformations [
1,
5,
6]. The first law contact with pathway spectral entropy is notably different. Specifically
SY↔Wrec and
SY↔Qrec bracket SY↔ΔU:
and:
In so doing, the spectral entropy of the work and heat exchanges provides upper and lower bounds for
SY↔ΔU. There is a single exception, namely when
Wrec and
Qrec exactly cancel at all points of a pathway; this renders
SY↔ΔU zero. More importantly, for isochoric and adiabatic pathways, (28) and (29) become equality statements:
The first law bearing on pathway spectral entropy is crucial. It emphasizes how the work and heat exchanges between a system and surroundings must be programmed in-parallel with each other.
SY↔ΔU could exceed
both SY↔Wrec and
SY↔Qrec only if the exchanges were independent, thus admitting different sets of Fourier coefficients. The first law and the nature of reversible pathways preclude this. For one of infinite possible examples,
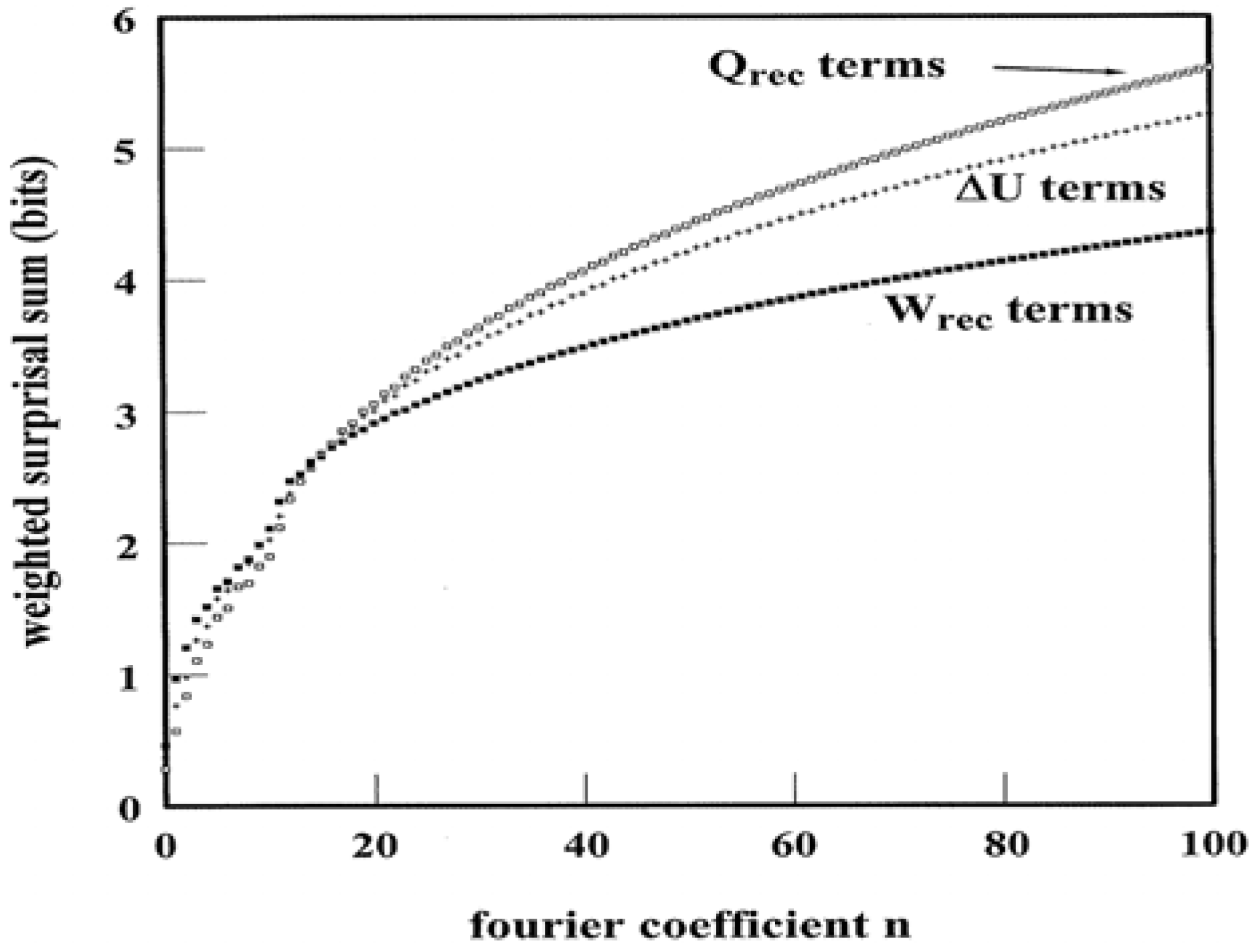
Figure 6 illustrates the weighted surprisal summations that yield
SY↔Wrec,
SY↔ΔU, and
SY↔Qrec for the
Figure 4 pathway. In this case, the condition in (28) holds. Evidently the complexity of programmed heat exchanges exceeds that of the work exchanges. Such a trait is not apparent from casual inspection of the pathway structure.
Figure 6.
Weighted Surprisal Sums based on ΔU, W
rec, and Q
rec Power Spectra. The data derive from the pathway illustrated in
Figure 4.
Figure 6.
Weighted Surprisal Sums based on ΔU, W
rec, and Q
rec Power Spectra. The data derive from the pathway illustrated in
Figure 4.
The second law of thermodynamics also impacts the spectral entropy; this is the subject of
Figure 7. The Caratheodory statement of the second law asserts that there exist neighboring states of a system which are impossible to access along an adiabatic path [
19]. A pathway's spectral entropy admits a parallel statement:
All systems possess neighboring states for which a
SY↔S = 0 path is non-existent.
Figure 7 shows four (of
infinite possible) arrows that pinpoint nearby states. For these, there exists no
SY↔S = 0 pathway that links the initial state without expression of positive
SY↔S. The Caratheodory principle emphasizes that adiabatic pathways are exceptional for systems, ideal and otherwise. The same principle establishes the rarity of
SY↔S = 0 pathways.
Figure 7.
Pathways and Neighboring States. The arrows point to several (of infinite possible) neighboring states that cannot be accessed by an adiabatic/isentropic path. The pathway identifies one (of infinite possible) that can link initial and final states. It is virtually always the case that changing paths incurs changes in the spectral entropy.
Figure 7.
Pathways and Neighboring States. The arrows point to several (of infinite possible) neighboring states that cannot be accessed by an adiabatic/isentropic path. The pathway identifies one (of infinite possible) that can link initial and final states. It is virtually always the case that changing paths incurs changes in the spectral entropy.
There follows a corollary:
There exist an infinite number of pathways that are able to link an initial to a final state. The curve in
Figure 7 represents one (of infinite possible) having positive
SY↔S,
SY↔V,
SY↔p,
etc. There exist
neighboring pathways for which a
non-zero change in
SY is impossible:
Y ↔
p,
T,
U,
μ,
etc. The reason is that altering a pathway inexorably modifies one or more weight coefficients in the Fourier representation. Neighboring states that admit fixed-entropy pathways are special by the Caratheodory principle. Neighboring pathways that pose zero change in the spectral entropy prove no less special.
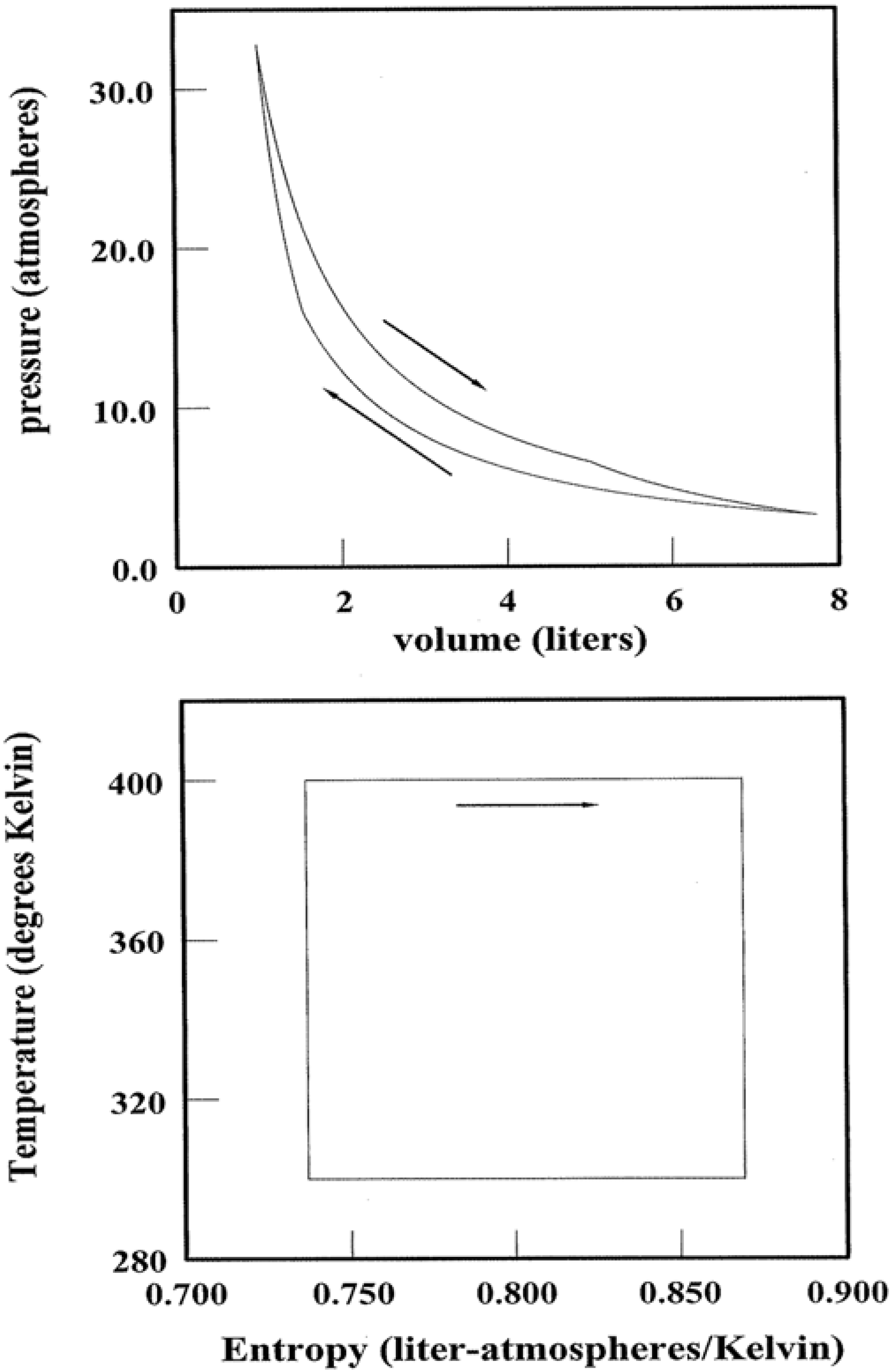
Figure 8.
Carnot Cycles and Pathways. A Carnot cycle for 1.00 mole of monatomic ideal gas is illustrated in both the pV and TS planes. The Carnot strategy in relation to pathway spectral entropy is discussed in the text.
Figure 8.
Carnot Cycles and Pathways. A Carnot cycle for 1.00 mole of monatomic ideal gas is illustrated in both the pV and TS planes. The Carnot strategy in relation to pathway spectral entropy is discussed in the text.
A final insight concerns heat engines, devices that transform a system along a cyclic pathway such that the initial and final states are identical. In simplest terms, heat is injected into the system (e.g., steam or combustion gas mixtures) at some high temperature; entropy is injected simultaneously. So that mechanical integrity is preserved, an equivalent amount of entropy must be ejected by the system somewhere along the pathway. The only feasible way is for the system to cast out “wasted” heat at some lower temperature. It follows that the conversion efficiency of injected heat → output work can never be 100%. The output work is at best equal to
Qinjected–
Qwasted [
6,
7].
Not all cyclic transformations are created equal. Thus Carnot identified the optimum pathways for heat → work conversions [
6,
7,
12,
13]. These entail minimizing the thermal gradients within the system while maximizing the temperature differences between the points of heat injection and ejection. The first strategy minimizes the irreversibilities that create
additional entropy; this extra entropy must also be ejected at some point of the cycle to maintain integrity. The latter strategy enhances the ejection efficiency as Δ
S scales inversely with temperature. One example of a Carnot cycle is represented in
Figure 8. Shown for both the
pV and
TS planes are the state point loci for 1.00 mole of a monatomic ideal gas operating over a temperature range of 300–400 K. Heat is injected along the upper isotherm while ejection occupies the lower. The work performed over each cycle equates with the area enclosed by each cyclic pathway.
Figure 9.
Cyclic Pathways and Spectral Entropy. Upper and lower panels illustrate highly similar cyclic pathways for 1.00 mole of monatomic ideal gas. The volume domains are identical while the pressure domains are nearly so. The heat → work conversion efficiency is greater—25% versus 12%—for the cycle in the lower panel because SY↔TS for the B segment is less than that for A.
Figure 9.
Cyclic Pathways and Spectral Entropy. Upper and lower panels illustrate highly similar cyclic pathways for 1.00 mole of monatomic ideal gas. The volume domains are identical while the pressure domains are nearly so. The heat → work conversion efficiency is greater—25% versus 12%—for the cycle in the lower panel because SY↔TS for the B segment is less than that for A.
Carnot’s strategy can be stated succinctly in spectral entropy terms:
At all points of the cyclic pathway, the following equality must be maintained:
SY↔T and
SY↔S are respectively zero for isothermal and adiabatic pathways. Thus Equation 32 reflects that the optimum algorithm for heat → work conversions is where
SY↔TS is limited
either by
SY↔T or
SY↔S. In effect,
SY↔T and
SY↔S establish an upper bound for
SY↔TS so as to minimize the spectral entropy. In other words, the pathway
SY↔TS must demonstrate a single source of thermal programming complexity for the maximum efficiency. Clearly all the pathway segments of
Figure 8 demonstrate this critical property. The condition is unmodified if the segments are subdivided arbitrarily. Note the Carnot segments to be radically different from the pathways illustrated of the previous figures where:
The
TS-spectral entropy provides an alternative assessment of pathway segments for their suitability in heat engine programs. As an example,
Figure 9 shows two (of infinite possible) cyclic pathways that have equivalent volume domains and nearly-equal pressure domains. The upper segments A and B are different, however. The heat → work conversion efficiencies are readily computed by conventional methods. Alternatively, a calculation of
SY↔TS for the A and B segments immediately identifies the more efficient program.
SY↔TS is ca. 10% less for B in the lower panel; the heat → work conversion efficiency is about double that for the upper panel cycle. This holds in spite of the nearly-double temperature domain covered in the upper cycle.