Abstract
This paper investigates the estimated return rate and optimal order quantity under three cross-border e-commerce return logistics modes: direct mail (from predecessor), in situ destruction (new), and insurance (new). The estimated return rate under each model was analyzed and it was found that different modes have different thresholds in delivery lead time (the time retailers need to deliver goods to customers), and within which the estimated return rate increases as the delivery lead time increases. And a size comparison of the estimated return rates for the three models was conducted. A profit model was constructed based on the estimated return rate model, the optimal order quantity was calculated, and the effects of different factors (tax, postage, and delivery lead time etc.) on it were analyzed. For the insurance model, the effect of bearing the insurance ratio between retailers and consumers on the optimal order quantity was examined. The goal of this paper was to construct a model of the estimated return rate for the two new modes and to compare the estimated return rate of the three modes, which provides a reference for retailers to choose among the diversified return logistics modes and then make the best ordering strategy according to the influence of different factors on the optimal order quantity.
1. Introduction
Cross-border e-commerce is a business model that enables international trade by selling goods or services over the internet, in different countries []. The main forms of cross-border e-commerce are B2B, B2C, and C2C []. This study focuses on B2C. Cross-border e-commerce B2C is the process of selling goods to consumers located abroad through online channels, or directly through proprietary websites [].
In recent years, global cross-border e-commerce transactions have shown dramatic growth, with revenues expected to reach around USD 35-2025 billion by 2025 [,]. It will grow to nearly USD 4.8 trillion by 2026 []. Meanwhile, Chinese cross-border e-commerce has also grown rapidly, with total transactions growing 32% annually [], and by 2021 China’s cross-border e-commerce market size had reached CNY 19.8 trillion []. According to data from the E-commerce Research Centre, in the first half of 2022 alone, the cross-border e-commerce market size had exceeded CNY 7 trillion, accounting for 35.85% of China’s total import and export of goods valued at CNY 19.8 trillion []. Although the market size has increased rapidly, the return rate by users of cross-border e-commerce has also increased year by year for various reasons.
The increase in the return rate has led to a considerable increase in costs for retailers as well. Currently, return costs account for 5–10% of the total cost of cross-border e-commerce []. Moreover, return logistics costs are an important influencing factor in return costs []. To reduce return logistics costs, retailers may choose a reasonable cross-border e-commerce return logistics mode. So how should retailers choose an appropriate cross-border e-commerce returns logistics model to reduce their returns logistics costs? This is the focus of this paper.
In this paper, a retailer (within a given country) purchases goods from a manufacturer (within the same country) at a purchase price and then sells the goods to consumers (outside the given country) through a cross-border e-commerce platform. After the consumer places an order, the goods are shipped from the seller’s country to the buyer’s country through cross-border logistics, during which the goods are subject to appropriate taxes and duties as they pass through customs. When the consumer returns the goods, the goods are sent to different places according to different modes. The specific structure of the different modes is shown in Section 3.
The current mainstream cross-border return logistics modes for retailers are direct mail, return insurance, and in situ destruction. First, we explore direct mail, a model that is currently used by platforms such as Lazada and Amazon []. The merchant can specify the value of the returned goods. If the value of the goods is less than or equal to the value of the goods specified by the merchant, the goods will be destroyed directly. If the goods value is greater than the merchant’s specified goods value, the platform will arrange for the goods to be returned to the warehouse specified by the merchant. Second, we explore return insurance; currently, eBay has introduced the eBay Free Return Care Returns Protection Program []. After the purchaser purchases and returns the goods within the scope and time agreed in the insurance agreement, the insurance company will compensate the seller for the loss of income in accordance with the policy agreement. Third, we explore in situ destruction, a model currently used by both Lazada and Shoppe []. The goods are not returned to the retailer nor refunded regardless of their value but, instead, are fully handed over to the e-commerce platform for in situ destruction. Retailers may sometimes incur increased costs due to the improper choice of mode. How should retailers choose between these three models?
At present, there are few studies on the selection of return logistics modes for cross-border e-commerce, and only Wang, Xie, and Fan [] have studied the problems related to return logistics modes for cross-border e-commerce, but their paper has the following shortcomings: First, it mainly focuses on three modes, namely direct mail, bonded warehouse, and overseas warehouse, but there are other modes that are more commonly used in real life, such as insurance and in situ destruction. Second, their paper compares the magnitude of the estimated return rates of the three modes but does not give a specific range. To compensate for their shortcomings in this regard, this paper selects their direct mail mode, as well as two other real-life modes: insurance and in situ destruction. The cross-border e-commerce return logistics model of these three modes was studied; on the other hand, this paper compares the size of the estimated return rate of the three modes and gives a more detailed range of values.
In this paper, we study the above three currently common modes to cross-border e-commerce return logistics. In so doing, we seek to address the following questions: (1) What is the estimated return rate and optimal order quantity for retailers under different modes? (2) How should retailers choose a cross-border e-commerce return logistics mode that suits their needs? (3) How should retailers decide on ordering under different modes? To answer these questions, we built three estimated return rate models based on a study by Wang, Xie, and Fan []; these three models are based on consumers’ time preferences. And we analyze and compare the estimated return rate under the different modes. The retailer can choose a mode with a lower estimated return rate to reduce the cost of returns, and then determine the ordering strategy based on the impact of factors such as taxes and postage on the optimal order quantity under that model.
First, there are thresholds of the delivery lead time for all three modes (see Section 3.2 for details). Within the threshold range, customers may choose to return the goods because of the extended delivery lead time [,]. Outside of the threshold range, consumers usually do not choose to return the goods, but consumers may not purchase again. After analyzing the estimated return rate, the in situ destruction mode has the largest estimated return rate, while the direct mail mode has the smallest estimated return rate.
Second, the paper also establishes a profit model based on the estimated return rate, through which the optimal order quantity of retailers in different modes and the influence of each factor (postage, taxes, delivery lead time, etc.) on the optimal order quantity are calculated; we find that the influence of factors such as postage and taxes on the optimal order quantity is different in different modes. For example, in the direct mail mode, when postage and taxes are high, retailers are advised to purchase more goods with higher salvage value; when postage and taxes are low, retailers are advised to purchase more goods with lower salvage value. Further details appear in Section 4.
Finally, the paper conducts numerical simulations on the estimated return rate as well as the optimal order quantity.
Under the more detailed model, this paper provides more detailed guidance for future research, as well as retailers’ model selection and ordering strategies. First, it provides more detailed cross-border e-commerce return logistics models so that retailers can have more guidance when selecting return logistics models. Second, under the insurance model, this paper provides different ordering strategy suggestions for different situations under the insurance ratio coefficient borne by consumers. Third, the three modes are compared in terms of size and a detailed range of values is provided so that retailers can choose the appropriate return logistics mode according to their own situation based on the comparison table.
The rest of the paper is organized as follows: In Section 2, we review the relevant literature. In Section 3, we build and analyze the estimated return rate model. In Section 4, we model the profit and calculate and analyze the optimal order quantity. In Section 5, we perform numerical simulations for the estimated return rate, as well as the optimal order quantity. In Section 6, we discuss the conclusions.
2. Review of the Literature
A number of scholars have studied this area of e-commerce logistics. For example, Andreas Risberg [] developed a framework for logistics decision making and reviewed how the research focus in the e-commerce logistics literature has evolved from multichannel logistics to, more recently, omnichannel logistics. Cano, Londoño-Pineda, and Rodas [] examined recent work on the sustainability of e-commerce logistics operations from the perspectives of last mile, distribution logistics, the main themes, trends, etc. Ahsan and Rahman [], on the other hand, devoted a systematic literature review to the study of e-commerce product returns.
Both consumer satisfaction and utility influence consumer behavior in e-commerce transactions. Vahdani, Niaki, and Aslanzade [] found that reducing delivery lead time or improving product quality to increase customer satisfaction changes consumer utility, which in turn improves the overall performance of the food supply chain. Some scholars also relied on the timeliness of perishable food or freshness to reduce cost, improve efficiency, and increase consumer satisfaction [,]. Lin et al. [] investigated the moderating effect between consumer perception and online purchase intention from the perspective of consumers’ perceived risk of aquatic products.
However, a higher purchase rate also leads to a higher return rate. In order to reduce the return rate, many scholars have studied the return management of goods.
Saarijärvi, Sutinen, and Harris [] studied the different stages of the return decision and the specific reasons for returns and showed that product defects, consumer benefits, etc., have an impact on return behavior. Araújo et al. [] showed, from a policy perspective, that it is possible to develop a return policy, improve return handling times, and control expenses to manage returns well. Zhang, Q.L Ding, and J.C Ding [] used two return strategies, environmental awareness and shipping insurance, to reduce the return rate and manage returns well. Walsh and Möhring [] used a money back guarantee, product reviews, and return labels to reduce the return rate, and the results showed that product reviews had a better effect on reducing the return rate.
Many retailers have started to move into cross-border e-commerce due to the rapid development of the internet. Cross-border e-commerce is similar to domestic e-commerce, but there are some differences, mainly in logistics, customs regulations, network security, customer relationship management, and payment []. However, the biggest difference is that purchasers and sellers in cross-border e-commerce usually belong to different countries or regions [,]. As a result, freight costs, customs efficiencies, etc., incurred between different regions are critical to consumer behavior [].
Most previous studies on cross-border e-commerce have focused on the perfect logistics system, the driving mechanism of consumer willingness (behavior), and its influence effect [], while less research has been performed on the key issue of cross-border e-commerce returns. In fact, good returns management can reduce return rates, improve efficiency and reduce costs. A more liberal returns policy can increase consumer purchase intent.
Yang, Ma, and Han [] examined the mediating role of a loose return policy in cross-border e-commerce, and found that a loose return policy positively moderates the mediating path of product content on purchase intention through product commitment. Shao et al. [] established a theoretical model of the effect of a loose return policy on consumers’ purchase intention in cross-border e-commerce, and the results show that when retailers adopt a loose return policy, consumers perceive higher quality and lower perceived risk, which in turn leads to higher purchase intention.
For clear return factors, Xu and Jackson [] investigated the factors influencing customers’ return channel loyalty. The results showed that four main factors, perceived risk, purchase-return channel consistency, price cost, and hassle cost, affect customers’ return channel loyalty, and perceived risk has the greatest impact on customers’ return channel loyalty. A study by Wang, Tian, and Fan [] showed that time preference affects consumers’ purchase behaviors, as well as return behaviors.
Choosing the right returns logistics model also enables better returns management. Today, cross-border logistics is mainly divided into international postal parcel, international commercial express, cross-border rail logistics, overseas warehousing mode, and transshipment mode [,]. Zha et al. [] studied the choice of direct mail and bonded warehouse modes with the advantage of market demand information. The results show that information sharing affects the logistics mode choice of overseas suppliers, and information sharing, and direct mail mode are more favorable for retailers. Wang, Xie, and Fan [] proposed a new method to describe customer utility based on customer time preference and constructed three cross-border logistics models: overseas-to-overseas (O2O) mode, overseas-to-domestic (O2D) mode, and domestic-to-domestic (D2D) mode. The results show that the O2O model is always a better choice than the O2D model, while the D2D model is better for retailers than the O2O model under certain conditions. To increase market demand, the O2O model is optimal for retailers selling high-priced goods, while the O2D model is optimal for retailers selling low-priced goods. Although Wang, Xie, and Fan [] consider three modes, they did not take into account real factors such as insurance and in situ destruction.
This paper, however, aims to provide reference for retailers’ cross-border e-commerce return logistics model selection and merchandise ordering strategy. It uses the real-life cross-border e-commerce return logistics mode and the mode from Wang, Xie, and Fan [] to study the direct mail mode, the in situ destruction mode, and the return insurance mode. In other words, this paper combines the three realistic factors of cross-border e-commerce, returns, and insurance to predict the return rates. And the retailer can select the appropriate returns logistics model based on the estimated return rate and then determine the optimal order quantity under that mode.
A summary of the literature review for this paper is shown in Table 1.

Table 1.
Summary of the literature review.
This paper refers mainly to Wang, Xie, and Fan [] and makes the following improvements, shown in Table 2.

Table 2.
Comparison table.
3. Estimated Return Rate Model of Cross-Border E-Commerce Return Logistics Mode
3.1. Problem Description and Notation
This paper studies a total of three cross-border e-commerce return logistics modes: the direct mail mode, the in situ destruction mode, and the return insurance mode.
Under the direct mail mode, the overseas retailer receives the consumer’s order and can send the goods directly from the retailer’s in situ area to the overseas consumer. When a return occurs, the consumer sends the goods directly back to the retailer’s in situ area. This means that the direct mail mode involves cross-border logistics from the seller’s country to the purchaser’s country in the forward direction and from the purchaser’s country to the seller’s country in the reverse direction. This mode is beneficial for overseas retailers to avoid inventory risk, but it also incurs higher logistics costs []. The direct mail mode is shown in Figure 1.
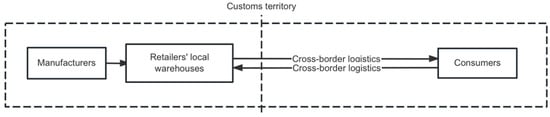
Figure 1.
Direct mail mode.
In the in situ destruction mode, the overseas retailer receives the consumer’s order and sends the goods directly from the retailer’s in situ area to the overseas consumer. When a return occurs, the consumer is required to send the goods directly to the centralized destruction office in their home country. That is, the in situ destruction mode involves cross-border logistics from the seller’s country to the purchaser’s country in the forward direction and centralized destruction office in the purchaser’s country in the reverse direction. The in situ destruction mode is shown in Figure 2.
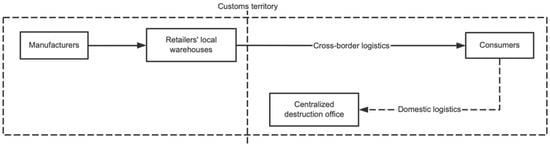
Figure 2.
In situ destruction mode.
Under the return insurance mode, the overseas retailer will take out insurance on the goods and, upon receipt of the consumer’s order, will send the goods directly from the retailer’s local area to the overseas consumer. When a return occurs, the consumer is required to send the goods directly to a centralized collection point in their home country, and the insurer will then compensate the retailer for the loss suffered in connection with the return. This means that the forward logistics of the return insurance mode is the cross-border logistics from the seller’s country to the purchaser’s country, while the reverse logistics is the inbound logistics to the processing center in the purchaser’s country. The return insurance mode is shown in Figure 3.
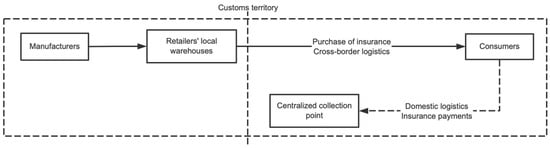
Figure 3.
Return insurance mode.
The notation description in this paper is shown in Table 3.

Table 3.
Definitions of symbols.
The assumptions in this paper are as follows (assumptions from Wang, Xie, and Fan []):
- (1)
- Only returns due to time preferences are considered.
- (2)
- Returns accepted by the retailer are false failure returns and the consumer is given a full refund.
- (3)
- Although the retailer may sell the goods at the same price on the second sale as on the first, there is a higher cost to the retailer due to the various post-return handling, so the value of the goods to the retailer is reduced.
- (4)
- The consumer is responsible for the logistics costs of purchasing and returning the goods, as well as tariff costs.
3.2. Model Construction
Wang, Xie, and Fan [] proved the direct mail model in their paper. This paper focuses on proving the insurance model and the in situ destruction model.
For the model construction of the estimated return rate for the direct mail mode, first the utility function is constructed, and the return behavior occurs when the utility is less than . Next, the number of consumers purchasing goods is calculated. Then the number of retained consumers is calculated. Finally, the consumer return rate can be found by finding the rate of consumers who keep the goods.
The consumption utility functions for the direct mail and in situ destruction modes is as follows:
A purchase occurs when the consumer’s utility is greater than zero.
The utility function of the consumer upon receipt of the goods is as follows:
Lemma 1.
The estimated return rate under the direct mail model is as follows:
Proof.
In the direct mail mode, if a return occurs, the consumer has to pay the postage for the return of the goods as well as the tax , so when the consumer’s utility after receiving the goods , which means that the consumer’s utility after receiving the goods is lower than the lost postage, as well as the tax, the consumer will choose to return the goods. When , the consumer will keep the goods. denotes consumers who will purchase the goods, denotes consumers who will not purchase the goods, denotes consumers who will keep the goods, and denotes consumers who will return the goods.
The number of consumers who will purchase the goods is calculated as follows:
Since . So has the following formula:
so, the number of consumers who will retain the goods is:
therefore, the number of consumers who will return the goods (i.e., the estimated return rate) is as follows:
□
Theorem 1.
In the direct mail mode, when , consumers will not return the goods after receiving the goods because of the long delivery lead time; when , consumers will return the goods after receiving the goods because of the long delivery lead time. When , there is , when the estimated return rate of the goods will increase with the delivery lead time. When , there is , when the estimated return rate of the goods will decrease with the delivery lead time.
Proof.
When , consumers will not return the goods after receiving them because the delivery lead time is too long. At this point we have , from which we obtain . So, the threshold for the delivery lead time at this point is .
Finding the first-order derivative of with respect to leads to the result that is shown below:
so, . And since , we have when and when . □
For the model construction of the estimated return rate for the in situ destruction mode, first the utility function is constructed, and the return behavior occurs when the utility is less than . Next, the number of consumers purchasing goods is calculated. Then the number of retained consumers is calculated. Finally, the consumer return rate can be found by finding the rate of consumers who keep the goods.
Lemma 2.
The estimated return rate in the in situ destruction mode is as follows:
Proof.
In the in situ destruction mode, if a return occurs, the consumer has to pay the postage for the return of the goods, as well as the tax , so when the consumer’s utility after receiving the goods , which means that the consumer’s utility after receiving the goods is lower than the lost postage, as well as the tax, the consumer will choose to return the goods. When , the consumer will keep the goods.
The number of consumers who will purchase the goods is calculated as follows:
because . So has:
so, the number of consumers who would retain the goods is:
therefore, the number of consumers who would return the goods (i.e., the estimated return rate) is calculated as follows:
□
Theorem 2.
In the in situ destruction mode, when
, consumers will not perform a return operation on the goods after receiving them because of the long delivery lead time. When
, consumers will perform a return operation on the goods after receiving them because of the long delivery lead time. When
, there is
, when the estimated return rate of the goods will increase with the delivery lead time. When
, there is
, when the estimated return rate of the goods will decrease with the delivery lead time.
Proof.
When , the consumer will not return the goods after receiving them because of the long delivery lead time. At this point, we have , from which we have . So, the threshold for the delivery lead time at this point is .
Finding the first-order derivative of with respect to leads to the result that follows:
and because , so when , we have , when , we have . □
The return insurance mode consumption utility function is as follows:
The utility function of the consumer upon receipt of the goods is as follows:
For the model construction of the estimated return rate for the insurance mode, first the utility function is constructed, and the return behavior occurs when the utility is less than . Next, the number of consumers purchasing goods is calculated. Then the number of retained consumers is calculated. Finally, the consumer return rate can be found by finding the rate of consumers who keep the goods.
Lemma 3.
The estimated return rate under the return insurance mode is as follows:
Proof.
In the return insurance mode, if a return occurs, the consumer has to pay the postage for the return of the goods, as well as the tax , so when the consumer’s utility after receiving the goods , which means that the consumer’s utility after receiving the goods is lower than the lost postage as well as the tax, the consumer will choose to return the goods. When , the consumer will keep the goods.
The number of consumers who would purchase the goods is calculated as follows:
because . So, has:
so, the number of consumers who would retain the goods is:
therefore, the number of consumers who would return the goods (i.e., the estimated return rate):
□
Theorem 3.
In the return insurance mode, when
, the consumer will not return the goods after receiving them because of the long delivery lead time. When
, the consumer will return the goods after receiving them because of the long delivery lead time return operation. When
, there is
, when the estimated return rate of the goods will increase with the delivery lead time. When
, there is
, when the estimated return rate of the goods will decrease with the delivery lead time.
Proof.
When , consumers will not return the goods after receiving them because of the long delivery lead time. At this point we have , from which we have . So, the threshold for the delivery lead time at this point is .
Finding the first-order derivative of with respect to leads to the result that follows:
and because , so when , we have . When , we have . □
3.3. Theoretical Analysis Related to Estimated Return Rate
Through our research we have made the following findings:
Firstly, there is a threshold for the delivery lead time for all three modes: direct mail, in situ destruction, and return insurance (, , ). The threshold is made up of factors such as the price of the goods, cross-border logistics shipping costs, inbound logistics shipping costs, taxes, and charges. When the delivery lead time exceeds this threshold, the consumer will not choose to return the goods due to the long delivery lead time, but the consumer may no longer purchase the goods from the retailer due to the unacceptable delivery lead time, and the retailer may compensate the consumer for the long delivery lead time. When the delivery lead time is less than this threshold, the consumer will return the goods after receiving them because of the long delivery lead time. So, in order to reduce consumer returns within this threshold, the retailer may need to consider how to set the price of the item, shipping costs, and so on.
Secondly, in the direct mail mode, when the price of the goods is less than the cross-border logistics freight costs, the estimated return rate of the goods will decrease with the increase of the delivery lead time; when the price of the goods is greater than the cross-border logistics freight costs, the estimated return rate of the goods will increase with the increase of the delivery lead time. In the in situ destruction and return insurance modes, when the price of the goods is less than the freight cost of domestic logistics, the estimated return rate of the goods will decrease as the delivery lead time increases; when the price of the goods is greater than the freight cost of domestic logistics, the estimated return rate of the goods will increase as the delivery lead time increases.
Finally, the study found that when the price of a goods is too high, the increased delivery lead time of the goods leads to more pronounced consumer returns. Therefore, when retailers sell higher-priced goods, they should use faster and more efficient logistics methods to reduce the delivery lead time of the goods. For example, choosing a courier company for air transport will reduce the estimated return rate for consumers. When the price of the goods is too low, the longer delivery time will not make the return behavior of consumers more obvious. Retailers can choose lower cost logistics companies and more affordable logistics modes to reduce costs.
3.4. Comparison of the Size of the Estimated Return Rate
The forward logistics under the three modes of direct mail, in situ destruction, and return insurance are all the same cross-border logistics, so the cross-border logistics time, freight, and taxes are the same for all three modes, and the forward cross-border logistics freight is always greater than the reverse domestic logistics freight; i.e., , , , .
Lemma 4.1.
.
Proof.
since , and , it is known that , so we have . □
Lemma 4.2.
When 0 , we have ; when , we have .
Proof.
since , and , it is only necessary to determine the size of the molecule. Because , the image of the function can be judged to be open downwards and to have two roots.
- when 0 , we have ,
- when , we have . □
Lemma 4.3.
for and ; for and ; for and ; and with ; i.e., .
Proof.
since , and , only the size of the molecule needs to be judged. Because , it is not possible to determine its magnitude directly. So, when , the image of the function opens downwards and has two roots. At this point the following formula is used:
and
This leads to:
when , ,
when , ,
when , ,
when , we have , i.e., . □
The comparison of estimated return rates in this paper is shown in Table 4.

Table 4.
Comparison of estimated return rates.
The study shows that as the reverse logistics of the direct mail mode is cross-border, while the reverse logistics of the in situ destruction and return insurance mode are in-country, in-country logistics is a better option for consumers. Therefore, the latter two modes are more likely to cause consumers to purchase and return goods than the direct mail mode. Thus, when retailers choose the in situ destruction and return insurance mode, they need to pay more attention to managing the return of goods.
The comparison shows that, in all cases, the estimated return rate is always greater for the in situ destruction mode than for the direct mail mode. However, high return rates are also accompanied by high purchase rates. Thus, when choosing between the two modes, retailers need to consider the balance between the two factors. For example, when a retailer sells lower-cost, higher-volume goods, they may choose the in situ destruction mode. When the retailer sells higher-cost, smaller-volume goods, it is still best to choose the direct mail mode.
When the three modes are compared, the insurance mode has the highest estimated return rate and the direct mail mode has the lowest estimated return rate when the price of the item is high. Although the estimated return rate for the return insurance mode is higher than that for the in situ destruction mode, the retailer is reimbursed by the insurance company for the goods and may be more profitable under this mode. The estimated return rate is always highest for the in situ destruction mode when the price of the goods is low. The direct mail and return insurance mode vary in size under different conditions, so retailers can refer to the table when considering the best mode and then choose the most appropriate return logistics mode for their own conditions.
4. Profit Model of Cross-Border E-Commerce Return Logistics Mode
4.1. Profit Function
4.1.1. Profit Function in the Direct Mail Mode
The first item represents the proceeds from the sale of the goods that were not returned by the consumer. The second item represents the profit from reselling returned goods. The third item represents the salvage value and inventory holding costs of goods that are not sold and are stored in the warehouse. The fourth item represents the retailer’s purchase costs.
Lemma 5.
In the direct mail mode, when , the optimal order quantity for the retailer is
Proof.
Finding the first-order derivative of with respect to yields the result that follows:
Finding the second-order derivative of with respect to yields the result that follows:
since and . So, when , we have . At this point, we let , then we have the optimal ordering quantity .
When we have the following:
Solving for this gives:
□
Theorem 5.1.
In the direct mail mode, when , we have and , indicating that the retailer’s optimal order quantity decreases as the tax and postage costs increase. When , we have and , indicating that the retailer’s optimal order quantity increases with the increase in tax and postage.
Proof.
Finding the first-order derivatives of with respect to , , respectively, yields the following:
because , and . So, when , i.e., when , we have and . When , i.e., when , we have and □
Theorem 5.2.
In the direct mail mode, the delivery lead time of the item has more influence on the optimal order quantity. When and or and , there is . In both cases, the retailer’s optimal order quantity decreases as the merchandise delivery lead time increases; when and or and , there is . In both cases, the retailer’s optimal order quantity increases as the delivery lead time of the goods increases.
Proof.
Finding the first-order derivative of with respect to yields the following:
Since the numerator , only the sign of the denominator needs to be determined. For the denominator, , , , and , so only the sign of , p-c_1 needs to be judged. So, when and , i.e., when and , we have . When and , i.e., when and , we have . When and , i.e., when and , we have . When and , i.e., when and , we have . □
Theorem 5.3.
In the direct mail mode, we have when . This indicates that the retailer’s optimal order quantity increases as the inventory cost increases. When , we have . This means that the retailer’s optimal order quantity decreases as the inventory cost increases.
Proof.
Finding the first-order derivative of with respect to yields the following:
Since , , . So, when , i.e., when , we have . When , i.e., when , we have . □
Theorem 5.4.
In the direct mail mode, when , there is
, indicating that the retailer’s optimal order quantity decreases as the value coefficient increases. When
, there is
, indicating that the retailer’s optimal order quantity increases as the value coefficient increases.
Proof.
Finding the first-order derivative of with respect to yields the following:
Since , , . So, when , i.e., when , we have . When , i.e., when , we have . □
Theorem 5.5.
In the direct mail mode, when , there is
, indicating that the retailer’s optimal order quantity decreases as the salvage value of the goods increases. When , there is
, indicating that the retailer’s optimal order quantity increases as the salvage value of the goods increases.
Proof.
Finding the first-order derivative of with respect to yields the following:
Since , , . So, when , i.e., when , we have . When , i.e., when , we have . □
The results of the study show that when the salvage value of the goods is low, an increase in taxes and postage costs leads to a decrease in the retailer’s optimal order quantity. When the salvage value of the goods is high, an increase in taxes and postage costs leads to an increase in the retailer’s optimal order quantity. Therefore, when the tax and postage costs of cross-border logistics are too high, retailers tend to increase the sales of goods with a higher salvage value and to sell fewer goods with a lower salvage value.
The delivery lead time of a goods does not single-handedly affect the retailer’s optimal order quantity. When a retailer sells high-priced goods with a low salvage value or low-priced goods with a high salvage value, a longer delivery lead time will result in a reduction in the retailer’s optimal order quantity. When a retailer sells low-priced goods with a low salvage value or high-priced goods with a high salvage value, a longer delivery lead time will lead to an increase in the retailer’s optimal order quantity. This means that when the delivery lead time is too long, retailers should purchase more low-priced goods with a low salvage value or high-priced goods with a high salvage value. When the delivery lead time is short, retailers should purchase more high-priced goods with a low salvage value or low-priced goods with a high salvage value.
When the retailer purchases goods from the manufacturer at a higher price, an increase in the cost of stocking the goods increases the retailer’s optimal order quantity. When the order price is lower, an increase in the cost of stocking the goods reduces the retailer’s optimal order quantity. Therefore, when the inventory cost is low, the retailer should increase the quantity ordered at a lower price. Conversely, when the cost of inventory is higher, the retailer should order more of the higher-priced item.
When the salvage value of the goods is low, an increase in the merchandise value coefficient reduces the retailer’s optimal order quantity. When the salvage value is high, an increase in the merchandise value coefficient will increase the retailer’s optimal order quantity. Therefore, when the merchandise value coefficient is low, the retailer should increase the order quantity of the lower salvage value item. Conversely, when the goods value coefficient is higher, the retailer should increase the order quantity of the goods with a higher salvage value.
When the retailer purchases goods from the manufacturer at a higher price, an increase in the salvage value of the goods leads to a decrease in the retailer’s optimal order quantity. When the order price is lower, an increase in the salvage value of the goods leads to an increase in the retailer’s optimal order quantity. This means that when the salvage value of the goods is low, the retailer should order more of the goods with a higher purchase price. When the salvage value of goods is high, the retailer should order more of the goods at a lower purchase price.
4.1.2. Profit Function in the In Situ Destruction Mode
The first item represents the revenue generated by the sale of the goods and the failure of the consumer to return them. The second item represents the retailer’s purchase cost.
Theorem 6.
In the in situ destruction mode, when , the optimal order quantity for the retailer is
Proof.
Finding the first-order derivative of with respect to yields the result that:
Finding the second-order derivative of with respect to yields the result that:
since , . So, when , we have . At this point, let , then we have the optimal ordering quantity . When we have:
Solving for this gives:
□
Theorem 6.1.
In the in situ destruction mode, there is
and , indicating that the retailer’s optimal order quantity decreases as the tax and postage costs increase.
Proof.
Finding the first-order derivatives of with respect to , , respectively, yields the following:
since , and . So, we have and . □
Theorem 6.2.
In the in situ destruction mode, when , there is
, indicating that the retailer’s optimal order quantity decreases as the delivery lead time increases. When , there is
, indicating that the retailer’s optimal order quantity increases as the delivery lead time increases.
Proof.
Finding the first-order derivative of with respect to yields the following:
since the numerator , only the sign of the denominator needs to be judged. For the denominator, , , , and , so only the sign of needs to be judged. When , i.e., when , we have . When , i.e., when , we have . □
The results of the study show that, in either case, higher taxes and postage costs lead to a reduction in the retailer’s optimal order quantity. Therefore, it is advisable for retailers to reduce their order quantity when tax and postage costs are high.
When the price of the goods is greater than the freight cost of domestic logistics, the longer delivery lead time leads to a reduction in the retailer’s optimal order quantity. When the price of the goods is less than the freight cost of the domestic logistics, a longer delivery lead time will lead to an increase in the retailer’s optimal order quantity. This means that when the delivery lead time is too long, the retailer should order more goods priced lower than the freight cost of the domestic logistics. When the delivery lead time is short, retailers should order more goods priced higher than the freight cost of the domestic logistics.
4.1.3. Profit Function under the Insurance Mode
The first item represents the proceeds from goods sold and not returned by the consumer. The second item represents the insurance company’s compensation for the returned goods after insurance. The third item represents the retailer’s purchase costs. The fourth item represents the cost to the retailer of purchasing the return insurance.
Theorem 7.
In the return insurance mode, when
, the retailer’s optimal order quantity is .
Proof.
Finding the first-order derivative of with respect to yields the result that follows:
Finding the second-order derivative of with respect to yields the result that follows:
since and . So, when , we have . At this point, we let , then we have the optimal ordering quantity . When we have the following:
Solving for this gives us the following:
□
Theorem 7.1.
In the return insurance mode, there is
and , indicating that the retailer’s optimal order quantity decreases as the tax and postage costs increase.
Proof.
Finding the first-order derivatives of with respect to , , respectively, yields the following:
Since 0 , , and since , and . So, we have and . □
Theorem 7.2.
In the return insurance mode, when
, there is
, indicating that the retailer’s optimal order quantity decreases as the delivery lead time increases. When , there is
, indicating that the retailer’s optimal order quantity increases as the delivery lead time increases.
Proof.
Finding the first-order derivative of with respect to yields the following:
Since the numerator , only the sign of the denominator needs to be determined. For the denominator, , , and , so only the sign of needs to be judged. When , i.e., when , we have . When , i.e., when , we have . □
The results of the study show that in either case, higher taxes and postage costs lead to a reduction in the retailer’s optimal order quantity. Therefore, it is advisable for retailers to reduce their order quantity when tax and postage costs are high.
When the price of the goods is greater than the freight cost of domestic logistics, the longer delivery lead time leads to a reduction in the retailer’s optimal order quantity. When the price of the goods is less than the freight cost of the domestic logistics, a longer delivery lead time will lead to an increase in the retailer’s optimal order quantity. This means that when the delivery lead time is too long, the retailer should order more goods priced lower than the freight cost of the domestic logistics. When the delivery lead time is short, retailers should order more goods priced higher than the freight cost of domestic logistics.
Theorem 7.3.
In the return insurance mode, we have when . This means that the optimal order quantity increases as the proportion of insurance borne by the consumer. When , we have . This means that the optimal order quantity decreases with the proportion of insurance borne by the consumer.
Proof.
Finding the first-order derivative with respect to for leads to the result that follows:
Only the sign of the numerator is judged. When , we have . When , we have . □
The results show that when the price of goods is high, the optimal order quantity of retailers increases with the increase of the proportion of consumers who bear insurance. When the price of goods is low, the optimal order quantity of retailers decreases as the proportion of consumers who bear insurance increases. In other words, when consumers have a higher percentage of insurance coverage, retailers should order more higher-priced goods. When consumers have less insurance coverage, retailers should order more lower-priced items.

Table 5.
The main findings.

Table 6.
The main recommendations.
5. Numerical Simulation
5.1. Values
In cross-border e-commerce, factors such as cross-border logistics costs, commodity prices, arrival lead time, and customs clearance taxes and fees all have an impact on the return rate of goods and the retailer’s optimal ordering strategy. Therefore, in order to test the impact of the above factors on the retailer’s choice of cross-border logistics model optimization, a series of computational experiments were carried out in this section to further analyze and validate the main conclusions of this paper based on the model in the previous paper. The experiments were examined using Mathematica software to analyze and validate the main conclusions of this paper.
Based on Wang, Xie, and Fan [], this paper takes face masks (low-value products), clothing (medium-value products), and digital cameras (high-value products) as the objects of study. The information from the experiments in this paper is shown in Table 7.

Table 7.
Information in the experiments.
5.2. Low-Value Goods
Figure 4 and Figure 5 show the estimated return rates and optimal order quantity for three modes of low-value goods.
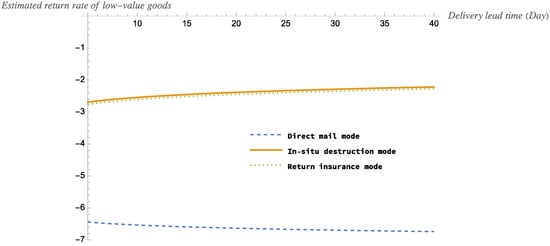
Figure 4.
The impact of delivery lead time on the estimated return rate of low-value goods.
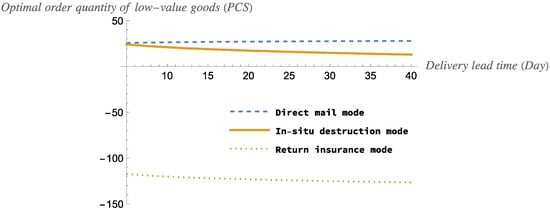
Figure 5.
The impact of delivery lead time on retailer’s optimal order quantity of low-value goods.
According to Figure 4 and Figure 5, for low-value goods, the estimated return rate of the goods will decrease as the delivery lead time increases and the optimal order quantity will increase as the delivery lead time increases under the direct mail mode, while the estimated return rate will increase as the delivery lead time increases and the optimal order quantity will decrease as the delivery lead time increases under the in situ destruction and return insurance modes. Specifically, we have made the following findings: Firstly, the return process is cumbersome for the consumer due to the low value of the goods. Thus, when consumers receive the goods, they want to return them but forgo returning them because they are too low value. As a result, in the case of low-value goods, the estimated return rate is negative for all three modes. Secondly, the estimated return rate is greatest for the in situ destruction mode and lowest for the direct mail mode. Thirdly, the optimal order quantity is greatest for the direct mail mode and lowest for the return insurance mode. Since the optimal order quantity for the return insurance mode is always less than zero, it is not recommended to purchase insurance for goods when the value of the goods is low.
5.3. Medium-Value Goods
Figure 6 and Figure 7 show the estimated return rates and optimal order quantity for the three modes of medium-value goods.
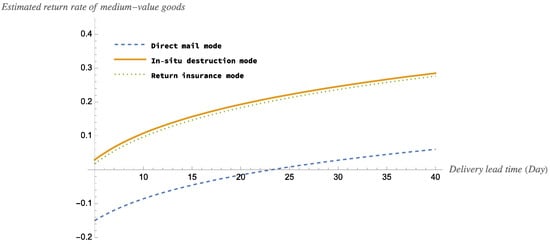
Figure 6.
The impact of delivery lead time on the estimated return rate of medium-value goods.
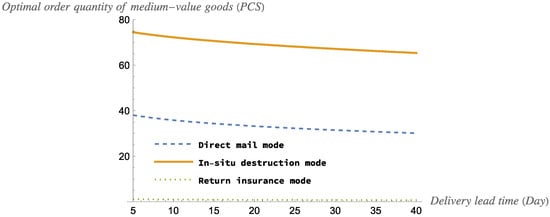
Figure 7.
The impact of delivery lead time on retailer’s optimal order quantity of medium-value goods.
According to Figure 6 and Figure 7, for medium-value goods, the estimated return rate of the goods will increase as the delivery lead time increases in all three modes. And the optimal order quantity will decrease as the delivery lead time increases in all three modes. Specifically, we have made the following findings: Firstly, the estimated return rate is greatest for the in situ destruction mode and lowest for the direct mail mode. This means that if the retailer can deliver the item within 23 days, the consumer will not return it because of time preferences. Therefore, if retailers want to reduce the estimated return rate, they should strictly control the clearance of goods, as well as the logistics time (e.g., by choosing faster logistics methods). Thirdly, the optimal order quantity is greatest for in situ destruction mode and lowest for the return insurance mode. Fourthly, the estimated return rate is highest for the in situ destruction mode because the goods are destroyed and cannot be re-sold, so retailers also have the highest order quantity in the in situ destruction mode to avoid running out of stock.
5.4. High-Value Goods
Figure 6 and Figure 7 show the estimated return rates and optimal order quantity for the three modes of high-value goods.
According to Figure 8 and Figure 9, for high-value goods, the estimated return rate of the goods will increase as the delivery lead time increases in all three modes. And the optimal order quantity will decrease as the delivery lead time increases in all three modes. Specifically, we have made the following findings: Firstly, the estimated return rate is greatest for the direct mail mode and lowest for the in situ destruction mode. The estimated return rate values for all modes is significantly smaller for high-value goods than for medium- and low-value goods. This means that high prices can limit consumers’ returns. Secondly, the threshold for the in situ destruction mode is around 5 days, the threshold for the return insurance mode is around 8 days, and the threshold for the direct mail mode is around 16 days. This means that if the retailer can deliver the item within the threshold, then the consumer will not return it due to time preference. Conversely, if the goods are delivered after the threshold has been exceeded, there is a risk that the consumer may be less inclined to purchase the goods or reverse the purchase due to time preference. Thirdly, the optimal order quantity is greatest for the direct mail mode and lowest for the in situ destruction mode. Fourthly, for the same delivery lead time, a mode with a lower estimated return rate also has a higher optimal order quantity. This means that a lower estimated return rate results in fewer items being available for secondary sales, so retailers need to order more items to keep up with market demand.
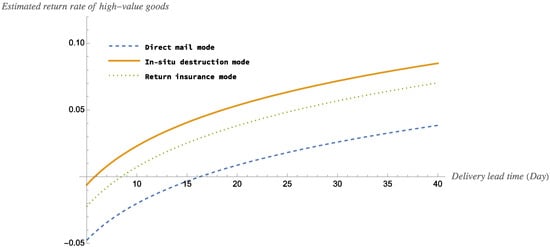
Figure 8.
The impact of delivery lead time on the estimated return rate of high-value goods.
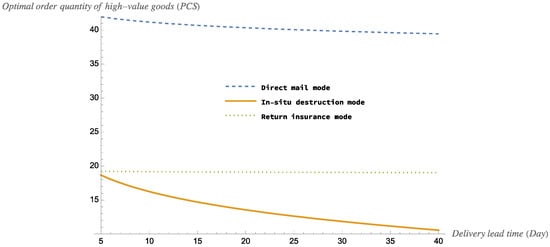
Figure 9.
The impact of delivery lead time on retailer’s optimal order quantity of high -value goods.
6. Conclusions
6.1. Conclusions
The main conclusions of this study are:
- (1)
- The estimated return rate is influenced by a variety of factors, such as tax, postage, price, and delivery lead time. Different modes have different thresholds. Within the thresholds range, consumers’ willingness to return goods changes as the delivery lead time increases; outside the thresholds range, consumers’ willingness to return goods does not change as the lead time increases changes. This means that retailers should choose faster or slower logistics depending on the mode. And in a close-to-realistic interval of delivery lead time, the return rate of goods increases as the arrival time increases.
- (2)
- By comparing the size of the estimated return rate of the three modes, this paper finds that the estimated return rate of the direct mail mode is always smaller than the other two modes in most cases. The estimated return rate of the in situ destruction mode is always larger than the other two modes.
- (3)
- This paper built a profit model based on the estimated return rate model and calculated the optimal order quantity based on the profit model. We analyzed them and found that the optimal order quantities all decrease as the delivery lead time increases. However, for products with different values, the order comparison of the optimal order quantity will be different.
- (4)
- The influence of postage and tax on the optimal order quantity is different in the different modes. Firstly, in the direct mail mode, when tax and postage are higher, it is recommended that the retailer orders goods with a higher salvage value. Conversely, it is recommended to order goods with a lower salvage value when the delivery lead time is longer. It is recommended to order more goods whose salvage value is proportional to the price and vice versa. When the inventory cost is higher, it is recommended to order goods with a higher price and vice versa. When the salvage value is higher, it is recommended to order goods with a lower price and vice versa. Secondly, in the on-site destruction mode, it is recommended to order more goods with a lower salvage value and vice versa. When the tax and postage are high, it is recommended to reduce the quantity of goods ordered and, conversely, to increase the quantity ordered. When the delivery lead time is longer, it is recommended to order goods with a lower price and, conversely, to order goods with a higher price. Finally, in the insurance model, when the tax and postage are high, it is recommended to reduce the quantity ordered and, conversely, to increase the quantity ordered. When the delivery lead time is long, it is recommended to order less expensive goods and, conversely, more expensive ones. And when the consumer pays a larger share of the insurance, it is recommended that retailers order more expensive goods and, conversely, less expensive ones.
6.2. Theoretical Implications
The following theoretical implications were obtained: (1) This paper extends the cross-border e-commerce return logistics model to the study of Wang, Xie, and Fan [], selecting the direct mail model of their, as well as two other real-life models: insurance and in situ destruction. It makes the current study of cross-border e-commerce return logistics modes more detailed. (2) The magnitude of the estimated return rates of the different modes is compared, and a more detailed reference range is given compared to Wang, Xie, and Fan []. (3) This study examines the impact of various factors on the optimal order quantity in a variety of models and summarizes the impact. In particular, the insurance model examines how the insurance premium rate paid by the consumer affects the retailer’s ordering strategy, which has not been found in previous studies.
6.3. Management Implications
The management implications of this study are as follows: (1) The retailer can reduce its return cost by the principle of the cross-border e-commerce return logistics mode suitable for the goods according to its tax, postage, and other factors. (2) Retailers can determine the optimal order quantity of goods according to the impact of various factors on the optimal order quantity that maximize profits, which is an important revelation for retailers’ ordering strategies.
6.4. Research Limitations
The limitations of this study are as follows: First, this paper only considers three modes of forward logistics as cross-border logistics, while it does not consider modes of forward logistics as domestic logistics, such as the overseas warehouse mode. Therefore, the overseas warehouse mode can be added in a future study for analysis and comparison. Second, this paper only studied the cross-border return logistics mode in a monopolistic environment. However, in the real world, there are always competitors. Therefore, the competitive environment can be used as a background in future work. Third, this paper assumes that the only returns are false failure returns and that the consumers choose to return goods based on the length of the delivery lead time, whereas in real life there are also other reasons for returns, such as quality of goods. Fourth, as for the simulation part, most of the data in this paper come from Wang, Xie, and Fan [], which represent the typical situation of low-, medium-, and high-value products, respectively. However, there are other situations in real life, and more detailed simulation studies should be carried out for different situations in the future.
Author Contributions
Conceptualization, Y.L. and Z.L.; methodology, Y.L. and Z.L.; software, Z.L validation, Z.L.; formal analysis, Z.L.; investigation, Z.L.; resources, Z.L.; data curation, Z.L.; writing—original draft preparation, Z.L.; writing—review and editing, Y.L.; visualization, Z.L.; supervision, Y.L.; project administration, Y.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yang, Y.; Chen, N.; Chen, H. The Digital Platform, Enterprise Digital Transformation, and Enterprise Performance of Cross-Border E-Commerce—From the Perspective of Digital Transformation and Data Elements. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 777–794. [Google Scholar] [CrossRef]
- Shojaiemehr, B.; Kuchaki Rafsanjani, M. A Multi-Agent Based Model for Collective Purchasing in Electronic Commerce. Int. J. Mach. Learn. Cyber. 2013, 4, 409–417. [Google Scholar] [CrossRef]
- Giuffrida, M.; Mangiaracina, R.; Perego, A.; Tumino, A. Cross-Border B2C e-Commerce to Greater China and the Role of Logistics: A Literature Review. Int. J. Phys. Distrib. Logist. Manag. 2017, 47, 772–795. [Google Scholar] [CrossRef]
- Cui, Y.; Mou, J.; Cohen, J.; Liu, Y. Understanding Information System Success Model and Valence Framework in Sellers’ Acceptance of Cross-Border e-Commerce: A Sequential Multi-Method Approach. Electron. Commer. Res. 2019, 19, 885–914. [Google Scholar] [CrossRef]
- Song, B.; Yan, W.; Zhang, T. Cross-Border e-Commerce Commodity Risk Assessment Using Text Mining and Fuzzy Rule-Based Reasoning. Adv. Eng. Inform. 2019, 40, 69–80. [Google Scholar] [CrossRef]
- Han, B.; Rizwanullah, M.; Luo, Y.; Atif, R. The Role of Cross-Border E-Commerce on the Export of Goods and Services. Electron. Commer. Res. 2024. [Google Scholar] [CrossRef]
- Wang, C. Analyzing the Effects of Cross-Border E-Commerce Industry Transfer Using Big Data. Mob. Inf. Syst. 2021, 2021, 9916304. [Google Scholar] [CrossRef]
- Li, Z.; Gao, G.; Xiao, X.; Zuo, H. Factors and Formation Path of Cross-Border E-Commerce Logistics Mode Selection. Sustainability 2023, 15, 3685. [Google Scholar] [CrossRef]
- Xi, X.; Wei, M.; Teo, B.S.-X. Analysis of the Key Influencing Factors of China’s Cross-Border e-Commerce Ecosystem Based on the DEMATEL-ISM Method. PLoS ONE 2023, 18, e0287401. [Google Scholar] [CrossRef]
- CITIC Institute. Cross-Border E-Commerce Logistics Industry Topics for the Transport Industry. 2020. Available online: http://www.cs.ecitic.com/newsite/zxzx/yjbg/ (accessed on 3 July 2023).
- Wang, X.; Xie, J.; Fan, Z.-P. B2C Cross-Border E-Commerce Logistics Mode Selection Considering Product Returns. Int. J. Prod. Res. 2021, 59, 3841–3860. [Google Scholar] [CrossRef]
- Lazada. Notes to Sellers. 2023. Available online: https://www.lazada-seller.cn/ (accessed on 3 July 2023).
- eBay. eBay Free Return Care. 2023. Available online: https://www.ebay.cn/efrc/ (accessed on 3 July 2023).
- Zhao, S.; Wu, F.; Jia, T.; Shu, L. The Impact of Product Returns on Price and Delivery Time Competition in Online Retailing. Comput. Ind. Eng. 2018, 125, 658–667. [Google Scholar] [CrossRef]
- Risberg, A. A Systematic Literature Review on E-Commerce Logistics: Towards an e-Commerce and Omni-Channel Decision Framework. Int. Rev. Retail Distrib. Consum. Res. 2023, 33, 67–91. [Google Scholar] [CrossRef]
- Cano, J.A.; Londoño-Pineda, A.; Rodas, C. Sustainable Logistics for E-Commerce: A Literature Review and Bibliometric Analysis. Sustainability 2022, 14, 12247. [Google Scholar] [CrossRef]
- Ahsan, K.; Rahman, S. A Systematic Review of E-Tail Product Returns and an Agenda for Future Research. Ind. Manag. Data Syst. 2022, 122, 137–166. [Google Scholar] [CrossRef]
- Vahdani, B. Production-Inventory-Routing Coordination with Capacity and Time Window Constraints for Perishable Products: Heuristic and Meta-Heuristic Algorithms. J. Clean. Prod. 2017, 161, 598–618. [Google Scholar] [CrossRef]
- Jiang, Y.; Lai, P.; Chang, C.-H.; Yuen, K.F.; Li, S.; Wang, X. Sustainable Management for Fresh Food E-Commerce Logistics Services. Sustainability 2021, 13, 3456. [Google Scholar] [CrossRef]
- Giallombardo, G.; Mirabelli, G.; Solina, V. An Integrated Model for the Harvest, Storage, and Distribution of Perishable Crops. Appl. Sci. 2021, 11, 6855. [Google Scholar] [CrossRef]
- Lin, W.; Xu, A.; Zheng, Q.; Ke, L.; Lin, J. Influence of Customer Perceived Value on the Online Shopping Intention of Aquatic Products under B2C E-Commerce. J. Discret. Math. Sci. Cryptogr. 2018, 21, 1189–1192. [Google Scholar] [CrossRef]
- Saarijärvi, H.; Sutinen, U.-M.; Harris, L.C. Uncovering Consumers’ Returning Behaviour: A Study of Fashion e-Commerce. Int. Rev. Retail Distrib. Consum. Res. 2017, 27, 284–299. [Google Scholar] [CrossRef]
- de Araújo, A.C.; Matsuoka, E.M.; Ung, J.E.; Massote, A.; Sampaio, M. An Exploratory Study on the Returns Management Process in an Online Retailer. Int. J. Logist. Res. Appl. 2018, 21, 345–362. [Google Scholar] [CrossRef]
- Zhang, S.; Ding, Q.; Ding, J. Return Strategy of E-Commerce Platform Based on Green and Sustainable Development. Sustainability 2023, 15, 11188. [Google Scholar] [CrossRef]
- Walsh, G.; Möhring, M. Effectiveness of Product Return-Prevention Instruments: Empirical Evidence. Electron. Mark. 2017, 27, 341–350. [Google Scholar] [CrossRef]
- Hazarika, B.B.; Mousavi, R. Review of Cross-Border E-Commerce and Directions for Future Research. J. Glob. Inf. Manag. 2021, 30, 1–18. [Google Scholar] [CrossRef]
- Zhu, W.; Mou, J.; Benyoucef, M. Exploring Purchase Intention in Cross-Border E-Commerce: A Three Stage Model. J. Retail. Consum. Serv. 2019, 51, 320–330. [Google Scholar] [CrossRef]
- Baek, E.; Lee, H.K.; Choo, H.J. Cross-Border Online Shopping Experiences of Chinese Shoppers. Asia Pac. J. Mark. Logist. 2019, 32, 366–385. [Google Scholar] [CrossRef]
- Cho, H.; Lee, J. Searching for Logistics and Regulatory Determinants Affecting Overseas Direct Purchase: An Empirical Cross-National Study. Asian J. Shipp. Logist. 2017, 33, 11–18. [Google Scholar] [CrossRef]
- Yang, X.; Ma, Y.; Han, J. Product Information the More the Better? A Moderated Mediation Model to Explain Consumer Purchasing Intention in Cross-Border e-Commerce. Asia Pac. J. Mark. Logist. 2023, 35, 2601–2620. [Google Scholar] [CrossRef]
- Shao, B.; Cheng, Z.; Wan, L.; Yue, J. The Impact of Cross Border E-Tailer’s Return Policy on Consumer’s Purchase Intention. J. Retail. Consum. Serv. 2021, 59, 102367. [Google Scholar] [CrossRef]
- Xu, X.; Jackson, J.E. Investigating the Influential Factors of Return Channel Loyalty in Omni-Channel Retailing. Int. J. Prod. Econ. 2019, 216, 118–132. [Google Scholar] [CrossRef]
- Wang, X.; Tian, J.; Fan, Z.-P. Optimal Presale Strategy Considering Consumers’ Preference Reversal or Inconsistency. Comput. Ind. Eng. 2020, 146, 106581. [Google Scholar] [CrossRef]
- Yang, Y. Selection Method of Cross-Border e-Commerce Export Logistics Mode Based on Collaborative Filtering Algorithm. J. Math. 2022, 2022, 6885432. [Google Scholar] [CrossRef]
- Xie, C.; Wang, H.; Jiao, J. Cross-Border E-Commerce Logistics Collaboration Model Based on Supply Chain Theory. Secur. Commun. Netw. 2022, 2022, 1498765. [Google Scholar] [CrossRef]
- Zha, X.; Zhang, X.; Liu, Y.; Dan, B. Bonded-Warehouse or Direct-Mail? Logistics Mode Choice in a Cross-Border e-Commerce Supply Chain with Platform Information Sharing. Electron. Commer. Res. Appl. 2022, 54, 101181. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).