Abstract
To bolster their competitiveness and profitability, prominent e-commerce platforms have embraced dual retailing channels: self-operating channels and online marketplaces. However, a discernible trend is emerging wherein e-commerce platforms are expanding their marketplaces to encompass competitive third-party suppliers. Motivated by this trend, this study sought to examine the strategic integration of a third-party product amidst the competition between a self-operating channel and a marketplace. This investigation involved the development of a game-theoretic model involving a platform and two representative suppliers—an incumbent supplier and a new entrant. Specifically, we delved into establishing an equilibrium partnership between the platform and the new entrant supplier while also evaluating the self-operating strategy of the established supplier. Our analysis uncovered a counterintuitive outcome: an escalation in the commission rate resulted in diminished profits for the established supplier. Furthermore, we ascertained that the economic implications of a competitive product entry pivot significantly on product quality. Lastly, we demonstrated that the revenue-sharing rate plays a pivotal role in influencing the self-operating strategy of the established supplier, and the market equilibrium hinges on the interplay among product quality, the commission rate, and the revenue-sharing rate. These insights provide invaluable guidance for marketers and e-commerce platforms in their strategic decision-making processes.
1. Introduction
E-commerce platforms have emerged as the dominant business format amid the growth of online retailing [1]. To enhance their competitiveness and profitability, giant e-commerce platforms such as Amazon and JD.com have adopted two retailing channels: the self-operating channel and the revenue-sharing online marketplace. The self-operating channel involves the platform partnering with upstream suppliers through either reselling or revenue-sharing modes. In the reselling mode, the platform operates as a reseller by purchasing products from suppliers and selling them in its own self-run stores. In the revenue-sharing mode, suppliers act as direct sellers and share a portion of their revenues with the platform, which, in turn, provides logistics and post-sales services [2]. In the online marketplace, upstream suppliers are permitted to open their own stores on platforms and directly sell their products to consumers by paying a commission to the platform. Based on these retailing channels, e-commerce platforms have experienced remarkable success and attracted merchants by leveraging the marketplace to obtain access to customers who may not have been aware of them otherwise [3,4].
Intuitively, both the platform and third-party suppliers benefit from the partnership if the suppliers sell products that differ from those sold by the platform, thereby avoiding direct competition [5]. However, in practice, a trend is emerging whereby e-commerce platforms allow third-party suppliers to sell the same kind of product, and third-party suppliers are occasionally permitted to carry identical products in the marketplace. For instance, cheersofa.com sells sofas in JD.com’s marketplace, and, interestingly, the platform itself also sells sofas within the same product category in its self-operated store. Similarly, lovelyskin.com sells skincare products on Amazon.com, some of which are also offered via Amazon itself. The proposition that allowing for third-party suppliers to participate in a platform’s marketplace constitutes a viable strategy that enhances the platform’s revenue streams is commonly intuited [6]. However, this approach may also elicit intense competition between the incumbent and entrant suppliers, leading to potential harm to both the suppliers and the platform [7]. Motivated by the above observations and the resulting ambiguity, this study sought to bridge these theoretical gaps by addressing the following research questions: What pricing strategies can the platform and suppliers adopt to optimize their respective interests? How does the entry of a competitive supplier impact the platform and the incumbent supplier? Under what conditions would the platform and the entrant supplier form their partnership? How does the incumbent supplier strategically choose a self-operating mode in response to a potential entrant rival?
Previous research on third-party sellers’ entry into platform-based markets has primarily focused on the impacts of such entries on pricing decisions [8], partnership relations [9,10], and product sales [11]. However, previous studies predominantly employed vertical differentiation models to represent the quality of their competing products, thereby creating a bias in favor of the supplier with the superior quality product [8,9]. Moreover, one notable difference between the self-operating channel and the online marketplace is that logistics services are provided by different parties [12]. In the self-operating channel, major e-commerce platforms deliver most products through their established self-supporting logistics service system (e.g., Chinese JD.com Logistics). In the online marketplace, logistics services are offered by the third-party suppliers themselves. There remains another gap in understanding how the logistics service impacts the third-party product’s strategic entry and price competition between the incumbent and the entrant. Addressing this question is critical for the e-commerce platforms, as the logistics service is a crucial component of the shopping experience for consumers on e-commerce platforms [13].
In the current research, we developed a game-theoretic model to address these questions. Specifically, we focused on an online market comprising a platform and two representative suppliers (i.e., an incumbent supplier and an entrant supplier). This platform has established a partnership with the incumbent supplier, selling a product through a self-operating channel. A third-party supplier seeks to join the marketplace and offer a substitutable product. We included two alternative modes in the self-operating channel: (i) a reselling self-operating mode, where the platform purchases products from the incumbent supplier at a wholesale price and resells them to online consumers; and (ii) a revenue-sharing self-operating mode, in which the incumbent supplier directly sells the product and shares a proportion of its revenue with the platform. Furthermore, we studied a four-stage game among the platform and suppliers. In the first stage, the incumbent supplier chooses a self-operating mode, which will either be a reselling one or a revenue-sharing one. In the second stage, the platform and the entrant supplier determine whether to form the partnership, i.e., the platform decides whether to open its marketplace to the third-party supplier, and this supplier determines whether to join the marketplace. In the third stage, the platform and suppliers make pricing decisions. In the last stage, customers observe the product prices and decide whether to buy a product and from which supplier. Specifically, according to the decisions in the first and second stages of this game, we considered four possible supply chain scenarios. Our findings revealed a counterintuitive result, in which an increasing commission rate decreases the incumbent supplier’s profits. The rationale behind this result hinges on the intensified competition incurred by a higher commission rate. Additionally, the economic implications of a competitive product entry crucially depend on the product quality. Finally, our findings indicated that the revenue-sharing rate has a crucial impact on determining the incumbent supplier’s self-operating mode selection decisions, and market equilibrium depends on the interplay among product quality, the commission rate, and the revenue-sharing rate.
This study offers three valuable contributions to the existing literature. First, it broadens the scope of research on cross-network externalities and formulates supplier-side network effects. Distinct from the previous studies in this stream, we investigated the pricing competition between a third-party supplier in the marketplace and an incumbent supplier under the self-operating channel. Second, it enriches the literature on platform operations under various business models. We explored the interactions among the incumbent supplier’s self-operating mode (i.e., reselling or revenue sharing), the openness of the platform, and the entry decisions of a third-party supplier, which have not yet been explored. Third, it contributes to the literature on product entry in platform-based markets. Specifically, we examined how the logistics service impacts the strategic entry of third-party products and price competition between the incumbent and the entrant, which is an important yet still underexplored area of research.
The remainder of this paper has been organized as follows. In Section 2, we review the related literature. In Section 3, we detail the model setting and key assumptions. Section 4 analyzes the optimal pricing strategies for the platform and suppliers under each supply chain scenario. Section 5 analyzes the equilibrium partnership between the platform and the entrant supplier, as well as the incumbent supplier’s strategic self-operating mode choice. Conclusions and a discussion regarding future research have been presented in Section 6.
2. Literature Review
In this section, we review three streams of the literature for a review of the existing research and the foundations of our study. The first relevant but under-researched stream is provider-side network effects in the context of a two-sided market. The second literature stream concerns platform operations under various business models. The last stream of the literature pertains to product entry in platform-based markets.
2.1. Provider-Side Network Effects in the Context of a Two-Sided Market
Platform-oriented markets are typically considered two-sided and are characterized via indirect network effects due to the interdependence between consumer demand for products and services on the platforms and the demand for their associated sellers [14]. Therefore, the decisions of one side of the network affect the dynamics of the other side due to cross-network externalities [15,16,17]. Previous studies have examined provider-side network effects in platform-based markets, exploring their impact on the user side from the perspective of the entrant platform’s operation, platform performance investment, revenue model choice, and partnership promotion. For example, Zhu and Iansiti (2012) [14] empirically examined indirect network effects from the application developer side to the consumer side in an application platform, highlighting the critical role that the strength of an indirect network effect plays in the entrant platform’s success. Anderson et al., (2014) [18] analyzed the optimal platform performance investment in the video game industry and demonstrated that the optimal performance investment increases as the strength of the indirect network effect on users from available content grows, particularly when the market attractiveness for content developers is significantly large. Chen et al., (2016) [19] developed an analytical model to evaluate a monopolistic platform’s strategic revenue model choice (i.e., brokerage or advertising) by considering the indirect network effects on buyers due to the increased variety among sellers. Chen and Guo (2022) [9] developed a game-theoretic model to investigate two-sided platform openness, revealing that indirect network effects on consumers resulting from an increased variety among suppliers can promote a partnership between the retailer and the third-party seller.
Our study followed this stream of research on cross-network externalities and formulated supplier-side network effects in our model setting. Distinct from the previous studies in this stream, we investigated the pricing competition between a third-party supplier in the marketplace and an incumbent supplier under the self-operating channel. Specifically, we focused on the impacts of supplier-side network effects on the incumbent supplier’s self-operating mode choice and marketplace openness, which have not been previously studied.
2.2. Platform Operations under Different Business Models
Several studies have focused on examining the effects of platform business models on optimal pricing strategies. For instance, Geng et al., (2018) [20] examined the interactions between a downstream online platform’s business model choice and an upstream firm’s add-on pricing strategy. Xu et al., (2021) [21] explored the effects of channel contract formats (i.e., the wholesale contract and the agency contract) on pricing strategies and profitability under a bundled distribution channel. Christen et al., (2022) [22] investigated value-based pricing under cross-platform settings. Moreover, several authors have investigated the impact of platform business models on product information disclosure. For instance, Kwark et al., (2017) [23] examined the interactions between an upstream manufacturer’s business scheme and third-party information on an online platform. Hao and Tan (2019) [24] explored the incentives that a platform and supplier have to facilitate information disclosure about consumers’ true product valuation under the agency and reselling modes.
Recently, several studies have examined the effects of platform business models with respect to other operational decisions, such as product demand uncertainty [25], supply-side competition [26,27], duopolistic competition [28,29], R&D evaluation [30], and the logistics service provision [31]. Our research diverges from the aforementioned literature in that it explores the interactions among the incumbent supplier’s self-operating mode (i.e., reselling or revenue sharing), the openness of the platform, and the entry decisions of a third-party supplier, which have not yet been explored.
2.3. Product Entry in Platform-Based Markets
There are two general lines underlying this research. One line focuses on the platform owner’s entry into third-party sellers’ product markets. These studies have primarily examined the impacts of a platform owner’s entry on product demand, product price, profitability, and innovation in third-party sellers’ product markets. For example, Jiang et al., (2011) [32] demonstrated that the platform owner’s entry can increase consumer demand for products, thereby benefiting third-party sellers. Lu and Liu (2015) [33] examined the impact of an e-commerce channel’s entry on the profitability under a physical distribution system. Li and Agarwal (2017) [34] suggested that the impact of a platform owner’s entry differs depending on the size of the third-party sellers, with positive spillover effects for larger third-party sellers, but potentially negative spillover effects for smaller ones. Forderer et al., (2018) [35] investigated the impact of platform owners’ entries into complementary markets on innovation under the platform ecosystem. Zhu and Liu (2018) [36] analyzed Amazon’s entry into third-party sellers’ product spaces and revealed that the platform owner shows a greater propensity to target successful product spaces. Wen and Zhu (2019) [37] examined the impact of Google’s entry into mobile app markets and found that such a threat can lead to reduced innovation among app developers and increased app prices. He et al., (2020) [38] conducted empirical research to examine the context-dependent impact of a platform owner’s entry on the demands of third-party stores.
In the other vein of available research, a number of recent studies have focused on investigating the entry of third-party sellers into platform-based markets. These investigations primarily aimed to explore the effects of third-party sellers’ entries on pricing decisions, partnership relations, and product sales within such markets. For instance, Ryan et al., (2012) [8] analyzed the optimal pricing decisions of third-party sellers when they join Amazon’s marketplace, which presents sellers with both valuation and awareness advantages. Mantin et al., (2014) [10] demonstrated that allowing for others to sell on a platform provides the platform owner with an external option, enabling them to allow for third-party sellers to sell substitute goods if a supplier cannot agree on a reasonable price. Chen and Guo (2022) [9] discovered that a third-party seller with a lower product valuation can leverage new media advertising to enter a large online platform and establish a partnership. Li et al., (2021) [11] empirically analyzed the impact of third-party sellers’ entries on product sales in a hybrid retail platform and determined that such an entry decreases the platform owner’s sales but increases the platform’s overall sales.
In summary, previous studies have mainly focused on vertical differentiation to model the quality of competing products, which can introduce a bias in favor of the supplier with the higher quality product. Our work, by contrast, considered cases where two competing products are horizontally differentiated so that, under equal prices, some consumers would inherently prefer the incumbent supplier’s product while others would favor the entrant supplier’s product. Furthermore, we examined how the logistics service impacts the strategic entry of third-party products and price competition between the incumbent and the entrant, which is an important yet still underexplored area of research [28].
3. The Model
We considered an e-commerce platform operating two online retail channels: the self-operating channel and the marketplace. Under the self-operating channel, there are two potential modes, namely reselling and revenue sharing. Under the reselling mode, the platform purchases products from an incumbent supplier at a wholesale price (w) and then resells them to online consumers at a retail price (P1; we refer to this self-operating mode as the reselling self-operating mode). Under the revenue-sharing mode, the incumbent supplier directly sells their products to their end consumers by sharing a proportion (λ) of its revenue to the platform, where λ∈(0,1) represents the revenue-sharing rate (we refer to this self-operating mode as the revenue-sharing self-operating mode). On the other hand, the platform also serves as a marketplace, and a third-party supplier chooses whether to join and engage in direct selling by paying a commission at a commission rate (ρ∈(0, 1)) as a fee to access consumers. The product retail price set by the entrant supplier was denoted as P2. We regarded the retail price, P1 or P2, as a total price of the bundle of the product and associated logistics service. The products offered by the two suppliers were completely substituted, and the marginal production costs were constant across the two suppliers, which were assumed to be zero without loss of generality. Both suppliers have no consumer base and can only reach their end consumers through the platform.
Under the self-operating channels, the incumbent supplier’s products are delivered through the platform’s self-supporting logistics service system. In the marketplace, however, the third-party supplier provides the logistics service itself. We let s1 and s2 denote the platform’s logistics service level and the third-party supplier’s logistics service level, respectively. On the consumer side, each consumer was assumed to have one unit of product demand and aimed to maximize their own utility. Based on the Hotelling model, we assumed that consumers’ product preferences are distributed uniformly on [0, 1], with the incumbent supplier’s product located at 0 and the entrant supplier’s product located at 1. If a consumer purchases a product that is distinct from their ideal product, they incur a misfit cost, which increases with the distance between their location and the given product. We let v denote the quality of the product sold by either supplier and t represent the disutility cost per unit distance; then, a consumer located at x derives the utility of v + s1 − tx when buying the product from the incumbent supplier and the utility of v + s2 − t (1 − x) when buying the product from the entrant supplier. We assumed that the consumer utility increases along with the logistics service level as a high-quality logistics service can enhance the customer experience and thus derive a higher consumer utility [39,40,41].
As a two-sided market, e-commerce platforms are generally characterized by positive indirect network effects on consumers due to their increased product variety [11,14,19,42]. In line with the literature, we also considered that the increased variety of suppliers on the platform attracts more customers, helping the platform to build a larger consumer base. In particular, we assumed that, with the supplier-side network effects, a customer obtains additional utility: α(v + si + N), where N is the supplier number and α denotes the strength of the indirect network effects, which measures how much consumers care about supplier-side variety. The approach to model the network effects as a function of product quality and the network size has been widely used in the existing literature (e.g., Baake and Boom, 2001 [43], Jing, 2007 [44], and Zhang et al., 2016 [45]). The third-party supplier has the option to join the marketplace to sell its products and needs to determine whether to do so. If the third-party supplier decides to enter, it bears an opportunity cost (c). We interpreted the opportunity cost as some of the other outputs the entrant supplier must sacrifice in operating an online retail. This is rational for those suppliers with a limited budget. In our analysis, we assumed that c is not so high (i.e., c < min{, }); otherwise, the third-party supplier would have no incentive to join the marketplace even if the charged commission was 0.
We studied a four-stage game among the platform, an incumbent supplier, and an entrant supplier. In Stage 1, the incumbent supplier chooses a self-operating channel mode, which will either be a reselling one or a revenue-sharing one. In Stage 2, the platform and the entrant supplier determine whether to form a partnership, i.e., the platform decides whether to open its marketplace to the third-party supplier, and the supplier determines whether to join the marketplace. Four scenarios are possible as a result of the first and second stages of this game (i.e., scenario RC, scenario RM, scenario SC, and scenario SM). In Stage 3, pricing decisions of the platform and suppliers are made. Specifically, in scenario RC, the incumbent supplier first determines the wholesale price (wRC), and then the platform and entrant supplier simultaneously determine the retail prices P1RC and P2RC, respectively. In scenario RM, the incumbent supplier first determines the wholesale price (wRM), and then the platform determines the retail price (P1RM). In scenario SC, the platform and the entrant supplier simultaneously determine the retail prices P1SC and P2SC, respectively. In scenario SM, the incumbent supplier sets the retail price (P1SM). In Stage 4, customers observe the product prices and decide whether to buy a product and from which supplier. The time sequence of this game is illustrated in Figure 1.
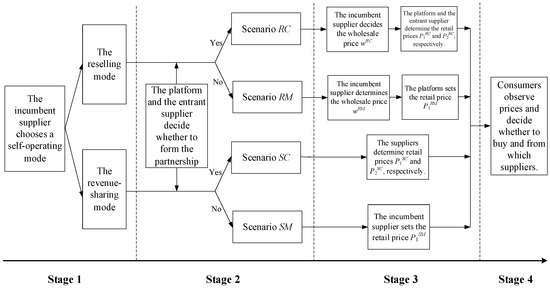
Figure 1.
The time line sequence of the game.
Note that we have attached a superscript (i∈{RM, RC, SM, SC}) to the decision variables to indicate the corresponding scenario. For instance, P1RC and P2RC indicate the retail prices in scenario RC. Table 1 summarizes the key notations that were used in this study.

Table 1.
Summary of notations.
4. Pricing Analysis
Given that both the self-operating mode choice in Stage 1 and the partnership decisions in Stage 2 were ex-ante determined, we first analyzed the optimal pricing strategies under four possible scenarios in Stage 3. To ensure that the market was fully covered in the competitive scenarios (i.e., scenario RC and scenario SC), we assumed that the disutility cost (t) was sufficiently small, i.e., t < min{, }.
4.1. Pricing Strategies without an Entrant Supplier
Without the entry of a third-party supplier, the incumbent supplier acts as a monopoly in the market. The consumer surplus function was set as U = v + s1 +α(v+s1 +1) − P1− tx. In Stage 4, consumers will buy the product as long as they derive non-negative utilities (i.e., U ≥ 0). By setting the surplus function as U = 0, we can obtain the location point of the marginal customer (). Among all the consumers in the market, those located in (0, x0) buy the product, and the others do not. As a result, we obtain the demand (). Figure 2 illustrates the market segmentation in this case.
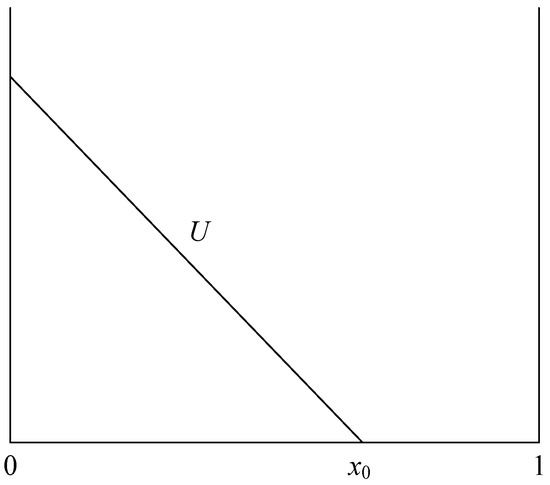
Figure 2.
Market segmentation without an entrant supplier.
This subsection mainly involves two scenarios: RM and SM. We accordingly analyzed the optimal pricing strategies under scenarios RM and SM.
In scenario RM, the profit functions of the platform and the incumbent supplier can be formulated as follows:
We applied the backward induction approach to characterize the equilibrium outcome. First, we solved the platform’s product pricing decision for a given wholesale price (wRM). We then derived the incumbent supplier’s optimal wholesale price based on the platform’s optimal response. Finally, we were able to obtain the optimal profits by inserting the optimal prices into the profit functions in Equations (1) and (2). The results are summarized in the following lemma (All proofs are provided in Appendix A, unless indicated otherwise).
Lemma 1.
In scenario RM, the optimal prices, demand, and profits are as follows:
.
From Lemma 1, we found that an increased indirect network effect intensity (α) would intuitively lead to an increase in the optimal wholesale price, retail price, demand, and the platform’s and incumbent supplier’s profits. Similarly, an increased logistics service level (s1) would lead to an increase in the optimal wholesale price, retail price, demand, and the platform’s and incumbent supplier’s profits. By contrast, the disutility cost (t) exerts negative impacts on the demand and the platform’s and incumbent supplier’s profits.
Under scenario SM, the profit functions of the platform and the incumbent supplier are given as follows:
In this scenario, the incumbent supplier has set a retail price to maximize its profits. Solving the incumbent supplier’s maximization problem with respect to produces the equilibrium results, which are given in the following lemma:
Lemma 2.
In scenario SM, the optimal prices, demand, and profits are as follows:
.
Compared to the equilibrium outcomes under scenario RM, the incumbent supplier chooses a lower retail price and thus gains a larger consumer demand under scenario SM (i.e., and ). This is because when both the incumbent supplier and the platform aim to maximize their individual profits, double marginalization will prevail under the reselling mode, which leads to channel inefficiency. Under the revenue-sharing mode, however, the double marginalization effect can be effectively mitigated.
4.2. Pricing Strategies with an Entrant Supplier
When a third-party supplier enters the marketplace and competes with the incumbent supplier, the consumer surplus of buying the incumbent supplier’s product is U1 = v + s1 + α(v + s1 + 2) − P1 − tx and that of buying the entrant supplier’s product is U2 = v + s2 + α(v + s2 + 2) − P2 − t(1 − x). Out of these two options, consumers choose the one that gives them the maximum surplus under Stage 4. By setting the surplus function as U1 = U2, we can obtain the location point of the marginal customer (). All consumers in the market are divided into two segments. Consumers located in (0, x1) buy from the incumbent supplier, as they derive the higher surplus from purchasing the incumbent supplier’ product than from purchasing the entrant supplier’ product. In contrast, consumers located in (x1,1) choose to buy from the entrant supplier. As a result, we found that and . Figure 3 illustrates the market segmentation in this case.
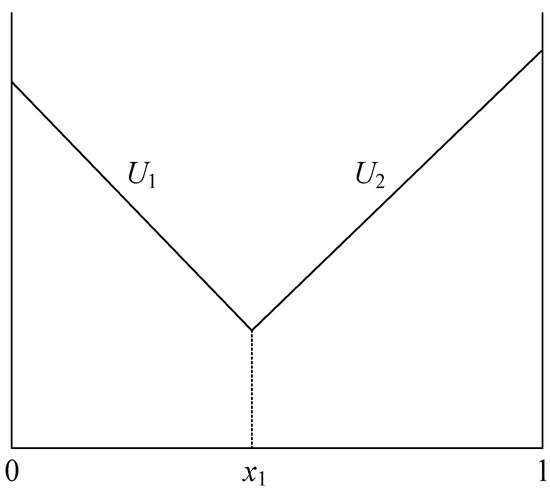
Figure 3.
Market segmentation with an entrant supplier.
This subsection mainly involves two scenarios: SC and RC. First, we analyzed the optimal pricing strategies under scenario SC. In this scenario, the profit function of the platform can be formulated as follows:
The profit function of the incumbent supplier is:
The profit function of the entrant supplier is:
Both suppliers set their corresponding retail prices to maximize their profits. Solving the incumbent supplier’s maximization problem with respect to and the entrant supplier’s maximization problem with respect to yields the equilibrium results, which are given in the following lemma:
Lemma 3.
In scenario SC, the optimal prices, demand, and profits are as follows:
Lemma 3 indicates that, under Scenario SC, the optimal prices, demand, and profits are related to the logistics service level (s1 and s2), the strength of the indirect network effects (α), the commission rate (ρ), and the revenue-sharing rate (λ). By examining the equilibrium outcome, we obtained the following corollary:
Corollary 1.
For scenario SC, we have:
- (1)
- ,,,, ,;
- (2)
- If si > sj, , ,,, , and ;
- (3)
- If , ; otherwise, ;
- (4)
- ,,,.
Corollary 1(1) indicates that a supplier’s optimal price, demand, and profits would increase as its logistics service level (si) increases or as its rival’s logistics service level (sj) decreases under scenario SC. This is intuitive, as a high-quality logistics service can enhance consumers’ utilities directly and thus strengthens the supplier’s competitiveness. Corollary 1(2) and corollary 1(3) examined the impact of indirect network effects on the equilibrium outcomes. The result revealed that the supplier with a logistics service quality advantage can benefit from an increasing indirect network effect intensity. For the platform, only if the network effect intensity is sufficiently large can an increasing indirect network effect enhance its profits. Corollary 1(4) identifies the varying profits via the commission rate or the revenue-sharing rate. We can find that the incumbent (entrant) supplier suffers from a higher revenue-sharing (commission) rate, whereas the platform always benefits from charging a higher revenue-sharing (commission) rate. Under scenario SC, both suppliers directly determine their retail prices, and the platform does not involve the price competition. As a result, the platform’s profits would increase as the revenue-sharing (commission) rate increases.
Next, we analyzed the optimal pricing strategies under scenario RC. Under this scenario, the profit function of the platform can be formulated as follows:
The profit function of the incumbent supplier is:
The profit function of the entrant supplier is:
Through employing backward induction, we first solved the product pricing decisions of the platform and the entrant supplier for a given wholesale price (wRC). We then derived the incumbent supplier’s wholesale price based on the optimal response. Finally, we derived the optimal profits by inserting the optimal prices into the profit functions in Equations (5)–(7). The following lemma solves these above profit maximization problems and characterizes the equilibrium outcome under this scenario:
Lemma 4.
In Scenario RC, the optimal prices, demand, and profits are as follows:
From Lemma 4, it is straightforward to show that the logistics service level (s1 and s2) and the indirect network effect intensity (α) have similar impacts on the equilibrium outcomes under scenario RC with what they carry out under scenario SC. However, one can observe that the commission rate (ρ) has more complicated impacts on the equilibrium outcomes under scenario RC. Thus, we focused on examining the impact of the commission rate under this scenario and provided the following corollary:
Corollary 2.
For scenario RC, we have:
- (1)
- ,,;
- (2)
- ,;
- (3)
- ,,.
Corollary 2(1) shows that the retail prices of the entrant supplier and platform increase, while the wholesale price of the incumbent supplier decreases via the commission rate (ρ). Corollary 2(2) indicates that the incumbent supplier’s demand decreases, while the entrant supplier’s demand increases via the commission rate. With a higher commission rate, a larger proportion of the entrant supplier’s sales go to the platform’s revenue, and the price competition between the platform and the entrant supplier is thus softened, which would increase the equilibrium retail prices. As the commission rate increases, the platform’s revenue gained from the commission prevails. In this case, the platform is more willing to decrease its demand and thus increase the entrant supplier’s demand by choosing a higher retail price. As a result, the incumbent supplier has to lower its wholesale price to maximize its profit. From corollary 2(3), we can further verify that both suppliers’ profits decrease, and the platform’s profit increases via the commission rate. It is intuitive that the platform directly benefits from a higher commission rate, as it gains a larger proportion of the entrant supplier’s revenue. A higher commission rate also softens the competition, which indirectly benefits the platform. The entrant supplier is harmed by a higher commission rate, as it has to transfer a larger proportion of the revenue to the platform, which cannot be compensated by the benefits of the softened competition. The incumbent supplier is harmed, as a higher commission rate will directly reduce its wholesale price and demand. Therefore, both suppliers suffer from a higher commission rate under this scenario.
5. Equilibrium Analysis
Based on the equilibrium outcomes under the four possible scenarios, we can further investigate the interactions among the platform and both suppliers during their early stages. In this section, we first examine the impact of a third-party supplier’s entry on the platform and the incumbent supplier. Then, we investigate the equilibrium partnership decisions between the platform and the entrant supplier. Finally, we analyze the incumbent supplier’s equilibrium self-operating mode choice.
5.1. Impact of a Third-Party Supplier’s Entry
In this subsection, we compare the equilibrium solutions between scenarios RM and RC and those between scenarios SM and SC to provide managerial insights into how the entry of a third-party supplier affects platform performance under the reselling self-operating mode and under the revenue-sharing self-operating mode. The following proposition summarizes the comparative results:
Proposition 1.
With the entry of a third-party supplier, we have that:
- (a)
- Under the reselling self-operating mode, the incumbent supplier charges a higher wholesale price (i.e., ) if v < v1 and gains a higher profit (i.e., ) if v < v3, and the platform charges a higher retail price (i.e., ) if v < v2 and gains a higher profit (i.e., ) if v < v4;
- (b)
- Under the revenue-sharing self-operating mode, the incumbent supplier charges a higher retail price (i.e., ) if v < v5 and gains a higher profit (i.e., ) if v < v6, and the platform gains a higher profit (i.e., ) if v < v7, where vi (i=1,…,7) is defined in Appendix A.
Proposition 1 identifies the conditions under which the platform and the incumbent supplier benefit from a third-party supplier’s entry under both self-operating modes. The results revealed that product quality plays a pivotal role in pricing and profitability comparisons. Specifically, when the quality of the entrant supplier’s product is sufficiently low, both the platform and the incumbent supplier are more beneficial from the product’s entry; otherwise, the platform and the incumbent supplier would suffer from the product’s entry. The rationale for this is as follows: Under a monopolistic market (i.e., scenarios RM and SM), the incumbent supplier acts as a monopoly so that both the supplier and the platform benefit from a higher product quality. As shown in Lemmas 3 and 4, the profits of the incumbent supplier and the platform both increase via the product quality variable (v). When the third-party supplier carrying the identical product enters the marketplace, the product market shifts from a monopolistic market to a competitive market, in which the incumbent’s product quality advantage wanes. Therefore, if the product quality is sufficiently high, both the platform and the incumbent supplier prefer a monopolistic market; otherwise, they prefer a duopolistic market.
5.2. Equilibrium Partnership
In our setting, the partnership between the platform and the entrant supplier can only emerge as an equilibrium when the platform is willing to open its marketplace and the third-party supplier has an incentive to join this marketplace; otherwise, the partnership cannot be formed, and the third-party supplier does not appear on the marketplace.
We first analyzed the platform’s decision regarding marketplace openness. The following lemma characterizes the conditions under which the platform has the willingness to open its marketplace to the third-party supplier:
Lemma 5.
When facing a third-party supplier with a product quality of v:
- (a)
- If v < v4, the platform would open its marketplace under both self-operating modes;
- (b)
- If v4 < v < v7, the platform would open its marketplace under the revenue-sharing self-operating mode;
- (c)
- If v > v7, the platform would not open its marketplace, where v4 and v7 are given in Proposition 1.
The key insights from Lemma 5 are as follows. The conditions required for the platform’s marketplace openness decision are driven via the product’s quality. When the product’s quality is low (i.e., Lemma 5a), the platform is willing to open its marketplace, regardless of the self-operating mode choice. When the product’s quality is medium (i.e., Lemma 5b), the platform is only willing to open its marketplace when the incumbent supplier chooses the revenue-sharing self-operating mode. When the product’s quality is high (i.e., Lemma 5c), the platform would not open its marketplace. The rationale behind this result is similar to that obtained under Proposition 1: when the product quality is low, the platform benefits more from a competitive market than from a monopolistic market; thus, it is more willing to open its marketplace to a third-party supplier.
We subsequently analyzed the third-party supplier’s entry decision. The following lemma presents the conditions under which the third-party supplier has an incentive to join the marketplace:
Lemma 6.
For an exogenous commission rate of ρ:
- (a)
- If ρ < ρ1, the third-party supplier would join the marketplace under both self-operating modes;
- (b)
- If ρ1 < ρ < ρ2, the third-party supplier would join the marketplace under both self-operating modes;
- (c)
- If ρ > ρ2, the third-party supplier would not join the marketplace, where ρ1 and ρ2 are defined in Appendix A.
Lemma 6 indicates that the commission rate exerts a crucial impact on determining the third-party supplier’s joining decision. When the commission rate is low in its level (i.e., Lemma 6a), the third-party supplier exhibits an incentive to join the marketplace, regardless of the self-operating mode choice. When the commission rate is medium in its level (i.e., Lemma 6b), the third-party supplier only has an incentive to join the marketplace when the incumbent supplier chooses the reselling self-operating mode. When the product’s quality is high (i.e., Lemma 6c), the third-party supplier would not join the platform. This rationale for this is intuitive. From corollaries 1 and 2, we noted that the entrant supplier’s profits decreases via the commission rate. If the platform charges a low commission fee, the third-party supplier obtains a positive profit from the competition and thus has an incentive to join. However, as the commission rate increases, the third-party supplier’s revenue cannot compensate for its opportunity cost incurred from joining the marketplace, which leads the third-party supplier to forgo the competition.
Through combining Lemmas 5 and 6, we can further investigate the equilibrium partnership between the platform and the entrant supplier. The following proposition prescribes the conditions to form this partnership:
Proposition 2.
Under equilibrium, three regions of v and ρ exist: R1 = {(v, ρ) | v < v4 and ρ < ρ1}, R2 = {(v, ρ)| v < v4 and ρ1 < ρ < ρ2}, and R3 = {(v, ρ)| v4 < v < v7 and ρ < ρ1 }, such that: (i) the platform opens its marketplace and the third-party supplier joins the marketplace under both of the self-operating modes if (v, ρ)∈ R1; (ii) the platform opens its marketplace and the third-party supplier only joins the marketplace under the reselling self-operating mode if (v, ρ)∈ R2; and (iii) the platform opens its marketplace and the third-party supplier only joins the marketplace under the revenue-sharing self-operating mode if (v, ρ)∈ R3; otherwise, the partnership between the platform and the entrant supplier cannot emerge as an equilibrium.
The equilibrium partnership between the platform and the entrant supplier can only be formed when both incentives of the platform and the third-party supplier are aligned. According to the various possible values of v and ρ, Proposition 2 identifies three regions in which the incentives of the platform and the third-party supplier may be aligned. Specifically, when both the product quality (v) and the commission rate (ρ) are sufficiently low (i.e., (v, ρ) falls into R1), the partnership between the platform and the entrant supplier can be always formed, no matter which self-operating mode is chosen. When v is sufficiently low and ρ is medium (i.e., (v, ρ) falls into R2), the partnership between the platform and the entrant supplier can only emerge as an equilibrium if the incumbent supplier chooses the reselling self-operating mode. When v is medium and ρ is sufficiently low (i.e., (v, ρ) falls into R3), the partnership between the platform and the entrant supplier can only emerge as an equilibrium if the incumbent supplier chooses the revenue-sharing self-operating mode. Otherwise, the partnership cannot be formed, and the third-party supplier does not appear on the platform’s marketplace in equilibrium.
5.3. Self-Operating Mode Choice
Anticipating the platform’s and the entrant supplier’s partnership decisions in Stage 2, we next analyzed the incumbent supplier’s strategic self-operating mode choice in Stage 1. Note that the incumbent supplier resells their products to the platform under the reselling mode and sells their products directly by sharing a proportion of its revenue to the platform under the revenue-sharing mode; the revenue-sharing rate (λ) is thus a determining factor of its self-operating mode selection decisions. By comparing the incumbent supplier’s profits when it chooses the reselling mode and when it chooses the revenue-sharing mode, we were able to conclude the equilibrium conditions for each scenario, as summarized in the following proposition:
Proposition 3.
Under equilibrium, the following holds (λ1, λ2, and λ3 are defined in Appendix A):
- (a)
- When (v, ρ) ∈ R1:(a1) If λ > λ1, the incumbent supplier chooses the reselling mode and scenario RC is under an equilibrium;(a2) If λ < λ1, the incumbent supplier chooses the revenue-sharing mode and scenario SC is under an equilibrium;
- (b)
- When (v, ρ) ∈ R2:(b1) If λ > λ2, the incumbent supplier chooses the reselling mode and scenario RC is under an equilibrium;(b2) If λ < λ2, the incumbent supplier chooses the revenue-sharing mode and scenario SM is under an equilibrium;
- (c)
- When (v, ρ) ∈ R3:(c1) If λ > λ3, the incumbent supplier chooses the reselling mode and scenario RM is under an equilibrium;(c2) If λ < λ3, the incumbent supplier chooses the revenue-sharing mode and scenario SC is under an equilibrium;
- (d)
- Otherwise, the third-party supplier does not appear on the platform’s marketplace and:(d1) If λ > 1/2, the incumbent supplier chooses the reselling mode and scenario RM is under an equilibrium;(d2) If λ < 1/2, the incumbent supplier chooses the reselling mode and scenario SM is under an equilibrium.
Proposition 3 provides a rich set of important insights into how the incumbent supplier’s self-operating mode selection strategies and market equilibrium are affected by the interplay among product quality, the commission rate, and the revenue-sharing rate. The incumbent supplier makes self-operating mode choices by considering the partnership between the platform and the entrant supplier. When (v, ρ) ∈ R1, the platform and the entrant supplier establish their partnership, no matter which self-operating mode is chosen. In this case, the incumbent supplier should compare the profit obtained under scenario SC (i.e., ) with that under scenario RC (i.e., ). If λ > λ1, , and the incumbent supplier would choose the reselling mode; if λ < λ1, and the incumbent supplier would choose the revenue-sharing mode. When (v, ρ) ∈ R2, the platform and the entrant supplier only form a partnership if the reselling mode is chosen; otherwise, their partnership cannot be formed. In this case, the incumbent supplier should compare its profit under scenario RC (i.e., ) with that under scenario SM (i.e., ). If λ > λ2, , and the incumbent supplier would choose the reselling mode; if λ < λ2, , and the incumbent supplier would choose the revenue-sharing mode. When (v, ρ) ∈ R3, the platform and the entrant supplier only form a partnership if the revenue-sharing self-operating mode is chosen; otherwise, their partnership cannot be formed. In this case, the incumbent supplier should compare its profit under scenario SC (i.e., ) with that under scenario RM (i.e., ). If λ > λ2, , and the incumbent supplier would choose the reselling mode; if λ < λ2, , and the incumbent supplier would choose the revenue-sharing mode. When (v, ρ) ∉ R1∪R2∪R3, the partnership between the platform and the entrant supplier cannot emerge as an equilibrium. In this case, the incumbent supplier should compare its profit under scenario RM (i.e., ) with that under scenario SM (i.e., ). If λ > 1/2, , and the incumbent supplier would choose the reselling mode; if λ < 1/2, , and the incumbent supplier would choose the revenue-sharing mode.
To make this more concrete, we applied a numerical example with v = 0.5, t = 1, c = 0.4, α = 0.2, and s1 = s2 = 0.1 to illustrate the equilibrium outcomes. Figure 4 depicts a spectrum of equilibrium regions depending on the revenue-sharing rate (vertical axis) and the commission rate (horizontal axis). As illustrated in Figure 4, the entire parameter space ((ρ, λ)∈[0, 1]2) is numerically divided into six regions. Since v < v4 was always satisfied in this numerical example, R1 and R2 were reduced to (0, 0.4) and (0.4, 0.78), respectively. First, moving horizontally from left to right, the equilibrium outcomes switch from competitive scenarios to monopolistic scenarios. Intuitively, this switching behavior was due to the impact of an increasing commission rate on the entrant supplier. As indicated in Lemma 6, an increasing commission rate lowers the third-party supplier’s willingness to join the marketplace. Second, moving vertically from low to high, the optimal self-operating mode shift from the revenue-sharing mode to the reselling mode. For instance, the equilibrium outcomes switch from scenario SC to scenario RC in R1, from scenario SM to scenario RC in R2, and from scenario SM to scenario RM in the other region. A larger revenue-sharing rate undermines the incumbent supplier’s profit, which leads to its choice of the reselling mode.

Figure 4.
Equilibrium regions depending on λ and ρ.
6. Conclusions and Discussion
In the current research, we developed a game-theoretic model to investigate the competition between a self-operating channel and a marketplace on an e-commerce platform, with a focus on examining the strategic entry of third-party products and self-operating mode choices. Specifically, we first analyzed the optimal pricing strategies for the platform and suppliers under four possible supply chain scenarios and examined the impacts of several key parameters (e.g., network effect intensity, logistics service level, disutility cost, and commission rate) on the equilibrium outcomes. Subsequently, we investigated the impact of third-party supplier entry on the pricing strategies and profitability of the platform and incumbent supplier. Our results demonstrate that the economic implications of a competitive supplier’s entry crucially depend on the quality of the product. Specifically, when the entrant supplier’s product quality is sufficiently low, both the platform and the incumbent supplier benefit from the product’s entry; otherwise, they would suffer from the product’s entry. Finally, we analyzed the equilibrium partnership between the platform and the entrant supplier and the incumbent supplier’s strategic self-operating mode choice, and further characterized the equilibrium conditions for each scenario. The results indicated that the market equilibrium depends on the interplay among product quality, the commission rate, and the revenue-sharing rate.
6.1. Theoretical Implications
Our research offers three significant theoretical contributions. First, this research broadens the current literature on provider-side network effects in the context of a two-sided market [14]. Previous studies have focused on provider-side network effects from the perspective of the entrant platform’s operation [14], platform performance investment [18], and partnership promotion [9]. Distinct from these studies, our study examined the pricing competition between a third-party supplier in the marketplace and an incumbent supplier in the self-operating channel. We investigated the impacts of supplier-side network effects on the incumbent supplier’s self-operating mode choice and the marketplace’s openness, which have not been previously studied.
Second, this research adds to the literature on the platform operations under different business models [3]. For example, some scholars have focused on the impacts of platform business models on optimal pricing strategies [20,22,46], while others have investigated the impact of platform business models on product information disclosure [23,24]. However, few studies have explored the interactions among an incumbent supplier’s self-operating mode (i.e., reselling or revenue sharing), the platform’s openness, and a third-party supplier’s entry decisions. Our research identified that the equilibrium conditions of the market are contingent on the interplay among product quality, the commission rate, and the revenue-sharing rate, which contributes novelty and complementary insights to the current body of knowledge.
Third, this research contributes to the existing literature on product entry in platform-based markets. Previous research has primarily examined vertical differentiation to model the quality of competing products, which may simply create a bias in favor of the supplier with the higher quality product [8,9]. In contrast, we considered cases where two competing products are horizontally differentiated, resulting in an inherent preference for the incumbent supplier’s product among others at equal prices. Moreover, we analyzed the impact of a logistics service on the third-party product’s strategic entry and price competition between the incumbent and the entrant, which is an important but underexplored area in previous research [28].
6.2. Managerial Implications
This study provides several important managerial implications for platform owners and market participants. First, our investigation underscores the varying functionalities of indirect network effects in shaping profitability outcomes across distinct market scenarios. For instance, under monopolistic scenarios, indirect network effects positively impact the platform and incumbent supplier’s profitability. Under the competitive scenarios, however, a strong network effect benefits the supplier with a superior logistics service quality, while negatively impacting the other supplier. For the platform, an increasing network effect first decreases and then increases its profits. This suggests that market participants aiming to leverage the additional supplier-side network effects should not always pursue the enhancement of network effects in a competitive market.
Second, our research highlights the significance of product quality in determining the economic effects of a third-party product entry on the incumbent. For instance, the platform and incumbent supplier only reap benefits from the entry of a third-party supplier if the entrant carries products of a low quality. The entry of high-quality products may cannibalize the incumbent’s monopolistic market, thereby weakening its profitability. Our research suggested that incumbents should take this influencing factor into account when establishing partnerships with third-party suppliers.
Third, our investigation provides managerial implications for platform owners. Platform owners should rationally comprehend the functions of the commission rate under platform operation and partnership decisions. A higher commission rate can not only effectively increase the platform’s profits but also reduce the entrant supplier’s profits and thus decrease the supplier’s incentive to join. Moreover, a higher commission rate can harm the incumbent supplier’s profits, further influencing the supplier’s self-operating mode choice. Therefore, platform owners should make a comprehensive consideration of the pros and cons of setting a higher commission rate when establishing partnerships with incumbent and entrant suppliers. Our study thus suggests that it is imperative that platform owners determine their underlying incentives carefully, which may require them to appropriately adjust their operations.
6.3. Limitations and Future Research
This study has several limitations that suggest potential directions for future research. First, we assumed that the commission rate was predetermined for analytical traceability. However, it would be interesting to investigate the situation in which the platform owner charges different commission rates to the entrant suppliers under different self-operating channel modes. For example, studies could explore cases where the platform conducts commission discrimination in the marketplace.
Additionally, this study did not consider the competition between third-party suppliers. To further reap more benefits from indirect network effects, the platform owner could allow multiple third-party suppliers to join the marketplace and introduce competition. It would be valuable to explore how competition among multiple third-party suppliers impacts the platform’s optimal strategies regarding product pricing and openness. Incorporating third-party supplier competition into our model framework could generate new insights. Therefore, future research could expand this model to consider more complex scenarios and investigate additional factors that may impact the platform’s profitability, such as multi-dimensional product differentiation, customer heterogeneity, and the impact of regulations on market structure.
Author Contributions
Conceptualization, B.X.; methodology, J.H.; validation, B.X., X.Z. and T.B.A.; formal analysis, B.X.; investigation, J.H.; writing—original draft preparation, B.X., J.H. and X.Z.; writing—review and editing, B.X., X.Z. and T.B.A.; supervision, T.B.A.; project administration, X.Z.; funding acquisition, B.X. and X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant numbers 72201031 and 71902003) and the China Ministry of Education Foundation for Humanities and Social Science (grant number: 19YJC630219).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data was used for the research described in the article.
Acknowledgments
The authors would like to thank three anonymous reviewers for very detailed and helpful comments and suggestions on this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Lemma 1.
By solving the first-order condition , we derive that . The objective function for the incumbent supplier follows by inserting the above solution into (2):
Solving the first-order condition () yields that . Inserting into and , we obtain that and . Inserting the optimal and into (1) and (2), we have that and . □
Proof of Lemma 2.
By solving the first-order condition () in (4), we derive that . Inserting into , we obtain that . Inserting the optimal into (3) and (4), we have that and . □
Proof of Lemma 3.
Solving the first-order conditions and simultaneously, we obtain that and . Inserting the above optimal prices into and , we obtain that and . Inserting the above optimal prices into (5), (6), and (7), we obtain the optimal profits under this scenario, as given in Lemma 3. □
Proof of Corollary 1.
Based on the optimal prices and profits under scenario SC, we can make the following calculations:
- (1)
- , ,, , ,, , , , and ;
- (2)
- If s1 > s2 holds, , ,,, , and ; if s1 < s2 holds, the following results can be derived similarly;
- (3)
- > 0 is equivalent to ;
- (4)
- ,,,. □
Proof of Lemma 4.
Given a wholesale price (wRC), we first solve the profit maximization problems of the platform and the entrant supplier in (8) and (10). By solving the first-order conditions and simultaneously, we obtain and . Inserting the above retail prices into (9), we obtain the profit maximization problems of the incumbent supplier as follows:
For the profit maximization problem of the incumbent supplier, solving the first-order condition of yields that . Inserting the optimal wholesale price into the above two retail prices, we can obtain that and . Then, we further obtained the corresponding demands and profits of the platform and suppliers, as summarized in Lemma 4. □
Proof of Corollary 2.
According to the optimal prices and profits under scenario RC, we can make the following calculations:
- (1)
- ,, and ;
- (2)
- , and ;
- (3)
- ;
- (4)
- ,
Proof of Proposition 1.
- (a)
- Denote , , , and . For the wholesale price, we can show that is equivalent to v < v1. For the incumbent supplier’s profit, holds if v < v3 is satisfied. For the retail price, is equivalent to v < v2. For the platform’s profit, holds if v < v4 is satisfied;
- (b)
- Denote , , and . For the retail price, we can show that is equivalent to v < v5. For the incumbent supplier’s profit, holds if v < v6 is satisfied. For the platform’s profit, holds if v < v7 is satisfied. □
Proof of Lemma 5.
From Proposition 1, we noted that if v < v4, the platform gains a higher profit by opening its marketplace (i.e., ) under the reselling self-operating channel mode. If v < v7, the platform gains a higher profit by opening its marketplace (i.e., ) under the revenue-sharing self-operating channel mode.
Next, we further proved that v4 < v7. It was easy to check that v7(λ) decreases via λ. Thus, we only needed to prove that min v7(λ) > v7(λ = 1) > v4, which is equivalent to . It was easy to show that , which is equivalent to the above inequation. As a result, we can conclude as follows: when v < v4, the platform would open its marketplace under both self-operating channel modes; when v4 < v < v7, the platform would open its marketplace under the revenue-sharing self-operating channel modes; when v > v7, the platform would not open its marketplace. □
Proof of Lemma 6.
According to corollaries 1 and 2, the entrant supplier’s profit functions under both self-operating channel modes decrease via the commission rate (ρ), i.e., and . Note that as 0 < c < min{, }, we can further obtain that , , and . Denote ρ1 = and ρ2 as the unique root of in ρ∈[0, 1]; thus, we found that and .
Next, we had to prove that ρ1 < ρ2. Since was equivalent to , which was always satisfied, we found that always holds. As ρ1 and ρ2 denote the roots of = 0 and , respectively, it was easy to show that ρ1 < ρ2.
As a result, we can conclude as follows: if ρ < ρ1, the third-party supplier would join the marketplace under both self-operating channel modes; if ρ1 < ρ < ρ2, the platform would join the marketplace under the reselling self-operating channel mode; and if ρ > ρ2, the platform would not join the marketplace. □
Proof of Proposition 2.
The partnership between the platform and the entrant supplier can only emerge as an equilibrium when the platform is willing to open its marketplace and the third-party supplier has an incentive to join this marketplace; otherwise, the partnership cannot be formed. According to Lemmas 5 and 6, if v < v4 and ρ < ρ1, both the platform and the third-party supplier have incentives to cooperate under the two self-operating channel modes. If v < v4 and ρ1 < ρ < ρ2, the platform is willing to open the marketplace under both self-operating channel modes, but the third-party supplier only has a willingness to join under the reselling self-operating channel mode. Thus, the partnership can only emerge as an equilibrium under the reselling self-operating channel mode. If v4 < v < v7 and ρ < ρ1, the third-party supplier is willing to join the marketplace under both self-operating channel modes, but the platform only has an incentive to open its marketplace under the revenue-sharing self-operating channel mode. Thus, the partnership can only emerge as an equilibrium under the revenue-sharing self-operating channel mode. In other cases, the incentives of the platform and the entrant supplier cannot be aligned in either self-operating channel mode, and the partnership cannot be formed in equilibrium. □
Proof of Proposition 3.
When (v, ρ) ∈ R1, the platform and the entrant supplier always cooperate, no matter which self-operating channel mode the incumbent supplier chooses. In this case, the incumbent supplier makes its decision by comparing and . By solving , we derived that λ1 = . If λ > λ1, , and the incumbent supplier chooses the reselling mode. If λ < λ1, and the incumbent supplier chooses the revenue-sharing mode.
When (v, ρ) ∈ R2, if the incumbent supplier chooses the reselling self-operating channel mode, the platform and the entrant supplier would form their partnership, and the incumbent supplier realizes a profit of . If the incumbent supplier chooses the revenue-sharing self-operating channel mode, their partnership cannot be formed, and the incumbent supplier would realize a profit of . The incumbent supplier needs to compare and . Solving yields λ2 = . If λ > λ2, and the incumbent supplier chooses the reselling mode. If λ < λ2, and the incumbent supplier chooses the revenue-sharing mode.
When (v, ρ) ∈ R3, if the incumbent supplier chooses the revenue-sharing self-operating channel mode, the platform and the entrant supplier would form their partnership, and the incumbent supplier realizes a profit of . If the incumbent supplier chooses the reselling self-operating channel mode, the partnership cannot be formed, and the incumbent supplier would realize a profit of . Thus, the incumbent supplier makes its decision by comparing and . Setting gives λ3 = . If λ > λ3, and the incumbent supplier chooses the reselling mode. If λ < λ3, and the incumbent supplier chooses the revenue-sharing mode.
When (v, ρ) ∉ R1∪R2∪R3, the platform and the entrant supplier do not cooperate, no matter which self-operating channel mode the incumbent supplier chooses. Thus, the incumbent supplier makes its decision by comparing and . It was easy to demonstrate that if λ > ½, , and the incumbent supplier would choose the reselling mode. If λ < 1/2, , and the incumbent supplier would choose the revenue-sharing mode. □
References
- Castell, C.; Kiefer, J.; Schubach, S.; Schumann, J.; Graf-Vlachy, L.; Konig, A. Integrating digital platform dynamics into customer orientation research: A systematic review and research agenda. J. Bus. Res. 2023, 163, 113911. [Google Scholar] [CrossRef]
- Song, W.; Chen, J.; Li, W. Spillover Effect of Consumer Awareness on Third Parties’ Selling Strategies and Retailers’ Platform Openness. Inf. Syst. Res. 2021, 32, 172–193. [Google Scholar] [CrossRef]
- Tian, L.; Vakharia, A.J.; Tan, Y.; Xu, Y. Marketplace, reseller, or hybrid: Strategic analysis of an emerging e-commerce model. Prod. Oper. Manag. 2018, 27, 1595–1610. [Google Scholar] [CrossRef]
- Rossmannek, O.; David, N.; Schramm-Klein, H. Suppliers’ loyalty to their sharing platform: The influence of multiple roles. J. Bus. Res. 2022, 143, 272–281. [Google Scholar] [CrossRef]
- Wu, W.; Huang, X.; Wu, C.; Tsai, S. Pricing strategy and performance investment decisions in competitive crowdfunding markets. J. Bus. Res. 2022, 140, 491–497. [Google Scholar] [CrossRef]
- Zhou, G.; Song, P. Third-party apps (TPAs) and software platform performance: The moderating role of competitive entry. Inf. Manag. 2018, 55, 901–911. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, Y.; Shen, Y.; Ge, C.; Jiang, J. Zooming in the impacts of merchants’ participation in transformation from online flash sale to mixed sale e-commerce platform. Inf. Manag. 2021, 58, 103409. [Google Scholar] [CrossRef]
- Ryan, J.K.; Sun, D.; Zhao, X. Competition and coordination in online marketplaces. Prod. Oper. Manag. 2012, 21, 997–1014. [Google Scholar] [CrossRef]
- Chen, J.; Guo, Z. New-Media Advertising and Retail Platform Openness. MIS Q. 2022, 46, 421–556. [Google Scholar] [CrossRef]
- Mantin, B.; Krishnan, H.; Dhar, T. The strategic role of third-party marketplaces in retailing. Prod. Oper. Manag. 2014, 23, 1937–1949. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Q.; Song, P. Third-party sellers’ product entry strategy and its sales impact on a hybrid retail platform. Electron. Commer. Res. Appl. 2012, 47, 101049. [Google Scholar] [CrossRef]
- Chang, S.; Li, A.; Wang, X.; Wang, X. Joint optimization of e-commerce supply chain financing strategy and channel contract. Eur. J. Oper. Res. 2022, 303, 908–927. [Google Scholar] [CrossRef]
- Orji, I.J.; Ojadi, F.; Okwara, U.K. The nexus between e-commerce adoption in a health pandemic and firm performance: The role of pandemic response strategies. J. Bus. Res. 2022, 145, 616–635. [Google Scholar] [CrossRef]
- Zhu, F.; Iansiti, M. Entry into platform-based markets. Strateg. Manag. J. 2012, 33, 88–106. [Google Scholar] [CrossRef]
- Mcintyre, D.P.; Srinivasan, A. Networks, platforms, and strategy: Emerging views and next steps. Strateg. Manag. J. 2017, 38, 141–160. [Google Scholar] [CrossRef]
- Song, P.; Xue, L.; Rai, A.; Zhang, C. The ecosystem of software platform: A study of asymmetric cross-side network effects and platform governance. MIS Q. 2018, 42, 121–142. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, K.; Wen, H.; Lin, J.; Zhang, K.; Tian, X.; Wang, S.; Lev, B. Integration of third-party platforms: Does it really hurt them? Int. J. Prod. Econ. 2021, 234, 108003. [Google Scholar] [CrossRef]
- Anderson, E.G.; Parker, G.G.; Tan, B. Platform Performance Investment in the Presence of Network Externalities. Inf. Syst. Res. 2014, 25, 152–172. [Google Scholar] [CrossRef]
- Chen, J.; Fan, M.; Li, M. Advertising vs. brokerage model for online trading platforms. MIS Q. 2016, 40, 575–596. [Google Scholar] [CrossRef]
- Geng, X.; Tan, Y.; Wei, L. How add-on pricing interacts with distribution contracts. Prod. Oper. Manag. 2018, 27, 605–623. [Google Scholar] [CrossRef]
- Xu, B.; Yao, Z.; Wu, S. Pricing strategies for a bundled channel with services network effects. Int. J. Prod. Res. 2021, 59, 3152–3168. [Google Scholar] [CrossRef]
- Christen, T.; Hess, M.; Grichnik, D.; Wincent, J. Value-based pricing in digital platforms: A machine learning approach to signaling beyond core product attributes in cross-platform settings. J. Bus. Res. 2022, 152, 82–92. [Google Scholar] [CrossRef]
- Kwark, Y.; Chen, J.; Raghunathan, S. Platform or wholesale? A strategic tool for online retailers to benefit from third-party information. MIS Q. 2017, 41, 763–786. [Google Scholar] [CrossRef]
- Hao, L.; Tan, Y. Who wants consumers to be informed? Facilitating information disclosure in a distribution channel. Inf. Syst. Res. 2019, 30, 34–49. [Google Scholar] [CrossRef]
- Belhadj, N.; Laussel, D.; Resende, J. Marketplace or reselling? A signaling model. Inf. Econ. Policy 2020, 50, 100834. [Google Scholar] [CrossRef]
- Wei, J.; Lu, J.; Zhao, J. Interactions of competing manufacturers’ leader–follower relationship and sales format on online platforms. Eur. J. Oper. Res. 2020, 280, 508–522. [Google Scholar] [CrossRef]
- Zennyo, Y. Strategic contracting and hybrid use of agency and wholesale contracts in e-commerce platforms. Eur. J. Oper. Res. 2020, 281, 231–239. [Google Scholar] [CrossRef]
- Vrankić, I.; Herceg, T.; Bach, M. Dynamics and stability of evolutionary optimal strategies in duopoly. Cent. Eur. J. Oper. Res. 2021, 29, 1001–1019. [Google Scholar] [CrossRef]
- Vrankić, I. Conflict and Corporate Social Responsibility in Duopoly. Bus. Syst. Res. Int. J. Soc. Adv. Innov. Res. Econ. 2022, 13, 36–46. [Google Scholar] [CrossRef]
- Georgiou, A. A Case Study of investor R&D Evaluation using Game Theory. Entren. Enterp. Res. Innov. 2022, 8, 91–98. [Google Scholar]
- Qin, X.; Liu, Z.; Tian, L. The optimal combination between selling mode and logistics service strategy in an e-commerce market. Eur. J. Oper. Res. 2021, 289, 639–651. [Google Scholar] [CrossRef]
- Jiang, B.; Jerath, K.; Srinivasan, K. Firm strategies in the “mid tail” of platform-based retailing. Mark. Sci. 2021, 30, 757–775. [Google Scholar] [CrossRef]
- Lu, Q.; Liu, N. Effects of e-commerce channel entry in a two-echelon supply chain: A comparative analysis of single- and dual-channel distribution systems. Int. J. Prod. Econ. 2015, 165, 100–111. [Google Scholar] [CrossRef]
- Li, Z.; Agarwal, A. Platform integration and demand spillovers in complementary markets: Evidence from facebook’s integration of instagram. Manag. Sci. 2017, 63, 3438–3458. [Google Scholar] [CrossRef]
- Forderer, J.; Kude, T.; Mithas, S.; Heinzl, A. Does platform owner’s entry crowd out innovation? Evidence from Google photos. Inf. Syst. Res. 2018, 29, 444–460. [Google Scholar] [CrossRef]
- Zhu, F.; Liu, Q. Competing with complementors: An empirical look at Amazon.com. Strateg. Manag. J. 2018, 39, 2618–2642. [Google Scholar] [CrossRef]
- Wen, W.; Zhu, F. Threat of platform-owner entry and complementor responses: Evidence from the mobile app market. Strateg. Manag. J. 2019, 40, 1336–1367. [Google Scholar] [CrossRef]
- He, S.; Peng, J.; Li, J.; Xu, L. Impact of platform owner’s entry on third-party stores. Inf. Syst. Res. 2020, 31, 1467–1484. [Google Scholar] [CrossRef]
- Zhang, M.; Fu, Y.; Zhao, Z.; Pratap, S.; Huang, Q. Game theoretic analysis of horizontal carrier coordination with revenue sharing in E-commerce logistics. Int. J. Prod. Res. 2019, 57, 1524–1551. [Google Scholar] [CrossRef]
- Cui, R.; Li, M.; Li, Q. Value of High-Quality Logistics: Evidence from a Clash between SF Express and Alibaba. Manag. Sci. 2020, 66, 3879–3902. [Google Scholar] [CrossRef]
- Wang, X.; Xie, J.; Fan, Z. B2C cross-border Ecommerce logistics mode selection considering product returns. Int. J. Prod. Res. 2021, 59, 3841–3860. [Google Scholar] [CrossRef]
- Xu, B.; Yao, Z.; Tang, P. Pricing Strategies for Information Products with Network Effects and Complementary Services in a Duopolistic Market. Int. J. Prod. Res. 2018, 56, 4243–4263. [Google Scholar] [CrossRef]
- Baake, P.; Boom, A. Vertical product differentiation, network externalities, and compatibility decisions. Int. J. Ind. Organ. 2001, 19, 267–284. [Google Scholar] [CrossRef]
- Jing, B. Network externalities and market segmentation in a monopoly. Econ. Lett. 2007, 95, 7–13. [Google Scholar] [CrossRef]
- Zhang, Z.; Nan, G.; Li, M.; Tan, Y. Duopoly Pricing Strategy for Information Products with Premium Service: Free Product or Bundling? J. Manag. Inf. Syst. 2016, 33, 260–295. [Google Scholar] [CrossRef]
- Chen, P.; Zhao, R.; Yan, Y.; Li, X. Promotional pricing and online business model choice in the presence of retail competition. Omega 2020, 94, 102085. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).