A Multi-Criteria Group Decision-Making Method for Risk Assessment of Live-Streaming E-Commerce Platform

Abstract

Live-streaming e-commerce is the future development direction of the retail industry. When retailers choose a live-streaming e-commerce platform, they face the test of various risks of the platform, such as insecure control of capital flow, insufficient support of public domain traffic, etc. Therefore, it is necessary to evaluate the risks of the platform to help retailers identify the platform with the lowest risk. Considering the complexity of the risks of live-streaming e-commerce platforms and the ambiguity of the decision-makers thinking, the current method for multi-criteria group decision-making (MCGDM) method in a fuzzy environment rarely discusses the decision-makers weight for the criterion. This paper proposes interval-valued intuitionistic fuzzy multi-criteria group decision-making based on the decision-makers’ professionalism to evaluate the platform’s risks. This method determines the decision-maker’s weight for the criterion based on the professionalism of the decision-maker and uses the technique for order preference by similarity to an ideal solution (TOPSIS) method to rank the alternative platforms. Finally, a risk assessment of the agricultural product live-streaming e-commerce platforms is used as a case study to demonstrate the feasibility and effectiveness of the proposed method. This research will not only provide practical guidance for retailers to choose the live-streaming e-commerce platform with the lowest comprehensive risk but also provide ideas for the research of live-streaming e-commerce from the perspective of risk assessment.

1. Introduction

With the rapid development of the economy, people’s demand for diversified and personalized consumption is getting stronger and stronger. In this context, the new business model of live-streaming e-commerce began to emerge [1,2]. The rapid application and popularization of modern information technologies such as big data, the Internet of Things, cloud computing, and the blockchain have provided complete technical support for live-streaming e-commerce [3]. However, because consumers are accustomed to the traditional offline retail model and are unwilling to make changes, the live-streaming e-commerce industry has not developed on a large scale [4]. Until 2020, COVID-19 had swept across over 200 countries and regions around the world. Faced with the tense situation caused by the spread of the epidemic, countries around the world have actively adopted prevention and control measures, such as travel restrictions. Influenced by the epidemic prevention and control policy, consumer habits began to change, and they started to shop more often in live-streaming rooms, which made the live-streaming e-commerce industry break through the difficulty of changing consumer habits [5].

Live-streaming e-commerce means that offline retailers use the online live-streaming platform to expand their customer base and sell products [6]. Its advantages mainly include the following three aspects: First, through the interactive communication in the live-streaming room, live-streaming e-commerce has stronger consumer stickiness compared with traditional offline retailers [7]. Second, because live-streaming e-commerce bypasses intermediate channels such as dealers, the price of products can often be much lower in the entire retail industry [8]. Last but not least, live-streaming e-commerce can show consumers the details of products in real-time videos, so that consumers can see the essence of products more intuitively and understand product information faster and more comprehensively, thereby igniting consumer enthusiasm for consumption and bringing a more immersive shopping experience [9]. The above advantages make live-streaming e-commerce stand out in the retail industry [10]. The “2022 China E-Commerce Development Trend Report: The Important Role of E-Commerce in High-Quality Economic Development” released by the China Council for the Promotion of International Trade (CCPIT) Research Institute shows that as of June 2022, the size of China’s live-streaming e-commerce users was 469 million, up 204 million from March 2020, accounting for 44.6% of the overall number of Internet users. The report shows that from May 2021 to April 2022, there were more than 9 million live streams per month on Tiktok, with more than 10 billion items sold. As of March 2022, the cumulative number of viewers of Taobao Live had exceeded 50 billion. These data show that live-streaming e-commerce has great potential for development and is the future direction of the retail industry.

The rapid development of live-streaming e-commerce has also led to the explosive growth of live-streaming e-commerce platforms, such as Tiktok in China, YouTube Live in the United States, and Niconico Live in Japan. This not only brings more choices to retailers but is also accompanied by some risks that affect their lasting and healthy development. For instance, the capital flow management and control of live-streaming transactions are not secure, the technical experience in the field of live-streaming is not professional, the public domain traffic support of live-streaming rooms is not sufficient, the competition pressure from other retailers or platforms is high, the cold chain logistics system is not mature, etc. Risk aversion is a common characteristic of all businesses, and choosing a live-streaming e-commerce platform with lower risk can help retailers effectively increase revenue, reduce costs, and improve competitiveness. Therefore, retailers must evaluate the risks of various aspects of the alternative platforms in order to determine the platform with the lowest overall risk and make the best platform selection choice.

In the face of numerous live-streaming e-commerce platforms, how to evaluate the risks of platforms to help retailers choose the platform is important. Previous studies on the risk assessment of live-streaming e-commerce platforms have mainly followed two streams [11]. The first stream focuses on the risks in the live-streaming e-commerce industry, using qualitative and quantitative methods to determine the types of risks. The second stream emphasizes risk evaluation methods. Since the live-streaming e-commerce industry has just emerged, research in this stream is relatively limited. By combing through previous studies, this paper proposes an interval-valued intuitionistic fuzzy MCGDM method based on the decision-makers’ professionalism, considering the complexity of the risks of live-streaming e-commerce platforms and the ambiguity of the decision-makers thinking. The method determines decision-maker weights for risk criteria based on the decision-makers’ professionalism, overcoming the problem of inaccurate decision results when the same weight is assigned to decision-makers for all criteria. Among them, decision-makers are individuals who have professional experience, knowledge, and skills in the field of live e-commerce and have attained a particular level of expertise, such as academics working on relevant research or professionals working on connected projects [12,13]. The term “decision-makers’ professionalism” refers to a specific level of expertise and skill that has been attained by decision-makers through research, education, and experience in a specific area [12,13]. In addition, the TOPSIS method is used to rank alternative live-streaming e-commerce platforms, which is simple to calculate and reliable, as well as more consistent with the realistic scenario of live-streaming e-commerce platform risk evaluation. Based on the above discussion, this study has the following contributions: First, the research will provide a method to assess the risk of live-streaming e-commerce platforms, which can help retailers identify the platform of entry. Further, this study will also urge live-streaming e-commerce platforms to reduce the risk brought to retailers and attract more retailers to enter. In addition, this study can provide ideas for studying live-streaming e-commerce issues from the perspective of risk evaluation.

The remainder of this study is organized as follows: Section 2 reviews related literature. Section 3 presents the basic theory of interval-valued intuitionistic fuzzy sets. In Section 4, this paper establishes the risk assessment model for a live-streaming e-commerce platform. Section 5 performs a case study to illustrate the feasibility and effectiveness of the method. In Section 6, this paper concludes and presents future research directions.

2. Literature Review

2.1. The Risks of the Live-Streaming E-Commerce Platforms

The live-streaming e-commerce industry has huge development potential, but similar to other industries, there are also some inevitable risks. In this regard, scholars have conducted qualitative research on the risks existing in the live-streaming e-commerce industry from various perspectives. For example, from the perspective of government officials’ live-streaming e-commerce, Deng et al. [14] studied the risks and challenges of the model of government live-streaming and agricultural assistance. Some scholars have used quantitative methods to study the risks existing in the live-streaming e-commerce industry. For instance, Wongkitrungrueng and Assarut [15] proposed a comprehensive framework to examine the relationship between customers’ perceived value of live-streaming e-commerce, customer trust, and engagement. Facing the product quality problems existing in the live-streaming e-commerce industry, Guo et al. [16] used a three-way evolutionary game model to study the three-way strategy selection and evolution of Internet celebrities, short video live-streaming e-commerce platforms, and consumers, and to a certain extent explained the current phenomenon of the proliferation of Internet celebrity product quality problems.

In this study, when evaluating the risks brought to retailers by live-streaming e-commerce platforms, two dimensions of systemic risk and unique risk were chosen for the comprehensive analysis. Among them, systemic risk is the risk faced by all categories of retailers [17]. For example, in aspects of finance, the live-streaming e-commerce platform does not safely control the capital flow of live-streaming transactions [18]. In aspects of technology, live-streaming e-commerce platforms lack technical expertise in live-streaming [19]. In aspects of operation, the live-streaming e-commerce platform failed to provide enough public-domain traffic support for retailers [20]. In aspects of the market, retailers face the threat of substitution from competitors in the same category of live-streaming e-commerce platforms [21]. The unique risk is the risk only faced by a certain category of retailers [16]. For instance, in aspects of logistics, agricultural product retailers may face the risk of incomplete construction of the platform’s cold chain logistics system [22]. The above five risks directly affect the sustainable and healthy development of retailers on live-streaming e-commerce platforms and therefore require special attention from retailers. As a result, this study has finalized five risk evaluation criteria to evaluate the risks of live-streaming e-commerce platforms: capital flow management and control of live-streaming transactions; technical expertise in the live-streaming field; public domain traffic support; competitive pressure from other retailers or platforms; and the maturity of the cold chain logistics system.

2.2. Risk Assessment Methods for Live-Streaming E-Commerce Platforms

As a nascent industry, there is little authoritative research on the risk assessment of live-streaming e-commerce platforms, but it is still possible to learn from risk assessment studies in other fields. By consulting the literature, it is found that in previous research on risk assessment, scholars have mostly used Bayesian theory, backpropagation (BP) neural networks, prospect theory, MCGDM in the fuzzy environment, and other related methods. For instance, Mina et al. [23] proposed a Bayesian network modeling framework that provides a powerful method to analyze project risk scenarios, which can be used to assess the risk of innovative projects. To improve the risk assessment and management of the fresh grape supply chain, Feng et al. [24] applied a neural network to evaluate the risk of the fresh grape supply chain, then established a neural network risk assessment model based on a single BP and optimized BP. Considering that the current risk assessment method based on Fine-Kinney cannot capture the detailed relationship between hazards and ignores the influence of risk assessment information bias, Wang et al. [25] proposed an improved Fine–Kinney model based on cumulative prospect theory for risk assessment.

When scholars use the MCGDM method in a fuzzy environment to conduct risk assessment research, some of them are based on a single MCGDM method for risk assessment. For example, Karaşan et al. [26] adopted an MCGDM method based on fuzzy set theory to assess blockchain risk. Jokar et al. [27] used fuzzy MCGDM techniques to determine the importance of risks and their priorities in research projects. There are also some studies on risk assessment that combine the MCGDM method with other theories. For instance, Dahooie et al. [28] proposed a method combining data envelopment analysis and dynamic MCGDM to assess the credit risk of customers, which solved the problem of ignoring time effects and changes in credit assessment standards. Liu et al. [29] proposed an MCGDM method based on improved failure mode to investigate and analyze the potential failure mode risk of cold chain green logistics, which considers the uncertain behavior of the expert group. Zhang et al. [30] proposed a hybrid credit risk assessment method based on the combination of MCGDM and fuzzy clustering.

The MCGDM in a fuzzy environment has emerged as the most popular risk assessment method. This is because the other risk assessment methods discussed above require decision-makers to provide evaluation information expressed in precise values. This is challenging to accomplish since the risk of the assessment object is unpredictable and complex, and the decision-makers’ thinking is fuzzy [31,32]. How to accurately represent and process uncertain information, how to reasonably determine decision-maker weights, and how to rank alternatives are key issues of MCGDM methods in fuzzy environments that have received a lot of attention from researchers. In terms of representing and processing uncertain information, Keshavarz et al. [33] proposed a method for evaluating third-party logistics providers that use interval type-2 fuzzy sets to handle uncertain information. Zhao et al. [34] proposed an MCGDM method based on probabilistic linguistic entropy and probabilistic linguistic cross-entropy weighting, which uses probabilistic language to deal with uncertain information. Peng et al. [35] proposed an MCGDM model based on hesitation and correlation coefficient in the environment of interval-valued intuitionistic fuzzy numbers, which uses interval-valued intuitionistic fuzzy sets to deal with uncertain information. Compared with interval type-2 fuzzy sets and probabilistic languages, interval-valued intuitionistic fuzzy sets are more flexible and accurate by considering the membership degree, the non-membership degree, and the hesitation degree while using interval numbers to deal with uncertain information.

In terms of ranking alternatives, Dezert et al. [36] proposed the stable preference ordering towards the ideal solution (SPOTIS) method, which simply compares the alternatives with the ideal solution without comparing the alternatives two by two. Rei et al. [37] proposed the characteristic objects method (COMET) method, a neural framework for training multilingual machine translation evaluation models that correlate with human judgments on a new level. Stoilova [38] proposed a new fuzzy multi-criteria approach based on the fuzzy linear programming method and sequential interaction model for urban systems (SIMUS). SIMUS takes each criterion as an objective criterion and applies linear programming methods to optimize according to each criterion. It does not need to calculate the weights of the criteria because the method calculates their relative importance internally and applies it in each iteration. Wątróbski et al. [39] proposed the data variability assessment of ideal solutions (DARIA-TOPSIS) method, which provides overall efficiency results for the performance of the alternatives being evaluated, taking into account the dynamic changes over the investigated time horizon. Krohling [40] proposed an approach based on TOPSIS for ranking evolutionary algorithms. Each of the above methods has its advantages in ranking alternatives and has been applied in different fields. The TOPSIS method is ultimately chosen to rank the alternatives in this paper after taking into account the benefits of the aforementioned methods and the distinctiveness of the research problem, such as focusing on the original thinking of experts and avoiding having to take into account time-dynamic changes.

In terms of determining decision-maker weights, Harish [41] proposed a decision-making method based on regret or pleasure to calculate decision-maker weights. Liu [42] proposed a two-path feedback consensus model to determine decision-maker weights based on a dynamic hybrid trust relationship. By summarizing the existing research, it can be found that most of the discussions on the decision-maker weight suggest that the weight of each decision-maker for all criteria is indifferent; that is, each decision-maker has the same weight for all criteria, which may be unreasonable and unrealistic [43]. Since the experience accumulation, knowledge level, and professional education background of decision-makers vary, each decision-maker is often only specializing in evaluating some criteria but not all criteria; that is, decision-makers often have different understandings and mastery of different evaluation criteria. Therefore, different weights should be given to decision-makers for different evaluation criteria. In summary, this study suggests a method for calculating the decision-maker weight for the criterion based on the decision-makers’ professionalism. This method gives decision-makers varying weights for various evaluation criteria based on their varied levels of expertise. Moreover, since the professionalism of decision-makers is a qualitative concept, this paper uses the expert scoring method to quantify the professionalism of decision-makers.

3. Overview of Interval-Valued Intuitionistic Fuzzy Sets

Considering the difficulty of using accurate real numbers to deal with fuzzy information, this paper proposes an interval-valued intuitionistic fuzzy MCGDM method based on the decision-makers’ professionalism to evaluate the risk of the live-streaming e-commerce platform. The method uses interval-valued intuitionistic fuzzy numbers to deal with uncertain information, and the TOPSIS method is used to rank the alternatives. The key to the approach is to determine the decision-maker’s weights for the risk criteria. Due to the different experience accumulation, knowledge levels, and professional education backgrounds of decision-makers, they have different understandings of different risk criteria, so different weights should be given to decision-makers for different risk criteria. The determination of the weight for the risk criteria is related to the decision-makers’ professionalism in the criterion. If the professionalism is stronger, it will be given a larger weight, and if the professionalism is weaker, it will be given a smaller weight. The basic theory of interval-valued intuitionistic fuzzy sets is briefly introduced below [44,45].

 Definition 1. 

Let X be a non-empty set, $A=\left\{<x,u_A(x),v_A(x)>|x\in X\right\}$ is an intuitionistic fuzzy set. Where, $u_A(x)$ and $v_A(x)$ represent the membership degree and non-membership degree of the element x belonging to the set X, respectively. In addition, they satisfy the condition $0\le u_A(x)+v_A(x)\le 1,\forall x\in X$. Since it is difficult to express the complexity and uncertainty of objective things with exact real values, it is proposed to extend the intuitionistic fuzzy set with interval numbers $u_A(x)$ and $v_A(x)$, where $u_A(x),$ $v_A(x)$ satisfy $u_A(x)\subset \left[0,1\right],v_A(x)\subset \left[0,1\right]$, respectively. Further, $\sup u_A(x)+\sup v_A(x)\le 1,\forall x\in X$.

 Definition 2. 

Let X be a non-empty set, $\left\{\prec x,\left[u_A{(x)}^{-},u_A{(x)}^{+}\right],\left[v_A{(x)}^{-},v_A{(x)}^{+}\right]\succ |x\in X\right\}$ be an interval-valued intuitionistic fuzzy set, and $\prec \left[u_A{(x)}^{-},u_A{(x)}^{+}\right],\left[v_A{(x)}^{-},v_A{(x)}^{+}\right]\succ$ be an interval-valued intuitionistic fuzzy number. Where, $\left[u_A{(x)}^{-},u_A{(x)}^{+}\right]$ and $\left[v_A{(x)}^{-},v_A{(x)}^{+}\right]$ represent the membership degree interval and non-membership degree interval of the element x belonging to the set X respectively. They satisfy the conditions $\left[u_A{(x)}^{-},u_A{(x)}^{+}\right]\subseteq \left[0,1\right],\left[v_A{(x)}^{-},v_A{(x)}^{+}\right]\subseteq \left[0,1\right]$, and $u_A{(x)}^{+}+v_A{(x)}^{+}\le 1,\forall x\in X$.

 Definition 3. 

Let $\tilde{\alpha }=\left(\left[a_1,b_1\right],\left[c_1,d_1\right]\right),\tilde{\beta }=\left(\left[a_2,b_2\right],\left[c_2,d_2\right]\right)$ be any two interval-valued intuitionistic fuzzy numbers, then the algorithm is

(a)

$\tilde{\alpha }+\tilde{\beta }=\left(\left[a_1+a_2-a_1{a}_2,b_1+b_2-b_1{b}_2\right],\left[c_1{c}_2,d_1{d}_2\right]\right)$;

(b)

$\tilde{\alpha }\cdot \tilde{\beta }=\left(\left[a_1{a}_2,b_1{b}_2\right],\left[c_1+c_2-c_1{c}_2,d_1+d_2-d_1{d}_2\right]\right)$;

(c)

$\lambda \tilde{\alpha }=\left(\left[1-{\left(1-a_1\right)}^{\lambda },1-{\left(1-b_1\right)}^{\lambda }\right],\left[c_1{}^{\lambda },d_1{}^{\lambda }\right]\right)$;

(d)

${\tilde{\alpha }}^{\lambda }=\left(\left[a_1^{\lambda },b_1^{\lambda }\right],\left[1-{\left(1-c_1\right)}^{\lambda },1-{\left(1-d_1\right)}^{\lambda }\right]\right)$.

 Definition 4. 

Let $\tilde{\alpha }=\left(\left[a_1,b_1\right],\left[c_1,d_1\right]\right),\tilde{\beta }=\left(\left[a_2,b_2\right],\left[c_2,d_2\right]\right)$ be any two interval-valued intuitionistic fuzzy numbers, then the normalized Hamming distance between them is

$$d\left(\tilde{\alpha },\tilde{\beta }\right)=\frac{1}{4}\left(\left|a_1-a_2\right|+\left|b_1-b_2\right|+\left|c_1-c_2\right|+\left|d_1-d_2\right|\right)$$

(1)

 Definition 5. 

Let $H=\left[\widetilde{{\alpha }_1},\widetilde{{\alpha }_2},\dots ,\widetilde{{\alpha }_n}\right]$ be a set of interval-valued intuitionistic fuzzy numbers, where $\widetilde{{\alpha }_i}=\left(\left[a_i,b_i\right],\left[c_i,d_i\right]\right)\left(i=1,2,\dots ,n\right)$. Then the n-dimensional interval-valued intuitionistic fuzzy weighted average operator (IIFWA) is

$$\begin{array}{l}IIFW{A}_{{\omega }_i}\left(\widetilde{{\alpha }_1},\widetilde{{\alpha }_2},\dots ,\widetilde{{\alpha }_n}\right)\\ ={\displaystyle \sum _{i=1}^n{\omega }_i\widetilde{{\alpha }_i}}=\left(\left[1-{\displaystyle \prod _{i=1}^n{\left(1-a_i\right)}^{{\omega }_i}},1-{\displaystyle \prod _{i=1}^n{\left(1-b_i\right)}^{{\omega }_i}}\right],\left[{\displaystyle \prod _{i=1}^n{c}_i^{{\omega }_i},}{\displaystyle \prod _{i=1}^n{d}_i^{{\omega }_i}}\right]\right)\end{array}$$

(2)

Among them, $\omega =\left\{{\omega }_1,{\omega }_{2,}\dots ,{\omega }_n\right\}$ is the criterion weight of $H=\left[\widetilde{{\alpha }_1},\widetilde{{\alpha }_2},\dots ,\widetilde{{\alpha }_n}\right]$, which satisfies $0\le {\omega }_i\le 1,{\displaystyle \sum _{i=1}^n{\omega }_i}=1,i=1,2,\dots ,n$.

4. Risk Assessment Model of Live-Streaming E-Commerce Platform

4.1. Problem Description

This paper uses the interval-valued intuitionistic fuzzy MCGDM method based on the decision-makers’ professionalism to evaluate the risk of live-streaming e-commerce platforms. The specific evaluation process is as follows: Firstly, for the live-streaming e-commerce platforms and related risk criteria, all decision-makers provide the interval-valued intuitionistic fuzzy risk evaluation matrix and the weight vector of the risk criterion. Then, according to the decision-makers weight for the risk criteria, the individual risk evaluation matrix of all decision-makers is assembled into a comprehensive risk evaluation matrix. Finally, the alternative live-streaming e-commerce platforms are sorted. In this process, two key issues need to be solved: the determination of the decision-makers weight for the risk criteria and the sorting of alternative live-streaming e-commerce platforms. Therefore, this paper proposes the following solutions: Firstly, the decision-makers weight for risk criteria is determined according to the decision-makers’ professionalism. Secondly, the TOPSIS method is used to rank alternative live-streaming e-commerce platforms. The specific process of determining the decision-makers weight for the risk criteria is divided into three steps. First, all decision-makers rate the professionalism of each decision-maker on the risk criterion to obtain the professional scoring matrix of the decision-makers. Second, the professional scoring matrices of all decision-makers are assembled to obtain the comprehensive professional scoring matrix of the decision-makers. Third, this paper normalizes them to obtain the decision-makers weight for risk criteria. 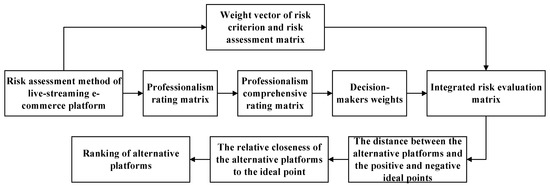The specific algorithm flow is shown in Figure 1.

The following notation is used to denote the involved aggregate quantities:

(a)

$A=\left\{A_1,A_2,\dots ,A_m\right\}$: The set of m alternative live-streaming e-commerce platforms concerned by decision-makers, where $A_i$ represents the i-th alternative live-streaming e-commerce platform, $i=1,2,\dots ,m$.

(b)

$U=\left\{u_1,u_2,\dots ,u_n\right\}$: The set of n risk criteria that decision-makers pay attention to when evaluating the risk of the live-streaming e-commerce platform, where $u_j$ represents the j-th risk criterion, $j=1,2,\dots ,n$.

(c)

$E=\left\{e_1,e_2,\dots ,e_n\right\}$: s decision-makers participating in the decision, where $e_k$ represents the k-th decision-maker, $k=1,2,\dots ,s$.

(d)

$\omega =\left\{{\omega }_1,{\omega }_2,\dots ,{\omega }_j\right\}$: Weight vector of risk criteria, where ${\omega }_j$ represents the weight or importance of the risk criterion, satisfying ${\omega }_j\ge 0$ and ${\displaystyle \sum _{j=1}^n{\omega }_j=1,j=1,2,\dots ,n}$. Here, the weight vector of the risk criterion can be given by the decision-maker.

(e)

${\lambda }_j^k$: Weight of decision-maker $e_k$ for risk criterion $u_j$.

(f)

$r_{ij}^k=\left(\left[a_{ij}^k,b_{ij}^k\right],\left[c_{ij}^k,d_{ij}^k\right]\right)$: The evaluation value of the decision-maker $e_k$ on the risk criterion $u_j$ of the alternative live-streaming e-commerce platform $A_i$, which is an interval-valued intuition fuzzy number, where $\left[a_{ij}^k,b_{ij}^k\right]$ and $\left[c_{ij}^k,d_{ij}^k\right]$ represent the decision-maker’s membership degree and non-membership degree of the alternative live-streaming e-commerce platform $A_i$ on the risk criterion $u_j$, respectively. Further, $\left[a_{ij}^k,b_{ij}^k\right]\subseteq \left[0,1\right],\left[c_{ij}^k,d_{ij}^k\right]\subseteq \left[0,1\right],b_{ij}^k+d_{ij}^k\le 1$.

(g)

$\widetilde{R^k}={\left(\widetilde{r_{ij}^k}\right)}_{m\times n}$: The risk assessment matrix of decision-maker $e_k$.

(h)

$T=\left\{T^1,T^2,\dots ,T^v\right\}$: The set of evaluation scales about the decision-makers’ professionalism for risk criteria. Where $T^{\epsilon }$ represents the $\mathit{\epsilon }$-th evaluation scale, $\epsilon =1,2,\dots ,v$. Generally, the larger $\epsilon$, the corresponding evaluation level is higher. For instance, in the specific example in the fifth part of this article, regarding the decision-maker’ scoring of the professionalism for the risk criteria, the scale set used is in the form of a 5-point scale, namely $T=\left\{T^1=1,T^2=2,T^3=3,T^4=4,T^5=5\right\}$. Where 1 indicates the least professionalism, and 5 indicates the highest professionalism.

(i)

$q_{gj}^k=T^{\epsilon }$: The professional score value of decision-maker $e_g$ on the risk criterion $u_j$ for decision-maker $e_{\mathrm{k}}$, where $e_g$ represents the g-th decision-maker, $g=1,2,\dots ,n$.

4.2. Risk Assessment Model of Live-Streaming E-Commerce Platform

The key to the risk assessment in this paper is to determine the decision-makers weight for the risk criteria. In order to determine the value of ${\lambda }_j^k$, it is necessary to consider the professionalism of decision-maker $e_k$ on risk criterion ${\omega }_j$, if decision-maker $e_k$ is highly specialized on risk criterion $u_j$, a larger weight ${\lambda }_j^k$ is given to decision-maker $e_k$ for risk criterion $u_j$. If decision-maker $e_k$ is weekly specialized on risk criterion $u_j$, a smaller weight ${\lambda }_j^k$ is given to decision-maker $e_k$ for risk criterion $u_j$. Among them, professionalism is a qualitative concept. For the convenience of calculation, the expert scoring method is used to determine the professional score of the decision-makers on the evaluation criteria. The specific algorithm of the expert scoring method is as follows: First, the decision-maker $e_g\left(g=1,2,\dots ,n\right)$ scores the professionalism of the decision-maker $e_k$ on the risk criterion $u_j$, and the score is $q_{gj}^k\left(g=1,2,\dots ,n\right)$. When $g=k$, namely $q_{kj}^k$, it means that decision-maker $e_k$ gives the self-professional score on the risk criterion $u_j$. When $g\ne k$, namely $q_{gj}^k\left(g=1,2,\dots ,n,g\ne k\right)$, it means that other decision-makers $e_g\left(g=1,2,\dots ,n,g\ne k\right)$ give the professional score of decision-maker $e_k$. In the professional scoring process, the scale set is setted as $T=\left\{T^1,T^2,\dots ,T^v\right\}$.

In order to comprehensively consider the self-scores and other decision-makers’ scores, the control coefficient $\eta \left(0\le \eta \le 1\right)$ is introduced to construct the professional comprehensive score $q_j^k$ of the decision-maker $e_k$ on the risk criterion $u_j$.

$$q_j^k=\eta q_{kj}^k+(1-\eta ){\displaystyle \sum _{g=1,g\ne k}^n{q}_{gj}^k}$$

(3)

A trade-off between the self-scores and other decision-makers’ scores can be achieved by changing the control coefficient $\eta$. When $\eta =1$, weight of decision-maker $e_k$ on risk criterion $u_j$ only depends on the self-scores of decision-maker $e_k$. When $\eta =0$, weight of decision-maker $e_k$ on risk criterion $u_j$ only depends on the scorings of decision-maker $e_k$ by other decision-makers.

By standardizing the comprehensive score $q_j^k$ of the decision-maker $e_k$, the weight of the decision-maker $e_k$ on the risk criterion $u_j$ is obtained as:

$${\lambda }_j^k=\frac{q_j^k}{{\displaystyle \sum _{k=1}^m{q}_j^k}}$$

(4)

According to Equations (3) and (4), the decision-makers’ weight matrix for the risk criterion of the live-streaming e-commerce platform can be obtained, and the weight vector of the risk criterion is given by the decision-maker. The next problem to be solved is to use Equation (2) to integrate the interval-valued intuitionistic fuzzy risk evaluation matrix of all decision-makers into a comprehensive interval-valued intuitionistic fuzzy risk evaluation matrix $\tilde{R}={\left(\widetilde{r_{ij}}\right)}_{m\times n}$, where,

$$\begin{array}{l}\tilde{R}={\left(\widetilde{r_{ij}}\right)}_{m\times n}\\ ={\left({\displaystyle \sum _{k=1}^s{\lambda }_j^k\widetilde{r_{ij}^k}}\right)}_{m\times n}={\left(\left[1-{{\displaystyle {\prod }_{k=1}^s\left(1-a_{ij}^k\right)}}^{{\lambda }_j^k},1-{{\displaystyle {\prod }_{k=1}^s\left(1-b_{ij}^k\right)}}^{{\lambda }_j^k}\right],\left[{{\displaystyle {\prod }_{k=1}^s\left(c_{ij}^k\right)}}^{{\lambda }_j^k},{{\displaystyle {\prod }_{k=1}^s\left(d_{ij}^k\right)}}^{{\lambda }_j^k}\right]\right)}_{m\times n}\end{array}$$

(5)

After obtaining the comprehensive interval-valued intuitionistic fuzzy risk evaluation matrix, the TOPSIS method is used to rank the alternative live-streaming e-commerce platforms. The TOPSIS method uses the positive ideal solution and the negative ideal solution to rank the schemes in the multi-criteria decision-making problem, which is a commonly used method in the field of multi-criteria decision-making. The steps are as follows:

Firstly, the maximum interval-valued intuitionistic fuzzy number is $\left(\left[1,1\right],\left[0,0\right]\right)$, so the positive ideal point of interval-valued intuitionistic fuzzy sets can be defined as: $\widetilde{X^{+}}=\left(\widetilde{X_1^{+}},\widetilde{X_2^{+}},\dots ,\widetilde{X_j^{+}}\right)$. Where, $\widetilde{X_j^{+}}=\left(\left[1,1\right],\left[0,0\right]\right),j=1,2,\dots ,n$. The minimum interval-valued intuitionistic fuzzy number is $\left(\left[0,0\right],\left[1,1\right]\right)$, so the negative ideal point of interval-valued intuitionistic fuzzy sets can be defined as:$\widetilde{X^{-}}=\left(\widetilde{X_1^{-}},\widetilde{X_2^{-}},\dots ,\widetilde{X_j^{-}}\right)$. Where, $\widetilde{X_j^{-}}=\left(\left[0,0\right],\left[1,1\right]\right),j=1,2,\dots ,n$.

Secondly, we use Equation (1) to calculate the distance between alternatives and the positive and negative ideal points of interval-valued intuitionistic fuzzy sets,

$$d\left(A_i,\widetilde{X^{+}}\right)={\displaystyle \sum _{j=1}^n{\omega }_{j}d\left(\widetilde{r_{ij}},\widetilde{X_j^{+}}\right)}$$

(6)

$$d\left(A_i,\widetilde{X^{-}}\right)={\displaystyle \sum _{j=1}^n{\omega }_{j}d\left(\widetilde{r_{ij}},\widetilde{X_j^{-}}\right)}$$

(7)

where,

$$d\left(\widetilde{r_{ij}},\widetilde{X_j^{+}}\right)=\frac{1}{4}\left(\left|a_{ij}-1\right|+\left|b_{ij}-1\right|+\left|c_{ij}-0\right|+\left|d_{ij}-0\right|\right)$$

$$d\left(\widetilde{r_{ij}},\widetilde{X_j^{-}}\right)=\frac{1}{4}\left(\left|a_{ij}-0\right|+\left|b_{ij}-0\right|+\left|c_{ij}-1\right|+\left|d_{ij}-1\right|\right)$$

Thirdly, we calculate the relative closeness of the alternatives to the ideal point. Since the purpose of this study is to determine the live e-commerce platform with the lowest risk, platforms with lower risks are preferred. Positive ideal points represent the greatest risk, and negative ideal points represent the smallest risk. Therefore, it is stipulated that the relative closeness of the alternatives to the ideal point is the degree that is far from the positive ideal point and close to the negative ideal point.

$$r\left(A_i\right)=\frac{d\left(\widetilde{r_{ij}},\widetilde{X^{+}}\right)}{d\left(\widetilde{r_{ij}},\widetilde{X^{+}}\right)+d\left(\widetilde{r_{ij}},\widetilde{X^{-}}\right)}$$

(8)

Fourthly, we sort the alternatives in descending order of relative closeness. The greater the relative closeness of the live-streaming e-commerce platform to the ideal point, the more the alternatives are far from the positive ideal point and closer to the negative ideal point; that is, the lower the platform risk, the more preferred it is. By calculating the relative closeness of each alternative to the ideal point, that is, the degree of distance between the positive ideal point and the negative ideal point, the alternative live-streaming e-commerce platforms are sorted, and the live-streaming e-commerce platform with the lowest comprehensive risk is identified.

5. Case Study

Agricultural products are closely related to people’s daily lives and are in great demand, which makes them a hot field for major e-commerce platforms and related professional websites. However, consumers are skeptical about the quality and safety of agricultural products because of their perishable nature, the inconvenience of storage, the intricate supply chain, and the virtual character of online transactions [46,47,48]. Compared with other categories of retailers, agricultural product retailers face more risks when choosing live-streaming e-commerce platforms to settle on. Therefore, in this section, we demonstrate the application of the risk assessment method of the live-streaming e-commerce platform by taking the example of choosing a live-streaming e-commerce platform for the agricultural product “Huaniu Apple”.

As a product of China’s National Geographical Indication, “Huaniu Apple” is the first apple variety in China to obtain an official trademark in the international market. However, due to the single sales channel and insufficient publicity, the demand market for “Huaniu Apple” has not been fully opened. For this reason, the local government decided to determine a platform with the lowest comprehensive risk from several alternative live-streaming e-commerce platforms to carry out live-streaming e-commerce business.

To help “Huaniu Apple” choose a live-streaming e-commerce platform with the lowest comprehensive risk, the local government invited four experts to conduct a risk assessment on five alternative live-streaming e-commerce platforms selected by the government. The five alternative live-streaming e-commerce platforms are Alibaba $\left(A_1\right)$, JD.com $\left(A_2\right)$, Pinduoduo $\left(A_3\right)$, Tiktok $\left(A_4\right)$ and Kuaishou $\left(A_5\right)$. Among them, the criteria for selecting experts are mainly the following two aspects: first, they have been engaged in the field of live-streaming e-commerce for 3 years and have live-streaming e-commerce-related professional experience, knowledge, and skills; second, they can perform their duties seriously, fairly, and honestly [45]. When choosing risk evaluation criteria, experts took into account the systemic and unique risks brought to agricultural retailers by live-streaming e-commerce platforms, such as easy perishability and deterioration, etc., and finally determined five risk evaluation criteria. The five risk evaluation criteria are: capital flow management and control of live-streaming transactions $\left(u_1\right)$, technical expertise in the live-streaming field $\left(u_2\right)$, public domain traffic support for agricultural product live-streaming rooms $\left(u_3\right)$, competitive pressure from other retailers or platforms $\left(u_4\right)$, and the maturity of the cold chain logistics system $\left(u_5\right)$ [49,50,51].

In the first step, the four experts evaluated the five risk criteria of the five alternative live-streaming e-commerce platforms. The evaluation values are in the form of interval-valued intuitionistic fuzzy numbers, and the interval-valued intuitionistic fuzzy risk evaluation matrix is obtained, as shown in

Table 1. Interval-valued intuitionistic fuzzy risk assessment matrix.

		${\mathit{u}}_1$	${\mathit{u}}_2$	${\mathit{u}}_3$	${\mathit{u}}_4$	${\mathit{u}}_5$
$e_1$	$A_1$	([0.6,0.8], [0.1,0.2])	([0.6,0.75], [0.05,0.2])	([0.6,0.65], [0.05,0.3])	([0.3,0.45], [0.35,0.4])	([0.4,0.5], [0.35,0.4])
	$A_2$	([0.7,0.8], [0.05,0.1])	([0.5,0.65], [0.25,0.3])	([0.45,0.6], [0.05,0.3])	([0.35,0.5], [0.3,0.4])	([0.45,0.5], [0.3,0.45])
	$A_3$	([0.4,0.6], [0.15,0.3])	([0.45,0.6], [0.2,0.35])	([0.7,0.85], [0.05,0.1])	([0.35,0.6], [0.25,0.3])	([0.4,0.45], [0.5,0.65])
	$A_4$	([0.3,0.5], [0.35,0.4])	([0.35,0.5], [0.35,0.45])	([0.6,0.75], [0.05,0.2])	([0.65,0.7], [0.15,0.5])	([0.25,0.3], [0.4,0.6])
	$A_5$	([0.3,0.45, [0.35,0.5])	([0.65,0.8], [0.05,0.15])	([0.3,0.45], [0.45,0.5])	([0.55,0.6], [0.3,0.35])	([0.3,0.4], [0.3,0.55])
$e_2$	$A_1$	([0.5,0.8], [0.05,0.2])	([0.65,0.75], [0.05,0.2])	([0.5,0.65], [0.05,0.3])	([0.3,0.55], [0.25,0.3])	([0.3,0.45], [0.45,0.5])
	$A_2$	([0.5,0.7], [0.15,0.3])	([0.65,0.7], [0.15,0.3])	([0.5,0.65], [0.15,0.3])	([0.25,0.4], [0.3,0.45])	([0.55,0.6], [0.3,0.4])
	$A_3$	([0.45,0.7], [0.05,0.2])	([0.4,0.55], [0.2,0.45])	([0.65,0.7], [0.15,0.25])	([0.4,0.55], [0.25,0.4])	([0.35,0.5], [0.4,0.45])
	$A_4$	([0.35,0.6], [0.15,0.3])	([0.55,0.7], [0.15,0.25])	([0.55,0.7], [0.15,0.2])	([0.55,0.8], [0.05,0.1])	([0.25,0.3], [0.4,0.7])
	$A_5$	([0.35,0.6], [0.35,0.4])	([0.65,0.7], [0.15,0.2])	([0.45,0.5], [0.2,0.35])	([0.45,0.8], [0.1,0.15])	([0.25,0.3], [0.45,0.7])
$e_3$	$A_1$	([0.45,0.7], [0.15,0.2])	([0.55,0.6], [0.15,0.25])	([0.45,0.6], [0.25,0.3])	([0.45,0.5], [0.25,0.3])	([0.35,0.4], [0.45,0.5])
	$A_2$	([0.55,0.6], [0.15,0.2])	([0.55,0.7], [0.15,0.25])	([0.55,0.6], [0.15,0.4])	([0.35,0.5], [0.3,0.4])	([0.4,0.6], [0.35,0.4])
	$A_3$	([0.4,0.65], [0.15,0.3])	([0.35,0.45], [0.4,0.55])	([0.6,0.75], [0.2,0.25])	([0.45,0.5], [0.2,0.45])	([0.35,0.5], [0.4,0.45])
	$A_4$	([0.55,0.6], [0.15,0.3])	([0.55,0.65], [0.05,0.2])	([0.55,0.7], [0.15,0.3])	([0.55,0.7], [0.05,0.2])	([0.15,0.2], [0.4,0.75])
	$A_5$	([0.45,0.5], [0.3,0.45])	([0.5,0.7], [0.15,0.25])	([0.35,0.4], [0.25,0.4])	([0.65,0.8], [0.05,0.1])	([0.05,0.2], [0.55,0.7])
$e_4$	$A_1$	([0.55,0.7], [0.2,0.25])	([0.45,0.7], [0.15,0.3])	([0.55,0.6], [0.3,0.35])	([0.55,0.6], [0.2,0.35])	([0.35,0.4], [0.4,0.55])
	$A_2$	([0.45,0.6], [0.15,0.3])	([0.5,0.7], [0.15,0.25])	([0.45,0.6], [0.25,0.4])	([0.3,0.55], [0.3,0.45])	([0.3,0.6], [0.35,0.4])
	$A_3$	([0.45,0.6], [0.15,0.3])	([0.35,0.4], [0.4,0.6])	([0.6,0.7], [0.2,0.3])	([0.4,0.55], [0.35,0.4])	([0.35,0.6], [0.25,0.3])
	$A_4$	([0.55,0.7], [0.15,0.4])	([0.5,0.65], [0.05,0.35])	([0.55,0.7], [0.15,0.2])	([0.55,0.7], [0.15,0.2])	([0.2,0.4], [0.5,0.6])
	$A_5$	([0.4,0.55], [0.35,0.4])	([0.5,0.75], [0.15,0.25])	([0.35,0.5], [0.45,0.5])	([0.65,0.8], [0.05,0.2])	([0.05,0.3], [0.55,0.7])

. All experts, considering the characteristics of live e-commerce platforms and agricultural products, jointly determine the weight vector of risk criteria through group discussion and consultation. It is $\omega =\left\{0.15,0.1,0.3,0.15,0.3\right\}$.

In the second step, the four experts score the professionalism of all experts on each risk criterion. The scale is set in the form of a 5-point scale when scoring, that is, $T=\left\{T^1=1,T^2=2,T^3=3,T^4=4,T^5=5\right\}$, where, 1 represents the lowest degree of professionalism and 5 represents the highest degree of professionalism. We obtain the expert’s professionalism score matrix, as shown in

Table 2. Experts’ professionalism scoring matrix.

		${\mathit{u}}_1$	${\mathit{u}}_2$	${\mathit{u}}_3$	${\mathit{u}}_4$	${\mathit{u}}_5$
$e_1$	$e_1$	2	1	3	2	4
	$e_2$	2	3	4	2	5
	$e_3$	3	4	1	4	3
	$e_4$	4	5	2	3	2
$e_2$	$e_1$	1	3	4	2	4
	$e_2$	3	2	3	1	5
	$e_3$	4	4	3	3	3
	$e_4$	4	3	2	5	2
$e_3$	$e_1$	2	1	4	1	5
	$e_2$	2	3	5	2	3
	$e_3$	4	3	2	5	3
	$e_4$	4	3	2	3	1
$e_4$	$e_1$	1	3	3	2	4
	$e_2$	2	1	5	1	3
	$e_3$	4	4	1	3	3
	$e_4$	4	5	1	4	2

.

In the third step, the weights of all experts for each risk criterion are calculated.

a. Calculate the professional comprehensive score of all experts on each risk criterion according to Equation (3), where let the control coefficient $\eta =0.5$, get the expert’s professionalism comprehensive scoring matrix, as shown in

Table 3. Expert’s professionalism comprehensive scoring matrix.

	${\mathit{u}}_2$	${\mathit{u}}_2$	${\mathit{u}}_3$	${\mathit{u}}_4$	${\mathit{u}}_5$
$e_1$	3	4	7	3.5	8.5
$e_2$	4.5	4.5	8.5	3	8
$e_3$	7.5	7.5	3.5	7.5	6
$e_4$	8	8	3.5	7.5	3.5

.

b. Normalize the professional comprehensive scores of all experts on each risk criterion according to Equation (4) to obtain the expert weights for the risk criterion, as shown in

Table 4. Expert weights for risk criteria.

	${\mathit{u}}_1$	${\mathit{u}}_2$	${\mathit{u}}_3$	${\mathit{u}}_4$	${\mathit{u}}_5$
$e_1$	0.13	0.17	0.30	0.16	0.33
$e_2$	0.20	0.19	0.38	0.14	0.31
$e_3$	0.32	0.31	0.16	0.35	0.23
$e_4$	0.35	0.33	0.16	0.35	0.13

.

In the fourth step, using Equation (5) and the expert weights for the risk criterion, the individual risk evaluation matrices given by each expert are assembled to obtain a comprehensive interval-valued intuitionistic fuzzy risk evaluation matrix (

Table 5. Comprehensive interval-valued intuitionistic fuzzy risk assessment matrix.

	${\mathit{u}}_1$	${\mathit{u}}_2$	${\mathit{u}}_3$	${\mathit{u}}_4$	${\mathit{u}}_5$
$A_1$	([0.52,0.75],[0.10,0.22])	([0.55,0.70],[0.10,0.25])	([0.55,0.65],[0.15,0.34])	([0.45,0.57],[0.27,0.36])	([0.37,0.46],[0.43,0.51])
$A_2$	([0.53,0.68],[0.10,0.19])	([0.55,0.69],[0.16,0.27])	([0.49,0.64],[0.15,0.40])	([0.32,0.54],[0.30,0.43])	([0.46,0.58],[0.33,0.41])
$A_3$	([0.43,0.67],[0.11,0.30])	([0.38,0.48],[0.32,0.51])	([0.65,0.78],[0.15,0.24])	([0.43,0.55],[0.25,0.38])	([0.37,0.52],[0.35,0.44])
$A_4$	([0.49,0.65],[0.20,0.36])	([0.50,0.64],[0.08,0.30])	([0.57,0.74],[0.12,0.25])	([0.57,0.75],[0.08,0.25])	([0.22,0.32],[0.43,0.66])
$A_5$	([0.40,0.55],[0.34,0.45])	([0.56,0.74],[0.13,0.22])	([0.38,0.50],[0.34,0.45])	([0.61,0.81],[0.11,0.20])	([0.20,0.32],[0.48,0.69])

).

In the fifth step, according to Equations (6) and (7), we calculate the distance $d\left(A_i,\widetilde{X^{+}}\right)$ and $d\left(A_i,\widetilde{X^{-}}\right)$ between the alternatives and the interval-valued intuitionistic fuzzy positive and negative ideal points, and the calculation results are shown in

Table 6. The distance between the alternatives and the positive and negative ideal points.

	${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$	${\mathit{A}}_4$	${\mathit{A}}_5$
$d\left(A_i,\widetilde{X^{+}}\right)$	0.38	0.37	0.38	0.39	0.47
$d\left(A_i,\widetilde{X^{-}}\right)$	0.62	0.63	0.62	0.61	0.53

.

In the sixth step, the relative closeness of the alternatives to the ideal point is calculated according to Equation (8). The calculation results are shown in

Table 7. The relative closeness of the alternatives to the ideal point.

	${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$	${\mathit{A}}_4$	${\mathit{A}}_5$
$r\left(A_i\right)$	0.3825	0.3749	0.3753	0.3931	0.4715

.

In the seventh step, the alternative live-streaming e-commerce platforms are sorted in descending order of relative closeness. The result of the sorting is: $A_5>A_4>A_1>A_3>A_2$. Therefore, the live-streaming e-commerce platform with the lowest comprehensive risk is Pinduoduo. Observing the weight vector of risk criteria given by experts, it can be seen that the two risk criteria, the platform’s public domain traffic support for agricultural product live-streaming rooms and the maturity of the cold chain logistics system, have the largest weights, both of which are 0.3. As a result, the above two risk criteria for the live-streaming e-commerce platform play a decisive role in its comprehensive risk assessment. Just as Alibaba’s daily department stores and JD.com’s 3C electronics, agricultural products are the important genes of Pinduoduo. Pinhaohuo, Pinduoduo’s predecessor, started with agricultural products such as fruits. After the establishment of Pinduoduo, commodities have moved closer to the whole category, but agricultural products still occupy a major position. Pinduoduo’s huge user traffic of agricultural products can provide the largest traffic support for “Huaniu Apple”. At the same time, relying on digitalization, Pinduoduo is continuing to invest heavily in the construction of infrastructures such as cold storage and fresh cold chain logistics systems and establishing a supply chain system suitable for fresh agricultural products, thereby improving circulation efficiency and reducing losses. In March 2021, Pinduoduo published a cold chain transportation patent, which includes a module diagram of a cold chain transportation system. This patent realizes cold chain transportation for agricultural products, fresh products, etc., to avoid the quality degradation and damage caused by traditional logistics and transportation methods during the transportation of products. It is because of the above two advantages that Pinduoduo can stand out among the alternative live-streaming e-commerce platforms and become the agricultural product live-streaming e-commerce platform with the lowest comprehensive risk.

6. Conclusions

When retailers choose a live-streaming e-commerce platform to settle in, they are faced with the challenges of various risks of the platform, such as the fact that the capital flow management and control of live-streaming transactions are not secure, the technical experience in the field of live-streaming is not professional, the public domain traffic support of live-streaming rooms is not sufficient, the competitive pressure from other retailers or platforms is high, etc. Therefore, how to evaluate the various risks of live-streaming e-commerce platforms to help retailers identify the platform with the lowest comprehensive risk is particularly important. Previous studies on the risk of live-streaming e-commerce platforms have mostly focused on the type of risk and less on the method of risk evaluation. However, a reasonable and effective method can directly influence retailers’ live-streaming e-commerce platform selection decisions. Therefore, considering the complexity of the risks of live-streaming e-commerce platforms and the ambiguity of the decision-makers thinking, this paper proposes an interval-valued intuitionistic fuzzy MCGDM method based on the professionalism of decision-makers. This method has the following advantages: First, facing the problems of complexity, fuzziness, and uncertainty in the risk assessment of live e-commerce platforms, the proposed method adopts interval-valued intuitionistic fuzzy sets to deal with uncertain information, which is more flexible and more accurate. Second, the method determines different weights for decision-makers for different risk criteria, which effectively solves the problem that the decision results may be unscientific when the same weight is given to decision-makers for different criteria. Finally, the use of TOPSIS to rank alternative live-streaming e-commerce platforms is more suitable and feasible for the characteristics of the e-commerce live platform ranking problem.

This research has the following two contributions: First, this paper can provide support for platforms and retailers in the live-streaming e-commerce industry. On the one hand, the risk evaluation method of the live-streaming e-commerce platform proposed in this paper can help retailers make a comprehensive evaluation of platform risks and identify a platform with lower comprehensive risks, thus helping retailers reduce costs and enhance competitiveness. On the other hand, the evaluation of live-streaming e-commerce platform risks can also help platforms identify and reduce risks, thus attracting more retailers to the platform, increasing profits, and enhancing competitiveness. Second, this work will also provide ideas for the research of the live-streaming e-commerce industry from the perspective of risk management.

For the risk evaluation method of live-streaming e-commerce platforms in this paper, the risk criterion weight information is jointly given by the decision-making group after negotiation, but the reality is that the risk criterion weight information is incomplete or even completely unknown. Therefore, the authors will further expand the risk evaluation method for live-streaming e-commerce platforms. In future work, the problem of incomplete or even completely unknown information on risk criterion weights will be investigated in more depth using methods such as linear programming.