Strategic Business Mode Choices for E-Commerce Platforms under Brand Competition

Abstract

Relying on the rapid development of information and internet technologies, e-commerce has boomed over the past decade. As a link between manufacturers and consumers, the e-commerce platform has a crucial position in the online retailing market. The e-commerce platform not only provides an online marketplace through which the manufacturers directly sell products to consumers but also purchases and resells manufacturers’ products to consumers. Therefore, when the e-commerce platform provides services to manufacturers, it is faced with the selection of two sales methods: reselling or marketplace. Using a game theoretic model, we focus on the strategic interactions between an e-commerce platform and two brand manufacturers in four different business modes. The results show that the e-commerce platform profits more when both brand manufacturers directly sell products through the online marketplace. From the two brand manufacturers’ points of view, using the e-commerce platform as a reseller is always more profitable than directly selling, no matter which business mode they are in. The above findings have important implications for the selling decisions of the e-commerce platform and brand manufacturers. Furthermore, an interesting and counterintuitive result is that the new brand manufacturer benefits more than the existing brand manufacturer when consumers’ acceptance of the new brand products is becoming lower. When production costs are low, only the two brand manufacturers can achieve a mutually beneficial situation by selling products to the e-commerce platform. Moreover, the competition among brand manufacturers is beneficial to the e-commerce platform. Our research provides a theoretical basis for brand manufacturers and the e-commerce platform to make more rational decisions, and it updates the existing knowledge about brand competition and e-commerce platform’s business mode choices.

1. Introduction

In recent years, online retailing through an e-commerce platform has grown strongly due to the speedy advancement of information technology and the Internet [1,2]. Since 2019, the global epidemic has also accelerated the process of online-ization of brick-and-mortar retail enterprises. The growth rate of the e-commerce business share of some brick-and-mortar companies is significant in 2020. Department stores with mainly optional consumption, as well as Best Buy’s online share have increased significantly. The United Nations Conference on Trade and Development (UNCTAD) reports that e-commerce is growing dramatically globally in 2020, which increases online retail’s share of all retail from 16% in 2019 to 19%. According to Statista, by 2021, more than 2.14 billion people worldwide purchased products and services online [3,4,5]. A recent report by the China Internet Network Information Center shows that by the end of 2021, there are 842 million online shoppers in China, accounting for 81.6% of all Internet users [6]. In 2021, online retail sales reached 13.1 trillion RMB, which was an increase of 14.1% over the previous year. The fast rise of the online retailing business has been fueled by the improvement of customers’ purchasing power and the integration of online shopping habits with mobile and social network shopping. As a key link connecting production and consumption, online and offline, urban and rural, domestic and international, online retailing is playing an active role in building a new development pattern [7,8].

Meanwhile, as a link between manufacturers and consumers, the e-commerce platform not only acts as a retailer that resells manufacturers’ products to consumers but also provides an online marketplace for manufacturers through which the manufacturers can directly sell the products to consumers [9]. The e-commerce platform has held a significant position in the online retailing market. In general, the two roles of the e-commerce platform, retailer and provider of the online marketplace, represent the two types of different business practices. When acting as a retailer, the e-commerce platform purchases products from manufacturers at wholesale prices and then resells them to consumers at retail prices. In contrast, when acting as a provider of the online marketplace, the e-commerce platform allows the manufacturers to determine the retail prices and charges commissions to manufacturers. For example, Amazon sells over 12 million products directly through Amazon.com, and the profits go straight to Amazon. In the meantime, Amazon also allows third-party sellers to sell on its e-commerce platform, Amazon Marketplace [8,10].

Furthermore, in the diversified market, the competition between different brands is increasingly fierce. Existing brands are those that have existed for many years, are widely recognized by consumers, and have strong financial advantages and large market demand [11,12]. For example, Apple and Samsung are widely recognized as existing brands in the mobile phone market. In contrast, new brands are those who enter the market shortly and have not been highly recognized by consumers. These brands face many risks and challenges in entering the market, such as high capital investment and low market demand in the early stage, but the new brands are bound to grab the existing market share of the existing brands [13]. For example, Xiaomi is a new brand that has just launched in recent years. According to Canalys, Xiaomi maintains third place in the global ranking by mobile phone shipments in Q2 2022, with a 13.8% market share. In recent years, as new brands continue to evolve and retailers continue to seek ways to differentiate and foster customer loyalty, new brand products have gradually become an important choice for customers and have taken a prominent place on the shelves of many types of retailers [14]. In this case, there is bound to be fierce competition between the existing and new brands.

The above findings inspire this research. Therefore, we consider an online supply chain in which an existing brand manufacturer (brand E) who is wildly recognized by consumers and has a stronger financial advantage, and a new brand manufacturer (brand N) selling differentiated but partially substitutable products through a common platform. The e-commerce platform is either a retailer that resells products from two brand manufacturers to consumers or a provider of an online marketplace that allows manufacturers to sell products directly to consumers. Both manufacturers could either sell wholesale products to the platform at wholesale prices or sell products directly to consumers at retail prices. Under these circumstances, the e-commerce platform faces a trade-off problem among four different business modes, i.e., a pure retailer mode (business mode R), a pure provider of the online marketplace mode (business mode M), a hybrid mode with only providing the marketplace to the new brand manufacturer (business mode HN), and a hybrid mode with only providing the marketplace to the existing brand manufacturer (business mode HE). Different business models affect the online supply chain members’ optimal decisions and profits.

We are seeking answers to the following questions. Under what circumstances could the e-commerce platform be more profitable? Under what circumstances can brand E and brand N’s profits be maximized? Could the e-commerce platform and manufacturers achieve a mutually beneficial situation? Is the competition between two brand manufacturers beneficial to the e-commerce platform?

First, by comparing the equilibrium results of the two brands, we note that the wholesale prices, retail prices and commissions paid to the platform for existing brand products are higher than those for new brand products. In addition, we obtain the counterintuitive results that brand N consistently outperforms brand E in terms of profitability when consumers’ acceptance of the new brand products is low, while brand N always outperforms brand E in terms of profitability when consumers’ acceptance of the new brand products is high.

Second, according to our analysis of various business modes, we find that the e-commerce platform is able to make the most profits when both brand manufacturers sell their products through the marketplace provided by the e-commerce platform. For two brand manufacturers, regardless of which business modes they are in, they earn higher profits when choosing the reselling mode.

Finally, we analyze the strategic selection between the two brand manufacturers. Specifically, when brand E chooses to sell products to the platform, brand N also prefers the same mode. Only when the production cost and consumers’ acceptance of the new brand products are all high, brand N decides to sell products through the online marketplace. When brand E sells products directly to consumers through the marketplace, brand N still prefers to sell the products to the platform. Only when the production cost and the consumers’ acceptance of the new brand products are relatively low, brand N may sell the products through the marketplace. Moreover, competition among brand manufacturers is beneficial to the e-commerce platform. The e-commerce platform is willing to cultivate new brands to compete with existing brands.

This research makes several innovations in the following respects. First, we consider the strategic interactions between two different upstream brand manufacturers and an e-commerce platform in four different business modes. Second, in the online marketplace business mode, we internalize commission fees, which enriches the previous related literature. Third, different from the conventional research studies of competition between national brand and store brand, we study the competition between existing brand and new brand, and we find the condition of how a new brand enters the market more smoothly. These several innovations not only enrich and develop the existing relevant literature but also draw conclusions that play an important guiding role for both the e-commerce platform and brand manufacturers’ decisions. The e-commerce platform and brand manufacturers are able to make pricing and mode selection decisions more scientifically under the theoretical guidance to maximize profits and also be more conducive to the sustainable development of the supply chain.

The remainder of this paper is organized as follows. The relevant literature is reviewed in Section 2. The model is described in Section 3. In Section 4, we analyze the equilibrium results of the model. Section 5 compares the equilibrium results of the e-commerce platform and manufacturers under four different business modes. In Section 6, we explore the impacts of the main parameters on the equilibrium results. Finally, in Section 7, we summarize the paper’s main results as well as future study directions. All proofs are presented in Appendix A.

2. Literature Review

In our paper, we investigate the game decisions between two horizontally different but substitutable brand manufacturers under four different business modes and the strategic interactions between two brand manufacturers and an e-commerce platform, which are widely studied by scholars. In this section, we review the streams of literature related to the research content, which are divided into the following three directions: strategic mode selection, brand competition and platform retailing.

2.1. The Strategic Mode Selection

The strategic mode selection among supply chain numbers is the subject of a wide range of literature, and it aims to reveal the trade-offs between conventional reselling and e-commerce platform marketing. Abhishek et al. (2016) [1] examine when should an e-retailer adopt an agency form to sell products instead of reselling by developing a theoretical model. Wang et al. (2018) [10] investigate that in order to complete existing brick-and-mortar retail channels, a manufacturer is faced with the choice of selling directly through themselves or distributing through a third party. Considering a supply chain that involves two suppliers who sell two substitutable products through a common online intermediary, Tian et al. [9] study the intermediary’s optimal mode selection by considering the interplay of order fulfillment cost and competition intensity in the upstream. In the context of the sharing economy, Li et al. (2020) [15] develop an analytical framework to examine the business model options for original equipment manufacturers. Wei et al. (2020) [16] investigate how suppliers producing complementary products and with different channel roles choose the optimal distribution contract by considering the combined effects of the supplier’s channel role, the e-retailer’s referral fee, the difference in the merchandise to complementarity levels, and the difference in the merchandise to potential demand. Zhang et al. (2021) [6] examine the best options for a manufacturer’s sharing mode by discussing the interaction between a manufacturer and a sharing platform. For the cross-selling supply chain, Li and Ai (2021) [5] build a game–theoretic model to study online retailers’ choices between “two-sided platforms” and “resellers”. Chen et al. (2022) [17] explore the selection of sales options when an e-commerce platform contracts with a manufacturer using a wholesale sales scheme or an agency sales scheme by considering consumer fairness. By considering a supply chain consisting of a manufacturer and a platform, Wang et al. (2020) [18] investigate the interaction between the manufacturer’s offline service effort strategy and the platform’s online sales model.

This stream of literature is concerned with the strategic choice of several modes. For retailers, there is a trade-off between choosing to adopt an agent form or to be a reseller, and the question of which mode should be chosen to maximize profits is examined under what circumstances. For manufacturers, there is a choice between selling their products directly to consumers or selling them through a third party. In addition, previous studies have considered several different sales models with mixed strategies, but there is still room for further research.

Different from previous studies, our paper contributes to this research stream in the following three ways. First of all, we explicitly consider the competition of two upstream brand manufacturers when determining the e-commerce platform’s optimal strategies. In addition, we consider four different business modes in which two brand manufacturers sell their products in the same or different ways through the e-commerce platform. Second, in reality, some platforms function as both retailers and providers of the online marketplace. This motivates us to consider these hybrid configuration modes in our paper for the manufacturers of both brands and the platform. Third, we consider the choice of equilibrium modes in the interaction between manufacturers and platforms and internalize the manufacturers’ commission fees in the online marketplace business mode.

2.2. The Brand Competition

The competition between different brands has received extensive attention from scholars at home and abroad recently. Luo et al. (2017) [19] investigate a supply chain in which retailers are supplied with differentiated brands by two manufacturers, a good brand and a generic brand, and develop a multi-stage game model to examine the impact of different power structures on the pricing decisions and profits of manufacturers and retailers. Li and Chen (2018) [11] examine pricing and quality competition in a supply chain through a game-theoretic model in which two manufacturers offer a quality-differentiated brand of products, a high-quality brand and a low-quality brand, to a common retailer. Yang et al. (2018) [20] investigate a dual-channel supply chain competition, where one national brand manufacturer has both online and retail channels and the store brand manufacturer has only retail channels and derive the conditions under which the supply chain members would like to participate in cooperative advertising. Wang et al. (2020) [21] examine the pricing strategies of competing dual-channel retailers through a Stackelberg game that considers a market with two competing retailers who sell two horizontally differentiated products. Zhou et al. (2020) [22] examine the impact of online recommendation on brand market management by developing a game model with no recommendation and with recommendation, and they explore the spillover conditions from national brand to store brand market. Furthermore, they discuss the effects of recommendation systems and pricing strategies on the competition between store brands and national brands and consumers’ search behavior, and they analyze the equilibrium strategies under uniform and differential pricing strategies. When a manufacturer contemplates launching an internet channel to sell its own national brand products, Wang et al. (2021) [23] consider the manufacturer’s channel strategy, whereas a brick-and-mortar retailer sells lower-quality national brand and own store brand products. Zhang et al. (2021) [24] use game theory to analyze the competition between manufacturer encroachment and the launch of a premium store brand or a store brand by retailers. Amrouche et al. (2022) [13] investigate the strategic value of combining mail-in rebates and brand coordination strategies in the context of a supply chain consisting of national brand manufacturers and traditional retailers.

In summary, the previous stream of literature on brand competition has focused on the competition between national brand and store brand, and the competition between two brands with quality differences such as high-quality products and low-quality products. Moreover, this literature has mostly studied the pricing issues between two brand manufacturers, and usually, the brands are selling their products through retailers. In addition, many scholars have previously studied the issue of manufacturer encroachment, which is also an issue of concern in brand competition.

Our paper extends this literature into two different directions as follows. First, different from previous studies, we consider competition between existing brands and new brands, which is a relatively novel concern. Second, this study not only examines pricing but also discusses the game situation when two brand manufacturers sell products through a platform under four different business modes.

2.3. Platform Retailing

Relying on the development of the Internet and big data, e-commerce is booming and research on platform retailing has attracted a lot of attention. Motivated by the Chinese consumer appliance market, Shen et al. (2019) [8] analyze how a manufacturer should engage with a platform retailer and a traditional distributor by examining a supply chain consisting of a manufacturer, a platform retailer, and a traditional distributor. Lin et al. (2020) [25] study the pricing and product bundling strategies of two platforms in a competitive setting. With two-sided network effects, Feng et al. (2020) [2] develop a two-stage game theoretic model to study a platform’s decision on the choice of high- and low-end product combinations and its pricing strategy. He et al. (2021) [7] present an analytical model for a retailer to implement offline store and omnichannel strategies (store shipping options) through the e-commerce platform’s self-run store, and they study the impact of this strategy on retailer and platform pricing decisions. Guo et al. (2021) [3] study the optimal bundling strategy for a retail platform through which two independent suppliers distribute their products by analyzing a two-stage Starkelburg game. Xu and He (2021) [26] develop an analytical model to study a retail platform that sells products to consumers and actively discloses product quality information using blockchain technology, and they explore the impact of disclosure strategies on pricing and consumers’ choice on the retail platform. Ha et al. (2022) [4] study the erosion and information-sharing decisions in the supply chain of manufacturers selling through online retail platforms by developing a game–theoretic model. The literature on platform retailing focuses on the strategic interactions between manufacturers, retailers and e-commerce platforms [27,28]. The choice of traditional retailing method and platform retailing method by retailers or platforms has always been a hot topic of research. In addition, theoretical studies on two-sided markets, such as network externality, two-sided network effects and strategic pricing, have also been widely studied in the field of platform retailing.

Based on previous related literature studies, we further investigate the decision making of the e-commerce platform under four different business modes as well as the strategic interactions between the two brand manufacturers and e-commerce platform, which leads to more diverse research related to platform retailing.

3. Model Description

We consider an online supply chain in which an existing brand manufacturer (brand E) who has a stronger financial advantage and a new brand manufacturer (brand N) sell differentiated but partially substitutable products through an e-commerce platform. The e-commerce platform can act as a retailer that resells two brand manufacturers’ products or a provider of the online marketplace that allows manufacturers to sell products directly. The two brands either manufacture wholesale products to the platform at prices $w_e$ and $w_n$, respectively, or sell products directly on the e-commerce platform at retail prices $p_e$ and $p_n$, respectively. In addition, brand E and brand N incur a production cost of $c_e$ and $c_n$, respectively. We assume $c_e=c_n=c$. Under these circumstances, the e-commerce platform faces a trade-off problem of business mode selection. Different business modes affect the online supply chain members’ optimal decisions and profits. The following are the four different business mode options that are evaluated and shown in Figure 1:

Retailer Business Mode R: The e-commerce platform acts as a reseller for both brand manufacturers. Two brand manufacturers sell their products at wholesale prices ($w_e$ and $w_n$) to the platform. The platform resells the products to consumers at retail prices ($p_e$ and $p_n$). For example, JD.com and Amazon’s self-run stores are all in this mode.

Online Marketplace Business Mode M: The e-commerce platform provides an online marketplace for both manufacturers. Two manufacturers sell their own products directly to consumers and pay commissions to the e-commerce platform for each successful sale. For example, Taobao.com is a typical example where a number of merchants open stores and pay commissions to Taobao.com.

Hybrid Business Mode HN: In this business mode, the e-commerce platform works as an online marketplace provider for brand N but as a retailer for brand E.

Hybrid Business Mode HE: In this business mode, the e-commerce platform works as an online marketplace provider for brand E but as a retailer for brand N.

Consumers are heterogeneous in the valuation of existing brand products and new brand products. We assume that the products’ customer evaluation v is uniformly distributed over [0, 1] within the market size (number of customers) from 0 to 1, which catches the individual difference in product valuation. Normally, compared with new brand products, consumers learn more about existing brand products and have a higher degree of trust. Therefore, we assume that the parameter $\theta \in (0,1)$ indicates the customer’s acceptance of the new products due to greater knowledge of the existing products. A consumer whose valuation is v may buy existing brand products if $v-p_e\ge 0$ and may choose new brand products if $\theta v-p_n\ge 0$. If $v-p_e>\theta v-p_n$, the customer chooses existing brand products instead of new brand products. Then, we indicate the indifferent values in whether the customer purchases or not the products as $v_e=p_e$, $v_n=\frac{p_n}{\theta }$, respectively. The indifferent value of which brand products to purchase is $v_{\mathrm{en}}=\frac{p_e-p_n}{1-\theta }$. Then, two scenarios should be considered:

(1) If $v_e>v_n(p_e>\frac{p_n}{\theta })$, we derive that $v_{\mathrm{en}}>v_e(\frac{p_e-p_n}{1-\theta }>p_e)$. Here, $v_n<v_e<v_{\mathrm{en}}<1$, namely, $\frac{p_n}{p_e}<\theta <1-p_e+p_n$; this implies that the customer whose product evaluation v is at $\left[v_{\mathrm{en}},1\right]$ purchases existing brand products while they purchase new brand products if v is at $\left[v_n,v_{\mathrm{en}}\right]$. The customer whose reservation price v is at $\left[0,v_n\right]$ purchases neither. Therefore, the demands for existing brand products and for new brand product are $D_e={\int }_{v_{\mathrm{en}}}^{1}1dv=1-v_{\mathrm{en}}=1-\frac{p_e-p_n}{1-\theta }$ and $D_n={\int }_{v_n}^{v_{\mathrm{en}}}1dv=v_{\mathrm{en}}-v_n=\frac{p_e-p_n}{1-\theta }-\frac{p_n}{\theta }$.

When $v_n<v_e<1\le v_{\mathrm{en}}(\theta \ge -p_e+p_n+1)$, no consumer purchases the existing brand products, and consumers whose product valuation v is at $\left[v_n,1\right]$ only purchase the new brand products. Therefore, the demands of existing brand products and new brand products are $D_e=0$ and $D_n={\int }_{v_n}^{1}1dv=1-v_n=1-\frac{p_n}{\theta }$.

(2) If $v_e\le v_n(p_e\le \frac{p_n}{\theta })$, $v_{\mathrm{en}}\le v_e$, then we have $v_{\mathrm{en}}\le v_e\le v_n<1(\theta \le \frac{p_n}{p_e})$. This implies that no customer purchases new brand products and customers only chooses existing brand products if v is at $\left[v_e,1\right]$. Therefore, the demands of existing brand products and new brand products are $D_e={\int }_{v_e}^{1}1dv=1-v_e=1-p_e$ and $D_n=0$.

In summary, the demand functions of existing brand and new brand products can be written as follows,

$$D_e=\left\{\begin{array}{cc}1-p_e,\hfill & \mathrm{if}0<\theta ⩽\frac{p_n}{p_e}\hfill \\ 1-\frac{p_e-p_n}{1-\theta },\hfill & \mathrm{if}\frac{p_n}{p_e}<\theta <1-p_e+p_n\hfill \\ 0,\hfill & \mathrm{if}1-p_e+p_n⩽\theta <1.\hfill \end{array}\right.$$

(1)

$$D_n=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}0<\theta ⩽\frac{p_n}{p_e}\hfill \\ \frac{p_e-p_n}{1-\theta }-\frac{p_n}{\theta },\hfill & \mathrm{if}\frac{p_n}{p_e}<\theta <1-p_e+p_n\hfill \\ 1-\frac{p_n}{\theta },\hfill & \mathrm{if}1-p_e+p_n⩽\theta <1.\hfill \end{array}\right.$$

(2)

There is complete information within the channel for two brand manufacturers and the e-commerce platform. This piecewise demand function enables us to intuitively comprehend how products’ retail prices and consumers’ preference for new brand products influence product demand. In addition, both the brand manufacturers and the e-commerce platform are risk-neutral and self-interested profit-maximizers.

4. Equilibrium Analysis

4.1. Retailer Mode

We first consider the retailer business mode. Under this setting, the platform acts as a retailer for both brand manufacturers. First, two brand manufacturers offer wholesale prices $w_e$ and $w_n$ to the e-commerce platform, and then, the e-commerce platform sets retail prices $p_e$ and $p_n$ for the consumers. The profits for the two brand manufacturers and the e-commerce platform are as follows:

$$\begin{array}{c}{\pi }_e=(w_e-c)D_e,\hfill \end{array}$$

(3)

$$\begin{array}{c}{\pi }_n=(w_n-c)D_n,\hfill \end{array}$$

(4)

$$\begin{array}{c}{\pi }_p=(p_e-w_e)D_e+(p_n-w_n)D_n.\hfill \end{array}$$

(5)

Backward induction is used to solve this game. In business mode R, the e-commerce platform and two brand manufacturers’ optimal prices and profits are given as follows, $w_n^R=\frac{(2+\theta )c+\theta -{\theta }^2}{4-\theta }$, $w_e^R=\frac{3c+2-2\theta }{4-\theta }$, $p_n^R=\frac{(2+\theta )c+5\theta -2{\theta }^2}{2(4-\theta )}$, $p_e^R=\frac{3c+6-3\theta }{2(4-\theta )}$, ${\pi }_n^R=\frac{(1-\theta ){(2c-\theta )}^2}{2\theta {(4-\theta )}^2}$, ${\pi }_e^R=\frac{(1-\theta ){(c-2)}^2}{2{(4-\theta )}^2}$, ${\pi }_p^R=\frac{(5\theta +4)c^2-(2{\theta }^2+16\theta )c+5{\theta }^2+4\theta }{4\theta {(4-\theta )}^2}$.

4.2. Online Marketplace Mode

Under this circumstance, the e-commerce platform serves as an online marketplace provider for two brand manufacturers. Firstly, the e-commerce platform sets the commissions $T_e$ and $T_n$, and then, the two brand manufacturers determine the retail prices $p_e$ and $p_n$. Hence, the profits for each brand manufacturer and the e-commerce platform under this business mode are as follows:

$$\begin{array}{c}{\pi }_e=(p_e-c-T_e)D_e,\hfill \end{array}$$

(6)

$$\begin{array}{c}{\pi }_n=(p_n-c-T_n)D_n,\hfill \end{array}$$

(7)

$$\begin{array}{c}{\pi }_p=T_e{D}_e+T_n{D}_n.\hfill \end{array}$$

(8)

In business mode M, the e-commerce platform and two brand manufacturers’ optimal prices and profits are given as follows, $T_n^M=\frac{\theta }{2}-\frac{c}{2}$, $T_e^M=\frac{1}{2}-\frac{c}{2}$, $p_n^M=\frac{(2+\theta )c+5\theta -2{\theta }^2}{2(4-\theta )}$, $p_e^M=\frac{3c+6-3\theta }{2(4-\theta )}$, ${\pi }_n^M=\frac{(1-\theta ){(2c-\theta )}^2}{4\theta {(4-\theta )}^2}$, ${\pi }_e^M=\frac{(1-\theta ){(c-2)}^2}{4{(4-\theta )}^2}$, ${\pi }_p^M=\frac{(\theta +2)c^2-6\theta c+{\theta }^2+2\theta }{4\theta (4-\theta )}$. Then, we compare the wholesale prices for two brand products in business mode R, the commissions paid by the two brand manufacturers to the platform in business mode M, and the retail prices and profits of two brand products under two business modes.

Proposition 1. 

(1) In business mode R, the existing brand products’ wholesale price is higher than that of new brand products, $w_n^R<w_e^R$; in business mode M, the commission charged by the e-commerce platform to brand E is higher than that of brand N, $T_n^M<T_e^M$; (2) In business mode R and M, existing brand products’ retail prices are higher than that of new brand products, $p_n^R<p_e^R$; $p_n^M<p_e^M$; (3) If $0<\theta <c^2$, ${\pi }_n^R>{\pi }_e^R$ and ${\pi }_n^M>{\pi }_e^M$, otherwise ${\pi }_n^R<{\pi }_e^R$ and ${\pi }_n^M<{\pi }_e^M$.

The above propositions show that in business mode R, the existing brand products’ wholesale price is higher than that of new brand products. In business mode M, the e-commerce platform charges brand E a higher commission than brand N. Furthermore, in both business modes, the final market prices for the existing brand products are higher than that for the new brand products. These results are not a surprise given that the existing brand products are more widely recognized than new brand products. To compete for the market with brand E, brand N has to reduce the wholesale price in business mode R to create a competitive advantage. Similarly, in business mode M, the preferential commission offered by the e-commerce platform to brand N is conducive to giving brand N’s relatively low market power. Therefore, the retail price of new brand products is always lower than that of existing brand products.

This is because when new brand products first enter the market, although consumers’ acceptance of the new brand products is low, brand N can gain more market share and therefore higher profits due to the lower retail prices of the new brand products. This result can provide a managerial implication for firms that it is easier for new brands to enter the market with the advantage of low prices. For example, when entering the Chinese market, Dell relies on a low-price strategy to capture more market share. However, as brand N gains more market share, brand E has to cut retail prices to compete with brand N, so brand E benefits more when consumers are more receptive to the new brand products.

4.3. Hybrid Mode with Platform Offering New Brand Marketplace

In this setting, the e-commerce platform acts as an online marketplace provider for brand N and a retailer for brand E. Brand N accepts a commission fee from the e-commerce platform, and brand E chooses to sell to the e-commerce platform. Therefore, the sequences of decisions are different for the two brands. For brand N, the e-commerce platform first determines the commission $T_n$. Then, brand N decides the retail price of new brand products $p_n$. On the other supply chain, brand E first decides the wholesale price of existing brand products $w_e$. Then, the retail price of existing brand products $p_e$ is determined by the e-commerce platform. The profits for the two brand manufacturers and the e-commerce platform are as follows:

$$\begin{array}{c}{\pi }_e=(w_e-c)D_e,\hfill \end{array}$$

(9)

$$\begin{array}{c}{\pi }_n=(p_n-c-T_n)D_n,\hfill \end{array}$$

(10)

$$\begin{array}{c}{\pi }_p=(p_e-w_e)D_e+T_n{D}_n.\hfill \end{array}$$

(11)

In hybrid business mode HN, the e-commerce platform and the manufacturers’ optimal prices and profits are given as follows, $T_n^{HN}=\frac{-(\theta -2)((7\theta -16)c-9{\theta }^2+18\theta )}{2(6{\theta }^2-29\theta +32)}$, $w_e^{HN}=\frac{(5{\theta }^2-24\theta +28)c-3{\theta }^3+16{\theta }^2-29\theta +16}{6{\theta }^2-29\theta +32}$,

$p_n^{HN}=\frac{({\theta }^2-8\theta +16)c-42{\theta }^2+42\theta +9{\theta }^3}{2(6{\theta }^2-29\theta +32)}$, $p_e^{HN}=\frac{(2{\theta }^2-13\theta +20)c+12{\theta }^2-51\theta +48}{2(6{\theta }^2-29\theta +32)}$,

${\pi }_n^{HN}=\frac{(1-\theta )(2-\theta ){(2\theta c-8c+3\theta )}^2}{2\theta {(6{\theta }^2-29\theta +32)}^2}$,

${\pi }_e^{HN}=\frac{(1-\theta ){(\theta c-4c+3{\theta }^2-13\theta +16)}^2}{2{(6{\theta }^2-29\theta +32)}^2}$,

${\pi }_p^{HN}=\frac{({\theta }^2-8\theta +16)c^2+(-6{\theta }^3+32{\theta }^2-44\theta )c+3{\theta }^4-13{\theta }^3+11{\theta }^2+8\theta }{4\theta (6{\theta }^2-29\theta +32)}$.

4.4. Hybrid Mode with Platform Offering Existing Brand Marketplace

In this setting, the e-commerce platform acts as an online marketplace provider for brand E and a retailer for brand N. The sequences of decisions are different for the two brands. For brand E, the e-commerce platform first determines the commission $T_e$. Then, brand E decides the retail price of existing brand products $p_e$. On the other supply chain, brand N first decides the wholesale price of new brand products $w_n$. Then, the retail price of new brand products $p_n$ is determined by the e-commerce platform. The profits for the two brand manufacturers and the e-commerce platform are as follows:

$$\begin{array}{c}{\pi }_e=(p_e-c-T_e)D_e,\hfill \end{array}$$

(12)

$$\begin{array}{c}{\pi }_n=(w_n-c)D_n,\hfill \end{array}$$

(13)

$$\begin{array}{c}{\pi }_p=T_e{D}_e+(p_n-w_n)D_n.\hfill \end{array}$$

(14)

In hybrid business mode HE, the e-commerce platform and the manufacturers’ optimal prices and profits are given as follows, $T_e^{HE}=\frac{(2-\theta )\left(\right(9\theta -18)c+16-7\theta )}{2(6{\theta }^2-29\theta +32)}$,

$w_n^{HE}=\frac{(3{\theta }^3-10{\theta }^2+16)c+{\theta }^3-5{\theta }^2+4\theta }{6{\theta }^2-29\theta +32}$, $p_n^{HE}=\frac{(16-7\theta )c+10{\theta }^3-45{\theta }^2+44\theta }{2(6{\theta }^2-29\theta +32)}$,

$p_e^{HE}=\frac{(3{\theta }^2-16\theta +22)c+11{\theta }^2-50\theta +48}{2(6{\theta }^2-29\theta +32)}$, ${\pi }_n^{HE}=\frac{(1-\theta ){((3{\theta }^2-13\theta +16)c+{\theta }^2-4\theta )}^2}{2\theta {(6{\theta }^2-29\theta +32)}^2}$,

${\pi }_e^{HE}=\frac{(1-\theta )(2-\theta ){(3c+2\theta -8)}^2}{2{(6{\theta }^2-29\theta +32)}^2}$,

${\pi }_p^{HE}=\frac{(3{\theta }^3-13{\theta }^2+11\theta +8)c^2+(-6{\theta }^3+32{\theta }^2-44\theta )c+{\theta }^3-8{\theta }^2+16\theta }{4\theta (6{\theta }^2-29\theta +32)}$.

Then, we compare retail prices of existing brand and new brand product and the profits of two manufacturers under two business modes.

Proposition 2. 

(1) In hybrid business modes HN and HE, existing brand products’ retail prices are higher than that of new brand products, $p_n^{HN}<p_e^{HN}$; $p_n^{HE}<p_e^{HE}$; (2) If $g_1(c,\theta )>0$, ${\pi }_n^{HN}>{\pi }_e^{HN}$, otherwise, ${\pi }_n^{HN}<{\pi }_e^{HN}$. Similarly, if $g_2(c,\theta )>0$, ${\pi }_n^{HE}>{\pi }_e^{HE}$, otherwise, ${\pi }_n^{HE}<{\pi }_e^{HE}$, where $g_1(c,\theta )=\frac{(2-\theta ){(2c(\theta -4)+3\theta )}^2}{\theta }-{(c(\theta -4)+\theta (3\theta -13)+16)}^2$, $g_2(c,\theta )=\left((\theta -2){(3c+2\theta -8)}^2\right)+\frac{{(c(\theta (3\theta -13)+16)+(\theta -4)\theta )}^2}{\theta }$.

Proposition 2 indicates that in both business modes HN and HE, the existing brand products’ retail prices are always higher than the retail prices of the new brand products. This is similar to what we have found in previous modes. Moreover, for both business modes, which brand is more profitable is jointly determined by the production cost c and consumers’ acceptance of the new brand products $\theta$. As shown in Figure 2, when the production cost is low, or brand N is not well recognized, brand E is always more profitable. When the production cost is becoming higher, the profits of the two brand manufacturers are closely related to $\theta$. Specifically, when $\theta$ is small, brand N is more profitable than brand E; otherwise, brand N is less profitable than brand E.

When the production costs are low and therefore the retail prices are low, the difference between the two retail prices are small. Therefore, for a given $\theta$, the indifference value is always in a small range. Thus, consumers are more likely to choose existing brand products when the costs are lower. Similarly, when the production costs are high and therefore the retail prices are high, the difference between the two retail prices are large. When $\theta$ is small, although consumers’ acceptance of the new brand products is low, consumers are more likely to choose the new brand products because the prices of the new brand product is much lower than the existing brand products. When $\theta$ is large, brand E reduces retail prices to attract more consumers, thus gaining more market share and more profits.

5. Strategic Mode Choice

In the previous section, we compare the equilibrium outcomes for the e-commerce platform and two brand manufacturers under four different business modes. In this section, we evaluate the strategic interactions between the e-commerce platform and manufacturers.

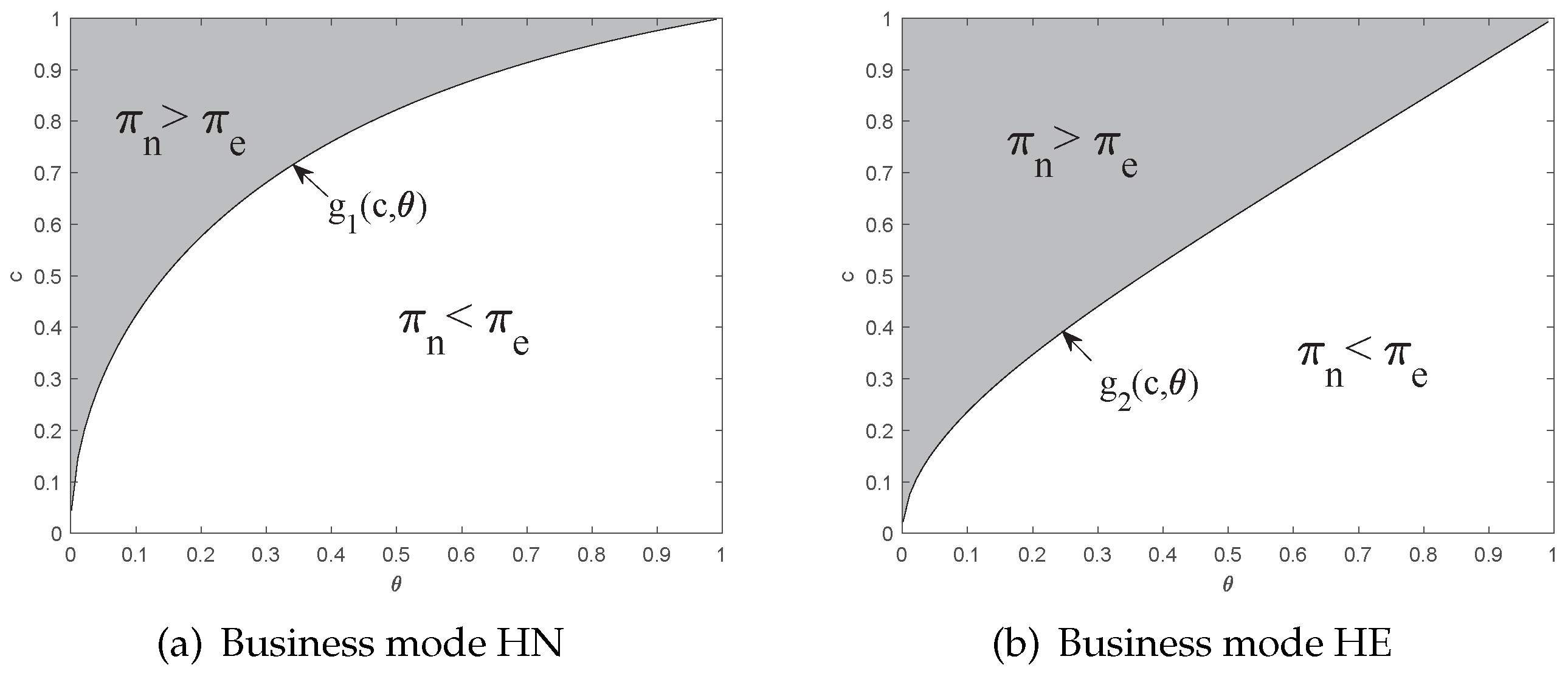
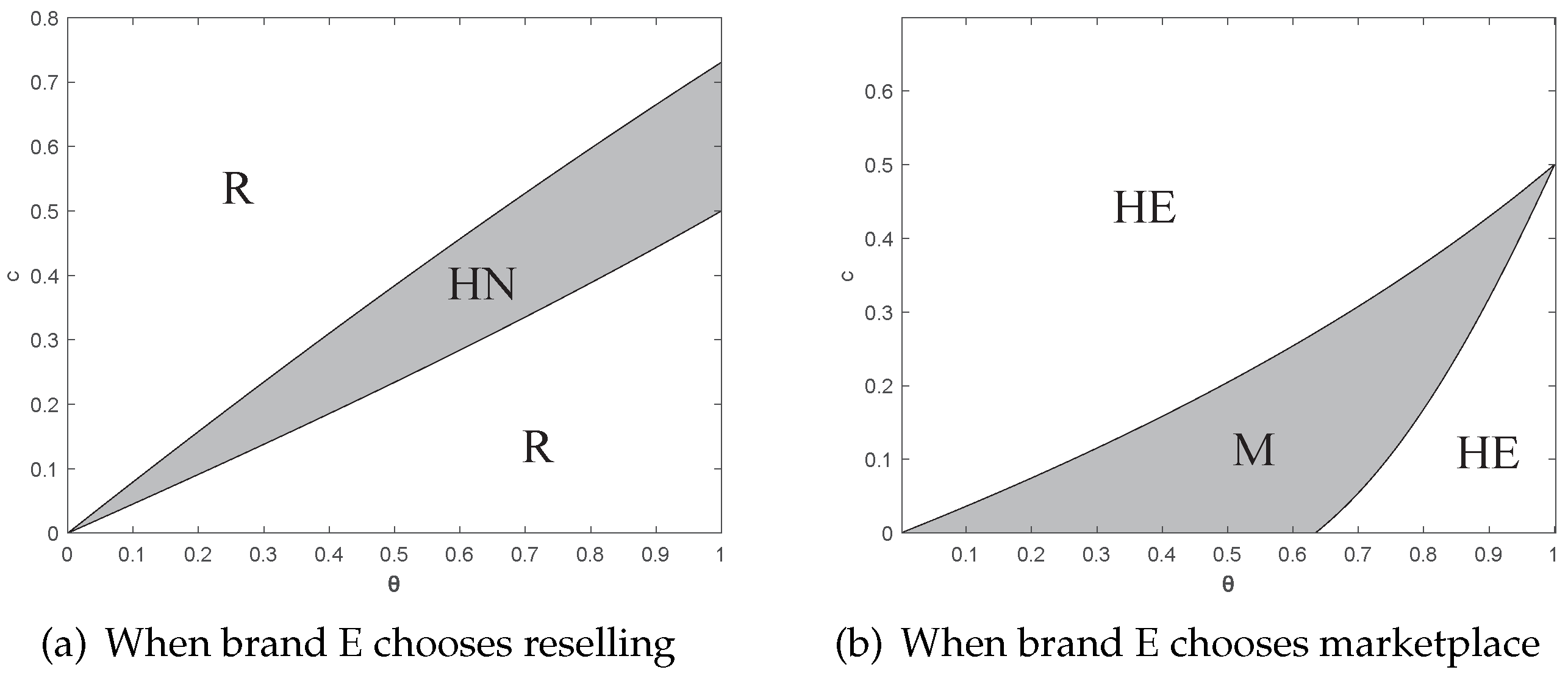
5.1. Comparison of Business Modes

In this section, we compare the business modes between the e-commerce platform and two manufacturers.

Proposition 3. 

(1) Under business modes R and M, the same brand products’ retail prices are the same, i.e., $p_n^R=p_n^M$, $p_e^R=p_e^M$; (2) In business modes R and M, the brand manufacturers prefer to resell products, that is ${\pi }_n^R=2{\pi }_n^M$, ${\pi }_e^R=2{\pi }_e^M$; the e-commerce platform prefers to act as an online marketplace, that is ${\pi }_p^R<{\pi }_p^M$.

As shown in the above proposition, the retail prices of the same brand products sold in modes R and M are the same. Comparing business modes R and M, we find that the brand manufacturers prefer to sell the products to the e-commerce platform instead of directly selling to consumers. However, the e-commerce platform is more likely to provide a marketplace for brand manufacturers than act as a retailer for both brands.

For brand manufacturers, when selling products to the e-commerce platform, the brand manufacturers have first mover’s advantage and determine the wholesale prices first, and the e-commerce platform responds by setting higher retail prices accordingly. For the e-commerce platform, when providing a marketplace to the brand manufacturers, the e-commerce platform has the first mover’s advantage and sets the commissions first, and then, the brand manufacturers set the retail prices based on the commissions. From this point of view, both brand manufacturers and the e-commerce platform prefer to be the leader of the game.

Proposition 4. 

(1) In hybrid business modes, the commissions and wholesale prices for existing brand products are higher than those for new brand products, $T_n^{HN}<T_e^{HE}$; $w_n^{HE}<w_e^{HN}$;

(2) The two brand products’ retail prices in business mode HE are higher than those in mode HN, $p_n^{HN}<p_n^{HE}$; $p_e^{HN}<p_e^{HE}$;

(3) Both brand manufacturers benefit more by reselling way, that is ${\pi }_n^{HN}<{\pi }_n^{HE}$; ${\pi }_e^{HN}>{\pi }_e^{HE}$; while for the e-commerce platform, if $0<\theta <c^2$, ${\pi }_p^{HN}>{\pi }_p^{HE}$, otherwise, ${\pi }_p^{HN}<{\pi }_p^{HE}$.

Comparing the hybrid modes HN and HE, the e-commerce platform charges higher commissions to brand E in mode HE than that to brand N in mode HN, and the wholesale price of existing brand products in mode HN is higher than that of new brand products in mode HE. This finding is in line with the findings in previous sections. Moreover, we find that the retail prices of both brand products in mode HE are higher than the retail prices in mode HN. Furthermore, in the hybrid modes, both brand manufacturers can make higher profits when they are the one who sells to the platform instead of directly selling to the consumers. This finding echoes our finding in Proposition 2, for the same reasons discussed in the previous proposition. In addition, if $\theta$ is small, the e-commerce platform gains more profits in mode HN than in mode HE. Otherwise, it makes more profits in mode HE than in mode HN. According to the previous propositions, it can be seen that the e-commerce platform benefits more when it provides a marketplace. In other words, the e-commerce platform makes profits mainly through commissions. When new brand products first enter the market, although the e-commerce platform charges a low commission to brand N, there is a large demand for new brand products due to the low price advantage. Therefore, the e-commerce platform charges more commissions and obtains more profits in mode HN than in mode HE when $\theta$ is small. As $\theta$ increases, brand E can capture more customers due to price reduction. As a result, the e-commerce platform charges more commissions from brand E when $\theta$ is small; then, the profits from mode HN is less than that from mode HE.

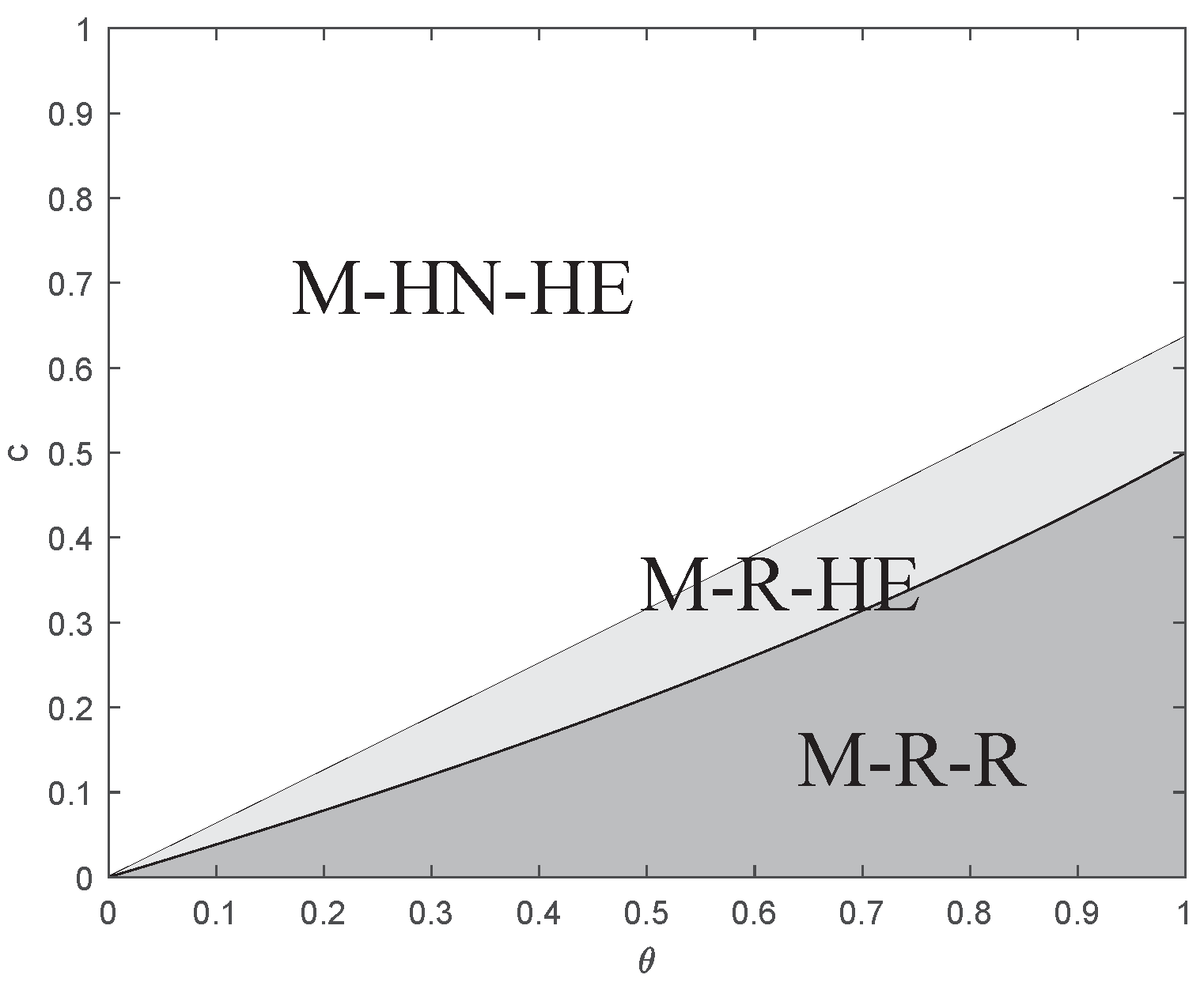
5.2. Strategy Selection

In this subsection, we analyze the strategic choices between two brand manufacturers.

Proposition 5. 

(1) There exists a threshold ${\theta }_1$, if $0<\theta <{\theta }_1$, $p_n^R>p_n^{HN}$; otherwise, $p_n^R<p_n^{HN}$; (2) If $g_3(c,\theta )>0$, ${\pi }_n^R>{\pi }_n^{HN}$; otherwise, ${\pi }_n^R<{\pi }_n^{HN}$, where $g_3(c,\theta )=\frac{{(\theta -2c)}^2}{{(\theta -4)}^2}+\frac{(\theta -2){(2c(\theta -4)+3\theta )}^2}{{(\theta (6\theta -29)+32)}^2}$.

The above proposition indicates that when consumers’ acceptance of new brand products is low, the retail price of brand N in mode R is higher than that in mode HN; otherwise, the retail price in mode HN is higher than that in mode R. The results provide management implications for manufacturers and platforms that when manufacturers and e-commerce platforms price new brand products, considering different sales methods, if consumers’ acceptance of new brand products is low, then the retail price for reselling should be higher, and conversely, the retail price should be higher for sales through marketplace.

It is seen from Figure 3a that when brand E chooses the retailer mode, brand N also prefers to sell the products to the e-commerce platform in general. However, brand N chooses to sell products through the platform’s marketplace only when the production cost c and consumers’ acceptance of the new brand products $\theta$ are all high. When selling the products to the e-commerce platform, brand N has the first mover’s advantage to enter the market more smoothly. As the production cost and consumers’ acceptance of new brand products increase, brand N’s profitability increases and it becomes more competitive to sell products directly to consumers through the marketplace.

Proposition 6. 

(1) There exists a threshold ${\theta }_2$, if $0<\theta <{\theta }_2$, $p_n^M>p_n^{HE}$, otherwise, $p_n^M<p_n^{HE}$; (2) If $g_4(c,\theta )>0$, ${\pi }_n^M>{\pi }_n^{HE}$, otherwise, ${\pi }_n^M<{\pi }_n^{HE}$, where $g_4(c,\theta )=\frac{{(\theta -2c)}^2}{{(\theta -4)}^2}-\frac{2{(c(\theta (3\theta -13)+16)+(\theta -4)\theta )}^2}{{(\theta (6\theta -29)+32)}^2}$.

Proposition 6 suggests that when consumers’ acceptance of new brand products is low, brand N prices the products higher in mode M compared to mode HE. Otherwise, it prices the products higher in mode HE than in mode M. Which mode is more profitable to brand N is jointedly determined by the production costs c and consumers’ acceptance of new brand products $\theta$.

As shown in Figure 3b, when brand E sells products directly to consumers through the marketplace, brand N still prefers to sell products by the reselling way in general. However, brand N may choose to sell products directly to consumers through the marketplace only when the production cost c and the consumers’ acceptance of the new brand products $\theta$ is relatively low. As we discussed before, by reselling, brand N has a first mover’s advantage and enters the market more smoothly. When the production cost and consumers’ acceptance of new brand products are low, the new brand products attract more demand due to the advantage of low retail prices. At this time, brand N chooses to sell products directly to consumers through the marketplace, which can gain a competitive advantage by having a more comprehensive understanding of consumer needs.

Proposition 7. 

For the e-commerce platform, mode M is the optimal mode selection, while for two brand manufacturers, the optimal selection is to sell products by the reselling way regardless of the mode.

By comparing four different business modes, we investigate the optimal mode selection of two brand manufacturers and the e-commerce platform. As shown in the Figure 4, we note that “M-HN-HE”, “M-R-HE” and “M-R-R” represent the areas of optimal mode selection combinations for the e-commerce platform and two brand manufacturers. For example, “M-R-R” means that the e-commerce platform is better off in mode M, while the two brand manufacturers are better off in mode R. Furthermore, there is no win–win situation for the e-commerce platform and two brand manufacturers. Only when the production cost is small, the two brand manufacturers can achieve a mutually beneficial situation. For the e-commerce platform, mode M is the optimal mode selection. As discussed in the previous propositions, this is the result of the influence of first mover’s advantage on the mode selection of the e-commerce platform and brand manufacturers.

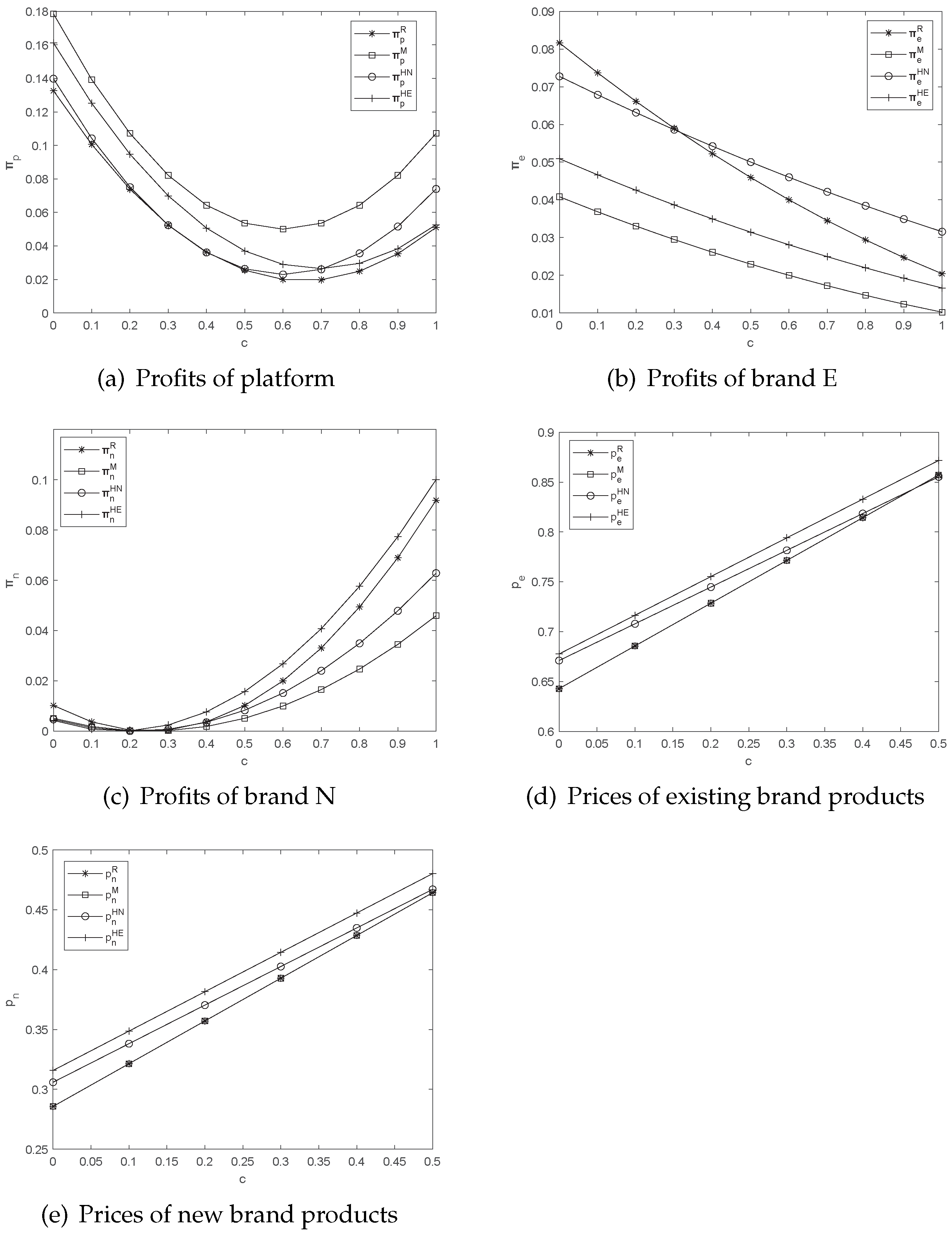
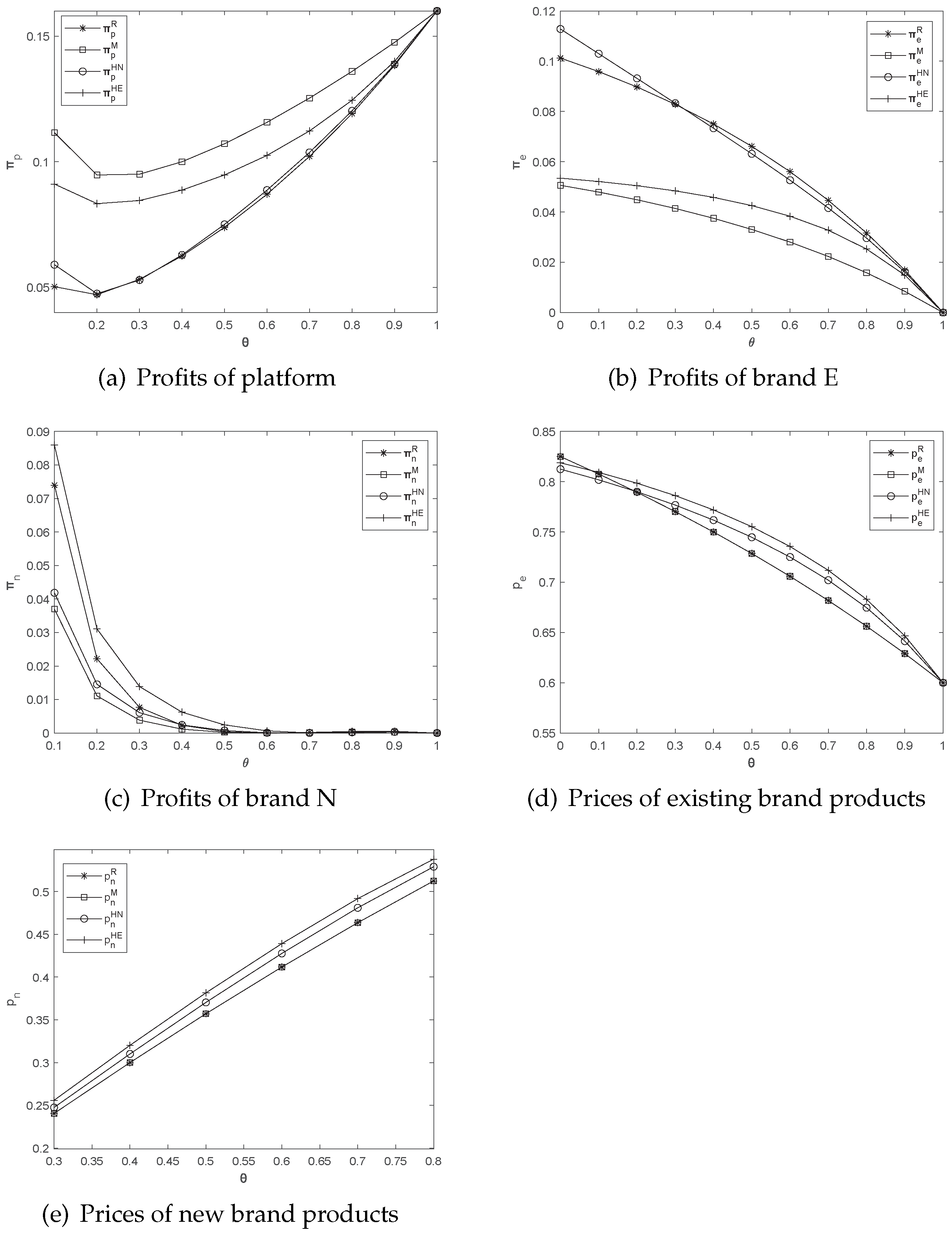
6. Sensitivity Analysis

In the previous section, we have compared the equilibrium outcomes of the four different business modes. In this section, we explore the effects of two important parameters, product production cost c and consumers’ acceptance of new brand products $\theta$ on the equilibrium retail prices and profits and shown in Figure 5 and Figure 6.

6.1. The Impact of Production Cost c

First, we study the impact of production cost c on wholesale prices, commissions, and retail prices, specifically, in four business modes, the wholesale and retail prices of both existing brand products and new brand products increase as production cost increases, while commissions decrease as production cost increases.

Obviously, when the production cost increases, brand manufacturers have to raise the wholesale prices to maintain the profits, and the retail prices increase accordingly. As production cost increases, if the e-commerce platform still charges the same or even higher commissions to brand manufacturers, the brand manufacturers have to give up selling their products through the e-commerce platform due to the high costs; therefore, the e-commerce platform reduces the commissions charged to brand manufacturers as production cost increases.

Corollary 1. 

${\pi }_e^R$, ${\pi }_e^M$, ${\pi }_e^{HN}$, ${\pi }_e^{HE}$ are decreasing in c; if $0<c<\frac{\theta }{2}$, ${\pi }_n^R$ is decreasing in c, otherwise ${\pi }_n^R$ is increasing in c; if $0<c<\frac{\theta }{2}$, ${\pi }_n^M$ is decreasing in c, otherwise, ${\pi }_n^M$ is increasing in c; if $0<c<\frac{3\theta }{8-2\theta }$, ${\pi }_n^{HN}$ is decreasing in c, otherwise, ${\pi }_n^{HN}$ is increasing in c; if $0<c<\frac{\theta (4-\theta )}{3{\theta }^2-13\theta +16}$, ${\pi }_n^{HE}$ is decreasing in c, otherwise, ${\pi }_n^{HE}$ is increasing in c.

The above corollary shows that under the four business modes, brand E’s profit always decreases as production cost c increases, while brand N’s profits are not so. Specifically, when the production cost is small, brand N’s profit decreases as the production cost c increases, and when the production cost is large, brand N’s profit increases as the production cost increases. For brand E, the increase in production cost makes the retail price of the existing brand products increase, and the high retail prices make consumers buy less of them. As a result, the demand for existing brand products decreases, resulting in a decrease in brand E’s profits. For brand N, when the production cost is small, the product input is low and the quality of the products is low. In this case, the increase in production cost leads to an increase in retail prices, and consumers cannot buy good quality products at high prices; as a result, there is less demand for new brand products and consequently less profits for brand N. When the production cost is large, the product is of good quality because of more production inputs. In this case, as the production cost increases, the retail prices increase, but consumers’ demand for new brand products is not significantly reduced by the increase in retail prices. Therefore, the profit of brand N increases subsequently.

Corollary 2. 

If $0<c<\frac{{\theta }^2+8\theta }{5\theta +4}$, ${\pi }_p^R$ is decreasing in c; otherwise, ${\pi }_p^R$ is increasing in c. If $0<c<\frac{6\theta }{2\theta +4}$, ${\pi }_p^M$ is decreasing in c, otherwise, ${\pi }_p^M$ is increasing in c. If $0<c<\frac{2\theta (3{\theta }^2-16\theta +22)}{2{(\theta -4)}^2}$, ${\pi }_p^{HN}$ is decreasing in c, otherwise, ${\pi }_p^{HN}$ is increasing in c. If $0<c<\frac{\theta (3{\theta }^2-16\theta +22)}{3{\theta }^3-13{\theta }^2+11\theta +8}$, ${\pi }_p^{HE}$ is decreasing in c; otherwise, ${\pi }_p^{HE}$ is increasing in c.

Corollary 2 states that under four business modes, when the production cost is small, the profit of the e-commerce platform decreases as the production cost increases. When the production cost is large, the profit of the e-commerce platform increases with the increase of the production cost. The e-commerce platform’s profit is mainly related to the consumers’ demand for the two brand products. Specifically, when the production cost is small, the product quality of both brand products is low. At this time, as the production cost increases, the retail prices increase, while the demand for the products decreases due to the increase in the retail prices. Therefore, the profit of the e-commerce platform decreases as the production cost increases. When the production cost is large, the quality of both brand products is improved, and the product quality further increases with the increase of production cost. Furthermore, the demand of products increases due to consumers’ pursuit of high-quality products. Therefore, the e-commerce platform’s profit increases as the production cost increases.

6.2. The Impact of Consumers’ Acceptance of New Brand $\theta$

In this subsection, we examine the effect of consumers’ acceptance of new brand on the equilibrium results of retail prices and profits.

Corollary 3. 

(1) The existing brand products’ wholesale prices $w_e^R$, $w_e^{HN}$, retail prices $p_e^R$, $p_e^M$, $p_e^{HN}$, and $p_e^{HE}$ are decreasing in θ, while new brand products’ wholesale prices $w_n^{HE}$, retail prices $p_n^R$, $p_n^M$, $p_n^{HN}$, and $p_n^{HE}$ are increasing in θ, and the exception is that only when θ is large enough, $w_n^R$ is increasing in θ. (2) $T_n^M$, $T_n^{HN}$ and $T_e^{HE}$ are increasing in θ, while $T_e^M$ is not related to θ.

The above corollary indicates that the wholesale and retail prices of existing brand products decrease as $\theta$ increases, while the wholesale and retail prices of new brand products increase as $\theta$ increases. As the customers’ acceptance of new brand products increases, more consumers choose new brand products; thus, brand E has to reduce existing brand products’ wholesale prices and retail prices to gain a competitive advantage. As for brand N, although the consumers’ acceptance of new brand products increases, brand N can only maintain profits by increasing new brand products’ wholesale prices and retail prices due to brand E reducing prices to gain a large demand. In addition, the range of $\theta$ has an impact on the wholesale price of new brand products under business mode R.

In addition, we find that the commission charged by the e-commerce platform to both brand manufacturers increases with $\theta$, but the commission may also be independent of $\theta$. For brand N, when consumers’ acceptance of new brand products is low, the e-commerce platform provides discounts to help new brand products enter the market better; thus, the commission charged is low. As acceptance increases, the profitability of brand N increases and the e-commerce platform needs to increase commissions to make profits. In addition, there are many factors affecting the commission, and $\theta$ may have a limited impact on it, so the decision should be made after comprehensive consideration.

Corollary 4. 

In four business modes, the profits of the two brand manufacturers are decreasing in θ; that is, brand E’s profits ${\pi }_e^R$, ${\pi }_e^M$, ${\pi }_e^{HN}$, ${\pi }_e^{HE}$ are decreasing in θ, and brand N’s profits ${\pi }_n^R$, ${\pi }_n^M$, ${\pi }_n^{HN}$, ${\pi }_n^{HE}$ are decreasing in θ.

Regardless of the business modes, the profits of both brand manufacturers decrease as $\theta$ increases. For brand E, as consumers’ acceptance of new brand products increases, brand E has to reduce prices to attract consumers. Although there is a large demand, it is not enough to offset the losses caused by lowering prices. For brand N, although consumers’ acceptance of new brand products increases, consumers are more likely to buy existing brand products due to the price reduction. As a result, brand N has to raise prices to maintain profits, but the price increase is not enough to compensate for the loss caused by the decrease in demand.

Corollary 5. 

If θ is small enough, the e-commerce platform’s profits are decreasing in θ; otherwise, the e-commerce platform’s profits are increasing in θ.

When $\theta$ is small, consumers’ acceptance of new brand products is low, and the market is almost monopolized by existing brand products at this time, which is harmful to the e-commerce platform, so the e-commerce platform’s profit decreases. When $\theta$ is large, consumers’ acceptance of new brand products is high and competition between new brand products and existing brand products is fierce, which is beneficial to the development of e-commerce platforms. As a result, competition among brand manufacturers is beneficial to e-commerce platforms, which increases profits by introducing new brands to compete with existing brands, and it also promotes the sustainable development of the whole supply chain.

7. Conclusions and Discussion

7.1. Conclusions

Online retailing through an e-commerce platform has grown rapidly in recent years, with the e-commerce platform playing an integral role as a link between upstream manufacturers and end consumers. The e-commerce platform not only provides an online marketplace for manufacturers but also acts as a retailer to resell manufacturers’ products to consumers. Thus, the two roles of the e-commerce platform also represent two choices of sales methods when the e-commerce platform provides services to manufacturers.

In recent years, the competition between different brands is increasingly fierce. The entry of a new brand is bound to impact the main position of the existing brand; thus, the competition between different brands is a valuable research question. Therefore, we also pay attention to the competition between the two brands. In this paper, we study the strategic interaction between an e-commerce platform and two manufacturers of different brands in four different types of business modes. Our key analysis findings and insights are summarized below.

First, when we compare the equilibrium results of the two brands, we find that the wholesale prices, retail prices, and platform commissions for existing brand products are higher than for new brand products. Furthermore, regardless of business modes, when consumers’ acceptance of the new brand products is low, brand N makes more profits than brand E, whereas brand E is more profitable than brand N when consumers’ acceptance of the new brand product is high.

Second, we discover that when both brand manufacturers decide to directly sell their products through the marketplace offered by the e-commerce platform, the e-commerce platform is able to gain the maximum profit out of all the alternative business modes. Regardless of the business modes they pick, two brand manufacturers are able to earn higher profits by choosing to sell their products to the e-commerce platform.

Finally, we analyze the strategic selection between the two brand manufacturers. Specifically, when brand E decides to sell to the e-commerce platform, brand N also prefers the same mode. When brand E chooses to sell the product directly to consumers through the marketplace provided by the e-commerce platform, brand N’s decision is determined by the joint action of the production cost c and consumers’ acceptance of new brand products $\theta$. Brand N is expected to sell products through the e-commerce platform’s marketplace once c and $\theta$ are both at a sufficient level. In the alternative, brand N may choose to sell the products through the marketplace. Additionally, the e-commerce platform benefits from brand manufacturers competing with one another. To compete with existing brands, the e-commerce platform is eager to cultivate new brands, which is also beneficial for the sustainability of the supply chain.

7.2. Discussion

This section compares the results obtained with similar previous research and with our paper’s opinion on the differences.

On the one hand, this paper investigates the strategic mode choice problem by exploring four different business modes, and we find different optimal modes for two brand manufacturers and the e-commerce platform, these different modes of reseller and marketplace are similar to those in the literature [9]. However, they are different from studying the intermediary’s strategic selections in different pure and hybrid modes; here, we make several innovations. First, we consider the problem of choosing four different business modes for the e-commerce platform, including two pure and two hybrid modes, and we find that the two brand manufacturers prefer to sell their products to the e-commerce platform, while the e-commerce platform prefers to let the two brand manufacturers sell their products directly to consumers through the marketplace. Second, we also consider the competition between the two upstream brand manufacturers. Third, in this paper, we internalize the manufacturers’ commission fees in the online marketplace business mode, which is also an innovation to the related literature.

On the other hand, this paper explores the competition problem between existing brands and new brands with respect to brand competition. In this regard, our paper mainly refers to certain studies [11,19,21]. Different from the mentioned studies, we make innovations in the following aspects. First, unlike the previous studies that analyze the competition between national brands and store brands, we study the game problem between existing brands and new brands that exist for different times under four different business modes. Second, not only do we consider the pricing problem between the two brands, but we also study the choice of sales modes between the two brand manufacturers, whether they sell directly to the e-commerce platform or to consumers, which makes the literature on brand competition more diverse.

7.3. Management Insights

This study establishes a theoretical foundation for the mode selection of the e-commerce platform and manufacturers. The research has a favorable impact on the growth of online retailing business modes. We summarize key management insights below. First of all, the research finds that the competition of multiple brand manufacturers improves efficiency, and the e-commerce platform also benefits from the competition. Therefore, the e-commerce platform improves the entire supply chain’s efficiency and benefits from the introduction of multiple brand manufacturers. In addition, the existence of multiple brand manufacturers also improves the supply chain’s ability to deal with risks. Second, the research finds that for the platform, providing manufacturers with an online marketplace is an optimal choice, while it is optimal to resell products for brand manufacturers. Therefore, the research results provide a theoretical basis for both platforms and brand manufacturers to provide and choose sales methods. Third, for manufacturers, selling products directly to the e-commerce platform enables higher profits compared to selling products to consumers through the e-commerce platform, so manufacturers should choose suitable sales mothods based on the relevant theoretical research and pay close attention to competitors’ decisions to make immediate adjustments to make themself more competitive and gain more profit.

7.4. Future Research Directions

At the end of this paper, we discuss certain limitations of our model as well as potential future research topics. To begin, in order to make the model easier to understand, we assume that existing brand products and new brand products have the same unit production cost, but in practice, the two product brands’ production costs are different. Hence, it can be expanded in future research, considering the changes in pricing and profit on the basis of different production costs of two brand products. Second, nowadays, all industries are promoting the concept of green development, and the research on the green supply chain is becoming more and more extensive. The supply chain model of the low-carbon cycle is a key direction for future research; therefore, adding the parameters related to the green supply chain in the basic model can also be an extended idea for the article.