Down with the #Dogefather: Evidence of a Cryptocurrency Responding in Real Time to a Crypto-Tastemaker
Abstract
:1. Introduction
2. Dogecoin
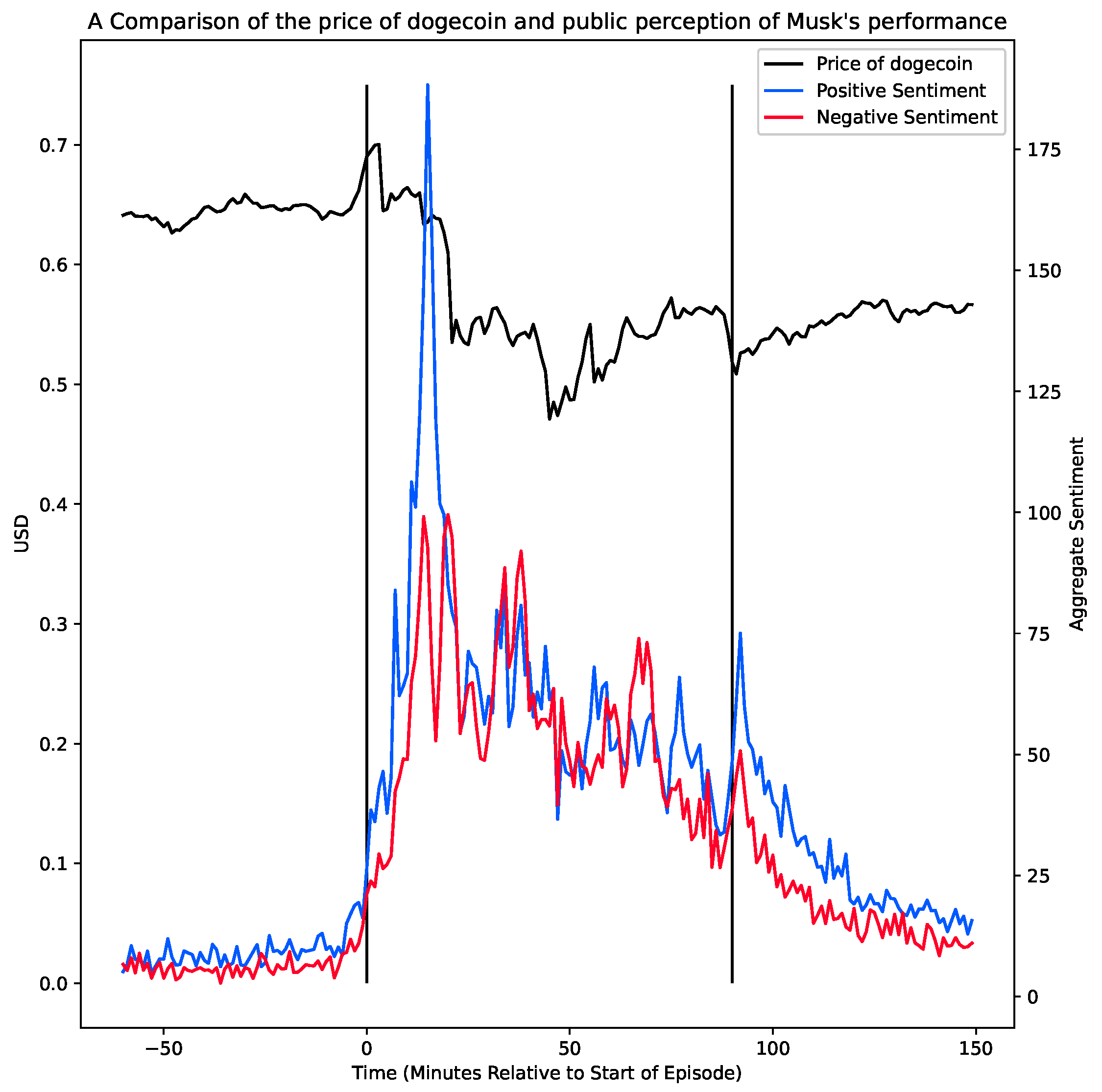
3. Data and Methodology
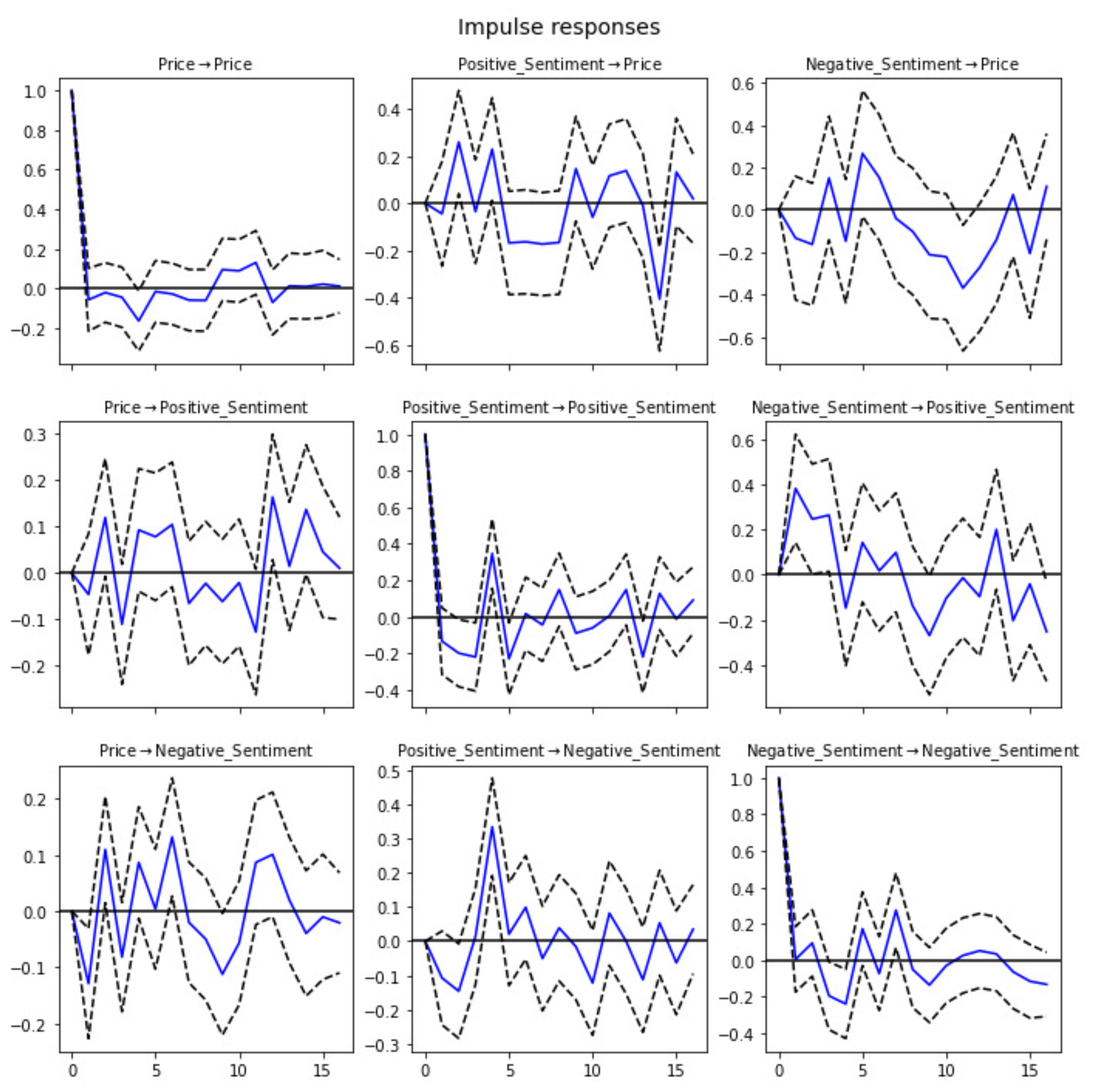
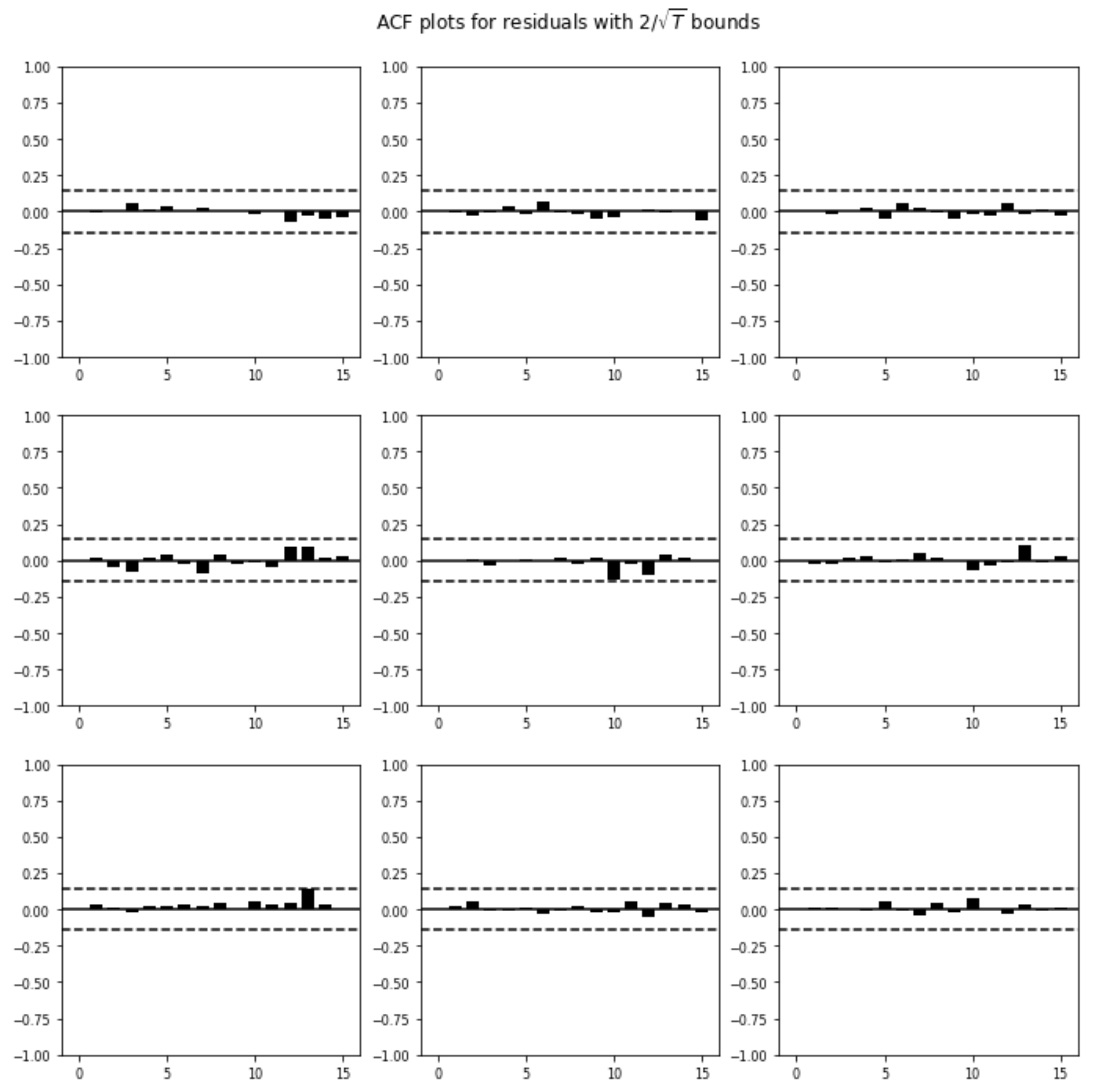
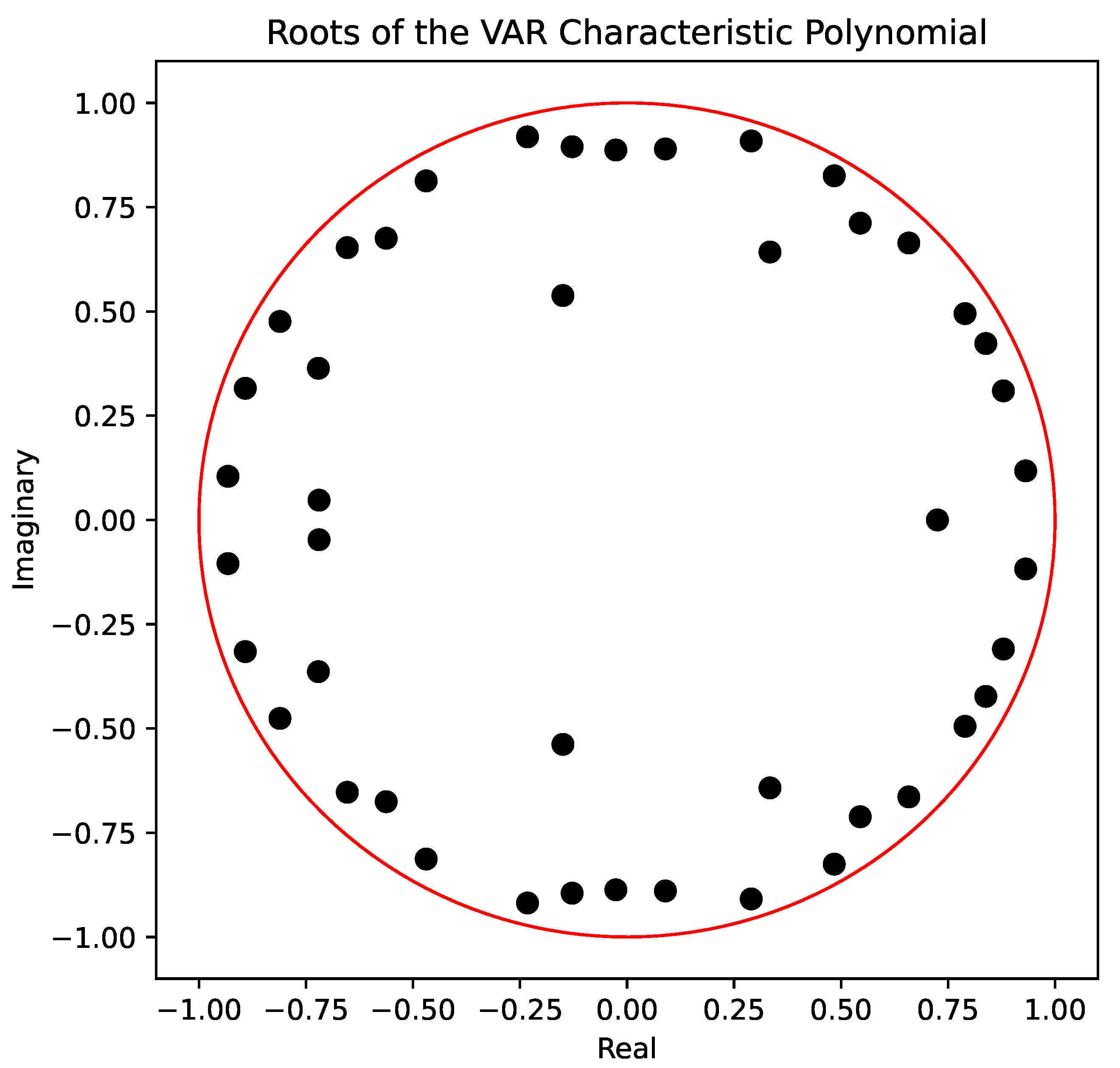
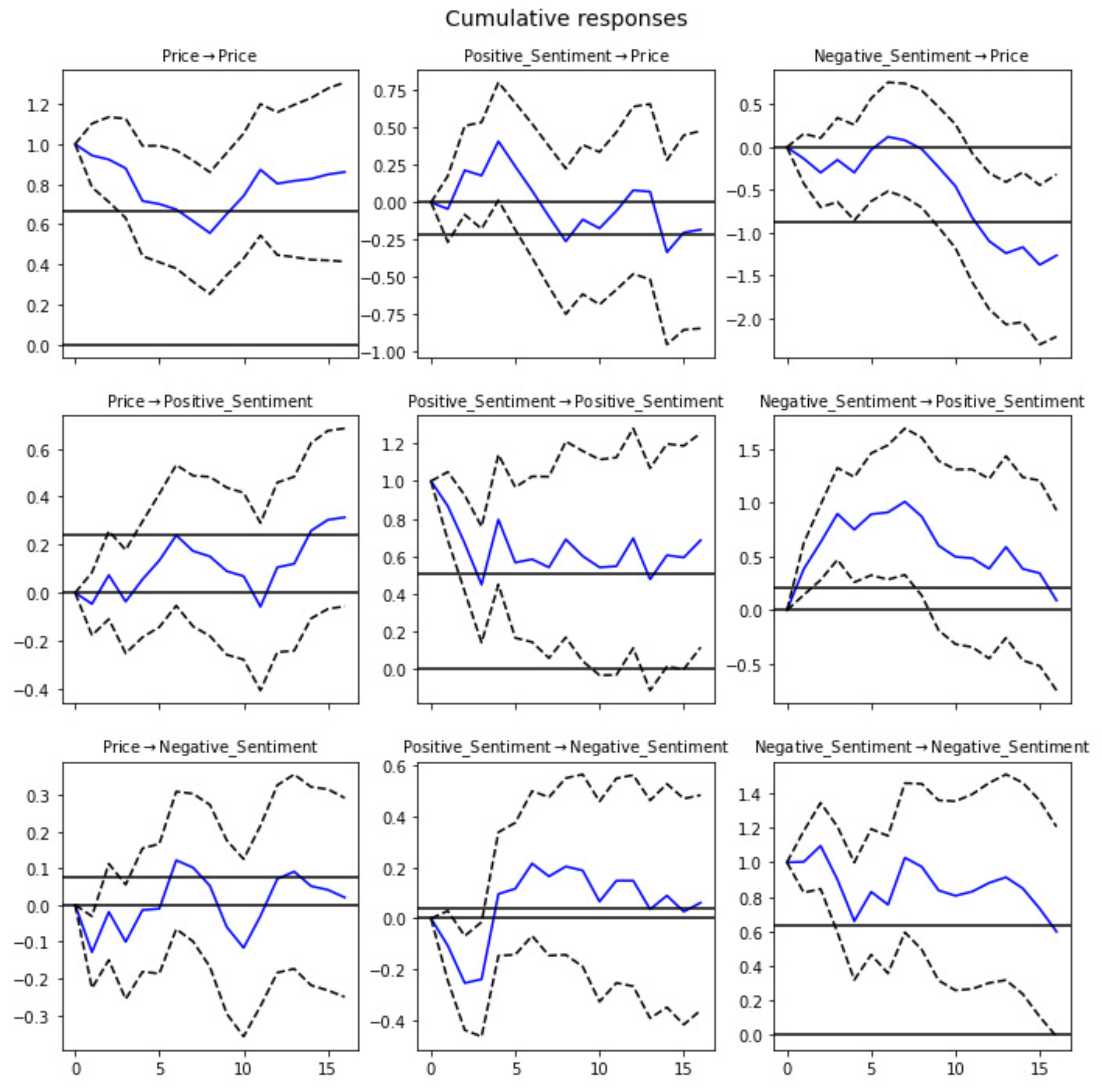
4. Results and Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. VAR Results
| Variable | Coefficient | Std. Err. | t-Stat | p |
|---|---|---|---|---|
| Constant | −0.0003 | 0.0007 | −0.4481 | 0.6541 |
| L1 Price | −0.0565 | 0.0811 | −0.6970 | 0.4858 |
| L1 Positive Sentiment | −0.0444 | 0.1131 | −0.3924 | 0.6947 |
| L1 Negative Sentiment | −0.1338 | 0.1489 | −0.8985 | 0.3689 |
| L2 Price | −0.0426 | 0.0767 | −0.5554 | 0.5787 |
| L2 Positive Sentiment | 0.2365 | 0.1108 | 2.1341 | 0.0328 |
| L2 Negative Sentiment | −0.1537 | 0.1534 | −1.0018 | 0.3165 |
| L3 Price | −0.0364 | 0.0783 | −0.4652 | 0.6418 |
| L3 Positive Sentiment | −0.0358 | 0.1132 | −0.3164 | 0.7517 |
| L3 Negative Sentiment | 0.0680 | 0.1548 | 0.4395 | 0.6603 |
| L4 Price | −0.1887 | 0.0786 | −2.3993 | 0.0164 |
| L4 Positive Sentiment | 0.2558 | 0.1109 | 2.3064 | 0.0211 |
| L4 Negative Sentiment | −0.1971 | 0.1614 | −1.2208 | 0.2221 |
| L5 Price | −0.0250 | 0.080 | −0.3131 | 0.7542 |
| L5 Positive Sentiment | −0.0253 | 0.1160 | −0.2181 | 0.8273 |
| L5 Negative Sentiment | 0.0061 | 0.1637 | 0.0375 | 0.9701 |
| L6 Price | −0.0542 | 0.0753 | −0.7191 | 0.4721 |
| L6 Positive Sentiment | −0.1438 | 0.1207 | −1.1918 | 0.2334 |
| L6 Negative Sentiment | 0.1467 | 0.1614 | 0.9093 | 0.3632 |
| L7 Price | −0.0498 | 0.0778 | −0.6396 | 0.5224 |
| L7 Positive Sentiment | −0.0709 | 0.1213 | −0.5844 | 0.5590 |
| L7 Negative Sentiment | −0.0612 | 0.1615 | −0.3789 | 0.7047 |
| L8 Price | −0.1269 | 0.0761 | −1.6678 | 0.0954 |
| L8 Positive Sentiment | −0.1935 | 0.1207 | −1.6028 | 0.1090 |
| L8 Negative Sentiment | −0.0623 | 0.1615 | −0.3859 | 0.6996 |
| L9 Price | 0.0476 | 0.0766 | 0.6217 | 0.5341 |
| L9 Positive Sentiment | 0.0915 | 0.1214 | 0.7537 | 0.4510 |
| L9 Negative Sentiment | −0.0143 | 0.1597 | −0.0897 | 0.9285 |
| L10 Price | 0.0742 | 0.0785 | 0.9449 | 0.3447 |
| L10 Positive Sentiment | −0.1283 | 0.1166 | −1.1002 | 0.2712 |
| L10 Negative Sentiment | −0.2174 | 0.1576 | −1.3795 | 0.1678 |
| L11 Price | 0.0761 | 0.0786 | 0.9681 | 0.3330 |
| L11 Positive Sentiment | 0.0118 | 0.1153 | 0.1025 | 0.9183 |
| L11 Negative Sentiment | −0.2561 | 0.1550 | −1.6521 | 0.0985 |
| L12 Price | −0.0401 | 0.0779 | −0.5144 | 0.6069 |
| L12 Positive Sentiment | 0.0812 | 0.1134 | 0.7165 | 0.4737 |
| L12 Negative Sentiment | −0.2535 | 0.1523 | −1.6641 | 0.0961 |
| L13 Price | 0.0825 | 0.0797 | 1.0350 | 0.3007 |
| L13 Positive Sentiment | −0.1346 | 0.1113 | −1.2099 | 0.2263 |
| L13 Negative Sentiment | −0.1352 | 0.1476 | −0.9157 | 0.3598 |
| L14 Price | 0.0305 | 0.0785 | 0.3886 | 0.6976 |
| L14 Positive Sentiment | −0.3995 | 0.1120 | −3.5670 | 0.0004 |
| L14 Negative Sentiment | −0.0198 | 0.1447 | −0.1369 | 0.8911 |
| L15 Price | 0.1195 | 0.0793 | 1.5071 | 0.1318 |
| L15 Positive Sentiment | 0.1268 | 0.1178 | 1.0766 | 0.2817 |
| L15 Negative Sentiment | −0.2441 | 0.1429 | −1.7083 | 0.0876 |
| Variable | Coefficient | Std. Err. | t-Stat | p |
|---|---|---|---|---|
| Constant | 0.0002 | 0.0006 | 0.4140 | 0.6789 |
| L1 Price | −0.0462 | 0.0667 | −0.6918 | 0.4891 |
| L1 Positive Sentiment | −0.1333 | 0.0930 | −1.4332 | 0.1518 |
| L1 Negative Sentiment | 0.3832 | 0.1226 | 3.1268 | 0.0018 |
| L2 Price | 0.1605 | 0.0631 | 2.5431 | 0.0110 |
| L2 Positive Sentiment | −0.1773 | 0.0912 | −1.9441 | 0.0519 |
| L2 Negative Sentiment | 0.2909 | 0.1262 | 2.3052 | 0.0212 |
| L3 Price | −0.0991 | 0.0644 | −1.5386 | 0.1239 |
| L3 Positive Sentiment | −0.1636 | 0.0932 | −1.7553 | 0.0792 |
| L3 Negative Sentiment | 0.3428 | 0.1274 | 2.6913 | 0.0071 |
| L4 Price | 0.1309 | 0.0647 | 2.0233 | 0.0430 |
| L4 Positive Sentiment | 0.2863 | 0.0913 | 3.1380 | 0.0017 |
| L4 Negative Sentiment | 0.0617 | 0.1328 | 0.4646 | 0.6422 |
| L5 Price | 0.0697 | 0.0658 | 1.0597 | 0.2893 |
| L5 Positive Sentiment | −0.2438 | 0.0954 | −2.5543 | 0.0106 |
| L5 Negative Sentiment | 0.1894 | 0.1347 | 1.4055 | 0.1599 |
| L6 Price | 0.1146 | 0.0620 | 1.8488 | 0.0645 |
| L6 Positive Sentiment | −0.1225 | 0.0993 | −1.2332 | 0.2175 |
| L6 Negative Sentiment | 0.2241 | 0.1328 | 1.6881 | 0.0914 |
| L7 Price | −0.0369 | 0.0640 | −0.5758 | 0.5648 |
| L7 Positive Sentiment | −0.1004 | 0.0998 | −1.0062 | 0.3143 |
| L7 Negative Sentiment | 0.1467 | 0.1329 | 1.1035 | 0.2698 |
| L8 Price | −0.0459 | 0.0626 | −0.7336 | 0.4632 |
| L8 Positive Sentiment | −0.1302 | 0.0993 | −1.3104 | 0.1900 |
| L8 Negative Sentiment | −0.0109 | 0.1329 | −0.0818 | 0.9348 |
| L9 Price | −0.0835 | 0.0630 | −1.3252 | 0.1851 |
| L9 Positive Sentiment | −0.0479 | 0.0999 | −0.4797 | 0.6314 |
| L9 Negative Sentiment | −0.2419 | 0.1314 | −1.8405 | 0.0657 |
| L10 Price | 0.0016 | 0.0646 | 0.0243 | 0.9806 |
| L10 Positive Sentiment | −0.1976 | 0.0960 | −2.0589 | 0.0395 |
| L10 Negative Sentiment | −0.0600 | 0.1297 | −0.4626 | 0.6437 |
| L11 Price | −0.0624 | 0.0647 | −0.9645 | 0.3348 |
| L11 Positive Sentiment | −0.0680 | 0.0949 | −0.7167 | 0.4735 |
| L11 Negative Sentiment | 0.0541 | 0.1275 | 0.4241 | 0.6715 |
| L12 Price | 0.1659 | 0.0641 | 2.5862 | 0.0097 |
| L12 Positive Sentiment | 0.1125 | 0.0933 | 1.2060 | 0.2278 |
| L12 Negative Sentiment | −0.0633 | 0.1253 | −0.5050 | 0.6136 |
| L13 Price | −0.0338 | 0.0656 | −0.5156 | 0.6061 |
| L13 Positive Sentiment | −0.0902 | 0.0916 | −0.9855 | 0.3244 |
| L13 Negative Sentiment | 0.2246 | 0.1215 | 1.8485 | 0.0645 |
| L14 Price | 0.1669 | 0.0646 | 2.5841 | 0.0098 |
| L14 Positive Sentiment | 0.1857 | 0.0921 | 2.0157 | 0.0438 |
| L14 Negative Sentiment | −0.1116 | 0.1191 | −0.9369 | 0.3488 |
| L15 Price | 0.1164 | 0.0653 | 1.7831 | 0.0746 |
| L15 Positive Sentiment | 0.0173 | 0.0969 | 0.1783 | 0.8585 |
| L15 Negative Sentiment | −0.0698 | 0.1176 | −0.5938 | 0.5527 |
| Variable | Coefficient | Std. Err. | t-Stat | p |
|---|---|---|---|---|
| Constant | 0.0001 | 0.0004 | 0.2079 | 0.8353 |
| L1 Price | −0.1288 | 0.0499 | −2.5803 | 0.0099 |
| L1 Positive Sentiment | −0.1070 | 0.0696 | −1.5359 | 0.1246 |
| L1 Negative Sentiment | 0.0033 | 0.0917 | 0.0365 | 0.9709 |
| L2 Price | 0.0980 | 0.0472 | 2.0762 | 0.0379 |
| L2 Positive Sentiment | −0.1651 | 0.0682 | −2.4197 | 0.0155 |
| L2 Negative Sentiment | 0.1167 | 0.0945 | 1.2353 | 0.2167 |
| L3 Price | −0.0589 | 0.0482 | −1.2207 | 0.2222 |
| L3 Positive Sentiment | 0.0219 | 0.0697 | 0.3143 | 0.7533 |
| L3 Negative Sentiment | −0.1159 | 0.0953 | −1.2163 | 0.2239 |
| L4 Price | 0.0611 | 0.0484 | 1.2624 | 0.2068 |
| L4 Positive Sentiment | 0.2521 | 0.0683 | 3.6914 | 0.0002 |
| L4 Negative Sentiment | −0.1634 | 0.0994 | −1.6432 | 0.1003 |
| L5 Price | −0.0091 | 0.0493 | −0.1853 | 0.8530 |
| L5 Positive Sentiment | 0.0732 | 0.0714 | 1.0247 | 0.3055 |
| L5 Negative Sentiment | 0.0968 | 0.1008 | 0.9604 | 0.3368 |
| L6 Price | 0.1543 | 0.0464 | 3.3251 | 0.0009 |
| L6 Positive Sentiment | 0.0828 | 0.0743 | 1.1142 | 0.2652 |
| L6 Negative Sentiment | −0.0941 | 0.0994 | −0.9472 | 0.3435 |
| L7 Price | −0.0023 | 0.0479 | −0.0489 | 0.9610 |
| L7 Positive Sentiment | 0.0496 | 0.0747 | 0.6640 | 0.5067 |
| L7 Negative Sentiment | 0.0919 | 0.0995 | 0.9237 | 0.3557 |
| L8 Price | −0.0279 | 0.0469 | −0.5960 | 0.5512 |
| L8 Positive Sentiment | −0.0365 | 0.0743 | −0.4914 | 0.6232 |
| L8 Negative Sentiment | −0.0170 | 0.0995 | −0.1709 | 0.8643 |
| L9 Price | −0.1617 | 0.0472 | −3.4295 | 0.0006 |
| L9 Positive Sentiment | 0.0526 | 0.0748 | 0.7029 | 0.4821 |
| L9 Negative Sentiment | −0.2434 | 0.0984 | −2.4742 | 0.0134 |
| L10 Price | −0.0501 | 0.0484 | −1.0358 | 0.3003 |
| L10 Positive Sentiment | −0.1080 | 0.0718 | −1.5032 | 0.1328 |
| L10 Negative Sentiment | −0.1346 | 0.0971 | −1.3868 | 0.1655 |
| L11 Price | 0.0459 | 0.0484 | 0.9478 | 0.3432 |
| L11 Positive Sentiment | 0.0101 | 0.0710 | 0.1421 | 0.8870 |
| L11 Negative Sentiment | 0.0189 | 0.0955 | 0.1985 | 0.8427 |
| L12 Price | 0.1147 | 0.0480 | 2.3908 | 0.0168 |
| L12 Positive Sentiment | 0.0729 | 0.0698 | 1.0439 | 0.2965 |
| L12 Negative Sentiment | −0.0868 | 0.0938 | −0.9253 | 0.3548 |
| L13 Price | −0.0609 | 0.0491 | −1.2404 | 0.2148 |
| L13 Positive Sentiment | −0.0424 | 0.0685 | −0.6182 | 0.5365 |
| L13 Negative Sentiment | 0.0477 | 0.0909 | 0.5241 | 0.6002 |
| L14 Price | 0.0462 | 0.0483 | 0.9568 | 0.3387 |
| L14 Positive Sentiment | 0.1419 | 0.0690 | 2.0582 | 0.0396 |
| L14 Negative Sentiment | 0.0179 | 0.0891 | 0.2011 | 0.8406 |
| L15 Price | 0.0871 | 0.0488 | 1.7832 | 0.0745 |
| L15 Positive Sentiment | −0.1290 | 0.0725 | −1.7775 | 0.0755 |
| L15 Negative Sentiment | −0.0307 | 0.0880 | −0.3485 | 0.7275 |
References
- Al Shehhi, A.; Oudah, M.; Aung, Z. Investigating factors behind choosing a cryptocurrency. In Proceedings of the 2014 IEEE International Conference on Industrial Engineering and Engineering Management, Selangor, Malaysia, 9–12 December 2014; pp. 1443–1447. [Google Scholar]
- Bouri, E.; Gupta, R.; Roubaud, D. Herding behaviour in cryptocurrencies. Financ. Res. Lett. 2019, 29, 216–221. [Google Scholar] [CrossRef]
- Ahn, Y.; Kim, D. Emotional trading in the cryptocurrency market. Financ. Res. Lett. 2020, 101912. [Google Scholar] [CrossRef]
- Da Gama Silva, P.V.J.; Klotzle, M.C.; Pinto, A.C.F.; Gomes, L.L. Herding behavior and contagion in the cryptocurrency market. J. Behav. Exp. Financ. 2019, 22, 41–50. [Google Scholar] [CrossRef]
- Vidal-Tomás, D.; Ibáñez, A.M.; Farinós, J.E. Herding in the cryptocurrency market: CSSD and CSAD approaches. Financ. Res. Lett. 2019, 30, 181–186. [Google Scholar] [CrossRef]
- Kallinterakis, V.; Wang, Y. Do investors herd in cryptocurrencies–and why? Res. Int. Bus. Financ. 2019, 50, 240–245. [Google Scholar] [CrossRef]
- Vidal-Tomás, D. Transitions in the cryptocurrency market during the COVID-19 pandemic: A network analysis. Financ. Res. Lett. 2021, 101981. [Google Scholar] [CrossRef]
- Stavroyiannis, S.; Babalos, V. Herding behavior in cryptocurrencies revisited: Novel evidence from a TVP model. J. Behav. Exp. Financ. 2019, 22, 57–63. [Google Scholar] [CrossRef]
- Aggarwal, G.; Patel, V.; Varshney, G.; Oostman, K. Understanding the social factors affecting the cryptocurrency market. arXiv 2019, arXiv:1901.06245. [Google Scholar]
- Huynh, T.L.D. Does Bitcoin React to Trump’s Tweets? J. Behav. Exp. Financ. 2021, 31, 100546. [Google Scholar] [CrossRef]
- Lamon, C.; Nielsen, E.; Redondo, E. Cryptocurrency price prediction using news and social media sentiment. SMU Data Sci. Rev. 2017, 1, 1–22. [Google Scholar]
- Philippas, D.; Rjiba, H.; Guesmi, K.; Goutte, S. Media attention and Bitcoin prices. Financ. Res. Lett. 2019, 30, 37–43. [Google Scholar] [CrossRef]
- Phillips, R.C.; Gorse, D. Predicting cryptocurrency price bubbles using social media data and epidemic modelling. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–7. [Google Scholar]
- Chohan, U.W. A History of Dogecoin. Discussion Series: Notes on the 21st Century. 2017. Available online: https://ssrn.com/abstract=3091219 (accessed on 13 August 2021).
- Young, I. Dogecoin: A Brief Overview & Survey. 2018. Available online: https://ssrn.com/abstract=3306060 (accessed on 13 August 2021).
- Ante, L. How Elon Musk’s Twitter Activity Moves Cryptocurrency Markets. 2021. Available online: https://ssrn.com/abstract=3778844 (accessed on 13 August 2021).
- López, M.; Sicilia, M.; Moyeda-Carabaza, A.A. Creating identification with brand communities on Twitter: The balance between need for affiliation and need for uniqueness. Internet Res. 2017, 27, 21–51. [Google Scholar] [CrossRef]
- Saura, J.R.; Reyes-Menéndez, A.; deMatos, N.; Correia, M.B. Identifying Startups Business Opportunities from UGC on Twitter Chatting: An Exploratory Analysis. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 1929–1944. [Google Scholar] [CrossRef]
- Mohammadi, A.; Hashemi Golpayegani, S.A. SenseTrust: A Sentiment Based Trust Model in Social Network. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 2031–2050. [Google Scholar] [CrossRef]
- Liu, B. Sentiment analysis and subjectivity. Handb. Nat. Lang. Process. 2010, 2, 627–666. [Google Scholar]
- Maiti, M.; Vyklyuk, Y.; Vuković, D. Cryptocurrencies chaotic co-movement forecasting with neural networks. Internet Technol. Lett. 2020, 3, e157. [Google Scholar] [CrossRef]
- Maiti, M.; Grubisic, Z.; Vukovic, D.B. Dissecting Tether’s Nonlinear Dynamics during Covid-19. J. Open Innov. Technol. Mark. Complex. 2020, 6, 161. [Google Scholar] [CrossRef]
- Vukovic, D.; Maiti, M.; Grubisic, Z.; Grigorieva, E.M.; Frömmel, M. COVID-19 Pandemic: Is the Crypto Market a Safe Haven? The Impact of the First Wave. Sustainability 2021, 13, 8578. [Google Scholar] [CrossRef]
- Yue, W.; Zhang, S.; Zhang, Q. Asymmetric news effects on cryptocurrency liquidity: An Event study perspective. Financ. Res. Lett. 2021, 41, 101799. [Google Scholar] [CrossRef]
- Ortu, M.; Uras, N.; Conversano, C.; Destefanis, G.; Bartolucci, S. On Technical Trading and Social Media Indicators in Cryptocurrencies’ Price Classification Through Deep Learning. arXiv 2021, arXiv:2102.08189. [Google Scholar]
- Matta, M.; Lunesu, I.; Marchesi, M. Bitcoin Spread Prediction Using Social and Web Search Media. In Proceedings of the UMAP 2015—23rd Conference on User Modeling, Adaptation and Personalization, Dublin, Ireland, 29 June 2015–3 July 2015; pp. 1–10. [Google Scholar]
- Bartolucci, S.; Destefanis, G.; Ortu, M.; Uras, N.; Marchesi, M.; Tonelli, R. The Butterfly “Affect”: Impact of development practices on cryptocurrency prices. EPJ Data Sci. 2020, 9, 21. [Google Scholar] [CrossRef]
- Mai, F.; Shan, Z.; Bai, Q.; Wang, X.; Chiang, R.H. How does social media impact Bitcoin value? A test of the silent majority hypothesis. J. Manag. Inf. Syst. 2018, 35, 19–52. [Google Scholar] [CrossRef]
- Rognone, L.; Hyde, S.; Zhang, S.S. News sentiment in the cryptocurrency market: An empirical comparison with Forex. Int. Rev. Financ. Anal. 2020, 69, 101462. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, X.; Pan, H.; Jia, J. Cryptocurrency, confirmatory bias and news readability–evidence from the largest Chinese cryptocurrency exchange. Account. Financ. 2019, 58, 1445–1468. [Google Scholar] [CrossRef]
| Time Series | Mean | SD | Min | Max |
|---|---|---|---|---|
| Price of Dogecoin in USD | 0.584 | 0.054 | 0.471 | 0.700 |
| Total Positive Sentiment | 29.67 | 37.58 | 4.79 | 188.35 |
| Total Negative Sentiment | 25.23 | 30.75 | 2.73 | 99.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cary, M. Down with the #Dogefather: Evidence of a Cryptocurrency Responding in Real Time to a Crypto-Tastemaker. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 2230-2240. https://doi.org/10.3390/jtaer16060123
Cary M. Down with the #Dogefather: Evidence of a Cryptocurrency Responding in Real Time to a Crypto-Tastemaker. Journal of Theoretical and Applied Electronic Commerce Research. 2021; 16(6):2230-2240. https://doi.org/10.3390/jtaer16060123
Chicago/Turabian StyleCary, Michael. 2021. "Down with the #Dogefather: Evidence of a Cryptocurrency Responding in Real Time to a Crypto-Tastemaker" Journal of Theoretical and Applied Electronic Commerce Research 16, no. 6: 2230-2240. https://doi.org/10.3390/jtaer16060123
APA StyleCary, M. (2021). Down with the #Dogefather: Evidence of a Cryptocurrency Responding in Real Time to a Crypto-Tastemaker. Journal of Theoretical and Applied Electronic Commerce Research, 16(6), 2230-2240. https://doi.org/10.3390/jtaer16060123






