2.1. Characteristics and Applicability of Decision Support System
The early beginning of Computer Decision Support Systems (DSSs) dates back to the 1970s. Their goal is to improve various fields of people’s lives by supporting decisions with the increasing use of information technology to improve the quality of decisions by recommending solutions [
15]. Decision Support Systems (DSS) were defined by Little in 1970 as computer information systems that help people solve different issues in a semi-structured or unstructured way involving data and judgment [
9,
16]. The modeling strategy is provided by DSS frameworks by integrating knowledge discovery and automated decision-making. In the early 1970s, DSSs were introduced as an innovative kind of tool that combines Data Mining (DM) with artificial decision-making. DSSs are described as an interactive computer-based system or subsystem used to support decision-makers in using communication techniques, data, documents, cognition, and patterns to identify and solve problems, perform decision-making tasks, and make judgments [
17].
Decision support is based on the necessary data collected and processed accordingly. Decision support systems can be based on expert knowledge to support decision-making in a given focus area effectively. A characteristic element of decision support systems is the presence of a mechanism that generates recommendations [
18]. Recommender systems solve the problem of the large amount of information that e-commerce platforms generate. They provide personalized information to improve user satisfaction. Recommender systems are used in many fields, such as e-commerce, health, industry, and e-learning. Generating personalized recommendations in RS can be done automatically using Machine Learning (ML) models, big data, Artificial Neural Network (ANN) models, Deep Neural Networks (DNN) models, Reinforcement Learning (RL), rules, and multi-criteria decision analysis methods (MCDA), and other methods, such as linear regression, decision trees, and logic rules [
19,
20,
21,
22].
More and more advanced algorithms are used to improve the accuracy of RS, such as fuzzy sets and genetic algorithms [
23]. Fuzzy set theory is becoming an increasingly popular approach in problems requiring data representation and user interaction, and information extraction from the user. An example is the Operations Research-based Intelligent Decision Support System (OR-IDSS) [
24]. Systems based on fuzzy rules are soft computing techniques introduced based on a fuzzy set theory proposed by Zadeh [
25]. Fuzzy sets are based on degrees of membership to represent uncertainty. In these techniques, membership functions and fuzzy rules are generated, which build the system’s knowledge base, and, based on it, prediction is possible. The fuzzy rules are discovered from the data provided to the system [
26].
RS are important in e-commerce development by implementing personalized and intelligent services. They provide recommendations based on information extracted from data and placed in a model that allows interactions and models user preferences. As a result, RSs minimize customer search costs and suggest products based on explicit and implicit feedback about customer behavior and preferences [
27]. Recommendation systems increase turnover by offering customized products and services to the client, suggesting additional products, helping to improve customer loyalty [
28]. In e-commerce, recommendation accuracy leads to increased sales and customer loyalty.
Recommender systems depend on consumer feedback and information about their shopping behavior. There are recommender systems that use agents to determine user interests and preferences based on historical transaction data. However, these systems have several problems, such as over-fitting the data of systems based on artificial neural networks and machine learning, and the difficulty of extracting from the available data that would represent human preferences accurately and objectively. Therefore, developing an objective and accurate recommendation system is necessary to provide personalized recommendations in e-commerce [
27].
As it can be noticed, there are many DSSs based on different algorithms, but for an accurate representation of human preferences, an approach based on Multi-Criteria Decision-Making seems to be more important. This approach allows the personalization of recommendations in the form of integrating multiple selected criteria and prioritizing them. In order to implement multi-criteria decision support systems (MCDSS), these systems were supplemented with MCDM tools. The decision-making process requiring aggregation of multiple incommensurable and conflicting dimensions is complex and requires commitment. The technology used in the DSS is supposed to simplify the decision-making process for decision-makers by combining their priorities and using data with models to handle multi-criteria decision-making problems [
29].
The use of MCDM in DSS increases their efficiency [
30]. DSSs consist of three main components: data integration, Data Mining (DM), and MCDM. In the third module, MCDM methods are used to evaluate the currently available alternatives, find the most satisfactory options, and make appropriate reactions in a timely manner [
31]. The performance of MCDM-based DSS requires a defined fixed set of criteria that presents the decision-maker with a clear representation of all available alternatives. The task essentially is to calculate the score of each alternative, thereby creating a ranking and selecting the one that maximizes that value [
32].
2.2. Overview of Various MCDM Methods Applied to Decision-Making Problems
Multi-criteria decision-making (MCDM) is the process by which the most suitable solution is selected from a set of alternatives considering evaluation criteria [
33]. Studies that consider MCDM methods are widely reported in the operations research (OR) literature. MCDM methods are used in solving multi-criteria problems to indicate to decision-makers the best alternative from a set of other options [
8]. The use of algorithms in MCDM models is now a standard in modern approaches to understanding some types of human thinking and decision-making process [
34]. Alternatives and criteria are the two main parameters considered in any multi-criteria problem. MCDM methods aim to provide a ranking of alternatives taking into account the criteria weights. The TOPSIS technique, which involves ranking the results in terms of similarity to the ideal solution, belongs to the methods of comparing and prioritizing alternatives [
35,
36].
MCDM methods are being developed all the time to be able to cope with the challenges that are specific to their domain. One such phenomenon is the rank reversal (RR) paradox. It consists of a change in the ranking of alternatives when an alternative is added or removed from their set. It results in a change in the order of priorities of decision-makers regarding two alternatives and is against the principle of independence of irrelevant alternatives. Research directions to develop methods resistant to the RR phenomenon are evident in the development of methods, such as Ranking of Alternatives through Functional mapping of criterion sub-intervals into a Single Interval (RAFSI) [
37], Stable Preference Ordering Towards Ideal Solution (SPOTIS) [
38], and the Characteristic Objects Method (COMET) [
39]. Other advantages of the COMET method worth noting are the high accuracy and the absence of the requirement for arbitrary weights [
40]. In literature, there are descriptions of studies in the successful application of this method to choose the most advantageous product, for example, electric scooters [
41], electric bikes [
42], and electric-powered cars [
43,
44].
Combined Compromise Solution (COCOSO) is another innovative and relevant MCDM method [
34]. Combined compromise solution (COCOSO) was first introduced initially by Yazdani et al. in 2019 [
45]. This method is among the most recent techniques of MCDM. In its performance, the comparability sequence is used in three ways. This method is effective in dealing with the ranking or selection of alternatives. Furthermore, they are assessed against specific criteria [
46]. It integrates simple additive weighting (SAW), step-wise weight assessment ratio analysis (WASPAS), and Exponentially Weighted Product (EWP) methods. Combining three different aggregation strategies distinguishes COCOSO from other MCDM methods and provides stable and reliable results [
47]. The literature reports a successful application of the COCOSO method in the selection of manufacturing technology [
48], personnel selection [
49], and sustainable supplier selection [
50].
Today, MCDM approaches are extensively applied to elucidate the problems, namely the mobile phone selection problem. However, MCDM problems differ according to the solution status and the approaches’ implementation. In recent literature, many research papers are available in which the solution of the multi-criteria problem of selecting the best mobile phone using MCDM based approach is presented. In the study of Aggarwal et al., the MCDM method called EDAS is used to select the most favorable mobile phone model from some previously selected mobile phones available in the Indian market [
10]. The result obtained from the averaged solution, which reduces the risk of expert bias against the alternative, is the main advantage that distinguishes EDAS from other MCDM methods. Additionally, the result obtained from the average solution already normalizes the data, significantly reducing the chances of deviation from the best solution. It follows that this method gives more reliable and more precise results for real-world multi-criteria problems, such as choosing the best mobile phone, than other well-known MCDM methods, such as TOPSIS or VIKOR.
Mishra et al., in 2021, applied an innovative procedure employing the multi-attribute boundary approximation area comparison (MABAC) to solve the smartphone selection problem [
12]. MABAC has an easy computational process, organized procedure, and an innovative direction that determines the foundation of real-world decision-making problems. Over the past few years, the MABAC approach is used by many scholars in different application areas. Furthermore, the outcomes of the analysis of the results demonstrate that the introduced method is well-ordered and effective with the existing ones. Therefore, MABAC appears to be an attractive explorative way to implement the MABAC in mobile phone selection.
MAIRCA is a technique recently proposed by Pamucar et al. This method is based on the definition of the difference between theoretical and actual results. It means that this method is based on the gap between ideal and empirical priorities [
51]. The main advantage of this method is related to the dissimilar linear normalization algorithm used. The described approach to linear normalization allows this method to achieve more efficient results [
52]. Stability of the solution, a well-structured analytical framework for ranking alternatives, the number of steps independent of the number of criteria, and suitability for cases with a large number of alternatives and criteria provide an appropriate ranking depending on a predefined dominance threshold [
51].
The MAIRCA method performs calculations given their proximity to ideal solutions, so it is the preferred method for evaluating decision alternatives. Furthermore, considering the studies in which this method has been applied, this study is expected to contribute to the literature as it is a novel method, and surveys using the MAIRCA method for evaluating mobile phones have not been evidenced yet. Finally, compared with some other MCDM methods, such as ELECTRE, MAIRCA was chosen due to its relative novelty and ease of use, as well as its requiring less computing time [
53].
Rankings provided by MCDM methods that require weights depend significantly on their determined values. Criteria weights have a direct impact on the final results of MCDM methods. The weights can be established by both objective and subjective methods. Weights determined by subjective methods require the active participation of the expert and are assigned by the expert based on knowledge and experience. Examples of subjective weighting methods include BWM (Best-Worst Method) [
51], AHP (Analytic Hierarchy Process) [
5,
54]. Objective methods set weights based on the data structure, taking into account each evaluation criterion’s actual degree of dominance.
The evaluation criteria in this study are quantitative measurement data. In such a case, the CRITIC method gets all the information included in the criteria of assessment. Therefore, CRITIC’s objective weighting methods may demonstrate more realistic results due to varying weights to criteria. This method, similar to Mean Weight (MW), Entropy method, Standard Deviation (SD), and Statistical Variance procedure, belongs to objective methods that calculate weights by solving mathematical equations omitting to take into account the decision-maker preferences [
55]. The use of subjective methods to determine weights raises questions about the reliability of the results obtained. Objective weighting techniques are used to overcome this problem. For this purpose, the CRITIC method was proposed by Diakoulaki et al. in 1995 [
56]. This method takes into consideration the intensity of the contrast occurring in the structure of the decision problem. Determination of contrasts between criteria is possible after performing fundamental statistical operations, such as correlation analysis [
57]. During the weighting process, both the standard deviation of a criterion and its correlation with other criteria are considered [
58]. The CRITIC method belongs to the class of correlation techniques. In this method, the intensity of contrast and conflict in the decision problem structure is considered. In addition, the decision matrix is examined to determine the information included in the criteria for assessing the alternatives [
59]. In the literature, many examples of the use of the CRITIC method for weights computation in combination with MCDM methods can be found, both known for many years and developed in recent times, employed to obtain the rankings of the assessed alternatives in multi-criteria problems, for example, TOPSIS [
58], VIKOR [
55,
60], MAUT [
61], WASPAS [
57,
62], AHP [
63], EDAS [
64], COCOSO [
65,
66], MULTIMOORA [
67], and CODAS [
60].
In
Table 1, the MCDM approaches used in the problem of selecting the most advantageous mobile phone model found in the most recent literature are listed. According to the recent literature, various MCDM strategies have been implemented to identify the most desirable mobile phone. Moreover, hybrid strategies of MCDM methods demonstrate high efficiency in analyzing real-world problems [
8]. It can be noticed that, for better results, a combined approach involving more than one method is often used in research. For example, in several publications from recent years, a combined MCDM procedure was adopted to select the best mobile phone model, where the weights are computed applying the Analytic Hierarchy Process (AHP). In the final stage, a set of alternatives was assessed employing the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) MCDM method to give an appropriate reference to the customer [
7,
8,
68]. Therefore, in the research presented in many publications, several MCDM methods are used to analyze in terms of comparison and conformity [
11,
34,
69]. Another approach described includes using AHP adopted to find out the criteria weights. In the next stage, two MCDM methods, named COPRAS and ARAS, are applied to obtain the rankings of the evaluated alternatives [
5].
Only one MCDM method, AHP, was used in Reference [
70], which is a subjective method. So, there is a lack of comparative analysis with other MCDM methods, which could give a different final ranking. Besides, only four mobile phones were evaluated in this study with five criteria. The situation is similar in Reference [
3], which also used only the AHP method to evaluate three criteria for mobile phone models. In Reference [
69], only five alternatives of mobile phones were evaluated. Many works dedicated to evaluating mobile phones using MCDM have used only one method [
6,
10,
12,
13,
71,
72]. In Reference [
5], 10 alternatives were evaluated with four criteria. Two MCDM approaches, AHP-COPRAS and AHP-ARAS, were used as methods to evaluate the alternatives, resulting in two rankings that were not identical. However, their similarity was not measured using an objective correlation coefficient. In addition, no strategy was proposed to present a consensus solution considering both rankings. Similar approaches considering no more than two MCDM methods for ranking alternatives can be observed in References [
11,
13,
14,
69]. In the case of the mobile phones evaluation problem, the small set of evaluated alternatives containing only 3–5 alternatives is a limitation of the study because it insufficiently represents the diversity specific to these devices. The same is true for the criteria, as their small number insufficiently represents consumer preferences. The use of one or two MCDM methods is also a limitation because different MCDM methods may give different solutions to the same problem. Thus, selecting an MCDM method to make a reliable decision is a challenge. In turn, using multiple MCDM methods may result in different rankings. Thus, a framework is needed that integrates the results of different methods and builds a reliable compromise ranking based on them. In Reference [
75], a set of six MCDM methods, including TOPSIS, VIKOR, PROMETHEE II, COPRAS, COMET, and SPOTIS, were used to evaluate electric bus alternatives. Based on the rankings obtained using the voting approach, compromise rankings were constructed and then compared with the rankings provided by the six MCDM methods using correlation coefficients. The compromise ranking was also used in the battery electric vehicles (BEVs) evaluation problem [
47]. It was generated from the SECA, MARCOS, ARAS, COCOSO, MAIRCA, and COPRAS rankings by applying the Borda technique and Copeland strategy.
The AHP method uses a scale to determine the importance of each criterion and a pairwise comparison matrix to scale the importance of each criterion [
54]. The requirement to perform only a pairwise comparison for all alternatives simplifies the decision-making process. Unfortunately, this method is not rank reversal-free [
76]. The AHP (Analytic Hierarchy Process) method is from the American school, similar to TOPSIS, VIKOR. Methods from the American school are based on the utility or value function. These methods use two types of relationships between the alternatives being evaluated: indifference and preference. However, they do not consider the incomparability of the options. It results in undesirable substitution effects (linear compensation) that occur even in their fuzzy extensions. The most popular methods from the European School include ELECTRE family and PROMETHEE II. Methods from the European school consider relations, the most common of which is indifference and weak or strong preference. They have a reduced linear compensation effect and are more oriented toward modeling user preferences. Methods from European school utilize outranking relations in the preference aggregation process. The described relationship is not transitive between pairs of evaluated alternatives. Researchers from European school point out that American school methods do not consider variability or uncertainty of expert judgements [
77]. The PROMETHEE II method results in numerical values calculated for each evaluated alternative. In contrast, the result of the ELECTRE family of methods is not quantitative, so the application of this method is limited depending on the results expected by the decision-maker, the need to combine different methods, or comparative analysis [
78]. The methods mentioned above are not resistant to the rank reversal paradox, evidenced by a change in rankings when some alternatives are added or removed. The problem of the occurrence of rank reversal paradox has been evidenced in studies for TOPSIS [
79,
80], AHP [
76,
81], PROMETHEE II [
82], and ELECTRE [
83]. Rank reversal paradox is a problem in the automation of decision-making processes [
76].
The COCOSO method, unlike the approaches mentioned above, considers three different aggregation strategies, Simple Additive Weighting (SAW), step-wise weight assessment ratio analysis (WASPAS), and Exponentially Weighted Product (EWP) methods, to obtain a stable and reliable solution [
34]. The main advantage of the ARAS method is that it has a utility function that enables an alternative to be proportioned to the optimal alternative. The COPRAS method helps find the similarity between each alternative and the optimal alternative by using degrees of utility [
5,
47]. The WASPAS method is a unique combination of the Weighted Sum Model (WSM) and Weighted Product Model (WPM). The main objective of the WASPAS method is to achieve the highest estimation accuracy by using weighted aggregate function optimization [
57].
The Characteristic Objects METhod (COMET) is an innovative method based on fuzzy set theory that successfully addresses the limitations in the previously mentioned approaches. The main advantage of this method is its resistance to the rank reversal paradox [
84]. This phenomenon consists in changing the ranking order when some alternatives are removed from the set under evaluation [
76]. The algorithm of the COMET method is based on a set of characteristic objects, which are reference points in the problem space. The characteristic objects are independent of the evaluated alternatives, so, even if an alternative is removed or added, there will never be a swap of places in the resulting ranking [
85]. In contrast to the previously mentioned methods, the algorithm of the COMET method has a complexity independent of the number of alternatives evaluated. This method provides accurate results, and operating on fuzzy numbers reflects adequately realistic problems where uncertainty and fluctuation are common. In this approach, the knowledge-dependent step for the decision-maker is a pairwise comparison of characteristic objects, the number of which depends on the number of criteria considered in the evaluation and their characteristic values. The possibility of creating a hierarchical model with an arbitrary structure in the decomposition process significantly reduces the number of comparisons required [
86]. However, the expert pairwise comparison stage is always the most laborious step of this method. In order to eliminate this subjective and time-consuming step, a novel hybrid approach named TOPSIS-COMET, combining another MCDA method, TOPSIS, with the COMET method, is proposed. TOPSIS is used in this case to evaluate a set of characteristic objects instead of a laborious pairwise comparison by an expert to fill in the Matrix Expert Judgement (MEJ). The proposed method is still rank reversal-free, just as in its classical version because TOPSIS, unlike its traditional application, is used here to evaluate characteristic objects instead of alternatives. The described approach was first presented in Reference [
87]. The decision to combine TOPSIS with COMET is justified by the fact that the TOPSIS method has many advantages, such as a simple, understandable, and widely used algorithm and returning the result in the form of a vector of numbers [
88], which plays the role of the SJ vector created in the classical version of the COMET method based on MEJ. The modular approach of the COMET method allows for further development and modification of the method, which is a significant advantage when considering this method as a DSS engine. Different MCDM methods may generate divergent solutions to the same problem due to their various methodological bases. The differences in results do not mean that the solutions are wrong. There is no complex or single method that is better than its equivalents. Although all MCDM methods are based on sound theoretical foundations, each technique has its advantages and disadvantages. Thus, a model must be proposed to achieve the compromise score and, thus, increase its reliability. In the approach presented in Reference [
47], the results from six different MCDM techniques are aggregated using the Borda and Copeland compromise ranking counting method. With this model, a consensus result can be achieved, and the reliability of the results is increased.
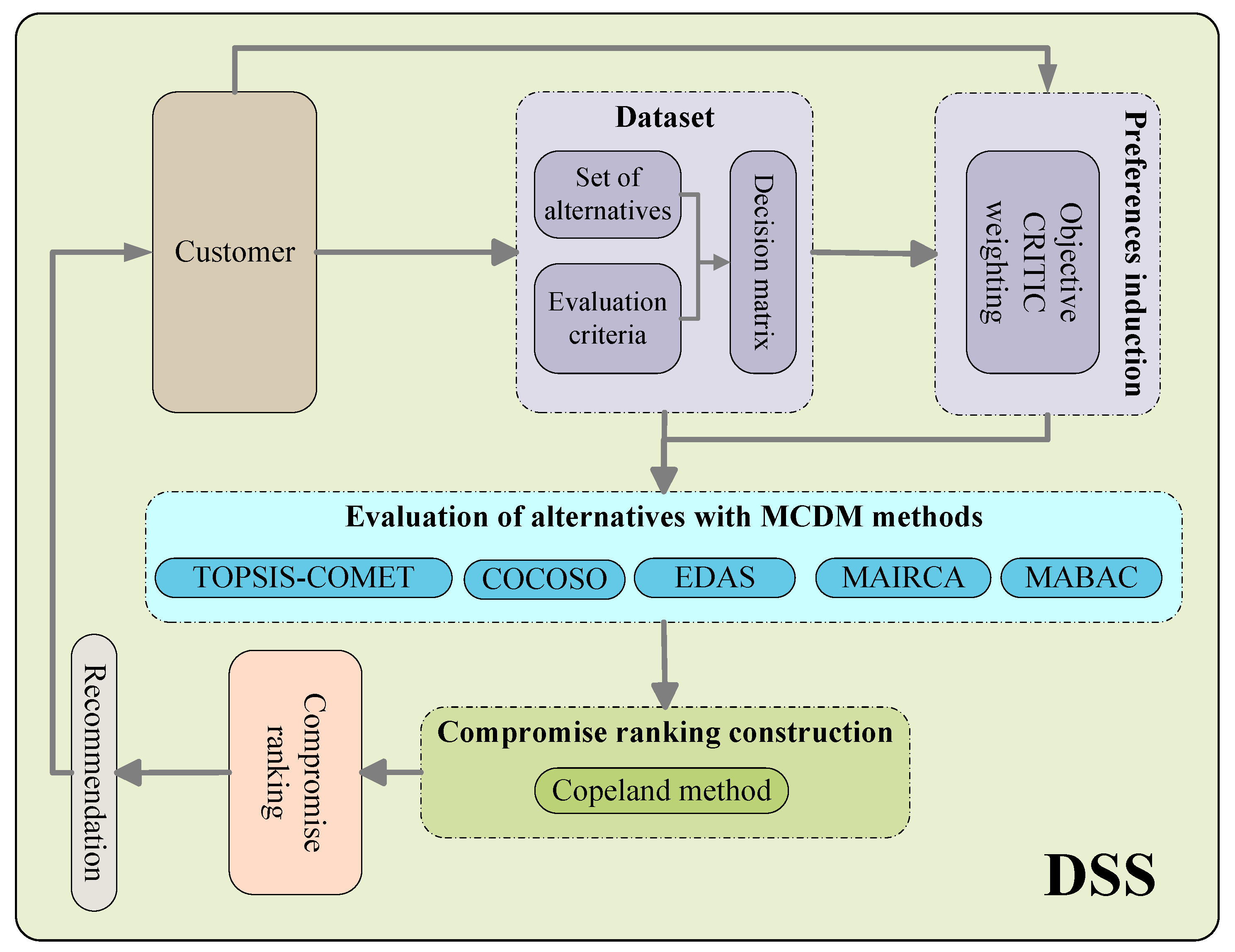
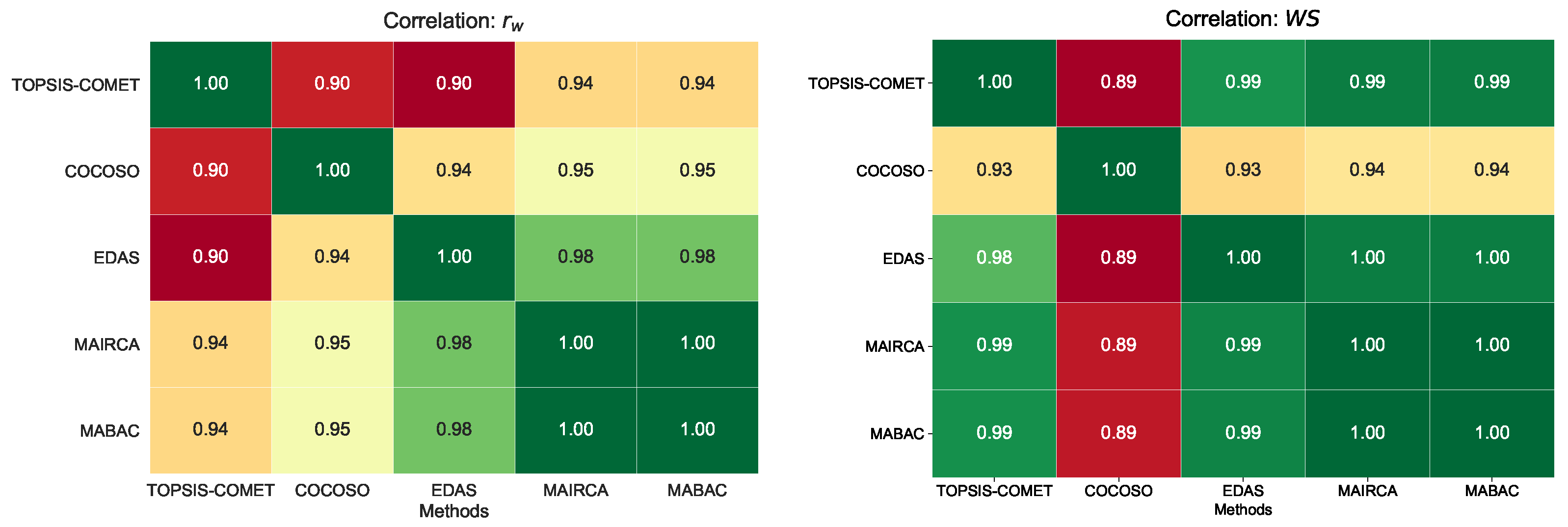
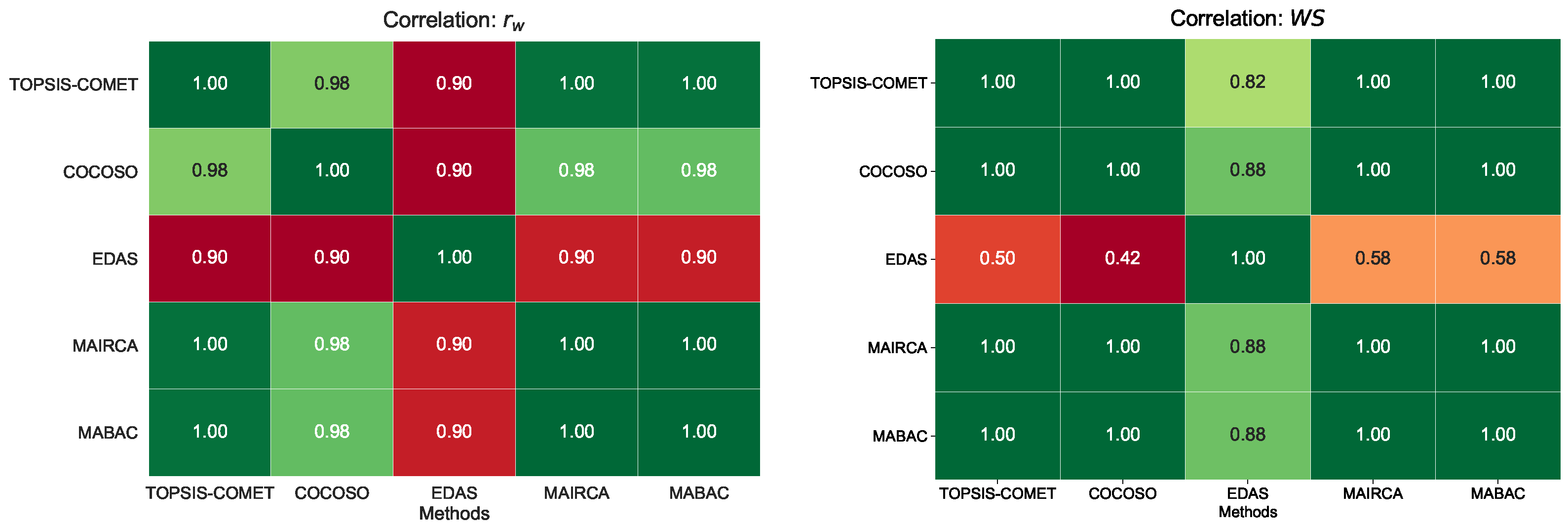
Due to the several advantages of the COMET method proved above, the authors of this work propose the TOPSIS-COMET hybrid approach as an engine of novelty DSS, which will be presented on an illustrative example of the problem of selecting the most advantageous mobile phone model. The authors propose an innovative DSS that recommends the compromise ranking that considers rankings from several relevant methods. Therefore, as a set of additional methods complementary for the innovative TOPSIS-COMET approach, the authors of this paper have chosen four MCDA methods: COCOSO, EDAS, MAIRCA, and MABAC. Based on the methods used, the Copeland strategy for constructing compromise ranking was applied, allowing multiple ranking lists to be combined into one. A sensitivity analysis was then performed on the compromise rankings candidates to calculate their match to the rankings provided by the methods used in the study. Correlation coefficients and were chosen as measures of matching.