Abstract
In online purchasing, customers may return products due to dissatisfaction with the quality of the product, and receive a refund based on the return policy, which is determined by online distributors. Online distributors can offer generous policies to attract more customers, but at the cost of reducing total profits. In this paper, the effect of the pricing and quality of complementary products (products sold together with other items) in online selling under the return policy is investigated. For this purpose, a mathematical model is developed to obtain optimal values for selling price, refund amount, and quality of products. Based on analytical results, a solution algorithm is proposed to solve the numerical examples and perform sensitivity analysis. Findings reveal that, while increasing the sensitivity of demand with respect to the refund amount, the price, quality, and refund on returned products should be increased. In addition, the online distributor should increase the quality of products when customers are more sensitive to the quality of products. Among other results, the selling price is shown to be negatively affected by demand elasticity with respect to price. In this situation, the online distributor should reduce the quality level and the refund amount for returned products to avoid a sharp decline in profit. In addition, when the quality cost is high, the price and quality should be decreased and the refund amount unchanged.
1. Introduction
Returning products from customers to vendors is a regular activity in many industries. In online purchasing, or e-shopping, the vendors inform their customers of a product’s details (i.e., quality, appearance, usage, time of delivery, among other characteristics) via a webpage. Then, the buyers decide to purchase a product based only on the webpage information and their needs. As we know, in online purchasing the customers do not have access to the physical product when they are purchasing; therefore, the return rate is higher than in physical purchases [1]. According to an Invesp infographic, the return rate in online purchasing is at least 30%, whereas it is lower than 9% in physical purchasing. Based on different product categories, shoppers return 30–40% of their purchases in shoes and clothing products [2]. This rate is higher for luxury and fashion products [3].
Nowadays, using a return policy has been proposed as a good strategy to encourage customers to purchase and boost the sales in e-commerce [4,5,6]. A return policy could have a high cost for managers. For example, the inventory of some products may increase, and managers may be forced to destroy them [7]. However, it will have a very positive impact on sales if online sellers manage it correctly [8,9,10]. If customers know that they can return a product that they are not satisfied with, they will be more inclined to buy the product and, correspondingly, increase sales [10,11,12]. To achieve the desired result from the implementation of the return policy, the managers must identify important factors influencing customer returns. Quality is closely related to return. Low quality in a product creates customer dissatisfaction and generates numerous returns. Conversely, high quality in a product creates high customer satisfaction and, therefore, a low number of returns [13]. However, high-quality products lead to high selling prices and a subsequent lower demand [14,15]. Thus, the return policy, pricing strategy and quality strategy are correlated decisions and online sellers should decide on them simultaneously. Dell is an example of successful e-commerce using a return policy. Dell determines a longer return duration for high-end computers that have a higher price and better quality. On the other hand, a one-year-after-sale service with no charge is used for computers with a low quality and price. With inspiration from the return policy of Dell, Li et al. [16] analyzed a pricing-quality problem in online direct selling. They considered an online distributor that used a return policy. It was assumed that customer demand was sensitive to the product’s price and return policy. The return policy and the product’s quality also affect the returned quantity of products. Later, Yoo [17] studied the relationship between return policy and product quality decisions in a decentralized system. Li et al. [18] constructed a two-stage Stackelberg game model to analyze the pricing strategy and return policy in a two-echelon supply chain.
In addition to return policies, another way to succeed in e-commerce is proposing products as complementary products. A complementary product is a product that adds value to another. In other words, they are two products that the customer uses together. Examples of complementary products include a cell phone and a charger, a bed and a mattress, a printer and a cartridge, and gaming portals and gaming DVDs. Proposing a product as complementary often helps customers to find a high-quality set of relevant products that are always bought and used together. Thus, the demand for complementary products is interrelated and the price of one product will influence the demand for another product. In practice, numerous e-commerce websites, such as eBay, Taobao, and Amazon, provide complementary products for their customers. Along with practical examples, researchers have also investigated the pricing of complementary products in online sales. The pricing problem of complementary products was analyzed by Zhao et al. [19]. They assumed a supply chain including two manufacturers and one retailer in which one of the two manufacturers uses both online and traditional channels to sell the products.
Due to the positive impact of the return policy and complementary products on e-commerce, the simultaneous use of these two policies can contribute to success in e-markets. To the best of our knowledge, no study has investigated the return policy in the context of complementary products. This research gap motivated us to conduct this study. In this paper, we propose a mathematical model to determine the optimal pricing and product quality of complementary products in online purchasing under the return policy. In line with this, we try to answer the following questions:
- How do online distributors determine the optimal selling price, optimal quality level, and optimal refund amount for two complementary products?
- How can online distributors maximize the total profits of the system when the conditions of the selling price, refund amount, and quality of products are all assumed to be at the optimum values?
- When customer’s demands are highly sensitive to the selling price, how should online distributors determine the optimal product quality and the refund amount?
- How should online distributors indicate the refund amount and product quality when the sensitivity of customers to product quality is high?
- When customers are more sensitive to refund amounts, how should online distributors set the optimal price and product quality?
This paper is structured as follows: In Section 2, we review the relevant studies. The problem definition and modeling are presented in Section 3 and Section 4, respectively. In Section 5, we analyze the proposed model, and the optimal value for decision variables is obtained. We provide a solution algorithm in Section 6. In Section 7, two numerical examples and sensitivity analyses are carried out, and managerial insight is presented. In Section 8, the research is concluded and some suggestions for future research are discussed.
2. Relevant Works
We briefly review the previous relevant studies in the following two categories: research investigating return policies and studies analyzing the pricing of complementary products.
2.1. Return Policy
The return policy has attracted considerable attention in the success of online selling, both in academia and the industrial world. On the first try, Pasternack [20] addressed the well-known newsvendor problem for a seasonal product with a fixed price and stochastic demand. In his model, a percentage of the lot size may be returned from retailers to the manufacturer. Later, Kandel [21] and Emmons and Gilbert [22] extended Pasternack’s [20] research to a case in which the demand is price sensitive. Emmons and Gilbert [22] analyzed the impact of a return policy in pricing and inventory decisions on a supply chain comprised of a manufacturer and a retailer. Lau and Lau [23] analyzed the pricing and return policies of a monopolistic manufacturer for single-period commodities. In addition, Webster and Weng [24], and Yao et al. [25] focused on return policies between the manufacturer and the retailer. Ringbom and Oz [26] proposed methods to determine the optimal rates of partial refunds on customers’ no-shows and cancellations. According to Mukhopadhyay and Setaputra [27], a good return policy increases a product’s demand. The reason for this is that some customers perceive the return as a motivator for their purchasing decisions. In the same year, Yue and Raghunathan [28] examined the full return policy’s impact on the supply chain with information asymmetry. They found that the retailer always benefits from a full return policy, in all situations, whereas the manufacturer and the supply chain are better off under some circumstances. Yao et al. [29] investigated the impact of price-sensitivity factors on features of return policy contracts in a single-period product, considering a stochastic and price-dependent demand. Yu and Wang [30] proposed a multi-dimensional framework to obtain the optimal returns policies under the direct sale channel. Su [31] studied the impact of full refund policies and partial refund policies on supply chain performance. On the other hand, Chen and Bell [32] addressed the problem of the joint determination of price and inventory replenishment when clients return items to the vendor. They conclude that the vendor should change the price and order quantity to reduce the negative effect of returns. Subsequently, Bonifield et al. [33] examined the relationship between quality and a flexible return policy. Afterward, Xiao et al. [34] studied the supply chain coordination with customer returns behavior and a buyback policy. They consider the order quantity as a decision variable, and the retail price and refund amount as given. Later, Chen and Bell [35] studied the impact of the returns from the customer on retailer’s price and order quantity, for both deterministic and stochastic demand, considering that returns from customers are dependent on the quantity sold or price, or both. One year later, Ai et al. [36] analyzed the decisions of retailers and manufacturers on two competing supply chains selling a substitutable product, with a demand uncertainty in the cases when manufacturers use or do not use full return policies. In their paper, Chen and Grewal [37] discussed how a new entrant retailer can practice either a full refund policy or a non-refund policy, to compete with a well-established retailer that always offers its customers a full refund. Afterward, Liu et al. [38] examined a supply chain with a single manufacturer and a single retailer considering uncertain demand. They investigated how customer returns impact the retailer’s ordering decisions as well as the manufacturer’s and retailer’s profits. Recently, Yoo et al. [39] analyzed the optimal pricing decision in a closed-loop supply chain under a return policy. Joint pricing and the environmental friendliness level model were presented by Giri and Bardhan [40]. Heydaryan and Taleizadeh [41] proposed a return policy depending on the selling price and refund amount for a two-echelon supply chain. They analyzed the proposed model by considering cooperative and non-cooperative games. Hu et al. [42] studied a dynamic pricing problem when customers can return their purchased products. They showed that this return policy can increase profit when the initial inventory and demand are moderate and high, respectively. Noori-daryan and Taleizadeh [43] modeled a pricing-inventory problem for a three-echelon supply chain. They considered the return policies between manufacturer, supplier and retailer. Ren et al. [44] studied the pricing and return policies of online retailers. This research dealt with pricing and inventory models for a single product.
All of the reviewed studies have been focused on modeling and analyzing the return policy along with other decision variables for single products. Our model differs from those in the existing literature in that it analyzes the pricing, quality, and return policy for complementary products.
2.2. Pricing of Complementary Products
In this section, we will review the relevant research that studies complementary products. It is well-known that an increment in the demand of one complementary product leads to an increment in the demand of the other. A product has a high degree of complementarity with others when it is sold together with another product i.e., a bed and a mattress, a computer and the operating system, a computer and a printer, just to name a few examples. Yue et al. [45] modeled a mixed bundling policy to sell two complementary products in a market with two independent firms. The model determined the optimal pricing strategy by maximizing the total profit. A pricing-quality model for complementary products was proposed by Bilotkach [46]. Later, Mukhopadhyay et al. [47] presented a leader-follower game to investigate the pricing strategy in a duopoly market. The benefits of the bundling strategy for complementary products were analyzed by Yan and Bandyopadhyay [48]. Most recently, Wei et al. [49] studied a two-level supply chain including two manufacturers and one retailer. They investigated the optimal pricing decisions for two complementary products. Wei et al. [50] derived the optimal policies for pricing and warranty duration in a two-echelon supply chain. Taleizadeh and Charmchi [51] proposed a joint pricing–advertising model for complementary products. Dehghanbaghi and Sajadieh [52] investigated the optimal policies for pricing, production, transportation, and inventory. Wang et al. [53] studied the pricing and service decisions for complementary products in a dual-channel supply chain. Taleizadeh et al. [54] dealt with pricing and inventory decisions jointly when complementary products were deteriorating. Findings revealed that the degree of complementarity influences the profit. Giri et al. [55] modeled a two-echelon supply chain. They assumed that two manufacturers sell two complementary products through one retailer. It was shown that profit would increase under a pure bundling policy. The effect of trade credit on the pricing of complementary products was analyzed by Ren et al. [56]. Shan et al. [57] studied a green supply chain by investigating the optimal pricing strategy for complementary products.
According to the reviewed studies, there are not any studies that analyze the joint pricing and quality decisions for two complementary products under a return policy.
3. Problem Definition and Modeling
We consider an online distributor that sells complementary products. The desire is to maximize the total profit from these products by determining the optimal pricing, refund amount, and product quality. Customers buy products via the internet based on the distributor’s description of the product. There are two possible outcomes when customers receive their product, as follows: (1) customers are satisfied with the quality of the product, or (2) customers are not satisfied because the product is not of the quality they expected. In this case, customers decide to return the product and request a refund.
Other assumptions will be stated as follows:
Assumptions:
- The two complementary products are considered;
- The product quality level refers to the consistency between the purchased product and its online description;
- The online distributor’s total profit is obtained by the summation of each product’s profit function;
- The demand for each product is sensitive to its price and the price of the other product;
- The refund amount for both products influences the demand;
- A low quality of product causes customer dissatisfaction and leads to an increase in the number of returns.
To model the problem, the following notations in Table 1 and Table 2 are used throughout this paper.

Table 1.
Notations and Parameters.

Table 2.
Continuous decision variables.
3.1. Demand Function
Customer demand decreases with an increasing product price. In addition, a return policy with a high refund has a positive impact on demand. Thus, we use the following functions to model the demand for both products:
and .
3.2. Return Function
After receiving a product purchased online, the customer decides whether to keep it or return it, based on their dissatisfaction with the purchased product, the return policy of the online distributor, and the refund amount. Therefore, the return quantity functions for the first and the second products are as follows:
and .
3.3. The Online Distributor’s Profit
The online distributor aims to maximize the profit that it gains from both complementary products by setting the optimal pricing, refund amount, and product quality. The profit function of the ith product is defined as the difference between revenue and cost (producing and quality costs). By considering Equations (1)–(4), the firm’s model can be formulated as follows:
and
4. A Special Case of the Proposed Model
In this section, to gain some qualitative insights into the proposed model, we apply a special form to the demand function, the return quantity and quality cost. As mentioned in the works of Coughlan [58], Wei et al. [49] and Mukhopadhyay et al. [47], we use a linear form of the demand function as follows:
In addition, the return quantity functions for the first and the second products, according to the definitions put forward by Li et al. [16] and Balachander [59], are as follows:
Here, the function of quality cost is considered (as used by Li et al. [16]), for the first and the second products as follows:
According to Equations (7)–(12), the profit function of the first and second products will be the following:
The total profit function (TPF) is the following:
5. Solution Method
The main purpose of this paper is to determine the optimal values for the decision variables that correspond to maximizing the total profit. To achieve our purpose, we first prove that the profit functions of both products are concave in Proposition 1. To prove the concavity of the profit function for the first and second products, the Hessian Matrix is applied [60,61,62].
Proposition 1.
The profit functions for both products are concave and have unique optimal solutions.
Proof.
See Appendix A. □
From the analysis carried out so far, we know that there are unique values for p1, q1, and r1 (p2, q2, and r2) that maximize the profit of selling the first product (and the second product).
Next, we study the conditions under which the total profit function is also concave in Proposition 2.
Proposition 2.
The total profit function is concave and has a unique optimal solution if the inequality (16) holds.
Proof.
See Appendix B. □
Thus, the optimal values for the decision variable can be obtained in Proposition 3.
Proposition 3.
The optimal policies of the online distributor for the first and the second products are as follows.
- (1)
- The optimal pricing for the first product is as follows:
- (2)
- The optimal refund amount for the first product is as follows:
- (3)
- The optimal quality policy for the first product is as follows:
- (4)
- The optimal pricing for the second product is as follows:
- (5)
- The optimal refund amount for the second product is as follows:
- (6)
- The optimal quality policy for the second product is as follows:where A, B, are defined in Appendix C.
6. Solution Algorithm
To gain more insight into the analytical results shown above, we need to solve the numerical examples. For this purpose, we proposed the following algorithm solution. A flowchart of the proposed solution algorithm is displayed in Figure 1.
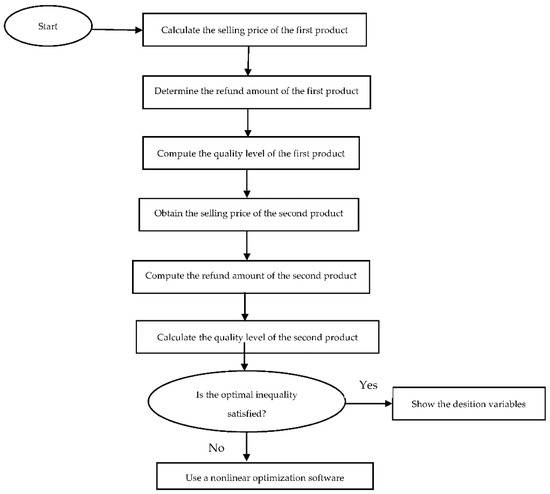
Figure 1.
Flowchart of the proposed solution algorithm.
Step 1: Calculate the selling price of the first product using Equation (17).
Step 2: Determine the refund amount for the first product using Equation (18).
Step 3: Compute the quality level of the first product using Equation (19).
Step 4: Obtain the selling price of the second product using Equation (20).
Step 5: Compute the refund amount for the second product using Equation (21).
Step 6: Calculate the quality level of the second product using Equation (22).
Step 7: Verify the inequality (16), if inequality (16) holds then the obtained values for the decision variables are optimal, stop; otherwise, go to step 8.
Step 8: Solve the nonlinear optimization problem in Equation (15) using any nonlinear optimization software to determine the optimal values for the decision variables.
7. Illustrative Example
In this section, numerical examples of complementary products with a deterministic demand are analyzed. The proposed model can be used in different industries in the real world, such as the electronic products industry. We considered the mobile phone industry when solving numerical examples. In this industry, cell phones and chargers are used as examples of two complementary products.
Example 1.
In this example, we supposed a market with a demand for 1400 and 1500 units of the first and second products, respectively. The values given for the other parameters considered are as follows:
Under these conditions, the online distributor is looking for the optimal values for the decision variables to maximize the total profit function. By using the proposed solution algorithm, we have the following:
Step 1: Calculate the selling price of the first product using Equation (17).
Step 2: Determine the refund amount for the first product using Equation (18).
Step 3: Compute the quality level of the first product using Equation (19).
Step 4: Obtain the selling price of the second product using Equation (20).
Step 5: Compute the refund amount for the second product using Equation (21).
Step 6: Calculate the quality level of the second product using Equation (22).
Thus, the optimal total profit function will be TPF= 894,497.4. In this example, using the given values for the parameters and the resulting value of the decision variables in inequality (16), we have the following:
The results showed that the online distributor should provide the first and second products with a quality of 56 and 49% and determined prices of USD 591.9 and USD 674.9 for them, respectively. It also returns USD 197.6 and USD 149.9 to the unsatisfied customers for the first and second products, respectively.
Example 2. In this example, we changed the parameters as follows:
By using the proposed solution algorithm, the optimal values for the decision variables were , and the optimal total profit function was TPF = 885,780.
7.1. Sensitivity Analysis
To study the effects of changes in the parameters on the optimal value of the decision variables, a sensitivity analysis was conducted by increasing and decreasing the parameters by 20 and 40%. Table 3 shows the results of the sensitivity analysis for the first numerical example presented in the previous section. Decision variables are considered as slightly sensitive whenever the rate of change in their values, due to changes in the model’s parameters, is less than 5%. When the rate of change falls between 5 and 30%, then the decision variables are considered to be moderately sensitive. A rate of change in the variables between 30 and 50% means that they are sensitive to parameter changes. For rates of change higher than 50%, the variables are said to be highly sensitive. Based on the results presented in Table 3, the following findings can be obtained:

Table 3.
Effects of parameter changes on optimal decision variables.
- For the first product, optimal values of the decision variables are highly sensitive to an increase in α1;
- is highly sensitive to a decrease in , and is highly sensitive to a decrease in ;
- Optimal values for decision variables are moderately sensitive to decreases in and ;
- is sensitive to an increase in , and is sensitive to an increase in ;
- Optimal values for decision variables are slightly sensitive to changes in and ;
- and are highly sensitive to a 40% decrease in parameter ;
- and are highly sensitive to a 40% decrease in parameter ;
- For the first product, optimal values of the decision variables are highly sensitive to a 40% decrease in parameter ;
- For the second product, optimal values of the decision variables are highly sensitive to a 40% decrease in parameter ;
- and are sensitive to a 40% increase in parameter ;
- and are sensitive to a 40% increase in parameter ;
- and are moderately sensitive to a 40 and 20% increase, respectively, parameter ;
- Change in the values of and does not have a significant effect on the optimal value of decision variables.
Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 show the changes in the total profit function concerning all parameters. Specifically, Figure 3, Figure 4, Figure 6, Figure 7, Figure 10 and Figure 11 show that by increasing the values of the parameters, the total profit function decreases. On the other hand, Figure 2, Figure 5, Figure 8 and Figure 9 show that by increasing the parameters’ values, the total profit function increases.
Figure 2.
Changes in the TPF with respect to α1, α2.
Figure 3.
Changes in the TPF with respect to λ1, λ2.
Figure 4.
Changes in the TPF with respect to γ1, γ2.
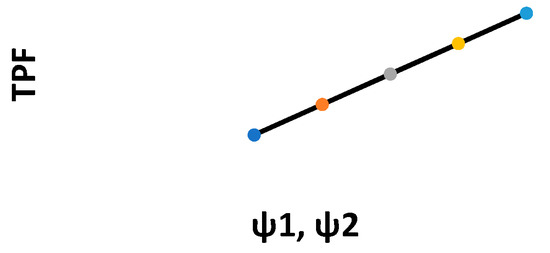
Figure 5.
Changes in the TPF with respect to ψ1, ψ2.
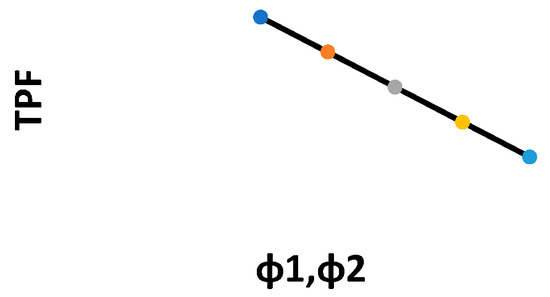
Figure 6.
Changes in the TPF with respect to ϕ1, ϕ2.
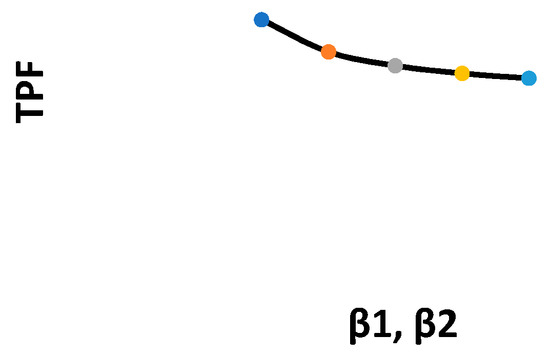
Figure 7.
Changes in the TPF with respect to β1, β2.
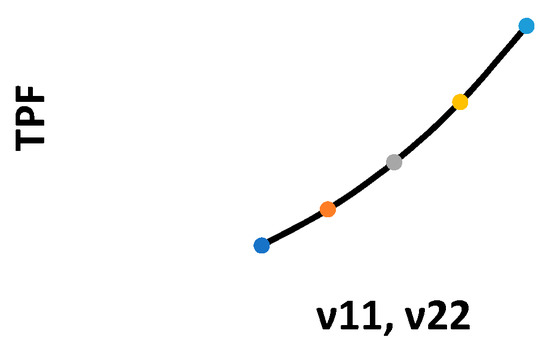
Figure 8.
Changes in the TPF with respect to υ11, υ22.
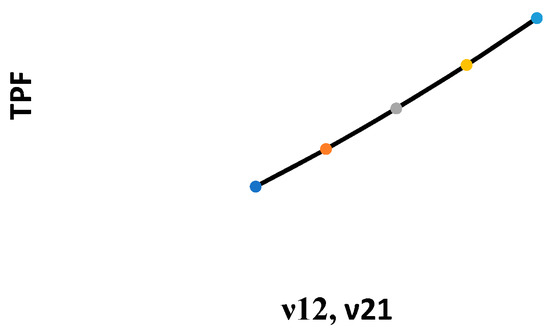
Figure 9.
Changes in the TPF with respect to υ12, υ21.
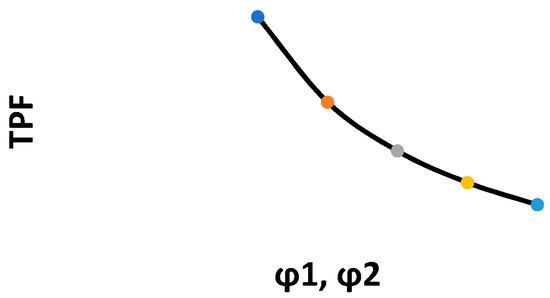
Figure 10.
Changes in the TPF with respect to φ1, φ2.
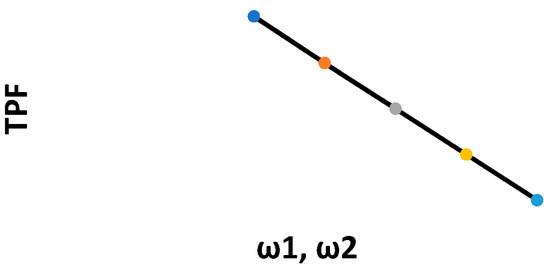
Figure 11.
Changes in the TPF with respect to ω1, ω2.
7.2. Managerial Insight
The following managerial insights can be drawn from our study:
- This study filled an important research gap in presenting a comprehensive model for two complementary products in online selling where a return policy exists, by deciding on the selling price, quality level, and refund amount for returned products.
- As the potential market demand has a positive effect on the online distributor’s profit, the managers should try to expand the target market of their products by applying appropriate marketing policies.
- Managers of two complementary products should spend more on the refund of returned products when the sensitivity of demand to refund amount is high. By applying this strategy, the demand will increase, and the online distributor can increase the selling price and quality.
- With an increasing sensitivity of returned quantity with respect to product quality, the online distributor should provide products with a higher quality and, correspondingly, retain the price and the refund amount.
- Managers should decrease the price of the first (or second) product by increasing the sensitivity of its demand to price. In contrast, they are advised to increase the price of the second (or first) product.
- The negative effect of the quality cost parameter on profit implies that managers should reduce the quality and keep the refund on returned products unchanged. In other words, they should take the position of “low quality and low price”.
- When customers are less sensitive to a return policy, they will pay more attention to quality. Thus, managers should seek a lenient return policy, such as increasing the quality and refund on returned products.
- The proposed model is a proper starting point to present a new model that considers other marketing variables, such as advertising.
8. Conclusions
In online sales, customers do not observe a product closely when deciding whether to buy a product; therefore, their concerns about product quality may prevent them from buying it. Thus, online vendors should use various policies to encourage customers to purchase products. One of the strategies that has been well documented in the literature is the return policy. In line with this, this paper focused on the pricing and quality of complementary products in online selling under a return policy. We considered an online distributor selling two complementary products with the aim of maximizing its profit by determining the optimal values for selling price, quality level, and the refund amount for returned products. We assumed that customer demand is sensitive to the product’s selling price and the refund amount for a returned product. In addition, the customer returns depend on the return policy and product quality. From a managerial perspective, the proposed model can be used to guide managers to make the best decisions in their e-commerce.
According to findings, when customer demand is highly sensitive to the selling price, online distributors should respond by providing policies to lower the price. They can achieve sales at lower prices by using the position of “low quality and low refund amount for returned products”. This helps to prevent an intense decline in total profits. Results showed that the quality and the refund amount for returned products are highly sensitive to a 40% decrease in the effect of the refund amount on the returned quantities. A 40% increment in the potential demands of the market leads to more than a 50% increase in the selling price and total profit. Thus, an online distributor should try to increase its market size by using heavy advertising. Results revealed that when increasing the quality cost, the quality and price should be decreased. When the sensitivity of customers to the refund amount is high, the policy of “low quality and low price” should be used. Further, when the customer’s return is sensitive to quality, the online distributor should focus on quality and provide a lenient return policy to guarantee customer demand for a high-quality product.
There were some limitations in this research. Firstly, we assumed that the demand was deterministic. As we know, demand uncertainty is present in the majority of the products, as is the case with stochastic demand and returns. Secondly, we used the assumed values for parameters in the mobile phone industry to conduct a numerical study. Considering a real data set makes our results more practical. Third, we did not investigate other operational decisions, such as inventory.
To address the above limitations, we provided the following extensions: The proposed model can be expanded by considering stochastic demand. Future research can create a more realistic model by extending this model with inventory decisions. An interesting extension to this work includes the consideration of a real data set for industries that sell products such as printers and cartridges, and gaming portals and gaming DVDs. In addition, inventory systems for both perfect and imperfect products are worth considering [63,64,65].
Author Contributions
Conceptualization, A.A.T. and L.E.C.-B.; Data curation, S.R.B.; Formal analysis, S.R.B. and L.E.C.-B.; Investigation, A.A.T., S.R.B., L.E.C.-B. and S.N.-G.; Methodology, A.A.T., S.R.B., L.E.C.-B. and S.N.-G.; Software, S.R.B. and L.E.C.-B.; Supervision, A.A.T. and L.E.C.-B.; Validation, S.R.B. and L.E.C.-B.; Visualization, S.R.B.; Writing—original draft, A.A.T., S.R.B. and L.E.C.-B.; Writing—review & editing, A.A.T., L.E.C.-B. and S.N.-G.. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data are self-content in the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. A Proof of the Concavity of the Profit Functions for the Both Products
For the first product, one has as follows:
And the second derivatives are shown by the following:
Consequently, the hessian matrix is as follows:
In order to proof the concavity, it is required to show that
Now, we have because .
Similarly, for the second product we have the following:
And the second derivatives are given as follows:
Therefore, the hessian matrix of the profit function for the second product is as follows:
In order to proof the concavity, it is necessary to show the following:
Now, one has because .
Appendix B. A Proof of the Concavity of the Total Profit Functions with Respect to Hessian Matrix
The total profit function is as follows:
Equation (10) is re-expressed as the following:
Using Equations (3) and (4), one obtains the following:
Using the following:
Then the total profit function is as follows:
The Hessian Matrix is as follows:
Appendix C. Deriving the Optimal Decision Variables
As we have shown previously, if the profit function of the first product is concave, then one obtains the first derivative of the total profit function, shown in Equation (10), with respect to the decision variables for the first product and then setting them equal to zero yields the following:
For the return policy, we have the following:
For the quality level, we obtain the following:
Similarly, for the second product we have the following:
For the return policy, we have the following:
For the quality level, we obtain the following:
In addition, after some algebraic simplifications we have the following:
where
References
- Chopra, S.; Meindl, P. Strategy, Planning, and Operation. In Supply Chain Management; Pearson: New York, NY, USA, 2001. [Google Scholar]
- Reagan, C. That Sweater You Don’t Like Is a Trillion-Dollar Problem for Retailers. These Companies Want to Fix it. 2019. Available online: https://www.cnbc.com/2019/01/10/growing-online-sales-means-more-returns-and-trash-for-landfills.html (accessed on 21 April 2021).
- Son, J.; Kang, J.H.; Jang, S. The effects of out-of-stock, return, and cancellation amounts on the order amounts of an online retailer. Retail. Consum. Serv. 2019, 51, 421–427. [Google Scholar] [CrossRef]
- Suwelack, T.; Hogreve, J.; Hoyer, W.D. Understanding money-back guarantees: Cognitive, affective, and behavioral outcomes. J. Retail. 2011, 87, 462–478. [Google Scholar] [CrossRef]
- Wai, K.; Dastane, O.; Johari, Z.; Ismail, N.B. Perceived risk factors affecting consumers’ online shopping behavior. J. Asian Financ. Econ. Bus. 2019, 6, 246–260. [Google Scholar]
- Khouja, M.; Ajjan, H.; Liu, X. The effect of return and price adjustment policies on a retailer’s performance. Eur. J. Oper. Res. 2019, 276, 466–482. [Google Scholar] [CrossRef]
- Pourhejazy, P. Destruction Decisions for Managing Excess Inventory in E-Commerce Logistics. Sustainability 2020, 12, 8365. [Google Scholar] [CrossRef]
- Mollenkopf, D.A.; Rabinovich, E.; Laseter, T.M.; Boyer, K.K. Managing internet product returns: A focus on effective service operations. Decis. Sci. 2007, 38, 215–250. [Google Scholar] [CrossRef]
- Tariq, A.; Bashir, B.; Adnan Shad, M. Factors affecting online shopping behavior of consumers in Pakistan. J. Mark. Consum. Res. 2016, 19, 95. [Google Scholar]
- Pei, Z.; Paswan, A. Consumers’ Legitimate and Opportunistic Product Return Behaviors in Online Shopping. J. Electron. Commer. Res. 2018, 19, 301–319. [Google Scholar]
- Cao, K.; Xu, Y.; Wang, J. Should firms provide online return service for remanufactured products? J. Clean. Prod. 2020, 272, 122641. [Google Scholar] [CrossRef]
- Fan, Z.P.; Chen, Z. When should the e-tailer offer complimentary return-freight insurance? Int. J. Prod. Econ. 2020, 230, 107890. [Google Scholar] [CrossRef]
- Kirmani, A.; Roa, A.R. No pain, no gain: A critical review of the literature on signaling unobservable quality. J. Mark. 2000, 64, 66–79. [Google Scholar] [CrossRef]
- Whitefield, R.I.; Duffy, A.H.B. Extended revenue forecasting within a service industry. Int. J. Prod. Econ. 2012, 141, 505–518. [Google Scholar] [CrossRef]
- Rabinovich, E.; Maltz, A.; Sinha, R.K. Assessing markups, service quality, and product attributes in music CDs’ internet retailing. Prod. Oper. Manag. 2008, 17, 320–337. [Google Scholar] [CrossRef]
- Li, Y.; Lei, X.; Li, D. Examining relationships between the return policy, product quality, and pricing strategy in online direct selling. Int. J. Prod. Econ. 2013, 144, 451–460. [Google Scholar] [CrossRef]
- Yoo, S.H. Product quality and return policy in a supply chain under risk aversion of a supplier. Int. J. Prod. Econ. 2014, 154, 146–155. [Google Scholar] [CrossRef]
- Li, G.; Li, L.; Sethi, S.P.; Guan, X. Return strategy and pricing in a dual-channel supply chain. Int. J. Prod. Econ. 2019, 215, 153–164. [Google Scholar] [CrossRef]
- Zhao, J.; Hou, X.; Guo, Y.; Wei, J. Pricing policies for complementary products in a dual-channel supply chain. Appl. Math. Model. 2017, 49, 437–451. [Google Scholar] [CrossRef]
- Pasternack, B.A. Optimal pricing and return polices for perishable commodities. Mark. Sci. 1985, 4, 166–176. [Google Scholar] [CrossRef]
- Kandel, E. The right to return. J. Law Econ. 1996, 39, 329–356. [Google Scholar] [CrossRef]
- Emmons, H.; Gilbert, S.M. Note: The role of returns policies in pricing and inventory decisions for catalogue goods. Manag. Sci. 1998, 44, 276–283. [Google Scholar] [CrossRef]
- Lau, H.S.; Lau, A.H.L. Manufacturer’s pricing strategy and return policy for a single-period commodity. Eur. J. Oper. Res. 1999, 116, 291–304. [Google Scholar] [CrossRef]
- Webster, S.; Weng, Z.K. A risk free perishable item returns policy. Manuf. Serv. Oper. Manag. 2000, 2, 100–106. [Google Scholar] [CrossRef]
- Yao, D.Q.; Yue, X.; Wang, X.; Liu, J.J. The impact of information sharing on a return policy with the addition of a direct channel. Int. J. Prod. Econ. 2005, 97, 196–209. [Google Scholar] [CrossRef]
- Ringbom, S.; Oz, S. Advance booking, cancellations, and partial refunds. Econ. Bull. 2004, 13, 1–7. [Google Scholar]
- Mukhopadhyay, S.K.; Setaputra, R. A dynamic model for optimal design quality and return policies. Eur. J. Oper. Res. 2007, 180, 1144–1154. [Google Scholar] [CrossRef]
- Yue, X.; Raghunathan, S. The impacts of the full return policy on a supply chain with information asymmetry. Eur. J. Oper. Res. 2007, 180, 630–647. [Google Scholar] [CrossRef]
- Yao, Z.; Leung, S.C.H.; Lai, K.K. Analysis of the impact of price-sensitivity factors on the return policy in coordinating supply chain. Eur. J. Oper. Res. 2008, 187, 275–282. [Google Scholar] [CrossRef]
- Yu, C.C.; Wang, C.S. A hybrid mining approach for optimizing return policies in e-retailing. Expert Syst. Appl. 2008, 35, 1575–1582. [Google Scholar] [CrossRef]
- Su, X. Consumer returns policies and supply chain performance. Int. J. Adv. Oper. Manag. 2009, 11, 595–612. [Google Scholar] [CrossRef]
- Chen, J.; Bell, P.C. The impact of customer returns on pricing and order decisions. Eur. J. Oper. Res. 2009, 195, 280–295. [Google Scholar] [CrossRef]
- Bonifield, C.; Cole, C.; Schultz, R.L. Product returns on the internet: A case of mixed signals? J. Bus. Res. 2010, 63, 1058–1065. [Google Scholar] [CrossRef]
- Xiao, T.; Shi, K.; Yang, D. Coordination of a supply chain with consumer return under demand uncertainty. Int. J. Prod. Econ. 2010, 124, 171–180. [Google Scholar] [CrossRef]
- Chen, J.; Bell, P.C. Coordinating a decentralized supply chain with customer returns and price-dependent stochastic demand using a buyback policy. Eur. J. Oper. Res. 2011, 212, 293–300. [Google Scholar] [CrossRef]
- Ai, X.; Chen, J.; Zhao, H.; Tang, X. Competition among supply chains: Implications of full returns policy. Int. J. Prod. Econ. 2012, 139, 257–265. [Google Scholar] [CrossRef]
- Chen, J.; Grewal, R. Competing in a supply chain via full-refund and no–refund customer returns policies. Int. J. Prod. Econ. 2013, 146, 246–258. [Google Scholar] [CrossRef]
- Liu, J.; Mantin, B.; Wang, H. Supply chain coordination with customer returns and refund-dependent demand. Int. J. Prod. Econ. 2013, 148, 81–89. [Google Scholar] [CrossRef]
- Yoo, S.H.; Kim, D.; Park, M.S. Pricing and return policy under various supply contracts in a closed-loop supply chain. Int. J. Prod. Res. 2015, 53, 106–126. [Google Scholar] [CrossRef]
- Giri, B.C.; Bardhan, S. Coordinating a supply chain under uncertain demand and random yield in presence of supply disruption. Int. J. Prod. Res. 2015, 53, 5070–5084. [Google Scholar] [CrossRef]
- Heydaryan, H.; Taleizadeh, A.A. Pricing strategy, return policy and coordination in a two-stage supply chain. Int. J. System Sci. Oper. Logis. 2017, 4, 384–391. [Google Scholar] [CrossRef]
- Hu, X.; Wan, Z.; Murthy, N.N. Dynamic pricing of limited inventories with product returns. Manu. Serv. Oper. Manag. 2019, 21, 501–518. [Google Scholar] [CrossRef]
- Noori-daryan, M.; Taleizadeh, A.A. Optimizing pricing and ordering strategies in a three-level supply chain under return policy. J. Ind. Eng. Int. 2019, 15, 73–80. [Google Scholar] [CrossRef][Green Version]
- Ren, M.; Liu, J.; Feng, S.; Yang, A. Pricing and return strategy of online retailers based on return insurance. Retail. Consum. Serv. 2021, 59, 102350. [Google Scholar] [CrossRef]
- Yue, X.; Mukhopadhyay, S.; Zhu, X. A Bertrand model of pricing of complementary goods under information asymmetry. J. Bus. Res. 2006, 59, 1182–1192. [Google Scholar] [CrossRef]
- Bilotkach, V. Quality coordination and complementary products. Appl. Econ. 2010, 42, 1875–1888. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.K.; Yue, X.H.; Zhu, X.W. A Stackelberg model of pricing of complementary goods under information asymmetry. Int. J. Prod. Econ. 2011, 134, 424–433. [Google Scholar] [CrossRef]
- Yan, R.; Bandyopadhyay, S. The profit benefits of bundle pricing of complementary products. J. Retail. Consum. Serv. 2011, 18, 355–361. [Google Scholar] [CrossRef]
- Wei, J.; Zhao, J.; Li, Y. Pricing decisions for complementary products with firms’ different market powers. Eur. J. Oper. Res. 2013, 224, 507–519. [Google Scholar] [CrossRef]
- Wei, J.; Zhao, J.; Li, Y. Price and warranty period decisions for complementary products with horizontal firms’ cooperation/noncooperation strategies. J. Clean. Prod. 2015, 105, 86–102. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Charmchi, M. Optimal advertising and pricing decisions for complementary products. J. Ind. Eng. Int. 2015, 11, 111–117. [Google Scholar] [CrossRef]
- Dehghanbaghi, N.; Sajadieh, M.S. Joint optimization of production, transportation and pricing policies of complementary products in a supply chain. Comput. Ind. Eng. 2017, 107, 150–157. [Google Scholar] [CrossRef]
- Wang, L.; Song, H.; Wang, Y. Pricing and service decisions of complementary products in a dual-channel supply chain. Comput. Ind. Eng. 2017, 105, 223–233. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Babaei, M.S.; Sana, S.S.; Sarkar, B. Pricing decision within an inventory model for complementary and substitutable products. Mathematics 2019, 7, 568. [Google Scholar] [CrossRef]
- Giri, R.N.; Mondal, S.K.; Maiti, M. Bundle pricing strategies for two complementary products with different channel powers. Ann. Oper. Res. 2020, 287, 701–725. [Google Scholar] [CrossRef]
- Ren, D.; Lan, Y.; Shang, C.; Wang, J.; Xue, C. Impacts of trade credit on pricing decisions of complementary products. Comput. Ind. Eng. 2020, 146, 106580. [Google Scholar] [CrossRef]
- Shan, H.; Zhang, C.; Wei, G. Bundling or Unbundling? Pricing Strategy for Complementary Products in a Green Supply Chain. Sustainability 2020, 12, 1331. [Google Scholar] [CrossRef]
- Coughlan, A.T. Distribution channel choice in a market with complementary goods. Int. J. Res. Mark. 1987, 4, 85–97. [Google Scholar] [CrossRef]
- Balachander, S. Warranty signaling and reputation. Manag. Sci. 2001, 47, 1282–1289. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Kalantary, S.S.; Cárdenas-Barrón, L.E. Pricing and Lot sizing for an EPQ Inventory Model with Rework and Multiple Shipments. TOP 2016, 24, 143–155. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Noori-Daryan, M. Pricing, Replenishments and Production Policies in a Supply Chain of Pharmacological Product with Rework Process: A Game Theoretic Approach. Oper. Res. Int. J. 2016, 16, 89–115. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Alizadeh-Pasban, N.; Sarker, B.R. Coordinated contracts in a two-level green supply chain considering pricing strategy. Comput. Ind. Eng. 2018, 124, 249–275. [Google Scholar] [CrossRef]
- Taleizadeh, A.A. Lot sizing model with advance payment and disruption in supply under planned partial backordering. Int. Trans. Oper. Res. 2017, 24, 783–800. [Google Scholar] [CrossRef]
- Lashgari, M.; Taleizadeh, A.A.; Ahmadi, A. Partial up-stream advanced payment and partial down-stream delayed payment in a three-level supply chain. Ann. Oper. Res. 2016, 238, 329–354. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Niaki, S.T.A.; Hosseini, V. Optimizing Multi Product Multi Constraints Bi-objective Newsboy Problem with discount by Hybrid Method of Goal Programming and Genetic Algorithm. Eng. Optim. 2009, 41, 437–457. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).