G-RCenterNet: Reinforced CenterNet for Robotic Arm Grasp Detection
Abstract
:1. Introduction
- AG-RCenterNet based on the CenterNet framework is proposed for industrial robotic arm grasping tasks, providing precise grasp box predictions through image analysis and improving grasp detection effectiveness.
- An efficient search strategy is introduced to enhance the channel and spatial attention mechanisms, significantly improving the network’s feature extraction capability and detection accuracy. This optimization allows for more flexible and precise attention to relevant features.
- An adaptive loss function is designed specifically for grasp detection tasks, enabling the model to effectively predict feasible grasp boxes and improving localization performance and overall detection accuracy.
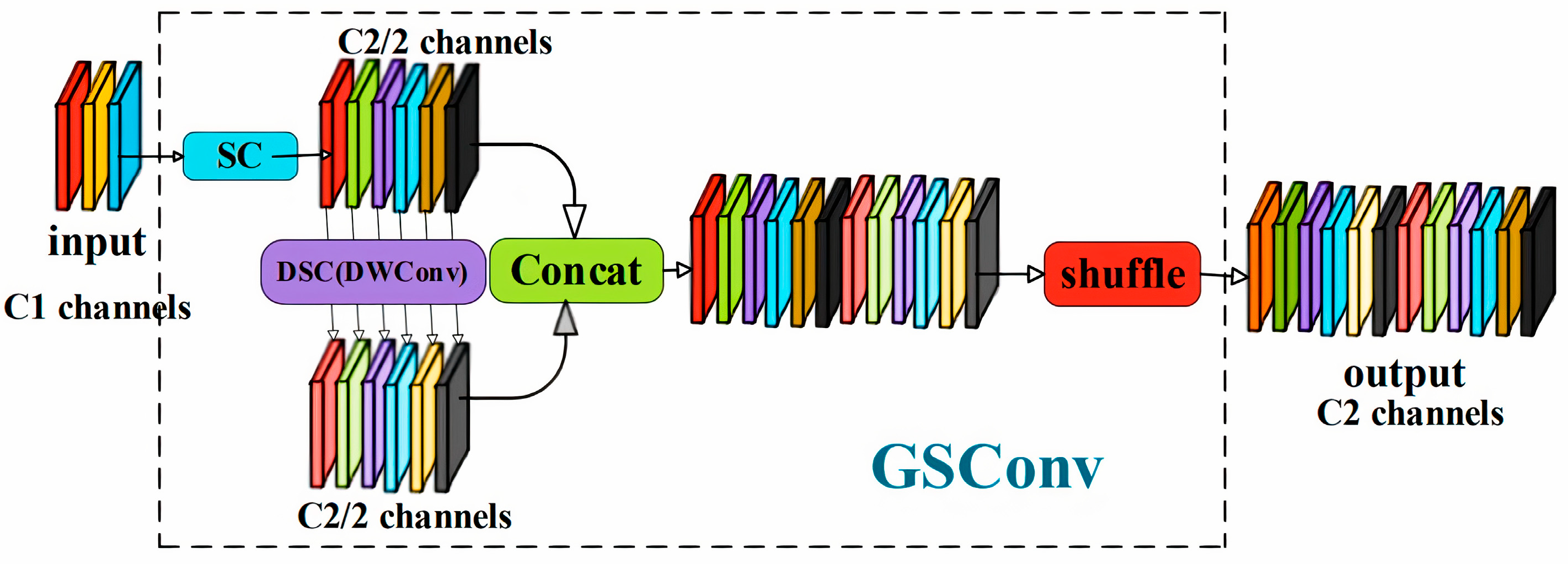
- The GSConv module is introduced in the prediction decoding phase to accelerate inference speed, ensuring real-time detection without compromising accuracy.
2. CenterNet Algorithm
3. Grasp-Reinforced CenterNet
3.1. Network Design
3.2. Loss Function Design
3.2.1. Key Point Estimation and Loss
3.2.2. Key Point Offset and Loss
3.2.3. Grasp Box Size Prediction and Loss
3.2.4. Grasp Angle Prediction and Loss
- (1)
- Identify the coordinates of the first two corner points, denoted as and .
- (2)
- Compute the direction vector by subtracting the coordinates of the first point from the second point, yielding .
- (3)
- Calculate the grasp angle using the arctangent function . The atan2 function returns the angle formed by the vector and the positive direction of the x-axis, with a range of . Since the grasp angle ranges from , the result of atan2 is adjusted accordingly.
3.2.5. Total Loss Function
3.3. Improved Convolution Block Attention Module
3.4. Lightweight Method Based on Improved Convolutional Modules
4. Experimental Validation
4.1. Grasp Detection Dataset
4.2. G-RCenterNet Training
4.3. Experimental Results and Analysis
- (1)
- The difference in rotation angle between the predicted and ground truth grasp boxes is within 30°.
- (2)
- The Jaccard index between the predicted and ground truth grasp boxes is greater than 25%.
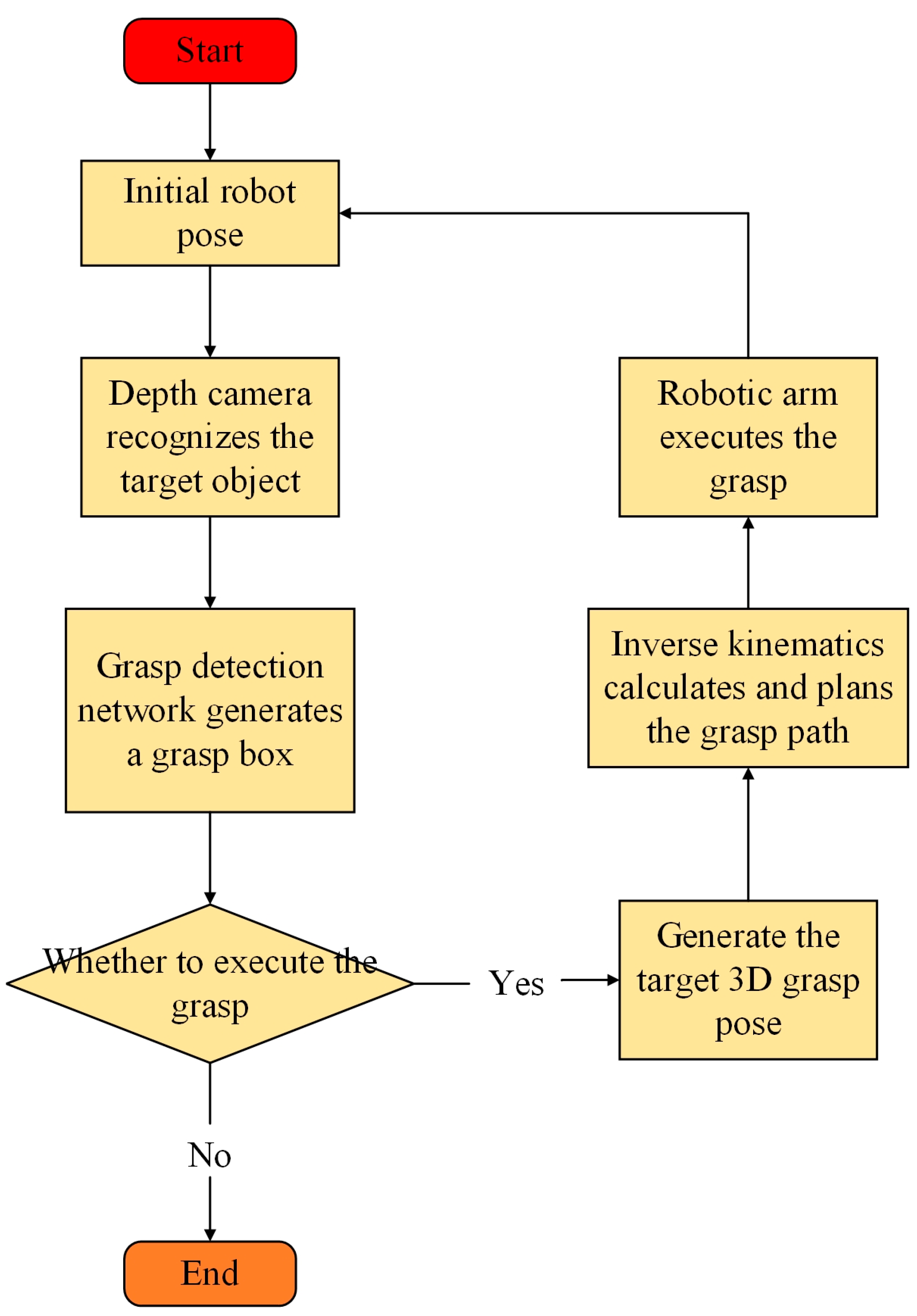
5. Robotic Arm Grasping Experiments in the Real World
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhong, M.; Zhang, Y.; Yang, X.; Yao, Y.; Guo, J.; Wang, Y.; Liu, Y. Assistive grasping based on laser-point detection with application to wheelchair-mounted robotic arms. Sensors 2019, 19, 303. [Google Scholar] [CrossRef]
- Xie, Y.; Tang, Y.; Zhou, R.; Guo, Y.; Shi, H. Map merging with terrain-adaptive density using mobile 3D laser scanner. Robot. Auton. Syst. 2020, 134, 103649. [Google Scholar] [CrossRef]
- Chen, F.; Wang, F.; Dong, Y.; Yong, Q.; Yang, X.; Zheng, L.; Gao, Y.; Su, H. Sensor fusion-based anthropomorphic control of a robotic arm. Bioengineering 2023, 10, 1243. [Google Scholar] [CrossRef] [PubMed]
- Veiga Almagro, C.; Muñoz Orrego, R.A.; García González, Á.; Matheson, E.; Marín Prades, R.; Di Castro, M.; Ferre Pérez, M. (MARGOT) Monocular Camera-Based Robot Grasping Strategy for Metallic Objects. Sensors 2023, 23, 5344. [Google Scholar] [CrossRef] [PubMed]
- Bai, Q.; Li, S.; Yang, J.; Song, Q.; Li, Z.; Zhang, X. Object detection recognition and robot grasping based on machine learning: A survey. IEEE access 2020, 8, 181855–181879. [Google Scholar] [CrossRef]
- Wong, A.; Wu, Y.; Abbasi, S.; Nair, S.; Chen, Y.; Shafiee, M.J. Fast GraspNeXt: A Fast Self-Attention Neural Network Architecture for Multi-task Learning in Computer Vision Tasks for Robotic Grasping on the Edge. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 2293–2297. [Google Scholar]
- Lenz, I.; Lee, H.; Saxena, A. Deep learning for detecting robotic grasps. Int. J. Robot. Res. 2015, 34, 705–724. [Google Scholar] [CrossRef]
- Kumra, S.; Kanan, C. Robotic grasp detection using deep convolutional neural networks. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 769–776. [Google Scholar]
- Mahler, J.; Liang, J.; Niyaz, S.; Laskey, M.; Doan, R.; Liu, X.; Ojea, J.A.; Goldberg, K. Dex-net 2.0: Deep learning to plan robust grasps with synthetic point clouds and analytic grasp metrics. arXiv 2017, arXiv:1703.09312. [Google Scholar]
- Zhou, X.; Lan, X.; Zhang, H.; Tina, Z.; Zhang, Y.; Zheng, N. Fully convolutional grasp detection network with oriented anchor box. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7223–7230. [Google Scholar]
- Liu, C.; Jiang, D.; Lin, W.; Gomes, L. Robot Grasping Based on Stacked Object Classification Network and Grasping Order Planning. Electronics 2022, 11, 706. [Google Scholar] [CrossRef]
- Hu, J.; Li, Q.; Bai, Q. Research on Robot Grasping Based on Deep Learning for Real-Life Scenarios. Micromachines 2023, 14, 1392. [Google Scholar] [CrossRef]
- Zou, M.; Li, X.; Yuan, Q.; Xiong, T.; Zhang, Y.; Han, J.; Xiao, Z. Robotic Grasp Detection Network Based on Improved Deformable Convolution and Spatial Feature Center Mechanism. Biomimetics 2023, 8, 403. [Google Scholar] [CrossRef] [PubMed]
- Villagomez, R.C.; Ordoñez, J. Robot grasping based on RGB object and grasp detection using deep learning. In Proceedings of the 2022 8th International Conference on Mechatronics and Robotics Engineering (ICMRE), Munich, Germany, 10–12 February 2022; pp. 84–90. [Google Scholar]
- Yu, S.; Zhai, D.H.; Xia, Y.; Wu, H.; Liao, J. SE-ResUNet: A novel robotic grasp detection method. IEEE Robot. Autom. Lett. 2022, 7, 5238–5245. [Google Scholar] [CrossRef]
- Li, Z.; Xu, B.; Wu, D.; Zhao, K.; Chen, S.; Lu, M.; Cong, J. A YOLO-GGCNN based grasping framework for mobile robots in unknown environments. Expert Syst. Appl. 2023, 225, 119993. [Google Scholar] [CrossRef]
- Gao, H.; Zhao, J.; Sun, C. A Real-Time Grasping Detection Network Architecture for Various Grasping Scenarios. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 7499–7519. [Google Scholar] [CrossRef] [PubMed]
- Weng, Y.; Sun, Y.; Jiang, D.; Tao, B.; Liu, Y.; Yun, J.; Zhou, D. Enhancement of real-time grasp detection by cascaded deep convolutional neural networks. Concurr. Comput. Pract. Exp. 2021, 33, e5976. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, T.; Du, B.; Zhao, J. Research on Deep Learning-Based Lightweight Object Grasping Algorithm for Robots. In Proceedings of the Computer Graphics International Conference, Shanghai, China, 28 August–1 September 2023; Springer Nature: Cham, Switzerland, 2023; pp. 438–448. [Google Scholar]
- Law, H.; Deng, J. Cornernet: Detecting objects as paired keypoints. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 734–750. [Google Scholar]
- Zhou, X.; Zhuo, J.; Krahenbuhl, P. Bottom-up object detection by grouping extreme and center points. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 850–859. [Google Scholar]
- Duan, K.; Bai, S.; Xie, L.; Qi, H.; Huang, Q.; Tian, Q. Centernet: Keypoint triplets for object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Long Beach, CA, USA, 15–20 June 2019; pp. 6569–6578. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Li, H.; Li, J.; Wei, H.; Liu, Z.; Zhan, Z.; Ren, Q. Slim-neck by GSConv: A better design paradigm of detector architectures for autonomous vehicles. arXiv 2022, arXiv:2206.02424. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.T.; Sun, J. Shufflenet v2: Practical guidelines for efficient cnn architecture design. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 116–131. [Google Scholar]
- Morrison, D.; Corke, P.; Leitner, J. Closing the loop for robotic grasping: A real-time, generative grasp synthesis approach. arXiv 2018, arXiv:1804.05172. [Google Scholar]
- Yun, J.; Jiang, D.; Huang, L.; Tao, B. Grasping detection of dual manipulators based on Markov decision process with neural network. Neural Netw. 2024, 169, 778–792. [Google Scholar] [CrossRef] [PubMed]
- Depierre, A.; Dellandréa, E.; Chen, L. Jacquard: A large scale dataset for robotic grasp detection. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 3511–3516. [Google Scholar]
- Chu, F.J.; Xu, R.; Vela, P.A. Real-world multiobject, multigrasp detection. IEEE Robot. Autom. Lett. 2018, 3, 3355–3362. [Google Scholar] [CrossRef]
- Karaoguz, H.; Jensfelt, P. Object detection approach for robot grasp detection. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4953–4959. [Google Scholar]
- Asif, U.; Tang, J.; Harrer, S. GraspNet: An Efficient Convolutional Neural Network for Real-time Grasp Detection for Low-powered Devices. In Proceedings of the IJCAI, Stockholm, Sweden, 13–19 July 2018; Volume 7, pp. 4875–4882. [Google Scholar]
- Kumra, S.; Joshi, S.; Sahin, F. Antipodal robotic grasping using generative residual convolutional neural network. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2020; pp. 9626–9633. [Google Scholar]













| Network Model | Accuracy (%) | FPS |
|---|---|---|
| G-CenterNet | 90.7 | 48.6 |
| G-CenterNet + CBAM | 94.4 | 44.8 |
| G-CenterNet + improved CBAM | 95.8 | 47.1 |
| G-CenterNet + GSConv | 89.9 | 54.1 |
| G-CenterNet + improved CBAM + GSConv (Proposed) | 95.6 | 53 |
| Backbone Network | Accuracy (%) | FPS |
|---|---|---|
| ResNet18 | 93.3 | 48.4 |
| MobileNetV2 | 91.7 | 41.1 |
| ResNet101 | 96.9 | 68.5 |
| ResNet50 (Proposed) | 95.6 | 53 |
| Source | Method | Accuracy (%) | FPS |
|---|---|---|---|
| Morrison [27] | GG-CNN | 73 | 52.63 |
| Kumra [7] | ResNet-50×2 | 89.2 | 9.71 |
| Lenz [6] | SAE, struct. reg | 73.9 | 0.74 |
| Chu [30] | Multi grasp RestNet-50 | 96.0 | 8.33 |
| Karaoguz [31] | GRPN | 88.7 | 5 |
| Asif [32] | GraspNet | 90.2 | 41.67 |
| Sulabh [33] | GR-ConvNet-RGB-D | 96.7 | 50 |
| Yu [15] | SE-ResNet | 97.1 | 40 |
| Proposed | G-RCenterNet | 95.6 | 53 |
| Category | Grasp Attempts | Successful Grabs | Success Rate (%) |
|---|---|---|---|
| Plastic bottle | 25 | 23 | 92 |
| Cup | 25 | 24 | 96 |
| Nut | 25 | 18 | 72 |
| Mouse | 25 | 21 | 84 |
| Total | 100 | 86 | 86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, J.; Cao, G. G-RCenterNet: Reinforced CenterNet for Robotic Arm Grasp Detection. Sensors 2024, 24, 8141. https://doi.org/10.3390/s24248141
Bai J, Cao G. G-RCenterNet: Reinforced CenterNet for Robotic Arm Grasp Detection. Sensors. 2024; 24(24):8141. https://doi.org/10.3390/s24248141
Chicago/Turabian StyleBai, Jimeng, and Guohua Cao. 2024. "G-RCenterNet: Reinforced CenterNet for Robotic Arm Grasp Detection" Sensors 24, no. 24: 8141. https://doi.org/10.3390/s24248141
APA StyleBai, J., & Cao, G. (2024). G-RCenterNet: Reinforced CenterNet for Robotic Arm Grasp Detection. Sensors, 24(24), 8141. https://doi.org/10.3390/s24248141





