Load-Balanced Dynamic SFC Migration Based on Resource Demand Prediction
Abstract
1. Introduction
- Considering the real SFC request scenario, we use a time-varying traffic dataset. We apply a CNN-AT-LSTM model to predict the short-term resource demands of VNFs. Using these predictions, we can proactively migrate VNFs in advance within a certain time frame.
- Considering that dynamic changes in traffic may lead to frequent VNF migration and uneven use of network resources, we introduce a load-balancing model to maintain network stability.
- In response to the multi-dimensionality and complexity of the VNF migration remapping problem caused by the dynamic network environment, we propose a DRL algorithm based on Proximal Policy Optimization (PPO) to enhance the effectiveness of VNF migration decisions.
2. Related Work
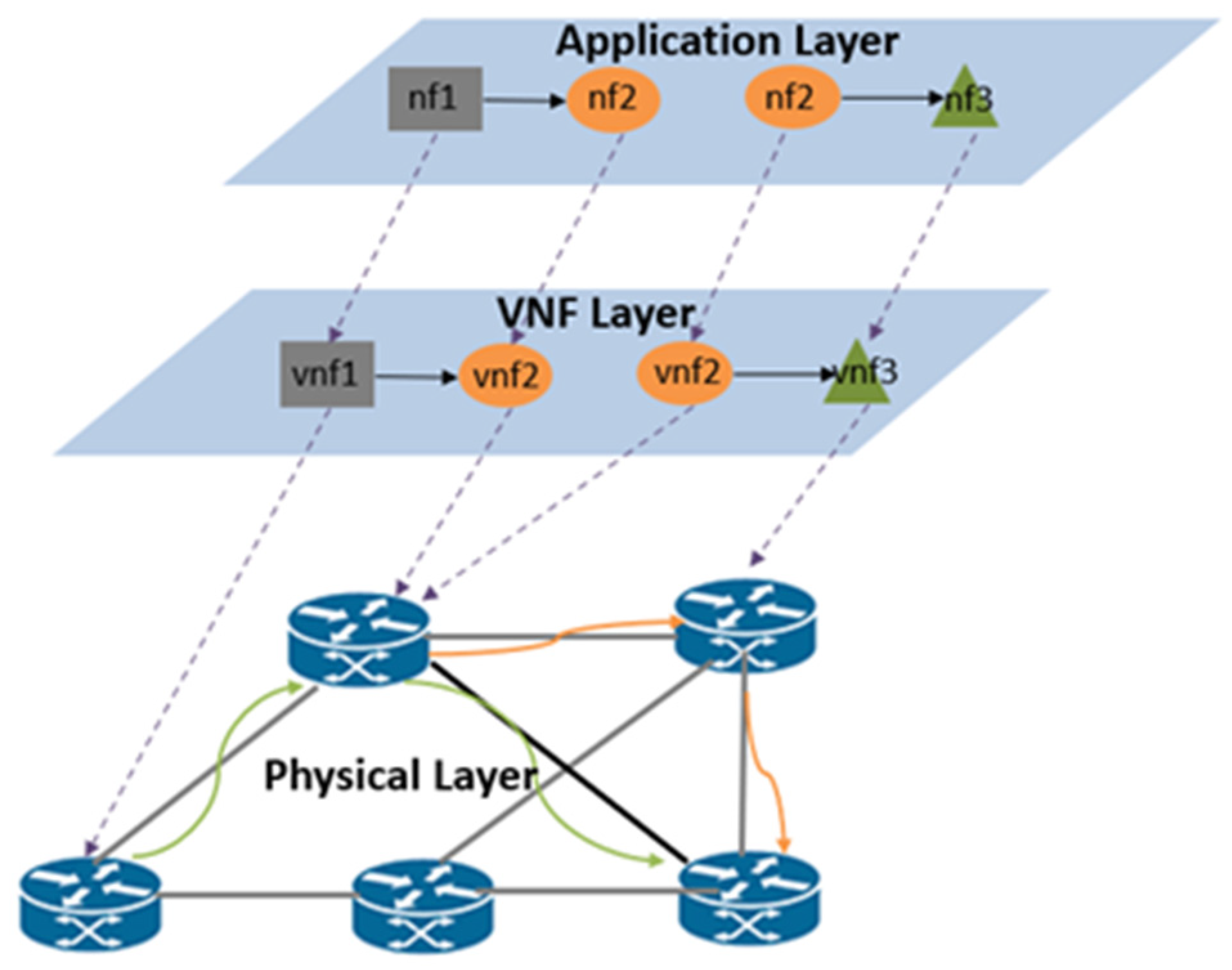
3. System Model and Problem Description
3.1. Network Model
3.2. SFC and VNF
3.3. Load Balancing Model
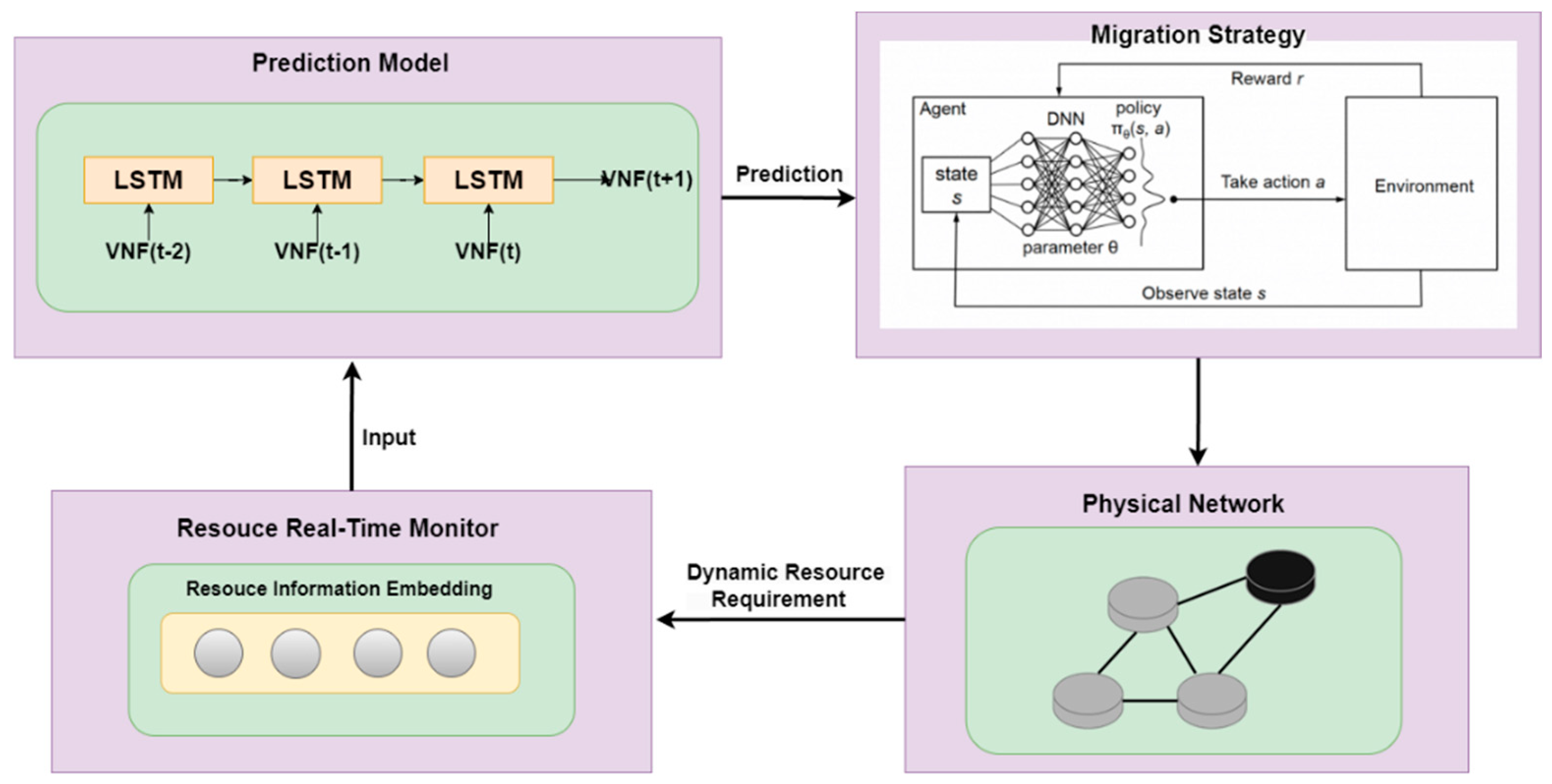
4. Algorithm Design
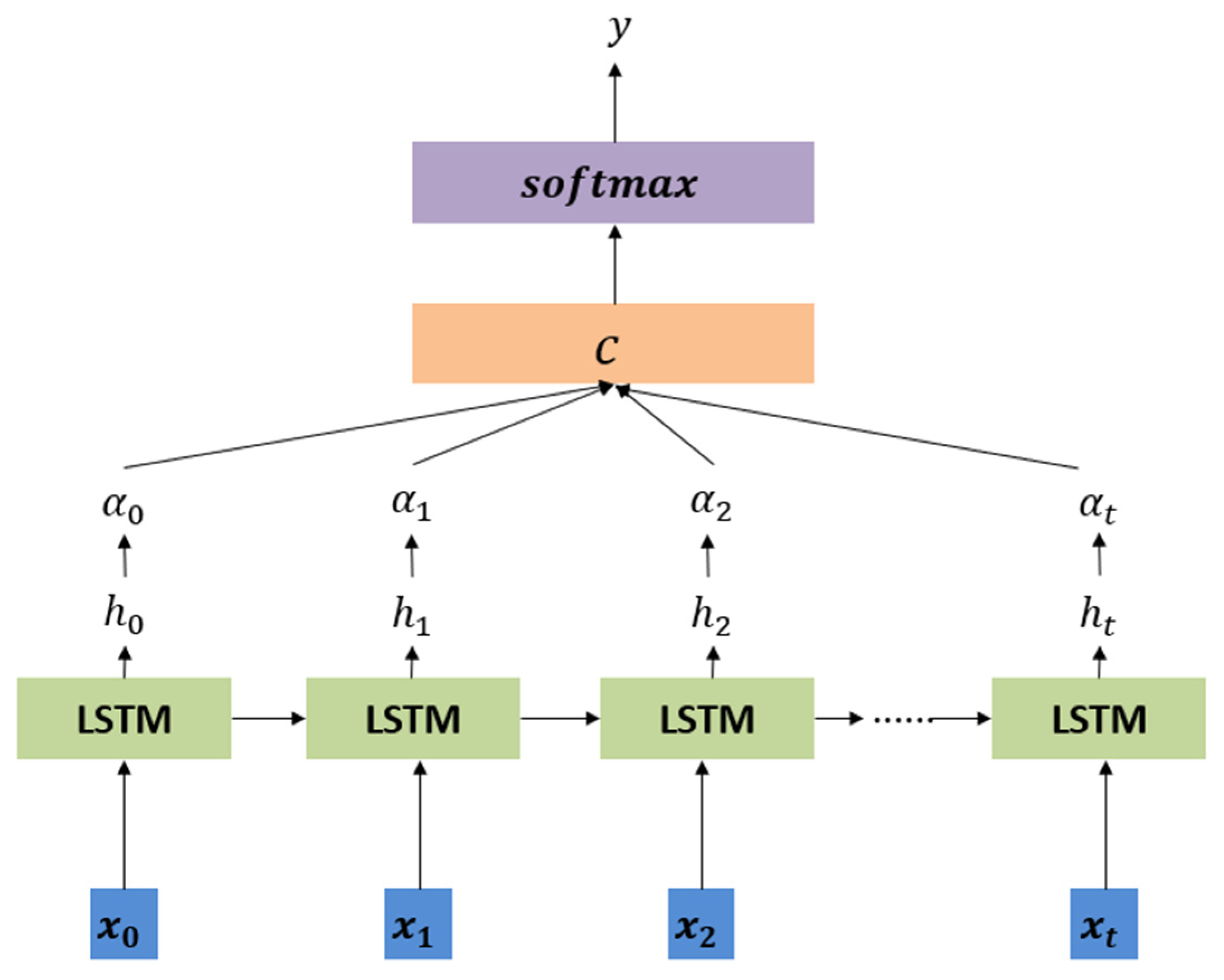
4.1. LSTM-Based Resource Demand Prediction Algorithm
4.2. PPO-Based SFC Migration Algorithm
4.2.1. MDP Model
4.2.2. Proximal Policy Optimization Algorithm
4.3. Resource Predictive Load Balancing SFC Migration Algorithm
| Algorithm 1 Resource Predictive Load Balancing SFC Migration Algorithm (RP-LBM) | |
| 1 | Input: Prediction result Physical network diagram ; SFC network diagram |
| 2 | Output: SFC mapping strategy ; |
| 3 | Calculate the resource utilization of each physical node according to the prediction result; |
| 4 | if then |
| 5 | Select an SFC to migrate on that node; |
| 6 | Initialize , M, (); |
| 7 | for episode = 1, …, M do |
| 8 | Select mapping actions from the strategies ; |
| 9 | if constraints are satisfied then |
| 10 | Execute the action , get the instantaneous reward |
| 11 | r and transfer it to the state s; |
| 12 | Obtain the advantage function ; |
| 13 | else |
| 14 | Set instantaneous reward r(t) = , and re-select the action from the policy network; |
| 15 | end if |
| 16 | Compute the clipped surrogate objective for PPO |
| 17 | Update the policy parameters using gradient ascent |
| 18 | Update the value function parameters using gradient descent |
| 19 | end for |
| 20 | end if |
5. Performance Evaluation
5.1. Simulation Setup
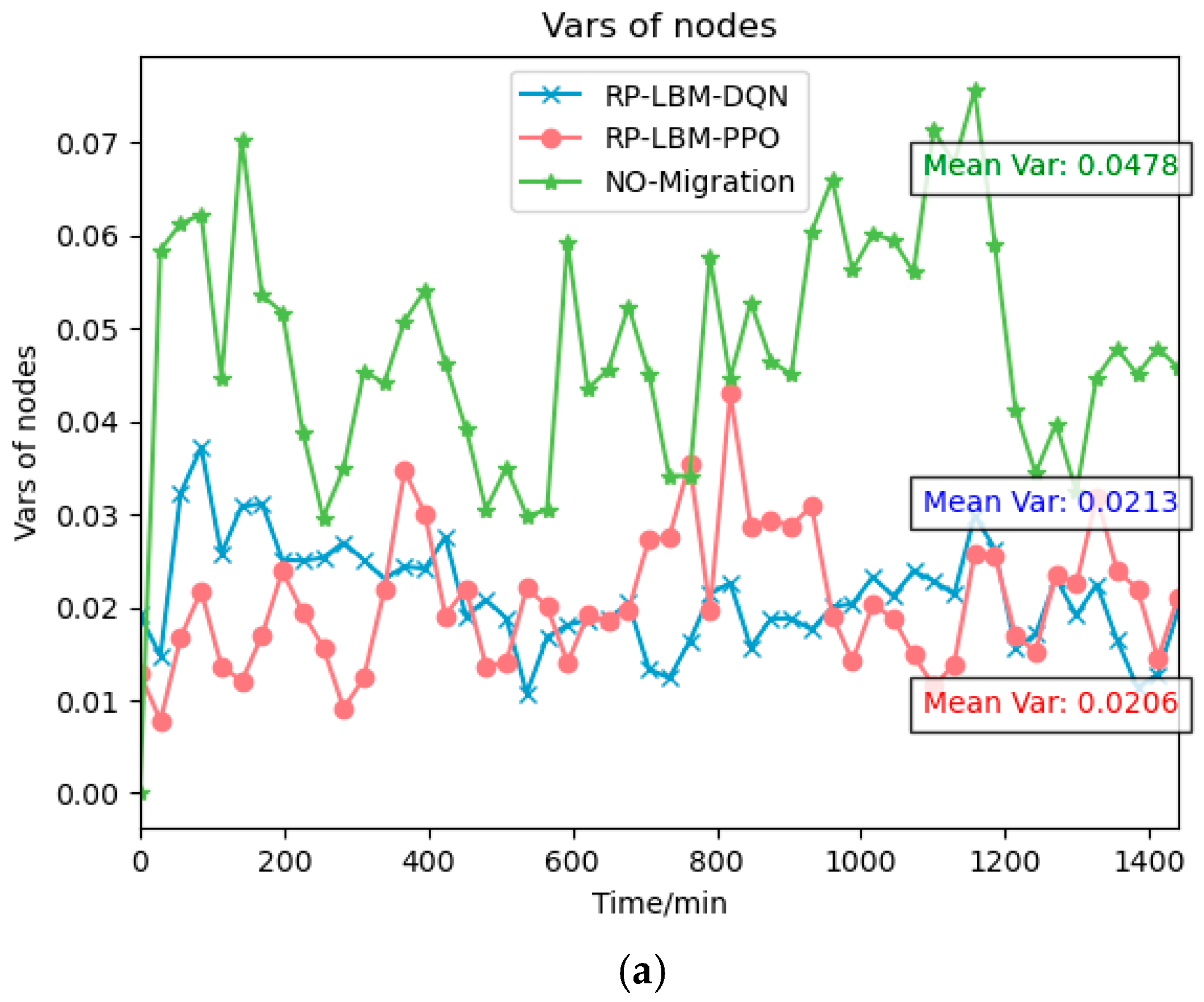
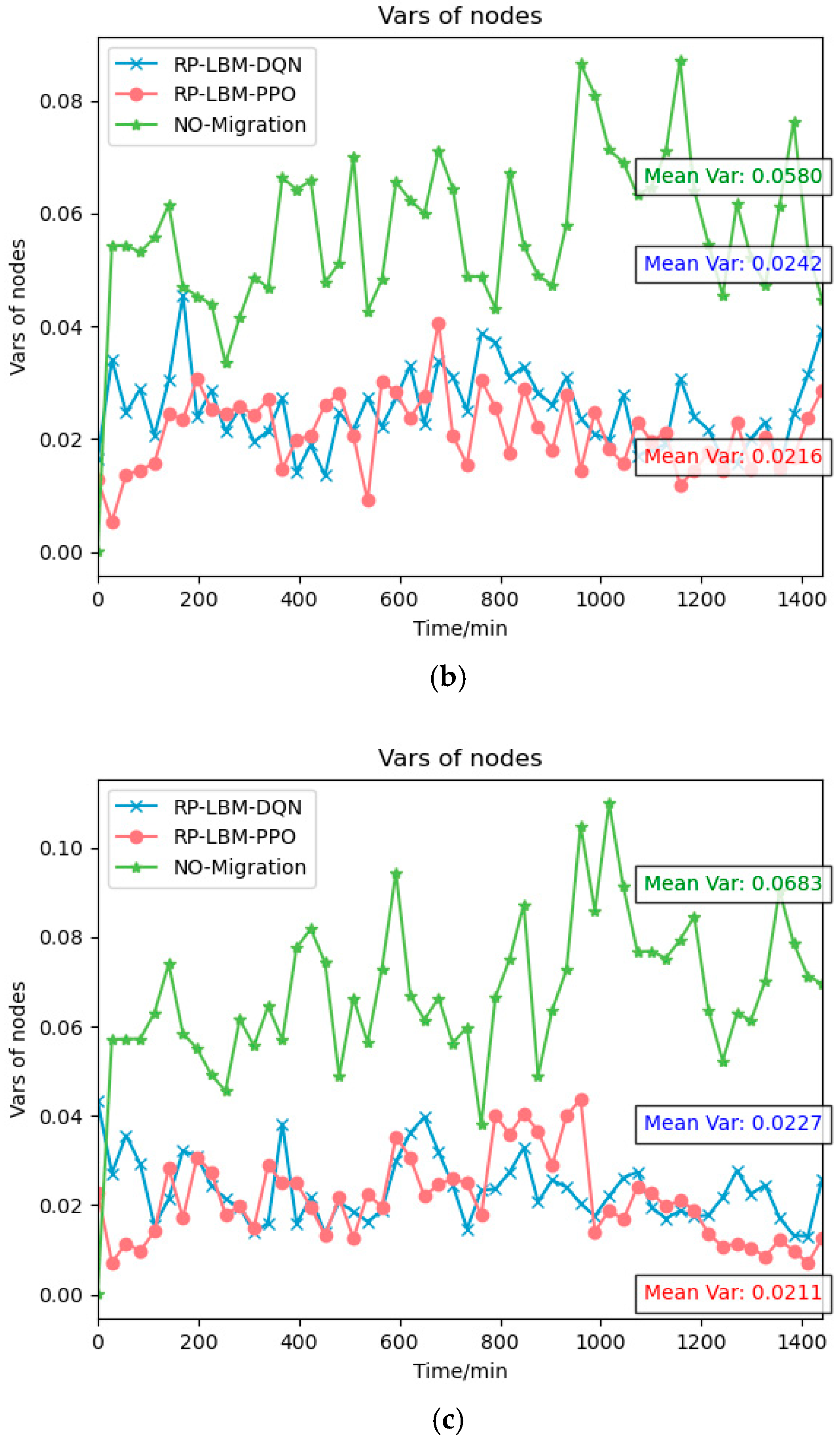
5.2. Simulation Result and Analysis
6. Conclusions
6.1. Summary of the Performance
6.2. Potential Future Research Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhamare, D.; Jain, R.; Samaka, M.; Erbad, A. A Survey on Service Function Chaining. J. Netw. Comput. Appl. 2016, 75, 138–155. [Google Scholar] [CrossRef]
- Qu, K.; Zhuang, W.; Shen, X.; Li, X.; Rao, J. Dynamic Resource Scaling for VNF over Nonstationary Traffic: A Learning Approach. IEEE Trans. Cogn. Commun. Netw. 2020, 7, 648–662. [Google Scholar] [CrossRef]
- Guo, Z.; Xu, Y.; Liu, Y.F.; Liu, S.; Chao, H.J.; Zhang, Z.-L.; Xia, Y. AggreFlow: Achieving Power Efficiency, Load Balancing, and Quality of Service in Data Center Networks. IEEE/ACM Trans. Netw. 2020, 29, 17–33. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Chen, J.; Cheng, X.; Guo, K.; Qin, Y. A Deep Q-Learning Based VNF Migration Strategy for Elastic Control in SDN/NFV Network. In Proceedings of the 2021 International Conference on Wireless Communications and Smart Grid (ICWCSG), Hangzhou, China, 26–28 November 2021; pp. 217–223. [Google Scholar]
- Tanuboddi, B.R.; Gad, G.; Fadlullah, Z.M.; Fouda, M.M. Optimizing VNF Migration in B5G Core Networks: A Machine Learning Approach. In Proceedings of the 2024 International Conference on Smart Applications, Communications and Networking (SmartNets), Harrisonburg, VA, USA, 28–30 May 2024; pp. 1–5. [Google Scholar]
- Afrasiabi, S.N.; Ebrahimzadeh, A.; Promwongsa, N.; Mouradian, C.; Li, W.; Recse, Á.; Szabó, R.; Glitho, R.H. Cost-Efficient Cluster Migration of VNFs for Service Function Chain Embedding. IEEE Trans. Netw. Serv. Manag. 2024, 21, 979–993. [Google Scholar] [CrossRef]
- Kim, H.G.; Lee, D.Y.; Jeong, S.Y.; Choi, H.; Yoo, J.H.; Hong, J.W. Machine Learning-Based Method for Prediction of Virtual Network Function Resource Demands. In Proceedings of the 2019 IEEE Conference on Network Softwarization (NetSoft), Paris, France, 24–28 June 2019; pp. 405–413. [Google Scholar]
- Bellili, A.; Kara, N. A Graphical Deep Learning Technique-Based VNF Dependencies for Multi Resource Requirements Prediction in Virtualized Environments. Computing 2024, 106, 449–473. [Google Scholar] [CrossRef]
- Zhu, R.; Li, G.; Zhang, Y.; Fang, Z.; Wang, J. Load-Balanced Virtual Network Embedding Based on Deep Reinforcement Learning for 6G Regional Satellite Networks. IEEE Trans. Veh. Technol. 2023, 72, 14631–14644. [Google Scholar] [CrossRef]
- Chiang, M.L.; Hsieh, H.C.; Cheng, Y.H.; Lin, W.L.; Zeng, B.H. Improvement of Tasks Scheduling Algorithm Based on Load Balancing Candidate Method under Cloud Computing Environment. Expert Syst. Appl. 2023, 212, 118714. [Google Scholar] [CrossRef]
- Wen, T.; Yu, H.; Sun, G.; Liu, L. Network function consolidation in service function chaining orchestration. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar]
- Li, B.; Cheng, B.; Liu, X.; Wang, M.; Yue, Y.; Chen, J. Joint Resource Optimization and Delay-Aware Virtual Network Function Migration in Data Center Networks. IEEE Trans. Netw. Serv. Manag. 2021, 18, 2960–2974. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, Y.; Li, X.; Yao, Z.; Zhao, D. On Dynamic Service Function Chain Reconfiguration in IoT Networks. IEEE Internet Things J. 2020, 7, 10969–10984. [Google Scholar] [CrossRef]
- Wan, A.; Chang, Q.; Khalil, A.B.; He, J. Short-Term Power Load Forecasting for Combined Heat and Power Using CNN-LSTM Enhanced by Attention Mechanism. Energy 2023, 282, 128274. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, H.; Wei, C.; Wang, J.; Bo, S.; Xiao, M. Research on Autonomous Driving Decision-Making Strategies Based Deep Reinforcement Learning. In Proceedings of the 4th International Conference on Internet of Things and Machine Learning, Nanchang, China, 9–11 August 2024. [Google Scholar]
- SFCSim Simulation Platform. Available online: https://pypi.org/project/sfcsim/ (accessed on 5 January 2021).
- Tang, L.; He, L.; Tan, Q.; Chen, Q. Virtual Network Function Migration Optimization Algorithm Based on Deep Deterministic Policy Gradient. J. Electron. Inf. Technol. 2021, 43, 404–411. [Google Scholar]
- VNFDataset: Virtual IP Multimedia IP System. Available online: https://www.kaggle.com/imenbenyahia/clearwatervnf-virtual-ip-multimedia-ip-system (accessed on 30 January 2021).
- Xu, L. Research on Key Technologies of Service Function Chain Orchestration Optimization for Mobile Scenarios. Ph.D. Dissertation, Beijing University of Posts and Telecommunications, Beijing, China, 2023. [Google Scholar]





| Metric | LSTM | CNN-AT-LSTM | LSTM–Encoder–Decoder |
|---|---|---|---|
| MSE | 21.973 | 15.579 | 19.653 |
| RMSE | 4.688 | 3.947 | 4.433 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Hu, H.; Zhang, S. Load-Balanced Dynamic SFC Migration Based on Resource Demand Prediction. Sensors 2024, 24, 8046. https://doi.org/10.3390/s24248046
Sun T, Hu H, Zhang S. Load-Balanced Dynamic SFC Migration Based on Resource Demand Prediction. Sensors. 2024; 24(24):8046. https://doi.org/10.3390/s24248046
Chicago/Turabian StyleSun, Tian, Hefei Hu, and Sirui Zhang. 2024. "Load-Balanced Dynamic SFC Migration Based on Resource Demand Prediction" Sensors 24, no. 24: 8046. https://doi.org/10.3390/s24248046
APA StyleSun, T., Hu, H., & Zhang, S. (2024). Load-Balanced Dynamic SFC Migration Based on Resource Demand Prediction. Sensors, 24(24), 8046. https://doi.org/10.3390/s24248046





