Surface-Dependent Isotopic Adsorption of CO on α-Al2O3: Role of Weak Interactions and Zero-Point Energy
Abstract
:1. Introduction
2. Results and Discussion
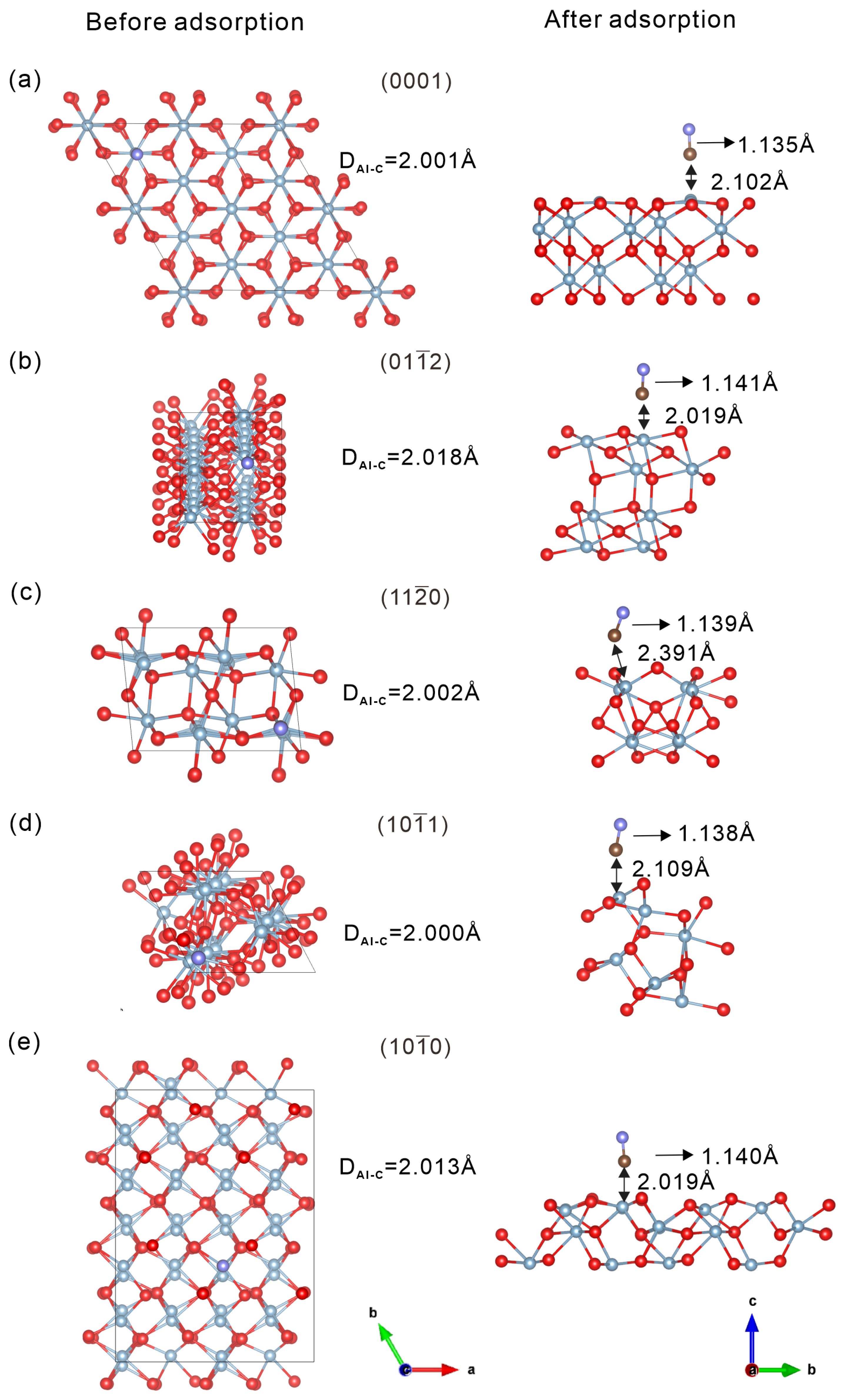
2.1. Surface Energy of Al2O3 Surfaces
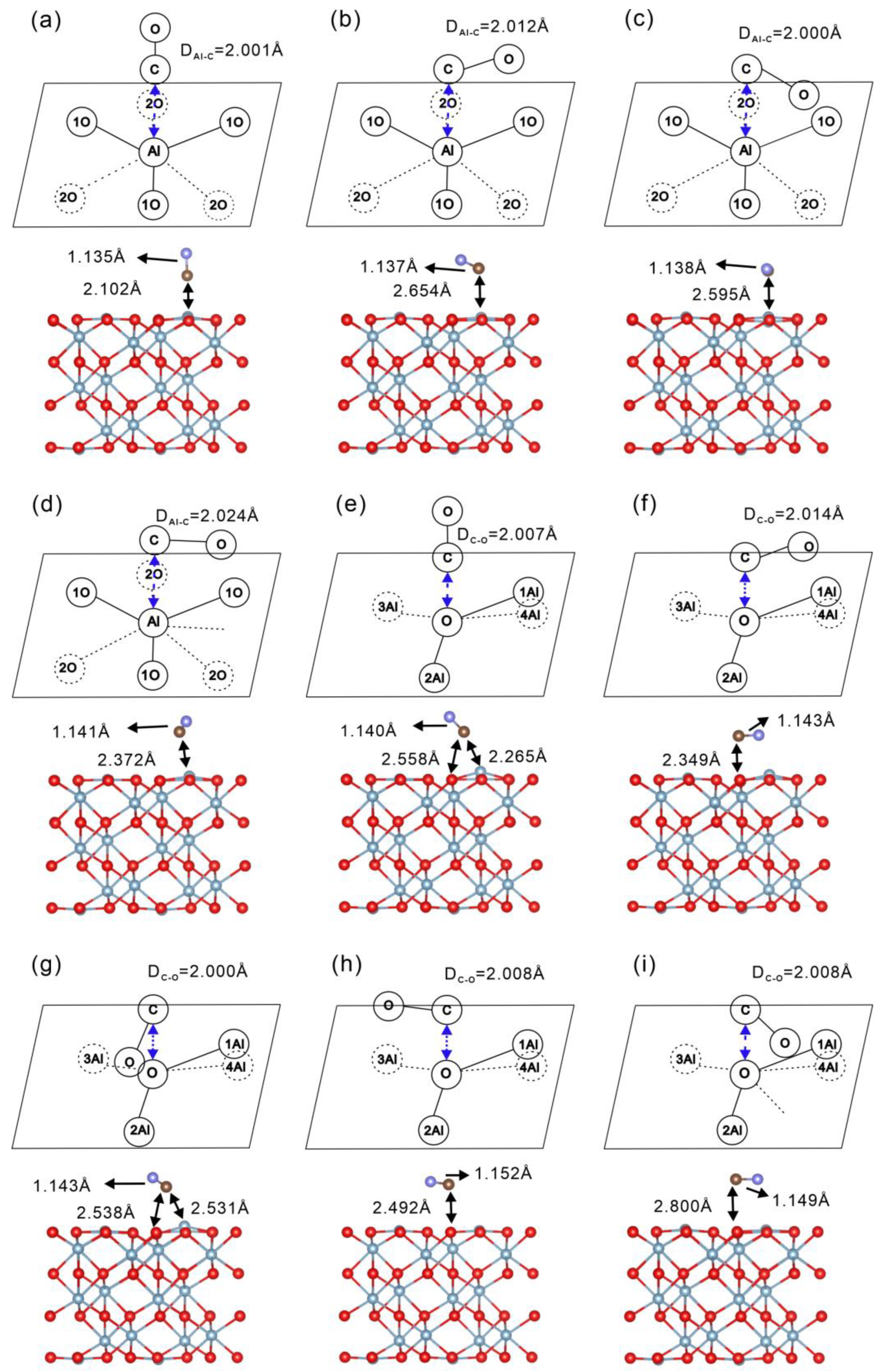
2.2. Adsorption of 12CO and 13CO on -Al2O3 ( ) Surface
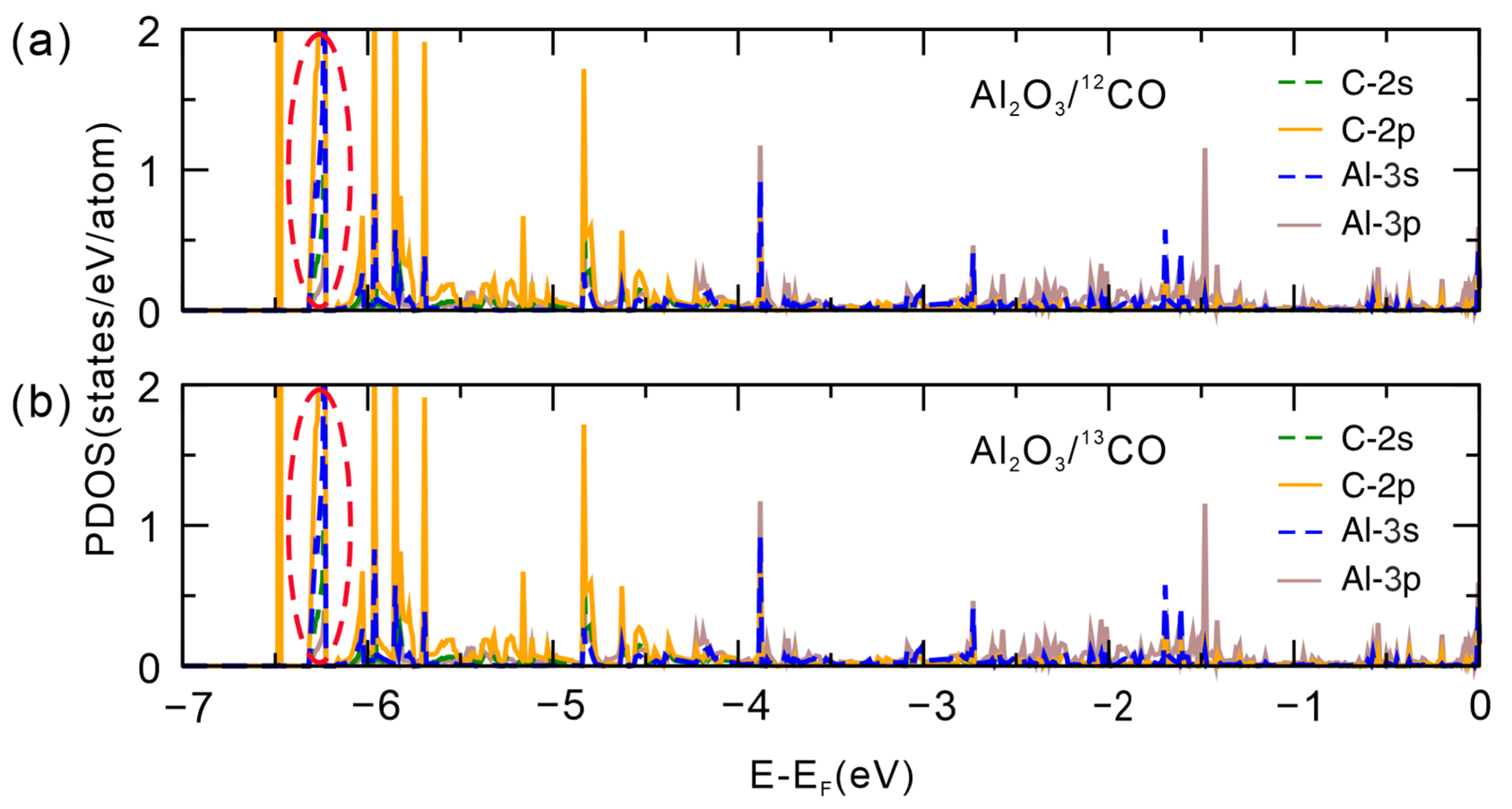
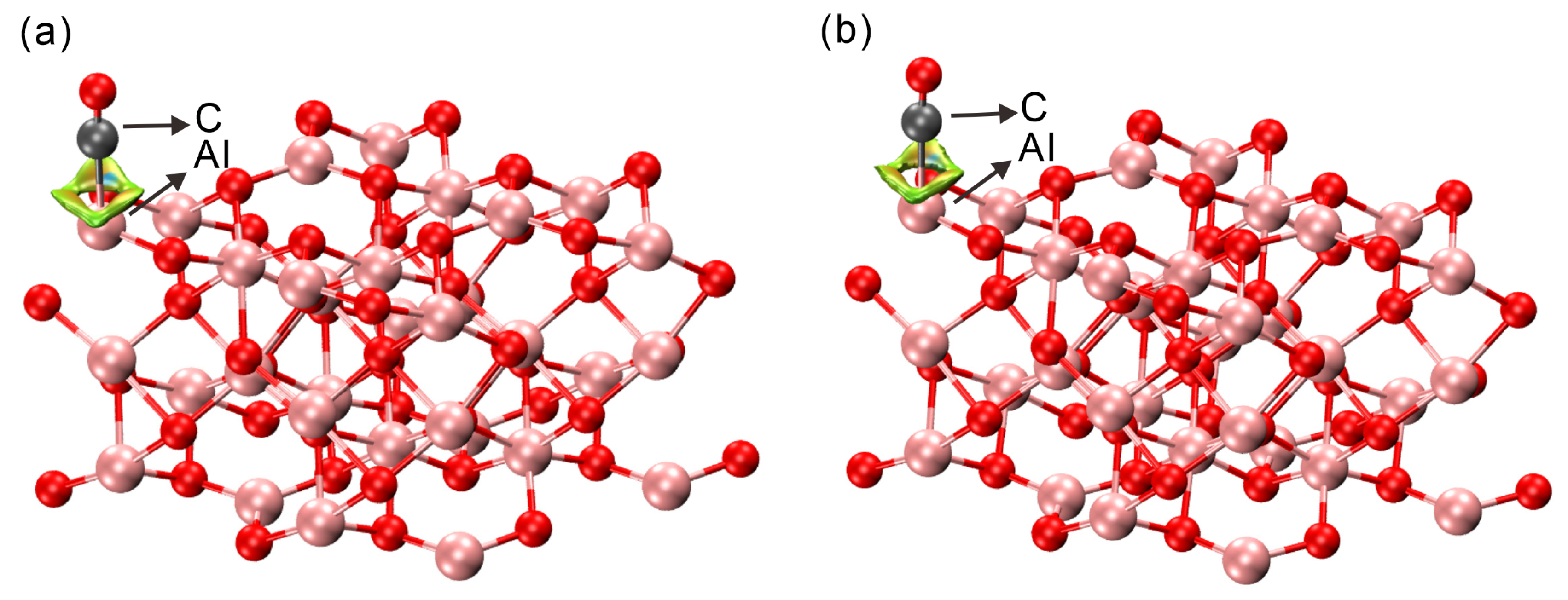
2.3. Bader Charge and Electronic Structure Analysis
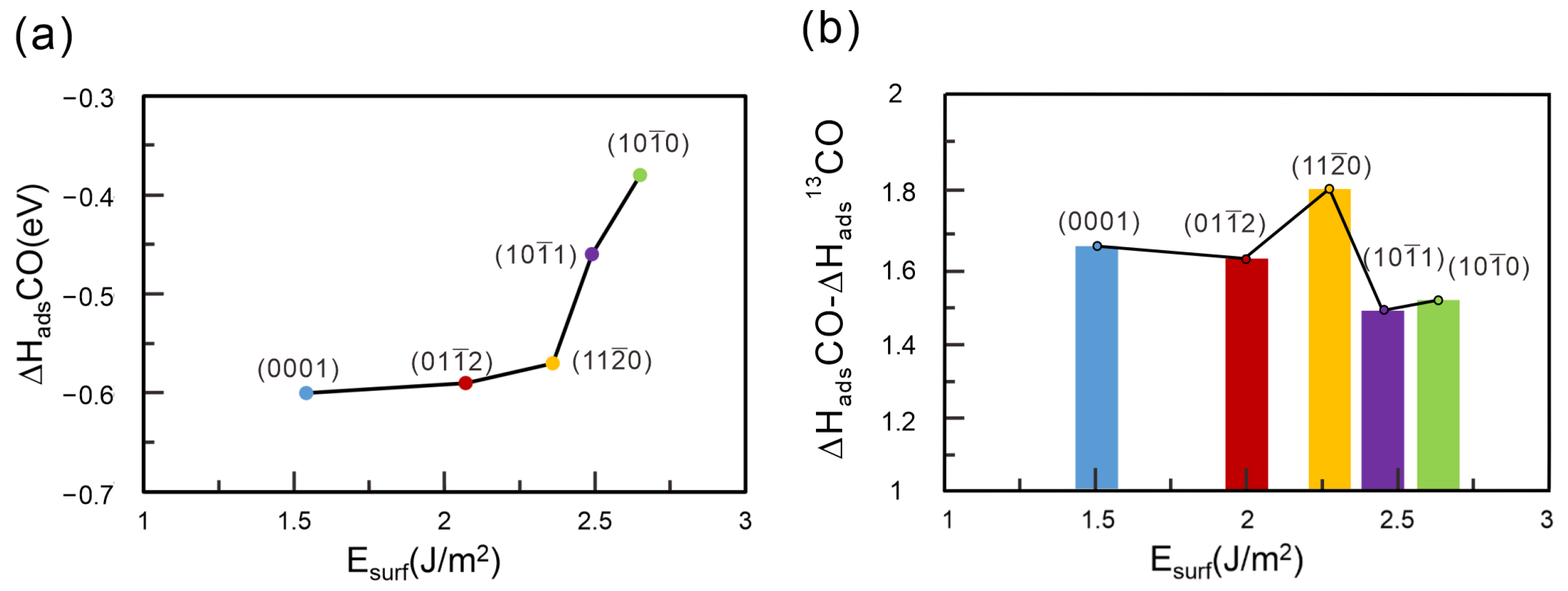
2.4. Comparison of 12CO and 13CO Separation Performance on Different -Al2O3 Surfaces
3. Computational Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wilkinson, D.J. Historical and Contemporary Stable Isotope Tracer Approaches to Studying Mammalian Protein Metabolism. Mass Spectrom. Rev. 2018, 37, 57–80. [Google Scholar] [CrossRef] [PubMed]
- Metallo, C.M.; Walther, J.L.; Stephanopoulos, G. Evaluation of 13C Isotopic Tracers for Metabolic Flux Analysis in Mammalian Cells. J. Biotechnol. 2009, 144, 167–174. [Google Scholar] [CrossRef] [PubMed]
- Davies, P.S.W. Stable Isotopes: Their Use and Safety in Human Nutrition Studies. Eur. J. Clin. Nutr. 2020, 74, 362–365. [Google Scholar] [CrossRef] [PubMed]
- Nelson, S.J.; Kurhanewicz, J.; Vigneron, D.B.; Larson, P.E.Z.; Harzstark, A.L.; Ferrone, M.; Van Criekinge, M.; Chang, J.W.; Bok, R.; Park, I.; et al. Metabolic Imaging of Patients with Prostate Cancer Using Hyperpolarized [1-13 C]Pyruvate. Sci. Transl. Med. 2013, 5, 198ra108. [Google Scholar] [CrossRef]
- Herold, R.; Becker, M. 13C-Urea Breath Test Threshold Calculation and Evaluation for the Detection of Helicobacter Pylori Infection in Children. BMC Gastroenterol. 2002, 2, 12. [Google Scholar] [CrossRef]
- Smith, B.N.; Epstein, S. Two Categories of13 C/12 C Ratios for Higher Plants. Plant Physiol. 1971, 47, 380–384. [Google Scholar] [CrossRef]
- Beenakker, J.J.M.; Borman, V.D.; Krylov, S.Y. Molecular Transport in Subnanometer Pores: Zero-Point Energy, Reduced Dimensionality and Quantum Sieving. Chem. Phys. Lett. 1995, 232, 379–382. [Google Scholar] [CrossRef]
- FitzGerald, S.A.; Pierce, C.J.; Rowsell, J.L.C.; Bloch, E.D.; Mason, J.A. Highly Selective Quantum Sieving of D2 from H2 by a Metal–Organic Framework as Determined by Gas Manometry and Infrared Spectroscopy. J. Am. Chem. Soc. 2013, 135, 9458–9464. [Google Scholar] [CrossRef]
- Kim, J.Y.; Zhang, L.; Balderas-Xicohténcatl, R.; Park, J.; Hirscher, M.; Moon, H.R.; Oh, H. Selective Hydrogen Isotope Separation via Breathing Transition in MIL-53(Al). J. Am. Chem. Soc. 2017, 139, 17743–17746. [Google Scholar] [CrossRef]
- Rae, H.K. Separation of Hydrogen Isotopes; ACS Publications: Washington, DC, USA, 1978. [Google Scholar]
- Hu, S.; Lozada-Hidalgo, M.; Wang, F.C.; Mishchenko, A.; Schedin, F.; Nair, R.R.; Hill, E.W.; Boukhvalov, D.W.; Katsnelson, M.I.; Dryfe, R.A.W.; et al. Proton Transport through One-Atom-Thick Crystals. Nature 2014, 516, 227–230. [Google Scholar] [CrossRef]
- Kim, J.Y.; Balderas-Xicohténcatl, R.; Zhang, L.; Kang, S.G.; Hirscher, M.; Oh, H.; Moon, H.R. Exploiting Diffusion Barrier and Chemical Affinity of Metal–Organic Frameworks for Efficient Hydrogen Isotope Separation. J. Am. Chem. Soc. 2017, 139, 15135–15141. [Google Scholar] [CrossRef]
- Su, Y.; Otake, K.; Zheng, J.-J.; Horike, S.; Kitagawa, S.; Gu, C. Separating Water Isotopologues Using Diffusion-Regulatory Porous Materials. Nature 2022, 611, 289–294. [Google Scholar] [CrossRef] [PubMed]
- Ujjain, S.K.; Bagusetty, A.; Matsuda, Y.; Tanaka, H.; Ahuja, P.; De Tomas, C.; Sakai, M.; Vallejos-Burgos, F.; Futamura, R.; Suarez-Martinez, I.; et al. Adsorption Separation of Heavier Isotope Gases in Subnanometer Carbon Pores. Nat. Commun. 2021, 12, 546. [Google Scholar] [CrossRef]
- Tian, Y.; Fei, W.; Wu, J. Separation of Carbon Isotopes in Methane with Nanoporous Materials. Ind. Eng. Chem. Res. 2018, 57, 5151–5160. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, M.; Lu, D.; Fei, W.; Wu, J. Computational Screening and Design of Nanoporous Membranes for Efficient Carbon Isotope Separation. Green Energy Environ. 2020, 5, 364–373. [Google Scholar] [CrossRef]
- Li, W.; Xie, K. Porous Single Crystals at the Macroscale: From Growth to Application. Acc. Chem. Res. 2023, 56, 374–384. [Google Scholar] [CrossRef]
- Li, X.; Li, W.; Zhang, J.; Yin, W.; Xia, Y.; Xie, K. Porous Single-crystalline Centimeter-sized α-Al2 O3 Monoliths for Selective and Durable Non-oxidative Dehydrogenation of Ethane. Angew. Chem. Int. Ed. 2024, 63, e202315274. [Google Scholar] [CrossRef]
- Parkinson, G.S.; Diebold, U. Adsorption on Metal Oxide Surfaces. In Surface and Interface Science; Wandelt, K., Ed.; Wiley: Hoboken, NJ, USA, 2016; pp. 793–817. [Google Scholar]
- Huang, Y.-C.; Zhao, K.-Y.; Liu, Y.; Zhang, X.-Y.; Du, H.-Y.; Ren, X.-W. Investigation on Adsorption of Ar and N2 on α-Al2O3(0001) Surface from First-Principles Calculations. Vacuum 2020, 176, 109344. [Google Scholar] [CrossRef]
- Yue, Y.; Melani, G.; Kirsch, H.; Paarmann, A.; Saalfrank, P.; Campen, R.K.; Tong, Y. Structure and Reactivity of α-Al2 O3 (0001) Surfaces: How Do Al–I and Gibbsite-like Terminations Interconvert? J. Phys. Chem. C 2022, 126, 13467–13476. [Google Scholar] [CrossRef]
- Zhu, Z.; Yu, Z.; Yun, F.F.; Pan, D.; Tian, Y.; Jiang, L.; Wang, X. Crystal Face Dependent Intrinsic Wettability of Metal Oxide Surfaces. Natl. Sci. Rev. 2021, 8, nwaa166. [Google Scholar] [CrossRef]
- Tamijani, A.A.; Bjorklund, J.L.; Augustine, L.J.; Catalano, J.G.; Mason, S.E. Density Functional Theory and Thermodynamics Modeling of Inner-Sphere Oxyanion Adsorption on the Hydroxylated α-Al2 O3 (001) Surface. Langmuir 2020, 36, 13166–13180. [Google Scholar] [CrossRef]
- Zhang, G.; Dou, S.; Lu, Y.; Shi, Y.; Lai, X.; Wang, X. Mechanisms for Adsorption, Dissociation and Diffusion of Hydrogen in Hydrogen Permeation Barrier of α-Al2O3: The Role of Crystal Orientation. Int. J. Hydrogen Energy 2014, 39, 610–619. [Google Scholar] [CrossRef]
- Elyasi Kojabad, M.; Nouri, M.; Babaluo, A.A.; Tavakoli, A.; Sardari, R.; Farhadi, Z.; Moharrami, M. Alumina-PEBA/PSf Multilayer Composite Membranes for CO2 Separation: Experimental and Molecular Simulation Studies. Sci. Iran. 2022, 30, 2043–2055. [Google Scholar] [CrossRef]
- Alioui, O.; Gueddida, S.; Benguerba, Y.; Lebègue, S.; Badawi, M. Potential of Nickel Nanoclusters Supported on α-Al2O3 (0001) Surface for CO2 Capture, Energy Production, and Dry Reforming of Methane. Appl. Surf. Sci. 2023, 610, 155474. [Google Scholar] [CrossRef]
- Hass, K.C.; Schneider, W.F.; Curioni, A.; Andreoni, W. The Chemistry of Water on Alumina Surfaces: Reaction Dynamics from First Principles. Science 1998, 282, 265–268. [Google Scholar] [CrossRef] [PubMed]
- Casarin, M.; Maccato, C.; Vittadini, A. Theoretical Study of the Chemisorption of CO on Al2O3 (0001). Inorg. Chem. 2000, 39, 5232–5237. [Google Scholar] [CrossRef]
- Rohmann, C.; Metson, J.B.; Idriss, H. DFT Study of Carbon Monoxide Adsorption on α-Al2O3(0001). Surf. Sci. 2011, 605, 1694–1703. [Google Scholar] [CrossRef]
- Manassidis, I.; Gillan, M.J. Structure and Energetics of Alumina Surfaces Calculated from First Principles. J. Am. Ceram. Soc. 1994, 77, 335–338. [Google Scholar] [CrossRef]
- Tasker, P.W. The Stability of Ionic Crystal Surfaces. J. Phys. C Solid State Phys. 1979, 12, 4977–4984. [Google Scholar] [CrossRef]
- Sun, J.; Stirner, T.; Matthews, A. Structure and Surface Energy of Low-Index Surfaces of Stoichiometric α-Al2O3 and α-Cr2O3. Surf. Coat. Technol. 2006, 201, 4205–4208. [Google Scholar] [CrossRef]
- Mackrodt, W.C.; Davey, R.J.; Black, S.N.; Docherty, R. The Morphology of α-Al2O3 and α-Fe2O3: The Importance of Surface Relaxation. J. Cryst. Growth 1987, 80, 441–446. [Google Scholar] [CrossRef]
- Ruberto, C.; Yourdshahyan, Y.; Lundqvist, B.I. Surface Properties of Metastable Alumina: A Comparative Study of κ- and α-Al2O3. Phys. Rev. B 2003, 67, 195412. [Google Scholar] [CrossRef]
- Alavi, S.; Sorescu, D.C.; Thompson, D.L. Adsorption of HCl on Single-Crystal α-Al2O3 (0001) Surface: A DFT Study. J. Phys. Chem. B 2003, 107, 186–195. [Google Scholar] [CrossRef]
- Hinnemann, B.; Carter, E.A. Adsorption of Al, O, Hf, Y, Pt, and S Atoms on α-Al2O3 (0001). J. Phys. Chem. C 2007, 111, 7105–7126. [Google Scholar] [CrossRef]
- Bedghiou, D.; Rahab, M.N.; Benali-Cherif, R.; Djelloul, A.; Boumaza, A. First Principles Unveiling Equilibrium Shapes for Understanding Morphological Growth Mechanisms in Alumina Polymorphs. Acta Mater. 2024, 281, 120450. [Google Scholar] [CrossRef]
- Huber, K.P.; Herzberg, G. Constants of Diatomic Molecules. In Molecular Spectra and Molecular Structure; Springer: Boston, MA, USA, 1979; pp. 8–689. ISBN 978-1-4757-0963-6. [Google Scholar]
- Chen, Y.; Bai, X.; Liu, D.; Fu, X.; Yang, Q. High-Throughput Computational Exploration of MOFs with Open Cu Sites for Adsorptive Separation of Hydrogen Isotopes. ACS Appl. Mater. Interfaces 2022, 14, 24980–24991. [Google Scholar] [CrossRef] [PubMed]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Blyholder, G. Molecular Orbital View of Chemisorbed Carbon Monoxide. J. Phys. Chem. 1964, 68, 2772–2777. [Google Scholar] [CrossRef]
- Pandey, I.; Lin, L.-C.; Chen, C.-C.; Howe, J.D. Understanding Carbon Monoxide Binding and Interactions in M-MOF-74 (M = Mg, Mn, Ni, Zn). Langmuir 2023, 39, 18187–18197. [Google Scholar] [CrossRef]
- Sung, S.S.; Hoffmann, R. How Carbon Monoxide Bonds to Metal Surfaces. J. Am. Chem. Soc. 1985, 107, 578–584. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, A.; Johnson, E.R.; Luaña, V. Critic2: A Program for Real-Space Analysis of Quantum Chemical Interactions in Solids. Comput. Phys. Commun. 2014, 185, 1007–1018. [Google Scholar] [CrossRef]
- Ono, S.; Rhim, J.H.; Gruen, D.S.; Taubner, H.; Kölling, M.; Wegener, G. Clumped Isotopologue Fractionation by Microbial Cultures Performing the Anaerobic Oxidation of Methane. Geochim. Cosmochim. Acta 2021, 293, 70–85. [Google Scholar] [CrossRef]
- McNeill, A.S.; Dallas, B.H.; Eiler, J.M.; Bylaska, E.J.; Dixon, D.A. Reaction Energetics and13 C Fractionation of Alanine Transamination in the Aqueous and Gas Phases. J. Phys. Chem. A 2020, 124, 2077–2089. [Google Scholar] [CrossRef]
- Bajdich, M.; Nørskov, J.K.; Vojvodic, A. Surface Energetics of Alkaline-Earth Metal Oxides: Trends in Stability and Adsorption of Small Molecules. Phys. Rev. B 2015, 91, 155401. [Google Scholar] [CrossRef]
- Gao, W.; Chen, Y.; Li, B.; Liu, S.-P.; Liu, X.; Jiang, Q. Determining the Adsorption Energies of Small Molecules with the Intrinsic Properties of Adsorbates and Substrates. Nat. Commun. 2020, 11, 1196. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Wyckoff, R.W.G.; Wyckoff, R.W. Crystal Structures; Interscience Publishers: New York, NY, USA, 1963; Volume 1. [Google Scholar]
- Corum, K.; Abbaspour Tamijani, A.; Mason, S. Density Functional Theory Study of Arsenate Adsorption onto Alumina Surfaces. Minerals 2018, 8, 91. [Google Scholar] [CrossRef]

| Reference | (0001) | (0) | (2) | (1) | (0) |
|---|---|---|---|---|---|
| [30] | 1.76 | 1.86 | - | 2.55 | 1.40 |
| [32] | 1.85 | 2.39 | - | 2.53 | 2.44 |
| [33] | 2.03 | 2.50 | 1.58 | 2.52 | 2.23 |
| [35] | 1.42 | - | - | - | - |
| [36] | 1.54 | - | - | - | - |
| [37] | 1.92 | 2.30 | 1.16 | - | - |
| This work | 1.54 | 2.36 | 2.07 | 2.49 | 2.65 |
| Adsorption Site | -Al2O3/CO | -Al2O3/12CO | -Al2O3/13CO | ||
|---|---|---|---|---|---|
| a | −0.6595 | 0.0560 | −0.6035 | 0.0543 | −0.6051 |
| b | −0.1813 | 0.0187 | −0.1626 | 0.0183 | −0.1630 |
| c | 0.0114 | 0.0172 | 0.0286 | 0.0169 | 0.0283 |
| d | −0.0858 | 0.0155 | −0.0702 | 0.0152 | −0.0705 |
| e | −0.6292 | 0.0538 | −0.5754 | 0.0524 | −0.5768 |
| f | −0.1165 | 0.0357 | −0.0808 | 0.0351 | −0.0814 |
| g | −0.4268 | 0.0389 | −0.3878 | 0.0379 | −0.3889 |
| h | −0.14167 | 0.0275 | −0.1141 | 0.0269 | −0.1147 |
| i | −0.1051 | 0.0230 | −0.0821 | 0.0225 | −0.0826 |
| Adsorption Site | O(e) | C(e) | CO(e) |
|---|---|---|---|
| a | −1.05 | +1.02 | −0.03 |
| b | −1.11 | +1.09 | −0.01 |
| c | −1.06 | +1.04 | −0.02 |
| d | −1.07 | +1.04 | −0.03 |
| e | −1.07 | +1.02 | −0.05 |
| f | −1.25 | +1.17 | −0.08 |
| g | −1.13 | +1.10 | −0.03 |
| h | −1.10 | +1.05 | −0.04 |
| i | −1.14 | +1.12 | −0.02 |
| Surface | (meV) | |||
|---|---|---|---|---|
| -Al2O3/CO | -Al2O3/12CO | -Al2O3/13CO | ||
| (0001) | −0.659499 | −0.603479 | −0.605166 | 1.69 |
| 2) | −0.631939 | −0.574888 | −0.576545 | 1.66 |
| 0) | −0.662079 | −0.591091 | −0.592936 | 1.85 |
| 1) | −0.511349 | −0.459618 | −0.461132 | 1.51 |
| 0) | −0.441109 | −0.386177 | −0.387719 | 1.54 |
| Surface | (meV) | ||
|---|---|---|---|
| -Al2O3/12CO | -Al2O3/13CO | ||
| (0001) | 0.056020 | 0.054333 | 1.69 |
| 2) | 0.057051 | 0.055394 | 1.66 |
| 0) | 0.070988 | 0.069143 | 1.85 |
| 1) | 0.054932 | 0.053390 | 1.51 |
| 0) | 0.051731 | 0.050217 | 1.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Cheng, X.; Xu, Q.; Deng, S. Surface-Dependent Isotopic Adsorption of CO on α-Al2O3: Role of Weak Interactions and Zero-Point Energy. Molecules 2025, 30, 2067. https://doi.org/10.3390/molecules30092067
Yang Q, Cheng X, Xu Q, Deng S. Surface-Dependent Isotopic Adsorption of CO on α-Al2O3: Role of Weak Interactions and Zero-Point Energy. Molecules. 2025; 30(9):2067. https://doi.org/10.3390/molecules30092067
Chicago/Turabian StyleYang, Qun, Xiyue Cheng, Qian Xu, and Shuiquan Deng. 2025. "Surface-Dependent Isotopic Adsorption of CO on α-Al2O3: Role of Weak Interactions and Zero-Point Energy" Molecules 30, no. 9: 2067. https://doi.org/10.3390/molecules30092067
APA StyleYang, Q., Cheng, X., Xu, Q., & Deng, S. (2025). Surface-Dependent Isotopic Adsorption of CO on α-Al2O3: Role of Weak Interactions and Zero-Point Energy. Molecules, 30(9), 2067. https://doi.org/10.3390/molecules30092067








